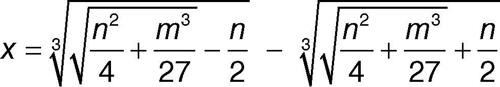I numeri complessi e le loro applicazioni

I numeri complessi e le loro applicazioni

I numeri complessi e le loro applicazioni

Sono caratterizzati da un numero indicato con una lettera perlomeno inusuale, i, detta unità immaginaria. Per di più, il quadrato di questo simbolo è un numero negativo: i ² = −1. Ce n’è a sufficienza per pensare ai numeri complessi come a una tipica astruseria matematica, che non ha riscontri nella realtà – numeri immaginari, appunto – e che per di più conduce a conclusioni paradossali, quali un quadrato espresso da un numero negativo. È invece sorprendente constatare che le applicazioni ci sono, e importanti, e che sin dalla loro apparizione i numeri complessi hanno consentito di risolvere problemi che oggi verrebbero classificati come di analisi reale. Certo, la loro introduzione fu tutt’altro che esente da difficoltà e incomprensioni, a partire da quelle di R. Bombelli e di G. Cardano che, a metà del Cinquecento, osservava come, con i numeri complessi, «progredisca la sottigliezza aritmetica il cui fine, come si dice, è tanto raffinato quanto inutile». Le radici quadrate di numeri negativi, i numeri complessi e i loro logaritmi crearono imbarazzo anche a Descartes (che utilizzò per primo il termine «immaginario»), Leibniz e Newton. Bisognerà arrivare all’algebra del Settecento e a Eulero e Gauss perché si delinei un quadro più chiaro del sistema dei numeri complessi e della loro importanza.

Per capirne la necessità anche in una classica questione algebrica, quale la risoluzione di un’equazione cubica, si consideri l’equazione x³ + mx + n = 0. Nel Cinquecento si dimostrò che una sua soluzione è data da:

Se si applica questa formula alla particolare equazione x³ − 3x + 1 = 0, si trova che una sua soluzione è data da:

Poiché lo studio della funzione f(x) = x³ − 3x + 1 permette di dedurre che la precedente equazione ammette tre radici, tutte reali, si ha che la soluzione trovata è un numero reale, pur essendo espressa mediante radici quadrate di numeri negativi. Dare significato all’operazione di radice quadrata di un numero negativo è pertanto esigenza che si impone già nel calcolo con i numeri reali.

In forma algebrica un numero complesso è una scrittura del tipo z = x + iy, con x e y reali. Il calcolo di addizioni, sottrazioni, moltiplicazioni e divisioni è sufficientemente comodo e rapido perché obbedisce a tutte le consuete regole e proprietà formali del calcolo con i numeri reali con l’unica “novità” costituita dal fatto che risulta i ² = −1. Si è però in imbarazzo nel calcolare le potenze zⁿ (al di là dei semplici casi del quadrato e del cubo) e soprattutto non si riesce a calcolare quell’operazione di radice n-esima che storicamente e concettualmente può essere considerata la motivazione strategica che ha portato all’introduzione dei numeri complessi. L’obiettivo, infatti, era stato quello di definire l’operazione di radice qualunque fosse il radicando e di superare l’asimmetria presente nel campo dei numeri reali: nel caso di indice dispari, l’operazione di radice ammette sempre un’unica soluzione; nel caso di indice pari, invece, l’operazione di radice ha due soluzioni quando il radicando non è negativo mentre non ne ha quando il radicando è minore di zero. Si preferisce allora scrivere z = x + iy nella cosiddetta forma trigonometrica, che si ricava da quella algebrica in modo semplice attraverso la rappresentazione nel piano. Per uno dei teoremi di trigonometria sui triangoli rettangoli, i due cateti x e y di un triangolo la cui ipotenusa è r si esprimono infatti come x = rcosα e y = rsinα. Si ha così z = r(cosα + isinα) dove

è la distanza dall’origine del punto P immagine nel piano del numero complesso z, mentre α è l’angolo che il raggio vettore

forma con la direzione positiva dell’asse x ed è assegnato dalla formula tanα = y/x.

Nel 1739 A. de Moivre dimostrò la formula (cosα + isinα)ⁿ = cos(nα) + isin(nα), che risolve il problema del calcolo della potenza di un numero complesso z, qualunque sia l’esponente intero n. Da qui si ottiene la formula per l’operazione inversa della radice n-esima:

con k = 0, 1, ..., n − 1. Pertanto, ogni numero complesso z ammette n radici n-esime che, rappresentate nel piano di Argand-Gauss, costituiscono i vertici di un poligono regolare di n lati inscritto nella circonferenza con centro nell’origine e di raggio

Il risultato viene generalizzato dal teorema fondamentale dell’algebra che afferma che ogni polinomio di grado n, con coefficienti complessi, ammette n radici in C.

Al di là dell’aggettivo “immaginaria” che qualifica l’unità i che permette di costruire i numeri complessi, le sorprendenti e “concrete” applicazioni di tali numeri spaziano in diversi campi. Essi contribuiscono innanzitutto a sviluppare in modo rigoroso specifiche teorie matematiche: dalla operazione di radice (nel senso prima illustrato) al calcolo degli autovalori di una matrice quadrata, dalla soluzione di un’equazione differenziale lineare di ordine superiore al primo a coefficienti costanti al calcolo di alcuni integrali impropri, dalla teoria dei numeri ad alcuni frattali definiti proprio attraverso i numeri complessi. Vi sono poi applicazioni più tecniche, in fisica e ingegneria. I numeri complessi sono utilizzati in fluidodinamica per descrivere il flusso potenziale in due dimensioni, in meccanica quantistica e nella teoria della relatività, dove alcune formule dello spazio metrico diventano più semplici con il loro impiego. Nell’elettromagnetismo, invece di considerare le intensità del campo elettrico e di quello magnetico come espresse da due entità reali separate, si preferisce descriverle attraverso un unico numero complesso (di cui la componente elettrica e quella magnetica sono, rispettivamente, parte reale e coefficiente dell’immaginario). I numeri complessi sono fondamentali nell’analisi dei segnali. Nell’ingegneria elettrica ed elettronica sono impiegati per indicare la tensione e la corrente, anche se in questi calcoli si usa tradizionalmente la lettera j per indicare l’unità immaginaria (dato che la i è riservata alla intensità di corrente).