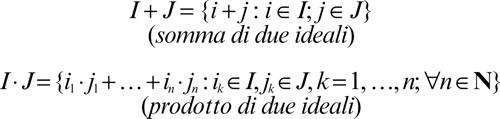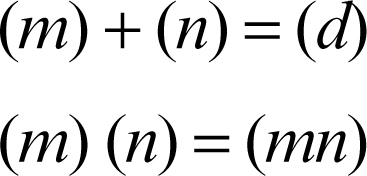ideale

ideale

ideale in algebra, sottogruppo I del gruppo additivo di un anello (A, +, ⋅) che soddisfa almeno una delle due condizioni seguenti:

a) se s appartiene a I, allora, per ogni a appartenente ad A, a ⋅ s appartiene a I;

b) se s appartiene a I, allora, per ogni a appartenente ad A, s ⋅ a appartiene a I.

Un ideale che soddisfa la condizione a) è detto ideale sinistro; un ideale che soddisfa la condizione b) è invece detto ideale destro. Un ideale che sia contemporaneamente sinistro e destro è detto ideale bilatero. Per esempio, nell’anello dei numeri interi, gli insiemi di tutti i multipli di un numero primo sono ideali bilateri. Gli ideali bilateri hanno, nel contesto degli anelli, un ruolo analogo a quello dei sottogruppi normali nel contesto dei gruppi: essi permettono di definire la nozione di anello quoziente (→ quoziente).

Un anello possiede sempre due ideali banali: l’ideale nullo, definito come I = {0}, e l’ideale I = A, che coincide con l’anello stesso pensato come ideale su sé stesso. Se l’anello è un campo, o più in generale se esso è un corpo, allora non vi sono altri ideali che questi. Se l’anello A è commutativo, allora le tre nozioni di ideale date vengono tutte a coincidere e si parla semplicemente di ideale.

Nel caso di un anello commutativo A, un ideale I è detto primo se, ogni qualvolta contiene un prodotto a ⋅ b, allora contiene almeno uno dei due fattori a oppure b; I si dice massimale se non esistono ideali che lo contengono, distinti da I e da A stesso. Ogni ideale massimale è primo. Il quoziente di un anello rispetto a un suo ideale primo è un dominio d’integrità; il quoziente di un anello rispetto a un suo ideale massimale è un campo.

Un ideale I è detto principale se è della forma A ⋅ a o della forma a ⋅ A, per un opportuno elemento a di A: ciò vuol dire che ogni elemento di I è multiplo di a. Un tale ideale è indicato con il simbolo I = (a); esso è il minimo ideale di A contenente a. Più in generale, I si dice generato da un suo sottoinsieme G se I è il minimo ideale che contiene G. L’ideale I si dice finitamente generato se esiste un sottoinsieme finito G di A, diciamo G = {i₁, i₂, …, i_n}, tale che ogni elemento s di I si scrive nella forma s = a₁ ⋅ i₁ + a₂ ⋅ i₂ + ... + a_n ⋅ i_n, per opportuni elementi a₁, a₂, ..., a_n di A; gli elementi di G sono detti generatori di I. Un ideale è principale se è finitamente generato da un solo elemento.

Due ideali I e J di un anello A possono essere addizionati e moltiplicati:

La somma I + J è un ideale di A che contiene l’unione I ∪ J (più precisamente esso è l’ideale generato dall’unione); il prodotto I ⋅ J è un ideale di A che contiene l’intersezione I ∩ J. Nel caso dell’anello degli interi Z, dove ogni ideale è principale, la somma e il prodotto di due ideali sono ben caratterizzati come segue:

dove d indica il massimo comune divisore di m e n. Dato un ideale I, si definisce il suo radicale come l’ideale, indicato con i simboli √(I) o Rad(I), costituito da tutti gli elementi che, elevati a un’opportuna potenza, appartengono a I: tale ideale coincide con l’intersezione di tutti gli ideali primi di A contenenti I. Per esempio, nell’anello Z degli interi, √(9) = (3).

Un ideale può anche coincidere con il proprio radicale e, in tale caso, è detto ideale radicale. In Z è tale per esempio l’ideale (6) perché √(6) = (6).

Tutti gli ideali primi sono radicali e il radicale di un ideale è sempre radicale:

Il radicale dell’ideale nullo è detto radicale dell’anello (o nihilradicale) ed è indicato con i simboli Rad(A) o √(A). Esso coincide con l’insieme degli elementi nihilpotenti di A. Un anello il cui radicale coincide con l’ideale nullo è detto ridotto.