identificazione

identificazione

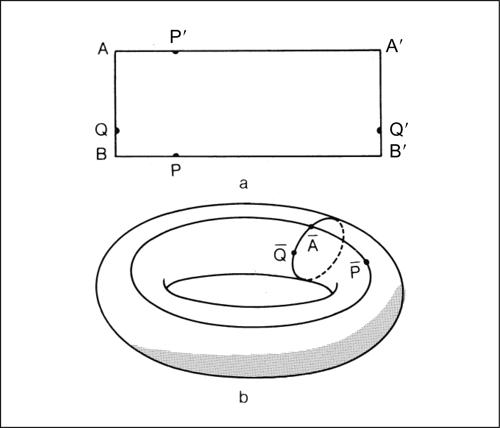
identificazione in topologia, procedimento che permette, a partire da un dato spazio topologico X, di costruire un nuovo spazio topologico ottenuto dal primo identificando alcuni suoi punti, vale a dire ponendo per definizione che essi coincidano (in qualche senso, si potrebbe dire che essi vengono “incollati”). Per esempio, dato un rettangolo di vertici (nell’ordine) A, B, B′, A′, tramite un’identificazione è possibile costruire un toro. Più in particolare, esso viene ottenuto identificando a coppie i punti del lato AA′ (presi nell’ordine che va da A ad A′ ) con i punti del lato opposto BB′ (presi nell’ordine che va da B a B′ ) e successivamente identificando a coppie i punti del lato AB (presi nell’ordine che va da A a B) con i punti del lato A′B′ (presi nell’ordine che va da A′ a B′ ). In questo modo i quattro vertici del rettangolo vengono tutti a coincidere in un unico punto, mentre i lati determinano, a coppie, due circonferenze sul toro. Similmente, a partire dallo stesso rettangolo, ma tramite una diversa identificazione, è possibile costruire una bottiglia di → Klein. Ciò può essere fatto identificando a coppie i punti del lato AA′ (presi nell’ordine che va da A ad A′ ) con i punti del lato opposto BB′ (presi nell’ordine che va da B a B′ ) e successivamente identificando a coppie i punti del lato AB (presi nell’ordine che va da A a B) con i punti del lato A′B′ (presi nell’ordine opposto, che va da B′ ad A′ ).

Più formalmente, dare un’identificazione consiste nel definire una relazione di equivalenza ∼ su uno spazio topologico X: se Y = X / ∼ è il quoziente di X rispetto a tale relazione, allora, a partire dalla topologia definita su X, è possibile definire univocamente una topologia su Y (detta topologia quoziente) rispetto alla quale si dirà che Y è ottenuto da X tramite l’identificazione ∼ (→ quoziente). Equivalentemente, un’applicazione continua e suriettiva ƒ: X → Y tra due spazi topologici X e Y è un’identificazione se e solo se gli aperti di Y sono tutti e soli i sottoinsiemi A ⊂ Y tali che ƒ ⁻¹(A) è aperto in X. Se ƒ: X → Y è una tale applicazione, allora Y è omeomorfo allo spazio topologico quoziente X / ∼, dove ∼ è la relazione di equivalenza su X che identifica i punti di X con la stessa immagine tramite ƒ.