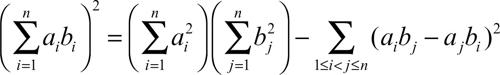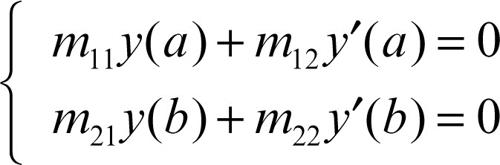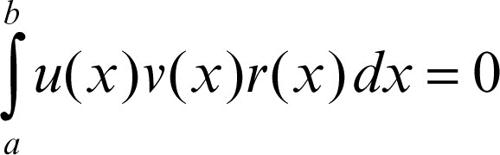Lagrange, identita di
Lagrange, identita di
Lagrange, identità di denominazione con cui si indicano più relazioni di identità, tutte riferibili a J.-L. Lagrange.
□ Nel campo dei numeri reali (o in quello dei numeri complessi), è la relazione
che può essere desunta a partire dall’identità di → Binet-Cauchy, ponendo in essa ci = ai e di = bi.
□ Nel calcolo vettoriale, è la relazione che lega quattro vettori arbitrari dello spazio ordinario a, b, c e d attraverso le operazioni di prodotto scalare (indicato con ⋅) e prodotto vettoriale (indicato con ×) nel seguente modo:
□ Nei problemi ai limiti per equazioni differenziali ordinarie, è una identità ricavabile a partire da un operatore differenziale in forma autoaggiunta L definito da
con p(x) > 0 di classe C1 e q(x) integrabile in un intervallo [a, b]. Se u e ν sono due funzioni di classe C 2([a, b]), vale allora l’identità:
(→ equazione differenziale, problemi ai limiti per una). Se inoltre u e ν soddisfano le condizioni ai limiti
integrando si ha
Ne consegue che se u e ν sono autosoluzioni del problema ai limiti per l’equazione differenziale Ly = λr(x)y, con r(x) > 0 in [a, b], corrispondenti rispettivamente agli autovalori distinti α e β, risulta
cioè u e ν sono funzioni ortogonali nello spazio di Hilbert con peso
Le ipotesi possono essere indebolite, consentendo al peso r(x) di annullarsi in punti isolati di [a, b], e, modificando opportunamente il problema ai limiti, di considerare un intervallo aperto (a, b), eventualmente illimitato.