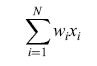Imparare a generalizzare
Imparare a generalizzare
Questo saggio fornisce un'introduzione alle teorie che mirano alla comprensione della capacità delle reti neurali di generalizzare a partire da esempi, con particolare attenzione al caso in cui le reti vengano usate a scopo di classificazione. Le prestazioni della rete possono essere quantificate dal cosiddetto errore di generalizzazione, che è la probabilità di classificare erroneamente un nuovo input, e del quale sono state ottenute espressioni approssimate. In questo saggio confronterò un approccio basato su idee tratte dalla fisica statistica, mirante alla modellizzazione del comportamento tipico di apprendimento, con uno schema introdotto nella statistica matematica da V.N. Vapnik e A. Chervonenkis, che fornisce limiti esatti per l'errore di generalizzazione nel caso peggiore. L'approccio di fisica statistica ha rivelato un comportamento nuovo e inaspettato di modelli semplici di reti, come, per esempio, una varietà di transizioni di fase. È un'eccitante questione aperta la possibilità che tali transizioni possano giocare un ruolo cognitivo nel cervello degli animali e degli uomini.
Introduzione
Le reti neuronali imparano da esempi. Questa affermazione è ovviamente vera per il cervello, ma anche le reti artificiali - o reti neurali - che sono divenute uno strumento potente per molti problemi di riconoscimento di pattern, adattano le intensità dei loro collegamenti interni a un insieme di esempi. Di solito le reti neurali sono composte da un numero elevato di unità di calcolo abbastanza semplici, organizzate in un'architettura spesso indipendente dal problema. l parametri che controllano le interazioni tra le unità si possono modificare durante la fase di apprendimento, e vengono spesso definiti accoppiamenti sinaptici. Dopo la fase di apprendimento la rete ha acquisito una certa capacità di generalizzare a partire dagli esempi, in quanto può effettuare delle previsioni su input mai visti prima: ha dunque cominciato ad apprendere una regola. In quale misura è possibile capire la complessità dell'apprendimento a partire dagli esempi attraverso i modelli matematici e le loro soluzioni? Questa è la domanda su cui intendiamo attrarre l'attenzione in questo saggio. Ci concentreremo sull 'uso delle reti neurali per la classificazione. In questo caso, si possono prendere delle specifiche caratteristiche, per esempio i pixel di una immagine, come pattern di input alla rete. Nel caso più semplice la rete dovrebbe decidere se un dato pattern appartenga, con probabilità elevata, a una certa classe di oggetti, e rispondere di conseguenza, a seconda dei casi, con l'output + 1 o -1. Per apprendere la regola di classificazione sottesa la rete viene addestrata su un insieme di pattern, dei quali sono disponibili le etichette di classificazione, fornite da un addestratore. Una strategia euristica per l'apprendimento consiste nel regolare i parametri della macchina (gli accoppiamenti della rete) utilizzando un algoritmo di apprendimento, in modo che gli errori compiuti sull'insieme degli esempi di addestramento siano piccoli, nella speranza che questo fatto aiuti a ridurre gli errori su dati nuovi. Quale capacità di classificare un input mai visto prima avrà una rete così addestrata? La prestazione su dati nuovi definisce la capacità di generalizzazione della rete. Da un lato questa capacità è influenzata dal problema della realizzabilità: la rete potrebbe non essere abbastanza complessa da apprendere la regola completamente, o potrebbero esservi ambiguità nella classificazione. Noi ci concentreremo principalmente su un secondo problema, legato al fatto che, nella maggioranza dei casi, l'apprendimento non è esaustivo, e che l'informazione sulla regola contenuta negli esempi non è completa. Le prestazioni della rete possono quindi variare da un insieme di apprendimento a un altro. Per poter trattare la capacità di generalizzazione in modo quantitativo, viene spesso usato un modello il quale ipotizza che tutti i pattern di input (sia quelli dell'insieme di addestramento che quelli nuovi, su cui viene verificato il comportamento della rete) abbiano una distribuzione di probabilità preassegnata, che caratterizza l'aspetto da classificare. Si assume inoltre che tali pattern provengano dall' ambiente che circonda la rete in modo casuale e indipendente, con la stessa distribuzione di probabilità. A volte, la distribuzione di probabilità usata per estrarre gli esempi e la classificazione di questi esempi viene detta regola. Le prestazioni della rete su dati nuovi possono così essere quantificate dal cosiddetto errore di generalizzazione, che è la probabilità di classificare erroneamente un nuovo input, detto input di prova, e possono essere misurate ripetendo lo stesso esperimento di apprendimento molte volte, con dati differenti.
Nell'ambito di un simile schema probabilistico, le reti neurali sono spesso viste come modelli statistici adattivi, in grado di fornire una spiegazione probabile dei dati osservati. In questo schema il processo di apprendimento risulta legato, dal punto di vista matematico, a un problema di stima statistica dei parametri (o accoppiamenti) ottimali della rete. La statistica matematica sembra perciò uno strumento appropriato per lo studio del comportamento di una rete neurale. In effetti sono stati applicati diversi approcci statistici, per quantificare le prestazioni in generalizzazione. Per esempio, sono state ottenute espressioni per l'errore di generalizzazione nel limite in cui il numero di esempi è grande rispetto al numero di accoppiamenti (Seung et al., 1992; Amari e Murata, 1993). In un caso simile ci si può attendere che l'apprendimento sia quasi esaustivo, in modo tale che le fluttuazioni statistiche dei parametri intorno ai loro valori ottimali siano piccole. In pratica, però, allo scopo di avere una rete flessibile, il numero di parametri è spesso piuttosto grande, e non è chiaro quanti esempi siano necessari affinché la teoria asintotica si possa considerare applicabile. La teoria asintotica potrebbe in effetti non cogliere comportamenti interessanti della cosiddetta curva di apprendimento, che mostra come cambia la capacità di generalizzazione all'aumentare dei dati di addestramento. Un altro importante approccio, introdotto nella statistica matematica negli anni Settanta da V.N. Vapnik e A. Chervonenkis (Vapnik, 1982; 1995), fornisce limiti esatti per l'errore di generalizzazione, validi per qualsiasi numero di esempi di addestramento. Questi limiti risultano inoltre completamente indipendenti dalla distribuzione degli input, e nel caso di regole realizzabili, essi sono anche indipendenti dallo specifico algoritrno, finché si assume che gli esempi di addestramento siano appresi alla perfezione. Dato che questa teoria è in grado di coprire anche le situazioni più difficili e sfavorevoli per il processo di apprendimento, non è sorprendente che essa possa fornire in alcuni casi risultati troppo pessimistici, che risultano anche troppo rozzi per rivelare un comportamento interessante nella regione intermedia della curva di apprendimento. In questo saggio l'attenzione sarà rivolta principalmente a un diverso approccio, che ha le sue origini nella fisica statistica, piuttosto che nella statistica matematica, e ne confronteremo i risultati con quelli ottenuti per i casi peggiori. Questo metodo ha come scopo lo studio del comportamento nel caso tipico, piuttosto che nel caso peggiore, e consente spesso il calcolo esatto della intera curva di apprendimento, per modelli di reti semplici con un numero molto alto di parametri. Poiché sia le reti neurali artificiali che quelle biologiche sono composte da un numero elevato di elementi, possiamo sperare che un simile approccio possa effettivamente rivelare caratteristiche importanti e interessanti.
A prima vista può sembrare sorprendente che un problema si debba semplificare quando il numero dei suoi costituenti diventa grande. Questo fenomeno è però ben noto per sistemi fisici macroscopici come gas o liquidi, che sono costituiti da un numero enorme di molecole. Chiaramente, non c'è alcuna speranza di studiare lo stato microscopico completo di un sistema simile, descritto dalle posizioni e dalle velocità, rapidamente fluttuanti, di tutte le particelle. D'altra parte, quantità macroscopiche come la densità, la temperatura e la pressione sono in genere proprietà collettive, influenzate da tutti gli elementi del sistema. Per queste quantità, le fluttuazioni si mediano nel limite termodinamico di un numero grande di particelle, e le proprietà collettive diventano in qualche misura indipendenti dal microstato. Analogamente, la capacità di generalizzazione di una rete neurale è una proprietà collettiva di tutti i parametri della rete, e le tecniche della fisica statistica permettono, almeno per alcuni modelli, semplici ma non banali, di effettuare calcoli esatti nel limite termodinamico. Prima di illustrare queste idee in maggiore dettaglio, fornirò nel seguito una breve descrizione delle cosiddette reti neurali feedforward (reti a propagazione in avanti).
Le reti neurali artificiali
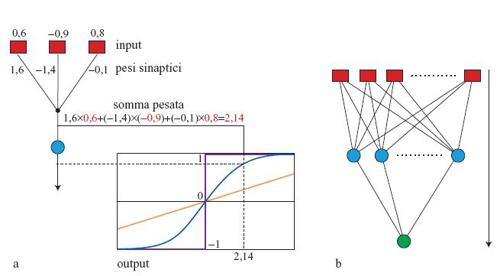
Le reti neurali artificiali, basate su modelli molto idealizzati delle funzioni cerebrali, sono costruite a partire da semplici unità elementari di calcolo, che sono a volte chiamate neuroni, per analogia con le loro controparti biologiche. Sebbene le realizzazioni hardware siano diventate un argomento importante di ricerca, le reti neurali sono ancora, per lo più, simulate su normali calcolatori. Ogni unità di calcolo di una rete neurale ha un solo output e diverse connessioni in input, che ricevono gli output di altre unità. A ogni connessione in input (contraddistinta dall'indice i) viene assegnato un numero reale, il cosiddetto peso sinaptico Wi, che è il parametro modificabile fondamentale della rete. Per calcolare l' output di una unità, tutti i valori in ingresso Xi vengono prima moltiplicati per i pesi Wi e poi sommati. Si veda la figura (fig. 1) per un esempio di un calcolo di questo tipo nel caso di tre accoppiamenti.
Il risultato viene filtrato attraverso una funzione di attivazione, che ha tipicamente la forma della curva blu nella figura la (una cosiddetta funzione sigmoide), e consente una classificazione graduale, tra - 1 e + 1. Altri casi importanti di funzione di attivazione sono rappresentati dalla funzione a gradino (in viola) e dalla funzione lineare (in giallo, usata per l'output del neurone in problemi di fit di funzioni continue). Nel seguito, per semplicità, ci limiteremo principalmente alla funzione a gradino. Unità semplici di questo tipo possono sviluppare un potere computazionale notevole, se interconnesse in un'architettura opportuna. Un tipo importante di rete è costituito dall' architettura feedforward mostrata nella figura 1b, che possiede due strati di unità di calcolo e accoppiamenti modificabili. l nodi di input (che non effettuano calcoli) sono accoppiati alle cosiddette unità nascoste, che inviano i risultati dell'elaborazione a una o più unità di output. Con un'architettura di questo tipo, e funzioni di attivazione di tipo sigmoide, si può approssimare con precisione arbitraria qualsiasi funzione continua degli input, purché il numero di unità nascoste sia abbastanza alto.
Il perceptron
Il tipo più semplice di rete è il cosiddetto perceptron (fig. 2), in cui si hanno N elementi di input Xi, N accoppiamenti sinaptici Wi, e l'output è positivo o negativo a seconda del segno di
formula [1]
Il perceptron ha un'architettura con un solo strato, e una funzione a gradino come funzione di attivazione (v. figura 1a). Nonostante la sua struttura semplice, esso può fornire delle prestazioni non banali di generalizzazione in molti problemi di apprendimento (Minsky e Papert, 1969), e si può usare come pnmo passo m un nuovo problema di classificazione. Come si può vedere confrontando le figure 2a e 1b, il perceptron è anche un componente elementare delle reti più complesse, a più strati. La comprensione teorica delle sue prestazioni può quindi migliorare anche la comprensione delle macchine più complesse. Per imparare un insieme di esempi, una rete deve regolare i suoi accoppiamenti in modo appropriato (spesso la parola accoppiamenti sarà usata per indicare il loro valore numerico, dato dai pesi Wi, con i= 1, ... ,N). Un fatto notevole è che per il perceptron esiste un semplice algoritmo di apprendimento che permette sempre alla rete di trovare i valori dei parametri, purché gli esempi possano essere appresi. Nell'algoritmo di Rosenblatt, i pattern di input vengono presentati alla rete in sequenze (per esempio, ciclicamente), e si verifica l'output prodotto. Ogni qualvolta un pattern non viene correttamente classificato, tutti gli accoppiamenti vengono cambiati simultaneamente. Si aumentano di una quantità fissata tutti i pesi per i quali l'unità di input e il valore corretto dell 'unità di output hanno lo stesso segno, e si diminuiscono per il caso di segni opposti. Questo semplice algoritmo ricorda la cosiddetta regola di apprendimento hebbiana, un modello fisiologico del processo di apprendimento nel cervello reale. Secondo questa regola, i pesi sinaptici vengono incrementati quando due neuroni sono simultaneamente attivi. Il teorema di Rosenblatt afferma che, in tutti i casi in cui esiste una scelta delle Wi per la quale tutti gli esempi vengono correttamente classificati (cioè un perceptron perfettamente addestrabile), l' algoritmo ora descritto trova una soluzione in un numero fmito di passi.
È spesso utile acquisire una comprensione intuitiva delle capacità di classificazione del perceptron attraverso una rappresentazione geometrica. Possiamo considerare i valori numerici degli input come le coordinate di un punto in uno spazio, solitamente a molte dimensioni. La figura 2b mostra il caso bidimensionale. Si costruisce anche il punto rappresentativo per i pesi Wi. Chiameremo vettore dei pesi, o vettore degli accoppiamenti, la freccia diretta dall' origine del sistema di coordinate verso questo punto rappresentativo. Applicando l'algebra lineare all'elaborazione che ha luogo nella rete, si può dimostrare che la retta perpendicolare al vettore degli accoppiamenti rappresenta il confine tra gli input che appartengono alle due diverse classi. I punti di input che giacciono dallo stesso lato del vettore degli accoppiamenti sono classificati come + l, mentre quelli che giacciono sul lato opposto sono classificati come - 1 (v. figura 2b).
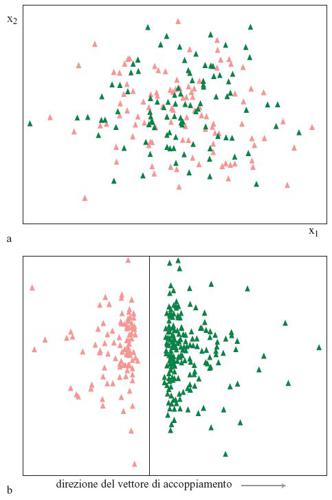
L'algoritmo di Rosenblatt mira all'identificazione di questa linea, nei casi in cui ciò è possibile. Questa rappresentazione si può generalizzare a più dimensioni, e in tal caso il ruolo svolto dalla retta nell' esempio a due dimensioni è giocato da un iperpiano. Possiamo ancora rappresentare la situazione in modo intuitivo effettuando una proiezione su piani in due dimensioni. Nella figura (fig. 3), su un piano generato da due assi coordinati arbitrari, sono proiettati 200 pattem di input con coordinate casuali, appartenenti a uno spazio a 200 dimensioni. Se invece usiamo per la proiezione un piano che contiene il vettore degli accoppiamenti (determinato da una variante dell'algoritmo di Rosenblatt), otteniamo la rappresentazione della figura 3b, in cui i punti sono chiaramente separati e in cui c'è perfino una separazione tra i due insiemi.
È chiaro che ci sono casi in cui i due insiemi di punti sono troppo mescolati, e non c'è nessuna retta (in due dimensioni) o iperpiano (in tre o più dimensioni) in grado di separadi. Ciò significa che la regola è troppo complessa per poter essere appresa perfettamente dal perceptron. In queste circostanze diventa interessante trovare la scelta degli accoppiamenti che minimizza il numero di errori compiuti su un insieme dato di esempi. In questo caso l'algoritrno di Rosenblatt non funziona, e il problema di trovare il minimo richiede l'utilizzo di algoritmi più complessi. L'errore di addestramento, cioè il numero di errori compiuti sull'insieme di addestramento, è di solito una funzione non regolare degli accoppiamenti della rete (cioè può avere grandi variazioni per piccoli cambiamenti degli accoppiamenti). Dunque, in generale, al di là del caso del perceptron perfettamente addestrabile, in cui l'errore finale è nullo, minimizzare l'errore di addestramento è di solito un compito arduo, che può assorbire una gran quantità di tempo di calcolo. Nella pratica, però, per addestrare la rete neurale si usano approcci iterativi, basati sulla minimizzazione di altre funzioni costo regolari (Bishop, 1995).
Capacità, dimensione di Vapnik-Chervonenkis e generalizzazione nel caso peggiore
Come abbiamo visto, i perceptron sono capaci di realizzare solo un tipo molto limitato di regole di classificazione, le cosiddette regole linearmente separabili. Quindi, indipendentemente dal problema di trovare il migliore algoritmo per apprendere la regola, ci si può chiedere in quanti casi il perceptron sarà capace di imparare alla perfezione un dato insieme di esempi di addestramento, se si scelgono arbitrariamente gli output. Per rispondere in modo quantitativo a questa domanda è opportuno introdurre alcuni concetti, come quelli di capacità, dimensione di Vapnik-Chervonenkis e generalizzazione nel caso peggiore, che si possono utilizzare nel caso del perceptron, ma che hanno un significato più generale.
Nel caso dei perceptron la domanda in questione ha avuto per la prima volta una risposta negli anni Sessanta, grazie a T. Cover (1965). Egli calcolò, per qualsiasi insieme contenente m pattem di input, la frazione di tutte le 2m possibili corrispondenze input/output - ognuna delle quali definisce una regola - che risultano linearmente separabili, e quindi tali da essere apprese da un perceptron. Questa frazione viene graficata in figura (fig. 4) come funzione del numero di esempi per accoppiamento, m/N, per diversi numeri di nodi di input (accoppiamenti) N. Si possono distinguere tre regioni:
1) regione in cui m/N≤1. Attraverso la semplice algebra lineare si vede che è sempre possibile imparare tutte le regole per le quali il numero m di pattern di input è minore o uguale al numero N di accoppiamenti (semplicemente, c'è un numero sufficiente di parametri da regolare).
2) Regione in cui m/N>1. Ci sono esempi di regole che non possono essere apprese. Però, finché il numero di esempi è minore del doppio del numero di accoppiamenti (m/N<2), se la rete è abbastanza grande è possibile apprendere quasi tutte le regole. Se si scelgono a caso le etichette di output di ognuno degli m input, uguali a + 1 o - 1 con uguale probabilità, la probabilità di trovare un insieme non realizzabile di accoppiamenti tende esponenzialmente a zero quando N tende all'infinito mantenendo fisso il rapporto m/N.
3) Regione con m/N>2. La probabilità che una regola sia realizzabile tende a zero esponenzialmente per N che tende all'infinito mantenendo fisso il rapporto m/N, cioè risulta proporzionale a exp[-Nf(m/N)]. La funzione f(α) che compare in quest'ultima relazione si annulla per α<2, ed è positiva per α>2. Questo fenomeno a soglia è il primo esempio di una transizione di fase, cioè di un cambiamento brusco di comportamento, che può aver luogo nel 'limite termodinamico' di grandi dimensioni della rete.
In genere, il punto in cui ha luogo una simile transizione definisce la cosiddetta capacità della rete neuronale. Sebbene la capacità misuri la possibilità, da parte della rete, di apprendere funzioni casuali dei suoi input, essa risulta anche legata alla sua capacità di apprendere una regola, cioè di generalizzare a partire dagli esempi. Ci chiederemo ora quali siano le prestazioni della rete su nuovi esempi, dopo che la rete stessa è stata addestrata su un insieme di m esempi.
Per dare un'idea intuitiva della connessione tra la capacità e la possibilità, da parte della rete, di generalizzare, ipotizziamo di avere un insieme di addestramento di dimensione m, e un solo pattern di prova. Supponiamo di definire una possibile regola attraverso una corrispondenza arbitraria (ma tale da poter essere appresa) tra input e output. Se m è molto più grande della capacità, per la maggior parte delle regole le etichette associate agli m pattern di addestramento che il perceptron è in grado di riconoscere determinano quasi univocamente gli accoppiamenti (e di conseguenza la risposta dell' algoritmo di apprendimento sul pattern di prova), e la regola può essere inferita in modo perfetto dagli esempi. Al di sotto della capacità, nella maggioranza dei casi vi sono due scelte diverse degli accoppiamenti che forniscono risposte opposte per il pattern di prova. Si ha dunque una corretta classificazione con probabilità 0,5, ipotizzando che tutte le regole siano equiprobabili. La figura (fig. 5) mostra i due tipi di situazioni per m = 3 e N = 2.
Questa relazione intuitiva può essere posta in termini più precisi. Vapnik e Chervonenkis hanno stabilito una relazione, valida per classificatori generici, tra una quantità simile alla capacità e la possibilità da parte della rete di generalizzare (Vapnik e Chervonenkis, 1971; Vapnik, 1982; 1995). La dimensione di Vapnik-Chervonenkis, Dvc, è definita come la dimensione del più grande insieme di input per il quale un dato tipo di classificatore può apprendere tutte le corrispondenze input/output. Per il perceptron la dimensione Dvc è uguale a N. Vapnik e Chervonenkis sono riusciti a dimostrare che, per qualsiasi insieme di addestramento di dimensione m maggiore di Dvc, la crescita del numero di corrispondenze realizzabili è limitata da un'espressione che cresce molto più lentamente di 2m (in effetti solo come un polinomio in m).
Questi autori hanno dimostrato che se il numero di esempi è ben al di sopra di Dvc, è molto improbabile avere una grande differenza tra l'errore di addestramento (cioè la percentuale minima di errori compiuti sull'insieme di addestramento) e l'errore di generalizzazione (cioè la probabilità di generare un errore sul pattern di test dopo aver imparato gli esempi) dei classificatori. Questo teorema implica che l'errore di generalizzazione aspettato è piccolo nel caso di apprendimento perfetto dell'insieme di addestramento. L'errore di generalizzazione aspettato è limitato da una quantità che cresce in modo proporzionale a Dvc, e decresce (trascurando le correzioni logaritmiche in m) come l/m.
Di contro, si può costruire una distribuzione di pattern di input corrispondente al caso peggiore, per la quale avere una dimensione dell'insieme di addestramento maggiore di Dvc è anche una condizione necessaria per una buona generalizzazione. Questi risultati dovrebbero in pratica permettere di selezionare la rete con la complessità appropriata, in modo da garantire il limite minimo sull'errore di generalizzazione. Per esempio, per trovare la dimensione ottimale dello strato nascosto di una rete con due strati, si potrebbero addestrare reti di diverse dimensioni sugli stessi dati.
La relazione tra questi concetti si può comprendere meglio se consideriamo una famiglia di reti di complessità crescente, che debbano apprendere la stessa regola. La figura (fig. 6) mostra una rappresentazione qualitativa dei risultati. Come indicato dalla curva, l'errore di addestramento minimo diminuisce al crescere della complessità della rete. D'altra parte, la dimensione Dvc e la complessità della rete crescono al crescere del numero di unità nascoste, e ciò porta a un aumento della differenza aspettata (intervallo di confidenza) tra l'errore di addestramento e quello di generalizzazione, come mostra la figura 6. La somma delle due curve ha un minimo, che fornisce il più piccolo limite sull'errore di generalizzazione. Come vedremo nel seguito, questa procedura conduce in qualche caso a stime non molto realistiche, a causa dei limiti piuttosto pessimistici della teoria. In altre parole, i limiti rigorosi, ottenuti per una rete e una regola arbitrarie, sono molto più alti di ciò che si ottiene per la maggior parte delle reti e delle regole.
Lo scenario tipico: l'approccio della fisica statistica
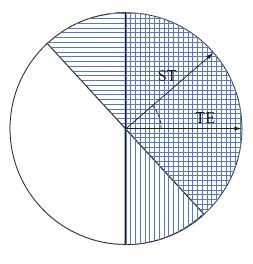
Nel caso in cui il numero di esempi sia confrontabile con la dimensione della rete, che per un perceptron è uguale alla dimensione Dvc, la teoria di Vapnik e Chervonenkis mostra che si possono avere situazioni sfavorevoli che impediscono la generalizzazione. In generale, però, non ci aspettiamo che il mondo si comporti come un nostro avversario. In che modo, dunque, si dovrebbe costruire un modello di una situazione più tipica? Per cominciare, si potrebbero costruire regole e distribuzioni di pattern che non agiscano reciprocamente come avversari. In questo contesto si è dimostrato utile il paradigma insegnante-studente. La regola da imparare è modellizzata da una seconda rete, la rete insegnante; in questo caso, se l'insegnante e lo studente hanno la stessa architettura e lo stesso numero di unità, la regola è chiaramente realizzabile. Le etichette di classe giuste per qualsiasi input sono fornite dall'output dell'insegnante. In questo schema è spesso possibile ricavare espressioni semplici per l'errore di generalizzazione. Nel caso del perceptron, possiamo utilizzare la rappresentazione geometrica per visualizzare l'errore di generalizzazione. Il perceptron studente, con vettore di accoppiamenti ST, classificherà un nuovo pattern di input in maniera errata solo se questo si trova tra i piani di separazione - la regione a righe nella figura (fig. 7) - definiti da ST e dal vettore di accoppiamenti dell'insegnante, TE. Se gli input sono tratti in modo casuale da una distribuzione uniforme, l'errore di generalizzazione è direttamente proporzionale all'angolo tra ST e TE. L'errore di generalizzazione è quindi piccolo se i vettori dello studente e dell 'insegnante sono vicini, e tende a zero quando coincidono.
Nel limite in cui il numero di esempi è molto grande, tutti gli studenti che imparano gli esempi di addestramento alla perfezione non saranno tra loro molto diversi, e i loro vettori di accoppiamenti saranno vicini a quelli dell'insegnante. l casi di questo tipo, con un errore di generalizzazione piccolo, sono stati trattati con successo usando stime asintotiche derivate con metodi di fisica statistica. D'altra parte, quando il numero di esempi è relativamente piccolo, vi sono molti studenti diversi che sono coerenti con l'insegnante sugli esempi di addestramento, e l'incertezza sui veri vettori di accoppiamento dell'insegnante è grande. Gli errori di generalizzazione possibili vanno da zero (se, per puro caso, un algoritmo di apprendimento converge all'insegnante) a un certo valore che corrisponde al caso peggiore. Si può dire che i vincoli che specificano il macrostato della rete (il suo errore di addestramento) non ne specificano univocamente il microstato. Ciò nonostante, ha senso parlare di un valore tipico per l'errore di generalizzazione, definito come il valore realizzato dalla maggioranza degli studenti. Nel limite termodinamico, noto dalla fisica statistica, in cui il numero di parametri della rete si assume grande, ci si aspetta che, in effetti, quasi tutti gli studenti appartengano a questa maggioranza, purché la quantità in esame sia il risultato di un effetto cooperativo di tutti i componenti del sistema. Come mostrato dalla visualizzazione geometrica dell' errore di generalizzazione per il perceptron, questo è quanto in effetti succede. L'approccio al problema che ora descriveremo, introdotto da E. Gardner (Gardner, 1988; Gardner e Derrida, 1989), è basato sul calcolo di V(ε), il volume nello spazio degli accoppiamenti per cui si ha un apprendimento perfetto di m esempi di addestramento e, allo stesso tempo, un dato errore di generalizzazione e. Per avere una rappresentazione intuitiva, pensiamo che siano permessi solo valori discreti per gli accoppiamenti; in questo caso V(ε) sarebbe proporzionale al numero di studenti. Il valore tipico dell'errore di generalizzazione è il valore di e che massimizza V(ε). Dobbiamo tenere a mente il fatto che V(ε) è un numero casuale, e fluttua da un insieme di addestramento a un altro; una trattazione corretta di questa casualità richiede tecniche matematiche piuttosto complicate (Mezard et al., 1987). Per ricavare una rappresentazione che spesso risulta qualitativamente corretta, possiamo sostituirlo con la sua media su molte realizzazioni degli insiemi di addestramento. Dalla teoria elementare della probabilità vediamo allora che questo numero medio si può trovare calcolando il volume A dello spazio di tutti gli studenti con errore di generalizzazione e indipendentemente dal loro comportamento sull'insieme di addestramento, e moltiplicando questo numero per la probabilità B = (l - ε)m che uno studente con errore di generalizzazione e dia m volte la risposta corretta su campionamenti indipendenti dei pattem di input. Si può mostrare che per N abbastanza grande, A ≈ [sin(πε)]N. Poiché A cresce esponenzialmente con il numero N di accoppiamenti (come i volumi tipici in spazi N-dimensionali), e B decresce esponenzialmente con m (poiché diventa sempre più improbabile dare m volte la risposta giusta per qualsiasi ε ≠ 0), i due fattori possono compensarsi se m cresce come m = αN. La grandezza α rappresenta una 'misura efficace' della dimensione dell'insieme di addestramento, quando N va all'infinito. Per avere quantità che rimangono fmite per N → ∞, è utile inoltre prendere il logaritmo di V(ε) e dividerlo per N; in questo modo trasformiamo il prodotto nella somma di due termini, S ed E. Il termine S = sin (πε), detto termine entropico, cresce al crescere dell'errore di generalizzazione, come indicato nella figura (fig. 8). Ciò succede perché vi sono moltissime reti che non sono simili all' inse gnante, ma ce n'è solo una uguale aesso. Quasi tutte le reti (si ricordi che il termine entropico non include gli effetti degli esempi di addestramento) hanno ε = 0,5, danno cioè la risposta corretta la metà delle volte, indovinando a caso. D'altra parte il secondo termine, E = αln(l- ε), decresce al crescere dell'errore di generalizzazione (v. figura 8), poiché la probabilità di dare la risposta giusta su un pattem in input cresce se la rete studente diventa più simile alla rete insegnante. Questo termine è spesso chiamato contributo energetico, perché favorisce stati della rete altamente ordinati (rispetto all'insegnante), come accade per gli stati dei sistemi fisici a basse energie. Ci sarà dunque un massimo di V(ε), come mostrato dalla curva di figura 8, per un certo valore di e il quale, per definizione, è l'errore di generalizzazione tipico.
Lo sviluppo del processo di apprendimento al crescere di m = αN si può comprendere in termini di una competizione tra il termine entropico, che favorisce configurazioni disordinate della rete (diverse dall'insegnante), e il termine energetico. Quest'ultimo domina quando il numero di esempi è grande. Vedremo nel seguito che questa competizione può dar luogo a un comportamento ricco e interessante al variare del numero di esempi. In figura (fig. 9) è mostrato il risultato per la curva di apprendimento di un perceptron, ottenuto attraverso un approccio di fisica statistica, trattando il campionamento casuale nel modo appropriato (Györgyi e Tishby, 1990; Sompolinski et al., 1990). Al contrario delle previsioni di caso peggiore della teoria di Vapnik e Chervonenkis, si può avere una capacità di generalizzazione al di sotto della dimensione Dvc. Come era da attendersi, l'errore di generalizzazione decresce monotonicamente, il che mostra che quanto più si impara, tanto più si capisce. Asintoticamente, l'errore è proporzionale a N e inversamente proporzionale a m, in accordo con le previsioni della teoria di Vapnik e Chervonenkis. Questo potrebbe non essere vero per reti più complesse.
Apprendimento basato su domande
Poco dopo il lavoro pionieristico di Gardner ci si è resi conto (Levin et al., 1989; Györgyi e Tishby, 1990; Opper e Haussler, 1991) che l'approccio ispirato alla fisica statistica è strettamente legato a idee tratte dalla teoria dell'informazione e dalla statistica bayesiana (Berger, 1985). In questi casi, l'attenzione è concentrata sulla riduzione di una incertezza iniziale relativa al reale stato del sistema (l'insegnante) attraverso l'osservazione dei dati. Il logaritmo del volume dei microstati significativi, definito nel paragrafo precedente, è una misura diretta di questa incertezza. Si può comprendere il lento progresso della capacità di generalizzazione mostrato nella figura 9 in considerazione del fatto che, al progredire dell'apprendimento, un nuovo esempio casuale fornisce sempre meno informazione sull'insegnante. In questo contesto il guadagno di informazione è definito come la riduzione di incertezza quando viene appreso un nuovo esempio. La decrescita del guadagno di informazione è dovuta all'aumento della capacità di generalizzazione. Questo è verosimile, poiché gli input per i quali la maggioranza delle reti-studente fornisce la risposta corretta portano meno informazione, rispetto a quelli per i quali è più probabile un errore. La situazione cambia se lo studente è libero di porre domande all'insegnante, se può cioè scegliere dei pattern di input che veicolano molta informazione. Per il perceptron, un'utile strategia basata su domande consiste nel selezionare un nuovo vettore di input perpendicolare all'attuale vettore degli accoppiamenti dello studente (Kinzel e Rujan, 1990). Tale input costituisce un pattern molto ambiguo, poiché cambiamenti anche piccoli degli accoppiamenti dello studente producono risposte di classificazione diverse. Per reti più complesse può essere difficile ottenere input ambigui con una costruzione esplicita. È stato proposto un algoritrno generale (Seung et al., 1992), che utilizza il principio di massimo disaccordo all'interno di un comitato (committee) di diversi studenti, come processo di selezione per i pattern di addestramento. Usando un'appropriata strategia casuale di addestramento si generano diversi studenti, che imparano tutti dallo stesso insieme di esempi. Ogni nuovo vettore di input viene quindi accettato per l'addestramento solo quando è massimo il disaccordo tra gli studenti circa la sua classificazione. Si può dimostrare che già per un comitato di due soli studenti, quando il numero di esempi è grande, il guadagno di informazione non decresce, ma raggiunge un valore positivo costante, e ciò ha come conseguenza una diminuzione molto più rapida dell'errore di generalizzazione. Invece di essere inversamente proporzionale al numero di esempi, la diminuzione dell' errore è ora esponenziale.
Buoni e cattivi studenti
Se è vero che il tipico perceptron-studente ha una curva di apprendimento regolare e monotonicamente decrescente, questo non esclude la possibilità che un qualche concreto algoritmo di apprendimento possa portare a un insieme di accoppiamenti dello studente che risultino piuttosto atipici, nel senso della nostra teoria. Per cattivi studenti, è possibile anche un comportamento non monotono della generalizzazione. Il problema di un algoritmo concreto di apprendimento può trovar posto nello schema della fisica statistica, se l'algoritrno minimizza una certa 'funzione costo'. Trattando i valori ottenuti per la nuova funzione costo come un vincolo macroscopico, si possono applicare nuovamente gli strumenti della fisica statistica. Come esempio è utile considerare il caso in cui l'insegnante e lo studente abbiano una diversa architettura: in uno degli esempi più semplici, si cerca di imparare a risolvere un problema di classificazione interpretandolo come un problema di regressione, cioè un problema di fit di una funzione continua attraverso dei dati. Specificamente, studiamo la situazione in cui la rete insegnante è ancora data da un perceptron che calcola output a valori binari dal segno dell'espressione [1].
Come studente scegliamo una rete con una funzione di trasferimento lineare (figura 1a) e proviamo a fare un fit di questa espressione lineare con le etichette binarie dell'insegnante. Se il numero di accoppiamenti è abbastanza grande (maggiore del numero di esempi), la funzione lineare (a differenza della funzione segno) è perfettamente in grado di adattarsi a valori continui di output arbitrari. Questo fit lineare è un tentativo di spiegare i dati in un modo più complicato del necessario, e per raggiungere questo fine bisogna regolare gli accoppiamenti in modo fine. Abbiamo trovato che lo studente addestrato in questo modo non generalizza bene (Vallet et al., 1989; Opper e Kinzel, 1995). Per poter confrontare le classificazioni da parte dell'insegnante e dello studente, dopo l'addestramento, su un nuovo pattern di input casuale, abbiamo infine convertito l'output dello studente in una etichetta di classificazione, prendendo il segno del suo output. Come mostriamo in figura (fig. 10), dopo un miglioramento iniziale delle prestazioni, l'errore di generalizzazione cresce nuovamente fino al valore pertinente al semplice indovinare a caso, ε = 0, 5 per α = 1. Questo fenomeno è chiamato overfitting. Per α>1, cioè per un numero di dati maggiore di quello dei parametri, non è più possibile avere un fit lineare perfetto attraverso i dati, ma si ha un fit con una piccola deviazione dalla funzione lineare che genera la seconda parte della curva di apprendimento. L'errore S decresce di nuovo, e si avvicina asintoticamente a zero per α che tende all'infinito. Ciò dimostra che quando sono disponibili dati sufficienti, sono meno importanti i dettagli dell'algoritmo di addestramento.
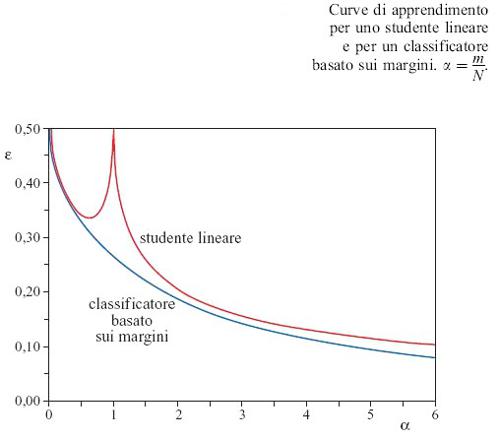
È ben nota la dipendenza delle prestazioni in generalizzazione dalla complessità del modello dei dati ipotizzato. Se si usa una classe di funzioni troppo complicata, si può fare un fit perfetto dei dati, ma la funzione trovata sarà molto sensibile alle variazioni nel campione dei dati, e ciò porta a previsioni inaffidabili su nuovi input. D'altra parte, funzioni troppo semplici sono tali che il fit migliore sia quasi insensibile ai dati e ciò impedisce di imparare abbastanza da loro. Si può anche calcolare la capacità di generalizzazione nel caso peggiore: per studenti-perceptron che imparano da un insegnante perceptron. L'errore di generalizzazione più alto si ottiene, come è chiaro pensando alla figura 7, quando si massimizza l'angolo tra i vettori degli accoppiamenti dell'insegnante e dello studente, sotto il vincolo che lo studente impari tutti gli esempi alla perfezione. Per quanto possa essere difficile costruire un algoritmo di apprendimento che realizzi in pratica tale massimizzazione, si può calcolare il conseguente errore di generalizzazione utilizzando l'approccio della fisica statistica (Engel e Van den Broeck, 1993). Il risultato è in accordo con la teoria di Vapnik e Chervonenkis: al di sotto della capacità non c'è previsione migliore dell'indovinare a caso. Mentre i precedenti algoritrni conducono a comportamenti peggiori di quelli tipici, considereremo ora il caso opposto, di un algoritmo che si comporta meglio. Siccome la capacità di generalizzazione di una rete neurale è legata al fatto che a vettori di input simili corrisponda lo stesso output, si può ipotizzare che tale proprietà possa essere migliorata se la separazione tra le due classi viene massimizzata, e ciò definisce una nuova funzione costo per un algoritrno. Questo perceptron con margine ottimale si può realizzare concretamente, e la sua applicazione a un insieme di dati dà luogo alle proiezioni della figura (fig. 11). Osserviamo, ed è un risultato notevole, che c'è una frazione relativamente grande di pattern posizionati esattamente sul margine; questi punti vengono chiamati vettori di supporto (support vectors). Per capire la loro importanza ai fini della capacità di generalizzazione, facciamo il seguente esperimento concettuale (Gedankenexperiment), assumendo, per il momento, che tutti i punti che non giacciono sul margine (i vettori non di supporto) vengano eliminati dal set di esempi di addestramento.
Dalla proiezione bidimensionale della figura 11 possiamo ipotizzare che, utilizzando l'algoritrno del margine massimo sugli esempi rimanenti (i vettori di supporto), non si riesca a creare una separazione più grande tra i punti. L'algoritmo convergerebbe dunque allo stesso iperpiano di separazione di prima. Questa rappresentazione intuitiva è in effetti corretta. Se si conoscessero in anticipo i vettori di supporto di un insieme di addestramento (sfortunatamente essi vengono identificati solo dopo aver utilizzato l'algoritmo), si dovrebbe addestrare il classificatore solo sui vettori di supporto, ed esso classificherebbe automaticamente in modo corretto il resto degli input di addestramento. Se, quindi, in un esperimento reale di classificazione, il numero di vettori di supporto risulta basso in confronto ai vettori non di supporto, ci si può attendere una buona capacità di generalizzazione.
In figura 10 mostriamo la curva di apprendimento per un classificatore basato sul margine (Opper e Kinzel, 1995) che impara da un insegnante-perceptron, calcolata con un approccio di fisica statistica. Recentemente il concetto di classificatore basato sul margine è stato generalizzato alle cosiddette macchine a vettori di supporto (Vapnik, 1995), per le quali gli input di un perceptron sono sostituiti da opportune quantità, costituite da funzioni non lineari degli input originali accuratamente scelte. In questo modo si possono apprendere regole non linearmente separabili e si può fornire un'interessante alternativa alle reti multistrato.
Il perceptron di Ising
L'approccio derivato dalla fisica statistica può sviluppare un potere predittivo specifico nelle situazioni in cui si desideri comprendere architetture o modelli nuovi di reti, per i quali attualmente non si conosca alcun algoritmo efficiente di apprendimento. Considereremo come esempio semplice un perceptron per il quale gli accoppiamenti Wi siano vincolati ad assumere valori binari (Gardner e Derrida, 1989; Györgyi, 1990; Seung et al., 1992). Questo sistema prende il nome di perceptron di Ising da E. Ising, che studiò un insieme interagente di elementi a valori binari come modello per un ferromagnete. Nel caso in esame, l'apprendimento perfetto degli esempi è equivalente a un difficile problema di ottimizzazione combinatoria, che, nel caso peggiore, si ritiene richieda un tempo di apprendimento che cresce esponenzialmente con il numero di accoppiamenti N.
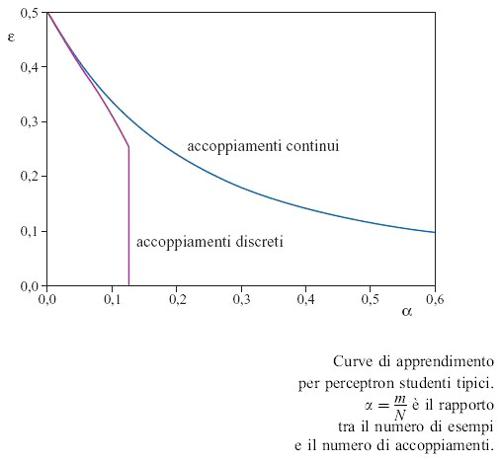
Per ricavare la curva di apprendimento per lo studente tipico possiamo procedere come prima, sostituendo a V(ε) il numero di configurazioni di studenti che sono coerenti con l'insegnante, e ciò porta a una corrispondente modifica del termine entropico. Se gli esempi sono forniti da una rete-insegnante dello stesso tipo binario, ci si può attendere che l'errore di generalizzazione decresca monotonicamente, come funzione di α. La curva di apprendimento è mostrata in figura 9. Per valori di α abbastanza piccoli, la natura discreta degli accoppiamenti non ha quasi effetto. Al contrario del caso continuo, però, una perfetta generalizzazione non richiede un numero infrnito di esempi, ma si ottiene già per un valore finito (α = αc = 1,24). Questo fatto non è sorprendente, poiché gli accoppiamenti dell'insegnante contengono solo una quantità frnita di informazione (un bit per accoppiamento), e ci si può attendere che non occorra molto di più di circa N esempi per apprenderli. Il risultato notevole e inaspettato dell'analisi sta nel fatto che la transizione alla generalizzazione perfetta è discontinua: l'errore di generalizzazione crolla istantaneamente da un valore non nullo a zero. Questo fatto dà un'idea della struttura complessa dello spazio di tutti gli studenti coerenti, e fornisce anche una traccia per comprendere il motivo per cui l'apprendimento perfetto, nel perceptron di lsing, sia un compito difficile. Per valori di α appena inferiori a αc il numero di studenti coerenti è piccolo, ma ciò nonostante i pochi rimanenti possono ancora differire tra loro, e dall'insegnante, per una frazione finita di bit, così che una generalizzazione perfetta risulta impossibile. Per valori di α appena superiori a αc sopravvivono solo gli accoppiamenti dell'insegnante.
Imparare con errori
L'esempio del perceptron di lsing ci insegna che non è sempre semplice ottenere un errore nullo nell'addestramento. Inoltre, un algoritrno che cerchi di ottenere questo scopo può imbattersi in minimi locali. Dunque, l'idea di permettere esplicitamente errori nella procedura di addestramento, introducendo un rumore appropriato, può aver senso. Una prima analisi di una simile procedura stocastica di apprendimento è stata fatta da P. Carnevali e S. Patarnello nelle cosiddette reti booleane, che possiedono unità elementari di calcolo diverse da quelle usate in reti neurali (Carnevali e Patarnello, 1987). Un algoritmo stocastico può risultare utile per sfuggire ai minimi locali dell'errore di addestramento, consentendo un apprendimento migliore dell'insieme di addestramento. Sorprendentemente, questo metodo può anche portare a capacità di generalizzazione migliore, se anche la regola di classificazione viene alterata da un certo livello di rumore (Györgyi e Tishby, 1990). Un algoritmo di addestramento stocastico si può realizzare usando il metodo Monte Carlo, che fu inventato per riprodurre gli effetti dovuti alla temperatura nelle simulazioni di sistemi fisici. In questo contesto è accettato qualsiasi cambiamento degli accoppiamenti della rete che causa una diminuzione dell'errore di addestramento durante l'apprendimento. Però anche un aumento dell' errore di addestramento viene accettato, con una probabilità che aumenta con la temperatura. Sebbene in linea di principio questo algoritrno possa visitare tutte le configurazioni della rete, per un sistema grande, con probabilità schiacciante, appaiono solo gli stati vicini a un determinato valore dell'errore di addestramento. L'applicazione dei metodi della fisica statistica a questa situazione ha dimostrato che, per temperature T abbastanza alte, si ottiene spesso una descrizione qualitativamente corretta se si ripete il calcolo per il caso senza rumore e si sostituisce il numero relativo di esempi, α, con un numero efficace, α/T. Le curve di apprendimento vengono 'deformate', ed un ancora possibile una buona generalizzazione, pagando il prezzo della necessità di un numero maggiore di esempi di addestramento.
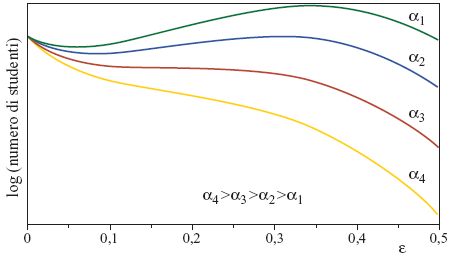
Nell'ambito dello schema stocastico, l'apprendimento (con errori) si può ora realizzare anche per il perceptron di lsing, ed è interessante studiare in maggior dettaglio il numero di configurazioni rilevanti dello studente in funzione di s (fig. 12). La curva verde è ottenuta per un valore piccolo di α per cui esiste un massimo pronunciato con errore di generalizzazione alto. Aumentando α il massimo diminuisce, finché diventa pari al secondo massimo, presente in ε = 0, indicando una transizione come quella della curva di apprendimento della figura 9. Per α maggiori, lo stato di generalizzazione perfetta dovrebbe essere lo stato tipico. Ciò nonostante, se l'algoritmo stocastico parte da uno stato iniziale che non ha nessuna somiglianza con l'insegnante (sconosciuto), cioè con ε = 0,5, trascorrerà nel massimo locale minore, il cosiddetto stato metastabile, un tempo che cresce esponenzialmente con N. Una transizione improvvisa alla generalizzazione perfetta sarà dunque osservabile solo per un numero di esempi che corrisponde alla curva superiore della figura 12, dove questo stato metastabile scompare. Per valori grandi di α (curva inferiore) l'algoritmo stocastico convergerà sempre allo stato di generalizzazione perfetta. D'altra parte, siccome lo stato con ε = 0 è sempre metastabile, un algoritrno stocastico che parta dagli accoppiamenti dell' inse gnante non porterà mai lo studente fuori dallo stato di generalizzazione perfetta. Chiariamo che le transizioni di fase nette sono una conseguenza del limite termodinamico, in cui lo stato macroscopico è completamente dominato dalle configurazioni tipiche. Nelle simulazioni di qualsiasi sistema finito si osserverà una attenuazione delle transizioni.
Complessità del calcolo per le reti multistrato
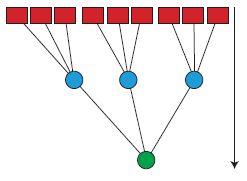
Per iniziare a comprendere la capacità di generalizzazione delle reti multistrato, si può studiare un'architettura che è più semplice di quella, completamente connessa, illustrata in figura 1b. L'architettura ad albero della figura (fig. 13) è diventata un modello frequentemente utilizzato. In questo caso ogni unità nascosta è connessa a un insieme diverso di nodi di input. Una semplificazione ulteriore risiede nella sostituzione degli accoppiamenti modificabili dalle unità nascoste al nodo di output con una funzione precablata fissa, che realizza la corrispondenza tra gli stati delle unità nascoste e l' output.
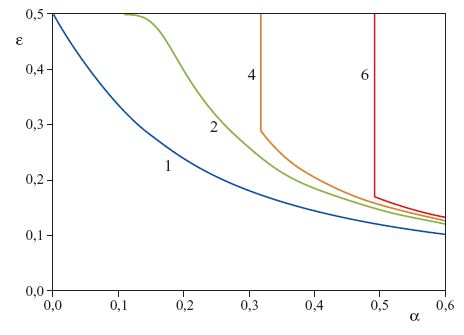
Due di queste funzioni sono state studiate in grande dettaglio. Per la prima, l'output fornisce solo il 'voto di maggioranza' delle unità nascoste: se la maggioranza delle unità nascoste è negativa, l'output totale è negativo, e viceversa. Questa rete viene detta committee machine ('macchina a comitato'). Per il secondo tipo di rete, la parity machine ('macchina a parità'), l'output è la parità degli output nascosti, cioè risulta un segno meno se si ha un numero dispari di unità nascoste negative, e un segno più per un numero pari. Per entrambi i tipi di rete è stata calcolata la capacità nel limite termodinamico di N grande, essendo N il numero di accoppiamenti del primo strato (Barkai et al., 1990; Monasson e Zecchina, 1995). Aumentando il numero di unità nascoste (ma mantenendolo sempre molto più piccolo di N) la capacità per accoppiamento e la dimensione Dvc si possono rendere arbitrariamente grandi. La teoria di Vapnik e Chervonenkis prevederebbe quindi che la capacità di generalizzare inizi a una dimensione dell' insieme di addestramento che cresce con la capacità. Le curve di apprendimento della tipica macchina a parità, addestrata da un insegnante a parità per 1, 2, 4 e 6 unità nascoste (fig. 14), sembrano coincidere almeno in parte con questa previsione.
Al di sotto di un certo numero di esempi si ha solo memorizzazione dei pattern appresi, senza generalizzazione. Superato un certo valore di soglia, ha luogo una transizione a una generalizzazione non banale (Hansel et al., 1992; Opper, 1994). Molto al di là della transizione, il decadimento delle curve di apprendimento diventa quello di un semplice perceptron (curva blu in figura 14), indipendentemente dal numero di unità nascoste, e quindi è molto più veloce del limite fornito dalla teoria di Vapnik e Chervonenkis. Questo dimostra come la curva di apprendimento tipica possa essere, in effetti, determinata da più di un parametro di complessità. Al contrario, le curve di apprendimento della tree committee machine (macchina a comitato con architettura ad albero) della figura 13 sono regolari, e richiamano quelle di un semplice perceptron (Schwarze e Hertz, 1992; 1993). All'aumentare del numero di unità nascoste (mantenendo N fisso e molto grande), l'errore di generalizzazione cresce, ma, malgrado la dimensione Dvc divergente, le curve convergono a una curva limite che ha un decadimento asintotico soltanto due volte più lento di quello del perceptron. Abbiamo quindi un esempio in cui il comportamento in generalizzazione tipico e quello per il caso peggiore sono completamente diversi.
Di recente è stata chiarita meglio la relazione tra lo scenario medio e quello del caso peggiore per la tree committee machine. Uno scenario di caso peggiore semplificato, in cui studenti con struttura di albero a comitato debbono imparare da un insegnante con la stessa struttura, è stato analizzato con metodi di fisica statistica (Urbanczik, 1996). Coerentemente con le previsioni, non ci sono molti studenti che mostrino una capacità di generalizzazione molto peggiore di quella tipica. Inoltre questi studenti potrebbero essere difficili da trovare per la maggior parte degli algoritmi ragionevoli di apprendimento, perché i cattivi studenti richiedono una regolazione molto fine dei loro accoppiamenti. Un calcolo degli accoppiamenti con precisione fmita richiede un numero di bit per accoppiamento che cresce più che esponenzialmente con α, e ciò, per α abbastanza grande, è oltre le capacità di algoritmi realistici. Ci aspettiamo dunque che, in pratica, un comportamento cattivo non venga osservato.
Le transizioni dell'errore di generalizzazione, come quelle osservate per la tree parity machine (macchina a parità con architettura ad albero), sono un aspetto caratteristico dei sistemi grandi con una simmetria che può essere rotta spontaneamente. Per spiegare questo punto, consideriamo il caso semplice di due unità nascoste. Se cambiamo simultaneamente il segno di tutti gli accoppiamenti per entrambe le unità nascoste, l'output di questa macchina a parità non cambia. Se quindi gli accoppiamenti dell'insegnante sono tutti uguali a + 1, uno studente con tutti gli accoppiamenti uguali a - 1 agisce esattamente come un cIassificatore identico. Se non ci sono molti esempi nell'insieme di addestramento, il contributo entropico dominerà il comportamento tipico, e lo studente tipico esibirà la stessa simmetria. Il suo vettore degli accoppiamenti consisterà in numeri casuali positivi e negativi; dunque non c'è preferenza per quell'insegnante o per un insegnante con tutti i bit invertiti, e la generalizzazione non è possibile. Se il numero di esempi è abbastanza grande, la simmetria è rotta, e ci sono due tipi possibili di studenti tipici: uno con più accoppiamenti positivi, e l'altro con più accoppiamenti negativi. Quindi, ognuno degli studenti tipici mostrerà qualche somiglianza con l'insegnante (o con la sua immagine negativa), e si innesca la generalizzazione. Un tipo simile di rottura di simmetria porta anche a una transizione di fase continua nella macchina a comitato completamente connessa. Questa si può considerare come un comitato di perceptron, uno per ogni unità nascosta, che condividono gli stessi nodi di input. Qualsiasi permutazione di questi perceptron lascia ovviamente invariato l'output. Di nuovo, se non vengono imparati molti esempi, lo stato tipico riflette la simmetria. Ogni perceptron studente esibirà, più o meno, la stessa somiglianza con tutti i perceptron insegnanti. Sebbene questo stato simmetrico permetta un qualche grado di generalizzazione, non gli è possibile recuperare completamente la regola dell 'insegnante. Dopo un lungo plateau, la simmetria è di nuovo rotta, e ognuno dei perceptron studenti si specializza su uno dei perceptron insegnanti, perdendo la sua somiglianza con gli altri. Questo porta a una rapida (ma continua) caduta dell'errore di generalizzazione. Questi tipi di curve di apprendimento con pIateau si possono effettivamente osservare nelle applicazioni delle reti multi strato completamente connesse.
Prospettive
L'approccio di caso peggiore (della teoria di Vapnik e Chervonenkis) e quello di caso tipico (della fisica statistica) sono importanti per modellizzare e comprendere la complessità dei processi con cui si apprende a generalizzare a partire dagli esempi. Sebbene l'approccio di Vapnik e Chervonenkis giochi un ruolo importante in una teoria generale della possibilità di imparare, le sue applicazioni pratiche alle reti neurali sono state finora limitate proprio dalla sua generalità. Poiché nella teoria entrano solo ipotesi deboli sulla distribuzione di probabilità e sulle macchine, le stime degli errori di generalizzazione sono state spesso troppo pessimistiche. Sviluppi recenti della teoria sembrano risolvere questi problemi. Usando dimensioni Dvc modificate, che dipendono dai dati che si sono effettivamente presentati, e che in casi favorevoli sono molto più piccole di quelle generali, sembra possibile ricavare risultati più realistici. Per le macchine a vettori di supporto (Vapnik, 1995) - generalizzazioni dei classificatori basati su margini che tengono conto di confini non lineari che separano due classi - Vapnik e i suoi collaboratori hanno mostrato l'efficacia dei risultati di Vapnik e Chervonenkis, modificati per la selezione del tipo ottimale di modello in applicazioni pratiche.
L'approccio di fisica statistica, d'altra parte, ha rivelato un comportamento nuovo e inaspettato di modelli semplici di reti, come, per esempio, una varietà di transizioni di fase. È una eccitante questione aperta la possibilità che tali transizioni possano giocare un ruolo cognitivo nei cervelli animali o umani. Gli sviluppi recenti della teoria mirano alla comprensione dei problemi dinamici dell'apprendimento. Per esempio il caso dell'apprendimento online (Saad, 1998), in cui il problema dell'apprendimento e quello della generalizzazione sono fortemente interconnessi, ha permesso lo studio di reti multistrato complesse e ha stimolato la ricerca sullo sviluppo di algoritmi ottimizzati. Oltre alla estensione dell'approccio a reti più complicate, una comprensione della robustezza del comportamento 'tipico' e un'interpolazione all'altro estremo (lo scenario di caso peggiore) è una importante direzione di ricerca.
Ringraziamenti
Ringrazio il Dipartimento di Fisica dei Sistemi Complessi dell'Istituto Weizmann a Rehovot, in Israele, presso il quale è stata scritta una parte di questo saggio.
Bibliografia citata
AMARI, S., MURATA, N. (1993) Statistical theory of learning curves nnder entropic loss. Neural Comput., 5, 140.
BARKAI, E., HANSEL, D., KANTER, I. (1990) Statistical mechanics of a multilayered neural network. Phys. Rev. Lett., 65, 2312.
CARNEVALI, P., PATARNELLO, S. (1987) Exhaustive thermodynamical analysis of boolean learning networks. Europhys. Lett., 4, 1199.
COVER, T.M. (1965) Geometrical and statistical properties of systems of linear inequalities with applications in pattern recognition. IEEE Trans. El. Comp., 14, 326.
ENGEL, A., VAN DEN BROECK, C. (1993) Systems that can learn from examples: replica calculation of uniform convergence bonnd for the perceptron. Phys. Rev. Lett., 71, 1772.
GARDNER, E. (1988) Space of interactions in neural networks. J. Phys., A 21, 257.
GARDNER, E., DERRIDA, B. (1989) Optimal storage properties of neural network models. J. Phys. A, 21, 271.
GYÖRGYI, G. (1990) First order transition to perfect generalization in a neural network with binary synapses. Phys. Rev. A, 41, 7097.
GYÖRGYI, G., TISHBY, N. (1990) Statistical theory of learning a rule. In Neural networks and spin glasses: proceedings of the STATPHYS 17 Workshop on Neural Networks and Spin Glasses, a c. di Theumann W.K., Koberle R., Singapore-River Edge, World Scientific.
HANSEL, D., MATO, G., MEUNIER, C. (1992) Memorization without generalization in a multilayered neural network. Europhys. Lett., 20, 471.
KINZEL, W., RUJAN, P. (1990) Improving a network generalization ability by selecting examples. Europhys. Lett., 13, 473.
LEVIN, E., TISHBY, N., SOLLA, S. (1989) Statistical approach to learning and generalization in neural networks. In Proceedings of the Second Workshop on Computational Learning Theory, a c. di Rivest R., Haussler D., Warmuth M., San Mateo, Morgan Kaufmann.
MÉZARD, M., PARISI, G., VIRASORO, M.A. (1987) Spin glass theory and beyond. Lecture Notes in Physics, 9, Singapore-River Edge, World Scientific.
MONASSON, R., ZECCHINA, R. (1995) Weight space structure and internaI representations: a direct approach to learning and generalization in multilayer neural networks. Phys. Rev. Lett., 75, 2432.
OPPER, M. (1994) Leaming and generalization in a two-Iayer neural network: the role of the Vapnik-Chervonenkis-dimension. Phys. Rev. Lett., 72, 2113.
OPPER, M., HAUSSLER, M. (1991) Generalization performance of bayes optimal classification algorithm for learning a perceptrono Phys. Rev. Lett., 66, 2677.
OPPER, M., KINZEL, W. (1995) Statistical mechanics of generalization. In Physics of neural networks III, a c. di van Hemmen J.L., Domany E., Schulten K., Berlino-New York Springer Verlag.
SAAD, D., a c. di (1998) Online learning in neural networks. Cambridge-New York, Cambridge University Press.
SCHWARZE, H., HERTZ, J. (1992) Generalization in a large committee machine. Europhys. Lett., 20, 375.
SCHWARZE, H., HERTZ, J. (1993) Generalization in fully connected committee machines. Europhys. Lett., 21, 785.
SEUNG, H.S., OPPER, M., SOMPOLINSKY, H. (1992) Query by committee. In The proceedings of the Vth Annual Workshop on Computational Learning Theory (COLT92). New York, Association for Computing Machinery, p. 287.
SEUNG, H.S., SOMPOLINSKY, H., TISHBY, N. (1992) Statistical mechanics of learning from examples. Phys. Rev. A, 45, 6056.
SOMPOLINSKY, H., TISHBY, N., SEUNG, H.S. (1990) Leaming from examples in large neural networks. Phys. Rev. Lett., 65, 1683.
URBANCZIK, R. (1996) Leaming in a large commitlee machine: worst case and average case. Europhys. Lett., 35, 553.
VALLET, F., CAILTON, J., REFREGIER, P. (1989) Linear and nonlinear extension ofthe pseudo-inverse solution for learning boolean functions. Europhys. Lett., 9, 315.
VAPNIK, V.N. (1982) Estimation of dependencies based on empirical data. Berlino-New York, Springer Verlag.
VAPNIK, V.N. (1995) Nature of statisticallearning theory, Berlino-New York, Springer Verlag.
VAPNIK, V.N., CHERVONENKIS, A. (1971) On the uniform convergence of relative frequencies of events to their probabilities. Theory of Probability and its Applications, 16, 254.
Bibliografia generale
ARBIB, M.A., a c. di, Handbook of brain theory and neural networks. Cambridge, Mass., MIT Press, 1995.
BERGER, J.O. Statistical decision theory and Bayesian analysis. Berlino-New York, Springer Verlag, 1985.
BISHOP, C.M. Neural networks Jor pattern recognition. Oxford, Clarendon Press, and New Y ork, Oxford University Press, 1995.
HERTZ, J.A., KROGH, A., PALMER, R.G. lntroduction to the theory of neural computation. Redwood City, Addison-Wesley, 1991.
MINSKY, M., PAPERT, S. Perceptrons. Cambridge, Mass., MIT Press, 1969.
WATKIN, T.L.H., RAU, A., BIEHL, M. (1993) Statistical mechanics of leaming a ruIe. Rev. Mod. Phys., 65, 499.