Imparare a vedere
Imparare a vedere
Il problema dell'apprendimento è centrale per comprendere l'intelligenza e per riprodurla in una macchina. In questo saggio passeremo in rassegna alcuni approcci specifici al problema della visione che fanno uso di tecniche di apprendimento. La maggior parte dei compiti grafici e visivi si può formulare in termini di addestramento di una 'scatola che impara' con appropriati insiemi di esempi, cioè di coppie di vettori input-output. La teoria su cui si basa questo approccio mette in relazione tecniche di approssimazione di funzioni, architetture di reti neurali e metodi statistici. Sono stati sviluppati sistemi che imparano a riconoscere oggetti in scene complesse, e algoritmi che imparano a sintetizzare nuove sequenze di immagini a partire da un piccolo numero di immagini reali. Illustreremo brevemente una nuova rappresentazione delle immagini basata sulla corrispondenza tra pixel, che è la chiave di tutti questi effìcienti sistemi di apprendimento. Infine, discuteremo alcune possibili implicazioni per il funzionamento del cervello, descrivendo dati fisiologici recenti che forniscono elementi di conferma ai modelli descritti.
Introduzione
La visione è una vera e propria forma di intelligenza. Da un punto di vista computazionale, il problema della visione è uno dei più complessi nell'ambito del problema globale della comprensione della mente che, a sua volta, è uno dei maggiori problemi che oggi la scienza si trova a dover risolvere, forse il più fondamentale di tutti. Da un punto di vista biologico il sistema visivo è una delle parti più sorprendenti del cervello, come risulta anche da un dato macroscopico: alla visione è dedicata in proporzione una parte della corteccia maggiore rispetto a quella dedicata ad altri aspetti dell'intelligenza, come per esempio il linguaggio. Nella seconda metà degli anni Novanta sia la visione computerizzata (che tenta di costruire macchine capaci di vedere) sia la neuroscienza della visione (che mira alla comprensione del funzionamento del sistema visivo) hanno subito nei loro approcci profonde modifiche. Piuttosto che tentare di comprendere tutti i dettagli della corteccia visiva, la neuroscienza della visione ha cominciato a focalizzarsi sui meccanismi che consentono alla corteccia di adattare i suoi 'circuiti' per imparare un nuovo compito. Invece di costruire una macchina cablata o un programma per risolvere un compito visivo specifico, gli studi di visione computerizzata stanno cercando di sviluppare sistemi che possano essere addestrati con degli esempi su un certo numero di compiti visivi. L'apprendimento sta diventando il problema centrale nel tentativo di comprendere l'intelligenza e di sviluppare macchine intelligenti. Dopo tutto, stiamo iniziando solo ora a renderci conto di quanto siano 'intelligenti' gli animali inferiori, e di come siano complessi i problemi che i nostri sensi risolvono abitualmente. Non è sorprendente che la nuova frontiera della visione computerizzata sia l'apprendimento. La sfida è lo sviluppo di macchine che imparino a svolgere compiti come l'analisi visiva e il riconoscimento visivo a partire da un insieme di esempi di addestramento. Ciò riflette una tendenza globale: costruire sistemi intelligenti che non abbiano bisogno di essere completamente e faticosamente programmati per compiti specifici. In altre parole, i calcolatori dovranno essere molto più simili al nostro cervello: dovranno imparare a vedere piuttosto che essere programmati per vedere. Così, l'apprendimento è anche la frontiera dove la visione computerizzata si incontrerà con la scienza della visione biologica. l sistemi visivi biologici sono più efficienti e flessibili di quelli per la visione artificiale, principalmente perché si adattano continuamente e imparano dall'esperienza. Le questioni in gioco sono sia applicative che scientifiche. Dal punto di vista delle applicazioni, la possibilità di costruire sistemi per la visione che si possano adattare a diversi compiti può avere un enorme impatto in numerosi settori, come l'analisi automatica, l'elaborazione delle immagini, l'editing video, la realtà virtuale, le banche dati multimediali, la grafica computerizzata e le interfacce uomo-macchina. Dal punto di vista biologico, la nostra comprensione attuale del funzionamento della corteccia potrebbe cambiare radicalmente se risultasse che l'adattamento e l'apprendimento giocano un ruolo essenziale. Anziché trovarsi di fronte a strutture corticali cabIate, come quelle semplificate dei lavori classici (per esempio quelli di D.H. Hubel e T.N. Wiesel), potremmo rivelare una plasticità neuronale importante, con proprietà neuronali e di connettività che cambiano in funzione dell'esperienza visiva su scale di tempo di pochi minuti o secondi. Diversi compiti visivi e grafici si possono formulare in termini dell'addestramento di una 'scatola che impara' con insiemi appropriati di esempi, cioè di coppie input-output, e la teoria su cui si fonda il metodo fa uso di tecniche di approssimazione di funzioni, architetture di reti neurali e metodi statistici. Sono stati sviluppati sistemi che imparano a riconoscere oggetti, in particolare facce, sistemi che imparano a trovare oggetti specifici in scene complesse, programmi che imparano a disegnare personaggi dei cartoni animati a partire da quelli prodotti da un disegnatore, algoritmi che imparano a sintetizzare nuove sequenze di immagini da un piccolo numero di immagini reali e dai quali ci si aspetta di poter ottenere compressioni estremamente elevate in applicazioni come le videoconferenze e la videoposta elettronica. Di pari importanza è il fatto che queste ricerche hanno conseguenze di vasta portata per la comprensione del funzionamento del cervello umano e animale nell'elaborazione visiva.
Compiti visivi e 'scatole che imparano'
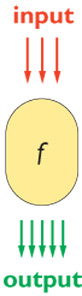
Con l'espressione apprendimento supervisionato (o apprendimento da esempi) ci si riferisce a un sistema che, anziché essere programmato, viene addestrato attraverso un insieme di esempi (insieme di addestramento). L'addestramento si può quindi considerare basato sull'utilizzo di coppie inputoutput come mostrato in figura (fig. 1). Lo scopo dell'addestramento è che, nel suo funzionamento, il sistema addestrato (la nostra 'scatola che impara') fornisca un output corretto per un nuovo input non contenuto nell'insieme di addestramento. Nei compiti di visione automatica l'input alla 'scatola che impara' descritta nella figura 1 è un'immagine digitalizzata, o una sequenza di immagini, e l'output è un insieme di parametri stimati dall 'immagine. Per esempio, nel sistema ALVIN, sviluppato da D. Pomerlau per svolgere il compito di guidare un veicolo, l'input è una serie di immagini della strada e l'output è l'angolo di sterzata. Questi compiti di visione automatica sono tipicamente compiti di analisi delle immagml.
Nell'approccio al problema dell' analisi di immagini basato sull' apprendimento da esempi, si addestra un modulo di apprendimento usando un insieme di esempi, come spiegheremo più avanti, per associare le immagini di input ai parametri di output. Tra i parametri di output vi può essere ciò che si chiama un'etichetta che identifica l'oggetto nell'immagine, così come altri parametri associati con esso, quali la sua posizione rispetto all'osservatore, la sua struttura tridimensionale o le sue proprietà materiali (fig. 2). Informazioni di questo tipo sono essenziali, per esempio, per afferrare un oggetto o per interpretare una scena. Dopo l'addestramento con un insieme di immagini e i corrispondenti parametri, ci si attende che la rete generalizzi in modo corretto, che classifichi cioè nuove prospettive dello stesso oggetto o di oggetti simili, riconosca un altro oggetto della stessa classe o sappia valutare i parametri che stimano la sua posizione o la sua espressione (nel caso di facce).
Il problema di analisi consistente nella stima delle 'etichette' dell'oggetto e degli altri parametri, è il problema della visione. Esso rappresenta il problema inverso di quello consueto dell'ottica classica e della moderna grafica computerizzata, che consiste nel sintetizzare immagini che corrispondano a superfici tridimensionali date, in funzione di parametri come la direzione di illuminazione, la posizione della macchina fotografica e le proprietà costitutive dell'oggetto. Nel nostro schema di apprendimento da esempi, risulta naturale usare un modulo di apprendimento per associare parametri di input a immagini in output (fig. 3). Questo modulo, quindi, potrà sintetizzare nuove immagini. La grafica computerizzata tridimensionale simula la fisica del mondo costruendo modelli tridimensionali, inserendo li in uno spazio tridimensionale, simulando le loro proprietà fisiche e infine producendone il rendering (visualizzazione realistica): in breve, simulando l'ottica geometrica. Il paradigma dell'apprendimento da esempi suggerisce un approccio abbastanza diverso e non convenzionale: prendere diverse immagini reali di un oggetto tridimensionale e creare nuove immagini generalizzando quelle date, sotto il controllo di parametri appropriati di posizione ed espressione, assegnati dall'utente durante la fase di addestramento.
Naturalmente questo approccio basato sulle prospettive all'analisi delle immagini (terreno tradizionale della visione computerizzata) e alla sintesi delle immagini (terreno della grafica computerizzata), non si può considerare sostitutivo degli approcci più tradizionali. L'approccio alla visione e alla grafica basato sull'apprendimento da esempi può comunque rappresentare una scorciatoia efficace per risolvere diversi problemi e, inoltre, possiede una notevole attrattiva in relazione alla descrizione del possibile meccanismo di funzionamento dei sistemi visivi biologici.
Teoria e applicazioni
Il modulo di apprendimento fondamentale usato nel nostro approccio si può definire una rete neurale, sebbene affondi le sue vere radici nella teoria dell' approssimazione di funzioni multivariate, cioè nella teoria dell'approssimazione di una funzione di molte variabili a partire da alcuni suoi valori.
Il modulo di apprendimento
Possiamo considerare l'apprendimento supervisionato come un problema di regressione che consiste nell'interpolare o approssimare una funzione multivariata a partire da pochi dati. In questo caso, i dati sono gli esempi. Nel caso dell'analisi di immagini della figura 2, i dati sono le coppie immagine-valori dei parametri. Generalizzare vuoI dire stimare il valore della funzione in punti dello spazio degli input per i quali non ci sono dati disponibili.
Una volta che il problema dell'apprendimento da esempi è stato formulato come un problema di approssimazione di funzioni, un approccio matematico moderno alla sua soluzione è costituito dalla regolarizzazione. La regolarizzazione impone dei vincoli di regolarità sullo spazio delle funzioni approssimanti. L'approccio della regolarizzazione funzionale si può anche formulare in un contesto statistico di tipo bayesiano.
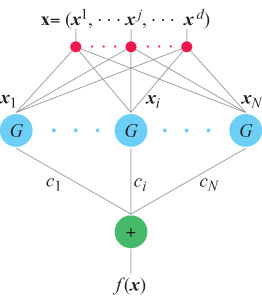
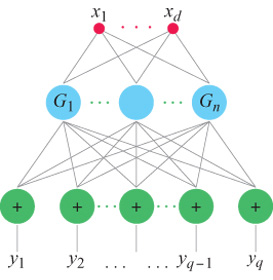
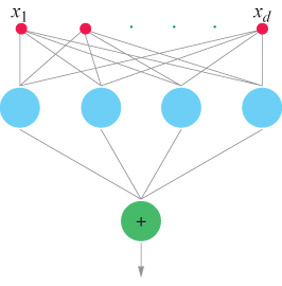
Un risultato cruciale, ottenuto per la prima volta nel contesto dell'apprendimento da T. Poggio e F. Girosi, è che, sotto condizioni abbastanza generali, la soluzione del problema di approssimazione formulato in termini di regolarizzazione si può esprimere come combinazione lineare di un insieme di funzioni di base, centrate sui punti rappresentativi dei dati e dipendenti dagli input x. Come hanno osservato Poggio e Girosi (1990a; 1990b) e, per il caso particolare delle funzioni di base radiali (RBF, Radiai Basis Function), D.S. Broomhead e D. Lowe (1988), si può sempre riformulare questa soluzione in termini di una rete con uno strato nascosto contenente un numero di unità pari al numero di esempi nell'insieme di addestramento (fig. 4). Si può considerare una rete semplicemente come una rappresentazione grafica di un'equazione che descrive il modo in cui i valori di output sono generati a partire da quelli di input. Lo strato nascosto è semplicemente lo strato centrale della rete, tra gli strati di input e di output. Le unità dello strato nascosto corrispondono alle funzioni di base, e si possono considerare come elaboratori che svolgono un'operazione specifica. l coefficienti Ci, che rappresentano i pesi delle connessioni con l'output vengono 'imparati' minimizzando l'errore sull'insieme di addestramento. Chiameremo queste reti reti di regolarizzazione (RN, Regularization Networks). Si può facilmente generalizzare il caso di un output scalare fin qui descritto al caso di molti output, cioè al caso dell' approssimazione di campi vettoriali (fig. 5).
Per comprendere ciò che fanno queste reti, consideriamo il caso particolare in cui le funzioni di base sono funzioni gaussiane (G) radiali. In questo caso, le reti RBF sono costituite da unità ognuna delle quali si modella su uno degli esempi attraverso una curva di attivazione a forma di campana. Ogni unità calcola la distanza IIx - Xi Il del vettore di ingresso X dal suo centro Xi (cioè la 'diversità' tra l'input e l'esempio immagazzinato in quella unità), e applica quindi la funzione G al valore della distanza, calcola cioè G I X - Xi I. Si noti che nel caso limite in cui G è una gaussiana molto stretta, la rete diventa una tabella di ricerca i cui elementi sono i centri delle unità.
Un compito di visione computerizzata: stimare posa ed espressione
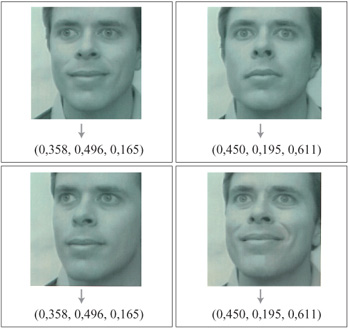
Per addestrare una rete con apprendimento a stimare pose ed espressioni arbitrarie, per esempio di una persona, bisogna 'etichettare' un insieme di immagini di esempio della persona stessa nello spazio delle pose e delle espressioni (fig. 6). L'input della rete, cioè la nostra rappresentazione dell'immagine, non è l'immagine stessa, ma il vettore di forma a essa associato, che viene calcolato a partire dall'immagine. Si può pensare il vettore di forma come una rappresentazione delle posizioni (x, y) delle caratteristiche facciali. Nella figura 6, l'output è costituito da tre parametri che rappresentano il grado di sorriso e di rotazione della faccia (destra-sinistra e alto-basso). Si addestra una rete come quella in figura 5 (con 8 unità nascoste) usando le 8 immagini di esempio mostrate nella figura 6. Dopo l'addestramento la rete è capace di generalizzare a nuove immagini della stessa persona, stimando i parametri di rotazione e di sorriso associati. In figura (fig. 7) sono mostrati degli esempi di immagini di input e dei loro parametri stimati.
Un compito di grafica computerizzata: sintetizzare nuove immagini
D. Beymer e collaboratori (1993) hanno usato una tecnica basata su esempi per generare immagini di corpi tridimensionali non rigidi in funzione di certi parametri di input. Il compito di sintetizzare immagini (un compito di grafica computerizzata) è il problema inverso dell'analisi delle immagini sopra discusso.
Daremo ora una dimostrazione di questa tecnica, applicata a immagini reali di facce con parametri di input quali la posa e l'espressione facciale, anche se si possono usare parametri diversi. La prima dimostrazione fu data da Poggio e R. Brunelli (1992), e in particolare da S. Librande (1992), insegnando a un computer a tracciare, sotto il controllo dell'utente, delle linee nuove a partire da un piccolo numero di disegni. Il primo passo consiste nel trovare delle corrispondenze tra pixel (i più piccoli elementi costitutivi dell'immagine) per calcolare la rappresentazione in termini di vettore di forma di ognuna delle immagini di esempio. Questo processo di riduzione a forma vettoriale viene sviluppato automaticamente usando i cosiddetti algoritmi di flusso ottico, che forniscono per ogni pixel di un'immagine il suo scostamento (x, y) rispetto a un'altra immagine, scelta come immagine di riferimento per il caso in analisi. Dopo aver posto in forma vettoriale le immagini di esempio può aver luogo la fase di apprendimento. Per addestrare la rete per la sintesi, l'utente associa ogni immagine di esempio a una posizione appropriata nello spazio dei parametri, utilizza una rete di regolarizzazione per stabilire la corrispondenza tra input e output e visualizza l'immagine in forma vettoriale come immagine a colori o a livelli di grigio.
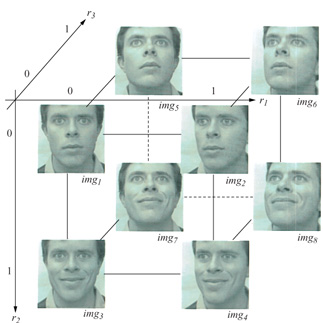
Dopo la fase di apprendimento la rete addestrata è in grado di sintetizzare una nuova immagine per qualsiasi ragionevole vettore di posizione in input. La rete per la sintesi ha in genere pochi input (i parametri di posizione) e molti output, ognuno dei quali corrisponde a un attributo di forma o aspetto superficiale relativo a un pixel dell'immagine. Nella figura 6 mostriamo otto esempi di una faccia e i parametri di posa associati in uno spazio tridimensionale di input. In figura (fig. 8) sono mostrate alcune teme di parametri (r1, r2, r3) e le immagini a colori prodotte dal modulo di sintesi. La sintesi delle immagini compiuta dalla rete è equivalente a un'interpolazione, o un'approssimazione, multi dimensionale; in questo caso si tratta di una forma di morphing multidimensionale, vale a dire di un processo che consente di visualizzare una trasformazione di un'immagine in un'altra, generando una serie di immagini intermedie che danno la sensazione di una transizione continua tra l'immagine di partenza e quella di arrivo.
La compressione di immagini nella videoposta elettronica
Le reti per l'analisi e la sintesi di immagini si possono usare in modo indipendente per molte diverse applicazioni. Le reti per l'analisi si possono considerare come interfacce uomo-macchina addestrabili. Un' applicazione interessante, adattabile a specifiche esigenze, consiste nel riconoscimento di gesti umani. Le reti per la sintesi, d'altra parte, costituiscono un modo alternativo per produrre grafica e animazione (per esempio per generare gestualità).
Un'applicazione particolarmente interessante delle reti di analisi e di sintesi è costituita dalla videoposta elettronica e dalla videoconferenza con ampiezza di banda molto piccola (fig. 9). Una rete per analisi, addestrata con poche immagini del particolare utente, analizza le nuove immagini in termini dei parametri di posa ed espressione. Questi parametri vengono inviati elettronicamente per ogni fotogramma e vengono utilizzati nella postazione ricevente da una rete per la sintesi precedentemente addestrata su immagini di esempio dello stesso utente, a partire dalle quali vengono sintetizzate le nuove immagini appropriate. Questo approccio basato su esempi può ottenere, in linea di principio, livelli di compressione molto alti. L'esempio che mostriamo in figura 9 necessita probabilmente di circa 3 byte per fotogramma per il suo funzionamento. Abbiamo anche sperimentato ulteriori parametri di controllo, come il grado di apertura o chiusura della bocca e degli occhi, la direzione dello sguardo e così via. Una stima realistica prevede circa 10 parametri da stimare e inviare, a cui ne vanno aggiunti pochi altri che defrniscono le trasformazioni dell'immagine nel piano, per un totale di circa 10÷20 byte per fotogramma. Naturalmente, l'effettiva praticabilità di questo schema rimane una questione aperta, così come il modo di combinarlo con altri metodi standard per la compressione di immagini stati che o in movimento.
Riconoscimento di facce e oggetti
Un'ovvia applicazione del nostro schema di apprendimento da esempi è costituita dal riconoscimento di oggetti. L'idea è semplicemente di addestrare il modulo di apprendimento con poche immagini dell' oggetto da riconoscere e con l"etichetta' corrispondente (come output). Questo è un caso particolare del problema di analisi della figura 2. Una classe interessante di oggetti da riconoscere è quella delle facce. Per diversi anni alcuni gruppi che si occupano di visione computerizzata hanno usato questo paradigma per sviluppare e far funzionare con successo sistemi per il riconoscimento delle facce. Nel nostro gruppo abbiamo sviluppato quattro diversi sistemi per il riconoscimento delle facce basati su diverse prospettive di esempio delle immagini di ogm persona.
Un sistema per il riconoscimento frontale delle facce. - Seguendo il lavoro svolto da R.I. Baron (1981) sul riconoscimento delle facce, Brunelli e Poggio (1993) hanno usato una strategia basata su fisionomie modello per riconoscere prospettive frontali di facce. A partire da una prospettiva di esempio, le facce vengono rappresentate usando fisionomie di riferimento per occhi, naso, bocca e per l'intera faccia. Per confrontare le immagini di input con le fisionomie di riferimento si usa la correlazione. Prima di ciò, le immagini di input si raccordano con le prospettive modello allineando gli occhi, il che normalizza gli input rispetto agli effetti di traslazione, scala e rotazione del piano dell'immagine. Questo passaggio fornisce una corrispondenza approssimata. Gli occhi vengono localizzati in una fase iniziale separata, utilizzando immagini di riferimento per gli occhi. La prestazione nel riconoscimento, su una base di dati molto piccola (47 persone, con 4 prospettive per persona), è stata del 100%, usando due prospettive come modello e le altre due per il test.
Un sistema per il riconoscimento delle facce basato su PC. - Usando un algoritmo molto simile, J.M. Gilbert e W. Yang (1993) hanno sviluppato un sistema veloce per il riconoscimento delle facce basato sull'uso di personal computer, che utilizzano un chip VLSI (Very Large Scale Integrated, integrato su larghissima scala) - dotato cioè di un livello molto alto di miniaturizzazione e conseguente alta densità di componenti integrati - specificamente progettato allo scopo di effettuare misurazioni veloci di somiglianza. Questo chip dedicato al calcolo della correlazione effettua un passo di calcolo della correlazione in termini di differenze assolute in 0,9 ms, e impiega solo 0,3 s per completare un insieme di 173 immagini modello. Una realizzazione su un PC 486, che utilizza questo chip in un'apposita scheda acceleratrice, ha impiegato circa 2 s dall'acquisizione al riconoscimento delle facce, con una percentuale di riconoscimento corretto superiore al 93%.
Un sistema per il riconoscimento delle facce invariante rispetto alle posizioni. - Mentre il sistema precedente funziona solo con prospettive frontali delle facce, Beymer (1994) ha sviluppato un dispositivo per il riconoscimento di facce invariante rispetto alla posizione, che usa 15 prospettive per persona, comprendenti diverse rotazioni fuori dal piano dell'immagine. Cinque diverse rotazioni da sinistra a destra e tre rotazioni dall'alto in basso sono mostrate in figura (fig. 10). Analogamente ai due sistemi precedenti, le traslazioni, le trasformazioni di scala e le rotazioni sul piano dell'immagine sono eliminate rilevando innanzitutto gli elementi corrispondenti agli occhi e al naso, e usandoli poi per raccordare le immagini di input con le prospettive modello. La fase di localizzazione degli elementi corrispondenti agli occhi e al naso utilizza un insieme di immagini modello di occhi e naso che comprende varie pose e fisionomie 'tipiche'. Una nuova immagine di input viene quindi confrontata con tutte le prospettive modello di tutte le persone, selezionando la migliore corrispondenza. La fase di confronto consiste in un raccordo geometrico basato sugli elementi corrispondenti agli occhi e al naso, seguito dal calcolo della correlazione utilizzando sagome modello di occhi, naso e bocca. La percentuale di riconoscimento corretto, su una piccola base di dati di 620 immagini (62 persone, 10 prospettive di test per persona) è stata del 98%. Le immagini di test erano costituite da un insieme di rotazioni delle immagini, sia sul piano dell'immagine che fuori di esso.
Verifica delle facce per l'autenticazione dell'utente nel collegamento a un calcolatore. - Il quarto sistema che discuteremo si occupa della verifica dell'identità di una persona, invece che dell'identificazione di una persona in una banca dati. In altre parole, esso verifica semplicemente se una nuova immagine rappresenta o no una certa faccia. Questo sistema (Romano et al., 1996) funziona in tempo reale su una stazione di lavoro basata su una workstation UNIX associata a una telecamera. Esso può rimpiazzare l'uso di una parola d'accesso nel collegamento a un calcolatore. Dopo che l'utente ha inserito il proprio nome identificativo, gli viene chiesto di guardare la telecamera anziché di inserire una parola di accesso. Il sistema è in grado di accettare in modo affidabile l'utente giusto e di rifiutare un utente che cerchi di collegarsi usando il nome di qualcun altro.
Rilevamento di oggetti: ricerca di persone. - Ancor più difficile del riconoscimento di un oggetto specifico isolato è il rilevamento di un oggetto di una certa classe in un'immagine complessa. Per esempio, è più semplice riconoscere una specifica faccia che non notare se in un'immagine complessa c'è o meno una faccia, e localizzarla. Un sistema sviluppato da K-K Sung e da Poggio (1994) ha mostrato di poter essere addestrato con successo a trovare facce, occhi e altri oggetti.
In figura (fig. 11) è mostrato un esempio delle prestazioni del sistema dopo che esso è stato addestrato a localizzare immagini frontali di facce. Come sarà spiegato più avanti, l'alto numero di esempi virtuali usati per l'addestramento è essenziale: sono necessari 3000 esempi virtuali di immagini di facce, oltre a 1000 esempi reali e a 50.000 esempi negativi di oggetti che non sono facce. B. Moghaddam e A. Pentland (1995) hanno realizzato un sistema molto simile. Più recentemente, H. Rowley, S. Baluja e T. Kanade (1995) hanno fatto funzionare un sistema con prestazioni di rilevamento simili ma più veloce.
Il flagello della dimensionalità e le prospettive virtuali. - Il problema centrale nell'uso pratico della maggior parte degli schemi di apprendimento basato su esempi è spesso la dimensione insufficiente dell'insieme di addestramento. Poiché i vettori di input hanno in genere una dimensionalità alta, cioè un alto numero di componenti (come il numero di pixel di un'immagine), il numero necessario di esempi di addestramento è molto elevato. Questo è ciò che potrebbe chiamarsi 'flagello della dimensionalità'. Un'idea interessante consiste nello sfruttare l'informazione nota a priori per generare esempi virtuali ulteriori a partire da un insieme piccolo di immagini di esempio reali. Per esempio, Poggio e T. Vetter (1992) hanno dimostrato che la conoscenza a priori delle proprietà di simmetria di una classe di oggetti tridimensionali consente la sintesi di ulteriori esempi. Le facce hanno approssimativamente una simmetria bilaterale, e quindi da un'immagine se ne può creare una nuova con una trasformazione speculare. In effetti ci sono prove di tipo psicofisico in favore dell 'utilizzo di questo approccio da parte del sistema visivo biologico. Più in generale, abbiamo proposto l'apprendimento delle trasformazioni tipiche per una certa classe di oggetti a partire da esempi tratti da oggetti della stessa classe.
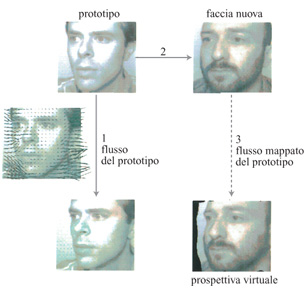
In figura (fig.12) è illustrato un modo per generare delle prospettive virtuali, applicando la trasformazione appresa da un prototipo della stessa classe. Nella figura successiva (fig. 13) si mostra il risultato dell'applicazione di questa tecnica per produrre diverse prospettive virtuali ruotate della stessa faccia a partire da una sola immagine reale. Le prospettive virtuali, usate come prospettive modello nel dispositivo per il riconoscimento invariante rispetto alle pose sviluppato da Beymer che abbiamo descritto prima, consentono di ottenere percentuali di riconoscimento corretto confrontabili con le prestazioni umane nella 'stessa' situazione (cioè sulla base di una sola prospettiva di esempio reale).
Rappresentazione delle immagini
Tutti gli approcci all'analisi e alla sintesi delle immagini che abbiamo descritto precedentemente poggiano su una condizione implicita essenziale: quella che le immagini devono essere rappresentate come vettori. Questa non è una richiesta banale: infatti i vettori, in quanto elementi di uno spazio vettoriale, sono oggetti che possono essere combinati linearmente producendo come risultato vettori appartenenti allo stesso spazio. In altre parole, nello spazio vettoriale devono essere definite, e avere senso, operazioni come per esempio l'addizione. Le immagini, d'altra parte, sono solo delle griglie di pixel, e non possiedono la struttura di uno spazio vettoriale. In particolare, l'addizione di due immagini a caso produrrà in generale una struttura senza senso.
I vettori di forma che abbiamo introdotto in precedenza rappresentano un modo per associare un vettore a ogni elemento di un insieme di immagini simili tra loro. Come abbiamo già detto, l'approccio alla vettorializzazione delle immagini richiede che si stabilisca una corrispondenza tra i pixel di una certa immagine e quelli di un'immagine di riferimento. In questo modo, un'immagine viene rappresentata come un vettore di forma delle posizioni (x, y) di elementi (o di pixel) 'etichettati', e un vettore relativo all'aspetto superficiale che contiene il colore di ogni elemento (o pixel). Questa corrispondenza determina una struttura di spazio vettoriale lineare in cui ogni componente ha un significato ben definito.
Come funziona il cervello
Come è dimostrato dalle varie realizzazioni descritte in precedenza, l'approccio basato sugli esempi risulta efficace in problemi concreti di riconoscimento di oggetti e di analisi e sintesi di immagini. Non è quindi strano chiedersi se il nostro cervello possa utilizzare un approccio simile. Le reti che apprendono a partire da esempi possiedono un'attrattiva ovvia, dato ciò che sappiamo dei meccanismi neuronali. A partire dalla metà degli anni Novanta, esperimenti psicofisici hanno in effetti fornito un supporto agli schemi basati su esempi e su prospettive. Recentemente, alcuni esperimenti fisiologici hanno fatto intravedere il modo in cui la corteccia inferotemporale potrebbe rappresentare gli oggetti per il loro riconoscimento. I risultati sperimentali sembrano essere in sorprendente accordo con i nostri modelli basati sulle prospettive.
In figura (fig. 14) è mostrato il nostro modulo elementare per l'analisi delle immagini descritto in precedenza, caso particolare del riconoscimento di oggetti. Il sistema di riconoscimento realizza lo stesso approccio basato sulle prospettive, sebbene non si basi esattamente sulla stessa rete. La classificazione o l'identificazione di uno stimolo visivo viene realizzata da una rete di unità elementari. Ogni unità è sintonizzata su una prospettiva particolare dell'oggetto, per esempio mediante l'adattamento agli elementi visibili in quella prospettiva. Dal punto di vista algoritmico questo si ottiene semplicemente immagazzinando ogni presentazione di quella prospettiva. Non si sa ancora come ciò si possa ottenere nei sistemi biologici, ma è quasi certo che vi giochi un ruolo un cambiamento delle connessioni sinaptiche dei neuroni adattati. Noi ci riferiamo alla prospettiva ottimale come al centro dell 'unità. Questo si può considerare come un modello di riferimento (o un insieme di modelli di riferimento) con cui vengono confrontati gli input. L'unità viene attivata al massimo quando lo stimolo corrisponde esattamente al suo modello di riferimento, ma risponde anche quando lo stimolo è solo simile a esso. La somma pesata delle attività di tutte le unità rappresenta l'output della rete.
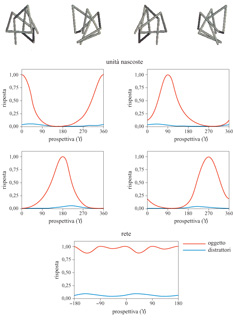
Si consideri il modo in cui la rete 'impara' a riconoscere le prospettive dell'oggetto mostrato in figura (fig. 15). In questo esempio gli input della rete sono le posizioni (x, y) dei vertici dell'oggetto filiforme nell'immagine. Vengono usate quattro prospettive di addestramento; dopo l'addestramento, la rete è costituita da quattro unità, ognuna delle quali è sintonizzata su una delle quattro prospettive. I pesi delle connessioni con le uscite vengono determinati minimizzando gli errori dovuti a un'errata classificazione delle quattro prospettive e usando dei distrattori, cioè degli esempi negativi (prospettive di altri oggetti simili).
La figura 15 mostra l'adattamento delle quattro unità a immagini dell'oggetto 'giusto'. Per ogni unità, la curva di adattamento è ampia e centrata sul centro dell 'unità, cioè sulla prospettiva di addestramento. Sorprendentemente, l'adattamento è anche molto selettivo, come indicato dalla risposta media di ognuna delle unità a 300 distrattori simili. Anche la massima risposta a uno di questi risulta sempre minore della risposta alla prospettiva ottimale. L'output della rete, essendo una combinazione lineare delle attività delle quattro unità, è essenzialmente invariante rispetto alle prospettive, ma comunque molto selettivo. L'attività delle unità misura la somiglianza globale del vettore di input al centro dell'unità stessa: per l'adattamento ottimale tutti gli elementi devono essere vicini al valore ottimale. Anche la mancata corrispondenza di una sola componente del modello può azzerare l'attività dell'unità. La semplice regola espressa da un'unità sintonizzata su una prospettiva è così la congiunzione di un insieme di predicati, uno per ogni elemento di input, che misurano la corrispondenza con il modello.
Naturalmente, le coordinate degli angoli utilizzati dalla 'rete giocattolo' che abbiamo descritto non possono essere caratteristiche biologicamente plausibili. Bricolo, N.K. Logothetis e Poggio hanno effettuato delle simulazioni di una rete più plausibile dal punto di vista biologico. lnnanzitutto un'immagine viene filtrata con un 'banco' di filtri direzionali con varie orientazioni e scale, simili ai neuroni corticali. Successivamente, in ogni punto del campo visivo un modulo di apprendimento confronta il vettore dei valori dei filtri con un centro, che rappresenta l'uscita dei filtri in corrispondenza a un pezzo dell'oggetto. È stato verificato che due centri, ognuno dei quali sintonizzato su un pezzo differente dell'immagine, sono sufficienti per il riconoscimento. Nonostante la sua grossolana ed eccessiva semplificazione, il nostro modello riesce a cogliere alcuni dei risultati psicofisici e fisiologici fondamentali, in particolare l'esistenza di unità sintonizzate sulle prospettive e di altre unità invarianti rispetto a esse, e la forma dei campi di riconoscimento misurati.
Gli esperimenti di fisiologia di Logothetis e J. Pauls (Logothetis e Pauls, 1995; Logothetis et al., 1995) sembrano fornire un supporto al nostro modello. Due scimmie sono state addestrate a riconoscere degli oggetti visualizzati da un calcolatore indipendentemente dalla loro posizione od orientamento. All'inizio si è consentito alle scimmie di esaminare un oggetto presentato da un certo punto di vista, e successivamente si è verificata la loro capacità di riconoscere lo stesso oggetto ruotato da 10° a 180° rispetto all'asse verticale. In alcuni esperimenti si è anche verificata la capacità degli animali di riconoscere prospettive dell'oggetto ruotato rispetto sia all'asse verticale che a quello orizzontale; in altri ancora, rispetto a tutti e tre gli assi. Le immagini venivano presentate in sequenza, con le varie prospettive dell'oggetto da riconoscere mescolate a un gran numero di altri oggetti (distrattori). A un pannello frontale della sedia su cui stava la scimmia erano assicurate due leve, e l'animale veniva ricompensato ogni volta che premeva la leva destra in risposta alla presentazione dell'oggetto da riconoscere. La scimmia doveva invece premere la leva sinistra alla presentazione di un distrattore. Le risposte giuste venivano premiate con succo di frutta.
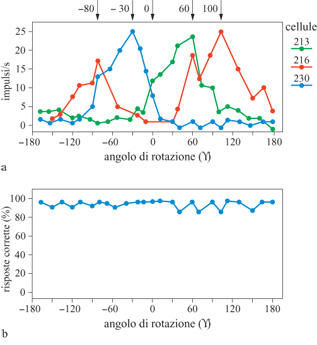
Durante lo svolgimento del compito di riconoscimento, usando dei microelettrodi si è registrata l'attività di un totale di 970 neuroni nelle due scimmie. Si è trovato che un numero significativo di neuroni mostrava una selettività notevole rispetto alle singole prospettive degli oggetti filiformi che la scimmia era stata addestrata a riconoscere. l neuroni che si adattavano alle prospettive dell'oggetto da riconoscere rispondevano vivacemente (fino a 50÷100 impulsi al secondo) alle prospettive che erano vicine a quelle di addestramento. Le prospettive generate con una rotazione di 36° in una delle direzioni hanno suscitato il 41 % della risposta massima, mentre prospettive a 50° rispetto a quelle di addestramento non hanno stimolato il neurone. Ci aspettavamo di trovare dei neuroni adattati a diverse prospettive dell'oggetto rispetto al quale la scimmia era stata addestrata. In effetti, per tre oggetti si è trovato più di un neurone adattato a prospettive differenti dello stesso oggetto. In figura (fig. 16) sono mostrate le risposte di tre unità che hanno risposto selettivamente a quattro prospettive diverse di un oggetto filiforme. All'animale era stato mostrato ripetutamente questo oggetto, e il suo comportamento ha mostrato un corretto riconoscimento del 95% delle prospettive verificate, come si può vedere dal grafico nella parte inferiore della figura. È interessante il fatto che uno dei tre neuroni risultava sintonizzato su una delle prospettive e sulla sua immagine speculare, il che è coerente con gli altri lavori teorici e psicofisici che abbiamo menzionato sull'elaborazione delle immagini simmetriche. La figura 16 è sorprendentemente simile alla figura 15, che mostra la risposta prevista per le unità nascoste sintonizzate sulle prospettive del modello in figura 14.
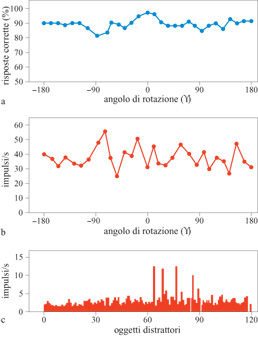
Una piccola percentuale delle cellule (8 su 773) rispondeva a oggetti filiformi presentati da qualsiasi punto di vista, mostrando caratteristiche di risposta invarianti rispetto alle prospettive, approssimativamente simili a quelle dell'unità di output del modello in figura l. Un esempio di neurone invariante rispetto alle prospettive di questo genere è descritto in figura (fig. 17). Il grafico in alto mostra le prestazioni della scimmia nel compito di riconoscimento, e il grafico al centro mostra l'emissione media di impulsi da parte del neurone. La cellula emette impulsi con una frequenza di circa 40 Hz per tutte le prospettive dell'oggetto da riconoscere. Il grafico in basso mostra la risposta della stessa cellula a 120 distrattori. L'attività è risultata uniformemente bassa per tutti gli oggetti presentati come distrattori, il che mostra che il segnale prodotto da questo neurone può servire per discriminare i vari oggetti, ed è correlato con la risposta comportamentale. Questo neurone, quindi, sembra comportarsi come l'uscita del modello in figura 14. Inoltre, crediamo che i nostri risultati riflettano una plasticità neuronale nella corteccia inferotemporale dipendente dall'esperienza, e questo costituisce uno degli aspetti essenziali dell'apprendimento. Ulteriori esperimenti serviranno ad approfondire questa idea, con lo scopo di determinare più precisamente la natura degli elementi che costituiscono gli input dei neuroni sintonizzati sulle prospettive, ovvero di comprendere meglio il 'vocabolario' che il cervello estrae dal mondo visivo.
Bibliografia citata
BARON, R.J. (1981) Mechanisms of human facial recognition. Int. J. Man-Mach. Stud., 15, 137-178.
BEYMER, D. (1994) Face recognition under varying pose. Proceedings IEEE conference on computer vision and pattern recognition, Seattle, 756-761.
BEYMER, D., SHASHUA, A., POGGIO, T. (1993) Example based image analysis and synthesis. A.I. Memo No. 1431, Artificial Intelligence Laboratory, MIT.
BROOMHEAD, D.S., LOWE, D. (1988) Multivariable functional interpolation and adaptive networks. Complex Systems, 2, 321-355.
BRUNELLI, R., POGGIO, T. (1993) Face recognition: features versus templates. IEEE transactions on pattern analysis and machine intelligence, 15, 1042-1052.
GILBERT, J.M., YANG, W. (1993) A real-time face recognition system using custom VLSI hardware. IEEE workshop on computer architectures for machine perception, 12, 58-66.
LIBRANDE, S. (1992) Example-based character drawing. Master's thesis, M.S., Media arts and science section, School of architecture and planning, MIT, 9.
LOGOTHETIS, N.K., PAULS, J. (1995) Psychophysical and physiological evidence for viewer-centered representations in the primate. Cereb. Cortex, 5, 270-288.
LOGOTHETIS, N.K., PAULS, J., POGGIO, T. (1995) Shape representation in the inferior temporal cortex of monkeys. Curr. Biol., 5, 552-563.
MOGHADDAM, B., PENTLAND, A. (1995) Probabilistic visuallearning for object detection. Technical report 326, MIT Media Laboratory, 6.
POGGIO, T., BRUNELLI, R. (1992) A novel approach to graphics. A.I. Memo No. 1354, Artificial intelligence laboratory, MIT.
POGGIO, T., GIROSI, F. (1990a) Regularization algorithms for learning that are equivalent to multilayer networks. Science, 247, 978-982.
POGGIO, T., GIROSI, F. (1990b) Networks for approximation and learning. Proceedings of the IEEE, 9, 78.
POGGIO, T., VETTER, T. (1992) Recognition and structure from one 2D model view: observations on prototypes, object classes and symmetries. A.I. Memo No. 1347, Artificial intelligence laboratory, MIT.
ROMANO, R., BEYMER, D., POGGIO, T. (1996) Face verification for real-time applications. In Proceedings of the image understanding workshop, San Francisco, Morgan Kaufmann.
ROWLEY, H., BALUJA, S., KANADE, T. (1995) Human face detection in visual scenes. Technical Report CMU CS-95-158R, School of computer science, Camegie Mellon University.
SUNG, K.-K., POGGIO, T. (1994) Example-based leaming for viewbased human face detection. In Proceedings of the image understanding workshop.
Bibliografia generale
EDELMAN, S., BULTHOFF, H.H. (1992) Orientation dependence in the recognition of familiar and novel views of 3D objects. Vision Res., 32, 2385-2400.
GIROSI, F., JONES, M., POGGIO, T. (1995) Regularization theory and neural networks architectures. Neural Computation, 7, 219-269.
HAYKIN, S. Neural networks, a comprehensive foundation, New York, MacMillan, 1994.
LOGOTHETIS, N.K., PAULS, J., POGGIO, T. (1994) View-dependent object recognition by monkeys. Curr. Biol., 4, 401-414.
NAYAR, S., POGGIO, T. Early visuallearning, Oxford-New York, Oxford University Press, 1996.
POGGIO, T., EDELMAN, S. (1990) A network that learns to recognize 3D objects. Nature, 343, 263-266.