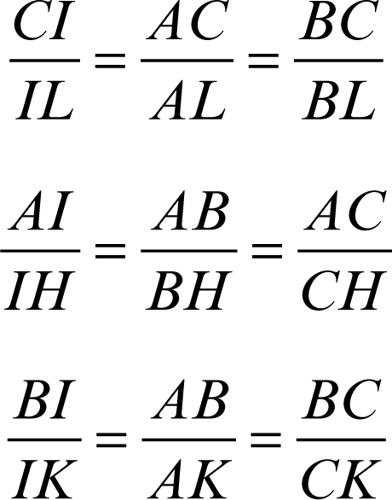incentro

incentro

incentro punto di un triangolo nel quale si intersecano le sue bisettrici. È il centro della circonferenza inscritta nel triangolo. Più in generale, l’incentro di un poligono, se esiste, è il punto equidistante da tutti i suoi lati, ottenuto come punto d’intersezione delle bisettrici dei suoi angoli al vertice e coincide con il centro della circonferenza inscritta nel poligono (donde il suo nome). Nel caso del triangolo, poiché le bisettrici concorrono sempre in un punto, l’incentro è sempre presente, mentre per un poligono esiste solo sotto particolari condizioni. Si può affermare che tutti i poligoni regolari sono dotati di incentro, in quanto in essi è iscrivibile una circonferenza. Esistono tuttavia poligoni dotati di incentro e non regolari. Nel caso dei quadrilateri, non solo il quadrato (poligono regolare) è dotato di incentro, ma anche ogni rombo, in quanto le sue bisettrici concorrono in un punto. I quadrilateri dotati di incentro sono caratterizzati dalla proprietà di avere costante la somma dei lati opposti.

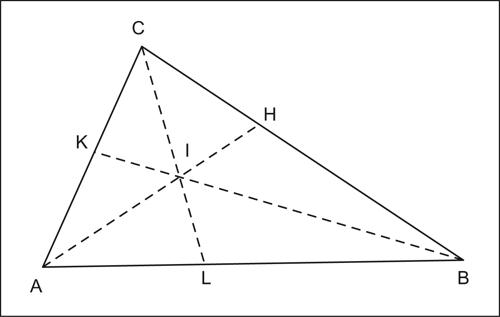
L’incentro di un triangolo divide ciascuna bisettrice in due segmenti che stanno fra loro come i lati del vertice da cui tale bisettrice ha origine stanno ai rispettivi segmenti staccati dalla stessa sul lato opposto. Con riferimento alla figura si hanno le seguenti relazioni:

Per estensione, si definisce incentro di un poliedro il punto equidistante da tutte le sue facce; tale punto esiste se e solo se esiste una sfera inscritta in esso, cioè se i piani bisettori di tutti i diedri interni si intersecano nello stesso punto. I poliedri regolari sono dotati di incentro (→ solido platonico).