induzione matematica, principio di

induzione matematica, principio di

induzione matematica, principio di procedimento che permette di inferire che una certa proprietà P vale per ogni numero naturale una volta che sia stato dimostrato che a) essa vale per 0 o per 1, intesi come elementi iniziali e che, b) se essa vale per n, allora vale anche per il successore di n, cioè per n + 1, qualunque sia n ∈ N. La proposizione a) è detta base dell’induzione mentre la b) è detta passo induttivo. Questo principio può essere metaforicamente esemplificato paragonando l’insieme dei numeri naturali alle tessere del domino disposte verticalmente su una fila: se una proprietà vale per il primo numero naturale, cioè se cade la prima tessera, e se dalla validità della proprietà per un qualsiasi numero discende la validità per il numero successivo, cioè se una tessera fa cadere la successiva, allora tutte le tessere cadono, ossia la proprietà vale per tutti i numeri naturali; su tale principio è basata la dimostrazione per induzione.

Il principio di induzione matematica, detto anche induzione completa, è incluso negli assiomi di → Peano per l’aritmetica e può essere anche formulato come segue:

«Sia I un sottoinsieme dell’insieme dei numeri naturali che soddisfa le seguenti proprietà:

• I contiene lo 0 (oppure I contiene 1) (base dell’induzione);

• se I contiene il numero n, I contiene anche n + 1 (passo induttivo), allora I coincide con l’insieme dei numeri naturali».

Il principio, come presentato precedentemente, è anche detto principio di induzione debole per distinguerlo da una sua formulazione equivalente, detta di induzione forte (o principio di induzione sul decorso dei valori) che può essere enunciata come segue:

«Una proprietà P vale per ogni numero naturale una volta che sia stato dimostrato che:

• P vale per 0 o per 1 (base dell’induzione);

• per ogni numero n, se P vale per tutti i numeri naturali minori di n, allora P vale anche per n (passo induttivo)».

Il principio di induzione forte deve il suo nome al fatto che le ipotesi richieste appaiono più restrittive rispetto a quelle del principio di induzione debole; tuttavia si può dimostrare che i due principi sono fra loro equivalenti ed entrambi sono anche equivalenti al cosiddetto principio di buon ordinamento secondo il quale «ogni sottoinsieme non vuoto dell’insieme dei numeri naturali ha un elemento minimo».

Una generalizzazione del principio di induzione matematica, fondamentale in teoria degli insiemi e in analisi, è l’induzione transfinita, che si applica a ogni insieme infinito ben ordinato. Un’ulteriore estensione è data dall’induzione transfinita di → Gentzen.

In termini più generali, il principio di induzione matematica stabilisce che una proprietà P_n, dipendente da un numero naturale n, vale per ogni numero naturale n ≥ k (dove k è tipicamente 0 oppure 1) una volta che sia stato dimostrato che:

a) P vale per k (base dell’induzione);

b) per ogni numero n ≥ k, se P vale per n, allora vale anche per il successore di n, cioè per n + 1 (passo induttivo).

Questo principio può essere euristicamente giustificato nella maniera seguente: il passo induttivo assicura che supponendo valida la proprietà per un generico numero naturale n, è possibile dimostrarla per il numero n + 1; d’altra parte, per la base dell’induzione, è noto che la proprietà P vale per il numero k, quindi la proprietà vale anche per k + 1 (passo induttivo) e allo stesso modo se vale per k + 1, grazie sempre al passo induttivo, vale anche per k + 2 e allo stesso modo vale anche per k + 3, e così via. Il principio di induzione rende quindi rigorosa l’idea intuitiva espressa dalla dicitura «e così via». Su tale principio è basata la dimostrazione per induzione illustrata dal seguente esempio. Si vuole dimostrare, utilizzando il principio di induzione, l’enunciato: «la somma delle ampiezze degli angoli interni di un poligono avente k + 2 lati è uguale a k angoli piatti». Per dimostrarlo occorre innanzitutto dimostrare la base dell’induzione per k = 1 (k = 0 non può essere accettato perché non esiste un poligono con 0 + 2 = 2 lati):

a) la somma degli angoli interni di un poligono avente 1 + 2 = 3 lati (cioè di un triangolo) è uguale a un angolo piatto, come è noto dalla geometria euclidea;

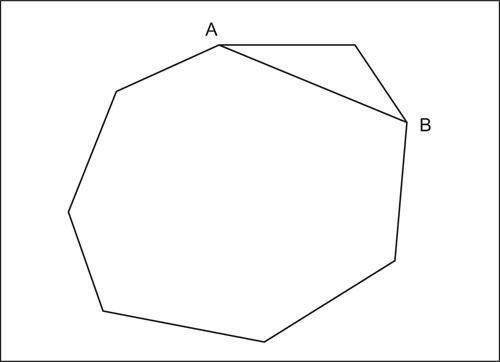
b) a questo punto è necessario dimostrare il passo induttivo. Supponendo che l’enunciato sia valido per k = n, si dimostra che esso è valido per k = n + 1; si suppone quindi noto che «la somma delle ampiezze degli angoli interni di un poligono avente n + 2 lati è uguale a n angoli piatti» e occorre dimostrare che «la somma delle ampiezze degli angoli interni di un poligono avente n + 1 + 2 = n + 3 lati è uguale a n + 1 angoli piatti». A tal fine si considera un poligono P di n + 3 lati (per semplicità si esamina solamente il caso di un poligono convesso) e si congiungono due vertici adiacenti a uno stesso vertice (come in figura i vertici A e B). In questo modo il poligono P è suddiviso in un poligono P′ di n + 2 lati (per il quale, per ipotesi induttiva, la somma degli angoli interni è uguale a n angoli piatti) e in un triangolo (la cui somma degli angoli interni è uguale a un angolo piatto): quindi la somma degli angoli interni del poligono P è data da n + 1 angoli piatti, come volevasi dimostrare.

Il principio di induzione è spesso utilizzato per dimostrare uguaglianze o disuguaglianze, come la disuguaglianza di → Bernoulli, (1 + x)ⁿ ≥ 1 + nx, dove x è un numero reale maggiore di −1 e n è un numero naturale, che coinvolgono numeri naturali. Va tuttavia osservato che esso ha carattere confermativo e dimostrativo di una proprietà (quale per esempio una uguaglianza o una disuguaglianza) già congetturata attraverso la sperimentazione di più casi.

Un principio analogo al principio di induzione matematica è utilizzato anche per dimostrare alcune proprietà delle formule logiche; esso prende il nome di principio di induzione sulla complessità (o sulla lunghezza) delle formule. Per enunciare tale principio si considerino le formule di un dato linguaggio logico, per esempio il linguaggio degli enunciati; per dimostrare che una data proprietà P vale per ogni formula ben formata del linguaggio degli enunciati, è sufficiente dimostrare che:

• la proprietà P vale per ogni formula atomica, cioè per ogni lettera enunciativa;

• se la proprietà P vale per le formule A e B, allora la formula vale per le formule che da esse si ottengono per mezzo dei connettivi, cioè: