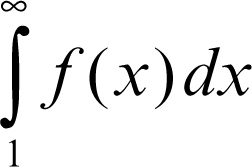infinito

infinito

infinito astrazione matematica (espressa dal simbolo ∞) che indica una grandezza illimitatamente grande o che può essere fatta crescere in modo illimitato. L’esempio più elementare è costituito dalla successione dei numeri naturali: 0, 1, 2, ... I tre puntini di sospensione indicano che tale sequenza può essere prolungata all’infinito, cioè che, comunque si prenda un numero “grande”, se ne può sempre trovare uno maggiore. In questa accezione, l’infinito è pensato come infinito potenziale, cioè come possibilità di ripetere una procedura quante volte si vuole (per esempio per trovare numeri sempre maggiori). È questo il concetto di infinito prevalentemente accettato nell’antichità e fino all’epoca moderna: seguendo Aristotele, non si potevano pensare, e non si dava loro possibilità di realtà effettiva, oggetti o enti matematici con un numero di elementi davvero senza fine. Si negava cioè che potesse esserci una realtà in atto infinita o, come si dice, un infinito attuale, mentre veniva accettata una forma di infinito in divenire. D’altra parte, fin dalla scoperta dei numeri irrazionali, l’introduzione di procedimenti infinitari aveva sollevato problemi di non facile soluzione che trovarono nei paradossi di Zenone forma esplicita: in apparenza ragionamenti viziosi, i paradossi di Zenone mostrano l’imbarazzo degli antichi di fronte a grandezze infinite (o infinitesime, prodotte per esempio da infinite suddivisioni di un segmento). Di fronte ai paradossi di Zenone, l’atteggiamento prevalente fu quello di bandire l’infinito dalla matematica. Nel calcolo delle aree e dei volumi Eudosso elimina il concetto di infinito con un procedimento di riduzione all’assurdo, mentre Archimede usa l’infinito in maniera euristica, ma dimostra i propri risultati riconducendosi alle procedure di Eudosso. Di questo horror infiniti che caratterizza la matematica classica vi è traccia ancora in Galileo e nella polemica di cui fu protagonista lo stesso Cavalieri sulla legittimità dell’uso degli «indivisibili» nel calcolo delle aree e dei volumi.

Il termine infinito (con il simbolo ∞ che lo rappresenta) entra in numerose locuzioni con significati affini, ma che debbono essere precisati dal contesto. In particolare, si hanno le seguenti accezioni:

• come punto di accumulazione della retta reale (o della sfera complessa), nel calcolo dei limiti, o comunque come punto improprio della retta proiettiva;

• (sostantivo) nel senso analogo a → infinitesimo, come funzione che ammette limite ∞;

• (aggettivo) nel senso della numerosità (→ cardinalità) degli insiemi;

• attuale (sostantivo o aggettivo) nella → analisi non standard.

L’infinito in analisi

Come si è detto, fino alla fine del xix secolo, l’unico infinito che veniva concepito era l’infinito potenziale: tale è l’infinito che emerge dall’analisi delle funzioni di variabile reale e la cui piena formalizzazione fu raggiunta con la teoria dei limiti, prima con A.-L. Cauchy e poi definitivamente con K. Weierstrass. Il simbolo ∞, introdotto da J. Wallis (nella sua opera De sectionibus conicis, del 1659: «Esto enim ∞ nota numeri infiniti»), può essere impiegato per rappresentare un punto astratto aggiunto formalmente alla retta reale per renderla compatta (→ compattificazione). Più frequentemente si utilizzano due punti, designati con −∞ e +∞, i cui intorni (unilaterali) sono dati rispettivamente dalle semirette {x < a} e {x > b}, che coerentemente sono indicate come intervalli della forma (−∞, a) e (b, +∞). Si noti che i valori ±∞ non vengono usualmente inclusi in tali intervalli, a meno che non si intenda operare sulla retta estesa [−∞, +∞], accettando esplicitamente tali valori come elementi del dominio e/o del codominio di una funzione. È in ogni caso escluso che ±∞ siano dei numeri reali, in quanto ciò risulterebbe incompatibile con la struttura di campo di R.

Ogni scrittura che contenga il simbolo ∞ (con o senza segno) è una forma di limite, sia che esso sia indicato esplicitamente col simbolo «lim», come in

o implicitamente come in

sia che il limite sia alla base di un altro processo dell’analisi matematica, come per esempio una → serie

un → integrale improprio

un → prodotto infinito o una → frazione continua. Sempre in analisi e come sostantivo, il termine infinito è utilizzato per indicare una funzione ƒ che ammette limite ∞: per esempio, la funzione

è un infinito per x che tende a 2, perché considerando valori di x sempre più vicini a 2 il suo valore diventa sempre più grande. Deve dunque essere considerato un infinito potenziale, cioè una quantità variabile che, in un opportuno insieme, diventa più grande (in modulo) di un valore assegnato ad arbitrio. La trattazione degli infiniti ripete l’analoga sugli → infinitesimi, con i cambiamenti naturali, per cui viene data qui una descrizione più sintetica. Sempre utilizzando la nozione di limite, è possibile confrontare diversi infiniti in uno stesso punto: se ƒ e g sono due diversi infiniti per x che tende a x₀, allora, considerato il

si dice che ƒ è infinito di ordine superiore, dello stesso ordine o di ordine inferiore rispetto a g se rispettivamente l = ∞, l è finito ma diverso da 0, l = 0. La nozione di ordine di un infinito può essere resa più precisa fissando delle funzioni campione. Si dice quindi che una funzione è un infinito di ordine α (per x → x₀) rispetto all’infinito campione g se per qualche α > 0 si ha

con l finito e diverso da 0. L’espressione l ⋅ g(x)^α è detta parte principale dell’infinito ƒ(x) ed è così detta perché in un piccolo intorno di x₀ tale parte principale approssima la funzione data. Per esempio, per x → +∞, la funzione

è un infinito di ordine 2/3 rispetto a x, e la sua parte principale è x ^2/3. Per altri esempi e per le applicazioni, si vedano → equivalenza asintotica, → O grande.

Come si è detto, la nozione analitica di infinito è molto vicina è quella di infinitesimo: una funzione ƒ è infatti un infinito per x che tende a x₀ se e solo se la sua inversa 1/ƒ è un infinitesimo per x che tende a x₀.

Per le speciali regole algebriche da utilizzare con il simbolo ∞, si veda la voce → forma indeterminata.

L’infinito in teoria degli insiemi

L’infinito, inteso come infinito attuale, viene pienamente accettato con la nascita della teoria degli insiemi, dovuta a G. Cantor, e in particolare con la sua teoria dei numeri cardinali. In teoria degli insiemi, secondo la definizione data da R. Dedekind, è detto infinito un insieme che può essere posto in corrispondenza biunivoca con una sua parte propria. Per esempio, l’insieme N dei numeri naturali è un insieme infinito perché si può stabilire la corrispondenza biunivoca tra esso e il suo sottoinsieme proprio P formato dai soli numeri pari (→ Galilei, paradosso di). L’infinità di un insieme è così definita non soltanto in termini negativi (come qualcosa di “non finito”), ma attraverso una proprietà verificabile. La teoria degli insiemi, inoltre, consentì a Cantor di distinguere tutta una gamma di diversi tipi di infinito attraverso l’introduzione delle nozioni di numero cardinale transfinito e ordinale transfinito, prima di allora sconosciute: per tali numeri transfiniti, egli definì anche un’estensione (detta aritmetica transfinita) delle usuali relazioni e operazioni aritmetiche soddisfatte dai numeri naturali, che coincidono con i cardinali finiti e con gli ordinali finiti. I più piccoli insiemi infiniti sono quelli che possono essere posti in corrispondenza biunivoca con l’insieme N dei numeri naturali (come per esempio gli insiemi Z dei numeri interi e Q dei numeri razionali): tali insiemi sono detti numerabili e ogni insieme infinito possiede un sottoinsieme di questa cardinalità. Molto importanti sono anche gli insiemi continui, vale a dire quelli che possono essere messi in corrispondenza biunivoca con l’insieme dei numeri reali R (o equivalentemente con l’insieme dei punti di una retta). Esistono infiniti altri tipi di infiniti attuali, per classificare i quali Cantor introdusse il simbolo ℵ (prima lettera dell’alfabeto ebraico, da leggersi alef ). In particolare, la notazione ℵ₀ (da leggersi «alef zero») indica la cardinalità del numerabile.

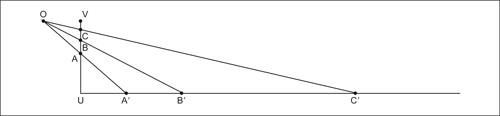
Se l’infinito potenziale aveva generato fin dall’antichità dei paradossi, come il paradosso di Zenone su Achille e la tartaruga, risolti dall’analisi matematica, la considerazione dell’infinito attuale generò paradossi e antinomie, cioè fatti non intuitivi e contrari al senso comune, ancora più radicali. Per esempio, i punti di un segmento, anche piccolo, sono tanti quanti i punti di una semiretta, come si può evincere dalla figura, in cui, proiettando i punti di un segmento UV da un punto O esterno, a ogni punto di UV corrisponde biunivocamente un punto della semiretta. Con tecnica analoga si può mostrare che un quadrato contiene tanti punti quanti un suo lato o che un piano contiene tanti punti quanti un segmento arbitrariamente piccolo. A questi paradossi, noti come paradossi dell’infinito, lo stesso Cantor stentò a credere tanto che così scrisse in una lettera a Dedekind: «Lo vedo, ma non lo credo!» (si veda anche → cardinalità).

Tra i tentativi condotti per superare le difficoltà aperte dalla «crisi dei fondamenti» si possono individuare diverse posizioni che si distinguono proprio per l’atteggiamento nei confronti dell’infinito: accettato il concetto di infinito attuale, anche se limitato al livello del numerabile, dai cosiddetti predicativisti come Russell e A.N. Whitehead, l’infinito veniva invece bandito in maniera radicale dagli intuizionisti come L. Brouwer, che riteneva sensata solo l’accettazione della reiterazione indefinita di processi generatori di un insieme. Il tentativo di salvare il più possibile dell’approccio cantoriano alla teoria degli insiemi fu condotto e operato dalla scuola formalista di D. Hilbert, il più tenace difensore del «paradiso (dell’infinito) svelato dai lavori di Cantor». L’esito di queste discussioni si confonde con l’esito della più generale questione dei fondamenti della matematica, mentre una rinnovata attualità doveva trovare l’infinito (e l’infinitesimo) attuale nella proposta di A. Robinson (1966) di un’analisi non standard.