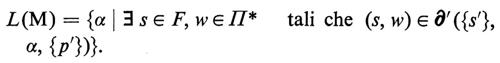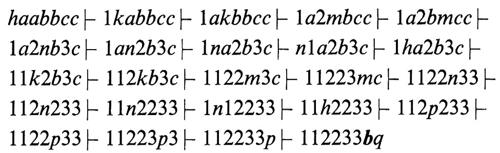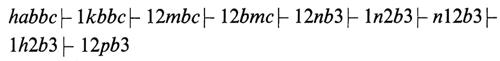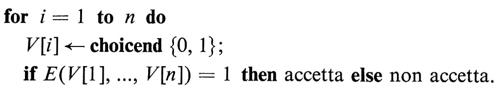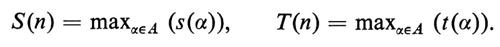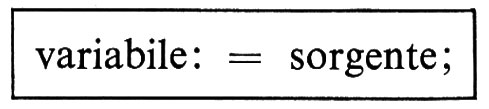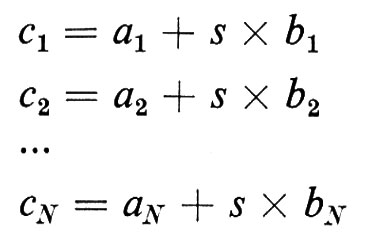Informatica

Informatica

Teoria della computazione  di Fabrizio Luccio

SOMMARIO: 1. Origine e motivazioni. 2. Notazione. 3. Automi finiti. 4. Automi a pila. 5. La macchina di Turing. 6. Decidibilità e indecidibilità. 7. Complessità di calcolo. 8. Problemi intrattabili. 9. I principali studi sull'argomento. □ Bibliografia.

1. Origine e motivazioni.

La necessità del calcolo, riconosciuta dall'uomo in tutte le civiltà ed epoche storiche, ha condotto a una sistematizzazione teorica della computazione solo in tempi recentissimi. Due fatti hanno contribuito in modo determinante allo sviluppo di questi studi: da un lato la formalizzazione del concetto di procedura di calcolo, che possiamo datare al 1936, anche se preceduta da rilevanti risultati di logica matematica ottenuti nei primi decenni del secolo; dall'altro lo sviluppo dei calcolatori a programma memorizzato, nati dal secondo conflitto mondiale e divenuti in breve tempo così importanti nelle più varie attività da richiedere approfonditi studi sull'efficienza della computazione. Nascono da questi fatti i due assi portanti della teoria della computazione, cioè la ‛computabilità' e la ‛complessità di calcolo', di cui ci occuperemo in questo articolo.

Il secondo problema di Hilbert sulla dimostrazione di compatibilità degli assiomi dell'aritmetica, posto all'inizio del secolo e rimasto insoluto anche nella formalizzazione dei Principia mathematica di Russell e Whitehead, aveva trovato una risposta negativa nel 1931 con il famoso teorema di incompletezza di Gödel, che provava l'esistenza di formule indimostrabili nel calcolo dei predicati del primo ordine, attraverso la costruzione di una di tali formule.

La prova di Gödel, basata sulla costruzione di una formula provatamente indimostrabile, lasciava aperto il problema della ‛formalizzazione della procedura' di dimostrazione, o più in generale della procedura di calcolo di una funzione. Gli anni che seguirono furono rivolti a ricercare tale formalizzazione, sotto l'ipotesi che ogni procedura dovesse consistere nella specificazione finita di una sequenza di passi, ciascuno eseguibile meccanicamente in tempo finito. Nel 1936 Turing introduceva la sua ‛macchina', che divenne il modello accettato di procedura e che rimane tale per la sua provabile equivalenza computazionale con ogni altro modello conosciuto, in particolare con i calcolatori di oggi (quando questi siano dotati di memoria sufficiente al calcolo richiesto), e per la sua equivalenza con ogni altro modello possibile, assenta nell'‛ipotesi di Church'.

La descrizione finita della procedura comporta come conseguenza che la classe di tutte le procedure è ‛numerabile', ovvero le procedure possono essere poste in corrispondenza biunivoca con i numeri naturali. Un modo pragmatico per convincersene è quello di formulare le procedure come programmi per un dato calcolatore, elencare questi programmi in ordine alfabetico rispetto ai caratteri che li compongono e assegnare poi a essi una numerazione progressiva: poiché si può banalmente dimostrare che i programmi ben formati sono infiniti, la classe dei programmi, e quindi delle procedure, ha la cardinalità degli interi.

Un argomento simile al precedente mostra che anche i dati su cui può operare una procedura, e i suoi risultati, rispondono a una descrizione finita e sono quindi numerabili. Ciò autorizza a considerare una procedura come meccanismo di calcolo di una funzione dai naturali sui naturali; anzi lo studio può essere limitato alle procedure ‛di decisione', che calcolano funzioni dai naturali su {o, 1} (decidono se accettare o respingere un'asserzione rappresentata dai dati), perché queste catturano tutte le proprietà interessanti della computabilità.

Questi fatti furono immediatamente posti in relazione con la non numerabilità della classe delle funzioni. Se infatti esistesse una numerazione f₀, f₁, ..., per esempio per le funzioni dai naturali su {0, 1}, si potrebbe legittimamente costruire la funzione g tale che

g(x) = 0, se f_x(x) = 1; g(x) = 1, se f_x(x) = 0;

per cui si avrebbe, per ogni i, g(i) ≠ f_i(i). Scelta comunque una numerazione di tutte le funzioni, giungeremmo pertanto alla contraddizione che g non fa parte dell'insieme.

La formalizzazione delle procedure mise quindi in evidenza un fatto dostinato a divenire uno dei cardini della teoria della computazione: poiché la classe delle funzioni non è numerabile, mentre la classe delle procedure è numerabile, devono esistere funzioni per le quali non esiste procedura di calcolo, cioè ‛funzioni non calcolabili' (o ‛non decidibili' nel caso di codominio {0, 1}). In sostanza non esistono procedure sufficienti a calcolare tutte le funzioni possibili. Se questo fatto era in qualche misura già atteso, molto meno ovvia fu l'individuazione delle prime funzioni non calcolabili, corrispondenti a problemi matematici significativi e ben posti, e tuttavia provatamente irrisolubili; ci occuperemo di tali problemi nel seguito.

Accanto alla macchina di Turing, altri modelli computazionali più semplici sono stati sviluppati nell'ambito di diverse discipline scientifiche. Tali modelli, concepiti in origine per la soluzione di specifiche classi di problemi, hanno trovato posto in una sistematizzazione generale della teoria della computabilità con il nome di ‛automi', assieme alla macchina di Turing, che è l'automa più potente e complesso e comprende tutti gli altri come casi particolari. Studieremo nel seguito le tre principali famiglie di automi e le classi di funzioni che essi calcolano: gli ‛automi finiti', nati come modelli di reti neuroniche e di circuiti elettrici, gli ‛automi a pila', nati in campo linguistico, e infine la ‛macchina di Turing' di cui già si è detto.

Affrontato il problema della calcolabilità, ci porremo quello della complessità dei procedimenti di calcolo, che ha origini molto più recenti. Benché possa apparire a prima vista sorprendente, lo studio dell'efficienza delle procedure ha riscosso attenzione crescente al crescere della velocità e delle dimensioni dei calcolatori ed è divenuto argomento centrale nella teoria della computazione solo nell'epoca attuale, caratterizzata da macchine estremamente potenti che dovrebbero rendere secondaria ogni preoccupazione sul modo più opportuno di impiegarle. Due motivi hanno invece generato l'effetto contrario.

Il primo, abbastanza semplice, è che l'uomo basa oggi il progresso economico e tecnologico sulla risoluzione numerica di problemi così vasti, da essere stati ritenuti praticamente non affrontabili prima dell'avvento dei grandi calcolatori. Non vi è però virtualmente limite alle dimensioni dei problemi che sarebbe utile poter risolvere e che sono ancora fuori della portata dei mezzi di calcolo: si tende perciò ad ampliare la potenza dei calcolatori e a raffinarne le tecniche di impiego, ed è a quest'ultimo aspetto che si rivolgono gli studi di complessità di calcolo.

Il secondo motivo, assai più sottile, è legato ai meccanismi del calcolo non deterministico. La macchina di Turing, nella sua più generale definizione, ha la possibilità di rispondere non deterministicamente alle stesse condizioni di ingresso, secondo un modello di comportamento definito matematicamente e simulato in pratica con l'esecuzione alternativa di tutte le azioni possibili a ogni passo. Il non determinismo non amplia la classe delle funzioni calcolabili, ma incide in modo cruciale sul tempo di calcolo, poiché una sequenza di n passi non deterministici, ciascuno dei quali preveda m alternative, è simulata attraverso mⁿ passi deterministici.

Nel decennio tra il 1960 e il 1970 si raggiunse la conclusione che la misura più significativa dell'efficienza di una procedura è l'espressione matematica del tempo che essa richiede in funzione della dimensione dei dati d'ingresso. Le procedure si divisero in ‛efficienti' e ‛inefficienti', a seconda che il tempo richiesto fosse polinomiale o esponenziale. In un famoso lavoro del 1971 sulla complessità delle procedure di dimostrazione, Cook provava che tutti i problemi risolubili con una macchina di Turing non deterministica in tempo polinomiale si riducono all'unico problema della soddisfattibilità di espressioni booleane. Negli anni seguenti si riconobbe che numerosissimi problemi ben posti e praticamente rilevanti sono computazionalmente equivalenti a quello della soddisfattibilità: esistono cioè procedure efficienti per risolverli nel modello non deterministico, ma la simulazione pratica di tali procedure è inefficiente poiché richiede tempo esponenziale. Se d'altra parte si scoprisse un algoritmo polinomiale deterministico per risolvere uno di questi problemi, lo stesso algoritmo sarebbe sufficiente a risolverli tutti in pari tempo.

L'unificazione di importanti problemi apparentemente molto diversi e il quesito formalmente ancora aperto dell'esistenza di un'efficiente procedura deterministica per risolverli hanno concentrato sugli aspetti di complessità gli studi attuali di teoria della computazione, influenzando profondamente il modo di affrontare la risoluzione algoritmica di un problema.

2. Notazione.

La teoria degli algoritmi è interamente basata su descrizioni finite e discrete. L'intera disciplina può essere appresa su un numero finito di testi di lunghezza finita, composti unicamente con i ‛caratteri' (o ‛simboli') di un insieme finito detto ‛alfabeto'. Non occorrono cioè illustrazioni composte di linee continue o colori sfumati, inflessioni di voce o altro, ma solo elementi tratti da un insieme che ha la cardinalità degli interi. Una volta appresa la disciplina, anche la pratica si avvale degli stessi mezzi di descrizione: tutte le computazioni eseguite da un uomo o da un calcolatore possono essere descritte con i caratteri di un alfabeto.

Poiché un alfabeto Σ è un insieme finito, la notazione di base è quella della teoria degli insiemi. Si definiscono l'insieme vuoto Ø, le relazioni di appartenenza e di contenimento, le operazioni di unione, intersezione e differenza. Si definisce la potenza 2^Σ dell'insieme Σ come l'insieme di tutti i sottoinsiemi di Σ; il prodotto cartesiano Σ × Γ tra gli insiemi Σ e Γ come l'insieme di tutte le coppie ordinate (s, g) tali che s ∈Σ , g ∈ Γ. Indicheremo in genere gli alfabeti con lettere greche maiuscole; i caratteri con le prime lettere latine minuscole o con cifre numeriche.

Una ‛stringa' (o ‛parola') w su un alfabeto Σ è una sequenza finita di caratteri di Σ; la sua ‛lunghezza' ∣ w ∣ è il numero di caratteri che contiene. ε indica la stringa vuota, ∣ ε ∣ = 0. Le stringhe si indicano in genere con le ultime lettere latine minuscole, o con lettere greche minuscole. La ‛concatenazione' di due stringhe v, w è la stringa composta da v seguita da w, e si indica con vw. Per ogni stringa w si ha: εw = wε = w.

La ‛stella' Σ * di un alfabeto Σ è l'insieme (infinito) di tutte le stringhe sull'alfabeto, inclusa la stringa vuota. Un ‛linguaggio' L è un insieme finito o infinito di stringhe su Σ, cioè L ⊆ Σ *. Ovviamente Σ * è numerabile, ma non è numerabile la classe di tutti i linguaggi su Σ.

I linguaggi si indicano specificandone le proprietà che caratterizzano le loro parole. La stringa costituita da un carattere c ripetuto i ≥ 0 volte si indica con cⁱ. Per esempio i seguenti insiemi L₁, L₂, L₃ sono linguaggi su Σ = {a, b, c}:

L₁ = {w ∣ w contiene un numero pari di simboli}; per esempio: abc² ∈ L₁;

L₂ = {w ∣ w = av, v ∈ Σ *}; cioè L₂ è formato dalle parole che iniziano con a, per esempio: acba, a, aab ∈ L₂;

L₃ = {aⁱbⁱ, i ≥ 0}; cioè L₃ è formato dalle parole che iniziano con un arbitrario numero di a seguito dallo stesso numero di b; per esempio: ab, ε, aaaabbbb ∈ L₃.

Consideriamo ora un automa (o procedura) A che dà risposte su {0, 1}. Detto Σ l'alfabeto con cui vengono codificati i dati d'ingresso, si ha che l'insieme di tutti i dati possibili è Σ * ovvero A calcola una funzione da Σ * su {0, 1}. Sotto una numerazione delle stringhe di Σ * si può affermare che tale funzione va dai naturali su {0, 1 }, ovvero A realizza una delle procedure di decisione il cui studio, come già affermato, contiene i risultati chiave della teoria della computazione. Se L è il sottoinsieme di Σ * per cui A dà risposta 1, diremo che L è il linguaggio ‛accettato' da A.

La computabilità potrà quindi essere vista come studio delle proprietà dei linguaggi accettati da diverse famiglie di automi e la complessità come studio del tempo necessario a tale accettazione, anche se l'intera questione sarà grandemente complicata dal fatto che l'automa potrebbe non fornire risposta in tempo finito.

3. Automi finiti.

Il primo modello computazionale che prendiamo in considerazione è l'‛automa finito' (brevemente a.f.). Esso è definito come un gruppo di cinque entità (S, Σ, s′, F, ∂), ove:

S è un insieme finito di ‛stati interni' (o semplicemente ‛stati');

Σ è l'alfabeto d'ingresso;

s′ ∈ S è lo ‛stato iniziale';

F ⊆ S è l'insieme degli ‛stati finali';

∂ è una ‛funzione di transizione' da S×Σ su S.

L'automa esegue una successione di ‛mosse'. Posto inizialmente nello stato s′, esso legge una stringa di ingresso α ∈ Σ * da sinistra a destra, un carattere per mossa, e assume a ogni mossa un nuovo stato indicato dalla funzione di transizione: più precisamente, posto che l'automa si trovi nello stato s ∈ S e legga il carattere c ∈ α, esso si porta nello stato ∂(s, c) e sposta la lettura sul carattere successivo di α. La stringa α è ‛accettata' se e solo se con la lettura del suo ultimo carattere l'automa si porta in uno stato finale f ∈ F.

Attraverso il meccanismo di transizione tra stati l'automa raccoglie e conserva informazione sullo svolgimento del calcolo, che consiste in sostanza nell'aggiornamento di tale informazione a ogni mossa, sulla base dei caratteri di α. Ogni stato di S corrisponde alla ‛memorizzazione' di una proprietà della porzione (‛prefisso') di a che termina sull'ultimo carattere letto. Poiché Σ * è infinito e S è finito, vi sarà in genere un numero infinito di stringhe prefisso che conducono l'automa nello stesso stato, per le quali cioè l'automa riconosce e memorizza la stessa proprietà. In particolare una proprietà è associata a ogni stato finale e caratterizza le stringhe accettabili.

La funzione di transizione si assegna indicandone i valori ∂(s, c) in una tabella, in funzione di s e c. In alternativa si usa un ‛grafo di transizione', di interpretazione immediata se è piccola la cardinalità del dominio di definizione S×Σ. I vertici del grafo corrispondono agli stati di S; gli spigoli sono orientati ed etichettati e corrispondono alle transizioni indicate dalla funzione ∂: se ∂(s, c) = t, vi è un arco di etichetta c diretto da s a t.

Consideriamo per esempio l'automa A = ({s′, s₀, s₁, s₂}, {0, 1}, s′, {s₀}, ∂), cui è associato il grafo di transizione della fig. 1 (lo stato finale s₀ è indicato a tratto spesso). A accetta tutte e sole le stringhe di 0 e 1 che rappresentano numeri binari multipli di tre, di almeno una cifra. Per esempio la stringa 10010 (codifica binaria del numero 18) causa la sequenza di transizioni s′ → s₁ → s₂ → s₁ → s₀ → s₀, che termina nello stato finale s₀ ed è quindi accettata da A. La stringa 1101 (codifica binaria di 13) causa le transizioni s′ → s₁ → s₀ → s₀ → s₁ e non è quindi accettata.

Per provare che l'automa A accetta tutte e sole le stringhe α ∈ {0, 1}* con le proprietà dette, indichiamo con [α] il numero binario rappresentato da α e associamo agli stati di A le seguenti proprietà delle stringhe prefisso β: s′ è lo stato iniziale, in cui si attende l'arrivo del primo carattere (ricordiamo che A non accetta la stringa vuota); s_i, con 0 ≤ i ≤ 2, è raggiunto per tutte e sole le stringhe β tali che [β] ≡ i mod 3 (cioè tali che i sia il resto della divisione tra [β] e 3), come si prova facilmente per induzione sulla lunghezza di β, notando che per β = ηc, con η ∈ {0, 1}* e c ∈ {0, 1}, si ha [β] = 2[η] + [c]. Per esempio, poiché si arriva in s₁ con stringhe β tali che [β] ≡ 1 mod 3 e concatenando βi con 0 si ha [β0] = 2[β] + 0 ≡ 2 mod 3, si pone ∂(s₁, 0) = s₂ (v. fig. 1). Lo stato finale è quindi s₀, associato a tutte le stringhe α con [α] ≡ 0 mod 3.

È utile estendere il dominio di definizione della funzione di transizione per designare il comportamento dell'automa in risposta a intere stringhe d'ingresso. Si introduce la nuova funzione ∂ da S×Σ* su S, definita ricorsivamente attraverso le relazioni:

∂(s, ε) = s;

∂(s, αc) = ∂(∂(s, α), c), con α ∈ Σ*, c ∈ Σ.

Si definisce allora il ‛linguaggio accettato' da un automa finito M = (S, Σ, s′, F, ∂) come l'insieme di stringhe L(M) = {α ∣ ∂(s′, α) ∈ F}. Un linguaggio (o insieme) L si dice ‛regolare' se esiste un automa finito M tale che L = L(M). Per l'automa A della fig. 1 abbiamo L(A) = {α ∣ [α] ≡ 0 mod 3, ∣ α ∣ > 0, dunque questo linguaggio è regolare.

Occupiamoci ora di una importante modificazione degli automi finiti, che ritroveremo anche negli altri modelli di calcolo. M = (S, Σ, s′, F, ∂′) è un ‛automa finito non deterministico' (brevemente a.f.n.d.) se, per uno stesso stato e uno stesso carattere letto dall'esterno, si definiscono più mosse per M. Il significato di S, Σ, s′ e F rimane invariato, mentre la funzione di transizione ∂′ è ora definita da S×Σ su 2^S, cioè: ∂′(s, c) = R ⊆ S, ove R è l'insieme di tutti gli stati in cui l'automa può portarsi dallo stato g leggendo il carattere c. Tutti questi stati devono essere ‛provati' dall'automa, che segue così una molteplicità di percorsi computazionali paralleli in relazione a una stessa stringa d'ingresso. La stringa è ‛accettata' se e solo se almeno uno di questi percorsi termina in uno stato finale f ∈ F. Si noti che 2^S contiene l'insieme vuoto, quindi potrebbe esistere una coppia s, c per cui ∂′(s, c) = Ø: in questo caso la nuova mossa non è definita e il percorso computazionale contenente s, c si arresta.

Immaginiamo di modificare l'automa A della fig. 1, in modo che accetti le stringhe α su {0, 1} che rappresentano numeri binari multipli di tre o di due, cioè: [α] ≡ 0 mod 3 o [α] ≡ 0 mod 2. Il nuovo automa B si costruisce spontaneamente come a.f.n.d., aggiungendo al grafo di transizione di A una nuova parte per il riconoscimento dei multipli di due e accedendo non deterministicamente da s′ all'una o all'altra parte del grafo per controllare entrambe le divisibilità. Si ha così

B = ({s′, s₀, s₁, s₂, s₃, s₄}, {0,1}, s′, {s₀, s₃}, ∂′),

con il grafo di transizione mostrato nella fig. 2. Il non determinismo è messo in evidenza nel grafo dall'esistenza di vertici (s′ nell'esempio) da cui partono spigoli con la stessa etichetta.

Il lettore potrà provare per proprio conto che l'automa B risolve correttamente il problema posto.

Poiché un a.f.n.d. M = (S, Σ, s′, F, ∂′) può assumere diversi stati in risposta alla stessa stringa d'ingresso, è utile introdurre una nuova funzione di transizione ∂′ da 2^S × Σ* su 2^S, definita attraverso le relazioni:

∂′(Q, ε) = Q, con Q ⊆ S;

∂′(Q, c) = ⋃_s∈Q ∂′(s, c), con Q ⊆ S, c ∈ Σ;

∂′(Q, αc) = ∂′(∂′(Q, α), c), con Q ⊆ S, α ∈ Σ*, c ∈ Σ.

Si definisce quindi il linguaggio accettato dall'a.f.n.d. M come l'insieme di stringhe L(M) = {α ∣ ???29??? s ∈ ∂′({s′}, α) tale che s ∈ F}. Per l'automa B della fig. 2 abbiamo: L(B) = {α ∣ ([α] ≡ 0 mod 3) ⋀ ([α] ≡ 0 mod 2), ∣ α ∣ > 0}.

Si può dimostrare che la classe dei linguaggi accettati dagli a.f.n.d. è esattamente quella dei linguaggi regolari. Se è ovvio che i linguaggi regolari siano accettati dagli a.f.n.d. (infatti ogni a.f. può essere considerato un caso particolare di a.f.n.d. in cui il codominio della funzione ∂′ è limitato a S), il seguente teorema dimostra che gli a.f.n.d. non accettano altri linguaggi, cioè il non determinismo non aumenta la potenza computazionale degli automi finiti.

Teorema. Sia L il linguaggio accettato da un a.f.n.d. arbitrario X. Allora esiste un a.f. (deterministico) Y che accetta L.

Il teorema si dimostra in modo costruttivo, indicando come costruire Y dagli elementi di X. In particolare ogni stato di Y, raggiunto in seguito alla lettura di una stringa a, corrisponde al sottoinsieme degli stati di X raggiunto con la lettura della stessa stringa. Quindi, se X ha n stati, Y può averne 2ⁿ ed è questa possibile esplosione delle dimensioni l'unico prezzo pagato al determinismo (vedremo che la situazione è molto diversa per le altre famiglie di automi).

Senza addentrarci nella prova del teorema, indichiamo nella fig. 3 il grafo di transizione di un a.f. C corrispondente all'a.f.n.d. B della fig. 2. I nomi degli stati di C indicano, con i loro indici, i corrispondenti sottoinsiemi di stati di B. I due automi hanno lo stesso stato d'ingresso e gli stati finali di C corrispondono a sottoinsiemi contenenti uno stato finale di B.

Abbiamo di nuovo: L(C) = L(B) = {α ∣ ([α] ≡ 0 mod 3) ⋀ ([α] ≡ 0 mod 2), ∣ α ∣ > 0}.

Tra le numerose proprietà di cui godono i linguaggi regolari, le seguenti sono assai notevoli.

Lemma. Per ogni linguaggio regolare L esiste una costante n > 0 tale che qualsiasi stringa α ∈ L, con ∣ α ∣ ≥ n può essere espressa come α = βγδ, con ∣ βγ ∣ ≤ n, ∣ γ ∣ ≥ 1, in modo che la nuova stringa α′ = βγⁱδ ∈ L per ogni i ≥ 0.

Il lemma è una diretta conseguenza del fatto che gli a.f. hanno un numero finito di stati. Posto n = ∣ S ∣, un'arbitraria stringa d'ingresso α condurrà l'automa almeno due volte in uno stesso stato s: la porzione di α che porta l'automa da s ancora a s può allora essere ripetuta un numero arbitrario di volte in α senza alterare l'effetto delle parti precedente e successiva della stringa.

Il lemma ha due importanti conseguenze. La prima è la possibilità di riconoscere che un linguaggio L non è regolare, se si individua una stringa α ∈ L che, comunque suddivisa in βγδ, genera stringhe α′ ∉ L. Consideriamo per esempio il linguaggio L = {aⁱbⁱ, i ≥ 1}. Posto che L sia regolare e che n sia la costante del lemma, la stringa α = aⁿbⁿ ∈ L potrebbe essere scritta come α = βγδ, con βγ = a^m≤n, e da questa si genererebbe la nuova stringa α′ = βγⁱ⁼⁰δ = βδ = a^pbⁿ, con p 〈 n. Poiché α′ ∉ L, questo linguaggio non è regolare. (Intuitivamente il motivo per cui un linguaggio apparentemente semplice come L non può essere accettato da un automa finito è che, per decidere se il numero delle b è uguale al numero delle a un automa dovrebbe aver ‛contato' le a, il che per una sequenza di a arbitrariamente lunga richiede memoria arbitrariamente grande).

La seconda conseguenza del lemma riguarda la possibilità di decidere se un linguaggio regolare è vuoto, finito o infinito. Dal lemma discende infatti che il linguaggio L(A) accettato da un a.f. A di n stati deve contenere almeno una stringa α tale che

∣ α ∣ 〈 n se L(A) ≠ Ø;

n ≤ ∣ α ∣ 〈 n, se L(A) è infinito.

Controllando la risposta di A su tutte le stringhe di lunghezza minore di n, o compresa tra n e 2n, si stabilisce se L(A) è vuoto o non vuoto, finito o infinito. Poiché tutte queste stringhe sono in numero finito, e l'automa A risponde a ciascuna di esse in tempo finito, il procedimento accennato è ‛effettivamente eseguibile' (anche se molto inefficiente; ma ne esistono di più rapidi). La teoria della computazione studia diverse proprietà degli insiemi, ma annette particolare importanza a quelle per cui esiste, ed è nota, una procedura di decisione.

Oltre alle proprietà viste, i linguaggi regolari godono di varie proprietà di chiusura, tra cui ricordiamo quelle espresse nel teorema seguente (la complementazione ¬L di un linguaggio L è definita come: ¬L = Σ* − L).

Teorema. La famiglia dei linguaggi regolari è chiusa sotto le operazioni di unione, intersezione e complementazione. Inoltre, dati due a.f. A₁, A₂, esistono (semplici) procedure per costruire un a.f. A₃ tale che

L(A₃) = L(A₁) ⋃ L(A₂);

L(A₃) = L(A₁) ⋂ L(A₂);

L(A₃) = ¬L(A₁).

Due automi che accettano lo stesso linguaggio si dicono ‛equivalenti'. Una conseguenza del precedente teorema è che si può costruire un automa A₄ che riconosce il linguaggio L(A₄) = (L(A₁) ⋂ ¬L(A₂)) ⋃ (¬L(A₁) ⋂ L(A₂)) e si vede immediatamente che L(A₄) = Ø se e solo se L(A₁) = L(A₂). Poiché sappiamo che esiste una procedura per decidere se L(A₄) = Ø, possiamo concludere col seguente teorema.

Teorema. Esiste una procedura per decidere se due automi finiti sono equivalenti.

4. Automi a pila.

La limitazione di potenza computazionale degli automi finiti deriva dalla finitezza della loro memoria. In particolare il ricordo di una situazione è legato unicamente allo stato assunto dall'automa: poiché l'insieme degli stati è finito, il numero di situazioni memorizzabili è anch'esso finito.

Per accrescere la potenza del modello si ammette che l'automa possa registrare un numero a priori illimitato di situazioni diverse; tale registrazione viene però effettuata su un mezzo esterno, perché l'automa conservi dimensioni finite. Il primo mezzo considerato è la ‛pila', definita come una struttura che può contenere una stringa di lunghezza illimitata, composta di caratteri di un proprio alfabeto Π. L'accesso alla pila avviene sul primo carattere p (‛testa') della stringa w ivi contenuta e ha lo scopo di ‛leggere' p e di memorizzare una nuova informazione mediante l'inserzione nella pila di una stringa x che sostituisce p (per consentire l'accesso, w non può essere vuota). Posto w = py, p ∈ Π, y ∈ Π* e x ∈ Π*, l'inserzione di x causa la trasformazione della stringa contenuta nella pila da w a xy e il conseguente spostamento della testa sul primo carattere di x.

Definiamo ora l'‛automa a pila deterministico' (brevemente a.p.d.) come un gruppo di sette entità (S, Σ, Π, s′, p′, F, ∂), ove:

S è un insieme finito di ‛stati';

Σ è l'alfabeto d'ingresso;

Π è l'alfabeto della pila;

s′ ∈ S è lo ‛stato iniziale';

p′ ∈ Π è il ‛carattere iniziale';

F ⊆ S è l'insieme degli ‛stati finali';

∂ è una ‛funzione di transizione' da S×Σ×Π su S×Π* (∂ può non essere definita sull'intero dominio S×Σ×Π).

Il funzionamento dell'automa è simile a quello dell'a.f., a parte l'impiego della pila. Esso è posto inizialmente nello stato s′, con pila contenente p′, e si appresta a leggere per scansione una stringa d'ingresso α ∈ Σ*. A ogni ‛mossa' l'automa si trova in uno stato s ∈ S, legge un carattere c ∈ α e il carattere p in testa alla pila; se ∂(s, c, p) = (t, x), con t ∈ S e x ∈ Π*, esso si porta nello stato t e inserisce x nella pila (cancellandovi p); se invece ∂(s, c, p) non è definita, la computazione si arresta. La stringa α è ‛accettata' se e solo se, con la lettura del suo ultimo carattere, l'automa si porta in uno stato finale f ∈ F; in particolare α non è accettata se la computazione si arresta prima che la stringa sia letta completamente.

La funzione ∂ si assegna di solito elencandone i valori ∂(s, c, p) in una ‛tabella di transizione', in cui le righe corrispondono agli stati s e le colonne alle coppie di caratteri c, p (la rappresentazione in forma di grafo è in questo caso meno chiara della tabella).

Consideriamo per esempio l'automa a pila deterministico

D = ({s₀, s₁, s₂, s₃}, {a, b}, {0, 1}, s₀, 0, {s₃}, ∂),

cui è associata la tabella di transizione della fig. 4. D accetta tutte e sole le stringhe del linguaggio L = {aⁱbⁱ, i ≥ 1}, che abbiamo riconosciuto come non regolare nel capitolo precedente. Per esempio la stringa d'ingresso aaabbb causa la seguente sequenza di transizioni tra stati, con associati contenuti della pila: s₀, 0 → s₁, 0 → s₁, 10 → s₁, 110 → s₂, 10 → s₂, 0 → s₃, 0, che termina nello stato finale s₃; la stringa è quindi accettata. La stringa aabbb causa le transizioni s₀, 0 → s₁, 0 → s₁, 10 → s₂, 0 → s₃, 0, e la computazione si arresta sulla lettura dell'ultimo carattere b, perché il valore ∂(s₃, b, 0) non è definito: la stringa non è quindi accettata.

Il lettore potrà dimostrare per proprio conto che l'automa D accetta tutte e sole le stringhe aⁱbⁱ, i ≥ 1.

Come sempre è utile estendere il dominio di definizione della funzione ∂, per designare il comportamento dell'automa in risposta ad arbitrarie coppie di stringhe di ingresso e di pila. Si introduce a tale scopo la funzione ∂ da S×Σ*×Π* su S×Π*, definita ricorsivamente come

Il ‛linguaggio accettato' da un a.p.d. M = (S, Σ, Π, s′, p′, F, ∂) è allora l'insieme L(M) = {α ∣ ∂(s′, α, p′) = (f, w), f ∈ F}. Per l'automa D abbiamo L(D) = {aⁱbⁱ, i ≥ 1}.

A differenza di quanto avviene per gli automi finiti, il non determinismo aumenta ora la potenza computazionale del modello. M = (S, Σ, Π, s′, p′, F, ∂′) è un ‛automa a pila non deterministico' (o semplicemente ‛automa a pila', brevemente a.p., perché questo è il modello più generale) se, per uno stesso stato, uno stesso carattere d'ingresso e uno stesso carattere in testa alla pila, si definiscono più mosse per M. Il significato di S, Σ, Π, s′, p′, F rimane invariato, mentre la funzione di transizione ∂′ è definita da S×(Σ ⋃ {ε})×Π su sottinsiemi finiti di S×Π*, cioè:

Con la lettura di c, p l'automa apre r percorsi computazionali distinti e la stringa d'ingresso è ‛accettata' se e solo se almeno uno di questi percorsi termina in uno stato finale. Se c = ε, l'automa procede allo stesso modo senza leggere il carattere d'ingresso (e non avanza quindi sulla stringa d'ingresso).

Poiché i caratteri in una pila si leggono in ordine inverso a quello in cui sono stati inseriti, un a.p. permette di riconoscere efficientemente se una stringa α è l'‛inversa' di un'altra, indicata con α^ι (cioè se α, letta da destra a sinistra, coincide con α^ι). L'automa a pila

E = ({r, s, t}, {a, b}, {0, 1, 2}, r, 0, {t}, ∂′},

cui è associata la tabella di transizione della fig. 5, accetta tutte e sole le stringhe αα^ι, con α ∈ {a, b}*. Nello stato r l'automa legge la stringa α e la ‛copia' nella pila, codificando i caratteri a, b rispettivamente con 1, 2; si porta poi nello stato s e prosegue la lettura, confrontando la stringa α^ι con quella contenuta nella pila, che viene cancellata carattere per carattere; se riemerge nella pila il carattere iniziale 0 quando la stringa d'ingresso è stata esaurita, l'automa accetta la stringa portandosi nello stato finale t per ingresso ε.

Il non determinismo interviene quando E si trova nello stato r e la stringa d'ingresso contiene due a, o due b, consecutive: in questo caso infatti l'automa non è ancora in grado di decidere se il secondo carattere appartiene anch'esso ad α o segna l'inizio di α^ι e considera entrambi i casi non deterministicamente. Ciò si riflette nei valori multipli: ∂′(r, a, 1) = {(r, 11), (s, ε)} e ∂′(r, b, 2) = {(r, 22), (s, ε)}.

Anche le transizioni per carattere ε possono causare comportamento non deterministico in relazione ad altre possibili transizioni, perché l'automa può procedere o non procedere nella lettura della stringa d'ingresso. Nell'automa E ciò avviene per esempio per i valori ∂′(r, ε, 0) = (t, ε), ∂′(r, a, 0) = (r, 10). Il lettore potrà verificare il funzionamento di E, provandolo su varie stringhe d'ingresso.

La risposta di un a.p. ad arbitrarie coppie di stringhe di ingresso e di pila può essere descritta con una funzione di transizione estesa ∂′, definita da 2^S×Σ*×(sottoinsiemi finiti di Π*) su (sottoinsiemi finiti di S×Π*), che indica l'insieme di stati, con relative stringhe nella pila, che l'automa può assumere. La definizione di ∂′ in funzione di ∂′ è ovvia ma piuttosto complicata, e non è riportata qui. Il ‛linguaggio accettato' da un a.p. M = (S, Σ, Π, s′, p′, F, ∂′) è allora l'insieme

Un linguaggio L si dice ‛libero' se esiste un automa a pila M tale che L = L(M). Tra questi linguaggi si trovano i principali ‛linguaggi di programmazione', per cui la teoria degli automi a pila riveste importanza fondamentale nella traduzione e interpretazione di programmi. Per l'automa E abbiamo L(E) = {αα^ι, con α ∈ {a, b}*}, dunque questo linguaggio è libero. La nostra precedente affermazione che il modello deterministico sia in questo caso meno potente si esprime con il fatto che i linguaggi accettati da automi a pila deterministici costituiscono un sottoinsieme proprio dei linguaggi liberi: si può per esempio dimostrare che non esiste un a.p.d. che accetta il linguaggio L(E).

I linguaggi regolari a loro volta costituiscono un sottoinsieme dei linguaggi accettati da a.p.d., come si deduce immediatamente notando che ogni a.f. è un caso particolare di a.p.d. che ‛non impiega' la pila (ovvero ∂(s, c, p′) = (t, p′) ovunque ∂ è definita). Inoltre tale sottoinsieme è proprio per quanto abbiamo provato sul linguaggio {aⁱbⁱ, i ≥ 1}.

Riportiamo ora alcune delle numerosissime proprietà di cui godono i linguaggi liberi. Il primo lemma è un'estensione di quello già discusso per i linguaggi regolari, ma la sua prova è ora complessa, né esso può essere giustificato facilmente in modo intuitivo.

Lemma. Per ogni linguaggio libero L esiste una costante n > 0 tale che qualsiasi stringa α ∈ L, con ∣ α ∣ ≥ n, può essere espressa come α = βγδζη, con ∣ γδζ ∣ ≤ n, ∣ γζ ∣ ≥ 1, in modo che la nuova stringa α′ = βγⁱδζⁱη ∈ L per ogni i ≥ 0.

Come nei linguaggi regolari, il lemma ha due importanti conseguenze. La prima è la possibilità di riconoscere che un linguaggio L non è libero se si individua una stringa α ∈ L che, comunque suddivisa in βγδζη, genera una stringa α′ ∉ L. Poniamo per esempio che il linguaggio L = {aⁱbⁱcⁱ, i ≥ 1} sia libero e che n sia la costante del lemma. La stringa α = aⁿbⁿcⁿ ∈ L potrebbe allora essere scritta secondo il lemma come α = βγδζη e in essa la sottostringa γδζ avrebbe lunghezza ≤ n, quindi non potrebbe contenere contemporaiìeamente a e c. La nuova stringa α′ = βγⁱ⁼⁰δζⁱ⁼⁰η = βδη non avrebbe allora lo stesso numero di a, b e c e non apparterrebbe a L in contrasto con il lemma. Concludiamo che {aⁱbⁱcⁱ, i ≥ 1} non è un linguaggio libero.

La seconda conseguenza del lemma è la possibilità di decidere se un arbitrario linguaggio libero L è vuoto, finito o infinito, con test di lunghezza finita condotti sull'a.p. che accetta L: il metodo consiste in una immediata estensione di quello già indicato per i linguaggi regolari.

Le proprietà di chiusura sono meno ricche per i linguaggi liberi che per quelli regolari. In particolare abbiamo il seguente teorema.

Teorema. 1) La famiglia dei linguaggi liberi è chiusa sotto l'operazione di unione; inoltre, dati due a.p. A₁, A₂, esiste una (semplice) procedura per costruire un a.p. A₃ tale che L(A₃) = L(A₁) ⋃ L(A₂); 2) la famiglia dei linguaggi liberi non è chiusa sotto le operazioni di intersezione e complementazione; inoltre, dati due a.p. A₁, A₂, non esistono procedure per decidere se L(A₁) ⋂ L(A₂) e ¬L(A₁) sono linguaggi liberi (cioè se esiste un a.p. che li accetta).

Il punto 2) del teorema afferma la non esistenza di una procedura di decisione per due quesiti posti sui linguaggi liberi, ovvero l'‛indecidibilità' di tali quesiti. Abbiamo riconosciuto nel cap. 1 che devono necessariamente esistere problemi indecidibili, ma tutte le prove di indecidibilità, inclusa quella del teorema, richiedono strumenti che saranno sviluppati nel prossimo capitolo. Similmente si può dimostrare che vale un altro drastico risultato negativo per i linguaggi liberi, espresso dal teorema seguente.

Teorema. Non esiste procedura per decidere se due arbitrari automi a pila A₁, A₂ sono equivalenti (cioè se L(A₁) = L(A₂)).

5. La macchina di Turing.

L'automa più potente dal punto di vista computazionale fu introdotto da A. Turing nel 1936. Si tratta di una macchina astratta di dimensioni finite, dotata di un organo (‛testa') che scandisce le ‛celle' consecutive di un ‛nastro' esterno di lunghezza illimitata, su cui esegue operazioni di lettura e scrittura. Tale scrittura consente la memorizzazione sul nastro di un numero illimitato di eventi, ma, a differenza dell'automa a pila, la macchina può percorrere il nastro in entrambe le direzioni e recuperare l'informazione registrata in qualsiasi posizione.

Formalmente la ‛macchina di Turing' (brevemente m.t.) si definisce come un gruppo di sette entità (S, Σ, Π, s′, b, F, ∂), ove:

S è un insieme finito di ‛stati';

Σ è l'alfabeto d'ingresso;

Π è l'alfabeto del nastro, con Σ ⊂ Π;

s′ è lo ‛stato iniziale';

b è un carattere speciale del nastro, detto ‛bianco': b ∈ Π − Σ;

F ⊆ S è l'insieme degli ‛stati finali';

∂ è la ‛funzione di transizione', da S×Π su S×Π×{Á, →} (∂ può non essere definita sull'intero dominio S×Π: in particolare non è definita su F×Π).

Ammettiamo che il nastro abbia un'origine ove si trova la sua prima cella e che sia illimitato verso destra: inizialmente esso contiene una stringa d'ingresso α ∈ Σ* registrata a partire dalla prima cella, seguita da una stringa di b illimitata a destra. La macchina inizia a operare nello stato s′, con la testa posta sulla prima cella del nastro; in ogni istante essa si trova in uno stato s ∈ S, legge un carattere c ∈ Π dal nastro ed esegue una delle azioni seguenti:

se ∂(s, c) = (t, d, m), con t ∈ S, d ∈ Π, m ∈ {Á, →}, la macchina si porta nello stato t, cancella c dal nastro e scrive al suo posto d, sposta la testa sul nastro di una posizione, a sinistra, se m = Á, a destra, se m = →;

se invece ∂(s, c) non è definita (come avviene per esempio nel caso che s sia uno stato finale, s ∈ F), o se la testa si sposta a sinistra dell'origine del nastro, la macchina si arresta.

Il meccanismo di cancellazione e riscrittura dei caratteri sul nastro fa sì che la stringa iniziale αbbb... si trasformi via via in un'altra, composta in genere con i caratteri di un alfabeto Π più ampio. La stringa α è ‛accettata' se la macchina si porta in uno stato f ∈ F (ove si arresta), in un numero finito di mosse. Si noti che a questo punto il nastro può contenere una stringa qualsiasi, completata a destra da infiniti b, e la testa può trovarsi in una posizione qualsiasi del nastro. Se la macchina si arresta in uno stato di S − F, o non si arresta mai, la stringa non è accettata.

La situazione della computazione di una m.t., in un dato istante, può essere completamente descritta indicando lo stato raggiunto dalla macchina, il contenuto del nastro e la posizione della testa. Si definisce a tale scopo la ‛descrizione istantanea' (d.i.) della macchina come la stringa xsy, con x, y ∈ Π* e s ∈ S, tale che:

s è lo stato della m.t.;

xy è la stringa contenuta nel nastro fino al carattere più a destra diverso da b, o, se più a destra di esso, fino al carattere a sinistra della testa (ciò avviene se la testa, spostandosi a destra, è entrata nella stringa illimitata di b);

la testa è posta sul primo carattere di y: se y = ε la testa si trova su un carattere della stringa illimitata di b. La posizione della testa è quindi indicata nella d.i. dalla posizione del simbolo dello stato s.

Una mossa della m.t. consiste nel passaggio tra due d.i., D₁, D₂, e si indica col simbolo: D₁ ⊢ D₂. La computazione, per la stringa d'ingresso α, è una successione di mosse che partono dalla d.i. iniziale s′α.

Consideriamo per esempio la macchina:

G = ({h, k, m, n, p, q}, {a, b, c}, {a, b, c, 1, 2, 3, b}, h, b, {q}, ∂),

la cui funzione ∂ è specificata nella ‛tabella di transizione' della fig. 6 (il valore ∂(s, j) si trova all'incrocio tra la riga s e la colonna j). G accetta tutte e sole le stringhe del linguaggio L = {aⁱbⁱcⁱ, i ≥ 0), che abbiamo riconosciuto come non libero nel capitolo precedente. Per esempio, in risposta alla stringa d'ingresso aabbcc ∈ L, la macchina esegue la computazione

che si arresta nello stato finale q (∂(q, b) non è definita) accettando la stringa. In risposta alla stringa abbc ∉ L la computazione è invece

e a questo punto la macchina si arresta nello stato non finale p (infatti ∂(p, b) non è definita): la stringa non è quindi accettata. Il lettore potrà approfondire il funzionamento di G su altre stringhe.

Il passaggio tra due descrizioni istantanee D₁, D₂ mediante un numero arbitrario ≥ 0 di mosse consecutive si indica col simbolo: D₁ ⊢* D₂ (la relazione ⊢* è cioè la chiusura riflessiva e transitiva di ⊢). Si definisce così il ‛linguaggio accettato' da una m.t. M = (S, Σ, Π, s′ b, F, ∂) come l'insieme L(M) = {α ∣ α ∈ Σ*, s′α ⊢* xsy con s ∈ F e x, y ∈ Π*}. I linguaggi (o insiemi) accettati dalle m.t. si dicono ‛ricorsivamente enumerabili' (brevemente r.e.). Per la m.t. G abbiamo L(G) = {aⁱbⁱcⁱ, i ≥ 0}, quindi questo linguaggio è r.e..

Mettiamo in evidenza ancora una volta che una m.t. M si arresta per tutte le stringhe di L(M), mentre può arrestarsi o non arrestarsi per le stringhe non in L(M). Non esiste però in genere alcun limite superiore al tempo necessario a M per accettare una stringa e perciò non esiste criterio generale per stabilire se una computazione in corso su una stringa d'ingresso α terminerà o no. Vi sono ovviamente m.t. che si arrestano su ogni stringa accettata o non accettata, come per esempio la G della fig. 6, ma, come vedremo nel prossimo capitolo, non tutti i linguaggi r.e. sono accettati da macchine di questo tipo: vi sono quindi linguaggi r.e. per cui non è possibile stabilire, entro un tempo fissato a priori, l'appartenenza di una stringa arbitraria al linguaggio.

Questa grave e inevitabile limitazione giustifica l'introduzione di un nuovo concetto: un linguaggio (o insieme) si dice ‛ricorsivo' se esiste una m.t. M che si arresta sempre in tempo finito, tale che L = L(M). Per esempio il linguaggio {aⁱbⁱcⁱ, i ≥ 0} è ricorsivo, perchè è accettato dalla macchina G. Da quanto affermato dobbiamo concludere che i linguaggi ricorsivi sono un sottoinsieme proprio dei linguaggi r.e.

La costruzione di una m.t. per il riconoscimento di un linguaggio dato L è sempre piuttosto complessa, anche se L è molto semplice. Sono allora stati studiati diversi ampliamenti del modello che risultano più comodi da impiegare, ma che non aumentano la potenza computazionale del modello originale, ovvero la famiglia dei linguaggi accettati. In particolare abbiamo i seguenti teoremi.

Teorema. Sia L il linguaggio accettato da una macchina di Turing X: 1) con nastro illimitato verso destra e verso sinistra; oppure 2) con k teste che agiscono contemporaneamente e indipendentemente sul nastro; oppure 3) con k teste che agiscono contemporaneamente e indipendentemente su k nastri indipendenti. Allora esiste una m.t. Y che accetta L.

Teorema. Sia X un qualsiasi calcolatore elettronico esistente, corredato di memoria infinita e di un programma per l'accettazione di stringhe (che abbia cioè uscita 0 o 1) e sia L l'insieme di stringhe accettate da X. Allora esiste una m.t. Y che accetta L.

La prova dei precedenti teoremi consiste nel mostrare come sia possibile costruire una m.t. Y che simula il funzionamento di X.

Anche per la macchina di Turing è significativo definire un modello non deterministico. Formalmente M = (S, Σ, Π, s′, b, F, ∂′) è una ‛macchina di Turing non deterministica' (brevemente m.t.n.d.) se, per lo stesso stato e lo stesso carattere letto sul nastro, si definiscono più mosse per la macchina. Il significato di S, Σ, Π, s′, b, F resta invariato, mentre la funzione di transizione ∂′ è ora definita da S×Π su 2^{SΠ×{Á,→}}. Una stringa è ‛accettata in t mosse' se almeno una delle computazioni cui tale stringa dà luogo raggiunge uno stato finale e la più breve computazione che raggiunge uno stato finale consiste di t mosse. Nonostante l'apparente potenziamento del modello, la famiglia dei linguaggi accettati dalle m.t.n.d. resta quella dei linguaggi r.e. Abbiamo infatti il seguente teorema.

Teorema. Se L è il linguaggio accettato da un'arbitraria m.t.n.d. X, esiste una m.t. Y che accetta L.

È interessante accennare alla prova di questo teorema. Stabilito, per ogni coppia (s, c), un ordinamento per tutti i valori della funzione ∂′(s, c) di X e indicato con k ≤ ∣ S×Π×{Á, →} ∣ il numero massimo di tali valori al variare della coppia (s, c), ciascuna delle computazioni di X per una stringa d'ingresso α potrà essere descritta con una sequenza di cifre comprese tra 1 e k, che indicano la scelta del valore ∂′ effettuata da X a ogni passo. La macchina Y genera ordinatamente una a una tutte le sequenze di cifre tra 1 e k, a partire dalle più corte. Nel nastro Y contiene α, seguita dalla sequenza di cifre β correntemente generata, seguita da una seconda copia di α su cui esegue la computazione. Questa avviene simulando la sequenza di mosse di X indicate passo per passo da β (se una cifra di β eccede il numero di mosse definite per X, Y si arresta). Se e solo se α ∈ L(X), Y si arresta accettando α.

Per quanto riguarda il numero di mosse eseguito dalle due macchine, possiamo osservare che una stringa α ∈ L accettata da X in t mosse è accettata da Y in t′ > k^t-1 mosse, con k costante.

Notiamo infatti che Y si arresta in corrispondenza della sequenza β′ che rappresenta la più breve computazione accettante di X e si ha t = ∣ β′ ∣. Poiché tutte le sequenze di lunghezza 〈 t vengono generate da Y prima della β′, e tra esse quelle di lunghezza t − 1 sono k^t-1 possiamo concludere che Y deve eseguire almeno k^t-1 simulazioni del funzionamento di X su α e che quindi il numero delle sue mosse t′ è (molto) maggiore di k^t-1.

Ammettendo che una mossa sia eseguita da una m.t. in tempo costante, i valori t e t′ rappresentano i ‛tempi di funzionamento' di X e Y per le stringhe accettate. Non ha invece particolare senso studiare il tempo di funzionamento di X, e quindi di Y, per una stringa α non accettata, poiché alcune computazioni potrebbero non terminare e non si può affermare che α non sarà accettata finché non si sono concluse tutte le computazioni.

Poiché il non determinismo non amplia la classe dei linguaggi accettati dalle macchine di Turing, gli studi di computabilità si conducono sulle m.t. (deterministiche). Il prezzo pagato è nel tempo di funzionamento, che cresce esponenzialmente se una m.t.n.d. X si simula con una m.t. Y nel modo sopra indicato. È importante però mettere in evidenza che la discussione precedente non esclude l'esistenza di una m.t. Y′ che accetti L in tempo inferiore a quello richiesto da Y, e in particolare in tempo polinomiale in t: quest'ultimo quesito è ancora irrisolto e sarà ripreso nella discussione generale sulla complessità di calcolo.

Nell'ambito dell'utilizzazione pratica dei calcolatori, le m.t.n.d. sono rappresentate da programmi ‛non deterministici' (n.d.), che prevedono l'esecuzione contemporanea di diverse frasi tutte egualmente accettabili. Ciò si ottiene in genere utilizzando il costrutto linguistico choicend A, che provoca la scelta non deterministica degli elementi di un insieme A, uno a uno. La computazione si divide quindi in ∣ A ∣ rami ogni volta che si incontra tale meccanismo, con lo stesso significato che la molteplicità di computazioni ha nella m.t.n.d.. Per essere praticamente eseguito su un singolo calcolatore, un programma n.d. X deve essere simulato da un programma deterministico Y, che realizza ogni costrutto choicend A scegliendo uno a uno in sequenza gli elementi di A. Il rapporto tra i tempi di esecuzione di X e Y è lo stesso indicato per le m.t.

I programmi non deterministici si prestano ad affrontare problemi risolubili in modo enumerativo, attraverso successioni di scelte. Un esempio importante è il seguente.

Problema della soddisfattibilità di espressioni logiche (P_sod). Data un'arbitraria espressione E costruita sulle variabili logiche x₁, ..., x_n con gli operatori ⋀, ⋀, ¬, stabilire se esiste un insieme di valori x₁′, ..., x_n′ che ‛soddisfi' la E, tale cioè che E(x₁′, ..., x_n′) = 1.

Un metodo per risolvere P_sod è quello di generare tutte le possibili n-ple di valori binari per x₁, ..., x_n e di valutare E per ciascuna di esse. Ciò è realizzato nel seguente programma n.d. di ovvio significato, in cui le n-ple vengono costruite nel vettore V attraverso l'assegnazione non deterministica dei valori 0, 1 a ogni suo elemento V[i]:

La E è soddisfatta se e solo se almeno una delle computazioni termina su ‛accetta'. Il tempo di funzionamento del programma nel caso di accettazione è, in ordine di grandezza, t ∈ O (n +t_E), ove n è il numero di operazioni per generare una n-pla e t_E è il tempo per calcolare il valore di E su tale n-pla.

Il programma n.d. può essere simulato in modo ovvio con uno deterministico, che costruisce sequenzialmente in V tutte le n-ple binarie, in un ordine preassegnato, e calcola il valore di E per ciascuna di esse. Poiché nel caso peggiore l'accettazione si stabilisce dopo aver esaminato 2ⁿ n-ple, il tempo richiesto è t′ ∈ O(2ⁿ • t_E) e cresce quindi esponenzialmente rispetto al tempo richiesto dal programma n.d.

6. Decidibilità e indecidibilità.

Abbiamo già incontrato varie volte problemi di decisione e abbiamo affermato l'esistenza o la non esistenza di procedure per risolverli. Discuteremo ora l'argomento in modo formale, impiegando la macchina di Turing come modello primitivo di calcolo.

Un problema ben posto deve avere una descrizione univoca, essere definito per uno o più ‛dati' e richiedere per essi un ‛risultato'. Da un punto di vista computazionale il problema è significativo se i dati possono assumere infiniti valori, ciascuno dei quali rappresenta un'‛istanza' del problema, e il risultato può assumere più di un valore. Non è infatti significativo un problema con un numero finito di istanze, poiché la computazione potrebbe ridursi alla consultazione di una tabella finita che listi i valori del risultato in funzione dei valori dei dati; né è significativo il caso in cui il risultato assuma un solo valore, perché, una volta noto per un'istanza, non sarebbe più necessario calcolarlo per le altre. Invece, come abbiamo già affermato, ha senso limitare lo studio a problemi che abbiano risultato binario (decisionali): in genere essi non chiedono di determinare una soluzione, ma solo di verificame una proprietà (per esempio l'esistenza) sufficientemente generale per mettere in luce la difficoltà intrinseca del problema.

Un esempio di problema decisionale con infinite istanze è P_sod, introdotto nel capitolo precedente. L'istanza generica è un'espressione E, il risultato è l'esistenza o meno di un insieme di valori delle variabili che soddisfi la E. Si noti che il procedimento indicato per risolvere P_sod scopre l'esistenza di una soluzione attraverso la sua generazione e potrebbe quindi essere applicato anche per determinare tale soluzione.

Codificate le istanze di un problema decisionale P come stringhe su un alfabeto, il linguaggio L relativo a P è definito come l'insieme delle istanze che prevedono risultato affermativo. Un procedimento di risoluzione di P può essere formalizzato come m.t. M, tale che L = L(M). Possiamo quindi trasformare il quesito sull'esistenza di una procedura effettiva di calcolo per P in uno equivalente sulla natura di L.

Se L è ricorsivo, esiste una procedura che genera sempre in tempo finito una risposta affermativa o negativa. In tal caso il problema P è ‛decidibile' e una m.t. che lo risolva è detta ‛algoritmo' per P. Se L non è ricorsivo il problema è ‛indecidibile' e non ammette algoritmo di risoluzione; tra tali problemi è comunque opportuno distinguere quelli che corrispondono a linguaggi r.e. da quelli che corrispondono a linguaggi non r.e., poichè per i primi esiste una m.t. che può non fornire tutte le risposte in tempo finito, per i secondi non esiste del tutto la m.t. Se le stringhe d'ingresso a una m.t. si interpretano come codifica di numeri naturali, la risoluzione di P corrisponde al calcolo di una funzione dai naturali su {0, 1}: problemi decidibili o indecidibili corrispondono allora a funzioni ‛calcolabili' o ‛non calcolabili'.

È a questo punto opportuno ricordare che le m.t. sono definite come gruppi di entità finite (S, Σ, Π, s′, b, F, ∂) e possono quindi essere descritte come stringhe di un opportuno alfabeto (in particolare si dimostra che è sufficiente l'alfabeto {0, 1} per descrivere tutte le m.t.). Tali stringhe possono poi essere ordinate alfabeticamente, dando luogo a un'enumerazione delle m.t., nella quale la macchina M_i corrisponde all'i-esima stringa dell'ordinamento. Similmente si possono enumerare le stringhe d'ingresso α per le m.t., indicando con α_i la stringa i-esima.

Indicheremo con M〈M> la stringa che descrive la m.t. M, con 〈M, α> la stringa che descrive M assieme alla sua stringa d'ingresso α. Sarà allora legittimo impiegare 〈M, α> come stringa d'ingresso per una diversa m.t. N, per rispondere a questioni circa il comportamento di M su α. N potrà simulare il funzionamento di M, svolgendo quindi la funzione di un calcolatore che esegue un arbitrario programma M sui dati α (si ricordi che una m.t. svolge in genere la funzione di un singolo programma).

L'argomento di conteggio sulla numerabilità delle procedure e la non numerabilità delle funzioni, introdotto nel cap. 1, può ora essere formalmente ripreso in relazione alla numerazione delle m.t. Tale argomento dimostra che devono esistere funzioni non calcolabili perché per esse non vi è m.t., ovvero devono esistere problemi indecidibili cui corrispondono linguaggi non r.e. Incontriamo ora il primo di questi linguaggi, detto ‛linguaggio diagonale' (L_d), composto da tutte le stringhe α_i che non sono accettate dalla m.t. M_i di pari indice.

Teorema. Il linguaggio L_d = {α_i ∣ α_i ∉ L(M_i), i = 0, 1, ...} non è r.e.

Il teorema si dimostra immediatamente notando che, comunque si costruisca l'enumerazione delle m.t., L_d non può essere accettato da alcuna di esse. Se infatti esistesse una M_j tale che L_d = L(M_j), la definizione di L_d condurrebbe alla contraddizione che α_j ∈ L_d se e solo se α_j ∉ L(M_j).

La scoperta che L_d non è r.e. permette di dimostrare l'indecidibilità di altri problemi, determinando la natura dei nuovi linguaggi in funzione della natura di L_d. Il primo di essi è relativo alla possibilità di stabilire se una m.t. arbitraria M accetta una stringa arbitraria α.

Teorema (Turing). Il linguaggio L_u = {〈M, α> ∣ α ∈ L(M)} è r.e. e non è ricorsivo.

L_u è detto ‛linguaggio universale', poiché pone la più generale delle questioni sulle macchine di Turing; la sua natura dimostra che i linguaggi ricorsivi sono un sottoinsieme proprio dei linguaggi r.e. In termini concreti il teorema afferma che non esiste algoritmo per stabilire il risultato di una computazione arbitraria (si noti che l'algoritmo non potrebbe consistere nella simulazione di tale computazione, poiché nel caso α ∉ L(M) la simulazione potrebbe non terminare in tempo finito).

Una conseguenza del teorema è che anche il linguaggio L_a = {〈M, a> ∣ la computazione di M su α si arresta} è r.e. e non è ricorsivo. Questo famoso risultato decreta l'indecidibilità del ‛problema dell'arresto' (P_a), ovvero stabilisce che non esiste algoritmo per decidere se una computazione arbitraria si arresta o meno.

I problemi indecidibili fin qui considerati pongono questioni sulle m.t., non sui linguaggi r.e. che esse accettano. Le questioni del secondo tipo sono di solito assai più generali. Si considerino per esempio i due linguaggi:

benché essi possano apparire simili, si ha L₁ ⊂ L₂, poiché il fatto che L(M) sia ricorsivo implica che esiste una m.t. M′ che lo accetta e si arresta sempre, ma non implica che sia M′ = M.

In effetti per le questioni inerenti i linguaggi r.e. vale un risultato generale di indecidibilità, espresso nel seguente teorema.

Teorema (Rice). Qualsiasi proprietà dei linguaggi r.e. è indecidibile, a meno che non sia banalmente verificata da tutti i linguaggi r.e. o da nessuno di essi.

Questo teorema ha ovviamente moltissime conseguenze, alcune delle quali sono espresse nel seguente corollario.

Corollario. Per un'arbitraria m.t. M, le questioni

sono indecidibili.

Per concludere l'argomento della decidibilità, accenniamo come esempio a due conseguenze dirette che i risultati esposti hanno nell'ambito delle applicazioni. La prima deriva dall'indecidibilità del problema dell'arresto P_a. Sarebbe molto utile poter inserire un ‛filtro' all'ingresso di un calcolatore, per decidere, prima di iniziare l'esecuzione di un programma, se questo terminerà la sua computazione o, presumibilmente perché contiene un errore, entrerà in un ciclo infinito. L'indecidibilità di P_a dimostra che tale filtro non può esistere.

La seconda conseguenza riguarda la possibilità di stabilire se due programmi A₁, A₂ sono equivalenti, cioè se per uguali dati producono uguali risultati. È questo il ‛problema dell'equivalenza' (P_e) e avrebbe grande importanza poterlo risolvere, per verificare, per esempio, se programmi scritti per calcolatori diversi generano esattamente gli stessi risultati. Notiamo però che per ogni programma arbitrario A e per dati arbitrari D, possiamo formulare il seguente programma A₁:

Chiaramente A₁ stampa ‛stop' se e solo se la computazione di A su D si arresta. D'altra parte possiamo anche formulare il programma A₂:

Poiché A₂ stampa sempre ‛stop', A₁ e A₂ sono equivalenti se e solo se la computazione di A su D si arresta. Un algoritmo per risolvere P_e consentirebbe allora di risolvere P_a, ma, poiché quest'ultimo problema è indecidibile, dobbiamo concludere che anche P_e è indecidibile, ovvero non esiste un algoritmo per decidere se due programmi sono equivalenti.

7. Complessità di calcolo.

L'argomento di conteggio attraverso il quale avevamo previsto l'esistenza dei problemi indecidibili permette di dimostrare, con opportuna estensione, che tali problemi sono la grande maggioranza di tutti i problemi possibili. E quindi piuttosto sorprendente che per scoprirli sia stato necessario il genio dei logici moderni, e forse l'unico modo di spiegare questa apparente contraddizione è che l'uomo tende a porsi spontaneamente problemi decidibili. E dunque a questi ultimi che ora ci riferiremo, con lo scopo di valutare la quantità di risorse di calcolo che essi richiedono: in particolare lo ‛spazio' e il ‛tempo'.

Ogni problema decidibile P è risolto da una m.t. (deterministica) M che si arresta per ogni istanza di P (M è un algoritmo per P). L'esistenza di M implica che P può essere risolto con infiniti algoritmi diversi, derivabili per esempio da M con banali aggiunte di mosse inutili; ma più interessante è considerare algoritmi che risolvano P con metodi sostanzialmente differenti e porli a confronto in base alla quantità di risorse richieste. Ciò conduce alle seguenti definizioni.

Nella computazione di M su un'arbitraria stringa d'ingresso α, sia s(α) il numero di celle diverse, oltre quelle contenenti α, visitate sul nastro dalla testa di M e sia t(α) il numero di mosse compiute da M. Considerato, per ogni numero naturale n, l'insieme A = {α ∣ ∣ α ∣ = n} di tutte le stringhe d'ingresso di lunghezza n, si dice che M ha ‛complessità in spazio' S(n) e ‛complessità in tempo' T(n), ponendo

Per ogni valore di n, la complessità di M in spazio e tempo si valuta dunque nel caso peggiore e costituisce un limite superiore alla complessità del problema P, poiché garantisce che P può essere risolto entro i valori S(n) e T(n). Si dice quindi che anche P ha complessità S(n) e T(n) in spazio e tempo, senza escludere l'esistenza di una diversa m.t. M′ che risolva P con complessità S′(n) 〈 S(n) e T′(n) 〈 T(n).

Definiamo ora le ‛classi di complessità' DSPAZIO(S(n)) e DTEMPO(T(n)) come le classi di tutti i problemi che hanno rispettivamente complessità in spazio S(n) e complessità in tempo T(n) (l'iniziale D nel nome delle classi indica che la m.t. risolvente è deterministica). Poiché per un'arbitraria m.t. di complessità in spazio o tempo f(n) è banalmente possibile costruirne un'altra che risolva lo stesso problema con complessità g(n) > f(n), abbiamo in genere DSPAZIO(f(n)) ⊆ DSPAZIO(g(n)) e DTEMPO (f(n)) ⊆ DTEMPO(g(n)). Il seguente teorema mostra che il contenimento è proprio e stabilisce una gerarchia tra le classi di complessità che contengono problemi sempre più complessi.

Teorema. Per ogni arbitraria funzione calcolabile f(n), esiste almeno un problema P tale che P ∉ DSPAZIO(f(n)) e P ∉ DTEMPO(f(n)).

Un importante legame tra le classi di spazio e tempo è espresso nel seguente teorema.

Teorema. Per un arbitrario problema P esiste una costante c tale che: 1) se P ∈ DTEMPO(f(n)), allora P ∈ DSPAZIO(cf(n)); 2) se P ∈ DSPAZIO(f(n)) e f(n) ≥ log₂ n, allora P ∈ DTEMPO(c^f(n)).

Il teorema mostra che la complessità in tempo è un parametro più critico della complessità in spazio, poiché può crescere esponenzialmente rispetto a quest'ultima. Approfondiremo quindi nel seguito lo studio della complessità in tempo T(n), che può essere anche detta semplicemente ‛complessità' quando tale dizione non sia ambigua, ricordando che esistono studi paralleli sulla complessità in spazio.

Si dice che una m.t. (o un algoritmo) M è ‛polinomiale' se esiste un polinomio p tale che, per ogni valore di n, sia T(n) ≤ p(n); il che equivale a dire che il problema P risolto da M appartiene a DTEMPO(p(n)). Ciò conduce alla definizione dell'importante classe P dei problemi per i quali esiste una m.t. polinomiale che li risolve:

Intuitivamente P è una classe di problemi che possono essere risolti efficientemente, poiché le m.t. deterministiche corrispondono agli usuali algoritmi programmabili e, come vedremo nel prossimo capitolo, la complessità polinomiale può essere ritenuta ragionevole anche per valori alti del grado del polinomio.

I concetti visti si estendono alla m.t. non deterministica M, e al problema P che essa risolve, con una puntualizzazione dovuta alla dissimmetria del funzionamento per le stringhe accettate e non accettate. Per una stringa d'ingresso α ∈ L(M), s(α) è il minimo numero di celle diverse visitate sul nastro, oltre quelle contenenti α, calcolato su tutte le computazioni di M e t(α) è il numero di mosse della computazione più breve. Se α ∉ L(M) si pone convenzionalmente s(α) = t(α) = 1. Considerato, per ogni n, l'insieme A = {α ∣ ∣ α ∣ = n}, le complessità in spazio e tempo di M e P si definiscono nuovamente come

Le nuove classi di complessità NDSPAZIO(S(n)) e NDTEMPO(T(n)) sono ora le classi di tutti i problemi che hanno rispettivamente complessità in spazio S(n) e complessità in tempo T(n) nel modello di calcolo non deterministico.

Limitando il nostro studio alla complessità in tempo, il risultato più generale sulla relazione tra le classi deterministiche e non deterministiche è espresso nel seguente teorema, che costituisce un sostanziale rafforzamento dell'osservazione sui tempi di funzionamento delle m.t. riportata nel cap. 5 (si noti che si pone ora un limite ‛superiore' alla complessità nel caso deterministico).

Teorema. Per un arbitrario problema P esiste una costante c tale che, se P ∈ NDTEMPO(f(n)), allora P ∈ DTEMPO(c^f(n)).

Anche una m.t.n.d. (o un algoritmo n.d.) M è detta ‛polinomiale' se esiste un polinomio p tale che, per ogni valore di n, sia T(n) ≤ p(n) ovvero se il problema P risolto da M appartiene a NDTEMPO(p(n)). Ciò conduce alla definizione della classe NP dei problemi per i quali esiste una m.t.n.d. polinomiale che li risolve:

Poiché possiamo considerare una m.t. come m.t.n.d. che non presenta mai scelte multiple, segue immediatamente dalle definizioni di P e NP la relazione: P ⊆ NP. Non esiste però alcuna prova che tale inclusione sia propria, cioè che P ≠ NP, benché ciò sia normalmente ritenuto vero a causa della capacità delle m.t.n.d. polinomiali di eseguire un numero esponenziale di computazioni, e della nostra ignoranza su un modo di ottenere gli stessi risultati con una m.t. polinomiale. In effetti il risultato più generale noto può essere espresso come corollario del teorema precedente, e nulla di sostanziale aggiunge alla nostra conoscenza sulla possibilità di simulare programmi non deterministici con programmi deterministici.

Corollario. Se un problema P può essere risolto da una m.t.n.d. in tempo polinomiale p(n), allora P può essere risolto da una m.t. in tempo c^p(n).

8. Problemi intrattabili.

La complessità gioca un ruolo fondamentale nello studio dell'efficienza degli algoritmi realizzati come programmi di un calcolatore. In questo caso la variabile indipendente n rappresenta lo spazio di memoria occupato dai dati d'ingresso, misurato come lunghezza della loro descrizione o qualunque numero proporzionale a essa; la funzione S(n) indica il massimo spazio di memoria occupato durante la computazione, misurato con lo stesso metro di n; la funzione T(n) indica il numero di operazioni elementari richiesto dalla computazione e risulta proporzionale al tempo di esecuzione del programma se si ammette che ogni operazione richieda lo stesso tempo costante.

Le funzioni S(n) e T(n) forniscono quindi valori proporzionali alle risorse di spazio e tempo richieste dal programma e si studiano in ordine di grandezza: questo permette di considerare tali funzioni come rappresentative dell'algoritmo prescelto, indipendentemente dal particolare calcolatore o linguaggio di programmazione impiegato. Come nel caso delle m.t., S(n) e T(n) costituiscono le ‛complessità in spazio' e ‛in tempo' del programma, o del problema che esso risolve; anche ora limiteremo lo studio alla funzione T(n), detta anche semplicemente ‛complessità'.

Per quanto esposto nel cap. 5 sui programmi non deterministici, la definizione della funzione T(n) può essere estesa a essi in modo ovvio. Le classi P e NP conservano il loro significato, poiché la loro definizione non è intaccata se la complessità si misura in ordine di grandezza, e restano valide le considerazioni fatte sulla loro relazione. In particolare, ricordando che i programmi non deterministici vengono simulati con programmi deterministici, dobbiamo limitare a P la classe dei problemi praticamente risolubili in tempo polinomiale.

I problemi per cui esistono, o sono noti, solo algoritmi di soluzione di complessità esponenziale sono detti ‛intrattabili', poiché il tempo richiesto per il calcolo cresce smisuratamente al crescere di n. Ovviamente anche un algoritmo polinomiale di grado molto elevato può richiedere un tempo inaccettabile al crescere di n, ma l'esistenza di un tale algoritmo autorizza a mantenere il problema tra quelli per cui vi è almeno speranza di soluzione futura, per il seguente non ovvio motivo.

Poniamo che un algoritmo di complessità polinomiale T(n) = n^c e uno di complessità esponenziale T(n) = cⁿ possano essere praticamente risolti fino a un (piccolo) valore di n su un calcolatore disponibile, e studiamo come cresce questo valore se si impiega un calcolatore più veloce. Detto m il nuovo valore trattabile in pari tempo di calcolo e osservando che impiegare un calcolatore k volte più veloce equivale a impiegare il calcolatore originale per un tempo k volte maggiore, abbiamo per l'algoritmo polinomiale: m^c = kn^c, cioè m = k^1/cn, che corrisponde a un incremento sensibile, benché percentualmente decrescente al crescere del grado c del polinomio. Per l'algoritmo esponenziale abbiamo invece c^m = kcⁿ, cioè m = log_c k + n, che corrisponde a un incremento trascurabile. Concludiamo che gli algoritmi di complessità esponenziale non traggono alcun giovamento dai progressi tecnologici dei calcolatori e rimangono inevitabilmente inefficienti.

Benché sia possibile dimostrare che alcuni problemi sono sicuramente intrattabili, poiché richiedono tempo esponenziale anche in un modello di calcolo non deterministico, quasi tutti i problemi intrattabili interessanti appartengono a NP: non si conosce cioè alcun algoritmo polinomiale deterministico per risolverli, ma non vi è prova che tale algoritmo non esista. Il meccanismo di base per indagare sui problemi intrattabili è quello di ‛riduzione'. Presi due problemi P₁, P₂ e i relativi linguaggi L₁, L₂ ⊆ Σ* (insiemi delle istanze che prevedono risultato affermativo per P₁ e P₂), una ‛riduzione polinomiale' da P₁ a P₂ è una funzione f: Σ* → Σ* tale che: 1 ) esiste un algoritmo polinomiale deterministico F che calcola f (si noti che in questo caso F non è un semplice algoritmo decisionale); 2) per ogni v ∈ Σ* si ha v ∈ L₁ se e solo se f(v) e L₂. Si dice allora che P₁ si riduce a P₂ e ciò si indica con P₁ ⇒ P₂. Si noti che la riduzione polinomiale è transitiva, cioè P₁ ⇒ P₂ e P₂ ⇒ P₃ implica P₁ ⇒ P₃.

L'importanza della riduzione da P₁ a P₂ deriva dalla considerazione che un algoritmo A₂ per risolvere P₂ può essere usato per risolvere P₁ attraverso le computazioni successive di F su v e di A₂ su f(v). Poiché F è polinomiale, la computazione complessiva ha la complessità di A₂, per cui P₂ ∈ P implica P₁ ∈ P, mentre P₂ ∈ NP implica P₁ ∈ NP, pur senza escludere che esista un algoritmo polinomiale deterministico per P₁: questa situazione si descrive dicendo che ‛P₂ è difficile almeno quanto P₁'. Se P₁ ⇒ P₂ e P₂ ⇒ P₁ due problemi si dicono ‛polinomialmente equivalenti' e sono ‛ugualmente difficili'.

Dalla discussione precedente discende che se tutti i problemi della classe NP si riducessero a uno di essi, questo sarebbe il più difficile problema di tale classe e sarebbe quindi il primo candidato a trovarsi in NP − P nel caso che fosse P ≠ NP. La ricerca di tale problema ha quindi importanza fondamentale nello studio della relazione tra le due classi.

Formalmente un problema P si dice ‛NP-completo' se P ∈ NP e per ogni altro problema P′ ∈ NP si ha P′ ⇒ P. I problemi NP-completi sono dunque i più difficili problemi in NP e sono tutti polinomialmente equivalenti. Come vedremo, se ne conoscono moltissimi, e il primo individuato tra questi è il problema della soddisfattibilità P_sod, già citato nel cap. 5. Si ha infatti il seguente teorema.

Teorema (Cook). P_sod è NP-completo.

La dimostrazione del teorema di Cook è piuttosto complessa. In sostanza, dopo aver provato che P_sod appartiene a NP, essa mostra come, per qualsiasi m.t.n.d. polinomiale M e per qualsiasi stringa d'ingresso α, Si possa costruire in tempo polinomiale un'espressione logica E che è soddisfatta se e solo se M accetta α. (Ricordiamo che il problema generale di stabilire se una m.t. accetta una stringa, espresso nel linguaggio L_u del cap. 6, è indecidibile. La M scelta sopra è però polinomiale e quindi non arbitraria: in particolare si arresta per ogni stringa d'ingresso).

La scoperta del primo problema NP-completo P_sod è di estrema importanza, poiché permette di dimostrare che altri problemi P ∈ NP sono NP-completi provando semplicemente che P_sod ⇒ P. In genere la classe dei problemi NP-completi si arricchisce di nuovi membri mostrando che un problema qualsiasi della classe si riduce a essi.

Poiché i problemi NP-completi sono polinomialmente equivalenti, l'esistenza di un algoritmo polinomiale deterministico per risolvere uno di essi implicherebbe che tutti i problemi NP-completi, e quindi tutti i problemi in NP, potrebbero essere risolti in pari tempo. Si avrebbe allora P = NP. Il fatto che tanti studi sull'argomento abbiano prodotto solo algoritmi esponenziali conforta la congettura che sia P ≠ NP, ma non sembra vicina la prova che tale affermazione sia vera o falsa, decidibile o indecidibile.

Un'altra osservazione importante su queste classi deriva dallo studio del ‛problema complementare' P^c per ogni problema P, definito in modo che abbiano risposta affermativa in P^c tutte e sole le istanze che hanno risposta negativa in P (dal punto di vista dei relativi linguaggi, poniamo L^c = {Σ* − L}). Per esempio Pc_sod ha per definizione risposta affermativa per tutte e sole le espressioni logiche non soddisfattibili. Dall'ipotesi che P sia decidibile discende che anche P^c è decidibile, poiché può essere risolto da una m.t. M^c che accetta l'ingresso se e solo se questo non è accettato dalla m.t. M che risolve P.

Consideriamo ora le classi dei problemi complementari di P e NP:

co-P = {P^c ∣ P ∈ P}, co-NP = {P^c ∣ P ∈ NP}.

Se la M scelta per risolvere P è deterministica, una M^c per P^c si costruisce semplicemente in forma anch'essa deterministica, invertendo in M le condizioni di accettazione e non accettazione. Ne risulta che M e M^c hanno la stessa complessità e quindi P = co-P. Se invece M è stata scelta in forma non deterministica, la suddetta costruzione per M^c non è più valida, poiché M^c deve accettare l'ingresso se e solo se tutte le computazioni di M terminano con non accettazione. Nulla cioè risulta per questa via sulla relazione tra NP e co-NP, ma è lecita la congettura che sia NP ≠ co-NP, poiché essa è più forte della P ≠ NP: infatti, poiché P = co-P, la NP ≠ co-NP implica P ≠ NP.

In effetti per molti problemi in co-NP non è noto il contenimento in NP, e in particolare ciò non è noto per tutti i problemi NP-completi. Vale infatti il seguente risultato.

Teorema. Se esiste un problema NP-completo P e P^c ∈ NP, allora NP = co-NP.

La classe dei problemi NP-completi contiene un grandissimo numero di problemi nati in campi diversi. Rimandiamo alla bibliografia per una elencazione anche approssimativa, citandone qui, oltre P_sod, tre di particolare importanza.

Problema del commesso viaggiatore (P_cv) Dato un grafo G di n vertici, ai cui spigoli sono associati pesi interi positivi, e un intero positivo k, stabilire se esiste in G un ciclo hamiltoniano la cui somma dei pesi sia ≤ k.

Problema dell'impaccamento (P_i). Dati un insieme A di n interi positivi e due interi positivi h, k, stabilire se esiste una partizione di A in k sottoinsiemi, tale che la somma degli elementi in ogni sottoinsieme sia ≤ h.

Problema delle equazioni diofantee quadratiche (P_edq). Dati tre interi positivi, a, b, c, di n cifre, stabilire se l'equazione ax² + by + c = 0 ha radici intere.

P_cv, P_i e P_edq sono rispettivamente i capostipiti, in forma decisionale, dei problemi di percorsi su grafi, dei problemi di allocazione in una o più dimensioni e dei problemi sulla risoluzione intera di equazioni. Se si passa dalla forma decisionale a una più generale forma risolvente, chiedendo che si generi una soluzione per tali problemi, essi diventano ‛difficili almeno quanto' i corrispondenti problemi decisionali e restano pertanto intrattabili.

A causa dell'importanza pratica di numerosissimi problemi intrattabili, sono state esplorate nuove vie di soluzione. Si è così sviluppata la teoria degli ‛algoritmi approssimati', in cui le soluzioni si ottengono in tempo polinomiale con preassegnata approssimazione, e quella degli ‛algoritmi probabilistici', in cui le soluzioni generate sono corrette con preassegnata probabilità. Questi argomenti potranno essere studiati nella letteratura specializzata.

9. I principali studi sull'argomento.

Per un primo approfondimento della teoria della computazione è utile riferirsi ad alcuni libri di testo, che forniscano un sicuro ancorché essenziale riferimento. Testi classici di computabilità sono quelli di Davis (v., 1958) e di Rogers (v., 1967), mentre la complessità di calcolo ha trovato una trattazione organica in tempi molto recenti con un testo di Aho, Hopcroft e Ullman (v., 1974), che ha influenzato grandemente la progettazione di algoritmi. Tra i testi più recenti e agili, che contengono elementi sia di computabilità che di complessità, ricordiamo quelli di Hopcroft e Ullman (v., 1979), Lewis e Papadimitriou (v., 1981), Davis e Weyuker (v., 1983), Salomaa (v., 1985) e quello di Börger (v., 1985), che mette in luce la relazione tra la teoria della computazione e la logica. Tra i contributi in lingua italiana ricordiamo una significativa opera di Ausiello (v., 1975) sulla computabilità e una introduzione di Luccio (v., 1982) alla complessità, rivolta alla costruzione di algoritmi efficienti.

Seguiamo ora, nella letteratura specializzata, le origini e i principali sviluppi degli argomenti trattati in questo articolo. Gli automi finiti furono introdotti da McCulloch e Pitts (v., 1943) come modelli di reti neuroniche e furono poi sviluppati da Huffman (v., 1954) e numerosissimi altri autori in relazione ai sistemi elettronici. Il modello di automa non deterministico e la sua relazione con quello deterministico si deve a Rabin e Scott (v., 1959). Le proprietà citate per i linguaggi regolari si devono a Bar-Hillel, Perles e Shamir (v., 1961) e a numerosi altri autori. L'equivalenza tra automi è conseguenza di risultati di Huffman (v., 1954) e Nerode (v., 1958). Due noti libri che trattano di automi finiti sono opera di Minsky (v., 1967) e Arbib (v., 1970).

Gli automi a pila e la loro relazione con i linguaggi liberi sono stati inizialmente studiati da Oettinger (v., 1961), Chomsky (v., 1962) e Schutzenberger (v., 1963). Molti altri autori hanno trattato l'argomento, per il quale rimandiamo ai fondamentali testi di Ginsburg (v., 1966), Hopcroft e Ullman (v., 1969) e Salomaa (v., 1973).

La macchina di Turing, con la prima dimostrazione di indecidibilità, fu proposta da Turing (v., 1936-1937). Altri equivalenti modelli di calcolo furono proposti da Kleene (v., 1936), Church (v., 1941), Post (v., 1943) e Kolmogorov e Uspenskij (v., 1958). Il teorema di Rice è apparso in Rice (v., 1953). Ottime fonti per approfondire questo campo sono i già citati testi sulla calcolabilità e un'ulteriore opera di Davis (v., 1965). La prova di equivalenza tra la macchina di Turing e i calcolatori elettronici può essere studiata in Aho e altri (v., 1974).

Dopo alcuni studi pioneristici sulla difficoltà di calcolo delle funzioni, il primo contributo organico di complessità di calcolo si fa risalire a Hartmanis e Stearns (v., 1965). Contemporanea è l'individuazione da parte di Edmonds dei problemi in P (v. Edmonds, 1965). Lo studio dei problemi NP-completi è nato con il fondamentale lavoro di Cook (v., 1971), immediatamente sviluppato da Karp (v., 1972). La più completa trattazione disponibile su tali problemi è contenuta nell'importante testo di Garey e Johnson (v., 1979). Tra i tanti testi di complessità concreta ricordiamo quelli di Savage (v., 1976) e di Papadimitriou e Steiglitz (v., 1982).

Mentre il problema sulle classi di complessità si sta spostando verso la logica (v., per es., De Millo e Lipton, 1979; v. Börger, 1985), si sviluppa la teoria degli algoritmi approssimati e probabilistici (v. Rabin, 1977) e la teoria degli algoritmi paralleli, in appoggio allo sviluppo dei circuiti elettronici integrati (v., per es., Haines e altri, 1982). Una utilissima rassegna bibliografica sull'intero argomento e dovuta a Cook (v., 1983).

Bibliografia.

Aho, A. V., Hopcroft, J. E., Ullman, J. D., The design and analysis of computer algorithms, Reading. Mass., 1974.

Arbib, M. A., Theories of abstract automata, Englewood Cliffs 1970.

Ausiello, G., Complessità di calcolo delle funzioni, Torino 1975.

Bar-Hillel, Y., Perles, M., Shamir, E., On formal properties of simple phrase structure grammars, in ‟Zeitschrift für Phonetik. Sprachwissenschaft und Kommunicationsforschung", 1961, XIV, pp. 143-172.

Börger, E., Berechenbarkeit, Komplexität, Logik, Braunschweig 1985.

Chomsky, N., Context-free grammars and pushdown storage, in ‟MIT. Research laboratory of electronics. Quarterly progress report", 1962, n. 65.

Church, A., The calculi of lambda-conversion, Princeton 1941.

Cook, S. A., The complexity of theorem proving procedures, in Proceedings of the 3rd Association for Computing Machinery symposium on theory of computing,New York 1971.

Cook, S. A., An overview of computational complexity, in ‟Comcomunications of the Association for Computing Machinery", 1983, XXVI, pp. 400-408.

Davis, M., Computability und unsolvability, New York 1958.

Davis, M. (a cura di), The undecidable, New York 1965.

Davis, M., Weyuker, E., Computability, complexity and languages, New York 1983.

De Millo, R., Lipton, R., Some connections between mathematical logic and complexity theory, in Proceedings of the 11th Association for Computing Machinery symposium on theory of computing, Conference record, New York 1979.

Edmonds, J., Paths, trees, flowers, in ‟Canadian journal of mathematics", 1965, XVII, pp. 449-467.

Garey, M. R., Johnson, D. S., Computers and intractability, San Francisco 1979.

Ginsburg, S., The mathematical theory of context-free languages, New York 1966.

Haines, L.S., Lau, R. L., Siewiorek, D. P., Mizell, D. W., A survey of high parallel computing, in ‟Computer", 1982, XV, pp. 9-24.

Hartmanis, J., Stearns, R.E., On the computational complexity of algorithms, in ‟Transactions of the American Mathematical Society", 1965, CXVII, pp. 285-306.

Hopcroft, J.E., Ullman, J. D., Formal languages and their relation to automata, Reading, Mass., 1969.

Hopcroft, J. E., Ullman, J.D., Introduction to automata theory, languages and computation, Reading, Mass., 1979.

Huffman, D. A., The synthesis of sequential switching circuits, in ‟Journal of the Franklin Institute", 1954, CCLVII, pp. 161-190, 275-303.

Karp, R. M., Reducibility among combinatorial problems, in Complexity of computer computations (a cura di R. E. Miller e J. W. Tatcher), New York 1972.

Kleene, S. C., General recursive functions of natural numbers, in ‟Mathematische Annalen", 1936, CXII, pp. 727-742.

Kolmogorov,A. N.,Uspenskij, V. A., On the definition of an algorithm, in ‟Uspechi Matematičeskich Nauk", 1958, XIII, pp. 3-28.

Lewis, H. R., Papadimitriou, C. H., Elements of the theory of computation, Englewood Cliffs, N. J., 1981.

Luccio, F., La struttura degli algoritmi, Torino 1982.

McCulloch, W. S., Pitts, W., A logical calculus of the ideas immanent in nervous activity, in ‟Bulletin of mathematical biophysics", 1943, V, pp. 115-133.

Minsky, M. L., Computation: finite and infinite machines, Englewood Cliffs, N. J., 1967.

Nerode, A., Linear automaton transformations, in ‟Proceedings of the American Mathematical Society", 1958, IX, pp. 541-544.

Oettinger, A. G., Automatic syntactic analysis and the pushdown store, in ‟Proceedings of symposia in applied mathematics of the American Mathematical Society", 1961, XII.

Papadimitriou, C. H., Steiglitz, K., Combinatorial optimization: algorithms and complexity, Englewood Cliffs, N. J., 1982.

Post, E., Formal reduction of the general combinatorial decision problem, in ‟American journal of mathematics", 1943, LXV, pp. 197-215.

Rabin, M. O., Complexity of computations, in ‟Communications of the Association for Computing Machinery", 1977, XX, pp. 652-633.

Rabin, M. O., Scott, D., Finite automata and their decision problems, in ‟IBM journal of research", 1959, III, pp. 115-125.

Rice, H. G., Classes of recursively enumerable sets and their decision problems, in ‟Transactions of the American Mathematical Society", 1953, LXXXIX, pp. 25-59.

Rogers, H. Jr., The theory of recursive functions and effective computability, New York 1967.

Salomaa, A., Formal languages, New York 1973.

Salomaa, A., Computation and automata, Cambridge 1985.

Savage, J. E., The complexity of computing, New York 1976.

Schutzenberger, M. P., On context-free languages and pushdown automata, in ‟Information and control", 1963, III, pp. 246-264.

Turing, A. M., On computable numbers with an application to the Entscheidungsproblem, in ‟Proceedings of the London Mathematical Society" (II Series), 1936, XLII, pp. 230-265; 1937, XLIII, pp. 544-546.

Algoritmi e strutture dei dati di Franco P. Preparata

SOMMARIO: 1. Introduzione. 2. La nozione di algoritmo: a) requisiti; b) la macchina di Turing. □ 3. Algoritmi: presentazione ed efficienza: a) il modello RAM e la presentazione degli algoritmi; b) complessità computazionale. 4. Strutture dei dati e paradigmi algoritmici: a) strutture dei dati; b) paradigmi algoritmici. 5. Conclusione. □ Bibliografia.

1. Introduzione.

Sebbene lo sviluppo di procedimenti di calcolo abbia interessato la mente umana da tempi remoti, il raffinamento del concetto di algoritmo come entità matematica rappresenta una conquista relativamente recente. Uno stimolo potente alla ricerca sugli algoritmi è stato fornito negli ultimi decenni dall'apparizione di strumenti automatici di calcolo, gli elaboratori elettrornci. Non solo la nozione di algoritmo è stata formalizzata, ma lo sviluppo di algoritmi e lo studio della loro efficienza sono al centro della disciplina nota come ‛informatica'.

Tipicamente, un algoritmo eseguito da un elaboratore opera una trasformazione di informazione in informazione. L'informazione, cioè i ‛dati', riveste un ruolo di importanza pari a quella del procedimento. Quindi lo studio dei dati, e della loro organizzazione, è importante quanto quello degli algoritmi. Infatti, come è stato osservato da vari autori (v., per esempio, Hoare, 1972), la relazione tra algoritmi e strutture dei dati è profonda, e N. Wirth ha giustamente suggerito l'espressione: algoritmi + strutture dei dati = programmi.

Questo articolo intende illustrare concisamente questa importante relazione, naturalmente con tutte le omissioni che la limitazione di spazio comporta. Nella prima parte si tenta di precisare la nozione di algoritmo, partendo dalla sua accezione prematematica per approdare alla sua formalizzazione nella macchina di Turing e nella tesi di Church-Turing. Nella seconda parte si considera il problema dell'efficienza degli algoritmi nel modello di calcolo oggi prevalente, cioè l'elaboratore di von Neumann. Ciò comporta un esame della rappresentazione degli algoritmi e dei criteri di valutazione della loro efficienza. Quindi la relazione tra algoritmi e organizzazione dei dati viene approfondita, illustrando alcune fondamentali strutture dei dati e alcuni importanti paradigmi algoritmici.

2. La nozione di algoritmo.

Nonostante le superficiali suggestioni di natura lessicale, il termine ‛algoritmo' non è associato nè ad ‛algebra' nè ad ‛aritmetica', ma deriva dal nome del matematico persiano Muḥammad ibn Mūsa al-Khuwārizmī, vissuto nel IX secolo. Al-Khuwārizmī (letteralmente ‛nativo di Khuwārizm'), uno dei maggiori pensatori della sua epoca, operò una fusione delle nozioni matematiche greche e indù e, agendo come tramite per il flusso di conoscenze, ebbe un'enorme influenza sullo sviluppo scientifico del Medioevo europeo. In realtà al-Khuwārizmī si occupò solo marginalmente di procedimenti di calcolo, tipicamente nella risoluzione analitica di equazioni lineari e quadratiche. Infatti il termine ‛algoritmo', nella versione arcaica ‛algorismo', veniva usato nel XIII secolo per denotare il sistema di numerazione arabo e, successivamente, i metodi dell'aritmetica (alla quale circostanza probabilmente va attribuita l'erronea attrazione lessicale). Solo in tempi più recenti, e in maniera definitiva negli ultimi decenni, il termine ha assunto la connotazione inequivocabile di procedimento formale di calcolo, che ci accingiamo a discutere.

a) Requisiti.

Intuitivamente, un algoritmo è una sequenza di operazioni avente come obbiettivo il conseguimento di un risultato designato. Pertanto un algoritmo presuppone un esecutore, tipicamente un essere umano (o qualunque dispositivo che possa soddisfacentemente sostituirlo in questa attività). In altre parole, dal punto di vista intuitivo, un algoritmo è un metodo per risolvere un problema, e un problema è considerato ‛risolubile' se si è prodotto un metodo per la sua soluzione. Chiaramente non si tratta di un concetto matematico; una sua formalizzazione (matematica) va accettata nella misura in cui costituisce un modello soddisfacente della nozione intuitiva.

Algoritmo è sinonimo di metodo o procedura; per esempio, una ricetta di cucina appartiene a questa classe intuitivamente definita in quanto essa prescrive come realizzare un piatto attraverso una successione di operazioni riguardanti quantità di ingredienti, tempi di cottura, eventuali azioni meccaniche, ecc. Nonostante la banalità della similitudine, una ricetta culinaria possiede alcune delle caratteristiche essenziali di un algoritmo, ma, come vedremo, generalmente difetta dell'importante attributo della definitezza.

Per apprezzare i requisiti fondamentali di un algoritmo è conveniente esaminare un esempio classico, l'‛algoritmo euclideo' per calcolare il massimo comune divisore MCD(m, n) di due interi m ed n. L'algoritmo è presentato qui come una sequenza di passi (intesi come ‛istruzioni' per l'esecutore), convenientemente numerati per facilitarne il riferimento:

1. Considerare due numeri, m ed n. Andare al passo 2.

2. Sottrarre n da m, e sia r la loro differenza. Andare al passo 3.

3. Se r = 0, allora MCD(m, n) = m e il processo termina; altrimenti, andare al passo 4.

4. Se r > 0, sostituire m con n e n con r, e andare al passo 2; altrimenti, andare al passo 5.

5. Scambiare m ed n, e andare al passo 2.

Questo semplice procedimento può essere eseguito senza alcuna difficoltà da chiunque abbia elementare dimestichezza con l'aritmetica (sottrazione e valutazione del segno). Innanzitutto sono dichiarati i dati (passo 1) e il risultato (passo 3); le operazioni - sottrazione, verifica di condizioni, scambio di dati, rinvio all'istruzione successiva - non danno luogo ad alcun equivoco d'interpretazione e ciascuna di esse è eseguibile speditamente; infine è possibile dimostrare che l'esecuzione termina sempre dopo un numero finito di passi. Ciò ci porta a enucleare le seguenti caratteristiche: 1. Specifica dei dati. Un insieme di zero o più dati viene fornito prima dell'inizio dell'esecuzione dell'algoritmo. Ciascun dato appartiene a un insieme ben definito, per esempio gli interi, ovvero i numeri razionali, ecc. (nell'esempio precedente i dati sono gli interi m ed n).

2. Specifica dei risultati. Un insieme di uno o più risultati è disponibile quando l'esecuzione dell'algoritmo termina. Ciascun risultato appartiene a un insieme ben definito (nell'esempio precedente il risultato è un intero).

3. Definitezza ed eseguibilità. Le azioni dell'algoritmo sono espresse in modo preciso, cioè appartengono a un insieme di operazioni, ciascuna delle quali è stata precedentemente specificata in maniera non ambigua. Inoltre, ciascuna delle possibili azioni deve essere eseguibile in un tempo finito (nell'esempio precedente le azioni sono la sottrazione, lo scambio di dati e la verifica di condizione: confronto di r con 0).

4. Terminazione, L'esecuzione dell'algoritmo termina dopo un numero finito di passi, per tutte le scelte ammissibili dei dati.

È facile rendersi conto che la verifica delle proprietà 1, 2 e 3 è un'operazione di natura relativamente semplice, in quanto comporta un'ispezione locale del testo dell'algoritmo, mentre la verifica della proprietà 4 implica l'analisi del comportamento dell'algoritmo e rientra nella verifica generale della sua correttezza, che consiste nell'accertarsi se l'algoritmo consegua o meno l'obbiettivo designato. La verifica di correttezza è un problema molto delicato, sul quale ritorneremo nel seguito.

La proprietà 3 merita un'ulteriore analisi, che ci condurrà a una definizione formale di algoritmo. Innanzitutto, l'‛eseguibilità' - cioè la possibilità di eseguire ciascuna operazione in un tempo finito - fa pensare, in prima istanza, a un esecutore umano fornito di carta e matita. Quando si aggiunga il requisito di non ambiguità, ci si rende conto che si fa appello alla diligenza e non alle capacità interpretative dell'esecutore, e che pertanto quest'ultimo può essere convenientemente sostituito da un dispositivo automatico. In conclusione, definitezza ed eseguibilità richiedono che siano forniti: a) un ‛linguaggio' (una rappresentazione simbolica), per esprimere le istruzioni impiegabili nell'algoritmo; b) una ‛macchina' (anche astratta), che possa interpretare ciascuna delle espressioni del linguaggio in maniera univoca come un'istruzione, ed eseguirla correttamente.

A prima vista può sembrare che le scelte di linguaggio e macchina comportino severe restrizioni rispetto a ciò che si suppone eseguibile da un essere umano con carta e matita. Questo punto importante verrà ulteriormente discusso nel seguito, dove, attraverso la nozione di equivalenza di macchine di Turing, verrà mostrata la generalità della scelta presente.

Il linguaggio consiste di un insieme finito di ‛stringhe' di simboli appartenenti a un alfabeto finito R; ciascuna stringa rappresenta un'istruzione eseguibile dalla macchina.

La macchina avrà due componenti fondamentali: a) la ‛memoria' per conservare le informazioni (dati iniziali, risultati intermedi e finali). Le informazioni sono rappresentate come stringhe di simboli di un alfabeto finito A; b) l'‛unità operativa e di controllo', per eseguire le operazioni elementari sui dati e per selezionare, una volta completata l'esecuzione di un'istruzione, l'azione da intraprendere successivamente (cioè quale istruzione eseguire o se terminare l'esecuzione).

Nell'ambito di queste direttive generali possiamo ora descrivere la macchina astratta definita da A. M. Turing nel 1936, e nota appunto come ‛macchina di Turing' (v. Turing, 1936-1937; v. Minsky, 1967; v. Lewis e Papadimitriou, 1981).

b) La macchina di Turing.

La memoria della macchina di Turing consiste in un nastro unidimensionale di lunghezza illimitata, suddiviso in celle, ciascuna delle quali è atta a contenere un simbolo dell'alfabeto A o l'assenza di simbolo * (denotato anche come simbolo ‛vuoto'). L'ipotesi di lunghezza illimitata serve solo ad assicurare che la macchina abbia sempre a disposizione tutta la lunghezza di nastro necessaria all'esecuzione del processo. Il tempo è discretizzato, cioè è suddiviso in unità - artificialmente concepite di durata costante - durante ciascuna delle quali la macchina compie un ‛passo' elementare. L'ingresso (lettura dal nastro) e l'uscita (scrittura sul nastro) di un simbolo avvengono per mezzo di una testina τ di lettura-scrittura, che può scorrere sul nastro; le celle del nastro definiscono le posizioni assumibili da τ in lettura o scrittura. Si assume che la macchina legga automaticamente il simbolo sul quale τ è posizionata.

L'unità operativa e di controllo, oltre che al nastro di memoria, ha accesso al ‛programma', cioè a una lista di comandi, o istruzioni, numerati consecutivamente (il numero di un'istruzione viene chiamato ‛etichetta' e identifica l'istruzione). L'unità può accedere a qualunque linea del programma, le cui istruzioni rappresentano le azioni eseguibili dalla macchina. Sorprendentemente, le istruzioni sono strutturalmente molto semplici e in numero molto limitato, e riguardano: scrittura sul nastro, movimento della testina e scelta dell'istruzione successiva. In dettaglio, abbiamo il seguente repertorio:

R: muovere τ di una cella a destra;

L: muovere τ di una cella a sinistra;

a: scrivere a ∈ A al posto del simbolo correntemente letto;

Sk: saltare incondizionatamente all'istruzione di etichetta k;

Sak: saltare all'istruzione di etichetta k se a ∈ A è il simbolo correntemente letto;

H: arresto.

(Si noti che questa formulazione suppone un meccanismo implicito per il ‛trasferimento di controllo', cioè per l'accesso all'istruzione successiva. Normalmente questo consiste nell'eseguire l'istruzione di etichetta (k + 1) dopo l'istruzione di etichetta k; le istruzioni di ‛salto' - Sk e Sak - consentono di deviare da questo meccanismo rigido). In conclusione, la macchina di Turing ha la struttura illustrata nella fig. 1, dove è mostrata mentre esegue l'istruzione b_k di etichetta k (b_k è rappresentata come una stringa sull'alfabeto B = A ⋃ {R, L, S, H} ⋃ K, dove K ⊆ ???OUT-N??? è l'insieme delle etichette delle istruzioni del programma). In questa formulazione l'unità di controllo è un automa a stati finiti, i cui dati di ingresso sono sia il simbolo letto da τ che l'istruzione. Una formulazione equivalente, che concettualmente separa i dati dal programma, si ottiene incorporando il programma nella struttura dell'unità di controllo. In tal modo ciascuna etichetta identifica uno stato della macchina. Formalmente la macchina di Turing M può essere definita come un sistema [K, A′, D, δ, k₀], dove:

K è l'insieme degli stati;

A′ = A ⋃ {*} è l'insieme dei simboli di ingresso/uscita;

D = {N, R, L} è l'insieme degli spostamenti della testina (N: nessuno spostamento, R: spostamento di una cella a destra, L: spostamento di una cella a sinistra);

δ = K × A′ → K × A′ × D è una funzione dallo stato corrente di M e dal simbolo corrente d'ingresso al simbolo corrente d'uscita, allo stato successivo di M e allo spostamento successivo di τ;

k₀ ∈ K è lo stato iniziale di M.

In questa formulazione la funzione δ, e quindi M stessa, sono descritte da un insieme finito di quintuple della forma: (stato corrente, ingresso corrente, stato successivo, uscita corrente, movimento successivo).

Si noti che la restrizione di D ai due elementi {N, R} (cioè l'eliminazione di L) specializza il modello di macchina di Turing a quello di automa o macchina a stati finiti. Ciò può fornire l'incauto suggerimento che la macchina di Turing sia essenzialmente un'estensione minore della macchina a stati finiti; la superficialità di quest'ipotesi, tuttavia, è resa evidente dal fatto che ogni estensione finora proposta della macchina di Turing - attraverso l'introduzione di più testine sul nastro, ovvero di più nastri, ovvero di nastri pluridimensionali - può migliorarne le prestazioni, nel senso che può ridurre il tempo impiegato a completare un calcolo, ma non ne altera le capacità, nel senso che non altera la classe di problemi da essa risolubili.

Per precisare questo concetto è opportuno analizzare la nozione di ‛problema risolubile'. Data una macchina di Turing M, il nastro iniziale contiene una stringa u sull'alfabeto A_IN ⊆ A′, delimitata da entrambi i lati da stringhe seminfinite di *. Il calcolo viene iniziato con τ posizionata sul primo simbolo di u; se, per ogni u, M termina nello stato H e il nastro contiene una stringa v sull'alfabeto A_OUT ⊆ A′ (similmente delimitata) e v = f(u), si dice che M calcola la funzione f da stringhe a stringhe e che la funzione f è Turing-calcolabile. Si noti che se il nastro iniziale non è del tipo specificato, l'operazione di M può non terminare mai. Allora, l'equivalenza tra macchine diverse viene stabilita attraverso il processo (concettuale) di ‛simulazione', nel quale si mostra costruttivamente che, data una macchina non standard M₁, esiste una macchina standard M₂ che ne imita il comportamento (cioè calcola la stessa funzione di M₁ e non si arresta quando M₁ non si arresta).

È abbastanza sorprendente che un dispositivo semplice come la macchina di Turing rappresenti il più potente strumento di calcolo conosciuto, nel senso che per ogni problema per cui è nota una procedura di soluzione è possibile formulare un algoritmo eseguibile da una macchina di Turing. Anche se ciò può bastare per accettare la macchina di Turing come la formalizzazione della nozione intuitiva di algoritmo, un ulteriore, e forse decisivo, sostegno è fornito dal fatto che altri due approcci indipendenti, e totalmente diversi, alla formalizzazione della nozione di calcolabilità sono stati dimostrati equivalenti alla macchina di Turing: questi approcci sono rappresentati dalle grammatiche a struttura di frase e dalle funzioni ricorsive. Questa evidenza corrobora la tesi di Church-Turing, secondo la quale ‛ogni processo che si possa chiamare algoritmo è realizzabile da una macchina di Turing'. La tesi di Church-Turing non è un teorema, in quanto propone una corrispondenza tra una nozione matematica (la macchina di Turing) e una nozione prematematica (la nozione naturale di algoritmo).

3. Algoritmi: presentazione ed efficienza.

Una volta accettata la tesi che la macchina di Turing rappresenta il dispositivo astratto per l'esecuzione di algoritmi, è opportuno volgere l'attenzione all'efficienza del calcolo. Chiunque per esercizio provi ad eseguire, usando carta e matita, un calcolo anche semplice (come la moltiplicazione di due interi) nello stesso modo in cui lo effettua una macchina di Turing, si accorgerà immediatamente della straordinaria inefficienza derivante dai passaggi ripetuti su porzioni di nastro per accedere ai dati. Se questa inefficienza (in tempo di calcolo) è il prezzo della notevole semplicità strutturale, è allora spontaneo cercare compromessi tra complessità di dispositivi e velocità di operazione. In questo modo è possibile tracciare, idealmente, se non storicamente, il cammino che porta dalla macchina di Turing all'elaboratore ordinario o di von Neumann. Il nastro illimitato ad accesso sequenziale è sostituito da una memoria (finita ma sufficientemente ampia) ad accesso casuale (random access), l'unità di informazione trattata da una singola istruzione (chiamata ‛parola') è scelta in modo da rappresentare entità importanti per l'utente (quali interi, ecc.), e il repertorio delle istruzioni è ampliato per fornire comandi atti a operare sugli oggetti matematici adottati (quali operazioni aritmetiche sugli interi, ecc.). In sostanza, la macchina di von Neumann, che d'ora in poi chiameremo ‛elaboratore', è un ‛equivalente' pratico della macchina di Turing.

Dato un elaboratore e un algoritmo da eseguire su di esso, è di grande interesse analizzare le prestazioni di quest'ultimo per quel che riguarda l'uso di risorse quali, per esempio, il tempo di calcolo e lo spazio di memoria. Tuttavia, piuttosto che considerare uno specifico elaboratore con le sue particolarità, per dare all'analisi un valore più generale è opportuno far riferimento a una macchina astratta, cioè a un modello di calcolo sufficientemente semplice nel quale siano riconoscibili le caratteristiche essenziali del tipico elaboratore.

a) Il modello RAM e la presentazione degli algoritmi.

Il modello comunemente adottato come conveniente astrazione dell'elaboratore di von Neumann è la RAM (Random Access Machine; v. Aho e altri, 1974), la quale possiede una memoria ad accesso casuale ed è dotata di istruzioni di accesso alla memoria (lettura/scrittura), aritmetiche, di trasferimento di controllo (condizionato e incondizionato) e di arresto.

Un algoritmo può essere dunque espresso come una lista di istruzioni per la RAM; una tal lista è chiamata ‛programma in linguaggio macchina'. Tuttavia è stato osservato che non è né necessario né desiderabile esprimere un algoritmo in linguaggio macchina. Piuttosto, per ottenere maggior chiarezza, efficacia di espressione e concisione, e quindi al fine di facilitare l'analisi della funzione di un algoritmo, si preferisce esprimere quest'ultimo in una forma più vicina alla sua formulazione verbale. Questo formalismo è fornito dai cosiddetti ‛linguaggi di programmazione ad alto livello' di tipo procedurale (o imperativo), quali il FORTRAN, l'ALGOL, il PASCAL, ecc. In particolare adotteremo negli esempi che seguono il cosiddetto Pidgin Algol, una versione informale e flessibile dei linguaggi di tipo Algol, che è rigoroso nella struttura di controllo, ma piuttosto informale nelle altre dichiarazioni, nelle quali l'uso di notazione matematica si alterna liberamente con l'uso di asserzioni (per quanto possibile non ambigue) in linguaggio naturale.

Per consuetudine i termini del linguaggio di programmazione sono in inglese. Dichiarazioni formali dei tipi di dati sono evitate, poiché il tipo di una variabile è reso evidente dal contesto. Inoltre non si ha un formato rigido per ‛condizioni' o ‛espressioni'. Un programma è chiamato procedure e ha il formato:

Un comando può essere sostituito da una sequenza di due o più comandi, compresi tra ‛parentesi' begin... end, nel modo seguente:

A sua volta un comando può essere espresso da una frase in linguaggio naturale ovvero apparire in uno dei seguenti formati.

1. Assegnazione:

La sorgente è un processo che genera il valore della variabile; questo processo è descritto da un' ‛espressione' su un insieme di variabili, che a loro volta possono essere espresse come function di altre variabili.

2. Condizionale:

A seconda della verifica o meno della condizione, si esegue il primo ovvero il secondo comando, rispettivamente. L'alternativa (else comando) è facoltativa.

3. Iterazione. Ne esistono tipicamente tre formati:

La variabile in 3a è l'indice dell'iterazione; questo indice assume consecutivamente tutti i valori da un valore iniziale a un valore finale.

Un comando di questo tipo appare in un programma del tipo function avente il formato:

L'espressione argomento di return diviene la sorgente di un'assegnazione.

Una volta precisato il modello di calcolo e il linguaggio per esprimere gli algoritmi, è opportuno considerare due aspetti fondamentali di un algoritmo: la ‛correttezza' e l'‛efficienza'.

Un algoritmo è ‛corretto' quando realizza l'obbiettivo per cui è stato concepito (la ‛specifica' dell'algoritmo), cioè la produzione del risultato corretto per ogni scelta ammissibile dei dati. La correttezza di un algoritmo, inteso come metodo di calcolo, è un teorema la cui dimostrazione - non diversamente dalla dimostrazione di qualsiasi proposizione matematica - ha l'obbiettivo di convincere l'interlocutore. Al livello più dettagliato di ‛programma' la correttezza è ancora stabilita come un teorema, ma in questo caso annotando il programma con asserzioni concernenti variabili del programma e dimostrandone la validità per mezzo del calcolo dei predicati. La verifica di correttezza dei programmi è oggetto di considerevole interesse scientifico, ma è tuttora in una fase di intenso sviluppo.

b) Complessità computazionale.

A uno stadio considerevolmente più maturo si trova l'analisi dell'efficienza degli algoritmi, cioè lo studio delle loro prestazioni per quanto concerne l'uso di memoria, di tempo e di altre risorse. Noto anche come ‛analisi e progetto di algoritmi' o ‛complessità computazionale', questo settore rappresenta una delle più attive e vitali aree di ricerca nelle discipline informatiche. L'obbiettivo è la caratterizzazione - attraverso la dimostrazione esistenziale di limitazioni inferiori e la dimostrazione costruttiva di limitazioni superiori - della complessità intrinseca dei problemi. Una limitazione inferiore (esistenziale) si applica a tutti i possibili algoritmi intesi a risolvere un problema dato; una limitazione superiore (costruttiva) scaturisce dall'analisi delle prestazioni di uno specifico algoritmo concepito per il problema dato.

Per illustrare lo spirito di questa disciplina prendiamo in considerazione il tempo di esecuzione di un algoritmo. Il tempo di esecuzione è ovviamente la somma dei tempi delle singole istruzioni eseguite. Poiché un programma in Pidgin Algol può essere trasformato in maniera abbastanza diretta in un programma in linguaggio macchina, otteniamo un metodo per valutare il tempo di esecuzione del programma. Tuttavia un simile approccio è noioso e scarsamente illustrativo: è certamente più interessante ricercare la dipendenza funzionale del tempo di esecuzione dalla dimensione del problema (quest'ultima normalmente espressa da uno o più interi, quali il numero di cifre binarie, il numero delle chiavi da ordinare, ecc.). Pertanto è convenzione esprimere il tempo di esecuzione - così come altre misure di prestazione - a meno di una costante moltiplicativa. Ciò si ottiene limitandosi a contare solo alcune ‛operazioni chiave', facilmente riconoscibili in un programma espresso in linguaggio procedurale. Questo campionamento è certamente legittimo nel contesto di limitazioni inferiori, poiché le operazioni non considerate possono solo accrescere la misura; nel contesto di limitazioni superiori, occorre accertarsi che le operazioni prescelte rappresentino una frazione costante delle operazioni complessivamente eseguite dall'algoritmo. Una notazione proposta da Knuth (v., 1976) è particolarmente adatta a esprimere limitazioni inferiori e superiori di misure di prestazione in funzione della dimensione N del problema:

O(f(N)) denota l'insieme delle funzioni g(N) tali che esistono costanti positive C e N₀ per cui ∣ g(N) ∣ ≤ C f(N) per N ≥ N₀.

Ω(f(N)) denota l'insieme delle funzioni g(N) tali che esistono costanti positive C e N₀ per cui g(N) ≥ C f(N) per N ≥ N₀.

θ(f(N)) denota l'insieme delle funzioni g(N) tali che esistono costanti positive C₁, C₂ e N₀ per cui C₁f(N)) ≤ g(N) ≤ C₂f(N) per N ≥ N₀.

Chiaramente la notazione O si riferisce a limitazioni superiori (cioè alle prestazioni di un dato algoritmo), mentre la Ω si riferisce a limitazioni inferiori (cioè alle prestazioni possibili per un dato problema) e la θ si riferisce in maniera naturale a un algoritmo ottimale, cioè a un algoritmo le cui prestazioni differiscono solo per una costante moltiplicativa dalle migliori prestazioni possibili. Questo tipo di analisi viene frequentemente denotato come ‛asintotico', in quanto assume piena validità per N considerevolmente grande.

Come esempio atto a illustrare i concetti ora esposti, si consideri il seguente programma per verificare se un dato intero N sia primo:

Una semplice analisi rivela che il tempo di esecuzione è proporzionale al numero di volte (al più (N − 2)) che l'iterazione while (linee 6-9) viene eseguita, in quanto le linee 2, 3, 5, 11, 12, 13 vengono eseguite ciascuna al più una volta sola; quindi, nel caso peggiore, il tempo di esecuzione è O(N). Una versione meno grossolana dell'algoritmo, che sostituisce alla condizione (j 〈 N) nella linea 6 la condizione (j² 〈 N), comporta un numero di iterazioni pari al più a √-N, e pertanto, nel caso peggiore, il tempo risulta O(√-N).

Il precedente tipo di analisi viene definito di ‛caso peggiore', in quanto fa riferimento al caso più oneroso che possa presentarsi all'algoritmo; nel tipo di analisi alternativo, detto di ‛caso medio', si presuppone una distribuzione di probabilità per le istanze del problema. Quest'ultimo tipo di analisi non è frequentemente praticato, sia per le considerevoli difficoltà analitiche, sia per la mancanza di consenso sulle distribuzioni di probabilità da adottare. L'esempio precedente illustra inoltre, nella sua semplicità, come un problema ammetta metodi di soluzione aventi prestazioni sostanzialmente diverse.

4. Strutture dei dati e paradigmi algoritmici.

Naturalmente il progetto di algoritmi è un'attività sintetica e come tale non può essere insegnata in maniera sistematica. La preparazione a un'attività sintetica si basa normalmente sullo studio attento di esempi e sul processo di astrazione, dalla moltitudine dei casi particolari, di schemi sufficientemente generali e, per così dire, unificatori. L'individuazione di schemi algoritmici generali, o ‛paradigmi', è attualmente un'area di ricerca attiva; ciascun paradigma rappresenta, per così dire, un differente approccio alla soluzione di problemi, e la risolubilità per mezzo del medesimo paradigma implica una relazione tra le ‛strutture' di diversi problemi. Nonostante gli algoritmi vengano frequentemente, e ragionevolmente, raggruppati sulla base degli oggetti matematici sui quali operano (per esempio, algoritmi per grafi, algoritmi matriciali, ecc.), l'approccio paradigmatico può offrire l'avvio a una sistematizzazione proficua per successivi sviluppi. È questo l'approccio scelto da vari autori - per esempio Horowitz e Sahni (v., 1978) - che seguiremo in questo articolo. Considereremo, senza pretesa di completezza, i seguenti paradigmi, per la maggioranza dei quali, ad evitare traduzioni goffe o bizzarre, useremo la denominazione in lingua inglese: divide-and-conquer, paradigma greedy, backtracking, branch-and-bound. Prima di procedere con questa rassegna, tuttavia, è opportuno volgere l'attenzione al problema delle strutture dei dati.

Come si è osservato precedentemente, vi è una profonda relazione tra il progetto di un algoritmo e quello dell'organizzazione dei dati con cui l'algoritmo interagisce. Infatti, le prestazioni sono determinate in egual misura da queste due fondamentali componenti.

a) Strutture dei dati.

In ogni applicazione di un elaboratore l'informazione viene opportunamente aggregata per rappresentare le entità matematiche che interessano. Alcune di queste entità, quali gli interi e i caratteri, sono normalmente disponibili e non devono esser create dall'utente; in altri termini, esse rappresentano le strutture ‛atomiche', non ulteriormente decomponibili. È invece compito dell'utente creare nuove strutture componendo strutture più semplici, a partire dalle strutture atomiche. Ciascuna struttura composita (o complessa) è caratterizzata da costi e prestazioni da valutare con cura in fase di progetto di algoritmi. Iniziamo dalle strutture elementari e, per semplicità, chiamiamo ‛elemento' la particolare struttura atomica pertinente all'applicazione considerata.

1. Strutture elementari. - Le strutture più semplici sono il record e l'array. Il primo è un vettore (x₁, ..., x_s), dove ciascuna componente x_i (detta ‛campo') appartiene a un insieme X_i; quindi un record è una sequenza inomogenea di elementi, mentre un array, denotato A[1 : N], è un allineamento di N records omogenei (A[j] essendone il j-esimo).

L'array può essere utilizzato per costruire una ‛lista' (v. fig. 2), che è strutturalmente una sequenza di records concatenati. La concatenazione di due records consecutivi è realizzata per mezzo di un ‛puntatore'; due speciali puntatori (l'uno da un record chiamato INIZIO, l'altro a un record NIL inesistente) segnalano l'inizio e la fine della lista. La lista viene realizzata per mezzo di un array; un particolare campo dell'array è il PUNTATORE, contenente l'indirizzo (come indice dell'array) del record successivo.

Sia l'array che la lista possono essere impiegati per rappresentare sequenze e insiemi, ciascuna delle due strutture con particolari vantaggi e svantaggi.

Nella rappresentazione di sequenze la ricerca del j-esimo elemento avviene con un accesso diretto nell'array e con una scansione nella lista; d'altra parte, una volta trovata la corretta posizione, l'inserzione o la rimozione di un record vengono effettuate nella lista attraverso la modifica di esattamente due puntatori.

Nella rappresentazione di un insieme A, la lista contiene ∣ A ∣ records, ciascuno corrispondente a un elemento di A, mentre l'array fa ricorso alla rappresentazione per mezzo della funzione caratteristica di A nell'universo U, e pertanto richiede ∣ U ∣ cifre binarie. Le operazioni previste sono l'appartenenza di un elemento a all'insieme A e l'unione e l'intersezione di due insiemi A e B. Nella lista l'appartenenza è verificata in un tempo proporzionale ad ∣ A ∣ e ciascuna delle altre due operazioni richiede un tempo proporzionale ad ∣ A ∣ + ∣ B ∣. Nell'array l'appartenenza è verificata in tempo costante, ma unione e intersezione richiedono un tempo proporzionale a ∣ U ∣ anziché ad ∣ A ∣ + ∣ B ∣.

Esistono utili varianti della lista, quali la lista doppiamente concatenata (per mezzo di due puntatori, uno progressivo e l'altro retrogrado), ovvero usi particolari della lista, quali la ‛coda' - per la quale a un'estremità hanno luogo inserzioni e all'altra rimozioni - e la ‛pila' per la quale inserzioni e rimozioni avvengono a una sola estremità.

Una volta introdotto l'uso di puntatori per rappresentare collegamenti tra records, è possibile sfruttare a pieno questo dispositivo per rappresentare topologie arbitrarie, cioè grafi diretti. Infatti dato un grafo G = (V, E), dove V è un insieme (di nodi) ed E ⊆ V × V è un insieme (di archi), è possibile rappresentare G nel modo seguente: con riferimento alla fig. 3 viene definito un array primario A[1 : ∣ V ∣], ciascun record del quale corrisponde a un nodo di G; il record A[j] contiene il puntatore iniziale della lista, arbitrariamente ordinata, degli archi originanti dal nodo associato ad A[j]. Qualora il numero degli archi uscenti da qualsiasi nodo di G sia limitato e sufficientemente piccolo, allora è possibile far ricorso a una struttura più efficiente, tipica della rappresentazione di ‛alberi', che ora esaminiamo.

Un ‛albero radicato' T è un grafo connesso tale che esattamente un nodo (detto ‛radice') è privo di archi entranti, e ogni altro nodo ha esattamente un arco entrante. I nodi privi di archi uscenti sono detti ‛foglie', e due nodi rispettivamente origine e destinazione di un arco sono in una relazione di ‛padre e figlio'. L'albero T è n-ario se n (il ‛grado') è il massimo numero degli archi uscenti da qualunque nodo di T; in un albero n-ario a ciascun arco uscente da un nodo è associato univocamente un intero da 1 a n (albero ‛ordinato'). In un albero radicato vi è un unico cammino dalla radice a un nodo generico; il ‛livello' di un nodo è il numero di archi in questo cammino, e la ‛profondità' di un albero è il massimo dei livelli dei suoi nodi. Gli alberi ordinati - in particolare gli alberi binari e ternari - hanno un'importanza eccezionale in informatica, sia come topologie di strutture dei dati sia come modelli astratti di processi di calcolo. Per gli alberi ordinati ciascun nodo è convenientemente rappresentato da un record, i cui puntatori sono in numero pari al grado n dell'albero, e sono posti in corrispondenza biunivoca con gli interi da 1 a n. Un albero binario è illustrato nella fig. 4. Per un albero di questo tipo è relativamente semplice esprimere procedure per la visita sistematica di tutti i nodi (‛attraversamento') in un ordine prescelto.

2. Strutture complesse. - Frequentemente i problemi da risolvere richiedono la manipolazione di insiemi di oggetti (per esempio, l'insieme dei nomi in una guida telefonica). Poiché - salvo rare eccezioni - i linguaggi di programmazione non offrono un repertorio di comandi per operare su strutture così complesse, è compito dell'utente progettare con estrema cura la struttura dei dati da fare interagire con un algoritmo applicativo. Una tale struttura dei dati deve essere concepita come un ‛modulo' operativo; essa non solo immagazzina i dati, ma è provvista di un repertorio di comandi per la sua gestione, azionabili dall'algoritmo applicativo. Prima di affrontare il problema strutturale, è opportuno esaminare quali siano le tipiche operazioni eseguibili su insiemi. Per semplicità, assumiamo di operare con insiemi estratti da un universo totalmente ordinato; nel caso contrario, poiché gli elementi dell'insieme sono rappresentati simbolicamente, si può sempre assumere l'ordinamento lessicografico. Le operazioni possono essere:

(Ricerca)

1. MEMBRO(m,P). Determinare se m ∈ P.

2. MIN(P). Estrarre il minimo elemento in P.

3. INSERISCI(m,P). Sostituire {m} ⋃ P a P.

4. RIMUOVI(m,P). Se m ∈ P, sopprimere m.

5. NOME(m). Dati gli insiemi P₁, ..., P_s, trovare il nome dell'insieme che contiene m.

(Manipolazione)

6. TAGLIA(m,P). Suddividere P in P₁ = {a: a ∈ P, a ≤ m} e P₂ = {a: a ∈ P, a > m}.

7. CONCATENA(P₁, P₂) Concatenare P₁ e P₂ in un singolo insieme P, nell'ipotesi che, per ogni a ∈ P₁ e b ∈ P₂, si abbia a ≤ b.

Queste operazioni di base possono essere richieste in varie combinazioni. L'esperienza suggerisce, per esempio, le aggregazioni indicate nella tabella, per ciascuna delle quali è stata coniata un' opportuna denominazione.

Si noti innanzitutto che ciascuna delle strutture riportate nella tabella potrebbe essere realizzata per mezzo di una struttura elementare, quale l'array o la lista. Tuttavia la semplicità realizzativa non compenserebbe certo la grave inefficienza operativa. Se le frequenze delle diverse operazioni sono confrontabili, si desidera realizzare una struttura per la quale i costi (come tempi di esecuzione) delle operazioni siano pure confrontabili, e possibilmente molto piccoli rispetto alla cardinalità dell'insieme in oggetto. La risposta a queste specifiche è fornita da un uso giudizioso di strutture ad albero, che ora descriviamo.

Per semplicità ci limitiamo agli alberi binari radicati. Ciascun elemento dell'insieme viene associato a un nodo dell'albero T e - utilizzando l'ordine - si prescrive che ogni elemento nel sottoalbero sinistro sia non minore della radice e che, analogamente, ogni elemento nel sottoalbero destro sia maggiore della radice (e che questa proprietà valga per ogni sottoalbero di T). Con questa organizzazione, e denotando con m(v) l'elemento associato al nodo v, la ricerca di un elemento m in T è effettuata dalla chiamata CERCA (m, radice(T)) del seguente algoritmo (dove si usano le abbreviazioni inglesi LSON e RSON per ‛figlio sinistro' e ‛figlio destro' rispettivamente):

È chiaro che, nel caso peggiore, la ricerca richiede un numero di passi proporzionale alla lunghezza del cammino più lungo a partire dalla radice dell'albero. E allora essenziale gestire l'albero modificandone dinamicamente la struttura - in modo da minimizzare la lunghezza del cammino più lungo. In altre parole, si desidera che l'albero sia ‛bilanciato', cioè che, per ogni nodo, le profondità dei sottoalberi destro e sinistro siano pressoché identiche. In tal caso la profondità dell'albero è pari al logaritmo del numero dei nodi. Fortunatamente è relativamente semplice assicurare che, per ogni nodo, le profondità dei due sottoalberi differiscano al più di una unità. Gli alberi che soddisfano questa condizione - noti come alberi bilanciati in altezza o alberi AVL, dai nomi Adelson, Velskii e Landis - sono impiegati con successo per realizzare ciascuna delle strutture dei dati illustrate nella tabella. Un'operazione di inserzione o rimozione può provocare la perdita di bilanciamento; tuttavia il bilanciamento può essere riottenuto (v., per esempio, Reingold e altri, 1977) per mezzo di ‛aggiustamenti' locali lungo il cammino tracciato dall'operazione, e pertanto in tempo pari al logaritmo della cardinalità dell'insieme. Vi sono metodi alternativi e analoghi per il conseguimento degli stessi obbiettivi - quali quelli basati sugli alberi 2-3 (v. Abo e altri, 1974) e sugli alberi bilanciati in peso - che non vengono considerati in questa sede.

b) Paradigmi algoritmici.

Consideriamo ora, con qualche dettaglio, i paradigmi algoritmici menzionati precedentemente. Questa discussione non può avere pretesa di esaustività, ma mira semplicemente a mettere in luce alcuni degli aspetti fondamentali dell'argomento.

1. Divide-and-conquer. - In questo paradigma il problema viene suddiviso (divide) in due o più sottoproblemi più semplici e dello stesso tipo del problema originario; i sottoproblemi vengono risolti separatamente (conquer), e le loro soluzioni vengono combinate per fornire la soluzione del problema dato. In tal modo il problema viene successivamente decomposto in sottoproblemi di dimensione decrescente, sino a che si giunge a sottoproblemi sufficientemente piccoli da potersi risolvere in maniera diretta. Rappresentando il problema dato come un ‛insieme' o una ‛sequenza' (un insieme ordinato) S, il paradigma ha il seguente formato:

Si noti che la definizione delle funzioni RISOLVI, DIVIDI e COMBINA dipende dalla natura del problema, così come la scelta del valore ‛piccolo' nella linea 2. Il paradigma è di natura ricorsiva, cioè usa (‛invoca') se stesso nel corso del programma (linee 6 e 7), il che giustifica la condizione che i sottoproblemi siano della stessa natura del problema originario. Inoltre la parte essenziale del paradigma è la funzione COMBINA usata nella linea 8, in quanto dalla sua efficienza dipende l'efficienza del paradigma. Infine è opportuno notare che il passo conquer (linee 6 e 7) può essere eseguito in parallelo sui sottoproblemi, qualora il dispositivo di calcolo abbia queste capacità.

Il paradigma divide-and-conquer è uno dei più comuni nella letteratura algoritmica e, naturalmente, costituisce la prima scelta di chi si accinga a progettare un algoritmo. Vari importanti problemi, sia numerici che combinatori, quali la trasformata discreta di Fourier, la moltiplicazione di matrici, la moltiplicazione d'interi, la fusione di due sequenze ordinate, l'ordinamento di un insieme, la ricerca del massimo in un insieme, ecc., sono efficientemente risolti da algoritmi del tipo divide-and-conquer. Ne diamo illustrazione con l'algoritmo di ordinamento per fusione, dove (s_i, ..., s_j) (j > i) denota una sequenza di numeri da ordinare:

Si noti l'uso delle funzioni ausiliarie MIN, MAX e MERGE.

2. Paradigma greedy. - Viene fornito di un insieme S di oggetti e le soluzioni del problema sono vettori con componenti in S e che rispettano certi vincoli. Si propone di costruire la soluzione incrementalmente, una componente alla volta; in altre parole, una volta acquisita, una componente appartiene alla soluzione finale (questa caratteristica spiega il nome greedy = avido, dato a questa classe di algoritmi). Occorre allora dotare lo schema di un meccanismo di selezione (la funzione SCEGLI) e di un meccanismo che accerti il rispetto dei vincoli (il predicato SODDISFA), e abbiamo il seguente formato dove, ancora una volta, S denota un insieme:

Chiaramente l'efficienza dell'algoritmo è determinata dall'efficienza delle operazioni SCEGLI e SODDISFA. Importanti esempi di questo paradigma estremamente semplice sono diversi problemi combinatori, fra i quali il knapsack, l'albero minimo di supporto, e l'ordinamento per selezione, dove SCEGLI viene specializzata alla funzione MAX e il predicato SODDISFA diviene vuoto (automaticamente soddisfatto):

Infine è bene rammentare che, complicando adeguatamente la funzione SCEGLI (cioè richiedendo non solo la selezione di un elemento di S, ma anche una sua opportuna elaborazione), si ottiene la sottoclasse di algoritmi di ‛scansione di spazio', che sono stati impiegati con notevole successo nella geometria computazionale (v. Preparata e Shamos, 1985).

3. Backtrack e branch-and-bound. - Questi due importanti paradigmi sono applicabili a problemi per i quali il metodo più immediato e grossolano è quello della ‛ricerca esaustiva'. Un problema di questo tipo ha per soluzione un vettore (x₁, ..., x_N) soddisfacente un insieme di vincoli, dove x_i ∈ X_i (i = 1, ..., N) e X_i è un insieme finito; la ricerca esaustiva consiste nel generare tutti i possibili vettori - in numero di ∣ X₁ ∣ • ∣ X₂ ∣ ... ∣ X_N ∣ - per scegliere tra essi la soluzione desiderata. L'insieme di questi vettori è convenientemente descritto per mezzo di un albero radicato (‛albero di ricerca'), in cui gli archi del j-esimo livello corrispondono per ciascun nodo alle scelte della variabile x_j in X_j secondo un ordine prestabilito (v. fig. 5). Naturalmente il numero di nodi dell'albero di ricerca può essere proibitivo, per cui ciascuno dei due metodi menzionati mira, in maniera diversa, a ridurre il numero dei nodi visitati nella risoluzione del problema.

Il paradigma backtrack costruisce il vettore soluzione componente per componente (a partire da x₁) e tenta di estenderlo quanto possibile; non appena l'estensione diviene impossibile, retrocede alla più vicina alternativa che non sia stata ancora esplorata. Abbiamo il seguente formato:

In questa versione elementare il metodo introduce sistematicità nella ricerca, in quanto evita la visita ripetuta del medesimo nodo, ma non riduce la complessità globale del compito. Quest'ultima può essere ridotta attraverso un meccanismo, noto come ‛preclusione', che consente di eliminare interi sottoalberi dell'albero di ricerca, in quanto la natura del problema assicura che non possono contenere soluzioni. Chiaramente un meccanismo di preclusione è specifico del problema in oggetto; tuttavia una classe abbastanza generale è rappresentata da problemi per cui si ricerchi una soluzione di minimo costo e tali che per le soluzioni parziali valga: costo (a₁, ..., a_j) ≤ costo (a₁, ..., a_j, a_j+1) per ogni scelta di a_j+1. Per questi problemi il paradigma di backtrack si specializza in quello di branch-and-bound, nel senso che una soluzione parziale viene estesa solo se il suo costo non eccede il costo minimo sinora ottenuto nella visita dell'albero di ricerca.

5. Conclusione.

In questo articolo si è cercato di discutere alcune questioni teoriche sulla nozione di algoritmo, di illustrare alcuni aspetti salienti della ricerca algoritmica e di mettere in luce la profonda interazione tra algoritmi e dati sui quali operano. Naturalmente i limiti di spazio hanno consentito solo una trattazione molto parziale, e a volte necessariamente superficiale, di un soggetto già maturo e tuttora attivamente studiato. Le omissioni sono state molte e vistose. Ci si è limitati alla macchina di von Neumann e, conseguentemente, ai linguaggi procedurali; tuttavia la metodologia e l'orientamento concettuale che sono stati illustrati possono essere una base proficua per lo studio di nuove interessanti direzioni di sviluppo, quali i linguaggi applicativi (e le relative architetture) e gli elaboratori paralleli.

Bibliografia.

Aho, A., Hopcroft, J. E., Ullman, J. D., The design and analysis of computer algorithms, Reading, Mass., 1974.

Hoare, C. A. R., Notse on data structuring, in Structured programming, New York-London 1972, pp. 83-174.

Horowitz, E., Sahni, S., Fundamentals of computer algorithms, Woodland Hills 1978.

Knuth, D. E., Big Omicron and Big Omega and Big Theta, in ‟Association for Computing Machinery SIGACT news", April 1976.

Lewis, H. R., Papadimitriou, C., Elements of the theory of computation, Englewood Cliffs, N. J., 1981.

Minsky, M., Computation: finite and infinite machines, Englewood Cliffs, N. J., 1967.

Preparata, F. P., Shamos, M. I., Computational geometry: an introduction, Berlin-New York 1985.

Reingold, E. M., Nievergelt, J., Deo, N., Combinatorial computing, Englewood Cliffs, N. J., 1977.

Turing, A. M., On computable numbers, with an application to the Entscheidungsproblem, in ‟Proceedings of the London Mathematical Society" (II Series), 1936, XLII, pp. 230-265; 1937, XLIII, pp. 544-546.

Matematica numerica di  Carl-Erik Fröberg

SOMMARIO: 1. Introduzione: a) algoritmi e complessità; b) funzioni generatrici. 2. Interpolazione: a) la trasformata di Fourier rapida (TFR); b) interpolazione con splines; c) estrapolazione di Richardson. 3. Sistemi di equazioni: a) metodi dei gradienti coniugati (GC); b) sistemi di equazioni non lineari; c) metodi di minimizzazione. 4. Problemi algebrici agli autovalori. 5. Quadratura e sommazione. 6. Equazioni differenziali ordinarie (EDO): a) metodi di Runge-Kutta (RK); b) metodi a passo multiplo; c) metodo di Cowell-Numerov; d) problemi con condizioni al contorno; e) problemi agli autovalori. 7. Equazioni differenziali alle derivate parziali (EDP): a) equazioni iperboliche; b) equazioni paraboliche; c) equazioni ellittiche. 8. Equazioni integrali. □ Bibliografia.

1. Introduzione.

Negli ultimi anni la matematica numerica si è sviluppata al punto da costituire una disciplina a sé stante. Un fatto da tenere presente è che la matematica, almeno dai tempi di Newton, ha avuto un'importanza decisiva come strumento generale a disposizione della maggior parte delle scienze tecniche e naturali. Fatto ancor più rilevante, questa situazione ha avuto un effetto ispiratore nello sviluppo di molte discipline matematiche; in questo modo nacque la matematica applicata. Prima dell'avvento dei calcolatori, i problemi che sorgevano ad esempio in astronomia, fisica, chimica e tecnologia, nella maggior parte dei casi dovevano essere affrontati principalmente con mezzi puramente matematici. Quando erano indispensabili calcoli numerici, questi dovevano essere effettuati a mano: questo capitava in balistica, idrodinamica e meccanica celeste, per citare solo poche aree di studio. La situazione cambiò drasticamente quando, a partire dal 1950 circa, si resero disponibili potenti calcolatori. L'interesse per i metodi numerici crebbe a dismisura e improvvisamente divenne possibile impiegare intere classi di algoritmi numerici che richiedevano troppe operazioni per poter essere accessibili al calcolo manuale. Tuttavia apparvero allora sulla scena certi fenomeni che prima erano vagamente noti soltanto a quelli che avevano più esperienza di lavoro nel calcolo manuale su larga scala. Questi fenomeni si rivelarono disastrosi in molti casi: mal-condizionamento, instabilità, mancata convergenza, accumulazione degli errori, e così via. Divenne subito necessario effettuare un'accurata analisi per individuare le cause delle difficoltà e per escogitare rimedi contro i danni. Quando vennero trovati metodi migliori, sorse anche una disputa intorno all'economicità. Si riscontrarono a questo riguardo enormi differenze tra vari metodi che erano apparentemente abbastanza simili. Risultò che alcuni metodi consumavano grandissime quantità di tempo macchina. Un approccio sistematico a questa problematica porta allo studio della ‛complessità algoritmica'. Si tratta di un campo nuovo in cui sono apparsi molti risultati inaspettati. A titolo di esempio ci limitiamo a menzionare il fatto che nel 1969 Strassen scoprì un metodo per effettuare il prodotto di due matrici n × n con O(n^2,81) moltiplicazioni, anziché con O(n³), come generalmente si riteneva necessario. Più tardi questo risultato è stato migliorato a meno di O(n^5/2). Tenendo presente questo sviluppo si capisce che il termine ‛analisi numerica' mette in evidenza le caratteristiche generali dei vari metodi numerici. La ‛matematica numerica' può essere vista come una materia in qualche senso più vasta, che include sia la tematica generale, sia i concetti puramente numerici. Il nome indica anche che non si tratta assolutamente di un tipo approssimativo di matematica: in effetti essa è rigida e coerente quanto la matematica ‛ordinaria'.

Storicamente la maggior parte dei metodi numerici concerneva l'interpolazione, la risoluzione di equazioni algebriche e trascendenti, il calcolo di integrali definiti e la risoluzione di equazioni differenziali ordinarie con l'uso delle semplici tecniche delle differenze finite. Nelle applicazioni moderne predominano la risoluzione di grossi sistemi di equazioni lineari (e, entro certi limiti, non lineari), l'approssimazione tramite famiglie ortogonali di funzioni e mediante splines, problemi agli autovalori, problemi di ottimizzazione, equazioni differenziali ordinarie (EDO) e alle derivate parziali (EDP). Bisogna anche notare che i metodi numerici giocano un ruolo importante persino nella scienza dei calcolatori. Problemi concernenti basi di dati, grafi, metodi di ricerca e ordinamento, decisioni logiche, crittografia e così via sono divenuti sempre più importanti e hanno addirittura portato a definire una nuova branca della matematica, detta ‛matematica finita'.

a) Algoritmi e complessità.

Possiamo definire l'‛algoritmo' come una procedura deterministica per risolvere una data classe di problemi. Un esempio classico ben noto è l'algoritmo di Euclide per trovare il massimo comun divisore di due interi assegnati.

Un'analisi dettagliata di una grande varietà di algoritmi ha rivelato che ci sono importanti differenze riguardo all'efficienza, che possono essere insignificanti quando un certo numero n, tipico del problema, è piccolo, ma possono essere proibitive quando n diventa grande. Per esempio, n può essere il numero di equazioni e di incognite di un sistema lineare. Risolvere un tale sistema con la regola di Cramer richiede un tempo proporzionale a n • n! > nⁿ e^-n se usiamo la definizione di determinante come la somma di tutti i prodotti degli elementi formata secondo le ben note regole, oppure un tempo proporzionale a n⁴ se calcoliamo i determinanti in maniera più pratica. Comunque già Gauss aveva ideato metodi di ordine O(n³), mentre, come si è detto sopra, oggi esistono algoritmi ancora migliori, vicini all'ordine O(n^5/2). Da quando nel lavoro pratico si affrontano coi calcolatori problemi di grandi dimensioni, ha importanza anche il fabbisogno di memoria, e spesso un metodo è caratterizzato da requisiti di ordine O(n^a) per il tempo e di ordine O(n^b) per lo spazio di memoria.

La maggior parte dei problemi computazionali è di ordine polinomiale, cioè di ordine O(n^a) con a reale positivo; questi problemi costituiscono una classe, detta classe P. Tuttavia esistono problemi, per la maggior parte di origine combinatoria, che sono di ordine esponenziale e dunque intrattabili. (Un algoritmo è di ordine esponenziale se il numero di operazioni elementari necessarie per risolvere con esso un problema a n variabili cresce come nⁿ, oppure come n! o come aⁿ). C'è anche una classe intermedia, comprendente un gran numero di problemi di grande importanza pratica. Per essi si conoscono solo algoritmi a tempo esponenziale, ma nessuno finora è stato capace di dimostrare che questi problemi non possono essere risolti in un tempo polinomiale. La maggior parte di essi appartiene a una classe detta NP (N sta per ‛non deterministico', P sta per ‛polinomiale'). Questa classe contiene problemi che si possono risolvere in tempo polinomiale su una macchina di Turing non deterministica, che si suppone sondi in parallelo tutti i possibili cammini computazionali senza ulteriori costi di tempo. Alcuni di questi problemi (se ne conoscono parecchie centinaia) sono più difficili degli altri: essi si dicono NP-completi (NPC). Se uno qualunque di questi problemi fosse risolubile su una macchina deterministica in un tempo polinomiale, allora anche tutti gli altri della classe NP sarebbero risolubili in un tempo polinomiale. Di fatto nessuno crede che ciò sia possibile, ma non c'è nessuna dimostrazione disponibile al riguardo e il problema di sapere se P = NP è una delle grandi questioni aperte nella matematica.

Per trattare i problemi della classe NP senza usare un tempo esponenziale sono stati suggeriti numerosi algoritmi approssimati o probabilistici. Un esempio di tali algoritmi è quello per stabilire se numeri molto grandi sono o non sono primi, in cui la probabilità che un certo numero sia composto può essere 〈 2^-N, dove N è il numero di prove che sono state effettuate a caso. Questo problema appartiene alla classe NP, ma si ritiene che non appartenga a NPC. Non è neppure noto se appartenga a P.

Un altro problema che per lungo tempo fu ascritto alla classe NP è quello della programmazione lineare; tuttavia nel 1979 il matematico russo Khacian provò che esso in effetti appartiene a P. Notiamo anche che il problema dell'ordinamento e la trasformata di Fourier rapida sono entrambi O(n • ln n); comunque sono stati fatti dei tentativi per trovare algoritmi di ordinamento che impieghino un tempo lineare, e sono stati pubblicati risultati promettenti.

Vogliamo ricordare anche alcuni problemi di scienza dei calcolatori, che sono stati ampiamente discussi negli ultimi anni. Oggigiorno i programmi per calcolatori sono quasi sempre scritti in un qualche linguaggio di programmazione di alto livello. La struttura interna di tali linguaggi è spesso convenientemente rappresentata per mezzo di grafi. Anche il processo di analisi spesso è meglio descritto con simili mezzi. Per questa ragione i concetti della teoria dei grafi suscitano un crescente interesse. Come esempi di importanti problemi citiamo gli isomorfismi di grafi, la planarità, gli algoritmi di ricerca e di ordinamento.

Un'applicazione molto particolare è data dal problema della segretezza dell'informazione, sia nella memorizzazione, sia nella trasmissione. Se abbiamo a che fare solo con piccole quantità di informazione, allora si può adoperare una chiave particolare, da usare una sola volta. Però, quando il volume dei dati è considerevole, si deve costruire qualche tipo di chiave più generale. È stato suggerito il sistema seguente: supponiamo che p e q siano numeri primi molto grandi, con N = pq. Scegliamo un intero T tale che 0 〈 T 〈 N − 1 (T rappresenta il testo iniziale da tradurre in codice). Denotando con [a, b] il minimo comune multiplo di a e b, poniamo λ(N) = [p − 1, q − 1]. Supponiamo dapprima che né p né q siano fattori di T. Allora, per il teorema di Fermat, si ha T^p-1 ≡ 1 (mod. p) e T^q-1 ≡ 1 (mod. q). Inoltre, scrivendo λ(N)/(p − 1) = w (w è un intero), abbiamo

T^λ(N) = (T^p-1)^w ≡ 1 (mod. p)

e similmente T^λ(N) ≡ 1 (mod. q). Dunque T^λ(N) − 1 è divisibile sia per p che per q e di conseguenza anche per pq = N. Se, d'altra parte, p è un fattore di T, ossia T = pT₁ (mentre q non è un fattore di T₁), allora T^λ(N) ≡ 1 (mod. q) e T^λ(N)+1 ≡ T(mod. q). Inoltre T ≡ 0(mod. p) e T^λ(N)+1 ≡ 0 ≡ T(mod. p) e dunque T^λ(N)+1 ≡ T(mod. N). La stessa congruenza sussiste se q, ma non p, è un fattore di T; infine p e q non possono essere entrambi fattori di T poiché T 〈 N − 1 〈 pq. Supponiamo ora che M = λ(N) + 1 si possa scomporre in due fattori: M = st (dove s e t non sono necessariamente primi); allora possiamo tradurre in codice per mezzo della congruenza C ≡ T^s(mod. N). La decodificazione può ora essere effettuata mediante

T ≡ C^t(mod. N),

in quanto

C^t ≡ (T^s)^t = T^st = T^M = T^λ(N)+1 ≡ T(mod. N.

Per esempio, siano

p = 197, q = 211, N = pq = 41.567, λ = [196,210] = 2.940

λ + 1 = 2.941 = 17 • 173, s = 17, t = 173.

Scegliamo T = 10.000. Allora C = 10.000¹⁷ (mod. 41.567) ≡ 6.045 (questo valore è trasmesso al destinatario). Decodificazione: T = 6.045¹⁷³(mod. 41.567) = 10.000. Non c'è bisogno di mantenere N e s segreti, ma N deve essere abbastanza grande da non poter essere fattorizzato, neppure con i supercalcolatori di oggi. Il limite pratico attualmente è dato da numeri di circa 75 cifre, quindi numeri di circa 200 cifre dovrebbero essere abbastanza sicuri. Inutile dirlo, quando si usano nella pratica simili algoritmi, occorre prestare una buona dose di attenzione.

b) Funzioni generatrici.

Vi sono parecchi problemi, particolarmente nelle applicazioni della scienza dei calcolatori, in cui si e interessati a una serie di interi a_n = a(n), n = 0, 1, 2, ... . In molti casi è assai conveniente introdurre un polinomio

dove x è una variabile puramente formale. Una tale funzione f(x) è detta ‛funzione generatrice'. Relazioni tra i coefficienti possono spesso essere tradotte in relazioni funzionali, che a loro volta possono dare informazioni supplementari, ad esempio sul comportamento asintotico, o in casi semplici fornire addirittura espressioni esplicite dei coefficienti. Un esempio semplice è quello del numero di alberi binari b_n con n nodi (b₀ = 1). Un tale albero può essere formato da un albero sinistro con k nodi e uno destro con n − k − 1 nodi (k = 0, 1, ..., n − 1), entrambi uscenti da un nodo iniziale. Perciò troviamo b_n = b₀b_n-1 + b₁b_n-2 + ... + b_n-1b₀, e ponendo B(x) = b₀ + b₁x + b₂x²+ ... si vede che xB(x)² = B(x) − 1 ossia B(x) = (1 − (1 − 4x)^1/2)/2x. Con facili calcoli si ottiene il risultato finale:

Un esempio un po' più complicato è il numero di arborescenze g₁, g₂, g₃, ...; posto g(x) = g₁x + g₂x² + g₃x³ + ..., si può dimostrare che

che fornisce g₁ = 1, g₂ = 1, g₃ = 2, g₄ = 4, g₅ = 9, g₆ = 20, g₇ = 48, g₈ = 115, g₉ = 286, g₁₀ = 719.

2. Interpolazione.

Ritorniamo ora agli argomenti più tradizionali della matematica numerica. Proveremo però a dar loro un'apparenza in qualche modo più moderna di quella usuale, cercando di evitare parecchi dei vecchi metodi quando se ne abbiano disponibili altri nuovi e più efficienti. In particolare tratteremo svariati metodi che sono basati su idee completamente nuove e rappresentano decisivi passi in avanti. Per ovvie ragioni daremo molto risalto alla loro utilità nel campo dei calcolatori.

Prima dell'era dei calcolatori si dedicavano molti sforzi al calcolo di funzioni, per farne uso in fisica teorica o in altre applicazioni. Per esempio, le funzioni di Bessel J_n(x) sono state tabulate per ogni intero n tra 0 e 135, e per 0 ≤ x ≤ 100. Per valori di x non tabulati, si poteva far uso di opportune formule interpolatorie per ottenere una risposta con un buon grado di precisione. Dunque non è sorprendente che la matematica numerica classica si occupasse in larga parte di tecniche di interpolazione. Naturalmente ci sono tuttora diverse situazioni in cui è ragionevole usare l'interpolazione di tipo tradizionale, ma non vogliamo entrare in una analisi più tecnica. Ci limitiamo a rilevare la potenza delle tecniche basate sugli operatori per la costruzione di formule interpolatorie alle differenze.

Ci occuperemo comunque di due concetti particolari, che hanno giocato un ruolo importante negli ultimi decenni, e cioè la trasformata di Fourier rapida (TFR) e l'interpolazione per mezzo di splines. Inoltre metteremo in evidenza anche l'utilità pressoché universale dell'estrapolazione di Richardson.

a) La trasformata di Fourier rapida (TFR).

In molti problemi pratici occorre trovare una formula interpolatoria trigonometrica che approssimi una data funzione. Ponendo

si sceglie un insieme di punti equispaziati x_k = 2πk/N, k = 0, 1, ..., N − 1, e si vogliono determinare i coefficienti c_r in modo tale che nei punti x_k si abbia esattamente p(x_k) = f_k, dove f₀, f₁, ..., f_N-1 sono grandezze assegnate. Posto w = exp (2πi/N), otteniamo il sistema lineare Ac = f dove A_rs = w^rs; esso ha la soluzione c = A^-1f, dove (A^-1)_rs = N^-1w^-rs. Quindi si trova

Per calcolare tutti i coefficienti occorrono in linea di principio N² moltiplicazioni. Tuttavia, come si capisce facilmente, ciascun termine compare più volte e ordinando i calcoli in maniera intelligente si può risparmiare un'enorme quantità di lavoro. La necessità di questa semplificazione sta nel fatto che in molte applicazioni, particolarmente in due o tre dimensioni, N diventa grande in modo proibitivo. Un rimedio è stato scoperto da Cooley e Tukey. L'artificio fondamentale è quello di formare espressioni lineari intermedie su differenti livelli. Il metodo ha validità generale, ma funziona meglio se N è una potenza di 2, N = 2ⁿ. In tal caso si impiegano n ≃ ln N livelli e l'ammontare complessivo di lavoro diventa O(N • ln N) invece di O(N²), il che costituisce un significativo e decisivo miglioramento. Per esempio, se N = 8, si ottiene via via (w⁸ = 1):

Questo metodo si chiama ‛trasformata di Fourier rapida' (TFR).

b) Interpolazione con splines.

Consideriamo il caso di N punti assegnati in un piano. Se essi formano una configurazione ragionevole, potremmo costruire un polinomio di grado N − 1 il cui grafico passi per i punti (x_k, y_k), k = 1, ..., N (interpolazione di Lagrange). Tuttavia è risultato che tali polinomi possiedono alcune proprietà indesiderabili che li rendono inadatti alla maggior parte degli usi numerici. In alternativa si preferisce spesso definire N − 1 polinomi cubici, imponendo la continuità di f, f′ e f′′ in tutti i punti interni e, ad esempio, f′′ = 0 in x₁ e in x_N. Questa costruzione è molto efficace e può essere considerata come un modello matematico di un curvilineo flessibile (spline), fatto passare per i punti dati. L'idea di usare funzioni distinte nei diversi intervalli è molto generale e può essere applicata in molti casi, anche in tre dimensioni. Ritorneremo su questo tipo di costruzioni, in particolare in relazione al trattamento delle equazioni differenziali ordinarie e alle derivate parziali.

c) Estrapolazione di Richardson.

Si tratta di un metodo molto generale per perfezionare i risultati che si ottengono nel calcolo di integrali, di soluzioni di EDO, di autovalori di EDO e di EDP, e in calcoli simili. L'idea è molto semplice e si basa sul fatto che gli errori di discretizzazione in generale sono della forma a₁h + a₂h² + ..., dove h è la lunghezza del passo. Ad esempio, supponiamo che sia y₁ = y₀ + ah² + bh⁴ + ...: allora raddoppiando la lunghezza dell'intervallo si ottiene y₂ = y₀ + 4ah² + 16bh⁴ + ...; trascurando i termini di ordine ≥ 4 otteniamo 4y₁ − y₂ ≃ 3y₀, il che fornisce un valore approssimato di y₀ corrispondente al caso limite h = 0. Le nuove grandezze hanno errori O(h⁴) e ripetendo l'estrapolazione si ha una formula del tipo 16z₁ − z₂ ≃ 15z₀.

3. Sistemi di equazioni.

Considereremo dapprima un sistema di m equazioni lineari in n incognite: Ax = b; A è una matrice m × n, x e b sono vettori n × 1 e m × 1 rispettivamente. Se m 〈 n, esiste di regola un'infinità di soluzioni. Se m = n e det(A) ≠ 0, esiste l'unica soluzione x = A^-1b, e descriveremo più avanti diversi metodi numerici per risolvere il sistema. Infine, se m > n, il sistema è sovradeterminato e in generale possiamo solo trovare una soluzione ‛ottimale', che è ottenuta minimizzando uno scarto convenientemente definito. Se A è una matrice rettangolare, il problema di risolvere il sistema Ax = b, come quello di trovare l'inversa A^-1 di A, perde, in qualche misura, il suo significato originale. Vi è una nozione che si è rivelata preziosa in questo caso, cioè la nozione di ‛pseudo-inversa'. Supponiamo di voler trovare una matrice X che soddisfi le seguenti relazioni:

AXA = A; XAX = X;

(AX)^H = AX; (XA)^H = XA,

dove H indica la trasposta coniugata (hermitiana).

Allora si può dimostrare che queste relazioni caratterizzano la soluzione completamente, e si ha

X = (A^HA)^-1A^H.

Chiameremo tale matrice X ‛pseudo-inversa' di A, e la indicheremo con A⁺.

La cosa più importante e interessante è che esiste un tipo di proprietà di diagonalizzazione detta ‛decomposizione dei valori singolari'. Per ogni matrice A (m × n), esistono due matrici unitarie, U (m × m) e V (n × n) tali che U^HAV = S, dove s_ik = 0, per i ≠ k, e s_ii = w_i (i = 1, ..., r), con w₁ ≥ w₂ ≥ ... w_r ≥ 0 essendo r il rango di A. Gli autovalori di A^HA sono non negativi e uguali a wi²; la matrice AA^H ha gli stessi autovalori tranne che per degli zeri in più se m 〈 n. Se la soluzione del problema sovradeterminato viene definita nel senso dei minimi quadrati, si vede che risulta x = A⁺b.

Veniamo ora al caso normale in cui m = n. Esistono molti metodi classici, sia diretti che iterativi. Tra i metodi diretti domina ancora la scena la ben nota eliminazione di Gauss, integrata da convenienti permutazioni di riga in modo da preservare pienamente la precisione. Come è ben noto, alcuni sistemi danno luogo a difficoltà dovute al mal-condizionamento, ossia al fatto che certe righe nella matrice dei coefficienti sono quasi linearmente dipendenti. Questa proprietà è intrinsecamente connessa al sistema dato e ovviamente non c'è modo di aggirarla.

Esiste anche una grande varietà di metodi indiretti, e noi discuteremo sia i metodi a gradiente che quelli puramente iterativi. I metodi a gradiente furono introdotti intorno al 1950 e suscitarono moltissimo interesse negli anni immediatamente successivi. L'interesse decrebbe poi in qualche misura, ma negli anni settanta tali metodi guadagnarono nuovo slancio e sono ora considerati tra i più validi.

I metodi iterativi hanno una lunga e affascinante storia. Già nel secolo XIX apparvero due metodi importanti, attribuiti uno a Jacobi e l'altro a Gauss e Seidel (Seidel era in effetti un allievo di Jacobi). Vi è una condizione fondamentale richiesta per tutti i metodi iterativi, cioè che la matrice dei coefficienti sia diagonalmente dominante. Questa condizione si può formulare nel modo seguente:

in cui deve valere la disuguaglianza stretta per almeno un valore di i. Un qualunque metodo iterativo produrrà una serie di vettori che approssimano la soluzione esatta x = A^-1b. Decomponiamo ora A in D + C, dove D è la diagonale di A con tutti zeri altrove. Partendo da un qualunque vettore x⁽⁰⁾, definiamo successivamente x⁽¹⁾, x⁽²⁾, ... in base alla legge x^(k+1) = − D^-1Cx^(k) + D^-1b = c + Bx^(k). Prendendo x⁽⁰⁾ = 0, troviamo x⁽¹⁾ = c, x⁽²⁾ = (I + B)c, x⁽³⁾ = (I + B + B²)c e così via. Supponendo ∥ B ∥ 〈 1 otteniamo

Questo è il metodo di Jacobi.

Nel metodo di Gauss-Seidel decomponiamo A in A₁ + A₂, dove A₁ contiene la parte triangolare inferiore, compresa la diagonale principale, e A₂ contiene la parte triangolare superiore. Poi poniamo A₁x^(k+1) = b − A₂x^(k). Posto A1^-1A₂ = E, si trova per induzione

Questo metodo comporta il fatto che nel ricavare la r-esima componente nella (k + 1)-esima iterazione si usano i migliori valori approssimati per le altre componenti, vale a dire la (k + 1)-esima approssimazione per le prime r − 1 componenti e la k-esima approssimazione per le ultime n − r componenti.

Negli anni cinquanta D. Young (v., 1971) inventò un metodo nuovo e potente, il metodo dei super-rilassamenti successivi (SRS). Scrivendo, come prima, A = D + C e moltiplicando l'equazione per D^-1, si ottiene

(I + D^-1C)x = D^-1b, ovvero x = Bx + c,

con B = − D^-1C e c = D^-1b.

Poiché tutti gli elementi sulla diagonale di B sono zero, possiamo decomporre B in una parte triangolare superiore R e una triangolare inferiore L : B = R + L. Il metodo SRS è allora definito da

x^(k+1) = (1 − w)x^(k) + w(Lx^(k+1) + Rx^(k) + c),

dove w è un parametro detto ‛di rilassamento'. Quando 0 〈 w 〈 1 abbiamo un sub-rilassamento e quando w 〈 1 un super-rilassamento. Se w = 1, torniamo al metodo di Gauss-Seidel. Si può dimostrare che la scelta ottimale è w = 2μ^-2(1 − √-1- -−- -μ-²), dove μ è il raggio spettrale di B. (Se λ_i sono gli autovalori di una matrice A, il raggio spettrale di A è definito dalla ρ(A) = max_i ∣ λ_i ∣). Si vede anche che il metodo SRS converge per 0 〈 w 〈 2, ma si ha super-rilassamento solo per 1 〈 w 〈 2.

In generale la velocità di convergenza del metodo iterativo x⁽ⁿ⁺¹⁾ = Mx⁽ⁿ⁾ + c è definita da R = − ln ρ(M), dove ρ(M) è il raggio spettrale di M. Si verifica facilmente che il metodo di Gauss-Seidel converge due volte più rapidamente di quello di Jacobi, mentre il metodo SRS, con un'intelligente scelta del parametro di rilassamento w, può dare considerevoli guadagni in velocità per grandi sistemi.

a) Metodi dei gradienti coniugati (GC).

Come spesso succede, alla base dei metodi GC c'è un modello geometrico. Supponiamo che A sia una matrice simmetrica e definita positiva, e consideriamo la funzione F(x₁, x₂, ..., x_n) = ½x^TAx − b^Tx. Essa può anche scriversi

Proviamo ora a minimizzare F: si ottiene

o, più concisamente, Ax = b.

In questa formulazione il sistema iniziale appare come una condizione di minimizzazione. Il vettore gradiente,

gioca un ruolo decisivo, in quanto è orientato nella direzione in cui la funzione F varia più rapidamente. Dato che stiamo cercando un minimo di F, potremmo procedere nel verso negativo, fintanto che F decresce, e poi calcolare un nuovo vettore gradiente. Tuttavia, poiché F definisce una famiglia di iper-ellissoidi, possiamo effettuare una mossa intelligente scegliendo la nuova direzione coniugata rispetto alla precedente. In questo modo raggiungiamo l'interno dell'ellissoide il più profondamente possibile. Non entriamo nei dettagli: basti osservare che questo processo richiede esattamente n passi; per sbarazzarsi degli errori di arrotondamento si raccomanda di effettuare un'ulteriore iterazione.

Durante l'ultimo decennio è stata introdotta una nuova tecnica basata sul cosiddetto ‛pre-condizionamento'. Dato il sistema Ax = b, noi risolviamo invece, iterativamente, il sistema B^-Ax = B^-1b, in cui sia A che B^-1 sono matrici simmetriche e definite positive. Poi si applica un metodo GC modificato, in cui a ogni passo viene risolto un sistema lineare avente B come matrice dei coefficienti. Da semplici considerazioni geometriche si capisce che la convergenza è migliore se gli autovalori sono più vicini l'uno all'altro, il che corrisponde al caso in cui l'ellissoide approssima una sfera. Frequentemente capita che B sia il prodotto di due matrici ‛sparse', rispettivamente triangolare superiore e inferiore. Il calcolo delle matrici sparse è numericamente stabile per le cosiddette ‛M-matrici', caratterizzate dalle proprietà a_ik ≤ 0, per i ≠ k, A non singolare e A^-1 ≥ 0.

b) Sistemi di equazioni non lineari.

Metodi per risolvere equazioni polinomiali o trascendenti in una variabile sono stati costruiti e analizzati già da secoli. Se l'equazione è della forma f(x) = 0, le proprietà della funzione f sono naturalmente decisive. Quando f è continua e ci interessiamo solo a un intervallo finito, esistono parecchi metodi ben noti (bisezione dell'intervallo, falsa posizione, ecc.). Se f(x) è anche differenziabile, è disponibile un'intera famiglia di metodi, comprendente il metodo di Newton-Raphson, definito da x_n+1 = x_n − f(x_n)/f′(x_n). Esistono anche numerosi metodi iterativi che si possono usare se l'equazione viene riscritta nella forma x = g(x) con ∣ g′(x) ∣ 〈 1 nell'intervallo considerato. Noi supponiamo che queste idee siano ben note e ci asteniamo da un'analisi più dettagliata. Esistono anche moltissimi buoni programmi, ma occorre sottolineare che è pressoché impossibile coprire tutti i casi che possono comportare difficoltà abbastanza particolari.

Se esistono anche radici complesse, molti metodi non sono in grado di trovarle, se i valori iniziali sono reali. In questo caso già ottenere una prima rozza localizzazione delle radici è un problema assai serio. Metodi per questo scopo hanno di solito origine nella teoria delle funzioni analitiche. Lehmer ha suggerito di sfruttare il fatto che l'integrale

dove P(z) è un polinomio e C una curva chiusa, fornisce il numero delle radici di P(z) che si trovano all'interno di C. Dato che il risultato deve essere un numero intero, il metodo è abbastanza affidabile e insensibile a fenomeni dipendenti ad esempio dall'accumularsi delle radici. Esiste un esempio particolare di grande interesse teorico, cioè la congettura di Riemann: essa stabilisce che tutti gli zeri non banali della funzione di Riemann

si trovano sulla retta critica z = 1/2 + it. Benché sia stato fatto qualche progresso, non è ancora stata trovata alcuna dimostrazione di questa congettura; ad ogni modo, sono stati calcolati almeno 500 milioni di zeri: i primi di essi sono t₁ = 14,134725, t₂ = 21,022040, t₃ = 25,010858; tutti giacciono esattamente sulla retta critica. Questi calcoli sono altamente specializzati e molto difficili, perché alcune radici sono molto vicine tra loro.

Veniamo ora al caso in cui si abbia un sistema di equazioni non necessariamente lineari. Considereremo solo il caso di radici reali. Il sistema si può scrivere

Introducendo i vettori x = (x₁, ..., x_n) e f = (f₁, ..., f_n), otteniamo la semplice forma f(x) = 0. Definiamo lo jacobiano nel modo consueto:

Proprio come nel caso 1-dimensionale si possono applicare metodi di punto fisso. Quindi è naturale riscrivere l'equazione nella forma

x = g(x).

Se x e g fossero scalari, potremmo usare la ben nota iterazione

x^(m+1) = g(x^(m)).

Questa idea si trasferisce direttamente al nostro caso e dà luogo a due differenti metodi: a) il metodo di Gauss-Jacobi,

xi^(m+1) = g_i(xi^(m), x2^(m), ..., xn^(m)), (1)

che converge se

e se l'approssimazione iniziale è sufficientemente accurata; b) il metodo di Gauss-Seidel,

In quest'ultimo caso le condizioni per la convergenza sono più complicate, ma nelle applicazioni pratiche non c'è alcuna difficoltà a stabilire se si ha convergenza oppure no.

Un altro metodo iterativo può essere costruito per mezzo dello sviluppo in serie di Taylor. Partiamo di nuovo dall'equazione vettoriale f(x) = 0. Supponiamo che la soluzione esatta sia il vettore z. Allora possiamo scrivere x = z + h, dove x è una approssimazione nota e il valore di h dovrà essere calcolato. Sia f(x) = f(z + h) = g; allora, trascurando i termini del secondo ordine, troviamo f(z) + Jh = g. Poiché z è la soluzione cercata, abbiamo f(z) = 0 e dunque h = J^-1g, dove bisognerà supporre che J sia non singolare. In questo modo si può costruire una formula iterativa: x^(m+1) = x^(m) − J^-1f(x^(m)). In dimensione 1 questa formula si riduce all'usuale formula di Newton-Raphson. Si noti, in particolare, che J cambia a ogni passo, per cui è ragionevole approssimare J(x^(m)) ad esempio con J(x⁽⁰⁾).

c) Metodi di minimizzazione.

Discuteremo ora il problema generale della minimizzazione, con l'intento di usarne i risultati per risolvere un sistema di equazioni non lineari. Sia y = F(x₁, x₂, ..., x_n) = F(x) una funzione assegnata. Vogliamo trovare un punto z di minimo locale. Consideriamo nuovamente lo sviluppo in serie di Taylor:

Osserviamo che (∂F/∂x_i) sono le componenti del vettore grad F, e introduciamo inoltre la matrice hessiana H con elementi (∂²F/∂x_i∂x_k). Allora la serie si scrive così:

F(x + h) = F(x) + h^T grad F(x) + ½h^THh + ...

Trascurando i termini di ordine superiore cerchiamo di scegliere h in modo da minimizzare F:

Si trova allora il metodo iterativo

x⁽ⁿ⁺¹⁾ = x⁽ⁿ⁾ − H(x⁽ⁿ⁾)^-1 grad F(x⁽ⁿ⁾).

In dimensione 1 questo è proprio il metodo di Newton-Raphson per trovare uno zero della derivata.

Ritorniamo ora al nostro sistema di equazioni f(x) = 0. A partire da questo costruiamo una funzione scalare

Per costruzione si ha F(x) ≥ 0; si tratta quindi di cercare un minimo di F(x) tale che sia F(x) = 0. In pratica spesso si cerca di spostarsi nella direzione negativa del gradiente fino a raggiungere un minimo locale, tuttavia può accadere che il minimo locale sia > 0; in tal caso dobbiamo cercare soluzioni in un'altra regione.

Recentemente è apparso un metodo elegante per trovare massimi e minimi globali. L'idea essenziale è di usare l'aritmetica degli intervalli, comprendente generalizzazioni di concetti fondamentali quali funzione, interpolazione, convergenza e sviluppo in serie di Taylor. In questo modo si riesce a determinare l'immagine della funzione.

In questo contesto si può fare un'importante osservazione, cioè la possibilità di riformulare un dato sistema di equazioni in modo da poterle interpretare come condizioni perché una certa funzione assuma valore minimo. Torneremo su questa idea quando tratteremo le equazioni differenziali, specialmente in connessione con problemi al contorno e agli autovalori.

4. Problemi algebrici agli autovalori.

Sia A una matrice quadrata n × n. Se esistono un vettore non nullo x e un numero λ tali che sia soddisfatta l'equazione Ax = λx, allora si dice che λ è un autovalore e che x è un autovettore.

L'equazione si può scrivere

(A − λI)x = 0,

cioè come un sistema omogeneo di equazioni, per il quale la condizione per avere soluzioni non banali è f(λ) = det(A − λI) = 0. Dunque λ deve essere uno zero di una equazione di grado n che, perlomeno in linea di principio, può essere scritta esplicitamente. È noto comunque che il calcolo degli autovalori eseguito direttamente a partire dall'equazione caratteristica è in generale un procedimento altamente instabile. Se gli a_ik sono interi e se, diciamo, n ≤ 10, si potrebbe (contrariamente alla regola generale) calcolare f(λ) per n valori distinti di λ e da questi risultati ricavare gli zeri.

Esistono due grandi famiglie di metodi per calcolare gli autovalori di una matrice: metodi iterativi e metodi di trasformazione. Nei metodi iterativi bisogna supporre che uno degli autovalori sia molto più grande degli altri. In altri casi si possono usare stratagemmi particolari, quale quello di considerare al posto di A la matrice A + aI, i cui autovalori sono stati traslati di una quantità a. I metodi di trasformazione si basano sulla ben nota proprietà che gli autovalori (ma non gli autovettori) sono invarianti rispetto alle similarità.

Nella maggior parte delle applicazioni le matrici hanno qualche buona proprietà particolare. In fisica teorica predominano le matrici hermitiane oppure unitarie. Le matrici hermitiane possono essere diagonalizzate per mezzo di trasformazioni unitarie e le matrici reali simmetriche per mezzo di trasformazioni ortogonali. Spesso invece si preferisce ridurre la matrice in forma tridiagonale (a_ik = 0, per ∣ i − k ∣ > 1).

Già più di 100 anni fa Jacobi inventò un metodo basato su ripetute rotazioni bidimensionali. L'idea era di scegliere il più grande elemento a_ik fuori della diagonale e di effettuare una rotazione nel piano (x_i, x_k), con l'effetto di rendere uguale a zero il coefficiente trasformato a′_ik. Dopo un numero sufficiente di rotazioni si ottengono gli autovabn sulla diagonale principale, mentre gli autovettori sono dati dal prodotto di tutte le matrici di trasformazione. A distanza di più di un secolo questo metodo in parecchi casi è ancora competitivo.

Se ci limitiamo a costruire matrici tridiagonali, l'opera può essere compiuta con successive trasformazioni ortogonali: o rotazioni (come suggerito da Givens), o riflessioni (come suggerito da Householder). In entrambi i casi saranno sufficienti (n − 1) (n − 2)/2 trasformazioni bidimensionali. Per trovare gli autovalori di una matrice tridiagonale simmetrica, si può applicare un elegante metodo iterativo. Come si dimostra facilmente, il valore del polinomio caratteristico in un dato λ può essere ottenuto con il seguente algoritmo:

f_k(λ) = (λ − a_k)f_k-1(λ) − b²_k-1f_k-2(λ); f_-1 = 0, f₀ = 1,

dove (a₁, a₂, ..., a_n) è la diagonale principale e (b₁, b₂, ..., b_n-1) ciascuna delle due diagonali adiacenti. Se si è interessati solo agli autovalori situati in un dato intervallo, è particolarmente semplice l'uso di questo metodo combinato con quello di bisezione, usando il fatto che f_k(Z) forma una successione detta di Sturm. Ciò significa che il numero di cambiamenti di segno V(z) nella successione f₀(z), f₁(z), ..., f_n(z) decresce di uno da V(−∞) = n a V(+∞) = 0 ogni volta che si incontra uno zero.

Vediamo infine un metodo molto efficiente con proprietà numeriche eccellenti, cioè il metodo QR introdotto da Francis. Se la matrice originale non è simmetrica, si raccomanda di metterla dapprima nella forma di Hessenberg superiore, caratterizzata da a_ik = 0 se i − k ≥ 2, con metodi simili a quelli sopra citati. Si può allora dimostrare che esiste un'unica fattorizzazione A = QR ove Q è unitaria e R è triangolare superiore. In pratica i calcoli si fanno in questo modo: partendo da A = A₁, costruiamo tre successioni di matrici A_s, Q_s, R_s per mezzo dell'algoritmo

A_s = Q_sR_s; A_s+1 = Qs^HA_sQ_s = Qs^HQ_sR_sQ_s = R_sQ_s.

Ponendo P_s = Q₁Q₂ ... Q_s e U_s = R_sR_s-1 ... R₁, otteniamo A_s+1 = Ps^-1A₁P_s. Il punto cruciale ora è che A_s+1 si avvicina sempre di più a una matrice triangolare superiore e quindi gli elementi della diagonale sono sempre più vicini agli autovalori. Il metodo QR si è rivelato molto affidabile ed è quello generalmente usato nella pratica. Esistono eccellenti programmi per calcolatore che effettuano i calcoli necessari.

5. Quadratura e sommazione.

Nel seguito considereremo procedimenti numerici per approssimare quantità definite da limiti, come integrali e derivate. Mentre la derivazione analitica è ‛facile', il suo analogo numerico è ‛difficile'. Il motivo è ovvio: la derivata in linea di principio è definita come il limite del quoziente di due quantità piccole:

Dal punto di vista numerico si ha cancellazione tra numeratore e denominatore. Al contrario, l'integrazione numerica è ‛facile', perlomeno quando la funzione da integrare non ha singolarità; se sono presenti singolarità, esse vanno rimosse in modo opportuno, ad esempio per sottrazione della parte singolare.

Per il calcolo numerico di un integrale non singolare su un intervallo limitato, apparvero sulla scena dapprima formule che usavano i valori della funzione in punti equispaziati. Quella più semplice è la formula dei trapezi, in cui l'area da determinare è approssimata da un trapezio. Poi si può ottenere un'intera famiglia di formule, se si approssima la funzione f(x) con un polinomio interpolatore di Lagrange. L'errore di troncamento è piacevolmente piccolo, ma formule di ordine maggiore sono estremamente instabili e vanno evitate. Comunque vi è un metodo molto bello per superare queste difficoltà: quello di usare ripetutamente la formula dei trapezi dopo aver dimezzato la lunghezza del passo, e attuare successivamente l'estrapolazione di Richardson. Questa tecnica è stata introdotta da Romberg.

Un altro metodo fu inventato da Gauss già all'inizio del secolo XIX. L'idea fondamentale è di scegliere un insieme di ascisse in modo che il termine di errore sia del maggior ordine possibile, ossia la formula risulti esatta per polinomi di ordine più alto possibile. Usando n ascisse possiamo sempre costruire un polinomio di grado n − 1 il cui grafico passi per i punti corrispondenti. Ma poiché possiamo scegliere tali punti liberamente, si può guadagnare precisione ulteriore, corrispondente a un termine di errore O(h²ⁿ) invece che O(hⁿ). Scrivendo

F(x) = (x − x₁)(x − x₂) ... (x − x_n)

e

dove

è il polinomio di Lagrange, calcoliamo l'integrale di f(x) con una data funzione peso w(x):

Qui i pesi sono

e il termine di resto è

I pesi sono univocamente determinati dalle ascisse x_k, k = 1 ..., n, mentre queste ultime sono ancora a nostra disposizione. È allora naturale richiedere che sia

Questa condizione è automaticamente verificata se F(x) appartiene a una famiglia di polinomi ortogonali. Come è noto, per tali polinomi P esiste una formula ricorrente a tre termini:

P_n+1 = (A_nx + B_n)P_n − C_nP_n-1.

Inoltre, ponendo P_r(x) = a_rx^r + b_rx^r-1 + ... e α_r = b_r/a_r − b_r-1/a_r-1, β_r = a_r-1/a_r, possiamo costruire una matrice tridiagonale T con diagonale principale α₀, α₁, ..., α_n e le due diagonali adiacenti date da β₁, ..., β_n. Le formule ricorrenti possono allora essere scritte sotto forma di sistema lineare con matrice dei coefficienti T. Dunque si comprende facilmente che gli zeri di P_n+1(x) sono autovalori di T. Essi sono esattamente le ascisse ottimali nella formula di Gauss corrispondente, definita dalla funzione peso w(x) e dagli estremi a e b. La formulazione matriciale permette di ricavare semplici proprietà degli zeri, ad esempio che essi sono tutti reali. Inoltre, dall'ortogonalità possiamo dedurre che tutti gli zeri sono semplici e appartengono all'intervallo (a, b).

Non sussistono più ragioni computazionali contrarie all'uso delle formule di Gauss nelle applicazioni pratiche da quando le tavole di ascisse e di funzioni peso possono essere facilmente immagazzinate nella memoria dei calcolatori. Cionondimeno, per la sua semplicità e il suo facile controllo degli errori, il metodo di Romberg è probabilmente quello attualmente dominante.

Le formule di sommazione si costruiscono agevolmente mediante l'uso di tecniche di operatori. A titolo di esempio consideriamo la serie

S = u₀ + u₁x + u₂x² + u₃x³ + ... .

Usando l'operatore di traslazione E, definito ad esempio da Eu_n = u_n+1, possiamo scrivere

ove Δ è l'operatore di differenza in avanti: Δ = E − 1. Questa è la ben nota trasformazione di Eulero. Ponendo x = − 1 otteniamo

Consideriamo anche un caso più generale:

S = f(x₀) + f(x₁) + ... + f(x_n).

Costruiamo la somma

qui x_r = x₀ + rh, U = h d/dx e i B_k sono i numeri di Bernoulli (B₁ = 1/6, B₂ = 1/30, B₃ = 1/42, ...). Quindi si ottiene

Questa è la famosa formula di sommazione di Eulero-Mac Laurin (qui scritta senza termine di resto). Quando si usa questa formula nel calcolo effettivo non c'è praticamente alcuna difficoltà nello stabilire la convergenza. Tuttavia esistono casi in cui bisogna fare un accurato esame del termine di resto. Prendiamo ad esempio la serie 1/3 + 1/5 + 1/7 + 1/11 + 1/13 + 1/17 + 1/19 + 1/29 + 1/31 + 1/41 + 1/43 + 1/59 + 1/61 + 1/71 + 1/73 + ... , che è la somma dei reciproci dei numeri primi gemelli. Quando n è circa 10⁶, abbiamo R_n ≃ 0,2; per arrivare a dimezzare R_n, dobbiamo prendere il quadrato di n, cioè circa 10¹².

6. Equazioni differenziali ordinarie (EDO).

La maggior parte dei fenomeni in fisica, astronomia, chimica, tecnologia e persino nelle scienze umane e sociali sono governati da equazioni differenziali ordinarie o alle derivate parziali. Un esempio tipico è il moto di un satellite nello spazio sotto l'azione delle forze gravitazionali. Disgraziatamente, solo un trascurabile numero di EDO è risolubile esplicitamente e per questa ragione bisogna ricorrere a metodi numerici. È interessante notare che parecchi metodi numerici furono inventati e usati nei calcoli pratici molto tempo fa, ma, a causa di ovvie limitazioni, molte difficoltà sfuggirono o vennero colte soltanto vagamente. Al contrario, dopo l'irruzione dei calcolatori, molte deficienze, più o meno serie, furono osservate e analizzate. Questo sviluppo è ancora nel pieno del suo corso.

È materia di discussione il momento in cui per la prima volta si fece uso delle parole ‛stabilità' e ‛instabilità' in rapporto ai metodi numerici per equazioni differenziali. Molto probabilmente ciò è avvenuto nel classico articolo di Courant, Friedrichs e Lewy sui ‟Matematische Annalen" del 1928, concernente la risoluzione numerica di un'equazione iperbolica con metodi alle differenze. Dapprincipio comunque il concetto di stabilità era definito abbastanza vagamente ed era spesso confuso con quello di convergenza. Intorno al 1950 un esempio di forte instabilità fu dato da Todd: egli mostrò come una semplice equazione differenziale del secondo ordine impazzisse quando si tentava di risolverla con un metodo alle differenze del quarto ordine.

Un passo avanti decisivo fu fatto negli anni cinquanta, quando Dahlquist, con una serie di articoli, dette l'avvio a un più fruttuoso studio teorico dei problemi di stabilità nell'integrazione numerica delle EDO. Cominceremo la nostra presentazione indicando brevemente alcune importanti classi di metodi di risoluzione; ci limiteremo a considerare l'equazione y′ = f(x, y). Analizzare solamente un'equazione del primo ordine non costituisce una limitazione molto forte, perché un'equazione di ordine maggiore si può banalmente scrivere come un sistema di equazioni del primo ordine; basta cioè considerare y e f come vettori anziché come scalari.

Prima di tutto osserviamo che, se f è analitica, possiamo calcolare le derivate di y(x) d'ordine più elevato e trovare il valore di y(x + h), per h sufficientemente piccolo, usando lo sviluppo in serie di Taylor. Tuttavia nella maggior parte dei casi lo sforzo computazionale risulta proibitivo e occorre usare altri metodi.

Un'idea del tutto naturale è quella di sostituire l'equazione differenziale con un'opportuna equazione alle differenze, e in effetti tale metodo fu suggerito già da Eulero. Egli approssimava y′_n con (y_n+1 − y_n)/h, il che comporta un errore locale di troncamento O(h²). Benché questo metodo sia molto rozzo, esso in effetti può essere fortemente migliorato usando l'estrapolazione di Richardson.

A questo punto è utile un po' di terminologia. Prima di tutto, usando un dato metodo, conveniamo di calcolare solo i valori y_k di y corrispondenti ad ascisse equispaziate x₀ + hk, k = 1, 2, 3, ... . Se y è la soluzione esatta, y_k dovrà allora essere una buona approssimazione di y(x_k). Se y_n+1 è calcolato a partire da y_n soltanto, abbiamo un metodo a un passo, o a passo singolo; se invece y_n+1 è ottenuto come funzione di più valori precedenti, y_n, y_n-1, ..., y_n-k, abbiamo un metodo a passo multiplo. Inoltre, se y_n+1 è dato sotto forma di una funzione esplicita di valori precedenti, abbiamo un metodo esplicito. Al contrario, se y_n+1 appare anche a secondo membro, abbiamo un metodo implicito. Per esempio, y_n+1 = y_n-1 + 2hf(x_n, y_n) è un metodo esplicito a due passi, mentre

è un metodo implicito a un passo. Ancora, un metodo della forma

y_n+1 = y_n + hf(s₀y_n + ... + s_ky_n-k),

con la derivata calcolata solo in un punto, è detto metodo a una tappa.

a) Metodi di Runge-Kutta (RK).

Intorno al 1900 si ebbe una serie di tentativi di costruire metodi nei quali l'incremento finale si ottenesse come media pesata di derivate calcolate in opportuni punti. Il punto di partenza fu il metodo di Eulero, che fu poi migliorato successivamente da Runge, Heun e Kutta. Infine emerse un metodo del quarto ordine che acquisì una ben meritata reputazione e fu usato per decenni nei calcoli pratici, per esempio in balistica. Di fatto il metodo è solo un membro di un'intera famiglia; comunque il più noto algoritmo è il seguente:

Il punto successivo è allora (x₀ + h, y₀ + k). L'errore globale asintotico è ε ≃ ah⁴ + bh⁵ + ..., il che non è molto sorprendente, perché quando f è una funzione della sola x il metodo si riduce alla formula di Simpson.

Come si è detto, il metodo classico RK è solo uno tra quelli di un'intera famiglia, e durante l'ultimo decennio ci si è dedicati alla ricerca di metodi RK più elaborati, in particolare impliciti. Quando i metodi RK si usano nei sistemi di equazioni possono sorgere alcune difficoltà. Il sistema

ha la soluzione particolare

Per x ≥ 1 si ha e^-21x 〈 10^-9, e da questa componente della soluzione non ci si aspettano difficoltà. Tuttavia, partendo da x = 1, y = 3,3111 (≃ 9 e^-1), z = 4,0469 (≃ 11 e^-1), con h = 0,2 si ottiene:

La spiegazione è la seguente. Scriviamo il sistema in forma matriciale:

Risolvendo col metodo di Runge-Kutta, dopo un passo si trova, come si vede facilmente,

u_RK = (I + C + C²/2! + C³/3! + C⁴/4!)u₀; C = hA,

mentre il valore corretto è u_{1 =} e^Cu₀. Con h = 0,2 gli autovalori di C sono λ₁ = − 0,2, λ₂ = − 4,2, come si deduce dall'equazione caratteristica λ² + 4,4λ + 0,84 = 0. In accordo con il teorema di Cayley-Hamilton si ha C² + 4,4 • C + 0,84 • I = 0. Esprimendo C², C³ e C⁴ in termini di C e I, dopo facili riduzioni si ottiene

con autovalori 0,8187333 e 6,2374. D'altra parte, scrivendo e^C = pC + qI, si ha

con autovalori 0,8187304 e 0,014996, ossia exp(− 0,2) e exp(− 4,2). Si vede pertanto che abbiamo ottenuto il valore exp(− 0,2) quasi esattamente, mentre siamo ben lontani dall'altro (6,2374 invece di exp(− 4,2) ≃ 0,014995...). Si comprende facilmente che un valore critico si ottiene dall'equazione 1 + x + x²/2! + x³/3! + x⁴/4! = 1 ed è dato da x ≃ − 2,7853, e se gli autovalori λ_i di A sono reali dobbiamo avere − 2,7853 〈 hλ_i 〈 0. Nel nostro esempio verrebbe 21h 〈 2,7853 e h 〈 0,1326. Si verifica che già con h = 0,1 si arriva a risultati soddisfacenti. Se sono presenti autovalori complessi, hλ_i deve appartenere a un dominio chiuso essenzialmente contenuto nel semipiano sinistro.

Questo tipo di fenomeni, in cui il comportamento di un dato metodo dipende criticamente dalla lunghezza del passo, è detto ‛instabilità parziale'.

Nell'esempio precedente abbiamo incontrato una complicazione abbastanza comune, cioè il fatto che sono coinvolte due scale dei tempi molto diverse (supponendo che la variabile indipendente sia il tempo). I problemi con questa proprietà sono detti stiff. Citiamo soltanto il decadimento di una sorgente radioattiva di intensità I = Σ a_i exp(− b_it). Un valore grande di b_i significa avere un grande contributo solo per valori piccoli di t, ed è naturale in questo caso usare un passo piccolo. Tuttavia, anche se l'influenza di tali termini si abbassa rapidamente, non possiamo aumentare il passo temporale a volontà. In tali casi è raccomandabile l'uso di formule implicite. Vediamo il risultato che si ottiene per il problema precedente, prima col metodo di Eulero e poi con una formula implicita. In entrambi i casi prendiamo h = 0,2. Col metodo di Eulero si ottiene

Ovviamente P ha per autovalori 1 − 1/5 = 0,8 e 1 − 21/5 = − 3,2; gli autovettori corrispondenti sono

Siamo partiti con il primo autovettore e vogliamo sopprimere l'altro; tuttavia ogni errore di arrotondamento farà rientrare in gioco questo vettore errato, e il processo si deteriorerà rapidamente.

Il metodo implicito è definito da

ovvero

Q ha autovalori (1 − 0,1)/(1 + 0,1) = 9/11 e (1 − 21/10)/(1 + 21/10) = − 11/31, con gli stessi autovettori di prima. La soluzione cercata si ottiene da u_n+1 = (9/11)u_n; si ha 9/11 = 0,81818 ..., in confronto con exp(− 0,2) = 0,818731. È chiaro che il restante autovettore non può creare alcuna difficoltà.

b) Metodi a passo multiplo.

Il metodo generale a k passi è definito dalla formula

È conveniente introdurre i due polinomi

Ovviamente ρ(z) è il polinomio caratteristico associato all'equazione alle differenze sopra scritta, quando h è posto uguale a zero. Siano z_i gli zeri di ρ(z). Allora la soluzione dell'equazione y′ = 0 con y(0) = 0 nel punto x_n = nh sarà approssimata da Σ_i a_iziⁿ e se vi è almeno una radice con modulo ∣ z_i ∣ > 1 ogni piccola perturbazione crescerà rapidamente oltre misura (forte instabilità). Questo caso fu illustrato già intorno al 1950 da Todd. Se vi sono radici sul cerchio unitario, queste devono essere semplici; altrimenti per le radici doppie si ottengono soluzioni della forma an +b.

Usando semplici equazioni di prova si possono dedurre ulteriori condizioni che devono essere soddisfatte da ρ(z) e σ(z). L'equazione y′ = 0 con y(0) = 1 ha la soluzione esatta y = 1. Poiché f(x, y) = 0 e y_r = 1 per ogni r, abbiamo α_k + α_k-1 + ... + α₀ = 0, ossia ρ(1) = 0. L'equazione y′ = 1 con y(0) = 0 ha la soluzione esatta y = x. Dunque y_r = rh e

Sottraendo nhρ(1) = 0 otteniamo ρ′(1) = σ(1). Le relazioni ρ(1) = 0, ρ′(1) = σ(1) sono dette relazioni di consistenza e sono necessarie per la convergenza.

Negli ultimi decenni sono state esaminate con estrema cura le proprietà di stabilità dei vari metodi. In molti casi si possono ottenere preziose informazioni dallo studio del comportamento di un dato metodo nei confronti dell'equazione scalare di prova y′ = qy. Citiamo qui soltanto la A-stabilità, se il semipiano sinistro del piano complesso appartiene alla regione di stabilità, e la A(α)-stabilità, se la regione di stabilità comprende il settore ∣ π − arg(qh) ∣ ≤ α.

Se riscriviamo l'equazione originale in forma di equazione integrale,

possiamo costruire un'intera famiglia di metodi a passo multiplo, sostituendo all'integrando un opportuno polinomio interpolatore, esprimibile per mezzo di differenze retrograde:

dove s = (t − x_p)/h. La scelta di diversi estremi di integrazione dà luogo a diversi metodi, come illustrato dallo schema seguente:

Nell'ultimo caso si ha la formula

con errore locale di troncamento − (1/90)h⁵y^(v)(ξ). La formula è implicita e spesso si parte con un valore rozzo (predittore) come primo passo, per poi usare una o più volte la formula precedente (correttore).

È illuminante analizzare il risultato che la formula di Miine-Simpson fornisce quando la si usa per le equazioni di prova y′ = y, y(0) = 1 e y′ = − y, y(0) = 1. Nel primo caso l'equazione alle differenze ha i valori caratteristici e^h + O(h⁵) e −e^-h/3 + O(h³). Ovviamente la seconda soluzione deve essere scartata, ma questo non provoca difficoltà. Nel secondo caso otteniamo e^-h + O(h⁵) e −e^-h/3 + O(h³), ma qui la soluzione indesiderata crescerà lentamente, anche se non è presente dal principio. Quando h → 0 entrambi i valori caratteristici si trovano sul cerchio unitario ed entrambi sono semplici; ciononostante il comportamento sopra accennato (debole stabilità) finisce per creare complicazioni.

c) Metodo di Cowell-Numerov.

Per le equazioni del secondo ordine in cui manca la derivata prima esiste un metodo particolare. Posto U = hD ≡ h(d/dx) e se δ = E^1/2 − E^-1/2 è l'operatore di differenza centrale (cosicché δy_n = y_n+1/2 − y_n-1/2), si può provare che

δ²/U² = 1 + δ²/12 − δ⁴/240 + ...

Se l'equazione differenziale è y′′ = f(x, y), si ha

ossia

L'errore di troncamento totale è ε ≃ c₄h⁴ + c₆h⁶ + ... .

Esistono altri metodi simili e, proprio come nel caso di equazioni del primo ordine, si hanno certe condizioni di stabilità e di consistenza. Se il metodo è scritto nella forma ρ(E)y_n = h²σ(E)f_n, allora tutti gli zeri di ρ(z) devono soddisfare la condizione ∣ z_i ∣ ≤ 1 e le radici sui cerchio unitario devono avere molteplicità ≤ 2. Inoltre bisogna avere ρ(1) = 0, ρ′(1) = 0, ρ′′(1) = 2σ(1).

d) Problemi con condizioni al contorno.

Per le equazioni dei primo ordine occorre dare una condizione iniziale, ad esempio y(x₀) = y⁰. Tuttavia, per equazioni di ordine più elevato, tali condizioni possono essere date in diversi punti e non c'è nessun modo semplice di trovare una soluzione che le soddisfi. Ci limiteremo qui a equazioni del secondo ordine y′′ = f(x, y, y′), con

Discuteremo anzi un problema ancora più semplice, e cioè

y″=f(x,y,y′); y(a)=c, y(b)=d,

e cercheremo di trovare una soluzione per a ≤ x ≤ b.

Esistono perlomeno cinque metodi differenti largamente usati per questi problemi, vale a dire il metodo dei ‛tiri' successivi, il metodo della collocazione, il metodo delle integrazioni ripetute, il metodo della matrice a banda e il metodo di minimizzazione (che comprende come caso particolare il metodo degli elementi finiti).

Il metodo dei tiri successivi va considerato come una tecnica di prove ed errori, combinata con l'interpolazione approssimata. Nel metodo della collocazione si costruisce una funzione

con p(a) = c, p(b) = d e q_i(a) = q_i(b) = 0. I coefficienti a_i sono poi scelti in modo che sia soddisfatta la relazione P′′(x_i) = f(x_i, P(x_i), P′(x_i)) in un determinato insieme di punti x₁, x₂, ..., x_n.

Il metodo delle integrazioni ripetute inizia con un opportuna funzione y₀(x), soddisfacente le condizioni al contorno. Poi si costruisce una successione di approssimanti della soluzione via via migliori, mediante la relazione y″_n+1 = f(x_n, y_n, y′_n), con costanti di integrazione calcolate in modo da verificare le condizioni al contorno.

Il metodo della matrice a banda è destinato preferibiimente a sistemi lineari, ma può anche essere applicato ad alcune equazioni ‛debolmente non lineari'. Discretizzando in punti equispaziati si ottiene un sistema di equazioni con matrice dei coefficienti a diagonale dominante. Generalmente è possibile ottenere miglioramenti (e anzi è raccomandabile) per mezzo dell'estrapolazione di Richardson.

Nel metodo di minimizzazione, introdotto da Ritz e Galerkin, si considera l'equazione differenziale come equazione di Eulero di un certo integrale da minimizzare. Spesso è possibile approssimare la soluzione cercata con qualche semplice funzione contenente un certo numero di parametri da determinare; naturalmente essi vanno scelti in modo che siano soddisfatte le condizioni al contorno. In particolare si possono usare funzioni di base molto semplici, ad esempio lineari a tratti. Questa idea è generalizzabile a dimensioni più alte (metodo degli elementi finiti).

Illustriamo la tecnica con un semplice esempio:

y′′ − y = 0, con y(0) = 0, y(1) = 1.

La soluzione esatta ovviamente è y = senh x/senh 1. Ora definiamo

e osserviamo che l'equazione di Eulero

ha la forma y′′ − y = 0, cioè esattamente l'equazione che stiamo considerando. La soluzione esatta dà G_min = coth 1 = 1,3130352855. Già y = x fornisce una approssimazione abbastanza buona: G =4/3=1,3333 ... . Poi, ponendo y = ax² + bx dobbiamo richiedere y(1) = a + b = 1. Dopo semplici calcoli si vede che occorre minimizzare G = (11a² − 5a + 40)/30 e quindi si ottiene a = 5/22, b = 17/22, G = 1,314394. Un calcolo analogo con tre parametri fornisce y = (77x³ − 8x² + 404x)/473 e G_min = 1,31303735.

Veniamo ora al metodo degli elementi finiti e definiamo

Nell'intervallo x_i 〈 x 〈 x_i+1 solo ϕ_i e ϕ_i+1 sono ≠ 0 e inoltre la funzione f(x) = aϕ_i(x) + bϕ_i+1(x) è lineare e tale che f(x_i) = a, f(x_i+1) = b. Facciamo una partizione dell'intervallo (0,1) in N parti uguali e cerchiamo nuovamente di minimizzare G sotto le condizioni y(0) = 0 e y(1) = 1. Con N = 4, ponendo y= aϕ₀ + bϕ₁ + cϕ₂ + dϕ₃ + eϕ₄, otteniamo immediatamente a = 0, e = 1. Dopo semplici calcoli troviamo

e le condizioni per avere il minimo,

diventano

Dunque b = 0,2147875, c = 0,4431405, d = 0,6994814.

Per un arbitrario valore di N si trova che gli elementi della matrice sono − (6N² − 1) e 12N² + 4. I parametri si determinano convenientemente come soluzioni di un'equazione alle differenze con equazione caratteristica

λ² − [(12N² + 4)/(6N² − 1)]λ + 1 = 0.

Denotandone le radici con λ₁ e λ₂, usando il fatto che a₀ = 0 a_N = 1, si ottiene

a_r = (λr₁ − λr₂)/(λ1^N − λ2^N) → senh(r/N)/senh 1.

I valori minimi sono:

Questa tecnica può essere generalizzata prendendo funzioni ben più elaborate, ad esempio polinomi di terzo grado. Per h = 1 e i = 0 otteniamo

Sia la funzione che la sua derivata sono continue nei nodi e inoltre si ha

e) Problemi agli autovalori.

Caratteristico di questi problemi è il fatto che l'equazione contiene un parametro e ha soluzione solo per certi valori di questo parametro. Un semplice esempio è offerto dal problema: y′′ + a²y = 0; y(0) = y(1) = 0. La soluzione generale è y = A cos ax + B sen ax. La condizione y(0) = 0 dà A = 0, mentre y(1) = 0 fornisce B sen a = 0. Se B = 0 abbiamo solo la soluzione banale y = 0; un'altra possibilità è che sia sen a = 0, cioè a = nπ, n = 1, 2, 3, ... . Ebbene, i valori n²π² sono detti ‛autovalori' e le corrispondenti soluzioni, sen(nπx), sono dette ‛autofunzioni'.

In casi più generali si possono trovare le soluzioni per mezzo di una opportuna discretizzazione, che porta a un sistema algebrico della forma (A − λI)y = 0, dove A è di solito una matrice a banda. Se questi autovalori algebrici sono calcolati per differenti partizioni, è possibile effettuare un qualche tipo di estrapolazione. Tuttavia occorre osservare che in questo modo si possono ottenere solo gli autovalori più piccoli.

Esempio: troviamo il minimo autovalore per il problema y′′ + λy/(1 + x²) = 0; y(0) = y(1) = 0. Prendiamo h = 1/2, 1/3, 1/4 e 1/5. Nel primo caso, scrivendo y(1/2) = y si ottiene 4(0 − 2y + 0) + λy/(5/4) = 0, ossia λ = 10. Poi con h = 1/3 e y(1/3) = y₁, y(2/3) = y₂ si ha

che fornisce

Similmente con h = 1/4 si ha

e con h = 1/5

Infine l'estrapolazione di Richardson dà λ = 12,336.

Osserviamo anche che in alcuni casi si può usare lo sviluppo in serie, che dà luogo a un'equazione algebrica con un infinito numero di termini.

7. Equazioni differenziali alle derivate parziali (EDP).

Le EDP si incontrano, ad esempio, in fisica teorica, nella teoria dell'elasticità, in idrodinamica e in meteorologia. Le equazioni del secondo ordine risultano di gran lunga predominanti e solo di queste ci occuperemo nel presente articolo. Supponiamo di avere un'equazione in due variabili indipendenti,

dove a, b, c ed e sono funzioni di x, y, u, (∂u/∂x) = p e (∂u/∂y) = q. Le EDP di questa forma si possono classificare in equazioni iperboliche, paraboliche ed ellittiche, a seconda che sia b² − ac > 0, = 0 oppure 〈 0. Il trattamento numerico risulta alquanto diverso in ciascun caso, benché vi siano alcuni metodi che possono essere usati universalmente. Bisogna osservare che, se i coefficienti a, b e c non sono costanti, può succedere che l'equazione appartenga a diverse classi al variare del dominio. Un esempio ben noto è il flusso dei gas, che può essere supersonico in certe zone e subsonico in altre.

a) Equazioni iperboliche.

Le equazioni iperboliche sono spesso collegate a qualche tipo di propagazione ondosa. Denotando con c (costante) la velocità, il più semplice esempio è l'equazione

la cui soluzione generale è u = F(x + ct) + G(x − ct), dove F e G sono funzioni arbitrarie. Spesso le condizioni iniziali sono della forma

(problema ai valori iniziali di Cauchy) e allora si ha la soluzione generale

In casi più complicati non si possono ottenere soluzioni esplicite e occorre invece affidarsi a tecniche numeriche. In molti casi si può far uso di sviluppi in serie. Esiste anche un metodo che utilizza le caratteristiche: è tipico allora il fatto che, partendo da valori su una curva che non sia una caratteristica, si può in linea di principio conoscere la soluzione in un dominio triangolare formato da questa curva e da due caratteristiche appartenenti a famiglie diverse.

Comunque sia, la discretizzazione è spesso assai efficiente: in tal caso si tratta di discutere piuttosto un'equazione lineare alle differenze. Già nel 1928 Courant, Friedrichs e Lewy trattarono l'equazione

esaminando quello che succedeva quando essa veniva sostituita da

con condizioni iniziali sulla retta y = 0. Questa potrebbe essere stata la prima volta in cui fu introdotto il concetto di stabilità, quantunque la definizione non fosse molto chiara. In ogni caso, essi trovarono la condizione di stabilità k ≤ h.

Esempio:

Scegliamo h = k = 0,1 e cominciamo col calcolare i valori ai livelli −1 e +1 (cioè per y = −0,1 e y = 0,1). Per esempio, abbiamo

Usando l'equazione alle differenze otteniamo d₁ + d_-1 = 0,04 +0,16, che dà d₁ = 0,17408. Il valore esatto è 0,09 + 0,01 + e^-0,3 senh 0,1 = 0,174205. Per quanto riguarda i valori a livelli più alti, si ha, per esempio,

c₂ + 0,04 = b₁ + d₁;

si noti che abbiamo bisogno dei valori interni a un triangolo rettangolo isoscele, come indicato nella figura. In questo modo si ottengono i seguenti risultati (tra parentesi riportiamo i valori esatti):

Lavorando con maglie di due diverse misure si può poi effettuare l'estrapolazione di Richardson nel modo usuale.

b) Equazioni paraboliche.

Una delle più semplici equazioni paraboliche non banali è l'equazione unidimensionale del calore:

Questa equazione si può discretizzare così:

Ponendo α = k/h² si ottiene

u_r,s+1 = αu_r-1,s + (1 − 2α)u_r,s + αu_r+1,s;

l'errore di troncamento risulta dell'ordine di

e quindi una scelta ragionevole sarebbe α = 1/6, ossia k = h²/6. Ciò significa che dovremmo usare intervalli estremamente piccoli nella direzione t, il che implica costi enormi in termini di calcolo. Per migliorare la situazione si potrebbe pensare di approssimare (∂u/∂t) con (u_r,s+1 − u_r,s-1)/2h, il che dà un errore di troncamento molto minore. Sfortunatamente questo metodo risulta instabile. Tuttavia, poiché (u_r,s+1 − u_r,s)/k può essere interpretato come un'approssimazione di (∂u/∂t) sull'intervallo (r, s + ½), un'idea sensata può essere quella di usare il valor medio di (∂²u/∂x²) ai livelli s e s + 1. Questo metodo, suggerito da Crank e Nicolson, è ovviamente implicito, ma gode di parecchie proprietà vantaggiose. Esso si può esprimere in forma matriciale:

(21+ aT)u₈+₁ = (21 - aT)u₈,

dove u_s è il vettore u al livello s e T è una matrice tridiagonale con tutti 2 nella diagonale principale e − 1 nelle due diagonali adiacenti. Quindi

u_s+1 = (I + ½αT)^-1(I − ½α)u_s = Cu_s,

Poiché gli autovalori di T sono λ_m = 4sen²(mπ/2M), dove m = 1, 2, ..., M − 1, per gli autovalori di C si ha (osservando che Mh = 1)

e si capisce dunque che il metodo è stabile per tutti i valori positivi di α. L'errore di troncamento è O(h²) + O(k²) e così si può scegliere h = ck (c costante) senza rischi di instabilità. Questo è un miglioramento sostanziale rispetto al metodo precedente.

c) Equazioni ellittiche.

Partiremo dalla discussione di qualche semplice equazione e poi esamineremo metodi più elaborati che possano essere usati nei casi generali. Prima di tutto osserviamo che, mentre è spesso possibile ottenere la soluzione generale di una equazione, il problema difficile è quello di adattarla alle condizioni al contorno. Considereremo qui l'equazione di Laplace

e l'equazione di Poisson

La prima equazione è un caso particolare della seconda con F = 0. L'equazione di Laplace ha la soluzione generale u = f(x + iy) + g(x − iy), dove f e g sono funzioni arbitrarie. L'equazione viene presa in esame all'interno di una regione assegnata R di bordo ∂R. Sono di solito discussi tre diversi problemi: a) il problema di Dirichlet, dove u = f(x,y) su ∂R; b) il problema di Neumann, dove la derivata normale (∂u/∂n) = g(x, y) è assegnata su ∂R; c) il problema di Robin-Churchill, con condizioni al contorno miste a(x, y)u + b(x, y)(∂u/∂n) = c(x, y) su ∂R.

Veniamo ora all'equazione di Poisson e tentiamo di risolverla con una conveniente discretizzazione. Usando una griglia quadrata di ampiezza h, si ha approssimativamente

Da qui è stato costruito il metodo iterativo di Liebmann:

Si parte da valori approssimati nei punti interni (o si pongono tutti uguali a 0), ma si usano valori esatti sulla frontiera. Poi si itera riga per riga, finché non si osserva più alcun cambiamento. In linea di principio si risolve un grosso sistema lineare col metodo di Gauss-Seidel.

Col metodo sopra descritto si effettua l'iterazione operando sul valore in ogni punto preso singolarmente e il metodo si può definire ‛iterativo-puntuale'. In linea di principio, lo si potrebbe scrivere nella forma u⁽ⁿ⁺¹⁾ = Mu⁽ⁿ⁾ + c e di conseguenza il metodo è esplicito. C'è anche un altro modo di affrontare il problema, cioè quello di lavorare con gruppi di punti presi insieme, ad esempio tutti i punti di una retta orizzontale. Questo metodo si definisce ‛iterazione a blocchi' ed è ovviamente implicito. Per illustrare ciò, esporremo un semplice esempio. Prendiamo un dominio rettangolare con 12 nodi interni equispaziati, 4 in ciascuna delle 3 linee orizzontali. Numerando i punti da sinistra a destra e dal basso in alto, applicando il metodo otteniamo una matrice 12 × 12 che può essere suddivisa in 9 blocchi quadrati 4 × 4, e il sistema può scriversi:

U, V e W sono vettori 4-dimensionali contenenti i valori delle tre righe richiesti, mentre A, B e C si ottengono dai valori al bordo. Il sistema può essere riscritto così:

ed è risolto dallo schema iterativo

È evidente che la risoluzione numerica di molte importanti EDP dipende in maniera critica dalla risoluzione di sistemi molto grandi di equazioni lineari. Nell'ultimo decennio sono apparsi nuovi metodi iterativi basati sul cosiddetto ‛pre-condizionamento'. Invece di risolvere il sistema Ax = b, possiamo risolvere iterativamente B^-1Ax = B^-1b, dove sia A che B^-1 sono matrici simmetriche e definite positive. Si può allora applicare una modifica del metodo GC, in cui a ogni passo viene risolto un sistema lineare con matrice B.

Daremo ora una breve descrizione del metodo degli elementi finiti (MEF), limitandoci all'equazione di Poisson

Costruiamo una maglia triangolare che sia più fitta nelle zone dove si possono prevedere rapide variazioni delle funzioni. Le parti della maglia, in questo caso triangoli, sono dette ‛elementi'. Al di sopra di ciascun nodo poniamo un punto ad altezza 1: in questo modo definiamo una piramide che a sua volta rappresenta una funzione base. Quindi possiamo approssimare la superficie cercata u(x, y) con figure piane, proprio come si può approssimare una linea curva mediante segmenti.

Tornando all'equazione di Poisson, vogliamo risolverla in una regione limitata S con la condizione u = 0 sulla frontiera ∂S. Tale soluzione u risolve anche il problema variazionale (∇u, ∇v) = (f, v), o, scritto per esteso,

per tutte le v(x, y) continue su S, nulle sulla frontiera e dotate di derivate limitate e continue a tratti. Integrando per parti si ha

dove la parte integrata è nulla perché è v = 0 su ∂S. Dunque si trova

Qui v è una funzione arbitraria e pertanto si conclude che deve essere Δu + f = 0. Con modifiche irrilevanti il ragionamento funziona anche nella direzione opposta e di fatto i due problemi risultano equivalenti.

Sviluppiamo ora in serie u rispetto alle funzioni ϕ_j a forma piramidale:

e usiamo la formula (∇u, ∇v) = (f, v) prendendo v uguale a ϕ_k:

(Σa_j∇ϕ_j, ∇ϕ_k) = (f, ϕ_k),

ovvero, in forma matriciale, Ca = g, dove

La matrice viene calcolata dapprima per ogni triangolo e poi i risultati per tutti i triangoli vengono raccolti insieme in una ‛matrice di rigidità'. Ovviamente, un elemento C_jk è ≠ 0 solo se i nodi N_j e N_k sono vertici dello stesso triangolo e da ciò si capisce che la matrice C è ‛sparsa', vale a dire ha molti elementi nulli. Si ottiene di nuovo un grosso sistema lineare che può essere risolto nel modo descritto prima. Il metodo degli elementi finiti può essere generalizzato anche alle equazioni paraboliche e iperboliche, e addirittura a equazioni non lineari. Esistono grossi programmi che sono utilizzabili nelle diverse situazioni e ciò testimonia dell'utilità del metodo in varie applicazioni pratiche.

Notiamo anche che i problemi agli autovalori nelle EDP possono essere trattati pressoché allo stesso modo che nelle EDO. Tuttavia la discretizzazione porta a sistemi piuttosto grossi; ma di regola l'estrapolazione di Richardson permette di raggiungere una precisione ragionevole. Nei problemi agli autovalori si può anche usare il principio di Ritz. Consideriamo per esempio l'equazione Δu + λu = 0 nell'ellisse x²/4 + y² = 1, con u = 0 sul bordo. Moltiplicando per u e integrando su un quarto S dell'ellisse si ha

Posto

si constata che I > 0. Una integrazione per parti fornisce I = − ∫∫_S uΔu dx dy e, dato che J = ∫∫_S u² dx dy > 0, troviamo λ = I/J > 0. Approssimiamo ora u con (4 − x² − 4y²)(a + bx² + cy²) e notiamo che con il valore esatto dell'autovalore λ si ha G = I − λJ = 0. Cerchiamo invece di minimizzare G come funzione di a, b e c, considerando λ come un parametro. Le condizioni

danno luogo a un sistema lineare omogeneo in a, b e c, e infine si ottiene un'equazione algebrica di terzo grado in λ. La radice più piccola è circa 3,57; con due parametri si trova 3,62, mentre un solo parametro fornisce 3,75.

8. Equazioni integrali.

Supporremo che le definizioni fondamentali e le classificazioni usuali siano note. In questa discussione concentreremo piuttosto la nostra attenzione sugli aspetti numerici, ma per ragioni di spazio possiamo solo fare dei brevi commenti.

Nella sua classica trattazione dell'equazione

Fredholm usò la tecnica generale di sostituire l'equazione integrale con un sistema di equazioni lineari Ay = f, ottenuto applicando la regola dei trapezi. Egli considerò quindi il valore limite D(λ) di det(A) allorché l'ampiezza dell'intervallo h → 0. Quando si usa una tecnica numerica bisogna lavorare con un valore finito di h e poi eventualmente eseguire l'estrapolazione di Richardson. Di norma λ deve essere tale che D(λ) ≠ 0. D'altra parte, se f(x) = 0, allora λ deve essere uno zero di D(λ) per avere soluzioni non banali, e si ha di fatto un problema agli autovalori.

Illustriamo questo caso con il seguente esempio:

dove

Ponendo λ = α², dopo due derivazioni si ottiene α²y′′ + y = 0 e y(x) = sen(x/α), dato che y(0) = 0. Introducendo questa funzione nell'equazione si trova la condizione tang(α^-1) + α^-1 = 0. Quindi

Se invece tentiamo una risoluzione numerica usando la regola di Simpson con h = 1/4, otteniamo, posto μ = 96λ,

Sviluppando si ha l'equazione μ⁴ − 32μ³ + 208μ² − 416μ + 256 = 0, con zeri 24,05311, 5,004228, 1,666243, 1,276419. Dunque si trovano gli autovalori approssimati λ = 0,250553, 0,052127, 0,0173567 e 0,013296. La precisione non è molto buona, ma può naturalmente essere migliorata prendendo h più piccolo e poi eseguendo l'estrapolazione di Richardson.

Come secondo esempio prendiamo un'equazione di Fredholm di seconda specie:

usando 2^N intervalli, con N = 2, 3, 4 e 5. Ovviamente y(−x) = y(x), e applicando di nuovo la regola di Simpson otteniamo un sistema di equazioni lineari che può essere risolto in modo standard. I risultati sono nella tabella seguente.

Dopo l'estrapolazione di Richardson in h⁴ l'errore è di qualche unità nell'ottava cifra decimale.

Per finire osserviamo che anche le equazioni integrali non lineari possono essere trattate con metodi numerici, naturalmente con l'ausilio di un calcolatore veloce. Notiamo anche che vi sono equazioni più complesse contenenti derivate, differenze e integrali, e di nuovo la discretizzazione offre una via di uscita. Comunque in questi casi possono avere buon esito tecniche di trasformate, preferibilmente la trasformata di Laplace. Una descrizione di questi metodi va oltre l'ambito di questa presentazione.

Bibliografia.

Abramowitz, M., Stegun, I. A. (a cura di), Handbook of mathematical functions with formulas, graphs, and mathematical tables, New York 1964.

Aho, A. V., Hopcroft, J. E., Ullman, J. D., The design and analysis of computer algorithms, Reading, Mass., 1974.

Ames, W. F., Numerical methods for partial differential equations, New York 1977².

Baker, C. T. H., The numerical treatment of integral equations, Oxford 1977.

Brigham, E. O., The fast Fourier transform, Englewood Cliffs 1974.

Cheney, E. W., Introduction to approximation theory, New York 1966.

Davis, P., Rabinowitz, P., Methods of numerical integration, New York 1975.

Forsythe, G., Malcom, M., Moler, C., Computer methods for mathematical computations, Englewood Cliffs 1977.

Fröberg, C.-E., Introduction to numerical analysis, London 1965, 1969².

Fröberg, C.-E., Numerical mathematics. Theory and computer applications, Menlo Park 1985.

Gerald, C. F., Applied numerical analysis, Reading, Mass., 1978.

Jacobs, D. (a cura di), The state of the art in numerical analysis, New York 1977.

Knuth, D. E., The art of computer programming, vol. II, Seminumerical algorithms, Reading, Mass., 1969.

Marchuk, G. I., Methods of numerical mathematics, New York 1975.

Ralston, A., Rabinowitz, P., A first course in numerical analysis, New York 1978.

Stoer, J., Burlisch, R., Introduction to numerical analysis, New York 1980.

Watson, G. A., Approximation theory and numerical methods, New York 1980.

Watson, G. N., A treatise on the theory of Bessel functions, Cambridge 1966.

Wilkinson, J. H., The algebraic Eigenvalue problem, Oxford 1965.

Young, D., Iterative methods for the solution of large linear systems, New York 1971.

Young, D., Gregory, R. T., A survey of numerical mathematics, 2 voll., Reading, Mass., 1972.

Supercalcolatori di Piero Sguazzero

SOMMARIO: 1. Introduzione. 2. Cenni storici. 3. Tecnologia microelettronica dei supercalcolatori: a) tecnologia dei circuiti logici; b) tecnologia delle memorie. 4. Organizzazione dei sistemi avanzati di elaborazione: a) l'architettura di tipo SISD; b) le architetture di tipo SIMD; c) le architetture di tipo MIMD; d) modello computazionale di un elaboratore parallelo. 5. Analisi delle prestazioni dei calcolatori paralleli. 6. Applicazioni dei supercalcolatori. 7. Algoritmi per elaboratori paralleli: a) equazioni alle derivate parziali; b) algebra lineare. 8. Software di sistema per elaboratori vettoriali e paralleli. 9. Linee di tendenza. □ Bibliografia.

1. Introduzione.

Uno dei fenomeni culturali più importanti degli anni ottanta è, secondo il premio Nobel 1982 per la fisica K. G. Wilson, il processo di ‟computerizzazione della scienza e della progettazione tecnica". Il processo è stato reso possibile dalla simultanea domanda e offerta sul mercato di una serie di nuovi sistemi di calcolo automatico con alte velocità di elaborazione e grandi dimensioni di memoria, in particolare ai due estremi dello spettro di potenza degli elaboratori, i calcolatori per uso individuale e le stazioni di lavoro (personal computers e workstations), da una parte, e i ‛supercalcolatori' (supercomputers) dall'altra. È contestualmente cresciuta in ‟importanza e rispettabilità intellettuale", nelle parole del matematico P. D. Lax, un'intera famiglia di nuove discipline scientifiche a carattere intermedio tra lo sperimentale e il teorico: le discipline computazionali come, ad esempio, la fisica, la chimica, la biologia e la matematica computazionali. Il processo, innescato nei grandi laboratori di ricerca che tradizionalmente hanno a disposizione gli elaboratori più potenti, in aree come la meteorologia, la progettazione di centrali nucleari e la fisica delle alte energie, sta coinvolgendo in quest'ultimo decennio università, industrie meccaniche, industrie di individuazione e di estrazione di idrocarburi, laboratori chimico-farmaceutici e perfino l'industria cinematografica. Comune a queste varie aree della scienza e della tecnologia è la necessità di effettuare simulazioni numeriche di fenomeni fisici, processi o prodotti industriali: la simulazione è spesso più veloce, più accurata e meno costosa dei metodi tradizionali di costruzione e verifica di prototipi e modelli fisici, come, ad esempio, le gallerie del vento nella progettazione di velivoli; per alcuni sistemi, inoltre, la simulazione numerica può essere l'unico strumento di verifica di una nuova teoria. In un numero crescente di laboratori industriali si è fatta strada la convinzione che un calcolatore di elevate prestazioni sia essenziale per la sopravvivenza in un ambito di concorrenza internazionale. Alla stessa conclusione sono pervenute, per ciò che riguarda la competizione scientifica, parecchie istituzioni scientifiche e universitarie: lo confermano le due principali iniziative nazionali in Giappone nel campo del calcolo avanzato (Japanese Super-Speed Computer Project) e in quello delle macchine di ‛quinta' generazione e la recente decisione della National Science Foundation degli Stati Uniti di finanziare cinque grandi centri universitari dotati di supercalcolatori. In altre parole, il mercato dei supercalcolatori e dei sistemi di calcolo di elevate prestazioni si sta allargando a vista d'occhio ed è cresciuto di conseguenza l'interesse per lo studio di sistemi di elaborazione avanzati, come testimonia il grande numero di articoli, libri e convegni dedicati all'argomento.

Questo articolo si propone di illustrare schematicamente gli sviluppi recenti dei supercalcolatori e le ragioni alla base degli aumenti di prestazioni, ovvero il progresso nella microelettronica dei circuiti e nella organizzazione (architettura) dei moderni sistemi di elaborazione. I nuovi sistemi, infatti, non solo sono costituiti, per ciò che concerne l'hardware, da componenti elettronici più veloci, più densi e più affidabili, ma sono anche caratterizzati da un elevato grado di complessità e replicazione che li mette in grado di eseguire molti processi di calcolo simultaneamente: sono dunque ‛macchine parallele'. L'articolo descrive inoltre alcune applicazioni tipiche degli elaboratori di alte prestazioni e le peculiarità degli algoritmi e del software di sistema per supercalcolatori.

2. Cenni storici.

Il termine ‛supercalcolatori' viene attribuito convenzionalmente agli elaboratori non specializzati (general-purpose) capaci di eseguire nell'unità di tempo un volume di istruzioni e di contenere una quantità di dati superiori alle altre macchine disponibili al momento. Poiché le innovazioni nella microelettronica e nell'organizzazione interna dei calcolatori (architettura) migrano costantemente dai sistemi di elaborazione avanzati ai sistemi a larga diffusione commerciale, si tratta di una identificazione transitoria che si modifica nel tempo con lo sviluppo della tecnologia. È invalso l'uso di misurare la velocità dei supercalcolatori in termini di quantità di operazioni aritmetiche in virgola mobile eseguibili al secondo (flop/s), poiché le applicazioni più comuni dei supercalcolatori, cioè i programmi di calcolo tecnico-scientifico, sono caratterizzate dalla prevalenza di operazioni aritmetiche su numeri in virgola mobile (floating-point).

La prima generazione di supercalcolatori moderni, nei primi anni settanta, è stata caratterizzata da velocità dell'ordine di 20-50 Megaflop/s (20-50 milioni di operazioni floating-point al secondo) ed è esemplificata dalla macchina a 64 processori ILLIAC IV, costruita per l'agenzia spaziale statunitense NASA, il cui utilizzo ha stimolato gran parte della ricerca iniziale su algoritmi e software per macchine parallele. Gli elaboratori di alte prestazioni disponibili sul mercato nella seconda metà degli anni ottanta eseguono da 100 a 1.000 milioni di operazioni floating-point al secondo, hanno pertanto velocità comprese tra 100 e 1.000 Megaflop/s. È questa la seconda generazione dei supercalcolatori moderni, iniziata con la creazione (1976) da parte di S. Cray della prima di una serie di macchine (Cray-1, Cray X-MP, Cray-2) vettoriali. È di Cray anche il progetto di base di una macchina vettoriale (CDC Cyber 205) con caratteristiche leggermente diverse, ma con prestazioni paragonabili. Gli anni successivi di questa seconda generazione di supercalcolatori sono stati segnati dalla diffusione del paradigma architetturale dei multiprocessori vettoriali e dall'ingresso sul mercato di macchine giapponesi (Hitachi, Fujitsu e NEC) e della IBM. Ancora nel quadro concettuale dei sistemi fin qui costruiti, sono in fase di avanzato sviluppo e sperimentazione macchine commerciali general-purpose capaci di fornire da 2 a 10 miliardi di operazioni floating-point al secondo (da 2 a 10 Gigaflop/s). Prestazioni simili sono da attendere, forse a scadenza più breve, da macchine di ricerca progettate per lo più per risolvere problemi di fisica computazionale (si vedano, ad esempio, i progetti GF11 del laboratorio T. J. Watson della IBM, APE dell'Università di Roma, VFPP della Columbia University). Sta contemporaneamente crescendo, nella scia del progetto giapponese di costruzione di macchine di ‛quinta generazione ,l'interesse per macchine con organizzazione architetturale ottimizzata per il calcolo logico, ad esempio per problemi di intelligenza artificiale, per le quali è più appropriata la scelta di una unità di misura di velocità come il Megalips (milione di inferenze logiche al secondo).

Il sorprendente ritmo del miglioramento delle capacità elaborative è spiegato, dal punto di vista dell'hardware, con l'aumento della velocità dei componenti elettronici e la loro miniaturizzazione, con conseguente diminuzione dei ritardi di propagazione nei circuiti, e, dal punto di vista dell'organizzazione dei sistemi, con l'introduzione del parallelismo, cioè con la complicazione dell'architettura per permettere a più operazioni di essere effettuate simultaneamente. Appare dunque abbandonata l'organizzazione seriale dei sistemi di elaborazione introdotta da von Neumann negli anni quaranta, caratterizzata da una struttura di singolare semplicità ed efficacia: una memoria singola e un processore singolo operante, un passo alla volta, su un flusso lineare di istruzioni. Sul fronte del software si è assistito alla crescita impetuosa di nuovi algoritmi, di nuovi linguaggi adatti all'utilizzo di macchine parallele e di nuovi compilatori capaci di effettuare in alcuni casi ben definiti un'efficiente traduzione in istruzioni-macchina anche di codici seriali (di alta qualità sono, ad esempio, i compilatori FORTRAN utilizzati dalle macchine vettoriali). Secondo gli esperti, il fattore che limita maggiormente lo sviluppo è costituito dallo sforzo industriale e scientifico richiesto per adattare o riformulare l'impressionante mole di algoritmi e software applicativi ora disponibili e originariamente concepiti per macchine più semplici.

3. Tecnologia microelettronica dei supercalcolatori.

I calcolatori elettronici sono sistemi di enorme complessità basati sulla replicazione di un numero estremamente ridotto di componenti semplici, essenzialmente circuiti logici elementari e celle di memoria.

a) Tecnologia dei circuiti logici.

Le operazioni binarie elementari in cui si decompongono le operazioni logico-aritmetiche vengono eseguite da dispositivi capaci di commutare stato in un tempo estremamente ridotto (transistori), miniaturizzati e integrati in complessi circuiti logici depositati con tecniche fotolitografiche su piastrine (chips) di semiconduttore, tipicamente silicio monocristallino, di qualche millimetro dilato. Lo sviluppo dei calcolatori è stato scandito in larga misura dall'avvicendamento di tecnologie di fabbricazione di transistori sempre più sofisticate, aventi per scopo l'aumento della velocità di commutazione e la riduzione delle dimensioni, della potenza elettrica dissipata e del costo. Nei moderni supercalcolatori, in cui il fattore prestazioni prevale sul fattore costo, i circuiti logici sono attualmente implementati con la tecnologia bipolare rapida ECL (Emitter Coupled Logic, logica a emettitori accoppiati; v. fig. 1), al momento capace di fornire porte logiche con tempi di ritardo sotto il nanosecondo (10^-9 s).

Alternative alla tecnologia ECL e a essa superiori in termini di densità circuitale, potenza dissipata e costo, ma non ancora in termini di velocità, sono le tecnologie dei transistori a effetto di campo (FET) e delle famiglie MOS (Metal Oxide Semiconducior), in particolare CMOS (v. fig. 2), utilizzati in genere nei circuiti logici degli elaboratori medio-piccoli.

Grandi possibilità di sviluppo appaiono avere le nuove tecniche FET e MOS basate sulla sostituzione del silicio con semiconduttori costituiti da un composto (per esempio l'arseniuro di gallio), che permettono velocità di commutazione da due a cinque volte superiori a quelle dei dispositivi basati sul silicio. Il tempo di commutazione dei dispositivi (o tempo di ritardo delle singole porte logiche dei circuiti) e il tempo di percorrenza dei circuiti da parte dei segnali elettrici influenzano la quantità fondamentale che esprime direttamente la velocità di una macchina, cioè il tempo di ciclo base (clock), che è l'unità minima di tempo necessaria a svolgere un'istruzione semplice ed è ora dell'ordine di pochi nanosecondi (10^-9 s) nelle macchine a prestazioni più elevate. La tecnologia microelettronica più spinta (circuiti e packaging) non permette di ridurre i tempi di ciclo-macchina al di sotto di questo limite con affidabilità e costi accettabili, mentre è di uso corrente circuiteria elettronica con ottimi requisiti di affidabilità con cicli base dell'ordine della decina di nanosecondi.

b) Tecnologia delle memorie.

Anche gli organi principali di memoria RAM (Random Access Memory) dei moderni elaboratori sono realizzati con chips di semiconduttori mediante tecniche MOS e FET, con caratteristiche di prestazioni e costi analoghe a quelle dei circuiti logici. L'estrema regolarità dei blocchi di memoria favorisce un'integrazione circuitale ancora più spinta e l'affermazione della tecnologia MOS. Gli standard odierni permettono di alloggiare su un singolo chip MOS oltre un milione di celle binarie (bits) e di costruire banchi di memoria con dimensioni tipiche di un centinaio di milioni di parole da 64 bits (100 Megawords). Il sistema delle memorie, per ragioni di costo, è organizzato gerarchicamente in sottosistemi di costo e prestazioni decrescenti, ma con capacità crescenti, ed è complementato da una base ancora più vasta di memorie ausiliarie di massa a tecnologia diversa, tipicamente dischi magnetici rotanti, con dimensioni dell'ordine del centinaio di Gigawords.

4. Organizzazione dei sistemi avanzati di elaborazione.

Con i limiti attuali della tecnologia circuitale non è possibile ottenere le prestazioni richieste dallo sviluppo delle scienze computazionali e dalle esigenze del calcolo per applicazioni tecnico-industriali restando nell'ambito delle organizzazioni architetturali tradizionali (seriali) dei sistemi di elaborazione.

Per fissare le idee, consideriamo una macchina con un ciclo base di 10 ns. Se l'architettura è tradizionale, un'operazione floating-point richiede da 4 a 5 cicli, cioè 50 ns e la velocità di elaborazione non può eccedere i 20 Megaflop/s. Per ottenere, diciamo, 1.000 Megaflop/s è necessario introdurre qualche forma di sovrapposizione di attività, cioè di ‛parallelismo' di esecuzione, in grado di produrre il richiesto incremento di 50 volte in velocità di elaborazione. Tutte le macchine di calcolo moderne fanno uso di qualche forma di parallelismo che modifica, complicandola, l'organizzazione degli elaboratori tradizionali (architettura di von Neumann).

a) L'architettura di tipo SISD.

L'architettura di von Neumann (v. fig. 3A) è schematicamente definita da un'unità di controllo (1) per l'interpretazione delle istruzioni e la loro assegnazione a un'unità aritmetico-logica (2) per l'elaborazione dei dati e da una memoria unica (3) per l'archiviazione di dati e di istruzioni, oltre che, ovviamente, da unità di ingresso/uscita (non riportate nella fig. 3). Le parti 1 e 2 costituiscono il ‛processore centrale' (Central Processing Unit, CPU). Caratteristica saliente della macchina di von Neumann o SISD (Single Instruction stream Single Data stream) è che tutte le operazioni (decodifica delle istruzioni, trasferimento di dati e istruzioni dalla memoria all'elaboratore centrale, operazioni aritmetico-logiche) avvengono in rigida successione: in particolare, l'unità di controllo carica dalla memoria un'istruzione alla volta, la decodifica e demanda all'unità aritmetico-logica l'esecuzione dell'operazione con dati risiedenti in memoria o, per ragioni di efficienza, in registri veloci, prima di passare all'istruzione successiva. La semplicità e l'efficacia dello schema SISD, e la sua aderenza allo schema intuitivo di algoritmo come successione di passi elementari, ne hanno fatto l'organizzazione architetturale predominante dei sistemi di elaborazione.

Allo scopo di migliorare le prestazioni, fin dagli anni sessanta questa organizzazione è stata marginalmente modificata, permettendo la sovrapposizione temporale di attività indipendenti, come, ad esempio, l'esecuzione di un'istruzione e la decodifica dell'istruzione successiva. Per ciò che concerne l'accrescimento della velocità di esecuzione delle istruzioni aritmetiche (di peso determinante nelle simulazioni numeriche), negli anni settanta è stata introdotta una modifica sostanziale dello schema seriale SISD, che porta il nome di architettura SIMD.

b) Le architetture di tipo SIMD.

1. Arrays di processori. - La prima, e concettualmente più semplice, esemplificazione dell'architettura SIMD (Single Instruction stream Multiple Data stream) consiste (v. fig. 3B) nella replicazione dell'unità di elaborazione di dati e nella conservazione dell'unicità dell'elaboratore di istruzioni. Questo schema architetturale permette l'esecuzione simultanea e parallela della stessa operazione aritmetico-logica su una molteplicità di operandi pari al numero di unità distinte di elaborazione dati. Il fattore atteso di miglioramento rispetto a una macchina SISD costruita con la stessa tecnologia microelettronica è ovviamente p, il numero di elaboratori replicati; un ulteriore vantaggio, il cosiddetto ‛risparmio SIMD', è costituito dal fatto che basta caricare e interpretare una sola istruzione di programma per poter eseguire p istruzioni aritmetico-logiche.

ILLIAC IV, ICL-DAP e Goodyear MPP. La prima macchina parallela di tipo SIMD è stato l'elaboratore ILLIAC IV, costruito in un unico esemplare per il Centro di Ricerca di Moffet Field (California) dell'agenzia spaziale statunitense NASA. ILLIAC IV, che all'inizio degli anni settanta ha rappresentato la punta avanzata del settore informatico in termini di tecnologia microelettronica, architettura e software, consisteva di 64 elaboratori aritmetici, organizzati a modo di matrice (array) quadrata (8 × 8), operanti con tempo di ciclo di 62,5 ns in maniera totalmente sincrona sotto il controllo di un unico elaboratore di istruzioni. Ciascun elaboratore aritmetico era dotato di una memoria privata di 2 kilowords ed era connesso attraverso registri di comunicazione ai suoi vicini immediati di griglia (nord, sud, est e ovest). La difficoltà più rilevante nell'utilizzazione efficiente di ILLIAC IV era costituita dalla necessità di ripartire il calcolo tra i 64 processori con strategie tali da non richiedere di norma a un processore di accedere a dati risiedenti in memorie private di processori a esso non contigui. Calcoli di meteorologia e aerodinamica su reticoli bidimensionali, e con schemi numerici richiedenti soltanto interazioni locali tra punti di griglia, sono stati effettuati con successo sull'ILLIAC IV, grazie anche alla disponibilità di una delle prime varianti parallele del linguaggio di programmazione FORTRAN.

Lo schema architetturale di connessioni a griglia di ILLIAC IV è in linea di principio particolarmente adatto all'elaborazione bidimensionale di immagini, per esempio di immagini raccolte da satellite con tecniche di telerilevamento. Essenzialmente per questo genere di applicazioni sono state costruite negli anni settanta due macchine SIMD ad array di processori, ICL-DAP e Goodyear MPP. La macchina DAP (Distributed Array Processor) consiste di una matrice di 4.096 microprocessori elementari capaci di elaborare, un bit alla volta, parole di lunghezza variabile. I 4.096 processori sono interconnessi a griglia (64 × 64) e sono dotati ciascuno di una memoria privata di 16 kilobits. La velocità operativa della macchina DAP è naturalmente dipendente dalla lunghezza delle parole elaborate e varia da circa 800 Megaop/s, per l'addizione di numeri interi a 8 bits, a circa 16 Megaflop/s, per la moltiplicazione di numeri floating-point a 32 bits. È interessante osservare che queste prestazioni sono ottenute solo grazie alla possibilità di avere simultaneamente 4.096 risultati alla volta, in quanto i singoli processori sono alquanto più lenti di un moderno calcolatore per uso personale. La macchina MPP (Massively Parallel Processor) può essere descritta come un DAP esteso a una griglia 128 × 128 con microprocessori un poco più complessi: la velocità di picco per l'operazione di moltiplicazione floating-point è, ad esempio, di 216 Megaflop/s.

Macchine sperimentali: VFPP, APE e GF11. Lo schema architetturale SIMD ad array di processori ha un'evidente potenzialità per problemi a struttura molto regolare e non si è imposto negli elaboratori general-purpose; ha dato però luogo, negli anni ottanta, a un'interessante serie di macchine sperimentali progettate per risolvere problemi di fisica computazionale. Esempi rappresentativi di questa classe sono l'elaboratore VFPP (Very Fast Parallel Processor), in costruzione alla Columbia University, New York, l'elaboratore APE, in costruzione all'Università di Roma, e la macchina GF11, in costruzione al Laboratorio IBM T. J. Watson di Yorktown Heights, New York. Si tratta di macchine progettate principalmente per la soluzione numerica di problemi di ‛cromodinamica quantistica', una teoria proposta per la spiegazione delle interazioni tra particelle elementari. Un tipico calcolo di cromodinamica quantistica, ad esempio la stima delle masse del protone, del neutrone e di qualche altra particella, richiede all'incirca 3 × 10¹⁷ operazioni floating-point, per lo più occorrenti nella forma di prodotti di matrici complesse 3 × 3. Con una macchina da 100 Megaflop/s questo calcolo richiederebbe circa 100 anni, mentre una macchina da 10 Gigaflop/s dovrebbe essere in grado di effettuare questo calcolo, di grande significato teorico, in meno di un anno. Ad esempio, GF11, una macchina ad architettura SIMD (v. fig. 4) con un elaboratore centrale di controllo e 576 processori aritmetici da 20 Megaflop/s, dotati di memorie individuali da 2 Megabytes, avrà una velocità di picco di 11,5 Gigaflop/s.

Una caratteristica interessante di GF11 è che i processori non sono organizzati in una rete di interconnessione statica (network), ma sono collegati da un dispositivo centralizzato di commutazione (switch), dinamicamente riconfigurabile a seconda delle esigenze del calcolo; al contrario, i 256 nodi computazionali da 16 Megaflop/s della macchina VFPP nella sua massima configurazione saranno organizzati in una griglia quadrata 16 × 16; i 16 processori da 64 Megaflop/s della macchina APE sono invece strutturati ad anello.

Macchine SIMD a elevatissimo parallelismo: Connection Machine. Si vanno facendo strada, con un dominio potenziale di applicazione forse più vasto del calcolo scientificotecnico, architetture SIMD con un numero elevatissimo p di processori (4.000÷1.000.000), ma di potenza e di memoria minori, strutturate in reti con diverse topologie di collegamento (v. fig. 5).

Questa classe di macchine è ben rappresentata dalla Connection Machine, originata dall'attività di ricerca del laboratorio di intelligenza artificiale del Massachusetts Institute of Technology (MIT). L'architettura della Connection Machine prevede fino a un milione di microprocessori, o, più esattamente, di ‛nodi intelligenti di memoria', ed è ora disponibile in una versione da 65.536 nodi: ne è prevista l'applicazione in problemi di elaborazione d'immagini e di fluidodinamica numerica, con metodi d'impiego mutuati dalla teoria degli ‛automi cellulari'.

2. Macchine vettoriali con pipeline. - Allo schema SIMD può essere ricondotta una seconda tecnica, che ha avuto il successo più grande nei supercalcolatori non specializzati: la tecnica di ‛segmentazione' o pipelining. Essa consiste nella strutturazione della CPU a modo di catena di montaggio, in più stadi, eseguiti da sottounità hardware indipendenti e in grado di operare simultaneamente su una ‛catena' di dati piuttosto che, serialmente, su un dato alla volta.

Un esempio notevole è rappresentato dalla segmentazione dell'operazione di addizione per dati in virgola mobile in più stadi (quattro, nell'esempio della fig. 6). Se ogni segmento della pipeline dell'addizione richiede un ciclo di macchina è chiaro che addizionare una sola coppia di numeri richiede un numero di cicli pari al numero dei segmenti della pipeline, quattro nel nostro caso; ma l'addizione di una serie di coppie di numeri può essere effettuata, a regime, al ritmo di un'addizione al ciclo, con un fattore di miglioramento pari al numero ν dei segmenti della pipeline.

Nella seconda metà degli anni settanta sono state introdotte macchine dotate di una o più pipelines, attivabili a programma da istruzioni aventi come operandi non più singoli numeri (operandi ‛scalari'), ma insiemi ordinati di numeri (operandi ‛vettori'). Tali macchine sono perciò dette ‛macchine vettoriali'.

Le macchine Cray-1 e CDC Cyber 205. La prima macchina dotata di istruzioni vettoriali, in aggiunta alle normali istruzioni scalari, che fece una comparsa non episodica sul mercato degli elaboratori fu il calcolatore Cray-1 (1976). Questa macchina (v. fig. 7) può avere una memoria centrale di dimensione massima eguale a un milione di parole da 64 bits, cioè un Megaword, divisa in 16 banchi indipendenti, e 12 unità funzionali indipendenti per tipi diversi di elaborazioni (operazioni logiche e aritmetiche su numeri floating-point e interi).

La caratteristica più notevole della macchina è che le unità funzionali indipendenti sono alimentate con dati residenti in un gruppo di 8 registri vettoriali da 64 parole ciascuno, a loro volta alimentati dalla memoria centrale. Ciascuna delle unità funzionali è strutturata con la tecnica pipeline con 5 o 6 segmenti. A ogni ciclo-macchina (12,5 ns) una coppia di operandi può entrare dai registri vettoriali in una pipeline e (a regime) può uscirne un risultato. Ciò corrisponde a un massimo di 80 milioni di operazioni al secondo per pipeline: poiché vi sono pipelines distinte per l'addizione e la moltiplicazione, per problemi di algebra lineare, in cui le due operazioni sono richieste simultaneamente su operandi vettori, la velocità di picco della macchina Cray-1 è di 160 Megaflop/s. La macchina Cray-1 è dunque un elaboratore SIMD con operazioni vettoriali ‛da registri a registri', che necessita di una ragguardevole velocità di trasferimento dati (larghezza di banda) tra memoria e registri per sostenere le notevoli capacità elaborative delle pipelines. Nel progetto iniziale dell'elaboratore la larghezza di banda era di una parola per ciclo-macchina, circa tre volte inferiore a quella richiesta nel caso di operazioni aritmetiche con due operandi da caricare dalla memoria centrale e un risultato da depositarvi: di conseguenza era facile verificare un sensibile scarto delle prestazioni medie rispetto alla velocità di picco. In versioni successive della macchina (Cray X-MP) tale squilibrio è stato corretto contestualmente alla riduzione del tempo di ciclo prima a 9,5 e poi a 8,5 ns con la messa a punto di uno schema architetturale di grande efficacia e di notevole successo commerciale.

Nella seconda metà degli anni settanta il mercato dei supercalcolatori è stato sostanzialmente conteso alla macchina Crayi soltanto dall'elaboratore CDC Cyber 205 (v. fig. 8). Benché progettata per lo stesso tipo di applicazioni, questa macchina differisce dalla precedente in molti dettagli architetturali. In breve, tutte le operazioni vettoriali sono direttamente eseguite su dati risiedenti nella memoria centrale, cioè ‛da memoria a memoria', senza l'intermediazione di registri vettoriali, da un gruppo di pipelines identiche; gli elementi degli operandi vettoriali devono però risiedere in posizioni contigue della memoria centrale. Poiché vi possono essere fino a 4 pipelines, ciascuna delle quali può fornire nel tempo di ciclo di 20 ns un'addizione e una moltiplicazione, la velocità di picco è di 400 Megaflop/s per numeri floating-point di 64 bits (o di 800 Megaflop/s per numeri di 32 bits).

Le macchine vettoriali giapponesi (Fujitsu, Hitachi e NEC). Nei primi anni ottanta e successivi è comparsa sul mercato un'interessante serie di macchine vettoriali di produzione giapponese (Fujitsu, Hitachi e NEC). Esse portano alle estreme conseguenze lo schema architetturale delle macchine Cray-1, consistente in un processore dotato di più pipelines aritmetiche per l'esecuzione veloce di istruzioni vettoriali. Così la macchina Fujitsu VP400 ha un banco di registri vettoriali a lunghezza riconfigurabile, 3 pipelines aritmetiche, 2 pipelines per il trasferimento dati da/per la memoria centrale di 32 Megawords, tempo di ciclo di 7 ns, 4 risultati per tempo di ciclo per pipeline, velocità di picco di 1.142 Megaflop/s; la macchina Hitachi S-810/20 ha 32 registri vettoriali di 256 elementi, 12 pipelines aritmetiche, 4 pipelines per il trasferimento dati da/per la memoria centrale di 32 Megawords, tempo di ciclo di 14 ns, velocità di picco di 630 Megaflop/s; la macchina NEC SX2 ha 40 registri vettoriali di 256 elementi, 4 distinte pipelines aritmetiche, 2 pipelines per il trasferimento dati da/per la memoria centrale di 32 Megawords (complementabile da una memoria di massa elettronica di 2 Gigabytes), tempo di ciclo di 6 ns, 4 risultati per ciclo e per pipeline, velocità di picco di 1.333 Megaflop/s.

c) Le architetture di tipo MIMD.

È apparso evidente negli anni ottanta che lo sviluppo di macchine a singola unità di controllo, anche con l'utilizzazione di tecnologia microelettronica sofisticata e di organizzazione vettoriale a pipeline o parallela a processori aritmetici replicati, avrebbe potuto non soddisfare le crescenti richieste di velocità di elaborazione da parte di applicazioni scientifico-tecniche non immediatamente riconducibili allo schema concettuale SIMD. Ciò ha portato, intorno alla seconda metà del decennio, molti laboratori di ricerca a investigare e le maggiori case costruttrici a offrire nuovi sistemi basati su multiple CPU (elaboratore di controllo + elaboratore di dati) dotate di memorie locali e con accesso a una grande memoria condivisa (shared memory) e/o a una rete di interconnessione per lo scambio di dati e di messaggi (message passing). Un multiprocessore di tale tipo è alquanto flessibile: può infatti essere utilizzato da più programmi totalmente indipendenti o da una sola applicazione decomponibile in tanti flussi d'istruzione separati quanti sono i processori, ma coordinati dalla consultazione di informazioni di controllo (‛semafori') nella memoria condivisa o dallo scambio di messaggi di sincronizzazione; si parla allora di programmazione e di architettura MIMD (Multiple Instruction stream Multiple Data stream), secondo la classificazione di Flynn illustrata nella fig. 3.

1. Multielaboratori vettoriali con piccolo numero di processori. - Multielaborazione MIMD (multitasking) e vettorizzazione SIMD sono due livelli diversi di parallelismo che si possono comporre per dare luogo al paradigma architetturale dei ‛multielaboratori vettoriali' a cui s'ispirano molti supercalcolatori disponibili sul mercato. Queste macchine sono per lo più costituite da un piccolo numero (p ≤ 10) di processori vettoriali molto potenti, che condividono un'ampia memoria centrale a vie multiple per permettere accessi simultanei da parte dei singoli processori.

Le macchine Cray X-MP, IBM 3090, Cray-2 e ETA-10. Esempi notevoli sono forniti dai multiprocessori Cray X-MP con 1, 2, 3 o 4 elaboratori vettoriali con architettura Cray-1, tempo di ciclo di 8,5 ns, velocità di picco di 235 Megaflop/s per processore, memoria centrale condivisa di dimensioni fino a 16 Megawords realizzata con tecnologia ECL nel modello più grande, complementabile da una memoria di massa elettronica con tecnologia MOS di ampiezza massima eguale a 512 Megawords, e dai multiprocessori IBM 3090 con 1, 2, 3, 4 o 6 elaboratori vettoriali con architettura S/370 estesa con istruzioni vettoriali, tempo di ciclo di 17,2 ns, velocità di picco di 116 Megaflop/s per processore, memoria centrale condivisa di dimensioni fino a 32 Megawords realizzata con tecnologia ECL, complementabile da un'estensione della memoria centrale realizzata con tecnologia MOS di ampiezza massima eguale a 256 Megawords, memoria virtuale con indirizzamento fino a 256 Megawords (v. fig. 9).

Le prestazioni più spinte entro lo schema dei multielaboratori vettoriali sono raggiunte dalla macchina Cray-2 (4 processori con istruzioni vettoriali da registri a registri, tempo di ciclo 4,1 ns, velocità di picco di 400 Megaflop/s per processore) e dalla macchina ETA-10 che raccoglie l'eredità architetturale e tecnologica dell'elaboratore Cyber 205 (tecnologia CMOS, raffreddata alla temperatura dell'azoto liquido, −200 °C, per ottenere prestazioni generalmente accessibili solo dalla tecnologia ECL; fino a 8 processori con istruzioni vettoriali da memoria a memoria; tempo di ciclo 10 ns, velocità di picco di 1.200 Megaflop/s per processore; memoria condivisa di ampiezza fino a 256 Megawords).

2. Macchine a elevato indice di parallelismo. - Lo schema architetturale dei multiprocessori vettoriali con piccolo numero di processori raggiunge nel caso della macchina ETA-10 il suo limite superiore di prestazioni, circa 10 Gigaflop/s, che potrà venire superato solo con l'utilizzazione di una tecnologia microelettronica diversa (transistori basati sull'arseniuro di gallio - di progettato impiego nella macchina Cray 3 - e transistori balistici). A causa di questo limite sono oggetto di sviluppo e sperimentazione, in molti laboratori di ricerca presso università e industrie, architetture avanzate, per lo più MIMD, miranti a raggiungere la fascia di 1-10 Gigaflop/s, ma capaci, in linea di principio, di obiettivi molto più ambiziosi. Esse sono caratterizzate da un uso marcato del parallelismo, con un numero p di processori variabile tra 100 e 1.000.

RP3 e CEDAR, due esempi di multielaboratori con comunicazione centralizzata. Tra i numerosi progetti di macchine parallele di questo tipo prendiamo in esame una macchina sperimentale denominata RP3 (Research Parallel Processor Project), in corso di sviluppo nel laboratorio IBM T. J. Watson di Yorktown Heights, N. Y., in collaborazione con il Courant Institute dell'Università di New York, e la macchina CEDAR, in corso di sviluppo all'Università dell'Illinois.

Il progetto RP3 ha come obiettivo la costruzione di hardware e software per una macchina parallela di tipo MIMD di caratteristiche molto generali. Nella sua configurazione completa la macchina RP3 (v. fig. 10) consterà di 512 processori da 32 bits e di 2 Gigabytes di memoria centrale. Questa massiccia memoria è distribuita uniformemente tra tutti i 512 processori dando luogo a 512 nodi PME (Processor-Memory Elements). Ciascun nodo PME è inoltre corredato da un modulo specializzato per la traduzione di indirizzi di memoria da indirizzi logici (di programma) a indirizzi fisici (di macchina).

Una caratteristica innovativa della macchina RP3 è che i 512 moduli di memoria possono essere ripartiti in proporzione variabile tra ‛memoria locale', cui accede individualmente ciascun processore, senza ritardi, e ‛memoria globale' distribuita, cui possono accedere - con tempi maggiori - tutti i processori attraverso un dispositivo centralizzato di commutazione. Questo dispositivo (combining switch), in congiunzione con i moduli di traduzione, permette di combinare efficacemente riferimenti di più processori agli stessi dati. Si tratta di una tecnica, proposta nell'ambito del progetto Ultracomputer del Courant Institute, che permette la creazione di algoritmi paralleli senza sezioni seriali e di conseguenza estendibili, senza perdita di prestazioni, a sistemi con un numero molto elevato di processori, attraverso l'uso di istruzioni primitive speciali, quale l'operazione fetch-and-add, che eseguono simultaneamente riferimenti a memoria e operazioni di sincronizzazione. Un secondo dispositivo di commutazione (non combining switch) consente lo scambio veloce di messaggi tra i processori. Questa flessibilità permette di sperimentare realisticamente l'efficienza di algoritmi e implementazioni a scambio di messaggi o a condivisione di memoria. Nella sua configurazione massima il sistema RP3 raggiungerà, si ritiene, solo 800 Megaflop/s, a causa della relativa potenza dei processori individuali, essenzialmente equivalenti a un personal computer in questa fase del progetto: si tratta dunque di una macchina più interessante per la novità del progetto architetturale che per l'immediata potenza di calcolo.

Il progetto CEDAR, in corso di sviluppo da parte del gruppo di D. Kuck all'Università dell'Illinois, ha l'ambizioso scopo di fornire un efficace paradigma architetturale per i supercalcolatori degli anni novanta, cui si richiederanno prestazioni dell'ordine dei Gigaflop/s, efficienza su un'ampia classe di problemi e semplicità d'uso. Il progetto CEDAR integra perciò diverse linee di ricerca informatica attive da più di un decennio all'Università dell'Illinois nel campo dello sviluppo di architettura, software e algoritmi per macchine parallele. Il progetto si articolerà in diverse fasi che porteranno, da qui agli anni novanta, alla creazione di prototipi di macchine con uno stesso impianto architetturale, ma con prestazioni e complessità crescenti. L'elaboratore parallelo CEDAR è organizzato gerarchicamente in sottosistemi (clusters, 4 nel prototipo iniziale, poi 16, infine 64) costituiti da 8 o 16 processori elementari (CE, Computational Elements), ciascuno dotato di capacità elaborative dell'ordine dei 10 Megaflop/s e di una piccola memoria individuale (v. fig. 11). In ogni sottosistema gli elaboratori elementari accedono attraverso una barra di trasmissione (bus) a una memoria globale di cluster, attualmente con dimensione di 8 Megawords. Attraverso un dispositivo centrale di commutazione (global switching network) essi possono accedere anche a una memoria globale di sistema costituita da 256 Megawords.

L'esecuzione di un programma di calcolo, anche originariamente scritto per una macchina seriale, sul multielaboratore CEDAR comporta l'individuazione, effettuata in maniera automatica, di ‛macromolecole' di calcolo (CF, Compound Functions), la cui esecuzione viene affidata ai singoli clusters sotto la supervisione di una unità di controllo generale. A loro volta ciascuno dei sottosistemi ripartisce ulteriormente l'unità di calcolo affidatagli tra gli elaboratori del cluster. Se il programma di calcolo lo consente, i dati richiesti nell'esecuzione delle compound functions sono pretrasportati automaticamente dalla memoria globale alle memorie di cluster. Questa articolazione gerarchica dell'architettura e del processo elaborativo permette l'efficiente cooperazione di tutti i singoli processori: massimizza le interazioni veloci ‛a corto raggio' tra membri di uno stesso cluster e riduce la necessità di interazioni ‛a lungo raggio' tra componenti di clusters diversi, che restano comunque possibili attraverso la rete di commutazione generale.

Le macchine RP3 e CEDAR illustrano un secondo fortunato paradigma di elaborazione avanzata, dopo quello, discusso inizialmente, dei multiprocessori vettoriali: esse infatti sono basate su un numero consistente di processori di media potenza, collegati tra di loro da un dispositivo centralizzato di commutazione (switch), che abbastanza frequentemente prende la forma di un commutatore a più stadi di tipo Omega (v. fig. 12).

Multielaboratori a interconnessione distribuita. Una terza famiglia di macchine MIMD sta ricevendo notevole attenzione. Essa è costituita da sistemi raggruppanti un numero elevato p, compreso tra 100 e 20.000, di nodi di elaborazione e memoria (PMF, Processor-Memory Elements, quasi sempre implementati su uno o pochi chips con tecnologia di integrazione circuitale su grande scala) collegati attraverso una ben evidente e spesso estesa rete di comunicazione (interconnection network). I singoli nodi possono scambiare direttamente dati con i nodi ‛vicini' nella rete, mentre la comunicazione ‛a distanza' di dati richiede l'inoltro e la ritrasmissione dei medesimi lungo una catena di nodi intermedi. La tecnica d'interconnessione distribuita è del tutto identica a quella vista per le macchine SIMD e ha dato luogo alle stesse varianti topologiche, quali, ad esempio, la struttura a griglia e la struttura ad albero. Poiché la struttura di interconnessione più completa, che connette direttamente ciascun elemento a ciascun altro, ha una complessità eguale al quadrato del numero p dei processori, e per p abbastanza grande non è realizzabile, si è posto il problema di realizzare topologie di collegamento con un buon equilibrio tra complessità (costo) ed efficienza, per esempio misurata con la distanza massima tra due nodi di rete. Tra le topologie di interconnessione, l'architettura variamente denominata ‛ipercubo', ‛n-cubo', ‛n-cubo booleano', ‛cubo cosmico' ha avuto il maggior seguito ed è una delle poche disponibili commercialmente. Un'architettura a n-cubo consiste di N = 2ⁿ nodi numerati da 0 a 2ⁿ − 1 e interconnessi in modo che vi è collegamento tra due processori se e solo se la rappresentazione binaria del loro numero d'ordine differisce per una cifra. Per n = 3, ad esempio, vi sono 8 = 2³ nodi che possono essere rappresentati come i vertici di un cubo (tridimensionale).

L'ipercubo di dimensione successiva, n = 4 (v. fig. 13), con N = 16 = 2⁴ nodi, si ottiene semplicemente congiungendo a due a due i vertici di due ipercubi tridimensionali e la stessa tecnica di duplicazione porta alle dimensioni successive. Il successo della topologia a ipercubo dipende dal numero limitato di interconnessioni richieste (in un ipercubo di 1.024 = 2¹⁰ nodi bastano 10 collegamenti per nodo), dalla buona efficienza (in un ipercubo di 1.024 = 2¹⁰ nodi, ad esempio, sono richiesti al più 10 passi intermedi per far arrivare un messaggio da un nodo a un altro) e dall'estrema regolarità della struttura, che favorisce la miniaturizzazione. Il primo ipercubo effettivamente operante (California Institute of Technology, 1983), un 5-cubo di 32 nodi costituiti ciascuno da un microprocessore Intel 8086 con coprocessore aritmetico Intel 8087, aveva modeste prestazioni, ma ha dimostrato la validità dell'impostazione architetturale e ha presto dato il via a ipercubi di dimensioni maggiori. Oggi sono proposti ipercubi commerciali con 1.024 = 2¹⁰ nodi e velocità di picco massima pari a 500 Megaflop/s, dalla Ncube, e numero di nodi N teoricamente uguale a 16.384 = 2¹⁴ e velocità di picco massima teoricamente eguale a 256 Gigaflop/s, dalla Floating Point Systems.

Tutte queste macchine sono MIMD (Multiple Instruction stream Multiple Data stream): ogni loro nodo è in grado di operare con programmi di calcolo indipendenti su dati indipendenti. Per ovvie ragioni di trattabilità le macchine MIMD a elevato numero di processori sono sovente adoperate in maniera SPMD (Single Program Multiple Data): in ogni nodo si trova cioè depositata una copia di uno stesso programma di elaborazione; durante il processo elaborativo i nodi possono però eseguire cammini diversi (branches) che tengano conto dell'identità dei singoli processori e dei dati presenti in questi ultimi.

d) Modello computazionale di un elaboratore parallelo.

Abbiamo fin qui proposto alcuni esempi di architetture avanzate di elaborazione, individuando il ruolo decisivo del parallelismo. Per comprendere in maniera più sistematica la complessità delle scelte che un progettista di sistemi di elaborazione paralleli deve affrontare, basterà qui ricordare che il ‛modello computazionale' di una macchina parallela richiede la specificazione di molteplici elementi, quali: 1) le entità atomiche di calcolo, cioè i tipi di dati elementari e le operazioni elementari permesse; 2) l'organizzazione dei dati nelle memorie, cioé le modalità di archiviazione e di accesso alle memorie; 3) il meccanismo di controllo, cioè le regole per raggruppare entità elementari di calcolo e assegnarle al sistema dei processori; 4) i modi e le strutture di comunicazione tra processori, onde permettere lo scambio di informazioni tra di essi; 5) i meccanismi di sincronizzazione, per assicurare la coerenza temporale delle azioni dei singoli processori.

Del tutto analogamente, la realizzazione di un elaboratore parallelo richiede di operare una scelta in uno spazio a più dimensioni progettuali, tra le quali, seguendo J. Schwartz, menzioniamo solo quelle corrispondenti ai cinque punti dell'elenco precedente: 1) numero dei processori; 2) potenza elaborativa di ciascun processore; 3) schema di controllo (SIMD, MIMD); 4) schema di comunicazione (a memoria condivisa, a scambio di messaggi); 5) struttura e caratteristiche dei dispositivi d'interconnessione.

Poiché per ciascuna di queste dimensioni progettuali ci si può attestare su diversi livelli, ci troviamo di fronte a una amplissima base di scelte: ciò spiega la sorprendente diversità delle architetture parallele di elaborazione degli anni ottanta e l'assenza a tutt'oggi di un modello architetturale concordemente riconosciuto superiore agli altri, come è avvenuto, per quasi tre decenni, nel caso della macchina di von Neumann.

5. Analisi delle prestazioni dei calcolatori paralleli.

Abbiamo visto nel capitolo precedente come il parallelismo di elaborazione sia realizzato principalmente attraverso la replicazione delle unità di calcolo (indice di parallelismo p) e la segmentazione (pipelining) delle operazioni elementari (indice di segmentazione v). La stima a priori del potenziale miglioramento di prestazioni dovuto all'applicazione congiunta di queste due tecniche è eguale al prodotto pν dei due singoli fattori di miglioramento. Qualche esempio mostrerà però che questa valutazione ha diversi limiti.

Supponiamo di dover eseguire uno dei nuclei operativi caratteristici dell'algebra lineare, ovvero l'operazione

tra gli elementi del vettore a = (a₁, a₂, ..., a_N) e del vettore b = (b₁, b₂, ..., b_N) per produrre il vettore c = (c₁, c₂, ..., c_N). Si tratta di effettuare N addizioni e N moltiplicazioni (2N operazioni floating-point), oltre che 3N trasferimenti tra memoria centrale e unità di calcolo (i vettori a e b provengono dalla memoria e c, il vettore risultato, vi deve essere portato).

Misuriamo sul multielaboratore vettoriale IBM 3090-200, dotato di due processori vettoriali, il numero dei cicli macchina necessari a eseguire questa operazione, per diverse lunghezze N dei vettori in gioco, effettuando ogni volta tre esperimenti: uso di un singolo processore scalare, uso di un singolo processore vettoriale (vector facility), uso di due processori vettoriali. La fig. 14 raccoglie i risultati degli esperimenti, effettuati mediante un semplice programma FORTRAN.

Vediamo subito che nel caso dell'esecuzione scalare (linea tratteggiata) il costo in cicli cresce in maniera lineare uniforme con la dimensione N e grosso modo corrisponde a 12 cicli per elemento c_l del vettore risultato. Nel caso dell'esecuzione vettoriale (linea continua) il costo in cicli scende a 3 cicli per elemento c_l, ma per ogni gruppo di 128 elementi vi è un costo addizionale di circa una novantina di cicli. Nel caso dell'esecuzione parallela con due processori vettoriali (linea punteggiata) il costo scende ulteriormente a 1 ciclo e mezzo per elemento, vi è sempre un costo addizionale di una novantina di cicli per ogni gruppo di 256 elementi e vi è un termine di costo iniziale di circa 600 cicli. È interessante notare che la dimensione N per cui esecuzione scalare e vettoriale sono equivalenti in costo è circa 12, mentre il punto di indifferenza tra esecuzione vettoriale su un solo processore e parallela con due processori vettoriali si ha intorno a N = 256. Va notato inoltre che in nessuno dei casi esaminati è stata raggiunta la prestazione teorica di picco dell'elaboratore, cioè due operazioni floating-point per ciclo per processore, che, nell'esempio esaminato, avrebbe consentito di produrre un elemento c_l del risultato ogni singolo ciclo con un solo processore e ogni mezzo ciclo con due: tale prestazione viene infatti raggiunta nel caso in questione solo se uno degli operandi a e b si trova già nei registri vettoriali e se il risultato c, che si forma nei registri, non deve subito venire portato in memoria (perché, ad esempio, deve venire riutilizzato in una successiva operazione). Non possiamo qui effettuare un'analisi a maggiore livello di dettaglio, per esempio esaminando le singole istruzioni di macchina in cui l'operazione c = a + s × b si decompone. Ci basterà osservare che l'esempio è indicativo di una situazione abbastanza generale.

Le prestazioni teoriche di picco di una macchina vettoriale e parallela sono di fatto limitate da una molteplicità di termini di costo, tra i quali segnaliamo qui quelli che sono emersi direttamente dallo studio dell'esempio precedente: 1) costo di avviamento delle istruzioni vettoriali (start-up); 2) costo di trasferimento degli operandi da e per le memorie nella loro articolazione gerarchica; 3) costo di sincronizzazione di più processori.

Un fattore di diminuzione di prestazioni, non presente nel semplice esempio della fig. 14, è costituito dalla ripartizione non equilibrata del carico di lavoro tra i processori di una macchina parallela, che può portare alla forzata inattività di alcuni nodi dipendenti per la prosecuzione dal completamento dell'attività assegnata ad altri.

Un'ulteriore ovvia limitazione emerge dall'analisi del seguente esempio. Si voglia calcolare una successione di iterate di una funzione, per un unico argomento scalare x, ad esempio

È chiaro che, in generale, non si potrà calcolare il termine f₂ fino a che non sia stato ultimato il calcolo di f₁, il termine f₃ fino a che non sia stato calcolato f₂ e così via. In altre parole, ci troviamo di fronte a una situazione di serialità (ricorsività) intrinseca, non parallelizzabile: avere a disposizione, diciamo, 1.000 processori non ci permette di ottenere i 1.000 valori f₁, f₂, ..., f_{1. 000} in un millesimo del tempo necessario per l'esecuzione del calcolo da parte di un singolo processore. Ben diverso è il caso in cui si voglia calcolare la successione delle iterate per un vettore x, perché allora parallelismo e pipelining svolgono egregiamente la loro funzione.

Siamo pronti ad accettare l'elementare constatazione che, per un dato problema, una macchina parallela (o vettoriale) porta a un incremento di prestazioni proporzionale non solo all'indice di parallelismo p (o all'indice di pipelining ν), ma anche, e si vorrebbe dire soprattutto, al coefficiente di ‛parallelismo intrinseco' del problema, α. Questa riflessione è espressa in forma molto convincente dalla cosiddetta ‛legge di Amdahl'. Dato un problema la cui soluzione comporta un costo C su una singola macchina scalare, supponiamo che C si possa dividere in due parti, αC e (1 − α)C, rappresentanti rispettivamente la parte parallelizzabile (vettorizzabile) e la parte intrinsecamente seriale. La soluzione del problema su una macchina parallela d'indice p richiederà ovviamente un costo pari a

L'incremento di prestazione (speed-up) tra esecuzione parallela ed esecuzione seriale è dunque

Identica è la situazione per lo speed-up vettoriale/scalare, fatta salva la sostituzione nella formula precedente dell'indice p con l'indice ν. La fig. 15 riporta per quattro valori di p, cioè 3, 5, 10 e 20, le curve di incremento di prestazione S(α, p) al variare di α tra lo 0% e il 100%, cioè tra il caso irriducibilmente seriale (scalare) e quello totalmente parallelo (o vettoriale). Si nota subito che per α = 0% evidentemente non c'è guadagno, per α = 100% il guadagno è p, il che non ci meraviglia, ma che anche in situazioni intermedie di buona parallelizzazione, diciamo α = 80%, l'incremento di prestazione varia piuttosto debolmente con p. In particolare, anche con un elevatissimo numero di processori, l'incremento di prestazione per α = 80% non può superare 1/(1 − a) cioè 5.

La ‛legge di Amdahl' nella forma citata trascura tutti i termini di costo additivi, ad esempio start-up e sincronizzazione, che pure abbiamo visto svolgere un ruolo importante. Includendo anche questi costi e indicandoli, in forma normalizzata, con ω(p) (overhead), la legge di Amdahl assume la forma

Una conseguenza leggermente paradossale di questa forma è che, se ω(p) cresce con p, l'incremento S(α, p) può anche decrescere al crescere di p, oltre un certo valore p_crit. Ciò avviene naturalmente quando il termine di overhead ω(p) vanifica la riduzione di tempo dovuta al parallelismo, cioè α/p.

Le considerazioni precedenti permettono di comprendere perché le prestazioni medie, per un dato problema, di un elaboratore ad architettura avanzata sono generalmente alquanto al di sotto delle prestazioni di picco ed evidenziano la difficoltà di confrontare dati di prestazione ottenuti su elaboratori con organizzazioni architetturali assai diverse. Resta inoltre confermata l'utilità di complementare l'usuale indice di prestazione, cioè la velocità di picco r^∞ espressa in Megaflop/s, con altri indici, quali quelli proposti da R. Hockney per connotare in forma direttamente percepibile dall'utilizzatore le caratteristiche architetturali del sistema: in particolare gli indici n_1/2, f_1/2, s_1/2, rispettivamente rappresentanti i tempi (morti) di avviamento di un'istruzione vettoriale, di accesso alla memoria, di sincronizzazione di un multielaboratore MIMD, tutti espressi in istruzioni floating-point equivalenti (che cioè si sarebbero potute eseguire durante queste attività accessorie). I tipici valori n_1/2 delle moderne macchine vettoriali sono compresi tra 20 e 400 flop (istruzioni aritmetiche equivalenti). Per le architetture MIMD più comuni s_1/2 può variare tra 500 e 50.000 flop, mentre f_1/2, a seconda della ‛distanza' processore-memoria, può variare tra qualche unità e qualche migliaio di flop.

6. Applicazioni dei supercalcolatori.

Lo sviluppo dei supercalcolatori è stato in massima parte pilotato dalla crescente richiesta di risorse elaborative da parte di un gruppo di applicazioni scientifico-tecniche caratterizzate da elevatissime quantità di operazioni aritmetiche (floating-point) su ampie basi di dati. Lo spettro delle applicazioni è estremamente ampio e non consente una classificazione rigorosa. A titolo esemplificativo la tab. I riporta alcune tradizionali aree di utilizzazione degli elaboratori di alte prestazioni.

Comune a tutte queste applicazioni è il ruolo del calcolatore come nuovo strumento d'indagine a fianco della sperimentazione fisica diretta e della speculazione teorica. Un valido ausilio alle discipline teoriche, che schematizzano mediante modelli matematici i nuovi fenomeni e processi continuamente proposti dalle discipline sperimentali, viene infatti offerto dalla ‛sperimentazione numerica'. Il punto di partenza di un esperimento numerico (per esempio di meteorologia) è un modello matematico che rappresenta un sistema fisico (l'atmosfera terrestre). La descrizione matematica del modello è data da leggi costitutive o evolutive, condizioni al contorno e condizioni iniziali, spesso espresse da equazioni algebriche ed equazioni differenziali che legano le variabili che interessano (nell'esempio in esame temperatura e velocità dell'aria). Se la teoria non offre soluzioni analitiche di queste equazioni - come accade quasi sempre per i sistemi non lineari - è necessario ricorrere a procedimenti risolutivi (algoritmi numerici) che conducano attraverso una successione di passi operativi ad accurate stime numeriche delle variabili in esame. L'approccio numerico permette di studiare il comportamento di sistemi o processi di enorme complessità o di difficile sperimentazione diretta; di prevederne l'evoluzione; di valutare l'effetto di variazioni di condizioni o di parametri. Gli unici limiti di questo approccio sono rappresentati dalla significatività dei modelli matematici di base e dall'ammontare dei calcoli richiesti. La tab. II riporta, ad esempio, una stima delle risorse di calcolo considerate come necessarie per l'avanzamento scientifico in alcune discipline.

7. Algoritmi per elaboratori paralleli.

L'aumento della velocità dell'hardware è soltanto uno dei fattori che controllano l'espansione della frontiera del calcolo avanzato (supercomputing). Egualmente importante è la disponibilità di metodi numerici (‛algoritmi') adatti alla complessità architetturale delle macchine di calcolo moderne.

Un'analisi critica del matematico P. D. Lax mostra che ‛nell'era di von Neumann' (1945-1970), delle macchine seriali, lo sviluppo di metodi numerici adatti a esse è stato sorprendente e ha addirittura superato in importanza i miglioramenti di prestazioni ottenuti nel medesimo periodo dall'evoluzione della tecnologia dei calcolatori: si pensi, ad esempio, alla comparsa, nel settore della dinamica ‛numerica' dei fluidi, del metodo dei passi frazionati, degli schemi alle differenze finite di elevato ordine di accuratezza, dei metodi spettrali e pseudospettrali, dei metodi agli elementi finiti e delle tecniche multigrid.

Lo sforzo della ricerca nel periodo 1945-1970 si è concentrato principalmente sulla progettazione di algoritmi a minimo costo di calcolo, il costo essendo semplicemente definito come il numero di operazioni floating-point (o più semplicemente ancora il numero delle moltiplicazioni) richieste dall'algoritmo. Questi algoritmi, con numero minimo di operazioni floating-point, ottimali per macchine seriali, non sono però automaticamente i più efficienti anche su macchine vettoriali e parallele per una molteplicità di ragioni, la più importante delle quali è la natura intrinsecamente seriale (ricorsiva) di molti di essi. Tra gli altri termini di costo che non possono essere trascurati nel bilancio complessivo ci sono i costi di avviamento (start-up) delle operazioni vettoriali, i costi di comunicazione e sincronizzazione tra processori e, sovente con un ruolo decisivo, i costi d'accesso dei dati alla gerarchia delle memorie con diverse velocità. Una maniera algoritmicamente assai efficace di rappresentare questi costi è tradurli con R. Hockney in operazioni floating-point ‛utili' che si sarebbero potute svolgere durante queste attività accessorie.

La ricerca in questo ultimo quindicennio (1970-1985) si è concentrata sulla riformulazione di determinati algoritmi, specie nel campo dell'algebra lineare e in quello delle equazioni alle derivate parziali, per adattarli a macchine parallele. Quattro sono le tecniche principalmente usate: a) riordinamento dell'algoritmo, per esempio per rinumerazione dei nodi di una griglia di calcolo o per alterazione (quando sia lecito) della struttura della sequenza di calcolo, al fine di rivelare una maggiore quantità di parallelismo o diminuire il traffico da/per la memoria o individuare pochi processi indipendenti di grosso ‛peso' piuttosto che molti di ‛peso' piccolo; b) partizione del dominio di calcolo in sottodomini da assegnare a processori indipendenti; c) decomposizione degli operatori di calcolo in operatori più semplici da assegnare a processori indipendenti; d) trasformazione del problema originale in un problema equivalente (per esempio attraverso una trasformazione di variabili), in cui la vettorizzazione e la parallelizzazione in genere siano di più facile attuazione.

a) Equazioni alle derivate parziali.

I modelli matematici di molti fenomeni e processi fisici (si pensi, ad esempio, alla dinamica dei fluidi) sono costituiti da una o più equazioni differenziali che esprimono le relazioni tra i valori che determinate variabili assumono nel corso del tempo e in un volume dello spazio (il ‛dominio' dell'equazione). Molti algoritmi di soluzione numerica di equazioni differenziali si basano sulla campionatura del dominio mediante una ‛griglia', nei nodi della quale sono da calcolare i valori delle variabili in esame, ed esprimono relazioni tra nodi contigui della griglia. La progettazione di architetture di elaborazione avanzate è stata influenzata dalla necessità di fornire efficaci strumenti di calcolo per questi algoritmi di soluzione numerica di equazioni differenziali e, reciprocamente, fissata un'architettura di elaborazione, sono stati cercati algoritmi ottimali (a minimo tempo di esecuzione) per essa. Un esempio caratteristico è costituito dalle architetture SIMD ad array di processori con interconnessione a griglia per la soluzione di equazioni ellittiche in 2 dimensioni con schemi alle differenze finite (v. informatica: Matematica numerica, suppl.).

Il classico metodo iterativo detto di Jacobi, per la soluzione numerica dell'equazione di Laplace

consiste nella ripetuta sostituzione del valore della variabile u in ciascuno dei punti di una griglia rettangolare (v. fig. 16) con la media dei valori dei nodi contigui (a est, ovest, nord e sud), consiste cioè nell'applicazione ripetuta della relazione di ‛smussamento'

in tutti i punti (i, j) della griglia, fino a che ulteriori smussamenti non producano più variazioni (convergenza). Lo schema di Jacobi è particolarmente adatto per architetture SIMD in quanto, a ogni ripetizione del ciclo, le sostituzioni della formula di smussamento nei diversi nodi sono indipendenti e possono essere effettuate simultaneamente. È interessante notare che lo schema di Jacobi è assai inefficiente a causa della sua lentezza di convergenza alla soluzione e in pratica è sempre stato sostituito da metodi più veloci, ad esempio lo schema iterativo detto di Gauss-Seidel

che consiste nell'utilizzare in ciascun punto i ‛nuovi' valori di u non appena essi siano disponibili. Si tratta di un algoritmo efficiente, ma intrinsecamente seriale. Nel caso specifico, con un opportuno riordinamento dei nodi di calcolo (ordinamento a scacchiera), è possibile ottenere uno schema efficiente come quello di Gauss-Seidel, ma sostanzialmente SIMD-parallelo come quello di Jacobi.

In generale non è possibile ottenere algoritmi che, su macchine parallele di indice p, abbiano prestazioni superiori di un fattore p al migliore algoritmo seriale noto, anche nel caso idealizzato di costo zero per comunicazione e sincronizzazione. Sono però stati proposti schemi che sulle architetture di elaborazione parallele più usate (multiprocessori vettoriali) hanno prestazioni interessanti: in particolare, per equazioni ellittiche, i metodi ‛a ripartizione di dominio' tra processi iterativi multipli e i metodi ‛caotici', senza sincronizzazione tra processi.

b) Algebra lineare.

Considerazioni analoghe sono sviluppabili per il problema della soluzione numerica di un sistema lineare

Ax = b,

in quanto la discretizzazione di un'equazione differenziale porge spesso direttamente un problema di algebra lineare. Anche qui i migliori algoritmi seriali, per l'ampia varietà di situazioni (matrici dense, sparse e strutturate, metodi iterativi e diretti), non sono facilmente generalizzabili ad architetture parallele. Offre particolari difficoltà l'implementazione, di grande interesse pratico, di efficienti metodi diretti per matrici sparse su macchine vettoriali, che porta a molte operazioni su vettori di piccole dimensioni e con elementi organizzati senza regolarità. Ottimi risultati sono invece ottenibili da varianti del classico algoritmo di eliminazione gaussiana su sistemi densi di equazioni, ed è in questo caso che le prestazioni medie dei supercalcolatori si avvicinano di più alle prestazioni di picco. Tra i metodi iterativi continua a ricevere grande attenzione il metodo del ‛gradiente coniugato' nelle sue numerose varianti.

Per problemi di algebra lineare con matrici a struttura regolare e per algoritmi consolidati, i migliori rapporti prestazioni/costo si possono però ottenere da architetture di elaborazione specializzate quali le ‛macchine sistoliche', che estendono a due dimensioni il concetto di pipeline lineare. Appare particolarmente interessante la possibilità, offerta dalla moderna tecnologia d'integrazione circuitale su grande scala, di realizzare questi dispositivi di calcolo specializzato a livello di chip.

8. Software di sistema per elaboratori vettoriali e paralleli.

Abbiamo visto come l'esistenza di efficienti algoritmi paralleli sia un requisito essenziale per lo sfruttamento delle moderne architetture di elaborazione. Di estrema importanza è anche la disponibilità di ‛ambienti' per lo sviluppo di software scientifico, che permettano agli utenti di accedere facilmente alle risorse dei supercalcolatori.

Nel passato l'utilizzatore tipico di supercalcolatori era un ricercatore con notevoli conoscenze informatiche pronto ad assumersi l'onere di creare il software applicativo e di base per sfruttare a pieno le potenzialità di una macchina dalle prestazioni avanzate. Con l'odierna diffusione dei supercalcolatori, il tipico utente, che non ha più il profilo sopra descritto, non vuole interagire direttamente con l'hardware dei calcolatori, ma è abituato a sfruttarli in maniera mediata, attraverso una serie di livelli intermedi di ‛linguaggi di programmazione'. Ciascuno di questi strati intermedi poggianti sopra il calcolatore reale costituisce un calcolatore virtuale con il suo linguaggio e il suo modello computazionale. I livelli coinvolti nella soluzione di un problema su una macchina parallela sono almeno quattro: 1) l'algoritmo, o descrizione ad alto livello dei processi di calcolo; 2) il linguaggio algoritmico ad alto livello, mediante il quale l'utente trasforma l'algoritmo in un programma di calcolo, o codice; 3) il sistema operativo, che assegna le risorse del sistema (i processori e le memorie, ad esempio) ai processi che ne fanno richiesta; 4) l'architettura del calcolatore reale con il suo insieme di istruzionimacchina eseguibili.

L'utilità totale di un sistema dipende dalla sua capacità di esprimere efficientemente le richieste algoritmiche ad alto livello in azioni del livello più basso; l'agevolezza d'uso di un sistema è direttamente proporzionale al grado d'invisibilità (trasparenza) degli strati inferiori.

Per quanto riguarda, ad esempio, l'agevolezza d'uso di una macchina SIMD (a replicazione di processori o con pipeline), grazie al software di sistema attualmente disponibile si può dichiarare pressoché risolto il problema. Esistono infatti linguaggi SIMD ad alto livello, con istruzioni operanti su oggetti complessi come vettori e matrici. Mediante linguaggi di questo genere, esemplificati tipicamente da APL (A Programming Language), è possibile esprimere in maniera naturale gli algoritmi vettoriali e contemporaneamente ottenere un'efficace implementazione hardware. Anche programmi scientifici composti nel linguaggio sequenziale (SISD) FORTRAN, in epoca antecedente alla comparsa di calcolatori dotati di pipelines e di istruzioni vettoriali, possono essere efficientemente eseguiti sulle modeme macchine vettoriali con piccole variazioni (quando, ben inteso, ne esistano le premesse algoritmiche). Esistono infatti ottimi ‛compilatori autovettorizzanti' in grado di rivelare automaticamente quali tra i cicli iterativi (DO-loops) di un programma in FORTRAN possano essere eseguiti mediante istruzioni vettoriali equivalenti e quali siano intrinsecamente ricorsivi e non riconducibili all'esecuzione SIMD. Ad esempio, il ciclo iterativo

anche se espresso (serialmente) mediante il programma FORTRAN, viene da questi compilatori agevolmente riconosciuto come ‛vettorizzabile', a differenza del ciclo ricorsivo

Più complesso è il caso della multielaborazione (multitasking), cioè della costruzione, della compilazione e dell'esecuzione di programmi per macchine MIMD. Alcuni gruppi di ricerca ritengono i linguaggi di elaborazione in uso nell'ambiente scientifico del tutto inadatti alle nuove architetture MIMD e propongono l'introduzione di nuovi linguaggi di elaborazione, ad esempio OCCAM, con efficaci e ben strutturate primitive di controllo e di intercomunicazione di processi concorrenti. Altri gruppi propongono leggere modifiche dei linguaggi in uso, e in particolare del FORTRAN, mediante l'introduzione di ‛direttive di parallelismo' o di estensioni del linguaggio, per permettere, ad esempio, l'esecuzione di un ciclo ripetitivo e privo di dipendenze su una molteplicità di processori. Se questo ciclo è uno dei più esterni di un programma e contiene chiamate a procedure interconnesse, spetta chiaramente al ‛programmatore parallelo' che ha utilizzato la direttiva di parallelismo sincerarsi che non vi siano interdipendenze di natura ricorsiva. L'indicazione può essere anche fornita attraverso istruzioni di ‛diramazione parallela' (fork) e ‛sincronizzazione' (join) (v. fig. 17), inserite in varia forma nel linguaggio di programmazione. In altre parole, è essenzialmente il programmatore che deve indicare esplicitamente nei casi più complessi quali processi possano essere eseguiti in parallelo.

Sono ancora in corso di sviluppo ‛compilatori autoparallelizzanti' per macchine MIMD, in grado di effettuare la complessa analisi interprocedurale e le valutazioni di efficienza ora richieste al programmatore. Di particolare rilevanza appare l'attività del gruppo di D. Kuck all'Università dell'Illinois, centrata attorno allo sviluppo di Parafrase, un rivelatore di parallelismo per programmi FORTRAN seriali.

9. Linee di tendenza.

Dal quadro qui tracciato appare chiaro che l'uso del parallelismo a tutti i livelli è attualmente la sola strada possibile per fornire le velocità di calcolo richieste da molte aree applicative. Tuttavia, mentre l'uso di macchine vettoriali è ormai pienamente accettato e diffuso, per quanto riguarda i multielaboratori la situazione è molto meno definita. In particolare la mancanza di compilatori autoparallelizzanti interprocedurali e la difficoltà di formulazione di algoritmi paralleli costituiscono una barriera che tiene ancora lontana la maggior parte degli utenti dall'uso di sistemi paralleli MIMD.

Non è inoltre escluso che i miglioramenti, attesi a scadenza medio-lunga, della tecnologia circuitale (transistori balistici, transistori a più stati, transistori fotonici, transistori a superconduzione) rendano nuovamente possibile ed economicamente vantaggioso realizzare supercalcolatori ad architettura seriale. A tale proposito è particolarmente illuminante ricordare che il primo supercalcolatore elettronico, la macchina ENIAC, costruita tra il 1943 e il 1948 all'Università di Pennsylvania, era una macchina a elevato parallelismo (era dotata di 20 accumulatori indipendenti) e con possibilità di interconnessioni variabili tra le diverse unità. Le difficoltà nella ‛programmazione parallela' di ENIAC, consistente nella coordinazione di molteplici pannelli di controllo, resero in pratica inevitabile un uso semplificato e seriale della macchina. L'incremento di velocità circuitale nelle macchine degli anni cinquanta, a partire da EDVAC, rese poi superflua la necessità, presente nel disegno di ENIAC, di accrescere le prestazioni con la replicazione delle unità e portò all'affermazione fino alla soglia degli anni ottanta dell'architettura di von Neumann. Se l'esempio è significativo, è dunque ragionevole considerare il parallelismo come una caratteristica necessaria, ma temporanea, dei sistemi di elaborazione attuali.

Bibliografia.

Amdahl, G. M., Validity of the single processor approach to achieving large scale computing capabilities, in ‟AFIPS conference proceedings", 1967, XXX, pp. 483-485.

Dongarra, J. J., Gustavson, F. G., Karp, A. K., Implementing linear algebra algorithms for dense matrices on a vector pipeline machine, in ‟SIAM review", 1984, XXVI, pp. 91-112.

Flynn, M., Some computer organizations and their effectiveness, in ‟IEEE transactions on computers", 1972, C-XXI, pp. 948-960.

Hockney, R. W., Jesshope, C. R., Parallel computers, Bristol 1981.

Hwang, K. (a cura di), Supercomputers: design and applications, Silver Spring, Md., 1984.

Kuck, D. J., A survey of parallel machine organization and programming, in ‟ACM computing survey", 1977, IX, 1, pp. 29-59.

Kuhn, R. H., Padua, D. A., Tutorial on parallel processing, Silver Spring, Md., 1981.

Kung, H. T., Lam, M., Wafer-scale integration and two-level pipelined implementations of systolica arrays, in ‟Journal of parallel and distributed computing", 1984, I, 1.

Ortega, J. M., Voigt, R. G., Solution of partial differential equations on vector and parallel computers, in ‟SIAM review", 1985, XXVII, 2, pp. 149-240.

Padua, D. A., Kuck, D. J., Lawrie, D. H., High-speed multiprocessors and compilation techniques, in ‟IEEE transactions on computers", 1980, C-XXIX, 9, pp. 763-776.

Paul, G. (a cura di), Special issue on supercomputers - Their impact on science and technology, in ‟Proceedings of the IEEE", 1984, LXXII, 1, pp. 1-144.

Rodrigue, G. (a cura di), Parallel computations, New York 1982.

Intelligenza artificiale di Piero Dell'Orco e Tomaso Poggio

SOMMARIO: 1. Che cos'è l'intelligenza artificiale. 2. Introduzione storica. 3. Ragionamento e percezione. 4. Risoluzione di problemi: a) tecniche di ricerca; b) la procedura MINIMAX; c) ottimizzazione continua. 5. Logica. 6. Rappresentazione della conoscenza: a) reti semantiche; b) ereditarietà, demoni, credenze, visuali; c) strutture (frames). 7. Sistemi esperti: a) generazione e verifica; b) sistemi basati su regole. 8. Linguaggio: a) sintassi e morfologia; b) dalla sintassi alla semantica. □ 9. Apprendimento: a) l'induzione di concetti e di regole da esempi; b) mutazione e selezione di regole. 10. Robotica e visione: a) la complessità della visione; b) l'organizzazione della visione; c) visione base; d) riconoscimento delle scene; e) architetture parallele. □ Bibliografia.

1. Che cos'è l'intelligenza artificiale.

Dell'intelligenza artificiale possono essere date varie definizioni, che però finiscono inevitabilmente per risultare o troppo generiche o troppo restrittive. In effetti una definizione di intelligenza artificiale dovrebbe comprenderne una di intelligenza, e definire l'intelligenza costituisce per un informatico (o uno psicologo) un problema tanto difficile quanto, per un biologo, quello di definire la vita. Nonostante questo, il termine ‛intelligenza' è usato nel linguaggio corrente, senza evidente ambiguità, per designare una facoltà normalmente attribuita agli esseri umani. Nel corso di questo articolo tale termine sarà usato senza ulteriore specificazione, in quanto il suo significato sarà reputato chiaro per il lettore.

Una delle principali finalità di questa disciplina consiste nell'ideare, produrre e utilizzare modelli computazionali di processi cognitivi, cioè schemi rigorosamente definiti (e, come tali, eseguibili da un elaboratore) di comportamenti ‛intelligenti'. Ciò significa costruire degli artefatti che abbiano un certo grado di intelligenza e, contemporaneamente, comprendere i principi che sono alla base di questa facoltà.

Un test (famoso, anche se non rigoroso) per determinare se un sistema segue un comportamento intelligente fu proposto dal matematico inglese A. Turing. Esso prescrive un'interazione scritta tra un essere umano e un'entità che egli non vede e che può essere un altro uomo o il sistema in esame. Il test è positivo quando il soggetto non distingue tra le risposte del sistema e quelle dell'uomo.

Prendendo spunto dalla particolare attività umana che l'intelligenza artificiale si propone di emulare, si possono individuare i diversi campi che costituiscono oggi questa disciplina: la percezione, le capacità di attuazione e di comprensione, l'apprendimento e l'uso di conoscenze generiche e specialistiche vengono emulati rispettivamente dai sistemi di percezione, dalla robotica, dai sistemi di analisi del linguaggio naturale e di apprendimento e dai sistemi esperti, come illustrato nella fig. 1.

È legittimo chiedersi, a questo punto, con quali mezzi sia possibile emulare tali attività. In linea di principio (e questo è quasi un dogma dell'intelligenza artificiale) qualsiasi mezzo (elettronico, ma anche meccanico) per elaborare l'informazione è adatto allo scopo, fatte salve le inevitabili differenze nella velocità di elaborazione, nell'ingombro e nel costo, in quanto la parte sostanziale è costituita dalla serie di istruzioni che la macchina deve eseguire. In particolare, rovesciando la prospettiva, il sistema nervoso umano può essere considerato una particolare macchina per l'elaborazione dell'informazione e si può ragionevolmente ipotizzare che esso utilizzi principi e metodologie analoghi a quelli di macchine di altro tipo: ciò rende l'intelligenza artificiale un campo di ricerca particolarmente rilevante per coloro che si interessano dell'intelligenza ‛naturale', e viceversa rende le scoperte e i risultati della psicologia cognitiva interessanti per gli studiosi di intelligenza artificiale.

Al momento attuale l'elaboratore elettronico è l'unico strumento in grado di offrire quell'insieme di caratteristiche di costo, ingombro e prestazioni che rendono praticabile la sperimentazione nel campo dell'intelligenza artificiale. Grazie a esso, infatti, è possibile, una volta formulata una teoria su qualche aspetto dell'intelligenza, esprimerla formalmente in un programma eseguibile e verificarla sperimentalmente. È proprio questa possibilità di verifica sperimentale che differenzia profondamente l'intelligenza artificiale dalle teorie filosofiche della mente formulate nel corso degli ultimi duemila anni. In questo modo l'elaboratore, emulando il comportamento umano, riveste un duplice ruolo: da una parte rappresenta una metafora dei meccanismi mentali umani e dall'altra è uno strumento di ricerca utilissimo. L'intelligenza artificiale, benché sia una scienza giovane, offre già svariate applicazioni pratiche, che comunque costituiscono, a detta di molti, solo una piccola percentuale di quelle che emergeranno in un futuro ormai prossimo.

2. Introduzione storica.

L'importanza che l'uso dell'elaboratore ha nell'intelligenza artificiale fa sì che essa sia spesso considerata una parte dell'informatica e quindi che la sua data di nascita sia ritenuta posteriore a quella dell'informatica stessa. Si può quindi chiamare convenzionalmente ‛preistoria' dell'intelligenza artificiale il periodo che vide lo sviluppo dei primi elaboratori. C. Babbage, matematico e astronomo inglese nato nel 1792, è spesso considerato il padre della scienza del calcolo automatico (e quindi dell'intelligenza artificiale) in virtù di due macchine, il ‛motore differenziale' e il ‛motore analitico', che egli progettò nel 1822 per eseguire calcoli astronomici. Nel 1943, durante la seconda guerra mondiale, il sistema Colossus veniva impiegato dagli Inglesi per decifrare i codici prodotti dai Tedeschi per mezzo del sistema Enigma. Molti dei giovani ricercatori che lavoravano a questo progetto, forse ispirati dalle particolarità del problema, avrebbero poi dato grandi contributi all'intelligenza artificiale. Tra questi c'era il matematico A. Turing, che aveva già legato, nel 1937, il suo nome al modello teorico di una macchina ideale, capace di descrivere ogni macchina reale in grado di eseguire completamente una qualsiasi procedura matematica. Qualche anno più tardi lo stesso Turing osservava profeticamente che le macchine avrebbero potuto emulare alcune funzioni intellettuali umane.

In seguito, quando ormai lo sviluppo degli elaboratori aveva fornito delle solide capacità di calcolo, il concetto di intelligenza artificiale fu ripreso su basi più pratiche; nel 1956 J. McCarthy organizzò, a Dartmouth, un convegno ‛storico' nel corso del quale fu coniato il termine ‛intelligenza artificiale' nel senso in cui lo usiamo oggi. Già in quel convegno vennero presentati i primi programmi capaci di un comportamento ‛intelligente': famoso, a questo proposito, il Logic theorist in grado di dimostrare teoremi di logica matematica.

A partire dal 1957 fu sviluppato un programma, il GPS (General Problem Solver), destinato a emulare il comportamento umano nella soluzione di problemi di tipo generale. Nel 1959 Gelertner costruì un programma per la dimostrazione dei teoremi di geometria, subito seguito da un altro programma per l'integrazione simbolica. Questi programmi utilizzavano per la prima volta, e in maniera massiccia, la capacità dell'elaboratore di manipolare simboli, oltre che numeri, secondo regole specificate dal programmatore.

Il successo di questi programmi, tanto vasto quanto inaspettato, dette luogo all'ipotesi (poi rivelatasi falsa) che le soluzioni fossero a portata di mano e quindi a una serie di aspettative infondate, se non negli obiettivi, quanto meno nei tempi di realizzazione. Quando tali aspettative andarono fatalmente disattese, l'intelligenza artificiale attraversò un periodo di crisi, per il brusco taglio dei finanziamenti e la cancellazione di molti progetti: ancora nel 1973 un rapporto di sir J. Lighthill sosteneva che nel Regno Unito la ricerca nel campo dell'intelligenza artificiale si era risolta sostanzialmente in un cattivo uso dei fondi governativi.

Nel frattempo i ricercatori avevano implicitamente adottato un codice di comportamento basato su un'estrema prudenza nella valutazione dei risultati e delle prospettive, per cui i programmi sviluppati durante gli anni settanta nel campo dei sistemi esperti poterono essere presentati con ragionevoli caratteristiche di solidità e affidabilità.

Oggi lo sviluppo dell'intelligenza artificiale ha assunto un andamento quasi esplosivo. Da un punto di vista scientifico, già nel 1981, alla prima conferenza UCAI (International Joint Conference on Artificial Intelligence) tenuta a Dartmouth in occasione del venticinquesimo anniversario della precedente conferenza storica, furono presentati più di duecento articoli relativi a otto diversi campi, alla presenza di delegati provenienti da più di venti nazioni. A fini applicativi tutte le grandi industrie hanno investito in misura notevole nell'intelligenza artificiale, mentre le piccole imprese specializzate in intelligenza artificiale stanno conoscendo uno sviluppo paragonabile solo a quello delle imprese impegnate nel campo della biologia molecolare. Lo sviluppo di tecnologie hardware e soprattutto software ha fornito la base per sistemi di intelligenza artificiale destinati a un'ampia gamma di professionisti finora toccati solo marginalmente dall'informatica - medici, insegnanti, chimici, geologi, biologi, avvocati, commercialisti, responsabili di fabbrica, ecc. -, per i quali questi mezzi si rivelano sempre più essenziali al successo professionale.

3. Ragionamento e percezione.

Da un punto di vista storico, le prime ricerche sull'intelligenza artificiale hanno avuto per oggetto gli aspetti che potremmo definire ‛profondi' dell'intelligenza: si sono cioè concentrate su attività che risultano essere più immediatamente in corrispondenza con il concetto intuitivo di intelligenza.

Per questo motivo si sono dapprima investigate le capacità di ragionare logicamente, di risolvere problemi, di capire testi scritti in qualche linguaggio naturale (inglese, italiano, ecc.), assumendo tacitamente che un sistema dovesse possedere queste capacità per essere reputato ‛intelligente' e che l'attività di interazione con il mondo esterno fosse un processo completamente trattabile nel quadro puramente fisico dell'elaborazione dei segnali e/o della meccanica. In realtà la mente umana interagisce essenzialmente in due modi con il mondo esterno: ricevendo da esso, attraverso i sensi, stimoli sotto forma di grandezze fisiche o variazioni di esse (radiazioni elettromagnetiche, onde sonore, ecc.) e immettendovi, attraverso l'apparato motorio, grandezze fisiche (onde sonore, forze meccaniche, ecc.); possiamo chiamare i due fenomeni rispettivamente ‛percezione' e ‛attuazione'.

I primi tentativi di emulare la percezione semplicemente sulla base dell'elaborazione dei segnali si rivelarono ben presto fallimentari, in quanto, come è risultato poi evidente, la facilità con cui l'uomo vede o sente è solo apparente: ogni forma di percezione ha bisogno di un'intelligenza periferica e specializzata estremamente complessa. Del tutto analogamente, i problemi di coordinazione motoria sono molto più sofisticati di quanto un'analisi superficiale possa far sospettare.

Il tipo di intelligenza che si richiede per risolvere questi problemi è leggermente differente da quello ‛profondo' visto prima, proprio perché le problematiche sono differenti: le facoltà ‛intellettuali profonde' (ragionamento, comprensione, ecc.) analizzano normalmente problemi caratterizzati da un'informazione completa, allo scopo di dedurne la soluzione corretta; l'attività percettiva, viceversa, consiste in genere nell'elaborazione di un'informazione incompleta al fine di interpretare l'immagine, sfruttando proprietà generiche del problema, degli oggetti del mondo fisico, ecc.

4. Risoluzione di problemi.

Sicuramente un'attività che viene reputata ‛intelligente' nella vita di ogni giorno, e che quindi rientra nella definizione intuitiva di ‛intelligenza', è quella di risolvere problemi.

I problemi alla cui soluzione sono destinate le metodologie dell'intelligenza artificiale consistono tutti, a prescindere dalla loro complessità intrinseca, nella ricerca di un ‛percorso operativo' che da uno stato iniziale, dato, porti a uno stato finale desiderato. In altri termini risolvere questo tipo di problemi significa trovare la successione delle operazioni che porta dallo stato iniziale a uno stato finale.

I problemi che si incontrano nella realtà sono spesso complicati da vari fattori, quali l'imperfetta definizione dello stato iniziale, dello stato finale e anche delle possibili mosse. Conviene quindi studiare l'argomento a cominciare da ‛realtà' che hanno poche semplici regole fisse, quali la dama, gli scacchi, il gioco del 16, ecc. Anche in questi casi, però, il numero degli stati possibili è spesso, per problemi non banali, molto elevato: per gli scacchi ogni configurazione della scacchiera costituisce uno stato; in totale essi sono 10¹²⁰ e un elaboratore che volesse esaminarli tutti, se anche impiegasse un milionesimo di secondo per operazione, impiegherebbe 10¹¹⁴ secondi, corrispondenti a un tempo dell'ordine di 10¹⁰³ millenni. Escludendo che la mente umana sia capace di prestazioni tali da ridurre questo tempo a pochi minuti, non resta che concludere che esiste un meccanismo che seleziona, da tutti gli stati possibili, solo quelli ‛rilevanti' e quindi ne riduce il numero totale in maniera drastica. L'obiettivo dell'intelligenza artificiale è, in questo caso, di risolvere questi problemi difficili limitando la ricerca delle soluzioni tramite strategie molto efficienti. Analizzando i meccanismi di scelta che la mente umana adotta in questi casi, si osserva che alla base di essi c'è sempre l'utilizzo di un'enorme quantità di conoscenza specifica del mondo. Infatti solo tenendo presenti le peculiarità del problema e dei suoi componenti si possono scartare a priori delle strade destinate a rivelarsi impraticabili. Questa conoscenza è utilizzata dalla mente umana anche nelle più semplici attività della vita di ogni giorno: anche la comprensione di semplici frasi del linguaggio naturale viene efficacemente raggiunta in maniera inconscia sulla base della conoscenza che il parlante ha del mondo e delle sue proprietà.

Nell'ambito di discipline ben circoscritte e specializzate (diagnostica medica, chimica organica, ecc.) l'utilizzo della conoscenza è sufficientemente chiaro e può essere quindi emulato dai cosiddetti ‛sistemi esperti', cioè da programmi che usano esplicitamente la conoscenza del dominio applicativo per dare consulenza a livello paragonabile a quello degli esperti umani.

La quantità di conoscenza necessaria per il funzionamento dei sistemi esperti, pur riferita a uno specifico dominio, è molto grande; un sistema svincolato dalla limitazione del dominio e che sia un risolutore generale di problemi richiede una quantità di conoscenza enorme, la cui rappresentazione pone problemi ancora insoluti. Ciò spiega come tentativi precedenti in questo senso, quale il GPS di Newell e Simons, si siano rivelati non funzionali. L'esperienza è servita comunque a chiarire alcuni punti fondamentali per la metodologia di risoluzione dei problemi, che possono essere riassunti come segue.

1. Identificare chiaramente il problema. Ciò significa identificare con esattezza e formalmente le caratteristiche fondamentali che descrivono esattamente lo stato iniziale, lo stato finale ed eventualmente gli stati intermedi, e definire dei metodi formali per accertarsi della loro presenza. Un semplice esempio è costituito dal ‛gioco del 16', in cui, in un quadrato 4 per 4 sono disposte 15 tessere, numerate progressivamente, che possono muoversi, occupando un posto prima libero, senza però uscire dal quadrato. Lo stato iniziale è dato dalle tessere in una disposizione qualsiasi, lo stato finale dalle tessere in disposizione ordinata. Naturalmente non per tutti i problemi, specie per quelli ‛reali', è cosi facile definire gli stati.

2. Sviluppare una rappresentazione appropriata. In pratica tradurre in simboli (sequenze di numeri, caratteri, o disegni) gli elementi costituenti il problema, per rendere possibile l'elaborazione dei simboli stessi invece che degli elementi del problema. Questa è un'esigenza presente in tutte le scienze: la chimica ha ricevuto indubbiamente un grande impulso dall'uso dei simboli e delle formule per indicare gli elementi e i composti. Nel nostro esempio una ragionevole rappresentazione potrebbe essere costituita dalla tabella ottenuta scrivendo i numeri delle tessere uno di seguito all'altro, quattro per riga, cominciando dall'angolo a sinistra in alto e procedendo lungo le righe.

3. Enunciare esplicitamente i vincoli del problema e tutte le condizioni che possono essere utili a ridurre il numero di stati da prendere in considerazione. Ciò equivale a esplicitare la ‛conoscenza del problema' o le ‛regole del gioco' e tutte le proprietà (per es. di simmetria) che rendono uno stato decisamente peggiore, migliore o equivalente a un altro. Nel caso del ‛gioco del 16' la ‛regola del gioco' potrebbe essere espressa stabilendo che, per ogni dato stato, può muoversi una delle tessere adiacenti alla casella vuota, occupandola.

4. Sviluppare delle procedure specifiche di soluzione. Ciò significa dare dei criteri e delle leggi per esaminare e giudicare gli stati, possibilmente senza enumerarli esaustivamente, eliminando dalla consultazione stati che si sa già che porteranno a situazioni non desiderate. Nel nostro caso una sequenza di mosse che porti a una configurazione già vista prima, di cui si sa già che non porta alla soluzione, è chiaramente ‛abortiva', va cioè scartata.

5. Verificare sperimentalmente. Questo fatto, sebbene non fondamentale dal punto di vista teorico, riveste invece enorme importanza dal punto di vista pratico, in quanto l'introduzione dell'elaborazione automatica permette di distinguere tra metodologie di interesse puramente speculativo e metodologie di applicabilità pratica, stimolandone nel contempo l'elaborazione di nuove, più generali ed efficaci.

Bisogna però notare subito che l'esposizione di questa metodologia generale non implica affatto la soluzione dei problemi, spesso formidabili, che l'attuazione di ogni suo passo comporta. Non esiste infatti una teoria generale che ci dica ‛come' effettivamente realizzare ciascuno dei punti sopra elencati: per esempio, sapere che è necessaria la ‛conoscenza del problema' non dà alcuna indicazione su come raggiungerla nè su come rappresentarla o utilizzarla in modo efficace.

Nei paragrafi successivi verranno illustrati alcuni procedimenti che cercano di realizzare al meglio i punti della metodologia esposta.

a) Tecniche di ricerca.

Per i problemi che si incontrano nel campo dell'intelligenza artificiale spesso non esiste una metodologia di risoluzione unica, ben determinata ed esprimibile in maniera formale. Un esempio di problema ‛classico', che cioè possiede una precisa metodologia di risoluzione, è offerto dal calcolo del fattoriale di un numero naturale (N), inteso come il prodotto di tutti i numeri naturali da 1 a N, tenendo conto del fatto che il fattoriale di 1 è 1. Una maniera di calcolarlo consiste nel moltiplicare il numero N per il fattoriale di N − 1, ammesso di conoscerlo; se questo non è il caso, si riapplica lo stesso ragionamento a N − 1, finché si raggiunge il numero 1, il cui fattoriale è noto. Come si può vedere, la soluzione di questo problema è unica, ed esiste una maniera di calcolarla, esprimibile in modo formale.

Nell'intelligenza artificiale problemi di questo genere costituiscono l'eccezione, più che la regola; nel caso del gioco del 16 non è possibile trovare una procedura diretta, unica per risolverlo. In effetti bisogna procedere per tentativi, provando a muovere alcune tessere, in una certa sequenza, e, se non si riesce a ottenere la soluzione, provando con un'altra sequenza. È quindi necessario far ricorso ad altri metodi di programmazione, più generali di quello visto, in grado di effettuare tentativi, cioè di cercare ed esaminare ‛stati' del problema in maniera più o meno ‛intelligente'. Perciò è importante determinare le strategie che permettono di effettuare il numero minimo di tentativi per giungere alla soluzione. Ciò significa sviluppare criteri che permettono di individuare stati ‛promettenti' e di produrli.

I concetti di determinazione dello stato iniziale, dello stato finale e delle operazioni di trasformazione di uno stato in un altro, di cui abbiamo parlato in generale, sono ovviamente validi anche in questo contesto. In più è conveniente stabilire una funzione di costo che esprima, per ogni stato, quanto esso disti dalla soluzione o, se vi sono più soluzioni, dalla più vicina di esse. In questo modo si può calcolare il costo di una successione di trasformazioni di stati, cioè di una traiettoria. Nel nostro esempio, una possibile maniera di calcolare i costi consiste nell'associare a ogni stato un costo proporzionale al numero delle tessere fuori sequenza: in questo modo una configurazione con molte tessere fuori sequenza risulterà ovviamente più ‛lontana' dalla soluzione di un'altra con quasi tutte le tessere in sequenza.

Un altro esempio, che può essere utile per introdurre alcuni termini, è la determinazione dell'itinerario più breve (o con meno attraversamenti, ecc.) da una città A a una città Z attraverso un insieme di città collegate da una rete autostradale, come illustrato nella fig. 2.

Astraendo dal particolare esempio, si può immaginare di sostituire le città con i possibili stati di un problema e i collegamenti autostradali con le operazioni di trasformazione di uno stato in un altro. La rete rappresentata nella fig. 2A viene chiamata il ‛grafo' del problema, ciascuna città corrisponde a un ‛nodo' del grafo, le strade corrispondono agli ‛archi'. La città A rappresenta lo stato iniziale e la città Z lo stato finale; l'itinerario (cioè la serie di archi che collegano A a Z) rappresenta la soluzione del problema.

Il grafo della fig. 2A può essere trasformato nel grafo della fig. 2B (chiamato ‛albero') semplicemente partendo da un dato nodo (chiamato ‛radice') e percorrendo tutti i cammini possibili da esso (senza, ovviamente, visitare stati gia visitati), passando da un nodo a quello a esso collegato (detti rispettivamente ‛nodo padre' e ‛nodo figlio') attraverso le connessioni (dette ‛rami') e arrestandosi ai nodi che non hanno figli (detti ‛foglie'). I grafi (e gli alberi) sono strumenti molto potenti e generali per rappresentare i problemi e le loro soluzioni: nel caso del gioco del 16, si può facilmente immaginare come dallo stato iniziale (radice) partano tanti rami quante sono le possibili mosse che portano ad altrettanti stati (nodi) intermedi, per ognuno dei quali si ripete la stessa situazione finché si raggiunge lo stato finale o uno stato già esaminato.

Ricerca in profondità e ricerca laterale. - Risolvere un problema equivale, astrattamente, a esaminare i nodi dell'albero che lo rappresenta fino a trovare una foglia che rappresenta lo stato desiderato o uno degli stati desiderati. In linea di principio, i nodi vanno esaminati tutti, anche se, come vedremo in seguito, esistono metodi che, tenendo conto delle peculiarità del problema, permettono di scartare alcuni nodi o addirittura interi sottoalberi senza nemmeno esaminarli.

Per ‛visitare' un albero (cioè per esaminare tutti i suoi nodi) esistono essenzialmente due strategie: una chiamata ‛in profondità' (o depth-first) e l'altra ‛laterale' (o breadthfirst). Entrambe forniscono un criterio per decidere quale nodo deve essere il prossimo da esaminare, a partire da un dato nodo. Nella ricerca in profondità si sceglie sempre il primo dei figli non ancora esaminati del nodo corrente; quando si raggiungono le foglie o si sono esaminati tutti i figli, si passa al fratello del nodo corrente, e si continua così finché tutto l'albero è stato visitato. Nella ricerca laterale, invece, si esamina il primo fratello non ancora esaminato del nodo corrente e, quando tutti i fratelli sono stati esaminati, si passa al primo figlio. Nella fig. 3A viene illustrata una ricerca in profondità, mentre la fig. 3B riporta un esempio di ricerca laterale.

Non esiste un criterio per decidere quale delle due strategie sia migliore in generale, ma ovviamente la forma dell'albero può suggerire di provare per prima una strategia anziché l'altra. Nel caso di alberi molto elongati, caratterizzati cioè da molti livelli, ognuno dei quali con pochi figli, con la ricerca in profondità si rischia di perdere molto tempo a percorrere rami infruttuosi, mentre, nel caso di alberi ‛a cespuglio' (con poche generazioni di molti figli ciascuna), con la ricerca laterale si rischia di abbandonare rami fruttuosi per esaminare altri nodi. Una modificazione di questa strategia è la cosiddetta ‛ricerca a raggio' (beam search), che consiste nell'esplorare, livello dopo livello, solo i figli dei nodi reputati più ‛promettenti', secondo un assegnato criterio di classificazione dei nodi. L'adozione di questa strategia mista permette una visita rapida ma non completa dell'albero (e quindi non garantisce l'ottimalità del percorso trovato) ed è condizionata dall'esistenza di un criterio che permetta di stabilire quando un nodo è ‛migliore' di un altro: va quindi utilizzata quando la forma dell'albero e le condizioni del problema lo consigliano.

Una procedura per esplorare i grafi. - Come illustrato nella fig. 2A, molti problemi di intelligenza artificiale possono essere rappresentati da un grafo, il quale può essere trasformato in un albero (v. fig. 2B) che opportuni metodi di ricerca consentono di esaminare per trovare il cammino dallo stato iniziale allo stato finale. È facile però rendersi conto che, se non si pone alcuna limitazione a questo processo, da un grafo possono essere ottenuti infiniti alberi, come potrebbe accadere se non si marcassero i nodi già visitati: è importante quindi fornire una procedura che permetta di ottenere l'albero (o gli alberi) da un grafo in maniera ordinata e senza ridondanze. Di questa procedura saranno illustrati solo i concetti fondamentali: essa è in realtà molto più dettagliata, in quanto deve essere eseguita dagli elaboratori elettronici. Essenzialmente, essa consiste dei seguenti passi.

1. Per ogni nodo N (a cominciare da quello iniziale):

A. Marcarlo come ‛esaminato'.

B. Considerare tutti i nodi a esso collegati.

C. Escludere da essi:

1) i nodi già esaminati;

2) il nodo (o i nodi) da cui si è raggiunto N.

D. Se l'insieme risultante è vuoto e non si è trovata precedentemente alcuna soluzione, il problema è irresolubile con questo metodo.

E. Se qualcuno di questi nodi è uno stato finale, si memorizza il cammino fino ad allora trovato, si risale al padre di tale nodo e si ricerca un altro cammino a partire da esso, smarcando opportunamente i nodi da esso dipendenti, che non siano suoi figli diretti. Se, per un dato nodo terminale, non esiste nemmeno uno tra i suoi antenati di qualsiasi livello che abbia figli ancora da esaminare, la procedura termina.

F. Ordinare, secondo un dato criterio di ‛merito' (anche arbitrariamente), i nodi così ottenuti.

G. Prendere il primo nodo, marcare l'arco che lo collega a N e considerarlo come nodo corrente.

2. Ripetere da 1.

L'insieme dei cammini costituisce l'albero di ‛ricerca' derivato dal grafo originale. In generale, come anche in questo caso, nella determinazione di un cammino su un grafo non è specificato a priori un metodo che permetta di scegliere, tra quelli possibili, il nodo più conveniente da raggiungere nel passo successivo. Un possibile criterio si basa sul costo dei passi necessari per raggiungere un nodo finale, o meglio si basa su una ‛stima' del costo, in quanto la sua valutazione effettiva presupporrebbe la visita del grafo e quindi la soluzione del problema.

Il costo minimo di un cammino che passi dallo stato iniziale (I) a uno degli stati finali F_i attraverso un dato nodo N si può esprimere come la somma del costo del cammino (già fatto) da I a N e del costo del cammino più ‛economico' che va da N al più ‛vicino' degli stati finali, intendendo ovviamente che si tratta di costi stimati e non di costi reali. Criteri di questo tipo vengono chiamati ‛euristiche', in quanto aiutano a scoprire il cammino ottimale.

b) La procedura MINIMAX.

Le procedure finora esposte si adattano, in pratica, a casi caratterizzati da un numero relativamente piccolo di stati, i cui alberi cioè non siano troppo grandi e che quindi possano essere visitati dalle euristiche a disposizione in un tempo relativamente breve. Problemi più complessi, come quelli delle fasi finali degli scacchi (per non parlare di quelli reali, che possono essere molto più difficili), generano alberi troppo grandi perché le euristiche note riescano a determinare il successivo nodo da visitare, con una certa attendibilità: come già detto, lo spazio degli stati degli scacchi contiene circa 10¹²⁰ configurazioni, quello della dama 10⁴⁰ e quello del semplicissimo gioco del ‛filetto' più di 360.000, cioè fattoriale di 9. In questi casi si può cambiare l'obiettivo di soluzione del problema, rinunciando alla ricerca dell'ottimo e cercando una soluzione praticabile. Una maniera di farlo consiste nel considerare, in un insieme di mosse possibili, per ogni mossa, le possibili risposte dell'avversario, determinare, tra le possibili controrisposte, quella più ‛favorevole' e, rifacendo il cammino all'indietro, scegliere la mossa che porta appunto alla situazione a noi favorevole.

È importante, perché sia possibile applicare queste tecniche, che si possa definire un ‛merito' misurabile che possa essere associato a ogni stato e che guiderà ogni successiva mossa. In quasi tutti i problemi di decisione, come in tutti i giochi, però, il vantaggio di un giocatore costituisce uno svantaggio per l'avversario. Evidentemente, una volta definito il ‛merito' di ogni stato, ci sarà una parte (convenzionalmente indicata con MAX) che tenderà a renderlo massimo e la parte avversa (indicata con MIN) che tenderà a renderlo minimo.

Una procedura del genere (che produce una ‛buona' strategia anche se non garantisce l'ottimalità, in quanto non esaustiva) viene per l'appunto chiamata MINIMAX.

c) Ottimizzazione continua.

L'idea del ‛merito' di uno stato e della sua influenza nella determinazione della strategia può essere illustrata mediante un'analogia fisica: in un territorio montagnoso disseminato di valli, alcune delle quali coperte dalla nebbia, si supponga di dover raggiungere la valle più profonda compiendo il cammino più breve. In mancanza di informazioni sulla struttura generale del terreno, l'unica alternativa è quella di esplorare tutte le valli. Se però si sa che la valle più profonda è raggiungibile con un cammino che è sempre in pianura o in discesa, ci si può muovere lungo la linea di discesa più ripida.

Questo metodo si può generalizzare ammettendo che vi siano anche dei tratti in salita, purché il dislivello non sia eccessivo. Matematicamente questo corrisponde a trovare il minimo di una funzione di più variabili. In casi relativamente semplici, quando la funzione ha un minimo, questo metodo risolve il problema; tuttavia, in generale, la soluzione richiede l'esplorazione esaustiva di tutti gli stati possibili per la determinazione del minimo.

Una metodologia interessante, proposta recentemente, prevede la combinazione della ricerca lungo la discesa più ripida con una certa quantità di ricerca casuale. Per tornare all'esempio precedente, una volta fissata l'altezza massima della salita che si può superare, la direzione di percorrenza viene determinata da una composizione tra una scelta casuale e la discesa più ripida. Ovviamente, se la ‛soglia di salita' è bassa, la componente casuale sarà determinante, altrimenti predominerà la componente deterministica. Questa metodologia, detta ‛ricottura simulata' (simulated annealing), prescrive di iniziare con soglie di salita piuttosto basse, in maniera da garantire l'esplorazione di un certo numero di stati, per poi innalzarle gradualmente per effettuare un'esplorazione deterministica e migliorare il risultato.

L'efficienza di questo metodo è essenzialmente probabilistica e dipende dalla differenza che intercorre tra la massima e la minima ‛soglia di salita' e da quanto gradualmente viene effettuato il passaggio dall'una all'altra. Alcune esperienze recenti hanno però mostrato che procedure deterministiche, che sfruttano i vincoli specifici del problema, possono essere più efficienti della ‛ricottura simulata'.

In definitiva si vede che procedure che sfruttano la conoscenza del problema sono efficienti, ma non generali, mentre procedure indipendenti dal problema rischiano l'inefficienza. È inoltre importante osservare che le procedure esposte (o quanto meno i principi su cui si basano) non hanno nulla di particolarmente specialistico: non sono altro che la versione formale di ragionamenti comuni, applicati a situazioni di ogni giorno.

5. Logica.

La capacità di ragionare in maniera rigorosamente consequenziale è sicuramente una caratteristica fondamentale dell'intelligenza.

La logica, cioè lo studio dei metodi di ragionamento rigoroso, è precedente all'intelligenza artificiale e può essere fatta risalire alle scuole filosofiche dell'antica Grecia, specie a quella aristotelica. Il fatto che la logica sia formale, e quindi meccanizzabile, la rende un aiuto prezioso alla risoluzione di problemi.

Per una trattazione della logica più completa e dettagliata si rinvia il lettore all'articolo di A. Robinson (v. logica matematica, cap. 5); qui basterà fornire una descrizione elementare del linguaggio del calcolo predicativo del primo ordine, su cui si basa la ‛capacità di ragionare' dei calcolatori.

Elencheremo nell'ordine: a) una serie di simboli atomici (o elementari), che costituiscono l'‛alfabeto' del linguaggio; b) dei criteri per costruire, a partire dai simboli atomici, espressioni formalmente corrette; c) delle ‛regole deduttive' che consentano di dedurre da enunciati veri altri enunciati veri.

L'alfabeto del linguaggio in esame è costituito da: a) ‛costanti individuali', a, b, c, ..., che servono per denotare oggetti; b) ‛variabili', x, y, z, ..., usate come contrassegni privi di riferimento individuale e suscettibili di essere sostituite da costanti individuali; c) ‛simboli di relazione' o ‛predicati', a uno, due, tre ... posti, R(.), S(..), ecc. (i punti fra le parentesi fungono da segnaposti), che denotano proprietà di oggetti (predicati a un posto) e relazioni fra oggetti (predicati a più posti); d) ‛connettivi', ¬ (‛non'), ⋀ (‛e'), ⋀ (‛o'), ⇒ (‛se ... allora ...'), che corrispondono alle ‛congiunzioni del linguaggio naturale (eccettuato il ¬, che corrisponde all'avverbio ‛non'); e) due ‛quantificatori', ???29???. (quantificatore esistenziale), che vuoI dire ‛esiste almeno un ...', e ∀. (quantificatore universale), che vuol dire ‛per ogni ...'; f) parentesi, ( e ).

Definiamo ora i criteri per costruire con i simboli dell'alfabeto espressioni formalmente corrette (che chiameremo ‛formule'): a) ogni predicato i cui posti siano occupati da variabili e/o da costanti individuali è una formula ('atomica', cioè non scomponibile in ‛sottoformule'); b) se X e Y sono formule, lo sono anche ¬ X, X ⋀ Y, X ⋀ Y, X ⇒ Y; c) se Q(x) è una formula nella quale compare la variabile x - che abbiamo messo in evidenza -, sono formule anche (???29???x) Q(x) e (∀x) Q(x). Tutte le formule del calcolo predicativo del primo ordine sono riconducibili strutturalmente ai casi contemplati in a), b) e c).

Naturalmente, perchè le formule costruite secondo i criteri dati abbiano un significato, è necessano ‛interpretare' i simboli del linguaggio formalizzato descritto, precisando l'‛universo di discorso' cui si intende riferirsi, cioè gli oggetti denotati dalle costanti individuali e le proprietà e le relazioni denotate dai predicati. Facciamo un paio di esempi.

Dato l'universo di discorso costituito dagli esseri umani e dalle proprietà e dalle relazioni che competono loro - fra cui, per esempio, le relazioni di parentela -, supponiamo di dover ‛tradurre' nel linguaggio del calcolo predicativo del primo ordine la frase ‛Giovanni è il padre di Marco'. Tutto quel che ci occorre sono due costanti individuali, g ed m, per denotare gli individui in questione, e un predicato a due posti, P(..), che indichi la relazione di parentela essere padre di'. Otterremo quindi la formula atomica P(g, m), che, in base all'interpretazione data ai simboli che la costituiscono, significa, appunto, ‛Giovanni è il padre di Marco'.

Sempre in riferimento allo stesso universo di discorso, stabilito che il predicato a un posto M(.) indichi la proprietà ‛essere mortale', la frase ‛tutti gli uomini sono mortali' si traduce nel linguaggio del calcolo predicativo del primo ordine (∀x) M(x), cioè ‛per ogni x (oggetto dell'universo di discorso) vale la proprietà essere mortale".

Gli esempi ora visti si riferiscono a una classe particolare di formule, la classe degli ‛enunciati'. Chiamiamo ‛enunciato' una formula di cui si possa dire che o è vera o è falsa (anche se non si è in grado di sapere quale dei due casi sussista). Un esempio chiarirà il concetto.

Assumiamo come universo di discorso l'insieme dei numeri naturali e scegliamo un predicato a due posti, M(..), per denotare la relazione d'ordine ‛essere maggiore di'. Allora la formula M(2, 3) e la formula M(3, 2) sono enunciati (il primo falso, perché 2 non è maggiore di 3, e il secondo vero), mentre la formula M(x, y) non è un enunciato, perché per poterle attribuire uno dei due valori di verità (‛vero' o ‛falso') bisogna prima sostituire le variabili con costanti.

Un altro modo per trasformare una formula (che già non sia un enunciato) in un enunciato consiste nel ‛vincolare' tutte le variabili che vi compaiono tramite quantificatori. Per esempio, sempre in riferimento all'insieme dei numeri naturali e al predicato usato precedentemente, la formula (???29???y) ((∀x) (¬ M(x, y)) è un enunciato (vero), che afferma l'esistenza di (almeno) un numero naturale non maggiore di un qualsiasi numero naturale dato (il numero cui si riferisce l'enunciato è lo 0).

In conclusione possiamo dire che una formula è un enunciato se non contiene variabili ‛libere', cioè se le uniche variabili che contiene (oltre alle costanti individuali) sono vincolate da quantificatori.

La verità di un enunciato ‛atomico' (cioè non composto da sottoenunciati) dipende naturalmente dall'universo di discorso. Per esempio, l'enunciato ‛non esiste un numero compreso fra 2 e 3' è vero se riferito all'insieme dei numeri naturali, falso se riferito all'insieme dei numeri razionali. Inoltre, come abbiamo già detto di sfuggita, di un enunciato possiamo dire sicuramente che o è vero o è falso, ma ciò non implica che sappiamo quale dei due casi sia quello giusto. Per esempio, dell'enunciato visto in precedenza, ‛Giovanni è il padre di Marco', si può affermare senza tema di smentita che o è vero, cioè Giovanni è effettivamente il padre di Marco, oppure è falso. Per appurare come stanno le cose sono necessarie indagini che esulano dalle competenze della logica.

La logica pertanto non si occupa dei criteri e delle metodologie che permettono di appurare la verità degli enunciati atomici: per esempio, l'enunciato ‛tutti i corpi dotati di massa sono soggetti alla forza di gravità' dev'essere verificato dalla fisica, l'enunciato ‛la derivata di x è 1' dall'analisi matematica, l'enunciato ‛soffriamo tutti del complesso di Edipo' dalla psicanalisi, ecc.

Di competenza della logica è invece il ‛calcolo' del valore di verità che un enunciato, composto tramite i connettivi, assume, in funzione dei valori di verità degli enunciati che lo compongono. Con ciò la logica non fa altro che sancire formalmente le norme logico-linguistiche che tutti applichiamo nei nostri ragionamenti quotidiani. Per esempio, dati due enunciati, p e q, l'enunciato p ⋀ q, congiunzione dei due, è vero, se entrambi gli enunciati componenti sono veri, falso, se almeno uno dei due è falso. Analogamente, se p è un enunciato vero, la sua negazione, ¬ p, è un enunciato falso (e viceversa). Per calcolare i valori di verità degli enunciati composti, in funzione dei valori di verità degli enunciati componenti, si sogliono utilizzare le cosiddette ‛tavole di verità' (a ogni connettivo ne corrisponde una distinta: v. fig. 4).

Ogni teoria, anzi ogni ragionamento, dal più rigoroso al più approssimativo, si sviluppa a partire da un certo numero, preferibilmente ristretto, di ipotesi di base, cioè di enunciati, esplicitati o meno, previamente verificati o assunti come veri. In logica e in matematica questi enunciati di partenza si chiamano ‛assiomi' e vengono esplicitati formalmente. Sempre in logica e in matematica si chiamano ‛teoremi' tutti gli enunciati deducibili, tramite l'applicazione di opportune regole deduttive (o ‛di inferenza'), dagli assiomi. Oltre che agli assiomi le regole deduttive si possono applicare anche a ipotesi introdotte ad hoc e in via provvisoria.

La logica è l'unica disciplina che esplicita formalmente (è questo uno dei suoi compiti principali) le regole deduttive. Anche in questo caso la logica si limita a precisare norme che tutti, più o meno consapevolmente, applichiamo nei nostri ragionamenti quotidiani. Illustriamo alcune di queste regole.

1. Specializzazione universale. Secondo questa regola da ∀xP(x) è deducibile P(c). A parole: ciò che si predica (tramite un qualsiasi predicato P(.)) di tutti gli oggetti dell'universo di discorso, si predica (a maggior ragione) di un singolo oggetto dell'universo (denotato da una qualsiasi costante c). Per esempio, precedentemente abbiamo interpretato l'enunciato ∀xM(x) come ‛tutti gli uomini sono mortali'; la regola di specializzazione universale ci autorizza a dedurre da questo enunciato l'enunciato M(g) (‛Giovanni è mortale').

2. Modus ponens. Secondo questa regola dai due enunciati p ⇒ q e p è deducibile l'enunciato q. Esempio: dai due enunciati ‛se piove, allora mi bagno' e ‛piove' è deducibile l'enunciato ‛mi bagno'.

3. Modus tollens. Secondo questa regola da p ⇒ q e ¬ q è deducibile ¬ p. Esempio: da ‛se piove, allora mi bagno' e ‛non mi bagno' è deducibile ‛non piove'.

Nel 1964 il logico A. Robinson propose un'altra regola di inferenza che aveva diversi vantaggi, quali la generalità (altre regole di inferenza sono suoi casi particolari), la facile meccanizzabilità (il procedimento si basa su passi molto semplici) e la fondatezza logica (che equivale, con una certa approssimazione, alla capacità di derivare tutti e soli i teoremi validi) e chiamò questa regola ‛principio di risoluzione'. Questa regola ricalca il principio della dimostrazione per assurdo, che si può enunciare come segue: se, unendo la negazione della conclusione alle ipotesi di partenza, si ottiene una contraddizione, la conclusione è valida, altrimenti non lo è.

Il principio di risoluzione costituisce anche la base di procedure che, a differenza di quanto visto prima, non solo dimostrano la verità o la falsità di una conclusione data, ma riescono anche a ‛costruire' una conclusione valida, per esempio trovando i valori che rendono vera una determinata formula.

Spesso, nell'ordinario ragionamento, vengono seguite regole che non trovano corrispondenza nella logica e che servono per ‛dedurre' conclusioni che, sebbene non sempre valide, possono tuttavia avere una grande attendibilità in molti casi. Un esempio di questo tipo di regole è la (impropria) regola di inferenza detta ‛di induzione': da p ⇒ q e q si deduce p.

Grafi ‛AND-OR'. - Le formule della logica possono essere rappresentate anche come dei grafi, nei quali alcuni archi sono collegati tra loro a coppie, in maniera tale da formare un cosiddetto ‛grafo AND-OR'. Questi grafi si prestano bene per effettuare dimostrazioni di teoremi, evitando alcuni problemi di esplosione combinatoria.

Una volta espressa la formula in maniera standard, si cerca il connettivo più ‛esterno' (cioè quello racchiuso dal minimo numero di parentesi) e si costruisce un albero, associando al nodo-radice la formula originaria, facendo partire da esso due rami e associando a ciascuno di essi rispettivamene la sottoformula a sinistra e a destra del connettivo più esterno.

Se il connettivo tra i due rami è ⋀ (AND) i due rami vengono connessi da un legame speciale, che invece non si traccia nel caso che il connettivo sia ⋀ (OR). Su ciascuna delle due sottoformule si ripete il procedimento, finché si ottiene un ‛letterale', cioè una formula atomica eventualmente negata. Si cerca poi se vi sono dei letterali (o fatti) di base (che non abbiano cioè variabili al loro interno) che corrispondono ai letterali ottenuti, eccetto per il fatto che contengono delle costanti al posto delle variabili. Se questi esistono, si cerca la combinazione di valori di costanti che, sostituita alle variabili, soddisfi i letterali, i nodi intermedi e infine la formula originale. In questo modo si ottengono non soltanto conclusioni valide dalle formule di partenza, ma anche i valori delle variabili che le rendono tali.

Per illustrare quanto appena esposto facciamo un semplice esempio.

Denotate rispettivamente con A(x, y), P(x, y) e C(x, y) le relazioni ‛x abita a y', ‛x possiede y' e ‛x conosce y' - onde, per es., A(Giovanni, Roma) significherà ‛Giovanni abita a Roma', P(Francesco, furgone) significherà ‛Francesco possiede un furgone' e C(Carlo, francese) significherà ‛Carlo conosce il francese' -, si considerino i seguenti fatti:

1. A(Giovanni, Roma)

2. A(Francesco, Milano)

3. A(Giuseppe, Roma)

4. A(Mario, Firenze)

5. A(Carlo, Milano)

6. P(Giovanni, autobus)

7. P(Giuseppe, automobile)

8. P(Francesco, furgone)

9. P(Mario, motocicletta)

10. P(Carlo, furgone)

11. C(Francesco, inglese)

12. C(Giovanni, tedesco)

13. C(Giuseppe, russo)

14. C(Mario, inglese)

15. C(Carlo, francese).

Si supponga quindi di dover rispondere, sulla base dei fatti elencati, alla domanda: ‟Chi conosce l'inglese e: o abita a Milano o possiede un furgone?". Rispondere a questa domanda significa individuare, se esistono, le terne di fatti (riguardanti ovviamente lo stesso individuo) che soddisfano la formula logica

C(x, inglese) ⋀ (A(x, Milano) ⋀ P(x, furgone)).

Seguendo la procedura descritta in precedenza otterremo il seguente grafo AND-OR:

11, 14; 2, 5; 8, 10 sono i fatti di base corrispondenti ai letterali ottenuti. Si vede facilmente che l'unica terna di fatti che soddisfa la formula è la terna 11, 2, 8 (corrispondente a x = Francesco).

6. Rappresentazione della conoscenza.

Si è fatto spesso cenno a come le procedure di risoluzione dei problemi e, in generale, di ricerca su grafi possano trarre enorme vantaggio dalla conoscenza dello specifico problema. È quindi ovvio che la rappresentazione della conoscenza sia un argomento importante dell'intelligenza artificiale, in quanto una rappresentazione appropriata costituisce spesso il passo fondamentale per risolvere un problema: basti pensare all'importanza che ha avuto, in chimica, la rappresentazione degli elementi con simboli e, in fisica, l'uso delle formulazioni matematiche per esprimere relazioni tra le grandezze fisiche. Mentre queste ultime possono essere considerate delle rappresentazioni specializzate della conoscenza, nell'intelligenza artificiale è spesso necessario rappresentare la conoscenza ‛comune' e quindi avere a disposizione un formalismo più generale, più flessibile e che permetta di effettuare non solo calcoli, ma anche deduzioni di fatti nuovi da altri già noti.

Non è facile introdurre una ‛buona' rappresentazione della conoscenza: essa infatti deve evidenziare le invarianti fondamentali del problema, deve poter esprimere i vincoli in esso presenti, deve essere completa, concisa, calcolabile.

Nel seguito saranno illustrati due formalismi di rappresentazione della conoscenza, paradigmatici delle principali tendenze che oggi vigono nell'intelligenza artificiale: le reti semantiche e le strutture (dette anche ‛frames'). Di entrambi sarà illustrata sia la sintassi (insieme dei simboli ‛legali' e delle loro disposizioni) sia la semantica (significato dei simboli stessi).

a) Reti semantiche.

Rappresentare la conoscenza sotto forma di formule logiche sicuramente aiuta a operare deduzioni su di esse; tuttavia spesso ciò non ha un potere evocativo tale da permeùere, senza un certo sforzo immaginativo, la visione generale del problema. Attraverso un opportuno insieme di convenzioni è possibile esprimere gli stessi concetti in una notazione equivalente dal punto di vista logico e dotata di un maggior potere evocativo.

Si può ottenere una rappresentazione grafica dei predicati con due argomenti semplicemente associando un nodo a ciascun argomento e connettendo tali nodi con un arco orientato che va dal primo al secondo argomento. Per esempio, l'enunciato ‛Piero è padre di Donato' può essere rappresentato come nella fig. 5.

Considerare esclusivamente predicati binari rappresenta una limitazione solo apparente, in quanto un predicato n-ario può essere sempre riscritto come una congiunzione di n + 1 predicati binari, di cui uno rappresenta l'evento e gli altri le relazioni degli altri elementi con quell'evento. Si può quindi generalizzare l'esempio prima visto, rappresentando i predicati binari con nodi e archi e facendo coincidere nello stesso nodo i nodi (ripetuti) che rappresentano la stessa entità (v. fig. 6).

Un insieme di formule logiche può essere rappresentato con la stessa metodologia, ottenendo come risultato una struttura chiamata ‛rete semantica'.

Le reti semantiche oltre a dare direttamente un'idea delle relazioni generali che esistono tra le entità in esame, suggeriscono anche possibili modi di passare da un'entità all'altra, fornendo quindi utili indicazioni per la loro memorizzazione in un elaboratore.

b) Ereditarietà, demoni, credenze, visuali.

Affermare che un oggetto appartiene a una certa classe equivale a dire, in maniera ‛compatta', che quel dato oggetto gode di determinate proprietà. A sua volta una classe può essere la sottoclasse di un'altra che gode di alcune delle proprietà della sottoclasse, e così via, fino a ottenere una classe generica che non gode di alcuna specifica proprietà.

Nelle reti semantiche questo processo di inclusioni successive può essere rappresentato collegando con archi del tipo ‛Elemento di' o ‛Sottoclasse di' i nodi rappresentanti gli elementi o le sottoclassi alle rispettive classi, dotando ogni classe delle proprietà che sono comuni a tutte le sue sottoclassi o a tutti i suoi elementi e dotando ogni sottoclasse o ogni elemento delle sue proprietà specifiche.

Spesso non tutte le informazioni relative a un dato nodo sono elencate o possono essere ereditate da altri nodi, tuttavia esse possono essere dedotte in altri modi, quale il ‛calcolo per mezzo di procedure'. Per esempio, sapendo che l'età di un qualsiasi animale è data dalla differenza tra la data attuale e la sua data di nascita, si può calcolare l'età di Fido ereditando la definizione di età dal nodo ‛animale' e applicandola alla ‛data nascita' di Fido. I meccanismi che attivano delle procedure il cui risultato è richiesto da particolari nodi per dare i valori di proprietà non esplicitamente elencate vengono chiamati ‛demoni', in quanto molto simili (almeno concettualmente) alle loro controparti favolistiche che, una volta evocate, esaudiscono i desideri dei loro padroni.

Un altro meccanismo che fornisce valori per le proprietà è quello delle ‛credenze' (defaults), secondo cui i valori vengono assegnati in base a criteri standard e vigono fino a quando non vengono esplicitamente corretti. Per esempio, in mancanza di altre informazioni, si potrebbe assegnare la proprietà ‛agile' a Fido, in base al fatto che i cani sono, in genere, agili. Tuttavia, questa affermazione non ha la stessa certezza dell'affermazione ‛i cani sono agili', per cui viene assunta (o ‛creduta') anche per Fido, a meno che un'esplicita informazione contraria non la neghi.

Negli esempi finora fatti si è assunto che, nelle reti semantiche, la relazione ‛Elemento di' (o ‛Sottoclasse di'), se esistente, fosse unica. Viceversa la stessa entità può essere considerata da diversi punti di vista: l'entità ‛pollo' può essere collegata dalla relazione ‛Elemento di' con la classe ‛uccello', ma anche con la classe ‛cibo' e con la classe ‛bipede'. Questi diversi punti di vista sono rappresentati in una rete semantica collegando un determinato nodo con un fascio di nodi corrispondenti alle diverse alternative (‛visuali').

c) Strutture (frames).

L'equivalenza, precedentemente illustrata, tra insiemi di formule logiche e congiunzioni di predicati binari può essere utilizzata sia per produrre la corrispondente rete semantica sia per ottenere una rappresentazione delle entità che gode di molte proprietà utili per la gestione automatica. Tale rappresentazione consiste di ‛strutture' (frames) che riportano, insieme all'identificatore dell'entità (che può anche essere un evento), una serie di caselle (slots), vuote all'inizio, ognuna delle quali fornita di un nome corrispondente al predicato binario che ha come argomenti il valore che occuperà quella casella e l'identificatore dell'entità.

Le strutture, proposte da Minsky, rappresentano però solo entità o situazioni statiche e non sono quindi adatte a rappresentare situazioni in evoluzione. Per questo sono state proposte da Schanck delle estensioni delle strutture chiamate ‛canovacci' (scripts). Esse agiscono proprio come il canovaccio per gli attori teatrali: determinano una sequenza temporale di eventi (o di classi di eventi), alcuni dei quali obbligatori, altri facoltativi, con variazioni più o meno grandi a seconda della particolare situazione. I canovacci estendono alle situazioni evolutive i meccanismi di ‛aspettativa' e di ‛credenza' propri delle strutture.

L'uso dei canovacci richiede però la capacità di trattare concetti relativi al tempo (quali ‛prima', ‛dopo', ‛contemporaneamente', ecc.) che sono estranei alla logica classica: per questo sono state proposte estensioni della logica dei predicati, che appunto tengono conto di questi e di altri concetti abitualmente usati dall'uomo.

Un altro problema, comune sia alle strutture sia ai canovacci, è quello relativo alla gestione delle credenze: nei casi visti prima ci si riferiva a un solo insieme di credenze, eventualmente aggiornate da informazioni esplicite. L'affermazione ‛Jumbo è un elefante' comportava quindi la credenza ‛Jumbo è di colore grigio': in altri termini, comportava la capacità di dimostrare che Jumbo era grigio, una volta che si fosse sicuri che non era di nessun altro colore, e cioè che non fosse un'eccezione tra gli elefanti. L'affermazione ‛Jumbo è un elefante albino' comporta un'altra credenza, più forte della precedente, sul colore di Jumbo, che è valida solo se si è sicuri che Jumbo non sia un'eccezione tra gli elefanti albini, e così via, in un processo infinito.

Sono stati quindi sviluppati sistemi, detti di ‛mantenimento della verità' (truth maintenance), che provvedono a evitare le contraddizioni che possono sorgere dall'applicazione indiscriminata di tali regole.

Risulta comunque evidente che la rappresentazione della conoscenza è il problema critico per lo sviluppo di una vera e propria intelligenza artificiale: probabilmente, in realtà, l'intelligenza utilizza una grande quantità di differenti rappresentazioni, adatte a diversi tipi di situazioni.

7. Sistemi esperti.

Una possibile applicazione delle tecniche di rappresentazione della conoscenza consiste nell'utilizzare la conoscenza stessa per dare alla macchina la capacità di fornire consulenza a livello paragonabile a quello degli esperti umani.

Dal punto di vista formale i sistemi esperti possono essere considerati come delle estensioni della capacità di reperimento delle informazioni e della capacità di ragionare su di esse. In effetti, un esperto può essere considerato tale solo quando è in grado di gestire, in maniera intelligente, le conoscenze che possiede e di effettuare deduzioni su di esse.

L'essere umano spesso utilizza queste informazioni attraverso logiche non standard, non equivalenti, cioè, al calcolo predicativo visto finora. E quindi uno degli obiettivi dei sistemi esperti quello di simulare l'utilizzo di queste logiche, oltre che, ovviamente, della logica dei predicati. Non è facile dare una definizione generale dei sistemi esperti. Da un certo punto di vista possono essere considerati come dei grossi programmi per la risoluzione di problemi che vengono in generale ritenuti ‛difficili' e normalmente risolti da persone con grande esperienza specifica. Questi programmi vengono detti ‛basati sulla conoscenza' perché la loro efficacia dipende criticamente dall'uso dei fatti e delle regole che sono forniti dell'esperienza. In un certo senso, essi possono essere considerati come la naturale evoluzione dei sistemi di reperimento delle informazioni. Infatti, per quel che riguarda questi ultimi, il problema principale é quello di reperire poche, specifiche informazioni da una vasta base di dati; per i sistemi esperti il problema si può spesso astrattamente ricondurre al reperimento non solo di informazioni esplicitamente memorizzate, ma anche di quelle ricavabili da esse secondo vari tipi di inferenza (deduttiva o di altro tipo). È quindi ovvia l'importanza di avere a disposizione una rappresentazione della conoscenza che sia efficace nel rappresentare le conoscenze dell'esperto e suscettibile di elaborazione automatica.

Per rappresentare la conoscenza nei sistemi esperti sono state finora seguite due filosofie alternative: una che rispecchia il paradigma del ‛generare e verificare' (generate and test) e un'altra che ubbidisce al paradigma delle regole. Il primo paradigma, essenzialmente, genera l'ipotesi di soluzione e verifica se questa ubbidisce ai vincoli del problema; nel secondo caso, invece, si parte dai dati che caratterizzano il problema e dalle regole che sono applicabili a essi e si cerca di dedurre la soluzione del problema come risultato dell'applicazione delle regole ai fatti.

a) Generazione e verifica.

Il primo paradigma (‛generazione e verifica') richiede, per la sua applicazione, l'azione di due moduli cooperanti: il generatore e il verificatore. Il generatore genera, una per una, tutte le soluzioni, mentre il verificatore verifica ciascuna soluzione rispetto a certi vincoli, per esempio il rispetto dei dati sperimentali. Questi sistemi trovano il loro campo di applicazione in problemi che prevedono un numero limitato di risposte.

Il primo (e forse più noto) esempio di questo tipo di sistemi esperti è il DENDRAL, un sistema esperto per la determinazione delle formule di struttura dei composti organici che può aiutare l'analista chimico organico nel suo lavoro. Questo sistema, dovuto a Feigenbaum, Buchanan e Lederberg (1980), accetta in ingresso dati provenienti dall'analisi chimica basilare, e cioè la cosiddetta ‛formula bruta' del composto, che definisce quanti atomi di carbonio, d'idrogeno o di ossigeno, per esempio, sono contenuti nella molecola del composto. Il sistema dispone di una base di conoscenze chimiche elementari: per esempio ‛sa' che il carbonio ha 4, 3 o 2 valenze, l'idrogeno ne ha sempre 1, l'ossigeno 2, e così via. Il generatore, sulla base dei dati sperimentali e delle regole del legame chimico, ipotizza formule di struttura che corrispondono alla formula bruta.

La seconda parte di questo sistema, cioè il verificatore, ‛contiene' l'esperienza che i chimici hanno accumulato scoprendo correlazioni tra particolari gruppi funzionali e proprietà specifiche. In pratica, attraverso una certa serie di esperimenti, la chimica è riuscita a dimostrare che particolari gruppi atomici, o sottomolecole, quali appunto i gruppi funzionali, hanno dei picchi di assorbimento (e quindi mostrano degli spettrogrammi caratteristici) in corrispondenza di particolari lunghezze d'onda della radiazione elettromagnetica, o hanno particolari spettri di risonanza magnetica nucleare, ecc. Il verificatore prende in considerazione una formula di struttura ipotizzata e calcola quale sarebbe lo spettrogramma corrispondente a tale formula, confrontandolo poi con lo spettrogramma reale. In questo modo vengono individuate le formule di struttura i cui spettrogrammi corrispondono a quello del composto in esame (v. fig. 7).

Un altro esempio è il sistema ACRONYM, ideato da Brooks e Binford. Questo sistema simula la competenza umana nella visione, in quanto deduce la struttura tridimensionale degli oggetti a partire da informazioni di natura bidimensionale. Le informazioni bidimensionali vengono utilizzate essenzialmente per produrre una serie di ipotesi sui possibili oggetti tridimensionali che possono corrispondere a quelle informazioni. Ognuna di queste ipotesi viene poi filtrata attraverso il verificatore che controlla la coerenza tra l'immagine corrispondente all'ipotesi e l'immagine bidimensionale.

b) Sistemi basati su regole.

Il secondo tipo di paradigma usa un altro tipo di conoscenza, espressa sotto forma di regole aderenti allo schema ‛SE... ALLORA...'. La struttura del sistema esperto, in questo caso, si compone di tre parti fondamentali: la base di conoscenza, il gestore della conoscenza (o motore inferenziale) e il modello della situazione (o modello del mondo).

Essenzialmente, il motore inferenziale fa scorrere, in un certo senso, le regole della base di conoscenza sui fatti della base di dati finché trova una regola applicabile ai fatti. La prima di tali regole viene applicata e viene quindi modificato il modello del mondo. Sul nuovo modello del mondo viene ripetuta l'operazione e quindi il modello del mondo cambia finché ci sono regole da applicare (v. fig. 8). L'analogia con il modo di operare dell'esperto umano è evidente: si tratta di applicare le regole al problema attuale con lo scopo di inferire nuovi fatti.

Oltre alle componenti essenziali del sistema descritte finora, ci sono altre componenti che sono comunque utili, e cioè il modulo di acquisizione della conoscenza, che gestisce l'accrescimento della base di conoscenza, il modulo di modifica di quest'ultima, il modulo che fornisce le spiegazioni del perché di una decisione suggerita o di una diagnosi effettuata dal sistema esperto.

Per realizzare questi sistemi basati su regole, i linguaggi tradizionali di programmazione non sono sufficienti, in quanto essenzialmente orientati a un tipo di programmazione che prescrive all'elaboratore cosa fare, passo dopo passo. Per i sistemi esperti sono invece necessari degli strumenti di programmazione che riescano a esprimere in maniera diretta le regole. Uno di questi strumenti è il Prolog, un linguaggio detto ‛di programmazione logica', che viene spesso utilizzato per la realizzazione di questi sistemi a regole. Le regole presenti in una base di conoscenza sono, a tutti gli effetti, paragonabili a un programma applicativo tradizionale e in generale sono espresse nella forma:

SE 〈congiunzione-di-condizioni> ALLORA 〈azione>.

Le condizioni che compaiono nella parte condizionale di ciascuna regola possono richiedere, per essere soddisfatte, l'applicazione di altre regole, e così via, in maniera ricorsiva. Un esempio di una regola di questo genere è il seguente:

SE il tipo di organismo è gram-positivo E

la morfologia dell'organismo è a bastoncello E

l'organismo è anaerobio

ALLORA è probabile (p = 0,7) che l'organismo sia Bacteroides.

Questo esempio, preso dal sistema esperto MYCIN, illustra parecchie caratteristiche: la prima è che le conclusioni possono essere o certe (avere cioè un coefficiente di verosimiglianza di 1) o ‛parzialmente' sicure, cioè avere una certa (incompleta) verosimiglianza (nel nostro caso si ha una sicurezza di 0,7). L'altro fatto che viene messo in evidenza da queste regole è che l'applicazione di una di esse modifica la situazione del mondo. Per esempio, l'applicazione di questa regola potrebbe essere stata richiesta da un'altra regola fornita, nella sua parte condizionale, della condizione ‛SE l'organismo è Bacteroides...'.

Qualche volta può accadere che più regole, avendo la stessa parte condizionale, siano in condizione di essere attivate dalla stessa base di dati. Si fa allora ricorso, per scegliere la regola applicabile, ad altre regole di tipo speciale (dette ‛metaregole'), che agiscono sulle regole stesse e le riordinano in maniera tale che venga scelta la regola più adatta secondo i criteri espressi dalle metaregole. In effetti possono esistere delle regole che agiscono anche sulle metaregole, cioè delle metametaregole: possono essere necessari molti livelli di regole se il sistema è complesso, come si prevede che saranno i sistemi esperti delle future generazioni, che conterranno un migliaio (e forse più) di regole, rispetto alle centinaia di regole dei sistemi esperti attuali. Queste regole possono essere applicate seguendo due diversi paradigmi: il primo, detto ‛ragionamento all'indietro' (backward chaining), risale dagli effetti ultimi alle cause prime; il secondo, detto ‛ragionamento in avanti' (forward chaining), cerca di trarre tutte le possibili conclusioni dai fatti noti e dalle regole applicate a essi.

Il primo di questi modi di procedere, esemplificato dall'operare del medico o del poliziotto, si applica tipicamente ai problemi di diagnosi: si prova infatti a vedere quali regole hanno le conclusioni uguali ai fatti della base di dati. Una volta trovate queste regole, si vede quali regole hanno nelle loro conclusioni la parte sinistra di queste regole, e così via, fino a risalire alle prime regole, la cui applicazione ha generato la situazione descritta dalla base di dati.

Viceversa, il secondo paradigma, esemplificato dal comportamento del giocatore di scacchi, consiste nell'applicare le opportune regole ai fatti attuali espressi nella base di dati: si cercano cioè le regole che hanno nelle loro parti condizionali i fatti che sono espressi nella base dei dati. Si applicano allora queste regole e si aggiungono dei nuovi fatti alla base dati, ripetendo il procedimento finché non ci sono più regole applicabili. Questo paradigma è particolarmente utile in problemi di pianificazione, in cui bisogna considerare gli effetti di decisioni prese sui fatti attuali.

Un terzo paradigma, relativamente recente, prevede che le regole siano organizzate secondo delle sorgenti indipendenti di conoscenza, che non comunicano le une con le altre e che operano su una base comune di dati, detta ‛lavagna' (blackboard). Questa base di dati contiene un insieme di ipotesi di soluzione parziale del problema, che rappresentano le conclusioni di varie regole. Queste ipotesi vengono poi confermate o refutate da ulteriori applicazioni di regole appartenenti alla stessa o a un'altra sorgente di conoscenza.

Molto spesso i sistemi esperti si trovano a dover trarre delle conclusioni logiche a partire da dati imprecisi o non perfettamente certi. È chiaro che la logica tradizionale non può soddisfare questa esigenza, per cui si rende necessario un approccio più flessibile. A questo scopo è stata proposta da Zadeh, nel 1965, una logica ‛diffusa' (fuzzy logics) che non presenta dei valori di verità definiti, come ‛vero' o ‛falso', ma solo valori di ‛attendibilità' compresi tra 1 e 1, dove 1 significa certezza del positivo, 1 certezza del negativo e 0 significa completa incertezza, con tutta la gamma dei valori intermedi. In questa logica le regole di inferenza della logica classica sono state modificate per renderle atte a trattare valori di attendibilità diversi da 1 e per poter calcolare i valori di verità di enunciati composti tramite i connettivi tradizionali, in funzione dei valori di verità ‛diffusi' degli enunciati componenti.

Questo tipo di ragionamento sembra essere la regola del ragionamento medico: infatti, termini come ‛rossastro', ‛piuttosto frequente', che non trovano una rappresentazione adeguata nella logica dei predicati del primo ordine, trovano invece una soddisfacente rappresentazione nei termini della logica diffusa.

L'esperienza fatta finora con i sistemi esperti ha dimostrato che è difficile programmare (o rendere esplicita) tutta la conoscenza di cui ha bisogno un sistema esperto per risolvere i problemi; il più delle volte l'esperto stesso trova defatigante trasferire, in maniera dettagliata, tutta la sua conoscenza a un sistema. Sono stati per questo sviluppati dei sistemi, detti ‛gusci' (shells) di sistemi esperti, che rendono facile la creazione di basi di conoscenza da parte di esperti umani, e, soprattutto, è stato dato il via a studi sulla possibilità di dotare i sistemi stessi della capacità di imparare dall'esperienza e quindi di formare nuove congetture e nuove regole, imitando molto, in ciò, l'azione dell'essere umano. Uno dei tentativi più noti (e più riusciti) in questo campo è il sistema EURISKO, che usa centinaia di regole o, meglio, di metaregole euristiche, che permettono di scoprire nuova informazione a partire dai dati del problema. Esempi di queste regole euristiche possono essere: ‛considerare casi estremi', ‛riprovare con la metodologia che prima ha dato buon esito', ecc. È importante osservare che questa metodologia è indipendente dal dominio semantico in cui si opera; quindi, in linea di principio, potrebbe essere usata per creare un sistema esperto in un campo qualsiasi. Usando questi programmi si vede che è molto importante disporre di rappresentazioni multiple della conoscenza, in quanto queste aiutano a produrre nuove euristiche e nuove regole.

8. Linguaggio.

Attualmente la comunicazione tra essere umano ed elaboratore passa attraverso interfacce formali che costituiscono un impedimento all'utilizzo generalizzato dell'elaboratore. Nella costruzione di sistemi esperti, per esempio, il processo di trasmissione della conoscenza al sistema, da parte di un esperto umano, è spesso fortemente limitato dal fatto che l'interfaccia tra l'uomo e il sistema non è ‛amichevole' verso l'utente, il quale deve diventare almeno parzialmente esperto di elaborazione dei dati per poter fornire conoscenza all'elaboratore. Questo problema non è proprio solo dei sistemi esperti ma, più in generale, dell'interazione tra l'uomo e la macchina. È quindi un'ovvia aspirazione dell'intelligenza artificiale quella di costruire sistemi che possano comprendere il linguaggio naturale, sia scritto, sia parlato. Così, per tornare all'esempio dei sistemi esperti, un'interfaccia amichevole, oltre a rendere facile l'acquisizione della conoscenza, potrebbe essere utile per spiegare la linea di ragionamento seguita e giustificare il ragionamento stesso, fare dei commenti, dare dei consigli, ecc. Inoltre, c'è un'ovvia e forte relazione tra linguaggio e intelligenza: è infatti considerato tipico delle specie intelligenti avere la capacità di astrarre dalle situazioni contingenti, generalizzandole, di tradurle in simboli linguistici e di comunicarle ad altri rappresentanti della stessa specie. Nell'uomo, in particolare, il linguaggio ha una struttura sintattica e semantica estremamente complessa.

L'essere umano apprende abbastanza presto a esprimersi verbalmente utilizzando in un primo tempo alcune sillabe solo apparentemente scoordinate, passando poi ai cosiddetti nomi-etichetta ('mamma', ‛papà', ecc.) e infine costruendo le prime strutture sintattiche; con ciò raggiunge una competenza linguistica strutturale che suggella definitivamente l'acquisizione di capacità astrattive (quando utilizza nomi-etichetta) e delle capacità di correlazione (quando costruisce frasi sintatticamente corrette). La comprensione del linguaggio naturale, essendo una delle più elevate capacità umane, è anche una delle più difficili da emulare. In effetti, il processo di comprensione del discorso dipende, in maniera critica, dalla conoscenza comune che entrambi gli interlocutori hanno e a cui fanno, spesso inconsciamente, riferimento. I significati di una parola vengono selezionati quando quella parola viene interpretata nell'ambito di un vasto spettro di aspettative che, a loro volta, sono influenzate dall'esperienza linguistica, dalla natura della situazione, ecc. In effetti, non è raro il caso in cui un interlocutore riesce ad anticipare ciò che l'altro sta per dirgli.

Il linguaggio, argomento centrale nell'intelligenza artificiale, può essere, almeno in prima approssimazione, visto come costituito di tre parti distinte: una acustico-fonetica, una morfologico-sintattica e una terza semantico-pragmatica (v. fig. 9).

Il compito del componente fonetico è quello di tradurre la successione delle onde sonore che forma le parole pronunciate in una serie di grafemi, cioè di simboli che le rappresentano. Questo problema è molto più difficile di quello che potrebbe apparire a prima vista, a causa soprattutto del fatto che le pause tra le parole hanno una corrispondenza solo occasionale con gli spazi bianchi che vengono lasciati tra le parole scritte. Una volta che si sia ottenuta la rappresentazione grafemica del parlato, la si passa al componente successivo, cioè a quello morfologico, il cui compito è quello di ricondurre ciascuna delle parole, cosi come vengono scritte nel testo, alle corrispondenti parole, così come si trovano nel dizionario. Per esempio, i nomi al maschile plurale saranno ricondotti al corrispondente maschile singolare, i verbi all'infinito e così via. In questo modo si può associare a ciascuna delle parole dell'enunciato il suo valore grammaticale (verbo, nome, ecc.) e il suo valore morfologico (maschile, participio, ecc.). Il compito del componente successivo (cioè del componente sintattico) è quello di ricevere in ingresso i risultati dell'azione del componente morfologico e di stabilire quali siano i legami di tipo sintattico che esistono tra i vari componenti dell'enunciato. In ogni linguaggio esistono regole per eseguire la lemmatizzazione (che consiste nel ricondurre le parole flesse o ‛forme' alle parole del dizionario o ‛lemmi') e l'analisi sintattica (o parsing). Una volta stabilito il ruolo che ogni parola ha nell'enunciato, si è ottenuta una rappresentazione formale della struttura sintattica della frase; il compito del componente successivo è quello di prendere in ingresso questa rappresentazione e di dare una rappresentazione formale del significato, sotto forma di una notazione che sia chiara, che rappresenti completamente il significato di ogni lemma e che sia usabile dal punto di vista informatico.

A ogni livello (a cominciare da quello fonetico) ci sono ambiguità, nel senso che le possibilità di analisi sono molteplici, possono cioè esistere diversi modi equivalenti di suddividere una singola emissione di fiato in diverse parole (per es. ‛la vena' e ‛l'avena'), di interpretare una singola forma (per es. ‛finissimo', aggettivo o verbo) e di scomporre un singolo enunciato in diverse parti del discorso (per es. ‛la vecchia porta la sbarra', come ‛articolo, sostantivo, verbo, articolo, sostantivo' o ‛articolo, aggettivo, sostantivo, pronome, verbo'). L'azione del contesto e della semantica può aiutare a eliminare questa ambiguità, che sembra essere una caratteristica fondamentale e permanente del linguaggio naturale. Ciò fu capito relativamente tardi e la mancanza di questa comprensione determinò il fallimento dei progetti di traduzione automatica iniziati negli anni cinquanta.

a) Sintassi e morfologia.

In linea di principio un linguaggio può essere definito semplicemente elencando tutti i suoi enunciati; in questo modo si potrebbe, dato un enunciato, determinare in maniera univoca la sua appartenenza al linguaggio dato. Si può facilmente vedere come questo metodo sia impraticabile, in quanto gli enunciati di un linguaggio possono essere addirittura infiniti, grazie alla presenza di vari meccanismi (detti ‛generativi') insiti nel linguaggio. L'italiano, come anche altri linguaggi, possiede un certo numero di meccanismi che lo rendono infinito: tra questi, per esempio, la ripetitività delle congiunzioni (per es. ‛Mario e Giovanni e Giuseppe e ...'), l'annidamento delle relative (per es. ‛Il cane che morse il gatto che mangiò il topo che...') e l'annidamento dei complementi di specificazione (per es. ‛L'attacco del cavo dell'apparecchio di lettura di...'). Per fortuna, però, gli enunciati possono essere scomposti in pochi elementi di tipo diverso (come ‛gruppo nominale', ‛gruppo verbale', ecc.), eventualmente ricorrenti. Questo fatto è alla base delle grammatiche formali, che essenzialmente sono dei meccanismi per specificare con un numero di regole finito (e normalmente abbastanza piccolo) i possibili enunciati di un linguaggio. Sostanzialmente l'idea è quella di specificare che un enunciato ‛legale' in un dato linguaggio è formato, per esempio, da un gruppo nominale seguito da un gruppo verbale; che il gruppo nominale può essere formato da un articolo seguito da un certo numero di aggettivi, seguiti a loro volta da un nome, ecc. Queste regole possono essere espresse in maniera formale e ciò le rende utilizzabili da un elaboratore attraverso degli algoritmi di analisi sintattica che riescono, dato un enunciato, a chiarire i legami sintattici tra gli elementi dell'enunciato stesso. Gli analizzatori sintattici hanno il compito di individuare le parti costituenti degli enunciati; vengono perciò detti, in inglese, parsers (dal latino pars = parte). I risultati di queste analisi sintattiche sono dati sotto forma di alberi che hanno come radice il simbolo corrispondente all'enunciato totale, come nodi intermedi i simboli delle parti del discorso di cui questo enunciato è costituito e come foglie le parole dell'enunciato stesso. Una rappresentazione ad albero di questo genere può agevolare l'esecuzione di procedure che calcolano la semantica, cioè il ‛significato' dell'enunciato, in quanto esplicita le relazioni tra le parole in esso contenute.

Grammatiche indipendenti dal contesto. - Una maniera conveniente di scrivere una grammatica formale, che possa cioè generare e anche analizzare tutti gli enunciati ammessi in un linguaggio, è quella di designare con un simbolo il gruppo che si vuoi definire (per es. GN per ‛gruppo nominale'), scriverlo facendolo seguire da una freccia, e scrivere a destra di questa freccia i nomi dei gruppi sintattici o delle parole che costituiscono tale gruppo; la regola per ‛gruppo nominale' sarà quindi

GN → Art Agg Sost

(cioè un gruppo nominale può essere formato da un articolo, seguito da un aggettivo, seguito da un sostantivo, per es. ‛il nuovo romanzo'). Regole di questo genere descriveranno la struttura dell'enunciato: per esempio

E → GN GV

afferma che l'enunciato può essere costituito da un gruppo nominale seguito da un gruppo verbale. Analoghe regole descriveranno la struttura del gruppo verbale, fino a ottenere una completa descrizione del linguaggio.

Dalla forma di scrittura di questa grammatica si può notare che a sinistra della freccia c'è solo un simbolo, il che implica che l'applicazione di ogni data regola dipende esclusivamente dal simbolo alla sinistra della freccia e non, per esempio, da quelli che lo precedono o lo seguono nella stringa. Le grammatiche che godono di questa proprietà vengono dette ‛indipendenti dal contesto' (context-free); nel caso invece in cui si voglia tener conto del contesto, si voglia cioè condizionare l'applicazione delle regole anche ai simboli che precedono e seguono quello considerato, si scriveranno delle regole nella cui parte sinistra, insieme al simbolo in questione, si riporteranno gli elementi del contesto di cui si vuoi tenere conto.

Per analizzare un enunciato con una grammatica indipendente dal contesto si possono seguire due differenti metodi: il primo consiste nell'andare ‛dall'alto verso il basso' (top-down) e il secondo nell'andare ‛dal basso verso l'alto' (bottom-up). Nella prima tecnica si parte dal simbolo iniziale e si applicano successivamente le regole della grammatica a ogni simbolo, cominciando ogni volta dal primo a sinistra e procedendo verso destra, come se si volesse effettivamente generare un enunciato. Al primo simbolo terminale (corrispondente cioè a una forma) che viene prodotto, si effettua un controllo dell'enunciato da analizzare per determinare se il simbolo prodotto è effettivamente presente: in caso affermativo l'analisi procede, cercando di sviluppare il secondo simbolo, e così via; in caso negativo si riesamina la regola applicata per ultima e si vede se ci sono delle altre regole che hanno la stessa parte sinistra e una differente parte destra. Se queste esistono, il processo riprende dalla prima di queste, continuando finché non si verifica uno dei seguenti casi: si ottiene ogni simbolo voluto (e in questo caso l'analisi riesce) oppure per un certo simbolo non ci sono alternative, e allora l'analisi fallisce.

Un procedimento alternativo consiste nell'usare la grammatica in senso inverso: si prendono delle sequenze di simboli presenti nell'enunciato e si cerca nella grammatica se esistono delle regole che hanno come parte destra tale sequenza. Se qualcuna di queste regole esiste, allora la sequenza di simboli viene sostituita dal simbolo che si trova alla sinistra della freccia. Si riapplica questo procedimento finché viene raggiunto il simbolo di enunciato, nel qual caso l'analisi è completata.

Quale che sia il metodo di analisi seguito, si può ottenere una rappresentazione grafica del procedimento di analisi semplicemente connettendo con dei segmenti ogni simbolo con i simboli da esso prodotti (per metodologie ‛dall'alto al basso') o con i simboli che lo producono (per metodologie ‛dal basso all'alto'); si ottengono degli alberi del tipo di quello illustrato nella fig. 10.

C'è da notare, in ogni caso, che il procedimento di analisi non è né semplice né diretto, in quanto normalmente esistono diverse regole di grammatica che, a parità di simbolo terminale, prevedono differenti sviluppi; è quindi chiaro che, anche in questi casi, si può avere una ‛esplosione combinatoria' (cioè una crescita incontrollata) del numero dei casi da trattare, che deve essere evitata con opportune metodologie.

Reti di transizione. - Esaminando le regole della grammatica viste sopra, si può capire come esse possano essere rappresentate da una rete ‛di transizione', in cui ogni simbolo viene considerato uno ‛stato' che, attraverso una transizione, passa in un altro stato. Ogni transizione viene condizionata dalla presenza (o dall'assenza) di certi altri particolari simboli. Nella fig. 11 è illustrata la rete di transizione equivalente a una grammatica del tipo visto prima. Si vede, per esempio, che nella transizione da E1 a E2 la condizione è ‛gruppo nominale'. Questa condizione non può essere verificata direttamente, per cui, prima che la transizione venga effettuata. viene attivata la sottorete che tratta i gruppi nominali, la quale cerca di effettuare la transizione dallo stato iniziale a quello successivo. Si vede che la condizione su questa transizione è semplicemente la presenza di un articolo determinativo, che è una condizione immediata: si può cioè constatare direttamente se tale simbolo è o meno il simbolo corrente dell'enunciato in esame. Se lo è, viene effettuata questa transizione e anche la successiva, che richiede un nome. Effettuata quest'ultima, può essere effettuata la precedente, nella prima sottorete, che dipendeva da essa. Procedendo in questo modo, si può analizzare l'intero enunciato: l'analisi di un enunciato consiste semplicemente nella serie di transizioni che sono state effettuate per raggiungere il nodo finale a partire dal nodo iniziale. Si possono anche vedere delle strade alternative che partono da un dato nodo: ciascuna di queste strade è caratterizzata dal simbolo che viene a essa associato e che serve per caratterizzarla.

Le grammatiche libere dal contesto, sia in forma tradizionale che in forma di rete, non possono tener conto di alcuni fenomeni linguistici quale, per esempio, la cosiddetta ‛trasformazione passivante', cioè la trasformazione di un enunciato dato in forma attiva nel suo equivalente in forma passiva. Per tener conto di questi fenomeni si sono sviluppate le cosiddette ‛grammatiche trasformazionali', che prendono in ingresso degli alberi di analisi e li trasformano, secondo certi criteri, in altri alberi che possono produrre altri enunciati derivati.

ATN (reti di transizione aumentate). - Alcune delle limitazioni delle reti di transizione possono essere superate fornendo ai nodi della rete alcuni attributi i cui valori possono guidare l'analisi: in questo modo si ottengono delle reti che sono molto più compatte e hanno un potere espressivo molto maggiore. Questi attributi, che sono molto simili alle caselle già viste per le strutture di rappresentazione della conoscenza, riportano informazioni di tipo morfologico (per es. genere, numero, ecc.) ed eventualmente anche semantico (per es. ‛umano/non umano', ‛animato/non animato', ecc.). In questo modo è possibile fornire dei criteri di scelta molto più rigidi, che guidano l'algoritmo di analisi evitando che faccia troppi tentativi inutili.

Il problema dell'efficacia dell'analizzatore è un problema centrale nell'analisi del linguaggio: infatti, se non si pongono delle limitazioni o comunque non si adottano delle ipotesi restrittive, il tempo impiegato dall'elaboratore per eseguire un'analisi cresce in maniera esponenziale rispetto alla lunghezza dell'enunciato da analizzare. Alcuni algoritmi adatti per grammatiche indipendenti dal contesto riescono invece a essere, nel peggiore dei casi, dipendenti solo dal cubo e spesso addirittura dalla prima potenza della lunghezza dell'enunciato da analizzare.

Un analizzatore basato su una grammatica ATN senza alcuna restrizione particolare può avere delle prestazioni non molto soddisfacenti; se però si adotta la restrizione che le uniche grammatiche ammesse sono quelle indipendenti dal contesto, le sue prestazioni aumentano notevolmente. Allo stato attuale della ricerca, per alcuni linguaggi naturali, come l'inglese, si sono scritte delle grammatiche formali che, anche se non coprono tutto il linguaggio, ne coprono la maggior parte. L'inglese, sebbene non sia un linguaggio indipendente dal contesto, lo è comunque abbastanza e ciò lo rende analizzabile da analizzatori basati su grammatiche formali.

Per aumentare l'efficienza degli analizzatori si può pensare di utilizzare i ‛suggerimenti' che provengono dai simboli che seguono il simbolo in esame, in quanto essi possono aiutare a scegliere la regola giusta da applicare ed evitare quindi i tentativi inutili.

b) Dalla sintassi alla semantica.

Come è stato accennato prima, il risultato dell'analisi sintattica, cioè l'albero di analisi, deve essere utilizzato dalle procedure che cercano di ricavare un significato dall'enunciato. Queste procedure si basano sulla rappresentazione del significato delle parole, che a sua volta si fonda su alcuni concetti elementari (reputati, per ciò stesso, ‛assiomatici') e su relazioni, anch'esse assiomatiche, tra di essi. Normalmente, siccome a ogni parola corrisponde più di un significato, si associa una rappresentazione del significato a ognuno dei sensi della parola. Per esempio, alla parola ‛piano' può corrispondere sia il significato (come avverbio) di ‛lentamente', sia quello (come aggettivo) di ‛liscio', sia infine quelli (come sostantivo) di ‛pianoforte', ‛piano di caseggiato', ‛progetto', ecc.

Anche tralasciando i primi due sensi di ‛piano', la rappresentazione del terzo significato comprenderà sicuramente una definizione di tipo (che provveda a collegare piano con strumento musicale) con in più alcune altre relazioni che, per esempio, dichiareranno che piano è uno strumento utilizzato da un singolo uomo. In tal caso il termine ‛uomo' o ‛essere umano' viene preso come elemento primitivo. Non sono assolutamente definiti (e variano di teoria in teoria) il numero e la natura di questi primitivi semantici; molte teorie però concordano sul fatto che essi esistano e siano in numero relativamente limitato. La semantica può aiutare anche la sintassi nella fase di analisi; per esempio, prendendo la frase ‛Giovanni va al parco con la moto' e confrontandola con ‛Giovanni va al parco con gli alberi', si vede che la sintassi dovrebbe formare nel primo caso un gruppo tra ‛va' e ‛moto', avendo ‛con' il significato di ‛mezzo', e invece, nel secondo caso, dovrebbe collegare ‛parco' e ‛alberi' essendo questa volta ‛alberi' una caratteristica di ‛parco'. Solo su basi semantiche può essere stabilita questa connessione: infatti, solo a livello semantico è possibile interpretare ‛moto' come ‛mezzo di trasporto' e quindi come possibile (e significativo) complemento di mezzo per il verbo ‛andare', mentre per ‛alberi' è valida solo l'interpretazione come attributo di ‛parco' e non come ‛mezzo' di ‛andare'. Come si vede, sono abbastanza forti le interazioni tra sintassi e semantica: in effetti, in alcuni metodi le due fasi sono alternate, si succedono, cioè, l'una all'altra durante l'analisi. Normalmente, appena viene formulata un'ipotesi di collegamento sintattico, la semantica viene consultata per verificarla; viceversa, le ipotesi semantiche vengono controllate dalla sintassi.

Per questo tipo di approccio un'architettura molto utile è un'architettura ‛a lavagna', in cui tutti i processi (sintassi, semantica ed, eventualmente, fonetica e acustica), si alternano l'uno all'altro registrando i loro risultati su una memoria condivisa (detta, appunto, ‛lavagna'), che viene usata da ogni processo per registrare l'attuale situazione dell'elaborazione, applicare le opportune regole e scrivere i risultati che verranno poi utilizzati da altri processi o dallo stesso processo. Nella fig. 12 è riportato lo schema del sistema HEARSAY, che è un sistema di comprensione del parlato, in cui tutti i componenti cooperano alla comprensione, comunicando i loro dati attraverso una lavagna.

Ruoli tematici. - Una maniera per rappresentare il significato di un enunciato consiste nell'esplicitare il ruolo di ciascun elemento della frase rispetto agli altri. Per esempio, data la frase ‛Giovanni porta il libro', una possibile maniera di spiegare il significato è dire che ‛Giovanni' è l'‛agente attivo' di una certa azione (‛portare') che è un sottotipo di ‛muovere', cioè ‛cambiare locazione', mentre ‛libro' è l'oggetto (‛paziente inanimato') di ‛muovere'. ‛Agente attivo', ‛paziente inanimato', ecc. costituiscono i cosiddetti ‛ruoli tematici', il cui numero e la cui natura variano di teoria in teoria da un minimo di 5-6 fino a un massimo di 40. In maniera approssimativa potremmo dire che essi tendono a un raffinamento del concetto di ‛complemento': sono infatti normalmente collegati a nomi (o a gruppi nominali), a verbi, ma anche a preposizioni.

Per stabilire i ruoli tematici, si prendono gli alberi prodotti dalle procedure di analisi sintattica e li si elabora associando a ogni parola la rappresentazione del suo significato, risalendo da questa parola al nodo che rappresenta il gruppo sintattico di cui essa fa parte e da questo ridiscendendo alla successiva parola che fa parte dello stesso gruppo sintattico. Per esempio, nella frase ‛Il ragazzo cammina', il nome ‛ragazzo' forma, insieme con l'articolo ‛il', un gruppo nominale, che è associato, attraverso il nodo sintattico ‛Enunciato', al gruppo verbale formato dal verbo ‛cammina'. Per stabilire quindi il ruolo tematico di ‛ragazzo', bisogna consultare un dizionario, cercare la definizione di ‛ragazzo' (che risulterà essere un sottotipo di ‛essere umano', a sua volta sottotipo di ‛animale', sottotipo di ‛animato', ecc.), risalire da ‛ragazzo' al gruppo nominale cui appartiene, da questo a ‛Enunciato', e da questo ridiscendere poi al gruppo verbale che contiene il verbo ‛cammina'. Nella definizione di ‛animato' si trova che esso ha la capacità di muoversi; nella definizione di ‛camminare' si trova che è un sottotipo di ‛muovere' e, nella definizione di quest'ultimo, si trova che uno dei possibili agenti è appunto un ‛animato'. Quindi ‛ragazzo', essendo un sottotipo di ‛animato', è un possibile agente attivo di ‛camminare', per cui, in questo caso, si può concludere che il ruolo tematico di ‛ragazzo' è ‛agente attivo'.

Nella fig. 13A è riportato un albero di analisi per l'esempio esaminato, mentre nella fig. 13B è riportato l'unico albero di analisi ‛sensato' per la frase ‛Il ragazzo porta la ragazza al cinema con la moto'. Dalla definizione di ‛ragazzo' si vede che esso può essere agente attivo di ‛portare' (qualsiasi ‛animato' può esserlo), si vede che ‛ragazza' è oggetto di ‛portare' (‛portare' può avere per oggetto qualsiasi cosa), ‛al cinema' è destinazione di ‛portare', che a sua volta è sottotipo di ‛muovere' (e quindi può avere una destinazione: ‛cinema' ha, in questo caso, la funzione di luogo). Per quello che riguarda ‛con la moto' si ha in questo caso un'ambiguità dal punto di vista sintattico in quanto la sintassi produce due analisi: una che riferisce ‛con la moto' a ‛porta' e l'altra che lo riferisce a ‛cinema', producendo quindi i gruppi ‛porta con la moto' e ‛cinema con la moto'. Dal punto di vista semantico, però, ‛portare', essendo sottotipo di ‛muovere', può essere collegato a un mezzo di trasporto' (di cui ‛moto' è sottotipo) che quindi assume il ruolo tematico di ‛strumento', mentre ‛cinema' non ha (normalmente) un ‛mezzo di trasporto' tra i suoi attributi. E quindi possibile, sulla base di queste considerazioni, eliminare (o attribuire una bassa attendibilità) alla seconda analisi.

L'esplicitazione dei ruoli tematici permette di rispondere a semplici domande su questo enunciato, quali: ‛Cosa porta il ragazzo?', ‛Dove il ragazzo porta la ragazza?', ‛Cosa usa il ragazzo per portare al cinema la ragazza?', ecc.

Significato e contesto. - Finora abbiamo trattato la comprensione del linguaggio naturale limitandolo all'enunciato. In realtà quello che l'essere umano comprende è il discorso, cioè l'insieme organizzato di enunciati. Inoltre nella comprensione umana si hanno altri meccanismi che permettono di inferire alcune informazioni che non sono esplicitamente date né nell'enunciato nè nel discorso: capire una storia è in realtà non solo capire il significato esplicito del discorso, ma anche dedurre tutta una serie di significati che, anche se non sono esplicitamente citati, sono comunque plausibili. Riprendendo l'esempio visto prima, dato che normalmente si va al cinema per vedere un film, in risposta alla domanda ‛Perché il ragazzo porta la ragazza al cinema?' si potrebbe indicare la visione del film come una plausibile finalità. Per fare questo genere di deduzioni occorre però un'enorme conoscenza del mondo e, in particolare, su come le persone elaborino dei piani per perseguire le loro finalità, sulle loro motivazioni, ecc. Questo processo rassomiglia molto, almeno in linea di principio, all'attraversamento di una rete semantica i cui nodi, collegati gli uni agli altri, vengono attivati o inibiti, a seconda dei casi; in questo caso la rete semantica è parecchio complessa, dovendo coinvolgere moltissimi concetti.

Una maniera relativamente diretta di realizzare, dal punto di vista delle macchine, tale architettura, è quella di disporre di numerose unità di elaborazione relativamente semplici e collegate in una rete, che si passano dei messaggi dopo aver elaborato, almeno parzialmente, i messaggi in arrivo. Questa architettura dovrebbe essere in realtà vista come uno stadio di preelaborazione, in cui i dati vengono preparati per essere elaborati dagli algoritmi di comprensione veri e propri, che sostanzialmente traggono vantaggio dal fatto che migliaia (o milioni) di interpretazioni inattendibili siano state scartate dalla preelaborazione, e quindi possono agire in maniera più ‛mirata'.

9. Apprendimento.

Per costruire sistemi esperti lo specialista, cioè il depositario della conoscenza, deve innanzitutto formalizzarla e poi introdurla nella macchina attraverso un processo che, oggi come oggi, è lungo e laborioso. Se invece l'elaboratore (o qualche sistema analogo) potesse imparare dall'esperienza, questa potrebbe essere senz'altro la chiave di volta per costruire sistemi esperti in maniera molto più facile, addirittura automatica. Una macchina che apprende inoltre rivoluzionerebbe la robotica: infatti, un robot capace di imparare a eseguire un particolare lavoro non richiederebbe alcun grosso sforzo di programmazione.

Dal punto di vista teorico, un problema che fin dai tempi di Locke ha affascinato gli studiosi della psicologia e dell'intelligenza è stato quello di determinare se esista un meccanismo generale che ci permette di imparare. È chiaro che, una volta che si sia individuato un meccanismo del genere, supposto che esista, si può costruire un modello funzionante dell'apprendimento stesso e quindi superare, d'un colpo, tutti i problemi di programmazione specifica.

A questo problema furono dedicate negli anni sessanta alcune ricerche condotte con particolari meccanismi detti perceptrons. Un perceptron, in sostanza, è un'architettura parallela di semplici unità di calcolo, ciascuna delle quali è capace di effettuare una semplice operazione.

Finora l'apprendimento è stato considerato essenzialmente un processo singolo; in realtà si dovrebbe più correttamente parlare di diversi tipi di apprendimento, a cui viene generalmente dato il nome di ‛apprendimento meccanico, ‛apprendimento parametrico', ‛apprendimento del metodo' e ‛apprendimento di concetti'.

a) L'induzione di concetti e di regole da esempi.

Nell'apprendimento umano riveste un ruolo importante la cosiddetta ‛individuazione dei concetti', dove per ‛concetto' si intende la rappresentazione mentale che sintetizza gli attributi specifici di una classe di oggetti. La costruzione di un concetto per via empirica si effettua esaminando una serie di esempi concreti del concetto da definire e individuandone le caratteristiche salienti.

È possibile indurre un sistema a ‛costruire concetti' fornendogli una serie di esempi ‛giusti' e ‛sbagliati' del concetto da definire: il sistema, confrontando le caratteristiche che distinguono gli esempi giusti da quelli sbagliati, ricava ‛per differenza' gli attributi specifici che concorrono alla definizione del concetto. Evidentemente hanno grande importanza, in questo caso, gli esempi ‛quasi giusti', cioè quelli che differiscono da un esempio giusto per un singolo attributo: il sistema può così individuare, con notevole precisione, quale sia l'attributo rilevante ai fini della definizione del concetto.

Alcuni sistemi, come, per esempio, quello sviluppato da Winston nel 1970, si basano sulla procedura descritta. Il sistema è stato effettivamente utilizzato per ricavare il concetto di ‛arco' da un insieme di esempi di archi e di altri elementi architettonici. Nella fig. 14A è riportato un esempio positivo; la fig. 14B, invece, illustra un caso di ‛quasi errore', consistente nel fatto che le colonne sono unite l'una all'altra. Questo ‛controesempio' mette in rilievo un importante attributo morfologico del concetto di arco: le colonne, per quanto vicine, non devono toccarsi; l'esplicitazione di questa caratteristica concorre alla definizione del concetto di arco.

Mentre gli esempi negativi servono a specializzare il concetto, restringendone la portata, gli esempi positivi contribuiscono a generalizzarlo: la fig. 15 può essere utilizzata come esempio positivo nel caso si voglia generalizzare il concetto di arco a strutture non curvilinee.

Il procedimento descritto prende il nome di ‛induzione'. Un procedimento del tutto analogo permette di ‛indurre' da una o più norme operative una regola di portata più generale. Un semplice esempio potrebbe essere il seguente. Supponiamo di prendere le mosse da una norma che prescriva di accarezzare ogni gatto in cui ci si imbatta. In termini espliciti questa norma potrebbe suonare così: ‛Se si esamina un oggetto e si stabilisce che esso è un gatto, allora lo si accarezzi'. Una prima generalizzazione di questa regola potrebbe far uso della rete semantica relativa alle specie animali per definire la classe cui appartiene ‛gatto'. Tale classe è ‛felino', per cui si può indurre la regola: ‛Se si incontra un felino, lo si accarezzi'. Notiamo che non si è tenuto conto, nella generalizzazione, di nessun altro attributo del gatto; oltre alla specie di appartenenza, non si e tenuto conto del suo colore, della sua grandezza, ecc. La regola precedente mostra però dei difetti: infatti non tutti i felini possono essere accarezzati impunemente, specie quelli di grossa taglia. Un esempio negativo per il sistema potrebbe appunto essere costituito dall'accarezzamento di un felino di grossa taglia. In questo caso emergerebbe l'importanza della taglia nella generalizzazione e quindi nell'induzione di regole: il fatto di avere un esempio ‛quasi positivo' (tutte le condizioni costanti, eccetto la taglia) rende subito evidente l'importanza di quest'ultima nella generalizzazione. Si può allora perfezionare la regola precedente come segue: ‛Se si incontra un felino di taglia non grande, allora lo si accarezzi'. Si può, a questo punto, provare a generalizzare da ‛felini' ad ‛animali' (purché piccoli) e così via, procedendo con esempi e controesempi.

Al fine di effettuare queste generalizzazioni si usano delle ‛metaregole' per poter modificare delle regole già esistenti o crearne delle altre. Per esempio, una di queste metaregole stabilisce che, in un esempio positivo, devono essere riportate alla classe immediatamente superiore le caratteristiche che lo rendono differente da altri esempi positivi, in maniera tale da generalizzare il più possibile tali caratteristiche. Ovviamente un tale sistema presuppone la capacità di paragonare due situazioni differenti tra loro e di trovarne le somiglianze; in altre parole, la capacità di fare il ‛paragone generalizzato' (matching). Questa operazione è, in generale, tutt'altro che diretta, in quanto non si tratta di stabilire delle uguaglianze o delle differenze ma delle ‛somiglianze'. Si deve allora ricorrere ad alcuni artifici, quali, per esempio, le reti semantiche. Le situazioni date sono allora riportate su un'opportuna rete semantica e si stabilisce se tra di esse esistono delle relazioni, e di che tipo. La caratteristica interessante di questi sistemi di apprendimento è che essi funzionano in maniera incrementale, cioè accumulano serie di esempi positivi e negativi: in questo modo il sistema comincia realmente a imparare quando sa già molto, sa cioè come confrontare situazioni almeno apparentemente diversissime e possiede già una rete semantica piuttosto estesa.

L'uso delle reti semantiche è piuttosto agevole soprattutto nell'ambito di settori delimitati già notevolmente formalizzati, come, per esempio, l'analisi matematica. Nel sistema LEX, sviluppato da Mitchell nel 1983, l'universo di discorso è costituito da espressioni simboliche da integrare servendosi dei normali procedimenti di integrazione simbolica. Data una formula, il sistema tenta di integrarla provando sequenzialmente tutti i metodi di integrazione finché ne trova uno con cui riesce a integrare la formula. Successivamente il sistema esamina le caratteristiche della formula stessa e comincia a generalizzare tutti i parametri rilevanti (sostituendo, per es., variabili al posto di costanti, classi di funzioni a singole funzioni, ecc.). Prova poi ad applicare la stessa metodologia di integrazione sulle formule che ottiene e si ferma al grado massimo di generalizzazione che preserva l'applicabilità del metodo di integrazione trovato. In questo modo il sistema può costruirsi delle regole del tipo: SE 〈 caratteristiche della formula da integrare > ALLORA 〈 operatore di integrazione >. Per esempio, per la formula

∫ 3x cos xdx,

LEX prova tutti i metodi di integrazione finché trova il metodo di integrazione per parti (abbreviato: IPP) e genera la regola: SE 3x cos x dx ALLORA IPP. Successivamente tenta di generalizzare la formula come illustrato nella fig. 16, in cui la prima formula è quella di partenza, che risulta integrabile per parti, mentre l'ultima è troppo generale perché l'integrazione per parti possa essere applicata. LEX allora constata che l'ultima generalizzazione è sbagliata e quindi prova con livelli minori di generalizzazione finché non trova, per esempio, che il 3 può essere sostituito da qualunque elemento appartenente alla classe delle costanti.

Recentemente sono stati proposti altri sistemi che, come il LEX, tentano di imparare regole.

Un sistema, proposto da Berwick, impara nuove regole sintattiche per l'analisi dell'inglese utilizzando i propri errori, cioè produce delle ipotesi di regole sintattiche quando non riesce a completare l'analisi di un enunciato. Ciò si può ottenere restringendo opportunamente il numero delle regole che si possono introdurre.

Winston ha proposto un altro sistema che, data una descrizione generale della funzione di un oggetto (per es. una tazza o una sedia) e alcune realizzazioni dell'oggetto (cioè particolari tazze o particolari sedie), può ottenere delle altre realizzazioni che possono essere utili per il trattamento della visione generalizzata e la comprensione delle scene.

Lenat ha sviluppato due sistemi i quali non si basano su esempi per l'apprendimento ma semplicemente esplorano lo spazio di ricerca, cioè le possibilità associate a ogni particolare situazione. Per esempio, il primo programma, chiamato AM, parte da alcuni assiomi sui numeri naturali e riesce a imparare delle regole di teoria dei numeri, semplicemente applicando determinate euristiche.

Un altro sistema, il già citato EURISKO (v. cap. 7, È b), in una sua applicazione particolare, si basa sulle proprietà delle navi e sulla situazione iniziale, determinata di volta in volta, per creare delle regole di gestione di una flotta in un gioco simulato di battaglia navale.

b) Mutazione e selezione di regole.

In tutti i sistemi che imparano visti finora è presente il meccanismo di ‛generazione-e-prova', cioè un meccanismo che accetta esempi positivi o negativi, induce da questi regole e concetti e ne verifica infine la correttezza. Questo processo artificiale è molto simile al processo naturale di mutazione e selezione: infatti, come gli organismi mutanti vengono esposti alla selezione naturale che determina la sopravvivenza dei più ‛idonei', così le regole vengono generate in via ipotetica e il loro confronto con gli esempi decide della loro sopravvivenza. C'è tuttavia una differenza fondamentale: nel caso dei sistemi artificiali c'è tutto un insieme di metaregole che decide quali sono i criteri da seguire per stabilire quali regole generare e in quale ordine provarle. Questi criteri vengono direttamente immessi nel sistema, ma evidentemente nulla vieta che tali criteri possano essere imparati. Si porrebbe allora il problema di creare delle metametaregole che possano aiutare a gestire le metaregole, e così via all'infinito, finché si potrebbe immaginare un processo (magari estremamente lento) che potrebbe partire dai primissimi criteri e arrivare alle regole più immediate dell'apprendimento.

Risulta in ogni caso evidente che i primi stadi dell'apprendimento sono i più difficili, proprio per la mancanza quasi assoluta di criteri guida. È possibile tuttavia pensare a un sistema che impari seguendo un procedimento puramente casuale, nei primissimi stadi, e sempre più deterministico man mano che si stabiliscono i criteri fondamentali di produzione delle regole. A questo stadio può aver luogo l'apprendimento, nel vero senso della parola; ciò conferma il fatto già messo in evidenza che l'apprendimento riesce solo se si sa già molto.

10. Robotica e visione.

La robotica è quella branca dell'intelligenza artificiale che si occupa della realizzazione di meccanismi (robot) capaci di svolgere in maniera autonoma e automatica determinate operazioni, ovvero capaci di intervenire sull'ambiente fisico circostante in modo da trasformarne uno stato iniziale dato in uno stato finale desiderato. Allo scopo questi meccanismi devono essere dotati di ‛facoltà percettive' e della capacità di agire secondo determinati fini sulla realtà percepita. Pertanto componenti essenziali dei robot sono: i ‛pianificatori', dispositivi che consentono al sistema di svolgere nella sequenza desiderata e secondo criteri prefissati i compiti di sua competenza; i ‛manipolatori', strumenti di azione diretta sul mondo fisico; i ‛sensori', dispositivi che conferiscono al robot la capacità di ‛percepire' la realtà circostante.

Questo capitolo è dedicato alla descrizione di un particolare tipo di percezione: la percezione visiva.

a) La complessità della visione.

Soltanto recentemente, nell'intelligenza artificiale, è stato affrontato il problema della visione dal punto di vista dei robot: dalla Conferenza di Dartmouth, nel 1956, all'inizio degli anni settanta le uniche attività prese in considerazione dall'intelligenza artificiale erano state quelle ‛profonde', come ‛dimostrare teoremi', ‛giocare a scacchi', ecc. Il perché di un atteggiamento di questo genere è ovvio: il ragionamento è un processo cosciente, che non necessita di un particolare sforzo introspettivo per essere descritto. Viceversa l'uomo non ha una precisa coscienza di quello che succede quando percepisce le immagini del mondo esterno e le elabora.

D'altronde le attività percettive (come, appunto, la visione) sembrano talmente ‛spontanee' da non richiedere una particolare intelligenza per la loro esecuzione; il tentativo di conferire la visione artificiale al robot ha invece portato alla consapevolezza che il sistema visivo è estremamente complesso dal punto di vista dell'elaborazione dell'informazione. Le ricerche fatte in questo campo hanno anche apportato importanti contributi alla neurofisiologia.

Quando un occhio o una telecamera riceve un'immagine del mondo esterno, che è evidentemente un mondo tridimensionale, riceve in realtà una proiezione bidimensionale della scena. Quando l'immagine, cioè il flusso luminoso, colpisce il ricettore (retina o elemento sensibile della telecamera), essa viene ‛vista' come un mosaico di elementi di immagine, detti picture elements o pixels, ognuno dei quali è omogeneo. Normalmente ognuno di questi elementi viene sottoposto a una particolare elaborazione, per essere inviato all'apparato ricevente (il cervello o l'apparecchio cui la telecamera è collegata) sotto forma di una serie di impulsi codificati che corrisponde all'immagine. Il numero di pixels in un'immagine tende a essere grande: un'immagine di non grande qualità, in bianco e nero, corrisponde a un mosaico di circa 500 × 500 pixels, mentre immagini discrete richiedono circa 1.000 × 1.000 pixels. Per avere un'idea della potenza dell'apparato della vista si deve tener conto che, in ciascun occhio umano, circa 30 di queste immagini devono essere elaborate ogni secondo per avere una visione in tempo reale. Ora, questa elaborazione, anche supponendo che sia molto semplice e si componga solo di una serie di addizioni e moltiplicazioni, comporta miliardi di operazioni da effettuare in tempo reale.

Questa capacità è parecchio al di là delle attuali prestazioni degli elaboratori, ma le nuove architetture, composte di centinaia e anche di migliaia di unità di calcolo che sono connesse tra di loro, in grado di elaborare indipendentemente l'informazione per poi fonderla insieme, aprono nuove prospettive. Si potrebbe, per esempio, far corrispondere una di queste unità a ogni pixel, per cui si potrebbe far eseguire in parallelo a ciascuna di queste unità tutte le operazioni relative al singolo pixel e poi integrare i risultati. Con tutto ciò, però, restano ancora dei grossi problemi di elaborazione dell'immagine per renderla ‛comprensibile': il fatto che venga utilizzata solo una proiezione dell'oggetto pone dei seri problemi di interpretazione, in quanto la proiezione può risultare estremamente ambigua. Per esempio, nella fig. 17 si vede quello che sembra essere il profilo di una sedia: il fatto che questa abbia quattro gambe non è assolutamente deducibile dalla proiezione bidimensionale, che invece ne mostra due, per cui è effettivamente solo la conoscenza del mondo esterno che ci permette di immaginare la presenza delle altre due gambe nascoste dalle due visibili. In definitiva, occorre una grande quantità di conoscenza del mondo fisico per poter interpretare le immagini

b) L'organizzazione della visione.

Nel campo delle ricerche sulla visione un criterio comunemente accettato è quello di dividere il processo in due fasi: una prima fase chiamata ‛visione base', o early vision, e una seconda, che possiamo chiamare ‛visione avanzata' o ‛comprensione delle scene'. Nella prima fase il sistema risale dalla matrice delle misure fisiche di luminosità, albedo, ecc. all'orientazione, alla distanza e ad altre caratteristiche geometriche dei singoli elementi che costituiscono la scena.

Il risultato di questa prima elaborazione è la cosiddetta ‛immagine intrinseca' che è costituita da un ‛amalgama' delle rappresentazioni così ottenute.

Una buona rappresentazione dell'immagine intrinseca è il cosiddetto ‛schizzo a due dimensioni e mezza' (2.5 D sketch), un'immagine non ancora ‛compresa', ma in cui vengono delineate le caratteristiche fondamentali dell'oggetto.

La seconda fase, che abbiamo chiamato ‛visione avanzata' o ‛comprensione delle scene', comporta la capacità di riconoscere oggetti noti, di descrivere nuovi oggetti, di tracciare traiettorie di movimento in vari ambienti e di guidare la manipolazione. Il paradigma già visto per l'analisi sintattica del linguaggio naturale è applicabile anche nel caso della funzione visiva: si possono cioè analizzare le immagini, nella prima e nella seconda fase, sia in modo bottom-up, sia in modo top-down. Entrambi questi metodi presentano vantaggi e svantaggi; i primi tentativi nel campo della visione furono caratterizzati dall'utilizzo di metodi top-down anche nella prima fase della visione. In questo modo si riusciva a ottenere un'analisi guidata dagli obiettivi, che portava a riconoscere abbastanza facilmente gli oggetti. Si è visto poi che questo tipo di analisi funziona abbastanza bene in un mondo molto limitato, in cui gli oggetti siano costituiti essenzialmente da forme note (blocchi, piramidi, ecc.) e sotto condizioni di illuminazione ben definite.

Tentativi successivi di ampliare l'ambito di applicabilità di queste metodologie portarono a stabilire che le metodologie top-down erano più adatte alla seconda fase della visione, mentre la visione base veniva trattata meglio con metodologie bottom-up (guidate dai dati). Attualmente si tende a partire dai dati e si cerca di ottenere delle descrizioni che possano essere utilizzate nella successiva fase della visione, guidata dall'obiettivo. Le metodologie guidate dai dati agiscono nella prima fase per stabilire obiettivi raggiungibili mediante le metodologie della seconda fase. Il metodo basato sugli obiettivi ha contribuito ad approfondire lo studio di aspetti particolari della visione, quali la stereopsi, la visione di oggetti in movimento, l'analisi di scene generalizzata, ecc.

Resta comunque tuttora aperto il problema di come fare interagire, in generale, i moduli della visione base con quelli a più alto livello e di come questi ultimi debbano guidare l'azione dei primi.

c) Visione base.

Il fine della visione base può essere visto come un problema di ottica inversa: infatti, mentre nell'ottica tradizionale, date le proprietà fisico-geometriche di un oggetto, si cerca di trovare l'immagine che esso genera in determinate condizioni di illuminazione, nel caso della visione si cerca di risalire alle proprietà fisico-geometriche dell'oggetto a partire dalla sua immagine.

Come ogni problema inverso, questo problema porta fatalmente a delle ambiguità le quali sono risolubili se si dispone di una notevole quantità di conoscenza sulle forme degli oggetti e sulle proprietà del mondo fisico (i cosiddetti ‛vincoli naturali'). Data una qualsiasi immagine, esistono diversi procedimenti (la tabella ne elenca i principali) che devono essere applicati per poter ricavare da essa la cosiddetta ‛immagine intrinseca'.

La struttura matematica del problema della visione. - Da un punto di vista matematico i problemi si possono dividere in problemi ben posti e problemi mal posti; un problema è ben posto se la sua soluzione: a) esiste; b) è unica; c) è una funzione continua delle variabili indipendenti (nel senso che a piccole variazioni delle grandezze in ingresso corrispondono piccole variazioni del valore della soluzione).

In generale i problemi della visione sono mal posti, in quanto non soddisfano alle condizioni suesposte. Se tali condizioni fossero soddisfatte, si potrebbe essere sicuri della stabilità numerica della soluzione anche in presenza di rumore; le fonti di rumore possono essere riflessi, zone d'ombra che coprono particolari, ecc.

Un esempio di problema mal posto è il problema della ‛rilevazione dei bordi' (edge detection), che è un problema fondamentale della visione. La tecnica generalmente utilizzata consiste nel misurare le rapide variazioni di intensità luminosa dell'immagine. Evidentemente il passo cruciale è la misura del cosiddetto ‛gradiente' (cioè della variazione di luminosità nei vari punti dell'immagine), che viene calcolata mediante operazioni di differenziazione numerica. Il problema che in tal modo ci si propone di risolvere è mal posto, in quanto non dipende in maniera continua dai dati iniziali.

Altrettanto mal posto, in quanto non ha un'unica soluzione, è il problema della ricostruzione di una superficie, date le coordinate di alcuni dei suoi punti. Un esempio potrebbe essere costituito dal problema della ricostruzione della superficie di una roccia, date le coordinate delle sue punte. Evidentemente esistono infinite superfici, comunque frastagliate, che passano per quei punti; una soluzione praticabile può essere quella di scegliere la superficie che unisce questi punti come li unirebbe una membrana di gomma tesa tra di essi.

Tecniche di regolarizzazione. - Molti problemi mal posti possono essere risolti ricorrendo ai metodi variazionali proposti da Tichonov, che permettono di regolarizzare il problema, cioè di restringere lo spazio delle soluzioni possibili, utilizzando delle specifiche proprietà del problema.

Nel caso della visione, l'obiettivo è quello di minimizzare un'opportuna combinazione di funzioni, la quale contiene la sommatoria di un termine che rappresenta la distanza della soluzione cercata dai dati (i quali contengono in generale del rumore) e di altri termini che misurano la deviazione della soluzione dalle condizioni che vengono ipotizzate. Nel caso della rilevazione dei bordi l'idea è quella di minimizzare il rumore relativo a un dato pixel, utilizzando le informazioni che provengono dai pixels vicini. In questo modo il valore dell'intensità luminosa di ciascun pixel verrà alterato in funzione dei pixels adiacenti, con il risultato che l'immagine finale sarà più pulita, cioè conterrà meno rumore. Con le tecniche di regolarizzazione si possono affrontare diversi problemi della visione base. Nel caso del problema dell'individuazione dei contorni le correzioni all'intensità dei pixels vengono apportate attraverso opportune funzioni chiamate ‛filtri'.

I filtri possono essere, in generale, della più svariata natura: uno, particolarmente importante e che viene utilizzato nel riconoscimento dei contorni, è basato sulla distribuzione, nelle due dimensioni del piano, di una gaussiana che ha il massimo nel pixel in esame. Questa preelaborazione, che viene già da tempo utilizzata, è effettuata, probabilmente, in tutti gli organi visivi dei Vertebrati da cellule ganglionari a ciò deputate.

Quella descritta non è l'unica tecnica impiegata nella visione base: per esempio, per risolvere il problema della stereopsi, che consiste nel trovare la corrispondenza tra gli elementi di due immagini lievemente differenti, si usano tecniche basate su altri principi; altre tecniche invece sono adatte per la determinazione dell'orientazione delle superfici in base alla riflettanza e ai gradienti della cosiddetta ‛tessitura', cioè della struttura della superficie e dell'immagine.

In effetti, siccome ogni passo del processo di visione base dà una certa descrizione dell'immagine, è un problema essenziale quello di combinare tutte queste descrizioni in una immagine coerente. Le varie proprietà fisiche che vengono misurate nei procedimenti di visione base, cioè l'‛albedo' (riflettanza nei vari colori), la distanza della superficie, la sua orientazione, ecc., devono coerentemente rispettare alcuni vincoli imposti dalla fisica della luce.

Uno dei principali obiettivi di questa ricombinazione delle misure è quello di individuare le discontinuità importanti dovute a spigoli, vertici e ad altre caratteristiche fondamentali dell'oggetto. Un approccio che viene tentato attualmente è quello di associare a ogni discontinuità delle proprietà attese, sulla base delle precedenti serie di discontinuità, seguendo un procedimento analogo al metodo delle catene di Markov. In questo modo si ottengono i cosiddetti Markov random fields, che permettono di ricavare da serie di discontinuità, e quindi di caratteristiche, quella più probabile, in base a serie di discontinuità precedentemente trovate.

Un altro approccio seguito consiste nell'utilizzare l'informazione numerica per passare a un'informazione simbolica e integrarla secondo la cosiddetta ‛regola di buon completamento', che probabilmente l'uomo stesso utilizza quando ricostruisce la forma di oggetti parzialmente occultati da altri. Per esempio, in riferimento alla fig. 18, la regola di buon completamento suggerisce che il tavolo, su cui il libro è appoggiato, abbia un bordo che continua dritto, mentre scarta o dà comunque attendibilità molto bassa ad altri tipi di continuazione, quale quello presentato nella fig. 18B. Evidentemente anche per applicare questa regola è necessaria una conoscenza del mondo piuttosto vasta e profonda.

d) Riconoscimento delle scene.

Una volta ottenuta la suddivisione dell'immagine in regioni ben delimitate ed etichettate, sorge il problema di riconoscere gli oggetti della scena, di descriverli, e di descrivere le relazioni che intercorrono tra di essi. Questo processo di riconoscimento, che appartiene al secondo stadio della visione, costituisce un problema ancora aperto, nel senso che non esiste un comune accordo sul fatto che esso consista almeno degli elementi illustrati nella fig. 19.

Rappresentazione delle forme. - Un sistema destinato al riconoscimento di oggetti deve, evidentemente, contenere un catalogo di descrizioni di oggetti con le quali confrontare quelle degli oggetti da individuare. Sorge allora il problema di come rappresentare gli oggetti in modo da ottenerne descrizioni indipendenti dalla scala, dalla posizione, dal grado di risoluzione e da altri parametri contingenti e inessenziali, e in modo che a oggetti simili corrispondano descrizioni simili.

Finora non è stato trovato un criterio di rappresentazione applicabile a tutti gli oggetti e in tutte le situazioni: a seconda degli scopi prefissi, che vengono stabiliti a un livello superiore, si ricorre a un particolare tipo di rappresentazione.

Un modo per rappresentare gli oggetti consiste nel descriverli in termini di cilindri ‛generalizzati' (cioè non necessariamente circolari, retti e a generatrici parallele): ogni oggetto viene scomposto in segmenti ‛cilindrici' (v. fig. 20), considerati alla stregua di elementi ‛primitivi' o ‛costitutivi' della forma complessiva. La situazione, a questo punto, diventa abbastanza analoga a quella del riconoscimento degli enunciati attraverso l'analisi sintattica. Come abbiamo visto, infatti, una volta rappresentato il significato delle singole parole e la struttura che le organizza, si può calcolare il significato dell'intero enunciato. Analogamente, descrivendo le caratteristiche di ciascun cilindro generalizzato elementare, e i suoi rapporti con gli altri, si ha una descrizione della figura, che a questo punto può essere immagazzinata e usata per un ulteriore riconoscimento. Il problema però è che questi cosiddetti ‛archetipi' memorizzati non corrispondono esattamente alla descrizione che di ogni dato oggetto reale si può dare in termini di cilindri generalizzati: si tratta quindi di risolvere un problema di ‛corrispondenza' e di ‛somiglianza' (più che di ‛uguaglianza'). Questo problema può essere reso difficile dal fatto che l'oggetto da individuare può essere descritto a un grado di risoluzione differente da quello al quale è stato memorizzato; inoltre l'oggetto da riconoscere può essere parzialmente occultato da altri oggetti.

Evidentemente, se di ogni oggetto da riconoscere si dovesse previamente memorizzare la descrizione, si andrebbe incontro a difficoltà insormontabili, in quanto il numero di oggetti possibili è sicuramente enorme e probabilmente infinito. Si deve quindi utilizzare una metodologia più potente di quella basata sul semplice ‛confronto-e-riconoscimento'.

Una metodologia particolarmente efficiente sotto questo aspetto è quella basata sul cosiddetto ‛albero di discriminazione': strutturando gerarchicamente le possibili caratteristiche di un oggetto in un albero, a partire dalle più generali, in modo che superare un nodo equivalga a scegliere fra diverse alternative, si ottiene alla fine del ‛percorso' la definizione dell'oggetto.

Finora abbiamo supposto che il riconoscimento riguardasse un singolo oggetto. Nel caso che la scena contenga più oggetti, sorge un problema preliminare rispetto a quello del riconoscimento, cioè il problema, estremamente complesso, della segmentazione. Questa consiste nell'individuare ed estrarre dalla scena tutti gli oggetti che la compongono, inclusi quelli che sono parzialmente coperti da altri. La segmentazione deve evidentemente essere eseguita correttamente, altrimenti il problema del confronto con le descrizioni contenute in un catalogo, specie se vasto, può risultare irresolubile.

e) Architetture parallele.

I processi di visione base consistono essenzialmente di ripetizioni, sui molti punti che costituiscono l'immagine, di semplici operazioni. Anche la stessa applicazione di filtri può essere considerata un'operazione molto semplice. Fare queste operazioni una dopo l'altra, cioè in maniera seriale, su tutti i punti dell'immagine può essere un processo molto lungo. Per ovviare a questo inconveniente si stanno realizzando macchine costituite da migliaia di semplici unità di calcolo collegate ciascuna con le sue vicine e capaci di effettuare un'elaborazione parallela dell'immagine. D'altra parte i procedimenti di comprensione dell'immagine richiedono la cooperazione di unità di calcolo non necessariamente vicine; queste macchine quindi devono anche essere capaci di effettuare dei collegamenti virtuali tra unità che non sono prossime tra loro. Una macchina di questo tipo (illustrata nella fig. 21 e chiamata connection machine) permette i collegamenti vicini per la visione base e i collegamenti virtuali tra elementi non vicini per procedimenti di visione ad alto livello. Questa macchina, che contiene 64.000 semplici unità di calcolo, dà effettivamente l'idea dei requisiti essenziali di macchine parallele che riescano a soddisfare le necessità di calcolo associate alla visione (v. informatica: Supercalcolatori, suppl.).

Bibliografia.

Ballard, D. H., Brown, C., Computer vision, Englewood Cliffs, N. J., 1982.

Barrow, H. G., Tenenbaum, J. M., Computational vision, in ‟IEEE. Proceedings", 1981, LXIX, 5, pp. 527-595.

Berwick, R. C., Weinberg, A., The grammatical basis of linguistic performance, Cambridge, Mass., 1983.

Brady, J. M., Hollerbach, J. M., Johnson, T. L., Lozano-Perez, T., Mason, M. T., Robot motion: planning and control, Cambridge, Mass., 1982.

Brooks, R. A., Symbolic reasoning among 3-D models and 2-D images, in ‟Artificial intelligence", 1981, XVII, pp. 285-348.

Charniak, E., McDermott, D., Artificial intelligence, Reading, Mass., 1984.

Chomsky, N., Lectures on government and binding, Dordrecht 1981.

Duda, R. O., Hart, P. E., Pattern recognition and scene analysis, New York 1973.

Geman, S., Geman, D., Stochastic relaxation, Gibbs distributions, and the Bayesian restoriation of images, in ‟IEEE transactions. Pattern analysis and machine intelligence", 1984, VI, pp. 721-741.

Grimson, W. E. L., From images to surfaces, Cambridge, Mass., 1981.

Hillis, D., The connection machine, Cambridge, Mass., 1985.

Horn, B. K. P., Robot vision, Cambridge, Mass. - New York 1986.

Lenat, D. B., Computer software for intelligent systems, in ‟Scientific American",s ettembre 1984, pp. 152-160.

Marr, D., Vision, San Francisco 1982.

Minsky, M., The society of mind, New York 1986.

Mitchell, T. M., Generalization as search, in ‟Artificial intelligence", 1982, XVIII, pp. 203-226.

Poggio, T., Torre, V., Koch, Ch., Computational vision and regularization theory, in ‟Nature", 1985, CCCXVII, pp. 314-319.

Robinson, J. A., The generalized resolution principle, in Machine intelligence, vol. III (a cura di D. Michie), New York 1968.

Simon, H. A., The sciences of the artificial, Cambridge, Mass., 1969.

Winston, P. H., Artificial intelligence, Reading, Mass., 1984.

Winston, P. H., Horn, B. K. P., LISP, Reading, Mass., 1981.