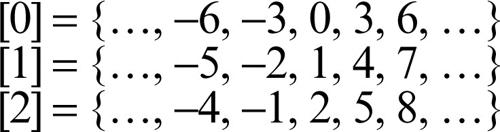Zn, insieme delle classi resto modulo n

Zn, insieme delle classi resto modulo n

Z_n, insieme delle classi resto modulo n in algebra, → insieme quoziente dell’insieme Z dei numeri interi rispetto alla relazione di congruenza, definita da a ≡ b (modn)(si legge «a congruo b modulo n») se e solo se n divide a − b, dove n è un intero maggiore di 1. Per indicare una classe di congruenza, è sufficiente indicare un suo rappresentante m: esso determinerà univocamente tutti gli altri elementi appartenenti alla sua classe; ci si riferisce pertanto alla classe di un intero m semplicemente scrivendo [m]. Per esempio, se n = 3, si hanno allora le tre classi

Convenzionalmente, si sceglie come rappresentante canonico della classe il minimo intero non negativo appartenente a essa. Per stabilire a quale classe appartenga un dato intero, basta dividerlo per n: il resto di tale divisione sarà il rappresentante canonico della classe di m. In questo modo, è possibile stabilire una corrispondenza biunivoca tra l’insieme Z_n delle classi di congruenza modulo n e i numeri naturali minori di n:

Le operazioni di addizione e moltiplicazione definite in Z passano al quoziente, vale a dire esse sono ereditate in modo naturale dall’insieme quoziente Z_n: se a e b sono due interi, si pone

Tali operazioni sono ben definite, nel senso che esse non dipendono dalla scelta del rappresentante della classe ed ereditano molte delle proprietà che soddisfano in Z le operazioni di addizione e moltiplicazione: più precisamente, esse determinano su Z_n la struttura di → anello commutativo unitario, con elementi neutri rispetto all’addizione e alla moltiplicazione, rispettivamente le classi [0] e [1], che con un piccolo abuso si indicano anche semplicemente con i simboli 0 e 1.

Da un punto di vista più astratto, Z_n, dotato della struttura di anello sopra definita, coincide con l’anello quoziente di Z rispetto all’ideale principale (n) generato dall’intero n. Per questo spesso si usa anche scrivere Z/(n) invece di Z_n.

A differenza di Z, non necessariamente l’anello Z_n è integro, vale a dire privo di divisori dello zero: per esempio, se n = 6, allora [2] ⋅ [3] = [6] = 0. Più precisamente, Z_n possiede divisori dello zero se e solo se n è un numero composto, mentre invece è un campo se e solo se n è un numero primo. I campi della forma Z_p, con p primo, sono particolarmente importanti perché a partire da essi è possibile costruire ogni altro campo finito (→ Galois, campo di).