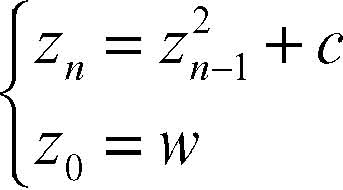Julia, insieme di
Julia, insieme di
Julia, insieme di oggetto della geometria frattale definito nel modo che segue. Fissato il valore c di un parametro complesso, sia w un punto del piano complesso, a partire dal quale si costruisce la successione ricorsiva:
L’insieme di Julia, relativo al punto c, è l’insieme di tutti i punti w per i quali zn non tende all’infinito. Al variare del parametro complesso c si hanno tutti i diversi insiemi di Julia. Il complementare di un insieme di Julia in campo complesso è detto polvere di Fatou. Gli insiemi di Julia possono risultare connessi o non connessi. L’insieme dei punti c del piano complesso che corrispondono a insiemi di Julia connessi è detto insieme di Mandelbrot. Se c non appartiene a tale insieme, il corrispondente insieme di Julia è omeomorfo alla polvere di Cantor.