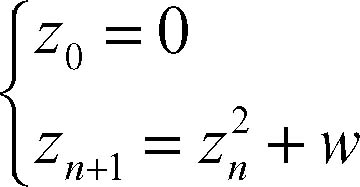Mandelbrot, insieme di
Mandelbrot, insieme di
Mandelbrot, insieme di oggetto frattale, costituito dall’insieme dei numeri complessi w (rappresentabile nel piano di → Argand-Gauss) per i quali non è divergente la successione
Al variare di w si possono infatti presentare le due seguenti situazioni:
• i punti della successione z1, z2, ... rimangono tutti in un intorno dell’origine;
• i punti della successione z1, z2, ... si allontanano definitivamente dall’origine e tendono all’infinito.
I punti liberi, cioè quelli che si allontanano verso l’infinito, formano l’insieme dei punti di fuga, gli altri formano l’insieme prigioniero o prigione. La forma della prigione dipende dalla scelta di w. L’insieme di fuga e l’insieme prigione sono separati da una frontiera detta insieme di → Julia. Sono punti di fuga quelli che si trovano a una distanza maggiore o uguale a 2 dall’origine; sono punti prigionieri quelli che si trovano a una distanza minore di 2 dall’origine. L’insieme di Mandelbrot è costituito dai punti w per i quali si ottengono insiemi di Julia connessi. Tale insieme permette pertanto di indicizzare gli insiemi di Julia. A ogni punto w del piano complesso corrisponde un diverso insieme di Julia che risulta connesso se w appartiene all’insieme di Mandelbrot, non connesso se non vi appartiene.