insieme
insieme
Collettività alla base della matematica d'oggi
Una foresta è un insieme di alberi; la folla sugli spalti di uno stadio è un insieme di persone; un gregge o una mandria sono insiemi di animali. Ecco alcuni termini (fra i molti esistenti) che si riferiscono a collettività, non a oggetti singoli. Usare parole che indicano un insieme è naturale e intuitivo. Raggruppare molti elementi sotto un unico concetto è tipico del modo di pensare dell'uomo, è un fatto elementare, che ognuno utilizza, ma, come spesso accade, sono proprio le idee elementari quelle più importanti. E così oggi il concetto di insieme è alla base di tutta la matematica che in ogni sua parte utilizza il linguaggio degli insiemi. Grazie a oggetti così primitivi, infatti, si fanno operazioni e si organizzano ragionamenti
Una prima descrizione
Il sostantivo insieme è utilizzato in matematica per indicare collettivamente oggetti di qualsiasi natura e quindi non soltanto i numeri o le figure di cui tradizionalmente si occupa tale scienza. Ogni insieme è caratterizzato dagli elementi che gli appartengono. Così si può considerare l'insieme delle vocali dell'alfabeto italiano e indicarlo con una lettera, per esempio V. I suoi elementi si elencano, racchiusi da parentesi graffe, in questo modo: V={a, e, i, o, u}. Quindi l'insieme è definito attraverso l'elenco dei suoi elementi. Per indicare che un oggetto è un elemento di un insieme si utilizza il simbolo ∈, che significa "appartiene". Per indicare, per esempio, che la vocale u appartiene all'insieme V si scrive: u∈V (si legge "u appartiene a V" oppure "u è elemento di V"). Un secondo modo di definire un insieme è quello di indicare la proprietà caratteristica dei suoi elementi. Possiamo per esempio scrivere gli insiemi delle vocali, dei numeri pari, dei dieci comandamenti in questa forma: V={vocali}; P={numeri pari}; D={dieci comandamenti}.
Gli insiemi vanno definiti con precisione perché deve risultare certo se un elemento vi appartiene oppure no. Una definizione quale S={persone simpatiche} non può essere accettata perché l'appartenenza a tale insieme dipende da un'opinione soggettiva.
Rappresentare un insieme con i diagrammi di Eulero-Venn
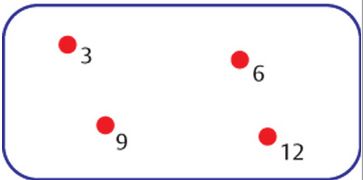
Talvolta un insieme è rappresentato attraverso un disegno, chiamato diagramma di Eulero-Venn, dal nome dei matematici che ne diffusero l'uso. In un diagramma di Eulero-Venn gli elementi sono rappresentati come punti all'interno di una linea chiusa. Possiamo per esempio così rappresentare l'insieme M={multipli di 3 minori di 15} (v. fig.).
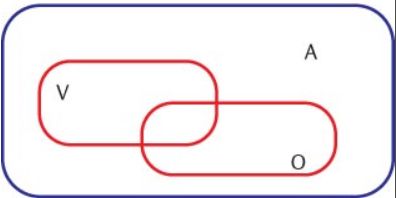
Gli insiemi sono utilizzati per classificare e spesso perciò è utile rappresentare più insiemi nello stesso diagramma. Per esempio nell'insieme A degli animali possiamo considerare l'insieme V dei vertebrati e quello O degli onnivori (v. fig.).
L'insieme V è un insieme contenuto nell'insieme A perché ogni vertebrato è anche un animale. Si dice in tale caso che V è sottoinsieme di A e si scrive: V⊆A.
Con i diagrammi di Eulero-Venn è possibile descrivere relazioni logiche. Per esempio se U={uomini}, M={mortali} la proposizione "tutti gli uomini sono mortali" è rappresentata dal diagramma mostrato che rende chiaro che non tutti i mortali sono uomini (v. fig.).
L'insieme di tutti i mortali che non sono uomini è chiamato insieme complementare di U rispetto a M e comprende, per esempio, animali e vegetali. In questo modo anche la negazione di una frase ‒ una tipica trasformazione di tipo logico ‒ è espressa attraverso una rappresentazione insiemistica.
Tra gli insiemi va considerato anche l'insieme vuoto, definito come l'insieme che non ha elementi ed è indicato con il simbolo Ø. L'insieme vuoto va considerato come il sottoinsieme minimo di ogni insieme. Anch'esso può essere definito attraverso una proprietà; basta ricorrere a una proprietà assurda, che cioè non può mai essere verificata, come nei seguenti casi: Ø={persone ancora in vita nate nel 19° secolo}={numeri positivi minori di 0}.
Operazioni tra insiemi
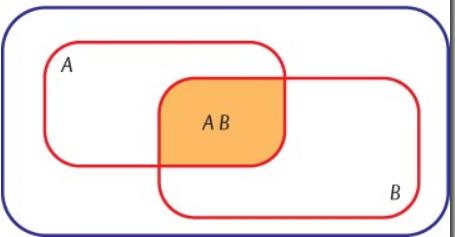
A partire da due o più insiemi è possibile formare altri insiemi. Possiamo per esempio considerare l'intersezione di due insiemi A e B, cioè l'insieme formato dagli elementi che appartengono sia ad A sia a B e che si indica con A ⋂B.
In un diagramma di Venn l'insieme intersezione è rappresentato dalla regione comune agli insiemi, rappresentata in colore (v. fig.).
Per esempio, se S={a, b, c, d, e, f} e V={vocali}, allora S ⋂V={a, e}.
Da un punto di vista logico l'intersezione di due insiemi corrisponde all'insieme formato dagli elementi che verificano le proprietà di entrambi gli insiemi: è cioè definito dalla congiunzione delle due proprietà attraverso la particella e. Per esempio, dati i due insiemi A={multipli di 3} e B={multipli di 5}, si ottiene A ⋂ B={multipli di 3 e di 5}. Si può anche scrivere A ⋂ B={multipli di 15}.
È possibile che due insiemi non abbiano alcun elemento in comune. In tale caso la loro intersezione è l'insieme vuoto: due insiemi con intersezione vuota si dicono disgiunti. Per esempio P={numeri pari} e D={numeri dispari} sono insiemi disgiunti (P ⋂ D=Ø) poiché i numeri sono o pari o dispari.
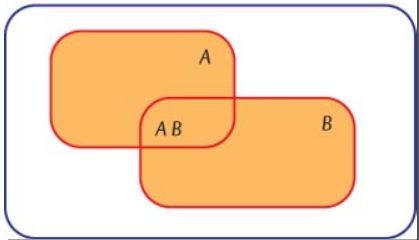
Oltre all'intersezione si definisce un'altra operazione tra insiemi, l'unione. Si dice insieme unione di due insiemi A e B quello formato dagli elementi che appartengono ad A, a B, oppure a entrambi. L'unione si indica con A ⋃ B. In un diagramma di Venn l'insieme unione è rappresentato dalla regione comune agli insiemi, qui in colore (v. fig.). Per esempio, se S={a, b, c, d, e, f} e V={vocali}, allora S ⋃V={a, b, c, d, e, f, i, o, u}.
Da un punto di vista logico l'intersezione di due insiemi corrisponde all'insieme formato dagli elementi che verificano le proprietà di uno oppure dell'altro degli insiemi: è cioè definito dalla disgiunzione delle due proprietà attraverso la particella o come in questo esempio: S={prime sei lettere dell'alfabeto}, V={vocali} e S ⋃V={prime sei lettere dell'alfabeto o vocali}.
Alla base della matematica
Attualmente tutta la matematica si basa sugli insiemi e ne utilizza il linguaggio. Si parla così di insiemi numerici (quali l'insieme dei numeri naturali, indicato con N, formato dai numeri che servono per contare, l'insieme dei numeri interi relativi Z, formato dai numeri interi positivi e negativi e dallo zero, e altri ancora (numero). Anche il piano e lo spazio sono insiemi di punti e, per esempio, le rette sono sottoinsiemi del piano. Negli insiemi sono poi definiti operazioni, relazioni o altri legami tra gli elementi e così si formano i diversi ambienti, le diverse teorie che costituiscono la matematica.
Venn ed Eulero
John Venn, matematico inglese vissuto tra Ottocento e Novecento, utilizzò i diagrammi per illustrare le diverse combinazioni logiche che si ottengono considerando proposizioni tra di loro connesse dalla congiunzione "e", dalla disgiunzione "o", dall'implicazione "se… allora", oppure negate con "non". Egli diffuse, più che inventare, l'uso di tali diagrammi che già erano stati utilizzati varie volte in precedenza, per esempio dal filosofo e matematico Leibniz e da Eulero.
Proprio Eulero, uno dei più versatili matematici di tutti i tempi, aveva utilizzato i diagrammi per spiegare le relazioni logiche alla principessa di Anhalt-Dessau, nipote del re di Prussia, della quale era precettore in matematica, fisica e filosofia.
Il paradosso del barbiere
Agli inizi del 20° secolo il matematico e filosofo Bertrand Russell ha messo in crisi la teoria degli insiemi, sulla quale si stava costruendo l'edificio della matematica. Egli infatti vi ha trovato una contraddizione poi illustrata con il cosiddetto paradosso del barbiere. In un villaggio c'è un barbiere che rade tutti gli uomini che non si radono da soli, e soltanto loro. Problema: il barbiere rade sé stesso?
Dividiamo tutti gli uomini del villaggio in due insiemi disgiunti: A={uomini che si radono da soli}, B={uomini che si fanno radere dal barbiere}. Chiamiamo b il barbiere. Se b∈A, se cioè il barbiere rade sé stesso, allora egli si fa radere dal barbiere, e quindi b∉A; se viceversa, b∈B cioè il barbiere si fa radere dal barbiere, allora egli si rade da solo e quindi b∉B.
Il paradosso di Russell ha portato a una crisi dei fondamenti della matematica e da questa crisi sono scaturite ricerche e definizioni più approfondite sul piano logico.