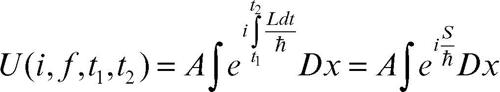cammino, integrale di
cammino, integrale di
cammino, integrale di nella meccanica quantistica, formulazione della dinamica dovuta al fisico statunitense Richard P. Feynman (New York 1918 - Los Angeles 1988); è anche detto integrale sui cammini o integrale di Feynman. Nella meccanica analitica classica, si definisce traiettoria di un sistema fisico la sua evoluzione nel tempo attraverso lo spazio delle fasi, ovvero lo spazio di tutte le possibili configurazioni del sistema. Per esempio, lo spazio delle fasi di un punto materiale è lo spazio 6-dimensionale delle tre coordinate spaziali e delle tre coordinate di velocità. Viene inoltre definita l’azione, una quantità scalare che ha le dimensioni di un’energia per un tempo, come funzionale della traiettoria:
dove C è la traiettoria nello spazio delle fasi e L è la lagrangiana del sistema fisico. Tra tutte le possibili traiettorie, quella effettivamente seguita dal sistema è quella tale da rendere stazionario il funzionale dell’azione. Nella meccanica quantistica, come affermato dal principio di indeterminazione di Heisenberg, non è possibile conoscere contemporaneamente la posizione e la velocità di una particella e pertanto non ha senso parlare di traiettoria nel senso classico. Lo stato del sistema viene allora definito mediante un vettore appartenente a un opportuno spazio di Hilbert. Questo vettore viene rappresentato nello spazio delle coordinate mediante una funzione a valori complessi, detta funzione d’onda, il cui modulo quadro rappresenta la densità di probabilità di trovare il sistema in una data configurazione spaziale. Si definisce inoltre ampiezza di transizione tra due stati una quantità complessa il cui modulo al quadrato rappresenta la probabilità di osservare una transizione del sistema tra i due stati. Nella formulazione dell’integrale di cammino, l’evoluzione di un sistema da uno stato all’altro è data dalla sovrapposizione di tutti gli infiniti possibili cammini tra i due stati. L’ampiezza di transizione da uno stato i a un tempo t1 a uno stato ƒ a un tempo t2 è data da
dove ħ è la costante di Planck divisa per 2π, A è una costante di normalizzazione e il simbolo Dx indica l’integrazione su tutti i possibili cammini. Se si fa tendere ħ a 0 (limite classico), i contributi di tutti i cammini lontani da quello classico si annullano reciprocamente e gli unici contributi significativi vengono dai cammini prossimi a quello classico. Questa formulazione della dinamica quantistica, che si dimostra essere equivalente a quella di Schrödinger, è molto laboriosa dal punto di vista del calcolo e non è particolarmente utile nei sistemi non relativistici; essa trova invece largo impiego nella teoria quantistica dei campi.