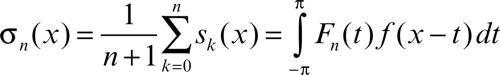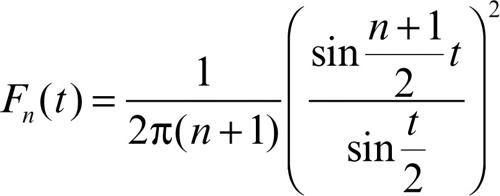Fejer, integrale di

Enciclopedia della Matematica (2017)

Fejer, integrale di


Fejér, integrale di particolare integrale che compare nello studio delle serie di → Fourier. Se infatti si studia la convergenza secondo Cesàro (→ sommazione, metodi di) di una serie di Fourier associata a una funzione ƒ, ci si imbatte nell’espressione della media a σn(x) delle somme parziali sk(x), data da

Enciclopedia della Matematica formula lettf 00480 001.jpg

Per tale media delle somme parziali, Fejér ha stabilito la relazione (teorema di Fejér):

Enciclopedia della Matematica formula lettf 00480 002.jpg

dove

Enciclopedia della Matematica formula lettf 00480 003.jpg

è il cosiddetto nucleo di Fejér. Si dimostra che se ƒ(x) è continua, la successione {σn(x)} converge uniformemente a ƒ(x) in R, mentre se ƒ ammette un salto in esso non si verifica il fenomeno di → Gibbs.

Vedi anche
anàlisi infinitesimale (o càlcolo) Parte della matematica (detta anche semplicemente analisi matematica) i cui metodi e sviluppi sono fondati sull'operazione di passaggio al limite. Suoi iniziatori sono considerati nel 17° sec. I. Newton e G.W. Leibniz, tuttavia ha avuto il suo sviluppo solo in seguito alla definizione rigorosa ... applicazione Matematica Il concetto di a. è una generalizzazione del concetto classico di funzione (➔ corrispondenza). Si parla di a. di un insieme P in un insieme Q, quando tra i due si stabilisce una corrispondenza del tipo seguente: a ogni elemento di P corrisponde un ben determinato elemento di Q, mentre un elemento ... distribuzione involutiva In matematica una distribuzione p-dimensionale ϑ su una varietà differenziale si dice distribuzione involutiva se, considerati due qualsiasi campi di vettori X, Y appartenenti a ϑ (ossia appartenenti agli spazi che costituiscono ϑ), anche il loro commutatore [X,Y] appartiene alla distribuzione. L’importanza ... Ulisse Dini Matematico italiano (Pisa 1845 - ivi 1918). Alunno della Scuola normale superiore di Pisa (1860-64), vi ebbe maestri O. Mossotti ed E. Betti. Prof. prima di geodesia e poi di analisi nell'univ. di Pisa (1865-1917) e direttore della Scuola normale (1874-76 e 1900-18). Socio nazionale dei Lincei (1882) ...
Tag
Vocabolario
integrale
integrale agg. e s. m. [dal lat. tardo integralis, der. di intĕger «integro, intero»]. – 1. agg., non com. Di elemento che fa parte di un tutto, che concorre alla costituzione di un intero (sinon. quindi di integrante): i corpi i. del mondo...
integralista
integralista agg. e s. m. e f. [der. di integrale] (pl. m. -i). – 1. agg. Relativo all’integralismo, ispirato all’integralismo, nelle due diverse accezioni del termine: il movimento i. del partito socialista italiano; la posizione i. della...