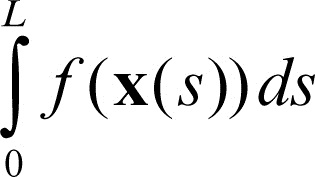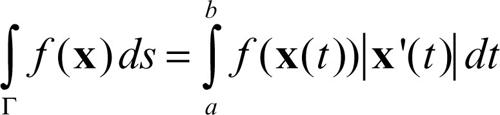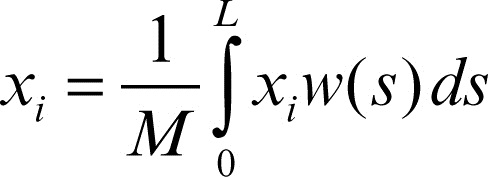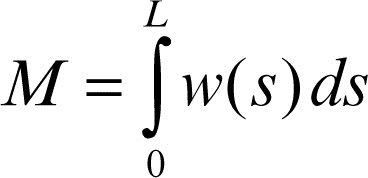integrale di linea
integrale di linea
integrale di linea integrale il cui insieme di definizione è una linea Γ che si può in prima istanza supporre regolare (→ curva). Vi sono due tipi di integrali di linea: a) gli integrali nell’ascissa curvilinea; b) quelli di forme differenziali lineari.
Nel caso a), l’integrale di una funzione ƒ(x) continua per x ∈ Γ, dove Γ è una linea regolare definita dalle equazioni parametriche x = x(s) nell’ascissa curvilinea s, s ∈ [0, L], è definito, in modo del tutto analogo a un → integrale definito in una variabile, come il limite di somme integrali del tipo
dove {si} è una partizione dell’intervallo [0, L], xi sono punti scelti ad arbitrio negli archi definiti da si−1 ≤ s ≤ si e δ la massima lunghezza di tali archi. Si mostra che il limite di tale somma esiste finito; tale limite si designa col simbolo
e si valuta tramite l’integrale definito
Nella pratica, non è necessario conoscere la rappresentazione di Γ mediante l’ascissa curvilinea, perché se x = x(t), t ∈ [a, b], è l’espressione di Γ mediante un generico parametro t, si ha
Questo tipo di integrali (detti anche integrali curvilinei di prima specie) si incontra nel calcolo di grandezze estensive dipendenti da una distribuzione di massa o di carica lungo una linea: per esempio, il baricentro di una linea Γ di densità lineare w(s) ha coordinate
dove
è la massa totale della linea; analogamente il potenziale gravitazionale generato dalla linea in un punto y ∉ Γè dato da
Per il caso b), ossia per gli integrali di linea intesi come integrali di forme differenziali lineari, si veda → forma differenziale.