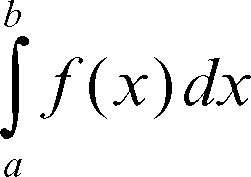Riemann, integrale di

Riemann, integrale di

Riemann, integrale di o integrale di Cauchy-Riemann, generalizzazione della nozione di → integrale definito secondo Cauchy, ottenuta non richiedendo a priori che la funzione integranda debba essere continua, bensì cercando delle condizioni sotto le quali le somme integrali convergano a un determinato limite al tendere a zero della dimensione della griglia che suddivide il trapezoide di cui si ricerca l’area. Le ipotesi sotto le quali una funzione è integrabile secondo Riemann sono date dal criterio di Lebesgue-Vitali, secondo cui condizione necessaria e sufficiente perché una funzione limitata in un intervallo [a, b] sia integrabile è che l’insieme dei suoi punti di discontinuità abbia misura nulla. Per esempio, la funzione di → Dirichlet (che è la funzione caratteristica dell’insieme Q dei numeri razionali) non è integrabile secondo Riemann in [0, 1] perché è discontinua in ogni punto. Si può verificare questo fatto usando la definizione, perché per ogni partizione vi sono sia somme integrali che valgono 0 (se come punti per calcolare ƒ si scelgono i punti ξ_k tutti irrazionali), sia somme che valgono 1 (se gli ξ_k sono tutti razionali).

Una ipotesi sufficiente è invece che la funzione sia monotòna in [a, b] o sia a variazione limitata e quindi differenza di funzioni monotone. Spesso, data una funzione reale ƒ(x) in un intervallo [a, b], per definire

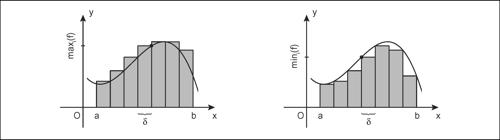
integrale definito di ƒ(x), si considera una suddivisione dell’intervallo [a, b] in sottointervalli [x_i−1, x_i] di ampiezza massima δ, con x₀ = a < x₁ < x₂ < ... < x_n = b, e per essa si considerano le somme per eccesso

e quelle per difetto

essendo M_i e m_i gli estremi superiore e inferiore di ƒ(x) in [x_i−1, x_i]. Se per δ → 0 tali somme ammettono lo stesso limite J, la funzione ƒ si dice integrabile. In questo modo si definisce il cosiddetto integrale di Darboux. Gli integrali di Darboux e gli integrali di Riemann sono equivalenti nel senso che se una funzione è integrabile secondo Darboux è anche integrabile secondo Riemann e viceversa; la funzione ƒ si dice integrabile secondo Riemann se esiste finito il seguente limite: