integrale indefinito

integrale indefinito

integrale indefinito di una funzione ƒ(x) è l’insieme di tutte le sue funzioni primitive, cioè di tutte le funzioni la cui derivata coincide con la funzione stessa in tutti i punti dell’intervallo [a, b], e si designa col simbolo

(si legge «integrale di effe di x in di x»). Si può usare anche la notazione più sintetica

che sottolinea il fatto che si tratta di un insieme di funzioni, che non dipende dal simbolo usato per indicare la variabile indipendente. Per il calcolo esplicito delle primitive si utilizzano sostanzialmente due metodi, che riducono l’integrale a casi noti, in particolare a integrali elementari o di funzioni razionali: l’→ integrazione per parti e l’→ integrazione per sostituzione. Si noti che non sempre la primitiva di una funzione elementare è a sua volta elementare: molte delle funzioni speciali sono definite come integrali di funzioni elementari. Si veda per esempio, il teorema di → Liouville sull’integrazione. Il teorema fondamentale del calcolo integrale lega le nozioni di integrale indefinito a quello di → integrale definito, riportando in molti casi il calcolo analitico di un integrale definito a quello di una generica primitiva della funzione integranda, cioè al suo integrale indefinito (→ funzione, primitive di una; → calcolo integrale, teorema fondamentale del).

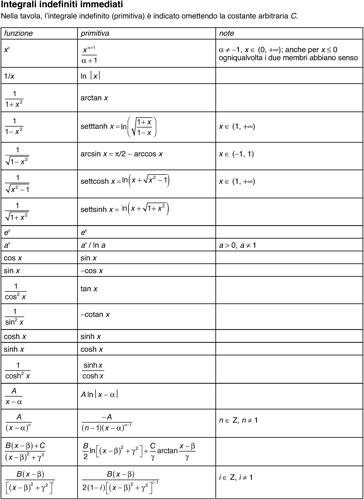
Per gli integrali indefiniti immediati, si veda la relativa tavola.