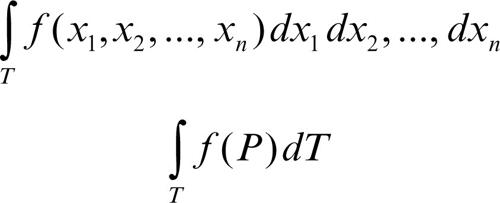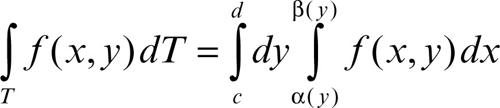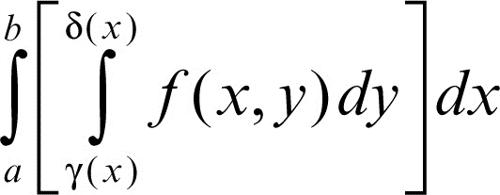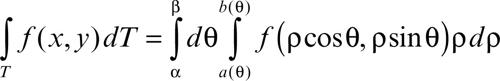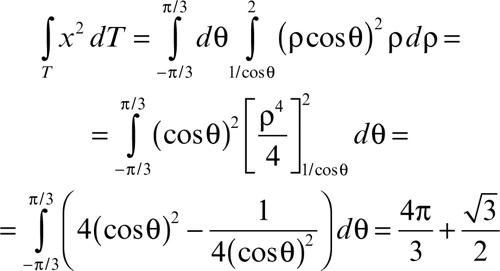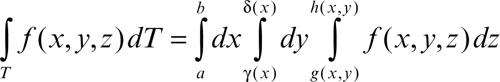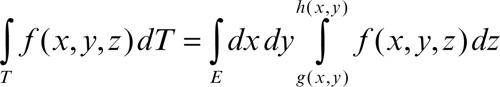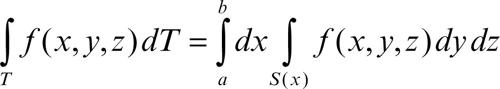integrale multiplo

integrale multiplo

integrale multiplo naturale estensione della nozione di integrale definito al caso di funzioni di più variabili. Facendo riferimento al caso più semplice, quello dell’integrazione secondo Cauchy, si considera una funzione ƒ(P) di n variabili, continua in un compatto T quadrabile di Rⁿ. Eseguita una decomposizione regolare di T,

(sostanzialmente, gli insiemi T_i non devono avere punti interni in comune, ma solo parte delle frontiere) e indicato con δ il massimo diametro degli insiemi T_i, si scelgano ad arbitrio punti P_i ∈ T_i e si costruisca la somma integrale

Per δ → 0 la somma S(δ) tende a un limite finito J, detto integrale n-plo di ƒ su T (in particolare doppio o triplo) e designato con le notazioni

o semplicemente

Soprattutto per gli integrali doppi (relativi al caso bidimensionale) o tripli (tridimensionale) si usano anche rispettivamente le notazioni seguenti:

e

Per contrapposto, nel caso di n = 1 si parla di integrale semplice.

Le proprietà degli integrali multipli sono analoghe a quelle dell’integrale definito, con l’avvertenza che Rⁿ non è ordinato, per cui non esistono estremi di integrazione e l’additività si esprime come

purché m(T₁ ∩ T₂) = 0.

L’integrale doppio ammette un’interpretazione geometrica analoga a quella dell’integrale semplice. Se ƒ è una funzione di due variabili a valori non negativi definita in T, il suo integrale esprime il volume con segno della porzione di spazio costituita da tutti i punti che hanno le prime due coordinate in T e la terza coordinata compresa tra 0 e ƒ(x₁, x₂).

Per il calcolo di un integrale multiplo si ricorre a formule di riduzione, che si fondano su successive integrazioni semplici, a cambiamenti di coordinate, oppure a metodi numerici.

Le formule di riduzione per integrali multipli sono formule che permettono di calcolare un integrale multiplo mediante una sequenza di integrali semplici, nell’ipotesi che il dominio T abbia una forma particolare; a tale ipotesi ci si può sovente ridurre decomponendo il dominio in un numero finito di parti

In particolare, per integrali doppi, se T è x-convesso, cioè se ogni sua intersezione con una parallela all’asse x si riduce a un segmento, e quindi può essere così descritto:

si ha:

mentre se T è y-convesso ed è quindi:

si ha l’analoga forma:

In queste formule si intende che l’integrazione che viene eseguita per prima è quella scritta più a destra, per cui, per esempio, l’ultimo integrale si deve intendere come

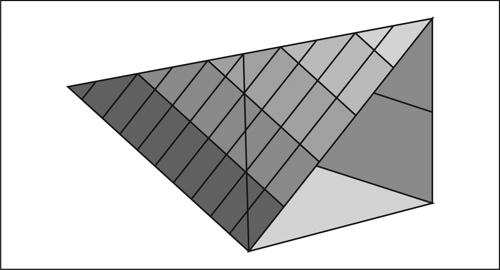
In tal modo l’integrazione nella variabile y produce un risultato dipendente dalla sola variabile x, che compare sia come argomento di ƒ che degli estremi di integrazione γ(x) e δ(x). Tale funzione di x viene quindi integrata tra estremi fissi, producendo così un risultato numerico, indipendente dalle variabili di integrazione (x, y). Per esempio, se T è il triangolo di vertici O(0, 0), A(1, 0), B(0, 2), si ha

(il volume della piramide in figura).

Se T non è convesso rispetto a nessuno dei due assi, è necessario decomporlo in parti che godano di tale proprietà per poter applicare a ciascuna di esse, separatamente, una delle due formule di riduzione.

È anche possibile scrivere una formula di riduzione in coordinate polari, quando T sia esprimibile nella forma T = {(ρ, θ) : α ≤ θ ≤ β, a(θ) ≤ ρ ≤ b(θ)}. Si ha allora:

in cui il fattore supplementare ρ corrisponde al determinante jacobiano (→ matrice jacobiana) della trasformazione tra coordinate cartesiane e polari.

Per esempio, se T è il segmento circolare definito da:

si ha:

In tre variabili (integrale triplo) esistono sei formule di riduzione, per esempio:

È possibile tuttavia eseguire anche delle riduzioni parziali di un integrale triplo, con le formule di integrazione per fili o per strati (detta anche per sezioni). La prima, per fili, esprime un integrale triplo come un integrale doppio il cui argomento è un integrale semplice: per esempio,

essendo E la proiezione di T sul piano Oxy e [g(x, y), h(x, y)] il segmento intersezione di T (supposto z-convesso) con una generica parallela all’asse z.

La formula di integrazione per strati (detta anche per sezioni) è invece

ed esprime l’integrale triplo come un integrale semplice su [a, b] dell’integrale doppio di ƒ esteso alla sezione S(x) di T con un generico piano perpendicolare all’asse x.

Per l’estensione di queste formule all’integrale di → Lebesgue, si veda il teorema di → Fubini.