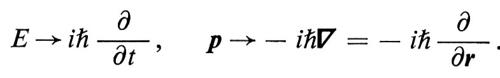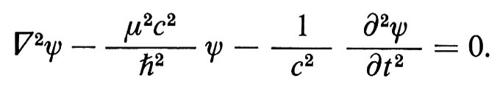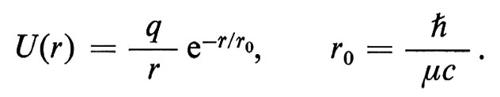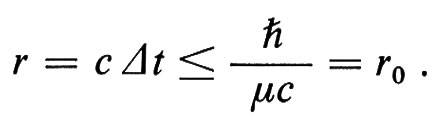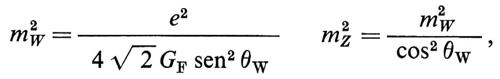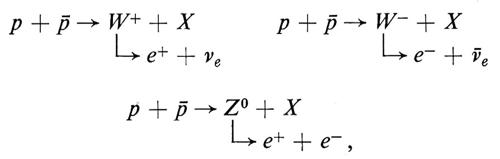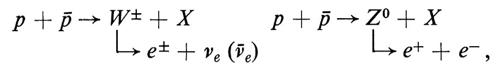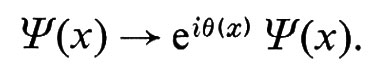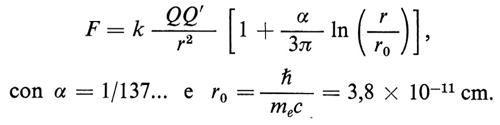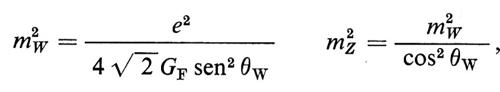Interazioni deboli

Interazioni deboli

sommario: 1. Particelle e forze elementari. 2. Le forze e la meccanica quantistica. 3. Le interazioni deboli. 4. Le correnti neutre. 5. La produzione diretta dei bosoni W e Z. 6. Osservazioni sperimentali. 7. Le interazioni deboli e le teorie di gauge. 8. Questioni aperte. □ Bibliografia.

1. Particelle e forze elementari

Non è troppo difficile immaginare che la materia sia costituita da oggetti puntiformi, le particelle elementari; è invece sorprendente il fatto che a formare l'intero universo, con la sua immensa varietà di forme, concorra un numero estremamente limitato di costituenti: i quarks, a carica frazionaria e colorati, e i leptoni, a carica unitaria o neutri.

A tutt'oggi si conoscono tre famiglie di particelle elementari, ciascuna comprendente due leptoni e due tripletti di quarks di tre colori diversi, con le corrispondenti antiparticelle. La materia ordinaria è dominata dalla prima famiglia e cioè dall'elettrone (e^-), dal neutrino (ν_e) e dai quarks di tipo u e d, a partire dai quali si sono formati il protone e il neutrone. Nei limiti della risoluzione degli esperimenti attuali (dell'ordine di 10^-16 centimetri) quarks e leptoni appaiono senza struttura interna, cioè ‛puntiformi'.

Le particelle elementari interagiscono tra di loro per formare la materia tramite l'azione di ‛campi di forze'. Le forze agiscono a distanze anche molto grandi e si propagano attraverso il vuoto. Assieme alle particelle elementari le forze costituiscono quindi il secondo ingrediente fondamentale dell'universo. È infatti grazie alle forze che le particelle elementari possono formare strutture più complesse: nucleoni, nuclei, atomi, molecole, pianeti, stelle, galassie e così via.

La forza più comunemente sperimentata è la gravità. Abbiamo l'esperienza del peso, poiché i quarks e i leptoni che si trovano nel nostro corpo interagiscono continuamente con i quarks e i leptoni che costituiscono il nostro pianeta. Questa proprietà mette in evidenza il carattere additivo delle forze, cioè il fatto che si possono costruire effetti molto grandi e a grandi distanze partendo da una forza elementare intrinsecamente debole.

Di gran lunga più rilevante nella nostra vita quotidiana è la forza elettrica, caratterizzata nella sua forma più elementare dall'interazione a distanza tra due cariche elettriche, descritta dalla ben nota legge di Coulomb. Sia nel caso delle forze elettriche sia in quello delle forze gravitazionali, per sorgenti di piccole dimensioni, la forza varia come l'inverso del quadrato della distanza. Vi sono però fra i due tipi di forze differenze importanti: la forza elettromagnetica è molto più potente e, a differenza di quella gravitazionale, può essere sia attrattiva che repulsiva (le cariche possono essere positive o negative). In pratica, la forza di gravità emerge nei fenomeni naturali solamente perché la cancellazione tra le cariche all'interno della materia è incredibilmente esatta, cioè Q_elettrone = Q_protone. Ciò nonostante, all'interno della materia il campo elettrico rimane forte a distanze piccole, dell'ordine di quelle interatomiche; a esso sono dovute tutte le proprietà meccaniche e chimico-fisiche della materia.

Sono stati fatti in passato diversi tentativi teorici miranti a una descrizione unificata della gravità e dell'elettromagnetismo, ma, come vedremo, tali tentativi erano destinati a fallire.

Sono stati osservati in natura altri due tipi di forze, che si manifestano esclusivamente a distanze submicroscopiche; è in gran parte per questo motivo che queste due forze, chiamate forza forte e forza debole, sono state studiate in maniera completa solo recentemente. La prima, cioè l'interazione forte, si manifesta quando due quarks si vengono a trovare a una distanza inferiore ai 10^-13 cm circa. A queste distanze gli effetti delle interazioni forti superano largamente quelli dovuti alle cariche elettriche delle particelle elementari. Come già accennato, i quarks esistono in tre stati differenti; questo grado di libertà interno a tre valori, chiamato ‛colore', viene oggi considerato la sorgente delle interazioni forti. L'effetto più vistoso di tale forza è la costruzione dei nuclei a partire dai quarks. L'energia termonucleare, ad esempio, deriva direttamente dall'utilizzazione di tale forza da parte dell'uomo.

L'altro tipo di forza, l'interazione debole, diventa importante quando quarks o leptoni si trovano a distanze ancora più piccole, inferiori ai 10^-16 cm. A tali distanze le forze elettromagnetiche e deboli hanno effetti paragonabili; questo non è casuale: come vedremo, recentemente, grazie soprattutto all'osservazione dei bosoni intermedi, si è riusciti a mettere in evidenza un legame strettissimo tra queste due forze, apparentemente così diverse.

Le interazioni forti e le interazioni deboli (più in generale tutti i campi di forze), oltre che producendo effetti cinematici classici, come ad esempio i ben noti effetti macroscopici dell'elettromagnetismo e della gravità, possono manifestarsi anche come trasformazioni tra particelle. Ad esempio, nel caso delle forze deboli, la radioattività consiste in reazioni in cui un neutrone si trasforma in un protone o viceversa, con l'emissione di una coppia elettrone-(anti)neutrino.

2. Le forze e la meccanica quantistica

Qual è il meccanismo responsabile delle forze? Quello dell'azione a distanza è stato uno dei problemi maggiormente ricorrenti nella storia della scienza. Alla fine del secolo scorso l'azione a distanza degli effetti elettromagnetici fu spiegata come dovuta all'etere, cioè a un mezzo, con proprietà fisiche straordinarie, in cui si supponeva che tutto l'universo fosse immerso. Come è ben noto, questa ipotesi, non priva di contraddizioni, fu confutata dalla famosa esperienza di Michelson, che aprì la strada alla teoria della relatività.

Al giorno d'oggi, per spiegare il meccanismo responsabile delle forze, si ricorre invece alla meccanica quantistica. Secondo la descrizione universalmente accettata, anche effetti macroscopici e a grande distanza sono in realtà una manifestazione di effetti quantici, consistenti nello scambio di quanti ‛virtuali' del campo. Le forze quindi sono una delle manifestazioni più spettacolari della meccanica quantistica nella materia e nel vuoto. Per spiegare meglio come l'azione a distanza di particelle separatamente inosservabili, o ‛virtuali', possa produrre un effetto osservabile, cioè la forza, ricordiamo che secondo la meccanica quantistica esistono limitazioni intrinseche al processo fisico di osservazione. In particolare il principio di indeterminazione di Heisenberg stabilisce una relazione tra le incertezze delle misure dell'energia e del tempo, come pure tra quelle della quantità di moto e della posizione:

ΔE Δt ≥ ℏ/2, Δp Δx ≥ ℏ/2,

dove ℏ = h/2π = 1,054 × 10^-27 erg s è la costante di Planck. La conseguenza più famosa di questa relazione è il fatto che non è possibile, neanche in linea di principio, localizzare esattamente l'orbita degli elettroni attorno all'atomo. È precisamente per questo motivo che i quanti virtuali (continuamente emessi e assorbiti dalle particelle che ne costituiscono le ‛sorgenti') sfuggono alla nostra osservazione.

Nella teoria quantistica dei campi ogni particella è associata a un operatore matematico, il campo quantistico, che è caratterizzato dai numeri quantici che definiscono la particella in questione, quali il momento angolare intrinseco, chiamato spin, la massa, la carica, ecc. Ricordiamo che, mentre nella meccanica classica il momento angolare può assumere qualsiasi valore, nella meccanica quantistica esso può avere solo valori che siano multipli di ℏ/2. Le particelle con spin semintero, cioè ℏ/2, 3ℏ/2, ecc., sono dette ‛fermioni', mentre quelle a spin intero, ℏ, 2ℏ, 3ℏ, ecc., sono dette ‛bosoni'. I fermioni obbediscono al principio di esclusione di Pauli, cioè due fermioni identici non possono occupare lo stesso stato quantico. Questo effetto è simile a una forza repulsiva a causa della quale due fermioni identici, in particolare quindi con spin uguale, non si possono trovare più vicini di una lunghezza d'onda. I bosoni invece possono liberamente addensarsi attorno a qualsiasi punto dello spazio.

Nella versione quantistica dell'elettromagnetismo il campo elettromagnetico è un campo di bosoni caratterizzato dai numeri quantici del fotone, cioè massa nulla, carica zero e spin uguale a un'unità di ℏ. Questo campo quantistico visualizza molto bene il ben noto dualismo fra l'aspetto ondulatorio e quello particellare, esso cioè rappresenta la probabilità di trovare il fotone in un dato punto spaziotemporale, mentre il campo classico misura l'ampiezza d'onda del campo elettromagnetico. Particelle cariche interagiscono quindi tra di loro scambiando fotoni. Nella fig. 2 si mostrano la descrizione classica (fig. 2A) e quella quantistica (fig. 2B) di due cariche puntiformi che interagiscono fra di loro attraverso il campo elettromagnetico. Così come classicamente la carica dell'elettrone è la sorgente del campo di forza coulombiano, da un punto di vista quantistico gli elettroni, e più in generale le particelle cariche, sono le sorgenti dei fotoni virtuali. La descrizione quantistica del campo di forze porta dunque a postulare l'esistenza di particelle: i quanti relativi al campo di forze.

È facile dimostrare che a un tipo di forza con raggio d'azione infinito vanno associati quanti di massa di riposo nulla, mentre quanti di massa non nulla generano forze a raggio d'azione finito. Supponiamo infatti di voler studiare la propagazione di un quanto di massa μ. La relazione relativistica tra l'energia totale E e l'impulso p di una particella libera di massa μ è data da

E² = p²c² + μ²c⁴,

dove c è la velocità della luce. L'equazione differenziale che descrive l'ampiezza d'onda di questa particella libera si ottiene sostituendo alle variabili dinamiche gli operatori quantistici corrispondenti secondo lo schema:

Si ottiene così la cosiddetta equazione d'onda di KleinGordon, che descrive la propagazione di una particella libera di massa μ:

Se ora si pone μ = 0, l'equazione diviene la ben nota equazione delle onde che descrive la propagazione di un'onda elettromagnetica. Nel caso indipendente dal tempo, e in presenza di una particella di carica q all'origine, l'equazione per il potenziale ha la seguente soluzione sfericamente simmetrica nella variabile polare r:

Questo potenziale diminuisce esponenzialmente all'aumentare della distanza e si riduce a zero per r ≫ r₀. Se invece il quanto è di massa nulla, come nel caso dell'elettromagnetismo, r₀ ⇒ ∞ e l'equazione ha come soluzione il campo elettrostatico di Coulomb: U(r) = q/r. Sperimentalmente la massa del fotone può essere determinata in vari modi. Un'indicazione suggestiva e accurata si può ottenere da misure elettrostatiche. Poiché una massa non nulla del fotone cambierebbe la legge di Coulomb, il campo all'interno di una sfera carica risulterebbe diverso da zero. Misure di questo tipo danno un limite superiore per la lunghezza d'onda Compton del fotone, r₀, pari a circa 10 km. Limiti più precisi si ottengono dallo studio a grandi distanze dei campi magnetici dei pianeti, con l'aiuto di sonde spaziali. Ad esempio, nel caso di un fotone di massa diversa da zero, il campo prodotto a una distanza r da un dipolo magnetico m acquisterebbe un termine addizionale di tipo esponenziale alla Yukawa pari a (m • r/r³) (1 + μ_γr)e^-μγr. Rilevazioni spaziali del campo magnetico di Giove permettono di dare a r₀ un limite superiore di circa 300.000 km. Limiti ancora più precisi si ottengono dalla misura del campo magnetico intergalattico, r₀ ≥ 10²² cm. Per capire meglio la relazione tra il raggio d'azione del campo di forze e la massa dei quanti virtuali a esso associati basta ricordare che, a causa del principio di indeterminazione, la creazione ‛spontanea' di una particella o di un quanto di massa μ associato al campo rimarrà irrivelabile almeno per un tempo

Δt ≤ ℏ/μc²,

dove per l'incertezza dell'energia ΔE abbiamo usato l'energia minima di riposo, E = μc². Durante questo intervallo temporale il quanto creato potrà propagarsi al massimo con la velocità della luce c e quindi a una distanza

Quindi più alta è la massa del quanto, più piccolo sarà r₀ e più breve sarà il raggio d'azione delle forze.

L'idea di un quanto elementare di massa non nulla fu introdotta nel 1935 dal fisico giapponese H. Yukawa per spiegare le forze tra il protone e il neutrone. Questo modello si basava su una generalizzazione del concetto di fotone in elettrodinamica quantistica e descriveva in modo fenomenologico le forze nucleari come dovute allo scambio di mesoni π fra i nucleoni. Poiché le forze nucleari agiscono solo su distanze assai brevi, era necessario introdurre una forza che diminuisse rapidamente a distanze grandi rispetto alle dimensioni nucleari. A questo scopo Yukawa assegnò al quanto propagatore delle forze nucleari una massa pari a circa 1/10 di quella del protone. Notiamo che gli esperimenti di questi ultimi anni ad altissime energie hanno dimostrato che sia i nucleoni sia i pioni sono di fatto formati da quarks e che le interazioni tra quarks sono mediate da quanti di massa nulla colorati, chiamati gluoni. Quindi l'ipotesi di Yukawa ha soprattutto un interesse storico. Tuttavia le considerazioni presentate sopra sono importanti per cercare di capire il ruolo delle masse dei bosoni intermedi nelle interazioni deboli.

3. Le interazioni deboli

La preistoria delle interazioni deboli è cominciata nel pomeriggio di domenica 1 marzo 1896, quando il fisico francese H. Becquerel scoprì che i sali di uranio emettevano una radiazione penetrante simile ai raggi X scoperti poco tempo prima dal fisico tedesco W. C. Röntgen. Questo nuovo fenomeno, a cui M. Curie diede il nome di radioattività, condusse più tardi ad abbandonare l'ipotesi dell'immutabilità dell'atomo. Per questo ci vollero però parecchi anni, dato che ben poco si sapeva sulla struttura atomica al momento della scoperta di Becquerel. I passi cruciali che portarono all'interpretazione esatta della radioattività e alla nascita delle interazioni deboli sono richiamati nella tab. I.

Il fisico svedese O. Klein fu il primo a suggerire che le interazioni deboli fossero mediate da campi carichi di massa non nulla e spin di valore unitario, quando nel 1938 fece uso dell'idea di Yukawa per costruire una forza a corto raggio d'azione. La proposta di Klein tuttavia va oltre il modello di Yukawa e stabilisce una connessione molto stretta fra l'elettromagnetismo e le interazioni deboli. Anche se all'epoca la teoria di Klein poteva apparire lontana dalla realtà, sappiamo oggi che essa rappresentava una visione premonitrice della moderna teoria delle interazioni deboli sviluppata da Glashow, Weinberg e Salam (nota come ‛modello standard'). Vale la pena di citare testualmente le parole di Klein sull'argomento: ‟Essendo il ruolo e le proprietà di queste particelle assai simili a quelli dei fotoni, potremmo chiamarle elettrofotoni (cioè fotoni carichi elettricamente)".

Nella notazione corrente queste particelle sono denominate W⁺ e W^-, anche se il nome suggerito da Klein sarebbe assai più pertinente. Si noti che le particelle di Klein erano simili al fotone, anche perché il valore del loro momento angolare era identico a quello del fotone. Esse erano cioè bosoni ‛vettoriali'.

Gli effetti delle interazioni deboli sono stati osservati da tempo sotto forma di reazioni di trasformazione spontanee all'interno dei nuclei. Tutte queste trasformazioni appaiono collegate a una coppia di reazioni elementari, che trasformano un protone in un neutrone e viceversa:

n ⇒ p + e^- + ν̄_e, p ⇒ n + e⁺ + ν_e.

Queste due reazioni sono note come decadimenti ‛, diretto e inverso rispettivamente.

Sul piano cosmologico le interazioni deboli hanno un ruolo assolutamente fondamentale. Per esempio, il processo debole

p + p ⇒ ²H + e⁺ + ν_e

controlla il ciclo delle reazioni principali che avvengono all'interno del Sole. L'aspetto più sorprendente di questi fenomeni è la loro straordinaria lentezza: alla temperatura e alla densità del centro del Sole, il processo di combustione produce una quantità di calore per unità di massa pari ad appena 1/100 di quello prodotto dal metabolismo umano. È proprio questa lentezza ciò che rende i processi deboli così preziosi, assicurando per esempio che sulla Terra vi siano le condizioni termiche appropriate allo sviluppo della vita. La lentezza dei processi deboli è una diretta conseguenza della grande massa dei quanti del campo d'interazione: i bosoni intermedi infatti sono le particelle elementari più pesanti prodotte finora con acceleratori.

Lo studio delle proprietà di vari decadimenti nucleari portò Enrico Fermi nel 1934 a formulare l'ipotesi che il decadimento β fosse determinato da un'interazione puntiforme fra i quattro campi quantistici che descrivono le particelle coinvolte. Ai decadimenti nucleari si sono successivamente aggiunti numerosi altri processi, che hanno permesso una descrizione sistematica delle interazioni deboli. L'universalità dei fenomeni dovuti alle interazioni deboli è attualmente interpretata sulla base dell'esistenza di un'interazione fondamentale fra i quarks e i leptoni, invece che fra nucleoni e leptoni. In altre parole, le reazioni fondamentali che danno luogo al decadimento β sono

[d] ⇒ [u] + e^- + ν̄_e, [u] ⇒ [d] + e⁺ + ν_e,

dove [u] e [d] sono i quarks di carica 2/3 e −1/3 (in unità di carica dell'elettrone) e le parentesi indicano che la reazione avviene all'interno dei nucleoni e non tra quarks liberi.

Cabibbo ha mostrato che l'universalità dell'accoppiamento debole delle varie famiglie di quarks può essere capita se si assume che vi sia mescolamento tra quarks differenti di carica 1/3 nelle correnti dovute alle interazioni deboli.

In maniera analoga le tre famiglie di leptoni - cioè (e, ν_e), (μ, ν_μ) e (τ, ν_τ) - hanno interazioni deboli simili, purché si tenga debito conto delle differenze fra le masse. Non è noto se (in analogia con il fenomeno di Cabibbo per i quarks) vi sia mescolamento fra i diversi stati dei neutrini, e cioè se si verifichi il cosiddetto fenomeno delle oscillazioni dei neutrini. Una conseguenza di tale fenomeno sarebbe che la natura dei neutrini provenienti ad esempio dal Sole subirebbe delle trasformazioni periodiche durante il percorso Sole-Terra.

A differenza delle altre interazioni più forti, come quella nucleare e quella elettromagnetica, le interazioni deboli violano un certo numero di leggi di conservazione. Questo comporta la non conservazione di numeri quantici quali la parità P, la coniugazione di carica C, il loro prodotto CP, la stranezza, il charm e altri. Onde poter spiegare il cosiddetto puzzle θ-τ, cioè il fatto che due mesoni una volta chiamati θ e τ (che, come oggi si sa, sono la medesima particella, un mesone K) avevano proprietà identiche malgrado una parità opposta nei loro stadi finali, Lee e Yang avanzarono l'ipotesi che la parità (P) non venisse conservata nelle interazioni deboli. Come è risaputo, l'operatore di parità (P) inverte le coordinate dello spazio (r È − r, riflessione rispetto all'origine delle coordinate). La non conservazione della parità significa quindi una rottura della simmetria tra la sinistra e la destra, fino ad allora considerata una proprietà fondamentale di tutte le leggi fisiche. È stato anche trovato che la non conservazione della parità va di pari passo con la non conservazione della coniugazione di carica (C), cioè l'operazione che trasforma un sistema di particelle nel sistema di antiparticelle corrispondenti. Per qualche tempo si è creduto, peraltro, che il prodotto CP delle due operazioni fosse strettamente conservato. Questa credenza era giustificata da un teorema fondamentale della teoria dei campi, il cosiddetto ‛teorema CPT' - che stabilisce l'invarianza delle leggi fisiche microscopiche sotto l'operazione CP e l'operazione T, che inverte la direzione in cui scorre il tempo -, e dall'ipotesi dell'invarianza di tutte le leggi della natura sotto la trasformazione T. Nel 1964 fu scoperta una violazione di CP nel decadimento del K⁰, con la corrispondente violazione della trasformazione rispetto a T. Questa scoperta ha avuto un grande impatto sulla fisica microscopica e sulla cosmologia.

La scoperta della non conservazione della parità nelle interazioni deboli diede luogo alla teoria del neutrino a due componenti, che attribuisce ai neutrini, supposti privi di massa, una polarizzazione totale nella direzione del moto, chiamata elicità, uguale e opposta a quella degli antineutrini. Nel 1957 Marshak e Sudarshan e, indipendentemente, Feynman e Gell-Mann rielaborarono la teoria di Fermi trasformandola in quella che viene comunemente chiamata la teoria V − A.

Per quanto in eccellente accordo con un grande numero di osservazioni sperimentali, la teoria di Fermi è tuttavia incompleta e insoddisfacente. Secondo la meccanica quantistica, nel calcolo di ogni processo di trasformazione bisogna tenere conto anche delle correzioni di ordine superiore, cioè del contributo di trasformazioni in cui avvengono simultaneamente transizioni multiple attraverso una varietà di stati intermedi. Questi contributi, di solito trascurati, appaiono infinitamente grandi e quindi fisicamente inaccettabili. A ciò si aggiunga che, ad esempio, usando la teoria di Fermi, l'estrapolazione ad alte energie del processo di diffusione

e + ν_e ⇒ e + ν_e

porta a gravi difficoltà teoriche, e cioè a una violazione della conservazione della probabilità, non appena l'energia disponibile nel centro di massa supera i 300 GeV.

La buona validità sperimentale della teoria di un'interazione puntiforme di Fermi si concilia con l'ipotesi di Klein dell'esistenza di bosoni intermedi, qualora si ammetta che questi abbiano una massa molto alta rispetto alla scala di energia a cui si effettuano gli esperimenti. In tal caso infatti essi vengono creati e riassorbiti entro tempi estremamente brevi, propagandosi su distanze molto più piccole di quelle accessibili di norma alle osservazioni sperimentali. L'esplorazione dei fenomeni fisici a tali distanze è diventata possibile solo negli ultimi anni, grazie allo sviluppo di nuove tecniche di accelerazione delle particelle elementari. Facendo collidere le particelle ad altissima energia è infatti possibile portare le particelle sempre più vicine ed esplorare distanze sempre più piccole. L'alta massa dei bosoni intermedi spiega dunque come mai le interazioni deboli appaiano puntiformi entro un grande spettro di energie. I quanti mediatori delle interazioni deboli sono stati scoperti nel 1983, quasi cinquant'anni dopo che ne era stata postulata l'esistenza; la loro massa è dell'ordine di 90 volte la massa protonica.

Nella fig. 3 sono riportati i grafici di Feynman che rappresentano, da un punto di vista quantistico, l'interazione debole fra i quarks e i leptoni, mediata da bosoni intermedi W^±. A sinistra si vede un quark di tipo [d] di carica −e/3 che emette un bosone W^- virtuale, trasformandosi in un quark di tipo [u] di carica +2e/3. Il bosone intermedio è riassorbito in una coppia elettrone-neutrino. A destra è mostrato il processo equivalente per la trasformazione [u] ⇒ [d].

Nella teoria viene introdotta una nuova costante di accoppiamento adimensionale, g, che rappresenta in un certo senso il valore della ‛carica' universale debole, identica per quarks e leptoni. Le misure sperimentali della velocità di disintegrazione dei nuclei, o di particelle elementari, non sono sufficienti per determinare direttamente il valore di g, il cui quadrato è legato alla costante di Fermi G_F = (1,16632 ± 0,00004) × 10^-5 GeV^-2 e alla massa del bosone intermedio m_W dalla relazione g² = 8 G_F m_W²/√-2. I fenomeni di interazioni deboli a energie piccole (rispetto alla massa dei bosoni intermedi) dipendono solamente dal rapporto g/m_W. Sono quindi necessari esperimenti ad altissima energia per mettere in evidenza il valore di m_W e quindi estrarre la costante fondamentale di accoppiamento g.

Anche se la massa rimane largamente indeterminata, le osservazioni sperimentali della natura vettoriale dell'interazione responsabile dei vari decadimenti (radioattività, ecc.) ci permettono di concludere che il momento angolare di spin del bosone intermedio deve essere uguale a 1 (in unità ℏ).

Vale la pena di ricordare che l'elettrofotone di Klein aveva non solo un momento angolare uguale a 1, come il fotone, ma anche una costante di accoppiamento g = e: in altre parole le costanti di accoppiamento elettromagnetica e debole erano uguali. Le enormi differenze macroscopiche tra l'elettromagnetismo e le interazioni deboli erano quindi dovute alle masse, straordinariamente grandi, dei bosoni W^±. Klein quindi predisse una massa del bosone intermedio di circa 38 GeV/c², non troppo lontana dal valore osservato sperimentalmente. Il modello standard predice masse per i bosoni intermedi che sono più elevate, principalmente a causa della presenza di bosoni vettoriali neutri, sconosciuti al tempo di Klein.

4. Le correnti neutre

Fu nel 1973 che esperimenti con neutrini ad alte energie, effettuati al Centro Europeo per le Ricerche Nucleari (CERN) e al Fermilab negli Stati Uniti, misero in luce un fenomeno interamente nuovo, che poteva essere interpretato in base all'esistenza di un partner neutro dei bosoni intermedi, chiamato Z⁰. In un numero considerevole di casi si osservarono infatti eventi del tipo

ν_μ + e ⇒ ν_μ + e

oppure del tipo

ν_μ + [q] ⇒ ν_μ + [q],

dove [q] rappresenta un quark all'interno di un protone o di un neutrone. Questi eventi erano prodotti con una frequenza confrontabile con quella delle interazioni ordinarie di neutrini, dovute alle interazioni deboli mediate da bosoni carichi, e non potevano essere dovuti a reazioni già conosciute, in quanto i neutrini non hanno né carica elettrica nè interazioni forti. D'altra parte i bosoni carichi W non possono accoppiare direttamente neutrini della famiglia μ a elettroni o quarks. La spiegazione più ragionevole, confermata poi da un grande numero di osservazioni relative a diversi esperimenti (collisioni elettrone-nucleo e muone-nucleo, collisioni di fasci di elettroni e positroni ad altissima energia, ecc.), è illustrata nel diagramma di Feynman della fig. 4, dove si mostra come le reazioni sopra indicate possano essere prodotte dallo scambio di un bosone neutro e massivo Z⁰. L'accoppiamento è caratterizzato da una costante g′, analoga alla costante g per i bosoni carichi.

Tuttavia ci si rese ben presto conto che i diagrammi della fig. 4 avevano caratteristiche ben diverse e più complesse di una semplice sostituzione Z ⇒ W accompagnata dalle corrispondenti modifiche delle cariche delle particelle interagenti. I valori sperimentali della costante g′/m_Z, ricavabili dai vari fenomeni in cui fu osservato l'effetto ‛correnti neutre', risultarono significativamente diversi a seconda che si trattasse dell'accoppiamento con neutrini, con leptoni carichi o con quarks, in contrasto con l'universalità del valore della costante g/m_W nel caso delle interazioni deboli ordinarie.

Questi fenomeni nuovi, invece di creare difficoltà, furono ben accolti, perché erano stati predetti poco prima da una teoria di Weinberg, Salam e Glashow, che postulava una forma possibile di unificazione tra le forze elettromagnetiche e deboli. Secondo questa teoria, mentre l'accoppiamento tra la Z⁰ e i neutrini è esattamente uguale a quello per i bosoni carichi W^± (cioè g), nel caso dell'accoppiamento della Z⁰ con particelle cariche esiste in più un termine analogo a quello dell'elettromagnetismo, cioè proporzionale alla carica elettrica. L'ammontare di questo termine proveniente dall'elettromagnetismo, e quindi il grado di ‛sovrapposizione' tra i fenomeni elettrici e deboli, era a quel tempo determinato a meno del fattore sen² θ_W, dove θ_W è il cosiddetto angolo di Weinberg, che, invece di essere predetto dalla teoria veniva estratto dai dati sperimentali. La validità del modello era quindi sostanzialmente basata sull'‛universalità' del valore di sen² θ_W (≈ 0,23), estratto da una moltitudine di disparati fenomeni fisici. Il modello di Weinberg, Salam e Glashow prevedeva tuttavia valori esatti per le masse dei bosoni intermedi W^± e Z⁰, pari a

dove e è la carica elementare e G_F è la costante di Fermi, sopra menzionata. Si noti che per sen² θ_W ≈ 1, e = g: siamo quindi ricondotti all'ipotesi di Klein. Per il valore sen² θ_W ≈ 0,23, si trova, per la massa dei bosoni W carichi, 83,0 GeV/c² e, per il bosone Z neutro, all'incirca 93 GeV/c². È da notare che la derivazione delle masse secondo il modello di Weinberg, Salam e Glashow implica l'esistenza del cosiddetto meccanismo di Higgs, che verrà discusso in seguito. Secondo questa ipotesi, il vuoto è dominato da fenomeni associati a un doppietto di campi scalari interagenti fortemente tra loro. La conseguenza sperimentale di tale modello, in aggiunta alla predizione ‛esatta' delle masse dei bosoni W e Z, è l'esistenza di una particella H⁰ neutra, di massa di riposo non nulla e di spin zero, la cosiddetta ‛particella di Higgs'. Non esistono predizioni affidabili circa la massa di H⁰. La ricerca ditale elemento, tuttora mancante, del modello standard è evidentemente della più grande importanza.

5. La produzione diretta dei bosoni W e Z

La ricerca diretta dei bosoni intermedi, cioè dei mediatori delle interazioni deboli, ha richiesto grandissimi sforzi; a essa è stata riservata una frazione apprezzabile delle attività svolte presso le grandi macchine acceleratrici negli ultimi decenni. L'eccellente accordo fra i dati sperimentali e la teoria di Fermi, che ipotizza un'interazione ‛puntiforme', lascia prevedere che la massa del W sia molto elevata. Ad esempio, esperimenti recenti di collisioni di neutrini contro quarks mostrano che la massa della particella W deve essere almeno di 60 GeV/c², cioè più di sessanta volte la massa del protone.

Per creare oggetti molto pesanti, come i bosoni intermedi, è necessario disporre di acceleratori di grandissima energia. Inoltre, poiché l'energia deve essere disponibile nel centro di massa delle particelli incidenti, si deve fare uso di collisioni tra fasci incrociati, per i quali si raggiunge la massima efficienza di trasferimento di energia tra l'acceleratore e il centro di massa della collisione. A questo scopo è stato realizzato al CERN un nuovo tipo di macchina, un anello di accumulazione in cui fasci densi di protoni si scontrano frontalmente con fasci di antiprotoni. A sua volta questa nuova macchina ha richiesto lo sviluppo delle tecniche di produzione e di accumulazione di un numero considerevole di antiprotoni. Una descrizione dettagliata di tali tecniche esula dallo scopo del presente articolo.

Come può avvenire la trasformazione di questa formidabile energia in materia destinata alla creazione di un bosone intermedio? Secondo la meccanica quantistica, i quanti dei campi di forza sono prodotti non solo quando due particelle sorgente si avvicinano l'una all'altra, ma anche quando una particella si annichila incontrando la sua antiparticella. Quando ciò avviene, tutta l'energia portata dalle due particelle che si annichilano è disponibile per la creazione di nuove particelle. Assumiamo che l'energia (inclusa la massa di riposo) delle particelle di ogni fascio sia uguale a E. Il quanto creato avrà un'energia totale uguale a 2E. Poiché la quantità di moto totale è zero, le condizioni cinematiche sono tali da produrre una particella reale a riposo con massa m secondo la legge mc² = 2E.

La produzione diretta di W^± e di Z⁰ può essere quindi ottenuta, in linea di principio, facendo scontrare una coppia quark-antiquark con un'energia totale uguale alla massa del bosone. I bosoni cosi prodotti decadono successivamente in una coppia elettrone-antineutrino nel caso della W e in una coppia neutrino-antineutrino o elettrone-positrone nel caso della Z⁰. La produzione di W e di Z da collisioni quark-antiquark può essere considerata simile alla formazione di stati risonanti in fisica nucleare. I dettagli del processo sono mostrati nella fig. 6, dove si vede che un quark [d], di carica −1/3, si annichila con un antiquark [ù], di carica −2/3, per formare un W^-. Analogamente, per produrre un W⁺, sono necessari un antiquark di tipo [ã], di carica +1/3, e un quark di tipo [u], di carica +2/3. Poiché i bosoni intermedi non hanno colore, il quark e l'antiquark devono sempre avere colori uguali (e opposti). In maniera analoga, coppie di quarks e antiquarks di tipo [u] e [d] dello stesso colore possono creare delle particelle Z⁰.

Purtroppo, in pratica, l'idea di produrre W^± o Z⁰ direttamente a partire da coppie di altissima energia di quarks e antiquarks è irrealizzabile, in quanto apparentemente i quarks non possono esistere allo stato libero. È quindi necessario usare protoni, cioè ‛pacchi' di quarks ricchi di quarks di tipo [u] e [d] contro antiprotoni che contengono i corrispondenti antiquarks. Si noti che fra i costituenti elementari del protone ci sono, seppure in misura alquanto minore, quarks di altri tipi (oltre a gluoni, ecc.).

Lo spettro energetico dei quarks di vari tipi all'interno del protone è noto da esperimenti di collisione di neutrini e mesoni μ su protoni ed è mostrato nella fig. 7. (Gli antiprotoni sono fatti esattamente come i protoni, eccetto che al posto dei quarks hanno antiquarks).

Indicando con x_p e x_-p le frazioni delle quantità di moto del protone e dell'antiprotone, ‛trasportate' rispettivamente dal quark e dall'antiquark, l'energia E_q-q nel centro di massa della collisione quark-antiquark è legata all'energia E_p-p delle collisioni protone-antiprotone dalla relazione E²_q-q = E²_p-px_px_-p. Quindi esiste un ‛continuo' di energie possibili anche a partire da fasci ben definiti di protoni e antiprotoni.

Il processo utilizzato in pratica è quindi del tipo

dove la quantità X rappresenta l'insieme di tutte le altre particelle prodotte nella frammentazione del protone e dell'antiprotone, a causa della presenza degli altri costituenti.

La probabilità di ottenere i processi sopra indicati è calcolabile facilmente partendo dalla probabilità elementare che la reazione associata ai bosoni intermedi avvenga come una collisione tra quarks e facendone la convoluzione con la probabilità di trovare la coppia quark-antiquark all'energia voluta. Per una massa del W di circa 82 GeV, e per un'energia dei protoni corrispondente a E_p-p = 540 GeV - il valore realizzato al CERN -, si ottiene un evento W^± del tipo sopra indicato ogni 100 milioni di interazioni protone-antiprotone. La probabilità per un evento tipo Z⁰ è circa 10 volte inferiore, si ha cioè un evento utile ogni miliardo di collisioni protone-antiprotone.

6. Osservazioni sperimentali

I processi da osservare sono dunque

dove X rappresenta la somma dei frammenti delle interazioni con gli altri partoni spettatori. La rivelazione di elettroni di alta energia è relativamente facile; l'osservazione dell'emissione del neutrino è invece un problema nuovo nella fisica delle alte energie. La probabilità di interazione secondaria del neutrino nell'apparato è infinitamente piccola e non può essere quindi di utilità pratica. È necessario pertanto ricorrere a metodi di rivelazione indiretti. A questo scopo si è realizzato un rivelatore sensibile su tutto l'angolo solido a particelle interagenti e in grado di misurare la loro energia complessiva: si tratta in sostanza di un insieme di calorimetri, costruiti alternando scintillatori e materiale assorbente in una struttura ‛a sandwich', in modo da ottenere una resa luminosa proporzionale all'energia e largamente indipendente dalla natura delle particelle incidenti. Le collisioni sono osservate nel centro di massa: quindi la direzione e l'energia di un neutrino eventualmente emesso sono ottenute indirettamente rilevando il difetto nel bilancio della quantità di moto (la cosiddetta ‛energia mancante'). La quantità di moto delle particelle cariche è ricavata dall'osservazione della curvatura, in un campo magnetico, delle loro tracce, mentre l'energia è misurata mediante sei strati concentrici di calorimetri, segmentati finemente nella lettura, che circondano il punto di collisione fino ad angoli dell'ordine di 0,20 rispetto alle direzioni dei fasci incidenti. Gli elettroni sono assorbiti dai primi strati; segue l'assorbimento delle particelle che interagiscono fortemente, cioè pioni, protoni, neutroni, particelle strane, ecc.; infine i mesoni μ, che attraversano facilmente l'apparato, sono registrati da rivelatori visualizzanti che circondano anch'essi il rivelatore.

Un tale strumento è capace di registrare eventi con un residuo dell'ordine di 4 GeV, dovuto agli errori strumentali, del bilancio energetico. Da notare che nel caso delle W^±, dove ci si aspetta l'osservazione di un elettrone isolato di alta energia, l'effetto della mancanza di bilancio energetico è spettacolare, in quanto dell'ordine della metà della massa del bosone, cioè di circa 40 GeV. Nel caso della produzione di Z⁰ ci si aspetta l'emissione di due elettroni di segni opposti e una quantità trascurabile di energia mancante.

Eventi dovuti alla presenza delle particelle W^± (v. fig. 10) e della Z⁰ furono scoperti al CERN nel corso dell'anno 1983; la loro scoperta valse a C. Rubbia e a S. Van der Meer il premio Nobel per la fisica nel 1984. Ci limiteremo a dare un breve sommario delle proprietà salienti di tali particelle.

Una delle proprietà più caratteristiche delle interazioni deboli è il fenomeno della violazione della parità. Evidentemente la particella W - come mediatore dei processi deboli - deve avere proprietà analoghe. Inoltre studi sul decadimento β hanno permesso di concludere che lo spin, o momento angolare intrinseco, della particella W deve essere J = 1 (in unità ℏ). Ambedue le predizioni sono state confermate sperimentalmente dall'osservazione della spettacolare asimmetria degli elettroni di decadimento della W rispetto alla direzione dei fasci incidenti.

Il campo dei quanti deboli deve avere un accoppiamento universale non solo con l'elettrone e con il neutrino corrispondente, ma con tutti gli altri doppietti di leptoni fondamentali e con tutti i doppietti di quarks. Questo implica, a parte piccole correzioni associate alle masse delle particelle di decadimento, l'uguaglianza dei rapporti di decadimento tra i processi

W → e + ν_e, W → μ + ν_μ, W → τ + ν_τ

e tra quelli riguardanti i quarks:

W → u + d_C, W → c + s_C, W → t + b_C.

Si noti che questi ultimi sono incrementati di un fattore tre a causa della possibilità che siano emessi quarks di tre colori diversi. L'indice C nei canali dovuti ai quarks indica la presenza del mescolamento di Cabibbo. Le reazioni leptoniche e le prime due reazioni con i quarks sono state osservate e sono, entro la precisione sperimentale del ± 20%, in accordo con le previsioni teoriche. L'ultima reazione è dovuta al quark t, il cosiddetto quark top, o sesto quark della famiglia. Alcuni eventi che sembrano essere interpretabili come dovuti a questo processo sono stati presentati nella letteratura. Se interpretabili in questo modo, essi sono consistenti con la massa del top, m_t ≈ 40 GeV/c². Le masse delle particelle W e Z sono ben misurate, m_W = (80,9 ± 2,0) GeV/c² e m_Z = (93 ± 2,0) GeV/c². I loro valori sono in ottimo accordo con le predizioni della teoria moderna delle interazioni deboli sviluppata da Weinberg, Salam e Glashow, che assume l'esistenza del cosiddetto meccanismo di Higgs. Il valore non nullo dell'angolo di mescolamento di Weinberg ricavato dai valori delle masse è inoltre in accordo eccellente con i dati dedotti da misure su fenomeni dovuti alle ‛correnti neutre' e alle basse energie.

7. Le interazioni deboli e le teorie di gauge

Il modello teorico su cui si basa la descrizione oggi universalmente accettata dalle interazioni deboli è quello delle cosiddette teorie di gauge. Data l'importanza che queste teorie hanno nella descrizione di tutti i vari tipi di forze fra le particelle elementari e in particolare per la comprensione delle proprietà dei bosoni intermedi, ne illustreremo brevemente i punti principali. L'altro ingrediente teorico fondamentale è il cosiddetto meccanismo di Higgs, che discuteremo pure brevemente.

I matematici capirono molto prima dei fisici l'importanza e la potenza considerevole delle proprietà di simmetria di un sistema. All'inizio del nostro secolo furono formulati vari principi di simmetria globali per sistemi fisici, il che permise di derivare proprietà come la conservazione dell'energia e della quantità di moto partendo dal principio dell invarianza dei fenomeni fisici rispetto a traslazioni nelle variabili spaziali e nel tempo. Fu per la prima volta con la relatività generale che ci si imbatté in un principio molto più potente: una simmetria valida separatamente in ciascun punto dello spazio e del tempo. L'idea alla base delle teorie di gauge è appunto che le leggi della fisica sono invarianti rispetto a una trasformazione continua e variabile da punto a punto, chiamata ‛trasformazione di gauge'. Il concetto di invarianza di gauge, che ha trovato la sua origine nello studio dell'elettromagnetismo, è diventato di importanza capitale nella formulazione teorica di tutti i campi fondamentali. La parola ‛gauge' (in tedesco eich) venne introdotta da Herman Weyl nel 1918, allorché egli avanzò l'ipotesi - più tardi riconosciuta errata - che il cambiamento del potenziale elettromagnetico dovesse corrispondere a un cambiamento da punto a punto della lunghezza di riferimento (gauge). Malgrado questa concezione errata, il nome rimase e viene correntemente usato per indicare trasformazioni caratterizzate da funzioni arbitrarie, in contrasto con trasformazioni (come ad esempio le rotazioni) che dipendono da uno o più parametri numerici.

L'invarianza dell'elettromagnetismo rispetto a trasformazioni di gauge riflette il fatto familiare che i potenziali - il vettore A e lo scalare ϕ - non sono direttamente osservabili, in quanto le uniche quantità osservabili sono i campi elettrici e magnetici. Quindi, senza alterare il fenomeno fisico osservabile, A e ϕ possono essere modificati da trasformazioni del tipo

A ⇒ A + 1/e grad Γ e ϕ ⇒ ϕ − 1/e ∂Γ/∂t,

dove Γ è una funzione arbitraria dello spazio e del tempo. Le equazioni di Maxwell sono invarianti rispetto a tali trasformazioni. L'invarianza rispetto alle trasformazioni locali di gauge porta alla conservazione della corrente elettromagnetica.

La potenza di tali tecniche è assolutamente impressionante. Si consideri per esempio l'invarianza delle leggi fisiche rispetto al gruppo delle trasformazioni che modificano la fase della funzione d'onda dell'ampiezza quantistica per le particelle, e cioè

Dall'invarianza rispetto a tale gruppo, chiamato U(1), è possibile ricavare l'esistenza di un campo vettoriale - il campo di gauge - identificabile con il campo elettromagnetico. E quindi possibile derivare l'insieme delle equazioni dell'elettrodinamica partendo dall'invarianza rispetto alle trasformazioni di gauge di tipo U(1) delle equazioni del moto.

In maniera analoga la forza forte, cioè la forza responsabile delle interazioni tra nuclei e quarks, può essere ricavata a partire da un'altra simmetria di gauge, applicata però ai gradi di libertà interni delle particelle. La simmetria, di tipo SU(3), si applica allo spazio dei colori dell'interazione forte.

Tuttavia - nonostante la loro impressionante efficacia - le simmetrie di gauge servono per trattare solo i casi in cui i quanti del campo abbiano massa nulla, cioè vanno perfettamente bene per i fotoni e i gluoni, ma non possono essere applicate direttamente nel caso delle interazioni deboli, i cui quanti, come abbiamo visto, hanno masse enormi. Il fatto che le particelle W^± e Z⁰ abbiano delle masse così grandi è dovuto molto probabilmente a una proprietà del vuoto, che però resta ancora da verificare sperimentalmente; attualmente questa verifica costituisce uno degli obbiettivi prioritari delle ricerche nel campo delle particelle elementari.

Come è fatto il vuoto? Seguendo la meccanica quantistica e in particolare il principio di indeterminazione, il vuoto oscilla continuamente tra uno stato di vuoto assoluto e uno stato di particella e antiparticella. In contrasto con l'immagine classica di assenza di materia, il vuoto diviene un campo aperto a tutte le forme possibili di materia. Tutte le possibili coppie particella-antiparticella si creano e si annichilano in intervalli di tempo brevissimi eludendo così, in virtù del principio di indeterminazione, ogni tentativo di osservarle direttamente. Gli effetti di queste fluttuazioni del vuoto possono comunque essere osservati in taluni fenomeni. Ad esempio, vicino alle sorgenti del campo elettromagnetico la creazione di coppie virtuali induce un effetto di polarizzazione che influenza la costante dielettrica del vuoto e quindi la legge di Coulomb. La dipendenza della forza di Coulomb dall'inverso del quadrato della distanza è una proprietà fondamentale, in quanto è derivata direttamente dal fatto che il fotone ha massa di riposo nulla. Ciononostante, a distanze piccole rispetto a r₀ = ℏ/m_ec = 3,8 × 10^-11 cm (dove m_e è la massa dell'elettrone, cioè della più leggera particella carica, e c è la velocità della luce) la legge appare modificata:

Quindi, a causa della struttura complessa del vuoto, a piccolissime distanze la forza elettrostatica diviene più forte di quanto predetto dalla legge di Coulomb.

Secondo un'ipotesi largamente condivisa al giorno d'oggi, anche la spiegazione del fatto che i mediatori delle interazioni deboli siano particelle di massa elevatissima è ricondotta alla struttura straordinariamente complicata del vuoto. Seguendo il fisico scozzese P. Higgs, si postula l'esistenza di un nuovo campo di forze, Φ, che interagisce così fortemente con se stesso che il suo valore medio esteso sul vuoto è molto grande

∣ 〈 vac ∣ Φ ∣ vac > ∣ ≈ 180 GeV.

Di massa nulla in assenza del campo di Higgs, le particelle W^± e Z⁰ acquistano una massa grazie alle interazioni continue con il campo di Higgs, onnipresente, per germinazione spontanea del vuoto. Questo campo non è solamente responsabile delle masse delle particelle W^± e Z⁰, ma anche delle masse di tutte le particelle conosciute e quindi di tutti gli oggetti. Naturalmente in questo modo non si spiega perchè, ad esempio, l'elettrone abbia una massa di riposo: si sostituisce il mistero della massa con un altro mistero, altrettanto impenetrabile, e cioè l'accoppiamento tra l'elettrone e il campo di Higgs.

Un'altra proprietà importantissima del modello è il fatto che il gruppo delle interazioni deboli e quello dell'elettromagnetismo si combinano in un principio di invarianza più largo: ne risulta una connessione diretta tra l'interazione debole e quella elettromagnetica. Il fotone fisico resta senza massa, mentre le particelle responsabili delle interazioni deboli ed elettromagnetiche si mischiano, generando il fotone e la particella Z⁰.

Cerchiamo di descrivere sommariamente i passi che ci portano da una teoria di gauge ai bosoni e al fotone reali. Le particelle dotate di interazioni deboli sono classificate in termini di due quantità, l'isospin T e l'ipercarica Y deboli. L'isospin T, essendo rappresentato in uno spazio bidimensionale, è determinato dal valore del modulo di T e dalla sua componente secondo un asse, T₃. Si noti anche la relazione fondamentale Q = T₃ + Y/2. I valori corrispondenti ai fermioni fondamentali sono elencati nella tab. II. I fermioni sono separati nelle due componenti di polarizzazione secondo la direzione del movimento, levogiro (f_L) e destrogiro (f_R). Si noti che questa classificazione è possibile in quanto a questo punto tutti i fermioni fondamentali hanno massa di riposo eguale a zero. Applicando una teoria di gauge allo spazio bidimensionale dell'isospin T e dell'ipercarica Y, si arriva a un gruppo di gauge di tipo SU(2), che genera tre quanti di campo con massa di riposo eguale a zero, W_μ⁽¹⁾, W_μ⁽²⁾ e W_μ⁽³⁾, e una costante fondamentale di accoppiamento g. Indipendentemente, l'invarianza U(1) già menzionata può essere usata per derivare nella sua forma iniziale l'elettromagnetismo, caratterizzato dal campo vettoriale B_μ con massa di riposo eguale a zero.

I risultati sperimentali sulle correnti neutre discussi in precedenza indicano che ci deve essere mescolamento tra i partners neutri delle due famiglie, nel quadro di una simmetria più vasta, e cioè SU(2) × U(1): questo mescolamento può essere parametrizzato introducendo un angolo di mescolamento debole, detto anche angolo di Weinberg, fra i due campi neutri B_μ e W_μ⁽³⁾. I due campi neutri sperimentalmente osservati, quello del fotone A_μ e quello delle particelle Z⁰, Z_μ risultano essere una combinazione lineare di questi due campi, tale che

A_μ = B_μ cos θ_W + W_μ⁽³⁾ sen θ_W

Z_μ = − B_μ sen θ_W + W_μ⁽³⁾ cos θ_W.

Se si impone che il neutrino non si accoppi al campo elettromagnetico A_μ e che l'elettrone abbia carica eguale a e, si possono ottenere le due relazioni seguenti:

g = e/sen θ_W ≥ e.

g′ = e/cos θ_W ≥ e.

Queste due relazioni mettono in rilievo il carattere unificato delle interazioni elettromagnetiche e deboli e mostrano come le due costanti di accoppiamento, g e g′, siano in realtà collegate fra loro da un parametro, l'angolo di Weinberg.

A questo punto, allo scopo di generare la massa dei fermioni e dei quanti del campo debole, si fa ricorso al meccanismo di Higgs, introducendo un doppietto di particelle scalari (spin eguale a zero) che si trasformano una nell'altra grazie a rotazioni nello spazio bidimensionale di SU(2). Queste particelle, oltre che interagire tra loro, hanno un accoppiamento con i fermioni fondamentali, proporzionale alle loro masse fisiche. Come menzionato sopra, la ragione di tutto ciò è - a questo stadio - sconosciuta.

Le interazioni con il suddetto campo di Higgs hanno conseguenze fondamentali su gran parte dei fenomeni naturali e cioè: 1) i bosoni deboli acquistano una massa di riposo, legata all'angolo di Weinberg,

dove G_F è la costante di Fermi; 2) la massa di riposo del fotone rimane rigorosamente nulla; 3) il campo di Higgs ‛partorisce' una particella neutra di massa ignota e di spin zero, la cosiddetta particella H⁰. Una delle proprietà più importanti delle teorie di gauge è la loro rinormalizzabilità, cioè il fatto che la teoria non contiene quantità che possono essere infinite all'aumentare dell'energia. Senza scendere nei dettagli della teoria, diciamo semplicemente che in generale la presenza di campi di gauge dotati di massa rovina la rinormalizzabilità, con effetti catastrofici, in quanto i fatti sperimentali richiedono masse abbastanza alte per i campi di gauge. L'introduzione del campo di Higgs risolve questa difficoltà, in quanto i campi addizionali cancellano le divergenze legate alla massa dei bosoni. La dimostrazione che questo meccanismo produce una lagrangiana rinormalizzabile è stata data da G. ‛t Hooft nel 1971.

Fino ad ora il meccanismo di Higgs rimane un'ipotesi teorica, che sembra tuttavia marciare molto bene: è quindi della più grande importanza verificarne la validità. In aggiunta alle masse delle particelle W^± e Z⁰, rimane tuttora da verificare la predizione di una particella pesante e neutra, la particella di Higgs H⁰. Quantunque le proprietà di interazione ditale particella siano predicibili, la sua massa è sconosciuta e incredibilmente ben nascosta nella fenomenologia esplorata dagli esperimenti d'oggi. Il meccanismo di Higgs rimane tuttora tra i misteri più fondamentali e più studiati della fisica delle particelle elementari.

8. Questioni aperte

Nonostante i progressi spettacolari degli ultimi anni, soprattutto grazie all'osservazione sperimentale prima delle correnti neutre e più recentemente dei bosoni intermedi e ai grandi progressi teorici collegati alle teorie di gauge, sussistono tuttora nel campo delle interazioni deboli numerose questioni aperte. Vorremmo menzionarne alcune.

La teoria di Weinberg, Salam e Glashow è esatta? E completa?

Esiste la particella di Higgs? Quali sono le sue proprietà?

Le interazioni deboli ed elettromagnetiche sono realmente descritte da una teoria di gauge, o questa è semplicemente un'approssimazione valida alle energie delle esperienze di oggi?

Qual è la spiegazione delle masse dei leptoni e dei quarks?

Qual è l'origine della violazione della parità?

Qual è l'origine della violazione di CP?

I neutrini sono realmente senza massa? Oscillano tra di loro?

Qual è l'origine dell'angolo di Cabibbo? E dell'angolo di Weinberg?

Esistono nuove famiglie di particelle elementari?

Quarks e leptoni sono veramente puntiformi, o hanno anch'essi una struttura interna?

Nuove, potenti macchine acceleratrici sono in costruzione o in progetto in Europa e negli Stati Uniti allo scopo di rispondere a questi quesiti.

bibliografia

Cheng, D. C., O'Neill, G. K., Elementary particle physics. An introduction, Reading, Mass., 1979.

Fritzsch, H., Quark, Torino 1983.

Los Alamos Science, Particle physics, estate-autunno 1984, n. 11, Los Alamos National Laboratory, Los Alamos, New Mexico 87545.

Okun, L.B., Leptons and quarks, Amsterdam 1982.

Perkins, D. H., Introduction to high energy physics, Reading, Mass., 1982.

Quigg, Ch., Gauge theories of the strong, weak and electromagnetic interactions, Reading, Mass., 1983.