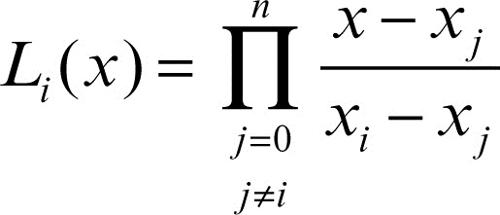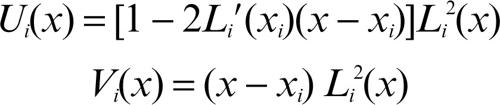interpolazione
interpolazione
interpolazione in statistica e in analisi numerica, procedimento mediante il quale, considerati come noti alcuni valori ordinati x1 < ...< xn di una variabile X e, in corrispondenza di questi, altrettanti valori y1, …, yn di una variabile Y, dipendente da X, si determinano valori non noti di Y in corrispondenza di valori di X che appartengano ancora all’intervallo [x1, xn], ma siano diversi dai precedenti. Per valori di X esterni all’intervallo [x1, xn] si parla invece di → estrapolazione.
Un caso elementare di interpolazione si ha quando si cerca, in tavole logaritmiche, statistiche o di altro tipo, un valore intermedio tra due valori noti, espressi nelle tavole stesse. In tale caso, date due coppie di valori successivi in una tabella (che per sua natura non può che essere discreta) (x1, y1) e (x2, y2), per trovare un valore corrispondente a xi, con x1 < xi < x2, si effettua una interpolazione lineare tra i due estremi come se in quell’intervallo la funzione descritta dalla tabella fosse lineare e quindi si approssima localmente il grafico della funzione con una retta. Si imposta perciò la proporzione
da cui si ricava il valore interpolato corrispondente a xi:
Tale metodo può essere applicato a qualunque altra coppia di valori consecutivi ed è usato nei metodi numerici di approssimazione locale di una funzione, di integrazione numerica e di calcolo delle soluzioni di un’equazione differenziale (si veda anche: → approssimazione (di una funzione), → approssimazione (di una soluzione) e → Newton, metodo di).
Se invece si vuole approssimare globalmente una funzione, allora non si interpola per coppie di punti, ma si considerano simultaneamente tutte le n coppie di valori a disposizione e, se si pensano X e Y come coordinate cartesiane, il problema dell’interpolazione si traduce geometricamente nel problema di tracciare una curva, detta curva interpolatrice, che in tutto l’intervallo [x1, xn] approssimi il grafico della funzione.
Più in generale, infatti, l’interpolazione è utile quando si vuole dare continuità a una sequenza di dati discreta e si cerca una legge matematica che, a partire dai dati osservati o rilevati, descriva il fenomeno. Presupposto per far ciò è che esista una certa regolarità nella dipendenza di Y da X.
Si distingue tra due tipi di interpolazione:
• interpolazione per punti (detta anche interpolazione analitica), più utilizzata negli ambiti dell’analisi matematica e numerica, in cui si cerca una funzione ƒ, detta funzione interpolatrice, tale che sia esattamente yi = ƒ(xi) per ognuna delle coppie (xi, yi) di valori dati, che in questo contesto sono detti poli. In tale caso il grafico della funzione passa per tutti i punti le cui coordinate sono le coppie di valori dati;
• interpolazione tra punti (detta anche interpolazione grafica), più utilizzata in ambito statistico, in cui non si richiede necessariamente che il grafico della funzione cercata passi per tali punti, ma soltanto che globalmente la funzione ben si adatti alle caratteristiche della distribuzione data; in questo secondo significato si parla più propriamente di → regressione. In tutti e due i tipi di interpolazione il problema ha infinite soluzioni giacché occorre prefissare la forma analitica della funzione interpolatrice, non univocamente determinata a priori. Tale scelta avviene o sulla base di considerazioni teoriche, quando una teoria propone una classe di funzioni di particolare interesse, oppure, come spesso accade, in base a considerazioni empiriche di semplicità e generalità. Nell’interpolazione tra punti, una volta scelta la funzione, occorre fissarne i parametri, e i principali metodi utilizzati a tale scopo sono il metodo dei minimi quadrati e il metodo della funzione di verosimiglianza, entrambi basati su diversi indici di scostamento.
Interpolazione per punti polinomiale
Dati n + 1 poli (x0, y0), ..., (xn, yn), con xi ≠ xj per ogni i e j, si vuole determinare il polinomio p(x) = a0 + a1x + a2x 2 + ... + anxn, di grado al più n, tale che p(xi) = yi per ogni i = 0, ..., n. I coefficienti di tale polinomio sono determinati imponendo che, in corrispondenza dei valori xi, il polinomio assuma i valori yi. Si tratta quindi di risolvere un sistema lineare di n + 1 equazioni in n + 1 incognite, che per n grande può risultare molto oneroso e numericamente instabile. Per tale motivo, per determinare tale polinomio si utilizzano altri metodi, numericamente più efficienti: l’interpolazione di → Lagrange oppure l’interpolazione di → Newton.
Un ulteriore tipo di interpolazione per punti polinomiale, detta interpolazione di Hermite, si ottiene se si considerano come dati non soltanto i punti della funzione, ma anche i valori relativi alla derivata della funzione, in modo da ricostruirne meglio l’andamento. In questo caso si considerano quindi non soltanto le coppie (xi, yi) ma anche i valori della derivata yi′ nei punti, per i = 0, ..., n. Il polinomio interpolatore di Hermite (detto anche polinomio osculatore), di grado al più 2n + 1, è allora:
dove i polinomi Ui (x) e Vi (x) sono a loro volta funzioni dei polinomi di Lagrange, relativi al polo (xi, yi)
e delle loro derivate Li′(xi)
Altri tipi di interpolazione per punti
Di notevole interesse applicativo in vari campi dell’analisi numerica è anche l’interpolazione di uno dei tipi descritti precedentemente e che si ottiene utilizzando come funzioni interpolatrici polinomi trigonometrici del tipo
oppure funzioni razionali.