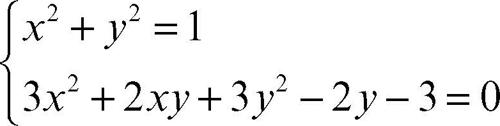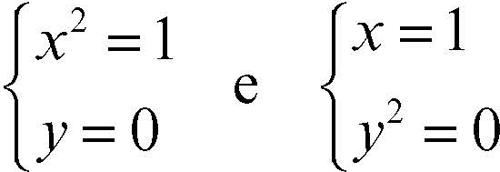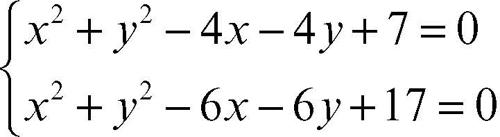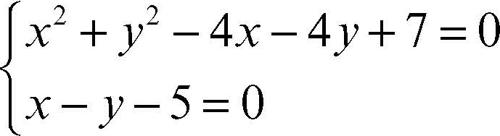coniche, intersezione di
coniche, intersezione di
coniche, intersezione di insieme dei punti comuni a due o più coniche. Analiticamente, l’intersezione tra due coniche si ricava impostando il sistema formato dalle loro equazioni, che risulta essere un sistema di quarto grado in due incognite, il quale può ammettere al massimo quattro soluzioni. In termini geometrici ciò sta a significare che due coniche possono avere da zero a quattro punti di intersezione, purché contati con la dovuta molteplicità. Nel caso in cui i punti di intersezione siano più di uno, alcuni di essi possono infatti anche coincidere. Per esempio il sistema
che rappresenta l’intersezione di una circonferenza con un’ellisse, è equivalente all’unione dei due sistemi:
Il primo sistema ha per soluzioni (−1, 0) e (1, 0), il secondo ha la soluzione doppia (1, 0). Il punto di intersezione P(1, 0) ha pertanto molteplicità 3, mentre il punto (−1, 0) ha molteplicità di intersezione 1.
Nel caso particolare in cui le due coniche sono due circonferenze, le intersezioni reali al massimo sono in numero di due. Infatti, poiché nel campo complesso tutte le circonferenze del piano passano per i due punti ciclici (→ Bézout, teorema di), le ulteriori intersezioni reali sono al massimo due. Ma si può dare di ciò anche una spiegazione strettamente algebrica. L’intersezione di due circonferenze conduce infatti a un sistema di quarto grado che, per la natura stessa delle equazioni che lo compongono, è sempre equivalente a un sistema di secondo grado, ottenuto sostituendo all’equazione di una delle due circonferenze, l’equazione, di primo grado, data dalla differenza delle loro equazioni.
Per esempio, il sistema
che rappresenta l’intersezione di due circonferenze è equivalente al sistema
che rappresenta l’intersezione di una circonferenza con una retta. La retta x + y – 5 = 0 è l’asse radicale delle due circonferenze e, nell’esempio considerato, passa per i punti in cui le circonferenze si intersecano.
