intorno

intorno

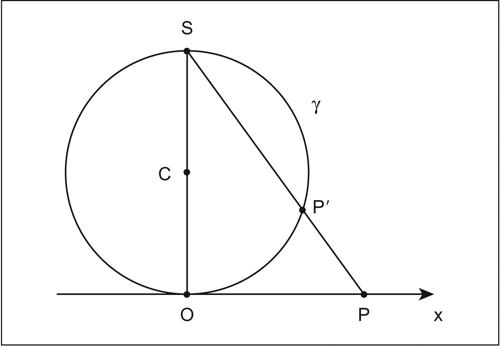
intorno in analisi, concetto che allude alla totalità di elementi “vicini” a un elemento dato. Poiché nella retta reale è definita la distanza tra due punti P₁ e P₂ come la lunghezza (senza segno) del segmento P₁P₂, si definisce intorno (simmetrico) di un qualsiasi punto P₀ (al finito) dell’asse x l’insieme dei punti P la cui distanza da P₀ non supera un certo r > 0; cioè, dette rispettivamente x e x₀ le ascisse di P e P₀, l’insieme dei numeri reali x per cui si verifica |x − x₀| ≤ r oppure l’analoga disuguaglianza stretta, cioè escludendo dall’intorno i suoi estremi. Più in generale, si considera intorno non simmetrico di P₀, cioè con estremi non equidistanti da esso, un qualsiasi intervallo (a, b) tale che a < x₀ e b > x₀; anzi, ponendo anche il segno di uguale in una delle due disuguaglianze si definiscono intorni unilaterali (destro o sinistro) in cui P₀ coincide con uno degli estremi. Il concetto di intorno così definito si estende anche al caso in cui si consideri non un punto P₀ al finito, bensì un punto all’infinito. Si può infatti osservare che i numeri reali possono anche rappresentarsi su una curva chiusa i cui punti siano posti in corrispondenza biunivoca con i punti della retta; per esempio su una circonferenza γ tangente all’asse x nell’origine O, su cui i punti vengano proiettati dal punto S della circonferenza diametralmente opposto a O. In tal modo al punto all’infinito dell’asse x corrisponde il punto S di γ e a un intorno di S sulla circonferenza corrisponde la parte della retta x esterna a un certo intervallo (−ω₁, ω₂). Si definisce allora tale parte della retta x come intorno del punto all’infinito della retta stessa. Se si considera ω₁ = ω₂ = ω, l’intorno è caratterizzato dalla disuguaglianza |x| ≥ ω. In R una disuguaglianza di questo tipo è definita appunto come intorno dell’infinito.

L’estensione del concetto a R² porta a definire l’intorno circolare di un punto P₀ come la totalità dei punti aventi da esso distanza non superiore a un fissato numero reale r non negativo, caratterizzato da una disuguaglianza analoga a quella che caratterizza l’intorno unidimensionale:

In tale caso P₀ e r sono rispettivamente detti centro e raggio dell’intorno. L’estensione a Rⁿ porta a definire intorni circolari di un punto nel corrispondente spazio n-dimensionale. Il concetto di intorno non si limita tuttavia a intorni circolari, ma va esteso a un qualsiasi dominio comprendente il punto P₀ al suo interno: nel caso bidimensionale, per esempio, è spesso utile riferirsi a intorni rettangolari definiti da a ≤ x ≤ b, α ≤ y ≤ β (con lati paralleli agli assi coordinati), attraverso cui si definiscono intorni incapsulati come successive celle c_n = (a_n ≤ x ≤ b_n, α_n ≤ y ≤ β_n) (con n = 1, 2, 3, …) tali che, dato ad arbitrio ε > 0, si può sempre trovare n tale che b_n − a_n < ε, β_n − α_n < ε (si dimostra che in tale caso esiste uno e un solo punto A interno a tutte le celle).

Il concetto di intorno non si limita comunque a Rⁿ, ma si estende a un più generale spazio topologico. In uno spazio topologico X l’intorno di un punto x è un sottoinsieme U di X contenente un aperto A cui appartiene x o, in altre parole, tale che x sia interno a U. Una base di intorni di x è una famiglia F di intorni tale che ogni intorno U di x contenga un membro della famiglia. Per esempio, in uno spazio metrico una base di intorni di un punto x è formata dagli intorni circolari B_r = {y : d(x, y) < r, con r > 0}, con cui è stato precedentemente introdotto il concetto di intorno. L’insieme degli intorni di un punto costituisce un → filtro.