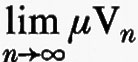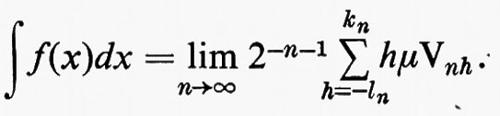Intuizionismo

Intuizionismo

di Arend Heyting

Intuizionismo

sommario: 1. Concetti fondamentali.  2. Aritmetica elementare.  3. Il principio del terzo escluso. 4. I numeri reali. 5. Ineguaglianza e separazione fra numeri reali. 6. Matematica e linguaggio. 7. Matematica applicata. 8. La teoria degli insiemi. 9. Spiegamenti. 10. Il soggetto creativo. 11. Relazioni d'ordine. 12. L'interpretazione delle costanti logiche. 13. L'induzione completa. 14. Nozioni che dal punto di vista classico sono equivalenti. 15. Misura e integrazione. 16. Matematica senza negazione. 17. Conclusioni. □ Bibliografia.

1. Concetti fondamentali

La concezione intuizionista della matematica è stata introdotta da L.E.J. Brouwer. Egli ne formulò le idee fondamentali nel 1907 e nel 1908; nel 1918 incominciò a sviluppare teorie matematiche ispirate ai suoi principi. Le sue idee furono accettate da pochissimi matematici, alcuni le rifiutarono violentemente perché non volevano rinunciare a quei metodi che, secondo Brouwer, erano infondati. Solamente a partire dal 1960 la matematica intuizionista incomincia a essere apprezzata e un gruppo di matematici elabora importanti lavori nel suo ambito, anche se non tutti condividono la filosofia di Brouwer.

Il termine ‛intuizionismo' è stato spesso causa di equivoci. Esiste una vaga o addirittura nessuna connessione fra la matematica intuizionista e le scuole filosofiche omonime. In particolare i matematici intuizionisti non pretendono di possedere una conoscenza immediata e intuitiva del mondo. Un'altra falsa idea è che Brouwer abbia inventato l'intuizionismo col proposito di evitare i paradossi logici. L'intuizionismo mira a fondare una base per la matematica che si possa capire immediatamente senza far ricorso a sottigliezze filosofiche; è una fortunata coincidenza che in tal modo si risolvano anche i paradossi.

Brouwer riuscì nel suo intento analizzando il procedimento del contare. Quando io conto degli oggetti, li considero uno per uno come entità isolate. Questo atto mentale di fissare la mia attenzione su un oggetto è alla base di tutto il pensiero organizzato. Brouwer lo chiama l'atto di ‟creare un'entità", sottolineando con ciò che si tratta di un'attività mentale. Dipende dalla mia volontà quali oggetti conto; per esempio, posso contare le persone che stanno in una stanza, ma posso anche contare le loro dita. In un dato momento, nella mia mente non c'e una collezione di oggetti distinti, ma un tutt'uno in cui io isolo determinate entità per mezzo di un atto mentale più o meno consapevole. Bisogna rendersi ben conto del fatto che il verbo creare nella espressione ‛creare un'entità' ha un significato diverso che nell'espressione, per esempio, ‛creare un'opera d'arte'. Dopo essere stato creato, un quadro esiste nel mondo esterno, mentre questo non avviene per le entità create mentalmente.

Un'ulteriore analisi mostra che io fisso la mia attenzione non su di un oggetto, ma su qualche sensazione. La nozione di oggetto è troppo complicata; nasce dalla combinazione di parecchie sensazioni, ricordi e aspettative. Vero è che nella maggioranza dei casi una sensazione è immediatamente e spesso inconsciamente associata alla nozione di un oggetto, tuttavia la sensazione deve essere considerata come primaria. Inoltre, in matematica, la natura della sensazione è inessenziale, si può astrarre da essa. Per esempio, nel costruire il numero 5, la natura delle entità che costituiscono questo numero è del tutto irrilevante.

Dopo aver creato un'entità, io posso fissare la mia attenzione su un'altra sensazione, trattenendo la prima nella memoria. Brouwer chiama questo atto un ‛passaggio di tempo". Iterando questo processo io costruisco mentalmente i numeri naturali. È chiaro che questi numeri, essendo costruiti mediante un atto mentale, non esistono al di fuori della mia mente; sono oggettivi per quel tanto che io posso indurre un'altra persona ad effettuare la corrispondente costruzione mentale.

Ogni tentativo di fondare la matematica intuizionista sulla logica o sulla filosofia è destinato a cadere in un circolo vizioso, poiché la logica e la filosofia, come qualsiasi altra scienza, fanno uso di un sistema di entità collegate da certe relazioni, e proprio questi sono i concetti fondamentali della matematica stessa. La matematica è una libera attività mentale; creare mentalmente un'entità è un atto che ognuno compie ogni giorno quasi continuamente. Possiamo costruire teorie filosofiche a proposito di questa attività, ma soltanto a posteriori. Questo vale in particolare per il presente articolo, che ha lo scopo di descrivere la matematica intuizionista, non di fondarla filosoficamente.

Seguendo Brouwer, chiamerò matematica classica la matematica nella forma usuale; dove scriverò ‛matematica' senza aggettivo, intenderò la matematica intuizionista.

2. Aritmetica elementare

Finora ho costruito mentalmente i singoli numeri naturali, ma non posso ancora fare affermazioni di carattere generale sui numeri naturali. Una proposizione del genere si può esprimere nella forma: ‛Supponiamo di aver costruito un numero naturale n, allora n ha la proprietà A". Tale proposizione contiene la nozione di costruzione ipotetica, che è fondamentale in matematica. Quasi ogni teorema si presenta nella forma: ‟Supponiamo che sia stata effettuata una costruzione A, allora posso effettuare anche la costruzione B". Una dimostrazione di questo teorema consiste in una costruzione C che, aggiunta alla costruzione A, fornisce la costruzione B. Per esempio, voglio dimostrare il teorema: ‟Se n è un numero naturale, allora esiste un numero primo più grande di n". La dimostrazione è la seguente. Supponiamo che sia stato costruito un numero naturale n (costruzione A). Voglio costruire un numero primo più grande di n (costruzione B). Si calcoli m = n! + 1 e si scomponga in fattori primi m; sia p il più piccolo fattore primo di m. Questa costruzione insieme con la dimostrazione che p > n costituisce la costruzione C. A rigore C non è una dimostrazione, ma un metodo generale di costruzione che può essere applicato a qualsiasi costruzione di un numero naturale.

Finora sono state necessarie le nozioni di ‛numero naturale', di ‛costruzione ipotetica' di un numero naturale e di ‛metodo generale' di costruzione da applicare a una costruzione ipotetica. Queste nozioni sono sufficienti per l'aritmetica elementare dei numeri naturali e razionali, che può essere costruita nel solito modo. Il significato dell'induzione completa in questa teoria sarà discusso più tardi (v. sotto, cap. 13).

3. Il principio del terzo escluso

La matematica intuizionista non tratta del mondo reale, nè di un mondo astratto di entità matematiche, bensì di costruzioni mentali. Ogni proposizione matematica P ha la forma: ‟Una costruzione A con tali e tali proprietà può venire eseguita". Una dimostrazione di P consiste nell'effettuare la costruzione A. Supponiamo che la proposizione Q significhi che la costruzione B può essere eseguita, allora la disgiunzione P ⋁ Q significa che almeno una delle costruzioni A e B può essere eseguita; P ⋁ Q si dimostra costruendo effettivamente o A o B. Si noti che non ha senso dire che o A o B è stata effettuata, senza sapere quale. Quindi come dimostrazione di P ⋁ Q noi abbiamo sempre una dimostrazione di P o di Q.

Supponiamo che P abbia lo stesso significato di prima. La negazione P significa che la costruzione A non può essere fatta; P si dimostra derivando una contraddizione dall'ipotesi che A sia stata effettuata. Quindi P ⋁ ¬ P si dimostra o effettuando A o derivando una contraddizione dall'ipotesi che A sia stata effettuata. Finché non si fa né una cosa nè l'altra, non si dispone di nessuna dimostrazione di P ⋁ ¬ P. In questo senso il principio logico del terzo escluso non vale nella matematica intuizionista. Per esempio, sia P la proposizione: ‟Esiste una coppia massima di numeri primi p, p + 2" (non si sa se la successione di queste coppie sia finita o infinita). Una dimostrazione di P consisterebbe nella costruzione di un'ultima coppia p, p + 2. Dato che una tale costruzione non è stata mai effettuata nè si è dimostrato che sia contradditoria, P ⋁ ¬ P in questo caso non è stata dimostrata. Dire che o esiste una coppia massima oppure no sarebbe un'affermazione relativa non a costruzioni mentali, ma a un mondo astratto di entità matematiche, di cui non si postula l'esistenza. Un tale postulato sarebbe un'ipotesi filosofica, che non può stare alla base della matematica.

Si è pensato a volte che il rifiuto del principio del terzo escluso significasse che oltre alla verità e alla falsità vi fosse un terzo valore di verità: il tertium. Quindi ogni proposizione sarebbe o vera o falsa o tertium. Questo è un equivoco. Consideriamo di nuovo la proposizione P che afferma che una costruzione A, dotata di determinate proprietà, può venir fatta. Quando viene effettuata una tale costruzione, noi diciamo che P è vera, quando deriviamo una contraddizione dall'ipotesi che A sia stata effettuata, diciamo che P è falsa; finché non viene fatta né l'una nè l'altra cosa, non possiamo dire niente su P; P non ha un terzo valore di verità, dato che in ogni momento può essere dimostrata vera o falsa.

Bisogna prestare una certa attenzione alla differenza fra l'uso della negazione in matematica e nel linguaggio quotidiano. In matematica la negazione ¬ P di una proposizione P può essere asserita quando è impossibile che P venga mai dimostrata, in altre parole, quando si sia derivata una contraddizione dall'ipotesi che P sia stata dimostrata. Nel linguaggio quotidiano la negazione è usata in senso più ampio. Quando dico che un certo evento non è accaduto, non voglio dire che fosse impossibile che accadesse. Per esempio, quando prima ho scritto che una coppia massima di numeri primi p, p + 2 non è stata trovata, non si trattava di una negazione matematica, poiché è perfettamente concepibile che una tale coppia venga trovata. Nel linguaggio ordinario si può dire che una proposizione P non è stata nè dimostrata nè confutata, ma in tal caso non si può affermare assolutamente niente a proposito di P in matematica. In matematica la negazione può comparire soltanto nel senso stretto della contraddittorietà, poiché ogni asserzione matematica deve esprimere una costruzione matematica e una dimostrazione di contraddittorietà è una costruzione. Questo articolo è scritto in linguaggio ordinario, di conseguenza le negazioni possono venire intese in senso debole, fuorché nelle asserzioni matematiche, dove devono sempre venir interpretate nel senso forte della contraddittorietà; l'ultimo significato è spesso messo in evidenza tramite locuzioni del tipo ‛impossibile', ‛contraddittorio', ‛assurdo'.

4. I numeri reali

L'introduzione dei numeri reali fa sorgere delle difficoltà per il costruttivista. Un numero reale è definito da una successione infinita di numeri razionali. In questo caso l'infinito è molto più essenziale che in aritmetica, dove compare soltanto nella forma: ‟Dopo ogni numero naturale ce n'è un altro". In analisi enunciamo proposizioni su ogni numero reale o, il che è lo stesso, su ogni successione infinita di numeri naturali. La difficoltà consiste nel fatto che noi non abbiamo una nozione chiara di successione ipotetica, poiché non esiste un metodo generale per costruire una successione, analogo al metodo di costruzione di un numero naturale.

Una soluzione fu resa possibile dalla teoria delle funzioni ricorsive. L'analisi ricorsiva è diventata un importante campo di ricerca, in cui sono stati ottenuti risultati molto fecondi dai matematici costruttivisti della scuola russa sotto la guida di A. A. Markov. Un importante lavoro nella stessa direzione è stato compiuto da E. Bishop (v., 1967). Egli definisce un numero reale tramite una successione convergente di numeri razionali che è data da una certa regola; chiameremo una tale successione ‛vincolata' (lawful). Da questa base egli sviluppa molti importanti capitoli dell'analisi.

Lo scopo di Brouwer era diverso. Era già stato dimostrato da Borel (v., 1914², p. 162) che la nozione di successione vincolata non può produrre il continuo così come viene generalmente concepito. È impossibile definire ogni punto del continuo con una successione vincolata, dato che l'insieme delle successioni vincolate è, in un certo senso imprecisabile esattamente, numerabile. Nella matematica non-costruttiva non c'è difficoltà: ci si limita a definire l'insieme di tutte le successioni convergenti, siano esse vincolate oppure no. Ma per i costruttivisti soltanto le successioni predeterminate esistono come individui. Brouwer si chiese come potesse venir definito costruttivamente il continuo. E trovò il modo introducendo la nozione di successione di scelte, cioè una successione i cui componenti sono scelti uno dopo l'altro. La libertà di scelta si può restringere mediante qualche legge; le successioni vincolate costituiscono un caso speciale di successioni di scelte.

Una definizione adeguata del continuo si ottiene usando successioni di frazioni duali {a_n/2ⁿ}, dove a_n è un intero, e garantendone la convergenza mediante la condizione ∣a_n~+1 − 2a_n∣ ≤ 1. Chiameremo questa rappresentazione la rappresentazione canonica del continuo.

Non si possono introdurre successioni di scelte nella matematica classica, poiché in essa le entità matematiche si considerano esistenti come oggetti definiti. Si possono studiare importanti settori della matematica costruttiva senza usare le successioni di scelte (v. Bishop, 1967), ma per molte ragioni è interessante prenderle in considerazione. Alcune di queste ragioni sono: 1) l'aritmetica dei numeri reali si può costruire con le successioni di scelte o senza di esse con uguale facilità. L'uguaglianza fra numeri reali è definita nella solita maniera e non vi è difficoltà nel definire la somma e il prodotto di due numeri reali definiti tramite le successioni di scelte. Ogni teorema dell'aritmetica elementare resta valido; 2) una nozione di continuo che corrisponda il più possibile alla nozione usuale si può ottenere soltanto usando successioni di scelte; 3) i ragionamenti sulle successioni di scelte e le loro proprietà presentano un interesse intrinseco e danno luogo a interessanti problemi.

Preciseremo ora la nostra terminologia definendo come entità matematiche: i numeri naturali, i numeri reali, le successioni vincolate e le successioni di scelte di numeri naturali o di numeri reali. Altre entità matematiche saranno introdotte al momento opportuno.

5. Ineguaglianza e separazione fra numeri reali

Vi sono due nozioni di ineguaglianza fra numeri reali. La prima, indicata con il simbolo ≠, è semplicemente la negazione dell'uguaglianza: a ≠ b si legge ‛a è diverso da b', e significa che si può dedurre una contraddizione dall'ipotesi a = b. Una nozione più forte è quella di separazione: a ???38??? b ‛a è separato da b', significa che si conosce un numero razionale positivo r tale che ∣ a − b ∣> r. Una delle ragioni per cui la relazione di separazione non può essere evitata è che la divisione è possibile soltanto rispetto a un numero separato da O; infatti per calcolare 1/a dobbiamo conoscere un effettivo limite inferiore positivo per ∣a∣ e quest'informazione non è necessariamente contenuta in una dimostrazione puramente negativa di a ≠.

La relazione di separazione gode delle seguenti proprietà: se a ???38??? b, allora, per ogni numero reale c, a ???38??? c oppure b ???38??? c. a ???38??? b implica a ≠ b. Se a ???38??? b è impossibile, allora a = b. Nessuna delle relazioni a = b, a ≠ b, a ???38??? b è decidibile.

La distinzione fra ≠ e ???38??? deve essere fatta sia per i numeri reali definiti da successioni vincolate, sia per quelli definiti da successioni di scelte. La relazione di separazione è fondamentale nell'analisi costruttiva, anche quando viene studiata senza le successioni di scelte. È anche importante in algebra, poiché deve comparire nella definizione di corpo; in questo caso la relazione di separazione può essere introdotta assiomaticamente.

6. Matematica e linguaggio

In primo luogo la matematica consiste di costruzioni mentali eseguite da un singolo matematico; tuttavia può essere comunicata. Non c'è una differenza essenziale fra l'uso del linguaggio per questo e per altri scopi. Noi usiamo il linguaggio per influenzare i pensieri e le azioni altrui. Quando un matematico scrive un articolo o un libro, egli intende suggerire costruzioni matematiche ai suoi colleghi, quando scrive appunti per ricordarsi dei risultati raggiunti, il suo io futuro riveste il ruolo di interlocutore. La comunicazione della matematica, come ogni tipo di comunicazione linguistica, è suscettibile di interpretazioni errate. È evidente che la costruzione di piccoli numeri naturali sia la stessa per tutti, ma anche un grande sforzo di chiarezza non può garantire una comprensione completa di strutture più complicate. Da questo punto di vista l'intuizionismo è esattamente l'opposto del formalismo.

Il formalista considera ogni ragionamento matematico intuitivo come inesatto. Egli studia il linguaggio in cui sono espressi tali ragionamenti e lo formalizza. Dal punto di vista intuizionista, il sistema formale ottenuto dal formalista appartiene alla matematica applicata; esso consiste in un sistema matematico molto semplice, applicato al linguaggio. Non c'è conflitto fra intuizionismo e formalismo fintanto che ognuno resta nel proprio ambito, finché cioè l'intuizionismo si dedica alle costruzioni mentali, e il formalismo alla costruzione di un sistema formale, attratto dalla sua intrinseca bellezza o dalla sua utilizzazione nel campo della scienza e della tecnica. Intuizionisti e formalisti si scontrano quando i formalisti pretendono che i loro sistemi esprimano il pensiero matematico. Gli intuizionisti muovono due obiezioni contro questa pretesa. In primo luogo non si possono esprimere esattamente, per mezzo del linguaggio, delle costruzioni mentali; in secondo luogo l'usuale interpretazione del sistema formale è insostenibile come costruzione mentale.

I formalisti hanno fatto molte ricerche sulle dimostrazioni di consistenza. L'importanza di una dimostrazione del genere è soprattutto pratica, giacché un sistema inconsistente non può essere molto utile. La pretesa che una dimostrazione di consistenza possa convalidare un'interpretazione del sistema formale è del tutto infondata.

Esiste una possibile applicazione dei metodi formali alla matematica intuizionista, in quanto rappresentano il modo migliore per investigare le ipotesi relative a una data dimostrazione. Recentemente il metodo formale è stato applicato con successo alle dimostrazioni nella teoria di Brouwer delle successioni di scelte (v. Kreisel e Troelstra, 1970). La formalizzazione della logica intuizionista ha anche un altro scopo, cioè quello di esprimere i teoremi logici in un linguaggio comprensibile per i matematici classici. Il lavoro metamatematico sul sistema formale della logica intuizionista, benché interessante in sé, ha poco a che vedere con la matematica intuizionista.

L'uso di assiomi. - Nessuna teoria matematica intuizionista è basata su assiomi. Per esempio, gli assiomi di Peano sono teoremi generali sui numeri naturali, che derivano dalla costruzione. Nell'ambito della matematica intuizionista gli assiomi sono usati come nella matematica classica. Quando si introduce la nozione di corpo tramite un sistema di assiomi A, si considera quest'ultimo semplicemente come un sistema di definizioni: una entità matematica F è un corpo se gode delle proprietà espresse da A. Un corpo particolare F viene determinato tramite una costruzione, indipendente dagli assiomi, dopodiché resta da dimostrare che F soddisfa A.

7. Matematica applicata

Il pensiero cosciente è un processo che consiste nel circoscrivere entità che l'osservazione ci mostra correlate; si tratta quindi di matematica applicata. Nella vita quotidiana la creazione di un'entità va di pari passo con la sensazione che essa rappresenta e con il complesso di memorie e di aspettative che è connesso con tale sensazione. Solo in un secondo tempo si può analizzare, più o meno in profondità, questo complesso nelle sue parti componenti. Esiste uno sviluppo graduale da questa attività naturale, che si svolge quotidianamente, alle scienze più astratte, costruite grazie all'intensa collaborazione di gruppi di scienziati. La scienza cerca di organizzare settori dell'esperienza che, per lungo tempo, sono sembrati del tutto isolati gli uni dagli altri, in una struttura più vasta che li comprenda tutti. Da questo punto di vista non c'è una differenza fondamentale fra la scienza in senso stretto e le scienze umane come la storia e la psicologia. La differenza essenziale fra le scienze non consiste nei metodi con cui cercano di strutturare il loro materiale, ma nel modo in cui ottengono il materiale grezzo.

Ogni scienza oltrepassa di gran lunga ciò che viene direttamente percepito, costruendo un modello matematico adatto alla spiegazione dei fenomeni. La struttura geometrica che noi imponiamo al mondo contiene molto di più di quello che noi possiamo effettivamente osservare. Analogamente gli storici cercano di sistemare i fatti che apprendono dai documenti nell'ambito di una struttura più vasta di eventi ipotetici.

La linguistica e la logica, l'ultima per quel tanto che non viene considerata un capitolo della matematica, appartengono alla matematica applicata. Lo stesso discorso vale per la filosofia se è studiata scientificamente.

Ricapitolando quanto detto possiamo affermare che: 1) la matematica è una libera attività della mente umana. Essa consiste nel costruire strutture a partire da entità correlate; 2) il pensare consiste nel costruire semplici strutture matematiche in relazione immediata con l'esperienza; 3) dato che la matematica appartiene ad ogni forma di pensiero, non ha bisogno di ulteriore fondazione; 4) la matematica pura consiste in strutture matematiche astratte, che non esistono al di fuori della mente umana; 5) la matematica si può comunicare per mezzo del linguaggio, ma non si può escludere in assoluto la possibilità che insorgano equivoci; 6) la logica si può studiare o come una parte della matematica o come un ramo della matematica applicata, ma non può costituire una fondazione per la matematica; 7) la filosofia scientifica appartiene alla matematica applicata. Il lavoro di molti filosofi non appartiene alla scienza ma alla letteratura. La matematica non può fondarsi sulla filosofia.

8. La teoria degli insiemi

La teoria classica degli insiemi pretende di descrivere un universo di insiemi che esistono indipendentemente dalla nostra mente. Nella matematica intuizionista la nozione di entità indipendenti dalla nostra mente è inammissibile. Un insieme S di entità matematiche è definito da una proprietà caratteristica P dei suoi elementi; P deve essere definita in maniera tale che, data un'entità a e una costruzione A, si possa decidere se A è una dimostrazione di aeS. Invece di ‛insieme' si usa il termine ‛specie'. Una specie è considerata un'entità matematica. Si può definire nel solito modo l'equivalenza fra specie. Non sempre è decidibile se due specie siano equivalenti, quindi il teorema di Schröder-Bernstein non vale. Le seguenti osservazioni sono importanti: 1) le entità matematiche sono introdotte per gradi. Ovviamente una specie S può contenere soltanto entità che possano essere definite prima che sia definita S. Per esempio, dopo che siano stati introdotti i numeri reali, si possono definire specie di numeri reali, quindi specie di specie di numeri reali, e così via. Questo procedimento conduce a una gerarchia analoga a quella della teoria dei tipi (v. Brouwer, 1924); 2) una specie S non può identificarsi con la collezione dei suoi elementi. La definizione di S e le definizioni dei suoi elementi sono completamente indipendenti l'una dalle altre; solo dopo che siano state date si può constatare che qualche entità è elemento di S; 3) non è necessario che sia decidibile la questione se un'entità a sia elemento di una specie S.

9. Spiegamenti

Definizioni. Una ‛direzione di spiegamento' D è una specie di successioni di numeri naturali che soddisfa le seguenti condizioni: 1) la successione vuota appartiene a D; 2) si può decidere per ogni numero naturale k se {k} è una successione a un solo membro in D oppure no; 3) se {a₁, a₂, ..., a_n, a_n+1} appartiene a D, allora {a₁, a₂, ..., a_n,} appartiene a D; 4) se {a₁, a₂, ..., a_n} appartiene a D, allora possiamo trovare almeno un numero naturale k tale che {a₁, a₂, ... , a_n, k} appartenga a D; 5) se {a₁, a₂, a_n} appartiene a D, allora si può decidere per ogni numero naturale k se {a₁, a_2~ ..., a_n, k} appartiene a D oppure no.

Uno ‛spiegamento' H è dato da una direzione di spiegamento D, una specie S e una legge F che assegna un elemento di S ogni elemento di D.

Se F{(a₁, ... , a_n)} = a_n per ogni successione in D, H si chiama spiegamento ‛svestito'.

Sia U = {a_n}_n una successione infinita tale che ogni segmento iniziale {a₁, ..., a_n} di U appartenga a D; allora la successione infinita F({a₁}), F({a₁, a₂}), ... è un elemento di H. La specie degli elementi di H si identifica con H. U può essere una successione vincolata o una successione di scelte.

La rappresentazione canonica del continuo (v. sopra, cap. 4) è data dal seguente spiegamento C. Definiamo D come segue: la successione {a₁, ..., a_m} appartiene a D se ∣a_n+1 − 2a_n ∣ ≤ I ⟨ 1 per ogni n ⟨ m. S è la specie dei numeri razionali. F({a₁, ..., a_m}) = a_m•2^-m. Un elemento di C è una successione infinita {a_m•2^-m}_m, dove gli a_m, soddisfano la condizione: ∣ a_n+1 − 2a_n ∣ ≤ 1 per ogni n.

Un sottospiegamento di uno spiegamento H si ottiene sostituendo D con una sottospecie D′ di D che sia una direzione di spiegamento. Per esempio, se, nel caso preso in considerazione sopra, aggiungiamo alla definizione di D la condizione 0 ⟨ a_n ⟨ 2ⁿ per ogni n, otteniamo uno spiegamento che rappresenta l'intervallo chiuso [0,1]. Si noti che in questo caso esiste un'unica possibilità di scelta per a₁ e, dopo che è stato scelto a_n vi sono tre possibilità di scelta per a_n+1; quindi ad ogni stadio esiste soltanto un numero finito di possibilità. Uno spiegamento con questa proprietà si chiama spiegamento ‛finitario' o ‛ventaglio'.

Un elemento α di uno spiegamento svestito H è una successione di scelte (che in casi speciali può essere vincolata). In ogni momento della sua generazione esso consiste di un segmento iniziale finito insieme con le restrizioni che regolano la sua continuazione. Se si assegna ad α mediante una certa regola f un numero naturale f(α), allora f(α) deve diventare noto dopo un tempo finito, quindi f(α) è definito da un segmento iniziale finito {a₁, ..., a_n} di a. Se f è definita per ogni elemento di H, allora f(β) avrà lo stesso valore per ogni elemento β di H che abbia {a₁, ..., a_n} come segmento iniziale. Questa proprietà è il ‛principio di continuità' di Brouwer. La specie delle successioni {a₁, ..., a_n} per cui il valore di f diventa noto è uno ‛sbarra- mento' in D. La definizione generale di ‛sbarramento' è la seguente: una sottospecie B di una direzione di spiegamento D è uno sbarramento in D se ogni successione infinita, ogni ‛segmento iniziale della quale appartenga a D, ha esattamente un segmento iniziale in B.

Uno sbarramento B in D e una funzione f da B ai numeri naturali definiscono una funzione ϕ su H nella maniera seguente: sia α ∈H e sia n il segmento iniziale di α in B, allora ϕ(α) = f(n). La stessa funzid~e f può essere usata per definire una funzione ψ da H alla specie delle funzioni di scelta di numeri naturali. Sia β una successione di scelte, allora ψ(β) = γ è definita da γ(n) = ϕ({n} * β), dove il simbolo * indica concatenazione: se {n} * β = δ, allora δ(l) = n e δ(m) = β(m − l)per μ > 1.

L'ultima definizione può essere usata per chiarire la nozione di successione di scelte. Non basta considerare solamente successioni libere (lawless), in cui ogni scelta non è sottoposta ad alcuna restrizione, dato che nessun'altra relazione oltre all'eguaglianza intensionale è concepibile fra successioni libere. Non appena una successione dipende da un'altra successione non è libera. Kreisel e Troelstra (v., 1970) propongono di ammettere successioni ψ(α), dove α è libera e ψ è definita come sopra. Essi costruiscono un sistema formale CS per la teoria di queste successioni, in cui valgono i principali teoremi della teoria di Brouwer. È un notevole risultato il fatto che la nozione di successione di scelte può venire eliminata da CS. Più esattamente, Troelstra e Kreisel dimostrano i seguenti teoremi. Qualsiasi formula A che non contenga variabili libere per successioni di scelte è equivalente in CS a una formula A′ senza variabili per successioni di scelte. Inoltre, quando A è dimostrabile in CS, allora A è dimostrabile in un sottosistema di CS in cui non occorrano variabili per successioni di scelte.

Allo scopo di formulare il principio di Brouwer di ‛induzione di sbarramento' (bar induction) introduciamo la nozione di ‛retroinduzione' (backward + induction). Una proprietà Q di successioni finite è ‛retroinduttiva' nella direzione di spiegamento D se gode della seguente proprietà: quando ogni immediata continuazione a₁, ..., a_n, b in D della successione a₁, ..., a_n gode della proprietà Q, allora a₁, ..., a_n gode della proprietà Q.

Principio di ‛induzione di sbarramento' (bar induction). Se Q è una proprietà retroinduttiva in D e ogni elemento di uno sbarramento in D gode della proprietà Q, allora la successione vuota gode della proprietà Q.

La dimostrazione che dà Brouwer di questo principio è notevole. Egli comincia col chiedersi: come possiamo sapere se B è uno sbarramento in D? Analizzando le possibili dimostrazioni di questo fatto, egli ricava il teorema. Sembra che così facendo Brouwer mescoli la matematica con considerazioni sulla matematica, ovvero, nella terminologia dei formalisti, la matematica con la metamatematica. Ma nella matematica intuizionista una dimostrazione è essa stessa una costruzione matematica che può essere trattata matematicamente come altre costruzioni. La sottile distinzione fra matematica e metamatematica non può essere mantenuta.

Il seguente teorema è un'importante conseguenza del principio di ‛induzione di sbarramento' (bar induction). Teorema del ‛ventaglio'. Ogni sbarramento in un ventaglio è finito. Dimostrazione. Sia H un ventaglio e D la sua direzione di spiegamento. Sia B uno sbarramento in D. A un elemento n di D corrisponde una sottospecie decidibile D(n) di D costituita dalle continuazioni in D di n. D(n) ⋂ B è uno sbarramento B(n) in D(n). Si applichi il principio di ‛induzione di sbarramento' (bar induction) alla proprietà: B(n) è finito.

Corollario. Se una funzione f associa un numero naturale a ogni elemento di un ventaglio H, allora possiamo trovare un numero naturale N tale che, per ogni elemento α di H, f(α) è determinato dalle prime N scelte di α.

Il teorema del ventaglio, appena dimostrato, ha conseguenze molto importanti in analisi.

Dal fatto che un intervallo chiuso del continuo coincide con un ventaglio, segue che ogni funzione reale che sia definita su un intervallo chiuso è uniformemente continua. Questo non significa che siano escluse dall'analisi funzioni discontinue; significa soltanto che una funzione del genere non può venire definita dovunque. Per esempio, la funzione che vale 0 per 0 ≤ x ≤ ½ e 1 per ½ ⟨ x ≤ 1 è indefinita per valori di x per cui non si sappia se ⟨ x.

Un'altra conseguenza del teorema precedente è che le uniche sottospecie decidibili del continuo sono la specie vuota e il continuo stesso. Infatti, se U è una sottospecie decidibile del continuo, allora la funzione che vale 1 su U e O sul suo complemento è definita ovunque e quindi è continua; dato che essa non assume altri valori oltre O e 1, è costante.

I teoremi che seguono sono ulteriori conseguenze del teorema del ventaglio. Una funzione definita ovunque su un intervallo chiuso E possiede su E un minimo confine superiore e un massimo confine inferiore. Se essa è dovunque positiva in E, il suo m.c.i. è positivo.

10. Il soggetto creativo

In alcuni dei suoi ultimi articoli Brouwer (v., 1948) ammette che il matematico effettui le scelte per una successione facendo dipendere le sue scelte dalla propria conoscenza matematica al momento della scelta. Egli usa tali successioni per la costruzione di controesempi a teoremi classici che non valgono dal punto di vista intuizionista. Il suo primo e più semplice esempio riguarda le nozioni di ineguaglianza fra numeri reali. Sia P una proposizione per cui non sia stato dimostrato nè ¬ P nè ¬¬ P. Il numero reale a sia definito dalla successione di scelte {a_n} nel seguente modo: finché né ¬ P nè ¬¬ P siano state dimostrate, io scelgo a_n = 2^-n ma se ¬ P o ¬¬ P viene dimostrata fra la scelta di a_m e quella di a_m+1, allora scelgo a_m+q = 2^-m per ogni q. Si osservi che a = 0 implicherebbe che né ¬ P nè ¬¬ P potrebbero mai essere dimostrate, il che è contraddittorio: quindi a ≠ 0. D'altronde a ???38??? 0 significherebbe che potremmo trovare un numero q tale che a > 2^-q; ne seguirebbe che o ¬ P o ¬¬ P sarebbe dimostrata prima della scelta di a_q. Ma questo possiamo saperlo soltanto se siamo effettivamente in grado di dimostrare o ¬ P ¬¬ P, il che nel caso attuale non si verifica. a è un esempio di numero reale per cui vale a ≠ 0, mentre non si sa se a ???38??? 0. Naturalmente a ???38??? 0 non può essere falso, poiché ciò implicherebbe a = 0.

11. Relazioni d'ordine

Una specie S è ordinata dalla relazione ⟨ se per ogni coppia di elementi a, b di S vale una delle seguenti proprietà: a ⟨ b, a = b, b ⟨ a. Il continuo non può essere ordinato, perché l'uguaglianza fra elementi del continuo non è decidibile. Ogni relazione d'ordine sul continuo è parziale. La relazione di separazione ???38??? dà luogo a una relazione d'ordine tale che a ???38??? b equivale a ‛o a ⟨ b, o b ⟨ a'. Questa relazine si chiama ‛pseudo ordine del continuo'. Brouwer definì una relazione più debole ???32???, tale che a ???32??? b equivale a ¬¬ (a ⟨ b). Comunque la relazione di pseudo ordine è più importante in analisi.

L'usuale definizione della nozione di insieme bene ordinato non è utilizzabile nella matematica intuizionista, neppure nella formulazione forte: la specie ordinata S è ben ordinata se ogni sottospecie decidibile di S che contenga almeno un elemento ha un primo elemento. Questo vale per specie col tipo d'ordine ω dei numeri naturali, ma non per specie con tipo d'ordine ω + 1. Controesempio: sia S la specie dei numeri naturali nel loro ordine solito, seguiti da un elemento a. Si consideri la sottospecie T che contiene a e quei numeri naturali n per cui le cifre dall'nesima alla (n + 9)-esima nello sviluppo decimale di π sono tutte 7. Non siamo in grado di trovare il primo elemento di T finché non si riesca a trovare dieci 7 successivi in π o si riesca a dimostrare che tale successione di 7 non può occorrere.

Nella matematica intuizionista non esiste alcuna nozione corrispondente alla nozione generale di insieme ben ordinato della matematica classica. In essa non compare la gerarchia di cardinali definita tramite tale nozione. Già la seconda classe di numeri concepita come un'entità compiuta non ha un equivalente in campo costruttivista. D'altronde c'è una stretta analogia fra la teoria intuizionista delle specie ben ordinate e la teoria classica degli ordinali ricorsivi; ma sussiste anche un'importante diversità di interpretazione. Gli ordinali ricorsivi sono definiti come sottoinsiemi di tutti gli ordinali, mentre Brouwer definisce direttamente la nozione di specie bene ordinata. La sua definizione procede così: a) la specie che contiene una sola entità matematica è ben ordinata; b) la somma ordinata di una successione finita di specie ben ordinate separate, precedentemente definite, è ben ordinata; c) la somma ordinata di una successione infinita di specie ben ordinate precedentemente definite è ben ordinata.

È facile vedere che ogni specie ben ordinata è finita o numerabile. Ogni successione discendente in una specie ben ordinata è finita. L'induzione transfinita è possibile in una data specie ben ordinata. Un ordinale è definito come specie di specie ben ordinate simili. Gli ordinali sono solo parzialmente ordinati, dato che l'uguaglianza fra ordinali non è decidibile. Ciò rende la teoria degli ordinali molto più complicata che nella matematica classica.

12. L'interpretazione delle costanti logiche

Noi usiamo le seguenti notazioni: ⋀ (congiunzione), ⋁ (disgiunzione), ¬ (negazione), → (implicazione), ∀ (quantificatore universale), ???29??? (quantificatore esistenziale). Questi connettivi si interpretano stabilendo che cosa si intenda come dimostrazione di una proposizione composta in termini di dimostrazioni delle proposizioni componenti.

Congiunzione. Una dimostrazione di P ⋀ Q consiste in una dimostrazione di P e in una dimostrazione di Q.

Disgiunzione. Una dimostrazione di P ⋀ Q è o una dimostrazione di P o una dimostrazione di Q. Quindi non basta dimostrare che P e Q non possono essere entrambe false.

Negazione. Una dimostrazione di ¬ P consiste in un metodo generale che trasformi ogni supposta dimostrazione di P in una contraddizione. La nozione di contraddizione si deve considerare fondamentale; 1 = 2 può essere preso come paradigma.

Implicazione. Una dimostrazione di P → Q consiste in un metodo generale che trasformi ogni data dimostrazione di P in una dimostrazione di Q.

Quantificatore universale. Una dimostrazione di ∀xP(x), dove il dominio di x è la specie S, consiste in un metodo M che porti al seguente risultato: se A denota la costruzione di un'entità a insieme con la dimostrazione che a∈5, allora M trasforma A in una dimostrazione di P(a).

Quantificatore esistenziale. Una dimostrazione di ???29???xP(x), dove il dominio di x è la specie S, consiste nella costruzione di un'entità a, in una dimostrazione di a∈S e in una dimostrazione di P(a).

Con questa interpretazione la logica diventa una parte della matematica, in quanto un teorema logico afferma che una certa costruzione può essere effettuata. Per esempio, ∀ x¬ P(x) →¬ ???29??? x P(x) afferma che esiste una costruzione che da una qualsiasi dimostrazione di ∀ x¬ P(x) conduce a una dimostrazione di ¬ ???29??? x P(x). Una tale costruzione si ottiene come segue: sia A una dimostrazione di ∀ x− P(x). Dobbiamo ricavare una contraddizione dall'ipotesi che si abbia una dimostrazione B di ???29??? x P(x). B ci darebbe un'entità a tale che P(a); ma A implicherebbe ¬P(a) e quindi da P(a) ricaviamo una contraddizione.

In questa interpretazione il principio del terzo escluso non vale. Di conseguenza non si può ignorare la doppia negazione. Si consideri per esempio un numero reale c di cui non si sappia se è razionale oppure no. Sia Q la proposizione c è razionale oppure c è irrazionale'. Per ipotesi non disponiamo di una dimostrazione di Q. È facile tuttavia vedere che Q non può essere falsa, perché, in tal caso, sarebbe falso, in particolare, che e sia un numero razionale, sicché e sarebbe irrazionale, e quindi Q sarebbe vera. In questo modo si può dimostrare che la doppia negazione di ogni caso specifico del principio del terzo escluso vale, ma il principio stesso non vale in ogni caso.

Diamo ancora un esempio. Definiamo un numero reale d come segue. Scriviamo lo sviluppo decimale di π e sotto di esso una frazione decimale d = 0,111..., in cui ogni cifra dopo la virgola è 1 finché non compaiano dieci 7 consecutivi in π, mentre dai primi dieci 7 consecutivi in π in poi, ogni altra cifra in d è 0. Quindi, se nello sviluppo di π compaiono a un certo punto dieci 7 consecutivi, d è una frazione decimale finita e rappresenta un numero razionale; se non compaiono dieci 7 consecutivi in π, d = 1/9. D'altronde la proposizione P: ‛d è razionale' non può esser detta vera, dato che per dimostrare P bisogna calcolare due numeri naturali p e q tali che d = p/q; allo stato attuale delle nostre conoscenze non siamo in grado di fare ciò. Tuttavia ¬¬ P è vera, poiché, supponiamo ¬ P, allora d sarebbe irrazionale, sicché in π non potrebbero comparire dieci 7 consecutivi, quindi sarebbe d = 1/9. Questa è una contraddizione, perciò ¬¬ P.

Naturalmente P implica ¬¬P, poiché se vale P, allora ¬ P è contraddittoria, sicché vale ¬¬ P; sostituendo ¬P a P otteniamo ¬ P → ¬¬¬ P. In questo caso vale anche il viceversa, cioè ¬¬¬ P → − P; infatti, supponiamo che valga ¬¬¬ P, allora ¬¬ P conduce a una contraddizione, quindi a fortiori P è contraddittoria. Non è necessario prendere in considerazione sequenze formate da più di due negazioni.

Una relazione si chiama estabile~ se è equivalente alla sua doppia negazione. Ogni relazione negativa è stabile poiché ¬¬¬ P equivale a ¬ P. L'uguaglianza fra numeri reali può essere considerata come una relazione negativa, poiché a = b è equivalente a¬ (a ???38??? b); quindi è stabile. La separazione non è stabile poiché ¬¬(a ???38??? b) è equivalente a a ≠ b, e non a a ???38??? b.

I quattro connettivi del calcolo proposizionale sono indipendenti. Nessuno di essi può essere definito in termini degli altri tre. Anche i due quantificatori sono indipendenti in questo senso. Da ¬ ∀ x ¬ P(x) segue che ¬¬ ???29??? x P(x), ma non che ???29??? x P(x). Controesempio: facciamo variare x sui numeri razionali e sia P(x): ‛x = d', dove d è il numero definito sopra. Analogamente, da ¬ ???29??? x ¬ P(x) segue che ∀ x¬¬ P(x), ma non che ∀ x P(x). Controesempio: facciamo variare x sui numeri reali e sia P(x): ‛x è razionale o x è irrazionale'.

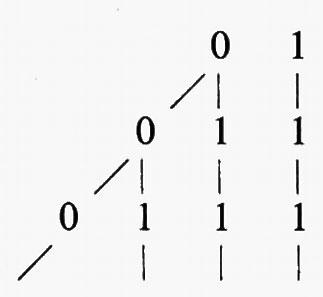
Il seguente esempio conduce a un notevole risultato. Consideriamo la direzione di spiegamento consistente in successioni di 0 e 1 con la restrizione che 1 può essere seguito soltanto da 1. D definisce un ‛ventaglio svestito' M che è illustrato dallo schema seguente:

La seguente regola A associa numeri a elementi di M: se a ∈ M e ogni membro di a è 0, allora A(a) = 1; se ogni membro di a è 1, allora A(a) = 2; se a consiste di n ‛zeri' seguiti da tutti ‛uno', allora A(a) = n + 2. Facciamo variare x su M e sia P(x): ‛A associa un numero a x'. Allora ∀ x ¬¬ P(x) è vera. Dimostriamo il teorema equivalente: ¬ ???29??? x ¬ P(x), deducendo una contraddizione dalla supposizione che A non associ alcun numero a un certo elemento a di M. Sotto tale ipotesi il primo membro di a non può essere 1, poiché in tal caso A(a) sarebbe 2; quindi il primo membro è 0. Il secondo membro non può essere 1, poiché A(a) sarebbe 3, sicché il secondo membro deve essere 0. Continuando in questo modo vediamo che ogni membro di a è 0; ne segue che A(a) = 1, risultato che contraddice l'ipotesi fatta. Quindi vale ¬ ???29??? x ¬ P(x) e anche ∀ x ¬¬ P(x). Tuttavia ¬¬ ∀ x P(x) non vale: possiamo persino dimostrare che vale ¬ ∀ x P(x). Supponendo che valga ∀ x P(x), il teorema del ‛ventaglio' ci permette di inferire che A(x) deve essere noto per ogni x dopo che sia stato dato un numero finito N di membri di x, ma questo contraddice evidentemente la definizione di A.

È importante apprezzare il significato ditali esempi costruiti artificialmente. Nella maggioranza dei casi il loro scopo è quello di mostrare che un certo teorema classico non vale dal punto di vista intuizionista. Tali esempi sono paragonabili ai controesempi della matematica classica, come quello di una funzione continua senza derivata. Il fatto che i matematici intuizionisti diano molti esempi del genere, allo scopo di mostrare in quali punti la matematica intuizionista si scosti dalla matematica classica, ha dato luogo alla falsa idea che tali esempi siano essenziali nella matematica intuizionista. Questo non è vero; la costruzione della matematica intuizionista è indipendente da tali controesempi.

Un sistema formale di logica intuizionista è stato dato da Heyting. Naturalmente un tale sistema non intende fornire una fondazione per la matematica intuizionista. Si tratta di un sistema linguistico e come tale può servire alla comunicazione, ma soltanto sulla base di una interpretazione semantica delle costanti come quella tracciata sopra.

Una dimostrazione è una costruzione. Kreisel (v., 1962) ha tracciato una teoria generale delle costruzioni da cui si possono dedurre le regole della logica intuizionista.

13. L'induzione completa

Le dimostrazioni per induzione completa sono valide nella matematica intuizionista. Sia P(x) una proprietà che può essere goduta da un numero naturale x. Supponiamo di aver provato P(i) e di possedere un metodo generale M che ci permetta di dedurre, per ogni numero naturale n, una dimostrazione di P(n + 1) da una dimostrazione di P(n). Sia x un qualsiasi numero naturale. Per dimostrare P(x) eseguiamo la costruzione di x e ad ogni passaggio da n a n + i applichiamo M per ottenere P(n + 1). Il risultato sarà una dimostrazione di P(x).

Questo ragionamento può essere considerato una dimostrazione generale di induzione completa. Comunque, non abbiamo bisogno del teorema generale per applicare l'induzione completa nei casi specifici.

14. Nozioni che dal punto di vista classico sono equivalenti

Accade spesso che una nozione della matematica classica scivoli nella matematica intuizionista trasformandosi in una nozione più forte e in una nozione più debole. Per esempio, la ineguaglianza fra numeri reali dà luogo alle relazioni di separazione e di differenza. Nella maggior parte dei casi la nozione più forte, essendo definita senza negazione, è la più importante, ma la più debole può avere interessanti proprietà.

La nozione di convergenza di una successione di numeri reali è un altro esempio. La nozione forte è definita nella solita maniera: la successione {a_n} è ‛convergente' al limite a se:

∀ k ???29??? n ∀ p(∣a_n+p − a∣ ⟨ 1/k). (1)

La successione {a_n} è una ‛successione di Cauchy' se:

∀ k ???29??? n ∀ p(∣a_n-+p − a_n∣ ⟨ 1/k). (2)

Si dimostra facilmente che ogni successione di Cauchy è convergente e che se ne può calcolare il limite. La successione {a_n} è ‛debolmente convergente' al limite a se:

∀ k ¬¬ ???29??? n ∀ p(∣a_n+p − a ∣ ⟨ 1/k); (3)

e ‛non oscillante' se

∀ k ¬¬ ???29??? n ∀ p(∣a_n+p − a_n∣ ⟨ 1/k). (4)

Come mostra il seguente esempio, non è vero che ogni successione non oscillante sia debolmente convergente. Sia a_n = 0 se non occorrono dieci 7 consecutivi fra le prime n cifre dello sviluppo decimale di π; a_n = i altrimenti. Per dimostrare che questa successione è non oscillante supponiamo di aver trovato un k tale che:

∀ n ¬ ∀ p(∣a_n+p − a_n∣ ⟨ 1/k₀) (*)

Supponiamo inoltre che in ‛ occorra una successione di dieci 7 consecutivi; allora avremo, per un n abbastanza grande, ∀ p(a_n+p = a_n = 1), in contraddizione con la (*). Quindi ∀ n(a_n = 0), che contraddice nuovamente la (*). Abbiamo derivato

¬ ???29??? k ∀ n ¬ ∀ p(∣ a_n+1 − a_n ∣ ⟨ 1/k),

che è equivalente alla (4). D'altronde non sappiamo se il limite sia O o 1, sicché non possiamo dire che la successione sia debolmente convergente.

Un teorema classico dice che una successione limitata monotona è convergente. Il seguente esempio mostra che questo non vale dal punto di vista intuizionistico. Sia a_n = 1 − 1/n se fra le prime n cifre dello sviluppo decimale di π non occorrono dieci 7 consecutivi; a_n = 2 − 1/n altrimenti. Si può dimostrare il seguente teorema più debole: ogni successione limitata monotona di numeri reali è non oscillante.

Teorema di Bolzano-Weierstrass. - L'ultimo esempio mostra anche che una specie limitata infinita di numeri reali non ha necessariamente un punto di accumulazione, sicché il teorema di Bolzano-Weierstrass non vale. In relazione con questo teorema si devono discutere differenti nozioni di finitezza e di infinità. Una specie è ‛finita' se si conosce un numero naturale che sia il numero dei suoi elementi. Si noti che una sottospecie di una specie finita è finita soltanto se è decidibile. Una specie è ‛limitata in numero' dal numero N se non può avere una sottospecie di N elementi. Una specie 5 è ‛numerabilmente infinita' se si conosce una corrispondenza biunivoca fra 5 e i numeri naturali. Una specie è ‛infinita' se contiene una sottospecie numerabilmente infinita. La seguente nozione è più forte: una specie S è ‛D infinita' se si conosce una corrispondenza biunivoca fra S e un sottoinsieme proprio di S.

L'usuale forma del teorema di Bolzano-Weierstrass non vale, nè vale la seguente forma che, dal punto di vista classico, è equivalente: una specie limitata di numeri reali senza un punto di accumulazione è finita. Brouwer ha dimostrato che valgono i seguenti teoremi.

Sia S una specie limitata infinita di numeri reali e siano m e n numeri naturali. Allora esiste un intervallo di lunghezza 2^-n che contiene almeno m elementi di S.

Se Q è una specie limitata di numeri reali con la proprietà che per ogni numero reale x si può trovare un numero naturale N(x) tale che l'intervallo (x - 2-~(z>, x + _2~N(z)) non possa contenere due differenti elementi di Q, allora Q è limitata in numero.

Topologia

In topologia la nozione di insieme aperto, definita nel solito modo, è meno importante della più costruttiva nozione di regione. Per convenienza consideriamo la topologia di una parte limitata del piano euclideo, per esempio un quadrato chiuso. Un ‛dominio elementare' V è definito da un insieme finito di rettangoli con vertici razionali e lati paralleli agli assi delle coordinate. Un punto P ‛appartiene a' V se è il limite di una successione di punti razionali in tali rettangoli. Una ‛regione' è l'unione di una successione {V_n} di domini elementari tali che V_n sta in V_n+1 per ogni n. Analogamente la nozione di specie chiusa può agevolmente essere sostituita da quella di ‛complemento di regione'. Un complemento di regione in una parte limitata del piano può anche venire definito come l'intersezione di una successione contraente (contracting) di domini elementari. Se P è un punto, A una regione, M un complemento di regione, allora P ∈ M è una relazione stabile, mentre P ∈ A non lo è.

Specie di punti localizzate

La ‛distanza' g(p, Q) di un punto p da una specie di punti Q è definita nel solito modo. Una specie di punti Q si chiama ‛localizzata' se g(p, Q) può essere calcolata per ogni punto p. Questa nozione è importante per i seguenti teoremi.

Ogni specie di punti localizzata chiusa e limitata coincide con un ‛ventaglio di punti canonico.

La chiusura di un ventaglio di punti canonico coincide con un complemento di regione localizzato.

Un ventaglio di punti canonico è definito in tal caso da una direzione di spiegamento D in cui ogni successione ha la forma {(a₁, b₁)}, ...,(a_m, b_m)}, dove ∣a_n+1 − 2a_n∣ ≤ 2^-n e ∣ b_n-1 −2b_n ∣ ≤ 2^-n per n ⟨ m, e F({(a₁, b₁), ..., (a_m, b_m)}) = (a_m2^-m, b_m2^-m).

Segue da questi teoremi che le proprietà di una funzione definita ovunque su un intervallo chiuso si possono estendere a funzioni definite ovunque su un complemento di regione localizzato; una tale funzione è uniformemente continua, ha un massimo limite inferiore, e, se è ovunque positiva, il suo massimo limite inferiore è positivo.

Il teorema di Heine-Borel vale per specie localizzate nella forma seguente: sia Q una specie di punti localizzata chiusa e limitata; se a ogni punto p di Q è associato un intorno U(p) di p, allora possiamo trovare un insieme finito U(q₁), ..., U(q_n~) di tali intorni in modo che Q sia contenuto nella loro unione.

15. Misura e integrazione

Misura di una regione

Essendo una regione definita da una successione {V_n} di domini elementari, è naturale definire la sua misura μA come

dove μV_n è l'area di V_n. Comunque, tale limite non esiste necessariamente, perché non è detto che una successione monotona limitata sia convergente. Se il limite esiste, A viene chiamata ‛regione misurabile' e il suo complemento M è un ‛complemento di regione misurabile'.

Definizione. Una specie di punti che contenga per ogni n un complemento di regione di misura più grande di 2^-n si chiama ‛quasi piena'. Una proprietà valida su una specie quasi piena si dice valida ‛quasi ovunque'.

La nozione generale di specie di punti misurabile può essere definita direttamente o per mezzo della definizione di funzione misurabile. Adotteremo il secondo metodo.

Funzioni misurabili. - Non ogni definizione classica di funzione misurabile può venire usata. Per esempio, se la funzionef assume il valore costante a e se b è un numero reale tale che non si sa se b = a, allora la specie di punti per cui f(x) = b non è misurabile, poiché la sua misura potrebbe essere tanto O quanto 1. Comunque, la definizione per mezzo di funzioni a gradini si può adattare. Consideriamo funzioni nel quadrato unitario E. La definizione è la seguente: la funzione f, definita su una sottospecie Q di E, è ‛misurabile' se per ogni numero naturale n sono date una regione misurabile A_n con μA_n ⟨ 2^-n e dei domini elementari V_nh(h = − l_n, ..., − 1,0,1, ..., k_n) tali che coprano semplicemente E, e in modo che siano rispettate le seguenti condizioni:

1) per x ∈ V_nh ⋂ (E − A_n), h ≠ 0, si abbia (h − 1) 2^-n-1 ???31??? f(x) ???31??? (h + 1)2^-n+1;

2) per x ∈ V_n0 ⋂ (E − A) ⋂ Q, si aabbia − 2^-n-1 ???31??? f(x) ???31??? + 2^-n-1;

3) V_nh ⋂ (E − _n) contenga almeno un punto interno (− l_n ≤ h ≤k_n).

‛L'integrale' della funzione misurabile f è così definito:

Quando f è limitata questo limite esiste sempre.

Una funzione limitata definita quasi ovunque in E è misurabile. Inversamente, ogni funzione misurabile limitata si può completare in una funzione misurabile definita quasi ovunque con lo stesso integrale.

Specie di punti misurabili. - La misura di una specie di punti limitata Q può essere definita per mezzo della funzione f_Q : f_Q(x)= 1 per x ∈ Q, f_Q(x) = 0 per x ∉ Q (per l'ulteriore sviluppo della teoria della misura e dell'integrazione v. Gibson, 1969; v. Heyting, 1971).

Altre parti della matematica che sono state sviluppate nei dettagli sono: l'algebra (v. Heyting, 1941), l'analisi funzionale (v. Ashwinikumar, 1966; v. Ashwinikumar e Shukla, 1971; v. Heyting, 1951), la topologia (v. Freudenthal, 1936; v. Troelstra, 1966).

16. Matematica senza negazione

Gli intuizionisti ammettono teoremi del tipo: ‟Un corpo di sei elementi non esiste". Griss (v., 1946 e 1950) obiettò che ogni nozione matematica deve avere la sua origine in qualche costruzione matematica che possa effettivamente venire eseguita; se la costruzione è impossibile, allora, afferma Griss, la nozione non può essere chiara. Se un campo di sei elementi non può esistere, come possiamo avere un'idea precisa di quel che sarebbe se esistesse?

In molti casi la dimostrazione di un teorema negativo suggerisce una forma positiva dello stesso teorema; per esempio: ‟Il numero degli elementi di un campo finito è una potenza di un numero primo". Griss cerca di evitare sempre la negazione. Quindi la relazione ≠ non può venire introdotta nella aritmetica dei numeri reali; l'unica relazione di differenza è ???38???. Al posto del teorema ¬(a ???38??? b) → a = b Griss usa: ∀ x (x ???38??? a → x ???38??? b) → a = b.

Il lavoro di Bishop (v., 1967) può essere considerato la realizzazione delle intenzioni di Griss per quel che riguarda l'analisi senza successioni di scelte. Egli evita la relazione ≠ introducendo la relazione ≤ come segue: a ≤ b significa che a − b > − r per ogni numero razionale positivo r, e dimostra che a ≤ b ⋀ b ≤ a → a = b. Una parte considerevole dell'analisi viene sviluppata nel libro di Bishop.

L'ulteriore sviluppo della teoria degli insiemi e della logica senza negazione porta ad enormi complicazioni. Nella teoria degli spiegamenti e delle specie non si può definire la specie vuota, poiché una proprietà di oggetti matematici può avere un senso chiaro soltanto dopo che si sia costruito un oggetto che la soddisfi. Di conseguenza, l'intersezione di due specie è definibile soltanto se contiene almeno un elemento. In logica non esiste calcolo proposizionale, poiché soltanto le proposizioni vere hanno senso. Inoltre si deve prendere in considerazione la restrizione nell'uso della congiunzione fra funzioni proposizionali, così come quella relativa all'intersezione di specie. Per tutte queste ragioni è possibile che la matematica senza negazione non verrà mai sviluppata al di là dell'analisi ordinaria, benché siano stati fatti numerosi tentativi per formalizzare la logica senza negazione.

17. Conclusioni

L'intenzione del matematico intuizionista è di rendere la matematica indipendente sia dall'esperienza sia da presupposti filosofici. I matematici classici non ottemperano a questa condizione poiché sono convinti dell'esistenza di un mondo di oggetti matematici. Per l'intuizionista gli oggetti matematici sono generati da una costruzione mentale; essi esistono soltanto nella mente. Nella vita quotidiana ognuno fa continuamente delle semplici costruzioni matematiche mediante le quali ordina la sua esperienza. C'è uno sviluppo graduale da questa forma primitiva di matematica alle complicate costruzioni astratte degli specialisti.

In linea di principio la matematica è indipendente dalle sue espressioni linguistiche; comunque il linguaggio è indispensabile per la comunicazione e per aiutare la memoria. L'uso del linguaggio è essenzialmente lo stesso in matematica e nella vita quotidiana. I matematici sono esseri umani e come tali possono sbagliare. Il linguaggio può aiutarli ad evitare confusioni, in particolare quando vengono studiate nozioni inusuali, fornendo l'opportunità di enunciare esattamente quali proprietà della nozione in questione verranno usate. Era questo il caso, in particolare, della teoria delle successioni di scelte, che non è mai stata abbastanza chiara prima che venisse costruito per essa un sistema formale. Ciò non significa naturalmente che il sistema formale sia più importante ovvero che preceda la nozione di successione di scelte, ma soltanto che era necessario fissare le proprietà delle successioni di scelte che devono essere usate nelle dimostrazioni.

In logica matematica si studia la combinazione di dimostrazioni; dato che una dimostrazione è a sua volta una costruzione matematica, la logica è una parte della matematica. Poiché la maggior parte delle dimostrazioni è complicata, la logica appartiene alla matematica superiore; non è a suo fondamento. Per dimostrare un teorema non abbiamo bisogno di una teoria generale delle dimostrazioni. La logica matematica deve essere mantenuta rigidamente distinta dall'indagine sulle regolarità del linguaggio. Questa forma tradizionale di logica appartiene alla matematica applicata.

La logica matematica intuizionista differisce dalla logica a due valori per l'interpretazione dell'esistenza matematica. Dire che un oggetto matematico esiste non può significare altro se non che tale oggetto è stato costruito mentalmente. La maggior parte dei matematici ragiona come se l'oggetto potesse esistere prima di venir costruito, o supponendo che l'oggetto sia stato costruito precedentemente; ma tali argomentazioni non appartengono alla matematica. La concezione costruttivista dell'esistenza matematica porta immediatamente al rifiuto del principio del terzo escluso come teorema matematico generale.

Molti capitoli dell'analisi possono essere sviluppati costruttivamente, anche senza l'uso della negazione, sicché vengono evitate anche le dimostrazioni indirette. Alcuni teoremi sono validi soltanto sotto condizioni ulteriori e alcune dimostrazioni sono più complicate, ma le complicazioni non sono intollerabili e sono bilanciate dal fatto che in esse viene convogliata una maggiore quantità di informazione, poiché ogni dimostrazione di esistenza fornisce nello stesso tempo un metodo di costruzione.

Le successioni di scelte sono necessarie per ottenere una soddisfacente teoria del continuo. Non esiste una teoria analoga nella matematica classica, dove non si può introdurre la nozione di successione di scelte. Quando si studia l'analisi sul continuo intuizionistico, alcuni risultati contraddicono verbalmente certi teoremi classici, ma le contraddizioni sono soltanto apparenti, poiché l'interpretazione è diversa. In un caso del genere, il teorema classico non possiede un'interpretazione intuizionistica, poiché presuppone, come dato essenziale, l'esistenza del continuo come un tutto.

La matematica intuizionista e quella classica partono entrambe in stretta connessione con l'esperienza; entrambe trascendono i limiti dell'esperienza in un libero sviluppo astratto. È in queste parti astratte che esse divergono in maniera più spettacolare. Per esempio, le parti della teoria degli insiemi che riguardano i grandi cardinali non hanno un equivalente intuizionistico. Alcuni matematici considerano questo fatto un impoverimento, ma l'intuizionista giudica le teorie per cui non dispone di alcuna interpretazione meno importanti delle sottili distinzioni logiche dell'intuizionismo e meno importanti degli interessanti problemi sollevati dalla teoria delle successioni di scelte, che a sua volta non ha un equivalente classico. Egli spera di contribuire, con il suo lavoro astratto, alla chiarificazione del pensiero umano in generale.

bibliografia

Ashwinikumar, Hilbert spaces in intuitionism (tesi), Amsterdam 1966.

Ashwinikumar, Shukla, S. L., Intuitionist determination of dual spaces of certain catalogued linear spaces, in ‟Indagationes mathematicae", 1971, XXXIII, pp. 240-260.

Bishop, E., Foundations of constructive analysis, New York 1967.

Borel, E., Leçons sur la théorie des fonctions, Paris 1914².

Brouwer, L. E. J., Over de grondslagen der wiskunde (tesi), Amsterdam 1907; in Collected works, vol. I, Amsterdam 1975, pp. 11-101.

Brouwer, L. E. J., De onbetrouwbaarheid der logische principes, in ‟Tijdschrift voor Wijsbegeerte", 1908, II, pp. 152-158; in Collected works, vol. I, Amsterdam 1975, pp. 107-111.

Brouwer, L. E. J., Zur Begründung der intuitionistischen Mathematik, in ‟Mathematische Annalen", 1924, XCIII, pp. 244-258, 1925, XCV, pp. 453-473, 1926, XCVI, pp. 451-489; in Collected works, vol. I, Amsterdam 1975, pp. 301-314, 321-340, 352-389.

Brouwer, L. E. J., Über Definitionsbereiche von Funktionen, in ‟Mathematische Annalen", 1926, XCVII, pp. 60-76; in Collected works, vol. I, Amsterdam 1975, pp. 390-405.

Brouwer, L. E. J., Consciousness, philosophy and mathematics, in Proceedings of the X^th International Congress of Philosophy, Amsterdam 1948, pp. 1235-1249; in Collected works, vol. I, Amsterdam 1975, pp. 480-494.

Brouwer, L. E. J., Collected works, Amsterdam 1975.

Dalen, D. van, Lectures on intuitionism, in Cambridge School in mathematical logic, Lecture notes in mathematics 337, Berlin-Heidelberg-New York 1973.

Freudenthal, H., Zum intuitionisstischen Raumbegriff, in ‟Compositio mathematica", 1936, IV, pp. 88-111.

Gibson, C. G., The intuitionist measure, in ‟Journal of the London Mathematical Society", 1969, XLIV, pp. 617-624.

Griss, G. F. C., Negationless intuitionistic mathematics, I, in ‟Indagationes mathematicae", 1946, VIII, pp. 675-681.

Griss, G. F. C., Negationless intuitionistic mathematics, II, in ‟Indagationes mathematicae", 1950, XII, pp. 108-115.

Heyting, A., Die formalen Regeln der intuitionistischen Logik, in Sitzungsberichte der preussischen Akademie der Wissenschaften, Berlin 1930, pp. 57-71, 158-169.

Heyting, A., Untersuchungen über intuitionistische Algebra, in ‟Verhandelingen Nederlandse Akademie van Wetenschappen", 1941, XVIII, 1^e sectie n. 2.

Heyting, A., Note on the Riesz-Fischer theorem, in ‟Indagationes mathematicae", 1951, XIII, pp. 35-40.

Heyting, A., Intuitionism, an introduction, Amsterdam 1971.

Kleene, S. C., Vesley, R. E., The foundation of intuitionistic mathematics, Amsterdam 1975.

Kreisel, G., Foundations of intuitionistic logic, in Logic, methodology and philosophy of science. Proceedings of the 1960 International Congress, Stanford 1962, pp. 198-210.

Kreisel, G., Troelstra, A. S., Formal systems for some branches of intuitionistic analysis, in ‟Annals of mathematical logic", 1970, I, pp. 229-387.

Markov, A. A., Teorija algorithmov, Moskva 1954.

Shukla, S. L., Intuitionist treatment of some spaces of sequences, in ‟Indagationes mathematicae", 1972, XXXIV, pp. 139-151.

Troelstra, A. S., Intuitionistic general topology (tesi), Amsterdam 1966.

Troelstra, A. S., Principles of intuitionism, Lecture notes in mathematics 95, Berlin-Heidelberg-New York 1969.

Troelstra, A. S., Informal theory of choice sequences, in ‟Studia logica", 1970, XXV, pp. 31-54.