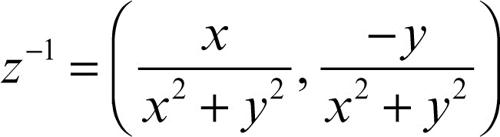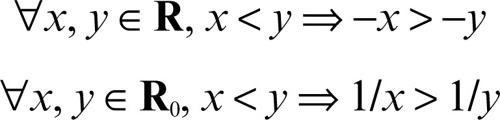inverso

inverso

inverso termine che assume differenti significati a seconda dell’oggetto cui si applica. Il termine è spesso usato in contrapposizione al termine «diretto», per cui si parla, per esempio, di operazione diretta e operazione inversa, così come di formula diretta e formula inversa, a seconda che si muti il soggetto della formula stessa. In modo analogo si parla di proporzionalità diretta e proporzionalità inversa tra due grandezze (→ proporzionalità).

☐ In algebra, l’inverso di un elemento x rispetto a una data operazione è quell’elemento (se esiste) che composto con x dà l’elemento neutro dell’operazione stessa: i due elementi sono allora inversi rispetto alla data operazione. Negli insiemi Q dei numeri razionali e R dei numeri reali, l’inverso di x rispetto all’addizione è −x ed è detto opposto, mentre l’inverso di x rispetto alla moltiplicazione (che esiste soltanto se x ≠ 0) è 1/x (o, che è lo stesso, x⁻¹) ed è detto reciproco. La reciproca della frazione 3/4, detta anche la sua frazione inversa, è per esempio 4/3. Nell’insieme C dei numeri complessi l’inverso additivo di z = (x, y) è −z = (−x, −y) mentre il suo inverso moltiplicativo (sempre se z ≠ 0) è

Nell’insieme Z dei numeri interi nessun elemento (salvo banalmente ±1) ha inverso moltiplicativo; nell’insieme N dei numeri naturali nessun elemento (salvo banalmente 0) ha inverso additivo. In generale, perché si possano considerare al suo interno gli inversi, un insieme G dotato di una operazione ∗ deve essere almeno un monoide e se u è il suo elemento neutro, l’inverso di un suo elemento x è un elemento y di G tale che x ∗ y = y ∗ x = u. Se un tale elemento y esiste, esso è unico e x è detto invertibile. Se ogni elemento di G è invertibile, allora G è un gruppo. In analogia con il caso numerico, se il monoide G è additivo con operazione +, due elementi x e y inversi l’uno dell’altro sono detti opposti e si scrive y = −x; se invece G è moltiplicativo con operazione ⋅, x e y sono detti reciproci e si scrive y = x⁻¹. Si può comunque considerare, nel caso in cui l’operazione ∗, definita in G e con elemento neutro u, non sia commutativa, anche l’esistenza di un elemento inverso a sinistra (rispettivamente, a destra) di un qualsiasi elemento di G. Se per ogni x ∈ G, esiste y ∈ G tale che y ∗ x = u, allora y è l’inverso a sinistra di x; analogamente se si ha x ∗ y = u allora y è l’inverso a destra di x, sempre rispetto all’operazione ∗. Ne consegue che un elemento y è inverso dell’elemento x rispetto all’operazione ∗ in G se e solo se ne è sia inverso destro, sia inverso sinistro.

La definizione dell’elemento inverso permette di definire un’operazione inversa rispetto a una data. Dato un gruppo G dotato di operazione ∗, l’operazione inversa di ∗, qui indicata con ∘, è tale che per ogni a, b ∈ G, a ∘ b = a ∗ b⁻¹, essendo b⁻¹ l’inverso di b rispetto all’operazione ∗. Così, in Q l’operazione inversa dell’addizione è la sottrazione, perché a − b = a + (−b), mentre l’operazione inversa della moltiplicazione è la divisione perché, se b ≠ 0, a /b = a ⋅ b⁻¹. Occorre osservare che se l’operazione non è commutativa (e quindi inverso destro e inverso sinistro non necessariamente coincidono) si possono avere due differenti operazioni inverse. Per esempio, l’elevazione a potenza aⁿ, definita in R, ha come operazioni inverse la radice ennesima se, dato b ∈ R, si cercano i valori della base a per cui aⁿ = b, e il logaritmo in base a, se, dato b ∈ R, si cerca il valore dell’esponente n per il quale aⁿ = b.

Un esempio di elemento inverso è dato dalla matrice inversa di una matrice quadrata A di ordine n e determinante non nullo: è la matrice A⁻¹ tale che A ⋅ A⁻¹ = I_n, essendo I_n la matrice identica di ordine n (elemento neutro del prodotto righe per colonne delle matrici dell’insieme).

☐ Ancora in algebra, la relazione inversa di una data relazione ρ, definita in un insieme A, è la relazione ρ⁻¹ per la quale x ρ⁻¹ y se e solo se y ρ x. Per esempio, l’inversa della relazione < definita in R è la relazione >. Si osservi che se per due numeri reali vale la relazione <, allora per i loro rispettivi inversi, sia additivi sia moltiplicativi, vale la relazione inversa:

Analogamente, data una corrispondenza tra due insiemi φ: X → Y, resta naturalmente definita la sua inversa tra Y e X (→ corrispondenza). Ne consegue che in geometria si considerano trasformazioni invertibili e, data una trasformazione (che è una particolare corrispondenza tra punti) se ne considera l’inversa.

☐ In analisi, data una funzione reale di variabile reale y = ƒ(x) la sua funzione inversa destra è la funzione g(y) tale che ƒ(g(y)) = x; essa ha come dominio l’immagine I di ƒ ed esiste solo nel sottoinsieme della controimmagine di I in cui ƒ è iniettiva; la funzione inversa sinistra di ƒ è invece la funzione h tale che h(ƒ(x)) = x e ha come dominio l’immagine di ƒ. Se una funzione ha sia la funzione inversa sinistra sia la funzione inversa destra, le due inverse coincidono, la funzione si dice invertibile e la funzione inversa è denotata con ƒ⁻¹; per esempio, l’inversa della funzione y = sinx, ristretta all’intervallo [−π/2, +π/2] in cui è iniettiva, è la funzione → arcoseno, indicata anche con sin⁻¹ e definita in [−1, +1].

In un riferimento cartesiano monometrico Oxy il grafico della funzione ƒ⁻¹ inversa di ƒ è il simmetrico del grafico di ƒ rispetto alla bisettrice degli assi di equazione y = x (→ funzione inversa; → invertibilità).

☐ In logica, dato un teorema enunciato sotto forma di implicazione, «se A allora B», il suo teorema inverso è il teorema «se B allora A» ottenuto scambiando tra loro ipotesi e tesi. Dato un teorema di tale forma, non necessariamente vale il suo inverso: per esempio, mentre è vero il teorema «Se due rette sono perpendicolari allora non sono parallele» non è vero che «Se due rette non sono parallele allora sono perpendicolari». Se valgono sia il teorema «Se A allora B» sia il suo inverso «Se B allora A», allora vale il teorema che si enuncia con la doppia implicazione «A se e solo se B».