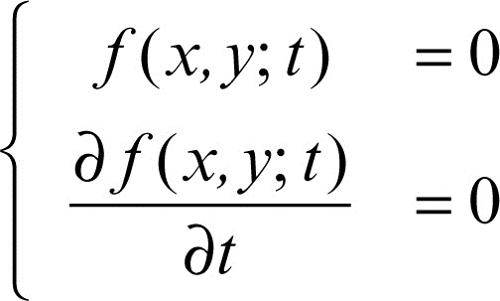inviluppo

Enciclopedia della Matematica (2013)

inviluppo


inviluppo per una famiglia F di funzioni dipendente da un parametro t è una curva Γ che in ogni punto è tangente a una curva della famiglia. Se F è scritta nella forma parametrica ƒ(x, y; t) = 0, l’inviluppo Γ è dato dal sistema

formula

Eliminando t da queste equazioni si ottiene Γ in forma implicita; risolvendo rispetto a (x, y) si ottiene Γ in forma parametrica. Nel caso in cui le curve di F posseggano dei punti singolari, il sistema definisce anche il luogo di tali punti. Per esempio, le parabole di tiro di un cannone posto nell’origine che spara proiettili a velocità ν con alzi differenti m sono date da y = mx − (1 + m2)gx 2/(2ν 2); derivando rispetto a m si ha 0 = x − mgx 2/v 2, ed eliminando m si ottiene l’inviluppo y = v 2/(2g) − gx 2/(2v 2), che è ancora una parabola (detta parabola di sicurezza) con fuoco nell’origine.

Il concetto di inviluppo si estende poi alle famiglie di superfici se si considerano i piani tangenti alle superfici anziché le rette tangenti.

INVILUPPO

Vedi anche
conica fig. 1ACurva che si ottiene segando un cono circolare (retto od obliquo) con un piano. Il cono va pensato come luogo di rette, e non di semirette, uscenti dal vertice V, cioè costituito, come si usa dire nel linguaggio elementare, da due ‘semiconi’ opposti al vertice. Si presentano tre diversi casi. ... retta Ente geometrico fondamentale, in genere assunto come primitivo nelle trattazioni assiomatiche. Astronomia R. d’altezza Proiezione di un tratto del cerchio d’altezza (➔ cerchio) sopra una carta di Mercatore. Le r. d’altezza sono utilizzate per le determinazioni del punto. Economia R. del bilancio del ... geometria In senso ampio e generico, ramo della matematica che studia lo spazio e le figure spaziali. Cenni storiciL’antichità - L’origine della g. è legata a concreti problemi di misurazione del terreno (nacque a scopi agrimensori nella zona del delta del Nilo); si trattava quindi essenzialmente di una g. empirica, ...
Tag
Altri risultati per inviluppo
  • inviluppo
    Enciclopedia on line
    In genere, qualsiasi cosa che avvolge strettamente. Matematica Inviluppo di una famiglia di curve piane È una curva L tale che per ogni suo punto P passi una e una sola curva della famiglia data avente ivi la stessa tangente della L. Se f(x, y, t)=0 è l’equazione delle curve Ct della famiglia, sotto ...
  • inviluppo
    Dizionario delle Scienze Fisiche (1996)
    inviluppo [Der. di viluppo, dal lat. faluppa "pagliuzza" incrociato con voluculum, da volvere "avvolgere"] [LSF] Avvolgimento, involucro che tiene insieme più cose e anche questo insieme. ◆ [ELT] I. di modulazione: la linea che passa per i successivi punti di massimo e di minimo delle alternanze di ...
  • INVILUPPO
    Enciclopedia Italiana (1933)
    Giovanni Lampariello 1. Si consideri un sistema di curve piane Ct dipendenti da un parametro arbitrario t variabile in un intervallo (t0, t1) che può essere anche tutto l'asse reale (− ∞, + ∞). Se esiste una curva Γ, tale che ogni Ct sia tangente in un suo punto alla Γ e, viceversa, la Γ sia in ogni ...
Vocabolario
inviluppo
inviluppo s. m. [der. di inviluppare]. – In genere, qualsiasi cosa che inviluppa, quindi involgimento, involucro e sim.; anche, insieme di cose inviluppate, avvolte insieme in modo più o meno confuso; fig.: un i. di frasi sconnesse. In...
inviluppaménto
inviluppamento inviluppaménto s. m. [der. di inviluppare]. – L’inviluppare o l’invilupparsi; l’essere inviluppato; in senso concr., insieme di cose inviluppate, inviluppo.