iperboloide

iperboloide

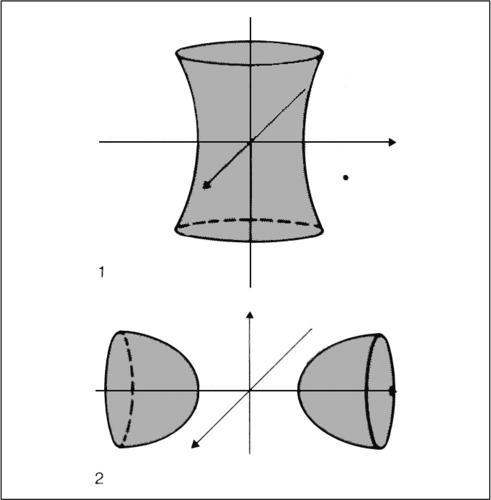
iperboloide superficie algebrica del secondo ordine, appartenente alla famiglia delle quadriche, i cui punti impropri formano una conica reale non degenere. Ammette un centro di simmetria, tre assi e tre piani di simmetria. Nello spazio euclideo si hanno due tipi di iperboloide: l’iperboloide ellittico, detto anche iperboloide a due falde, e l’iperboloide iperbolico, detto anche iperboloide a una falda.

L’iperboloide ellittico è costituito da due parti non connesse (falde) che si estendono all’infinito. La sua equazione canonica è

avendo scelto come assi coordinati gli assi di simmetria. Ampliando lo spazio con l’aggiunta degli elementi impropri, le due falde si congiungono lungo la conica all’infinito. Ha un solo asse trasverso (asse x) e le sue sezioni con piani perpendicolari all’asse trasverso o sono vuote o sono ellissi oppure si riducono a un punto (vertice). Se b = c la superficie è rotonda e l’iperboloide a due falde si può ottenere dalla rotazione di un’iperbole intorno al suo asse trasverso (asse x). Un iperboloide ellittico rotondo può anche essere definito come il luogo dei punti dello spazio che hanno costante, in valore assoluto, la differenza delle distanze da due punti fissi che prendono il nome di fuochi dell’iperboloide.

L’iperboloide iperbolico è costituito da una sola falda connessa che si estende all’infinito. La sua equazione canonica, in un riferimento che ha per assi coordinati i suoi assi di simmetria, è

Ha due assi trasversi (asse x e asse y) e le sue sezioni con piani perpendicolari all’asse z sono ellissi. In particolare, la sezione con il piano z = 0 è detta ellisse di gola. Se risulta a = b la superficie è rotonda e l’iperboloide a una falda può essere ottenuto dalla rotazione di un’iperbole intorno al suo asse non trasverso (asse z). In generale, un iperboloide iperbolico è una superficie rigata formata da due sistemi lineari di rette reali. Per ogni punto della superficie passano due rette, una per ciascun sistema lineare. Nel caso in cui risulta a = b, l’iperboloide iperbolico si può ottenere facendo ruotare una retta intorno a una seconda retta sghemba rispetto a essa.

Un iperboloide degenere è una quadrica rappresentata da un’equazione del tipo

Se a = b si ha un cono circolare, se a ≠ b si ha un cono ellittico.