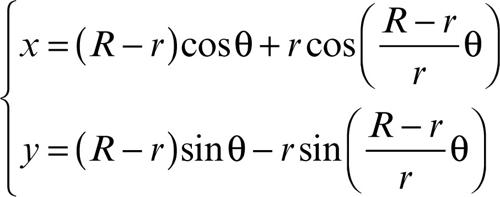ipocicloide

Enciclopedia della Matematica (2013)

ipocicloide

ipocicloide curva piana descritta da un punto P solidale a una circonferenza (epiciclo) che rotola senza strisciare internamente a una circonferenza fissa. In un piano cartesiano avente l’origine degli assi nel centro della circonferenza fissa, l’ipocicloide ha equazioni parametriche

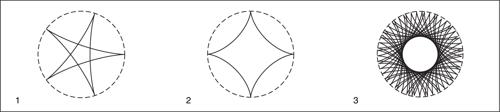
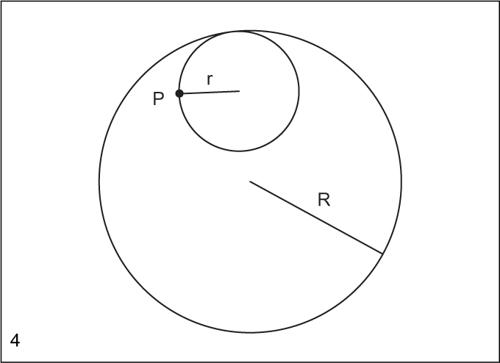
dove r e R indicano, rispettivamente, il raggio della circonferenza mobile e il raggio della circonferenza fissa. La forma dell’ipocicloide è determinata dal rapporto R /r. Se R /r = 2, l’epicicloide si riduce a un segmento (il diametro). Se il rapporto R /r è un numero razionale, l’ipocicloide è una curva chiusa con R cuspidi. Nel caso particolare in cui R /r = 4, l’ipocicloide si chiama → asteroide o tetracuspide. Se R /r è un numero irrazionale, l’ipocicloide è una curva aperta.

Una ipocicloide ordinaria può essere generata da due epicicli di raggi tali che la loro somma sia uguale al raggio della circonferenza fissa. Se il raggio dell’epiciclo è metà di quello della circonferenza, l’ipocicloide ordinaria si riduce a un diametro della circonferenza stessa (teorema di Cardano). Si possono considerare anche ipocicloidi accorciate o allungate considerando un punto all’interno o all’esterno della circonferenza anziché su di essa.

ipocicloide

Enciclopedia on line

La curva descritta da un punto P rigidamente collegato a un cerchio c (v. fig.), detto epiciclo, tangente internamente a un cerchio fisso k del suo piano e che rotoli senza strisciare su k. L’i. è ordinaria, accorciata o allungata a seconda che il punto P sia, rispettivamente, sul cerchio mobile, al ...
ipocicloide

Dizionario delle Scienze Fisiche (1996)

ipociclòide [Comp. di ipo- e cicloide] [ALG] La curva piana descritta da un punto P rigidamente collegato a una circonferenza C, di raggio r, che rotoli senza strisciare in un'altra circonferenza K del suo piano, di raggio R>r, mantenendosi tangente internamente a essa; si parla di i. ordinaria, ...