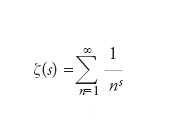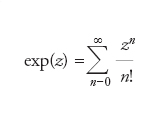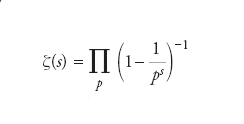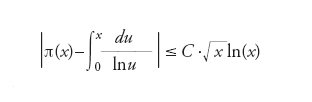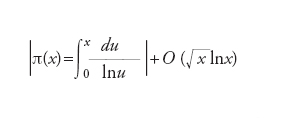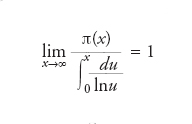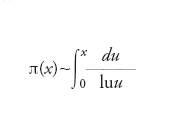ipotesi di Riemann

ipotesi di Riemann

Congettura sulla distribuzione degli zeri nella funzione zeta di Riemann. La funzione zeta di Riemann ζ(s) è la serie L di Dirichlet associata al carattere di Dirichlet banale definito dalla condizione χ(n)=1 per ogni intero n. Esplicitamente, tale funzione è definita dalla serie:

dove n^σ indica exp(s log n) e

è l’esponenziale complessa (convergente su tutto il piano complesso); il simbolo n!=(n−1)∙∙∙2∙1 indica il fattoriale di n, con la convenzione che 0! valga 1. Come tutte le serie L di Dirichlet, anche la funzione zeta di Riemann converge assolutamente nel semipiano {s∈ℂ tali che R(s)>1} formato dai numeri complessi s con parte reale ✄(s) maggiore di 1, converge (non necessariamente assolutamente) nel semipiano {s∈ℂ tali che R(s)>0} e può essere prolungata analiticamente a tutto il piano complesso a una funzione meromorfa, indicata con lo stesso simbolo ζ(s). La funzione ζ(s) ottenuta tramite prolungamento meromorfo a tutto il piano complesso ha come unica singolarità un polo semplice in s=1 con residuo uguale a 1. Inoltre, i suoi zeri godono delle seguenti proprietà: ζ(s) ha zeri semplici in s=−2k per k>0 numero intero. Questi zeri della funzione ζ sono detti zeri banali. Gli zeri di ζ(s) che non sono della forma −2k (con k>0 un numero intero) sono situati nella striscia critica {s∈ℂ tali che 0≤R(s)≤1} formata dai numeri complessi la cui parte reale è compresa tra 0 e 1. Questi zeri della funzione ζ(s) sono detti zeri non banali. È possibile dimostrare che gli zeri non banali di ζ(s) sono simmetrici sia rispetto all’asse reale sia rispetto alla retta {s∈ℂ tali che R(s)=1/2} formata dai numeri complessi la cui parte reale vale 1/2 (tale retta è detta retta critica). L’ipotesi di Riemann consiste nella seguente congettura: gli zeri non banali di ζ(s) stanno tutti sulla linea critica. In altre parole, l’ipotesi afferma che se ζ(s₀)=0 e s₀ non è un intero negativo, allora la parte reale di s₀ vale 1/2. Verifiche computazionali hanno provato che tutti gli zeri non banali di ζ(s) con parte immaginaria minore di 10⁹ stanno sulla linea critica e sono semplici. Non esiste però al momento alcuna dimostrazione dell’ipotesi di Riemann, che resta uno dei più importanti problemi aperti della matematica. La funzione zeta di Riemann può essere espansa in un prodotto di Euler:

dove il prodotto si intende esteso a tutti i numeri primi p (per definire un tale prodotto infinito è necessario ricorrere a una conveniente nozione di convergenza che per semplificare l’esposizione non sarà introdotta). Una delle ragioni per le quali Bernhard Riemann introdusse la funzione ζ(s) nel 1859 consiste nel fatto che, grazie al prodotto di Euler precedente, essa può essere utilizzata per studiare la distribuzione dei numeri primi. Più precisamente, detto π(x) il numero dei numeri primi minori di un fissato numero reale positivo x, Helge von Koch dimostrò nel 1901 che l’ipotesi di Riemann è equivalente alla seguente congettura: esiste un numero reale C tale che, per ogni numero reale positivo x, si abbia

La formula precedente si esprime generalmente in modo più compatto utilizzando la seguente notazione standard:

Per quanto riguarda la crescita di π(x), è noto, grazie ai lavori di Jacques Hadamard e Charles Jean de la Vallée-Poussin, che

Tale formula fu congetturata da Carl Friedrich Gauss sulla base di evidenze sperimentali. Essa si esprime generalmente in modo più compatto utilizzando la seguente notazione standard:

L’ipotesi di Riemann può essere estesa alle serie L(ζ;s) di Dirichlet. La congettura che si ottiene prende il nome di ipotesi di Riemann generalizzata. Come accade per la ζ(s) di Riemann, anche la congettura di Riemann generalizzata è legata alla distribuzione dei numeri primi. Più precisamente, la congettura per la serie L(χ,s) associata a opportuni caratteri di Dirichlet χ modulo m è legata al calcolo dei numeri primi minori di un dato numero reale positivo x e che siano congruenti a zero modulo m.

→ Fondamenti della matematica e teoria algoritmica dell’informazione