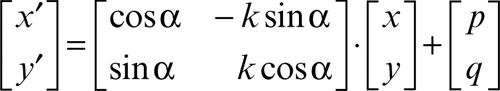isometria

isometria

isometria o trasformazione isometrica, corrispondenza biunivoca ƒ del piano (o dello spazio, o più in generale tra spazi metrici) in sé, che conserva le distanze, cioè tale che, per ogni coppia di punti A e B risulta d(A, B) = d(ƒ(A), ƒ(B)). Due figure che si corrispondono in una isometria sono dette figure congruenti. La congruenza tra due figure è una relazione di equivalenza. L’insieme delle isometrie del piano euclideo (e in generale di uno spazio euclideo di dimensione n) è un gruppo non commutativo, rispetto all’operazione di composizione di isometrie, detto anche prodotto di isometrie (→ isometrie, gruppo delle). Le isometrie possono definirsi nello stesso modo in qualsiasi spazio metrico e anche come applicazioni di uno spazio metrico E su uno spazio metrico F. Si chiama inoltre isometria o applicabilità tra due superfici una biiezione tra i punti delle superfici in cui archi di curva corrispondenti hanno uguale lunghezza. Le superfici applicabili sul piano sono quelle sviluppabili (→ sviluppabilità). Lo studio delle proprietà delle superfici invarianti per isometria costituisce l’oggetto della geometria metrica intrinseca della superficie.

Isometrie nel piano

Nel piano euclideo ogni isometria ha le seguenti proprietà:

• trasforma punti allineati in punti allineati e punti non allineati in punti non allineati (è una → collineazione);

• trasforma rette parallele in rette parallele e rette perpendicolari in rette perpendicolari;

• trasforma una circonferenza in una circonferenza di uguale raggio;

• trasforma un angolo in un angolo di uguale ampiezza.

Le precedenti proprietà rappresentano invarianti di una isometria.

In particolare, una trasformazione isometrica ƒ è detta isometria diretta o isometria pari se, dati tre punti non allineati A, B, C, i rispettivi trasformati ƒ(A), ƒ(B), ƒ(C) hanno lo stesso orientamento (orario o antiorario) di A, B, C; in caso contrario è detta isometria inversa o isometria invertente o isometria dispari (alcuni autori utilizzano in modo specifico il termine isometria invertente per non confondere l’isometria inversa con l’inversa di una isometria). Le isometrie dirette formano un gruppo, che è un sottogruppo del gruppo delle isometrie del piano. Il prodotto di un qualsiasi numero di isometrie è una isometria diretta o inversa a seconda che il numero di isometrie inverse che compaiono nel prodotto risulti pari o dispari. Si dicono punti uniti (o fissi) di un’isometria ƒ i punti P per i quali si ha ƒ(P) = P. Non tutte le trasformazioni isometriche hanno punti uniti. Una isometria è univocamente determinata quando sono assegnati tre punti allineati e le rispettive immagini.

Nel piano euclideo sono isometrie l’→ identità, la → simmetria centrale, la → glissosimmetria, la → traslazione, la → rotazione e la → simmetria assiale. In particolare, componendo queste ultime tre si ottengono tutte le isometrie del piano. Fondamentale nello studio delle isometrie è il teorema che stabilisce che ogni isometria può essere ottenuta come prodotto di al più tre simmetrie assiali. Il teorema permette di tracciare un quadro sintetico delle trasformazioni isometriche. Si può infatti osservare che:

a) la composizione di tre simmetrie assiali è

• una simmetria assiale se i tre assi delle simmetrie passano per uno stesso punto P;

• una glissosimmetria se i tre assi delle simmetrie non passano per uno stesso punto;

b) la composizione di due simmetrie assiali è

• una traslazione se gli assi delle simmetrie sono paralleli;

• una rotazione se gli assi delle simmetrie sono incidenti.

Da quanto detto segue che una qualsiasi isometria del piano, escludendo le identità, rientra in uno dei quattro tipi riportati in tabella.

Nel piano, riferito a un sistema di riferimento cartesiano, ogni isometria si può rappresentare con equazioni che legano le coordinate (x, y) di un punto e quelle (x′, y′ ) del suo trasformato. Utilizzando la scrittura matriciale si ha:

con la condizione k = ±1. Se la matrice quadrata M, detta anche matrice dell’isometria, è la matrice identica, si ha una traslazione di vettore v(p, q). In ogni caso, si ha che il determinante detM = ±1 a seconda che k = ±1. In particolare se detM = +1 si ha una isometria diretta, se detM = −1 si ha una isometria inversa.

Isometrie nello spazio tridimensionale

Una isometria si definisce in R³ nello stesso modo che nel piano, cioè come corrispondenza biunivoca dello spazio in sé che conserva le distanze. Alle proprietà delle isometrie nel piano se ne aggiungono altre, che riguardano l’ambiente tridimensionale. In particolare, una isometria in R³ trasforma punti complanari in punti complanari, sfere in sfere di ugual raggio, diedri in diedri di uguale ampiezza. Anche per le isometrie nello spazio si distingue tra isometrie dirette e isometrie invertenti. Sono isometrie dirette l’identità, la traslazione, che si estende naturalmente allo spazio considerando un vettore con tre componenti, la simmetria centrale, definita come nel piano, la rotazione attorno a un asse, che fa corrispondere a ogni punto P dello spazio un punto P′ ruotato sul piano perpendicolare all’asse di rotazione e la simmetria assiale, che coincide con una rotazione di 180° attorno allo stesso asse. Sono invece isometrie invertenti la simmetria planare rispetto a un piano π, che è tale che a ogni punto P del piano di simmetria π fa corrispondere sé stesso e a ogni punto non appartenente al piano π fa corrispondere un punto P′ situato sul semispazio opposto rispetto a π e tale che d(P′, π) = d(P, π). Nello spazio le simmetrie planari giocano un ruolo analogo a quello delle simmetrie assiali nel piano e, da esse, si possono ottenere tutte le altre isometrie. In particolare, componendo due simmetrie planari con piani paralleli si ottiene una traslazione, componendo due simmetrie planari con piani incidenti si ottiene una rotazione, componendo tre simmetrie planari si ottiene ancora una isometria (genericamente detta glissosimmetria). Le isometrie dello spazio formano un gruppo rispetto all’operazione di composizione; suoi sottogruppi sono il gruppo delle traslazioni e quello delle rotazioni con lo stesso asse.