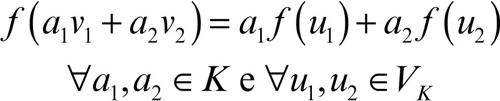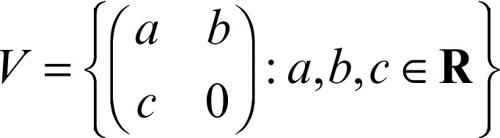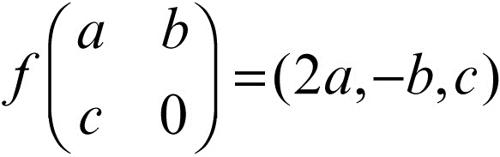isomorfismo

isomorfismo

isomorfismo termine che, nel linguaggio naturale, significa identità di forma; è utilizzato in diversi ambiti della matematica per identificare due strutture che, seppure sono “concretamente” diverse per origine o formalismo, hanno le stesse proprietà strutturali. In generale, un isomorfismo è una biiezione ƒ tra due insiemi dotati di strutture della stessa natura (d’ordine, algebriche, topologiche) tale che sia ƒ sia ƒ ⁻¹ sono dei morfismi, cioè applicazioni che conservano le relative strutture.

Gli isomorfismi determinano una relazione di equivalenza tra insiemi dotati di una stessa struttura, permettendo di stabilire se due di tali insiemi abbiano o meno la stessa forma rispetto alla struttura considerata: essi rivestono dunque una particolare importanza perché permettono di chiarire il concetto stesso di classificazione, alla base di tutta la matematica. La nozione di isomorfismo include così una serie di nozioni più specifiche come quelle di biiezione (tra insiemi privi di struttura algebrica), di isomorfismo d’ordine (tra insiemi parzialmente ordinati), di isomorfismo lineare (tra spazi vettoriali), di isomorfismo (tra gruppi, tra anelli, tra campi ecc.), di omeomorfismo (tra spazi topologici), di diffeomorfismo (tra varietà differenziabili), di applicazione biregolare (tra varietà algebriche). In tutti questi contesti, se sussiste un isomorfismo tra due insiemi A e B, dotati di una stessa struttura, si dice che A e B sono isomorfi, e talvolta si dice che sono uguali a meno di isomorfismo, e si scrive A ≅ B. Un isomorfismo di un insieme su sé stesso è detto automorfismo.

Relativamente ai gruppi, per esempio, un isomorfismo ƒ tra due gruppi (G, ∗) e (H, ∘) è una biiezione tale che, per ogni elemento a, b ∈ G, si ha ƒ(a ∗ b) = ƒ(a) ∘ ƒ(b), dove ƒ(a) e ƒ(b) appartengono a (H, ∘). Per esempio, la funzione esponenziale ƒ(x) = e^x realizza un isoformismo del gruppo additivo dei numeri reali (R, +) sul gruppo moltiplicativo dei numeri reali positivi (R⁺, ⋅) perché, per ogni a, b ∈ R, e^a+b = e^a ⋅ e^b e viceversa si ha ƒ ⁻¹ = ln (logaritmo naturale) che è tale che ln(a ⋅ b) = lna + lnb.

□ In geometria, un isomorfismo tra due spazi vettoriali V_k e W_k su un campo K è una applicazione lineare biunivoca ƒ: V_k → W_k tale che risulti

Per esempio, dati gli spazi vettoriali

e

l’applicazione ƒ: V → W, tale che

è un isomorfismo. Tutti gli spazi vettoriali sullo stesso campo aventi la stessa dimensione sono tra loro isomorfi. Tutti gli spazi vettoriali su R aventi la medesima dimensione costituiscono pertanto uno spazio vettoriale astratto. In questo senso, ogni spazio vettoriale di dimensione finita n si identifica, a meno di un isomorfismo, con lo spazio Rⁿ.

□ Nella teoria dei grafi, un isomorfismo tra due grafi G e G′ è una corrispondenza biunivoca ƒ tra i nodi di G e i nodi di G′ tale che esiste un arco tra i nodi ƒ(A) e ƒ(B) del grafo G′ se e solo se esiste un arco tra il nodo A e il nodo B del grafo G, in modo tale da conservare eventuali orientamenti degli archi.

□ In topologia, un isomorfismo tra due spazi topologici S e S′ (detto in questo contesto omeomorfismo) è una mappa biiettiva e bicontinua che conserva le topologie degli spazi, nel senso che manda aperti in aperti e mantiene le proprietà topologiche (separabilità, connessione, compattezza ecc.).

□ Più in generale, nel contesto delle categorie, con il termine isomorfismo ci si riferisce a un morfismo invertibile tra due oggetti A e B appartenenti a una stessa categoria.