istogramma

istogramma

Tipo di diagramma cartesiano al quale si ricorre per rappresentare graficamente la distribuzione di frequenza di una o più variabili quantitative. Lo scopo dell’i. può essere semplicemente descrittivo, oppure quello di fare inferenza (➔ inferenza statistica) circa la densità o la distribuzione ignota della popolazione da cui i dati sono stati estratti. L’i. consiste in rettangoli adiacenti, le cui basi rappresentano intervalli discreti dei possibili valori della variabile, mentre l’area o l’altezza di ciascun intervallo è uguale alla frequenza, assoluta o relativa. Gli i. si distinguono da altri tipi di diagrammi simili, come il diagramma a barre o a colonne, in quanto raffigurano distribuzioni quantitative continue, i cui valori possono essere divisi in intervalli adiacenti. n

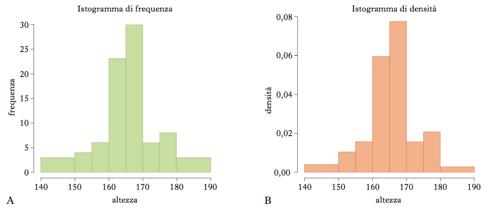
Istogramma di densità

Quando l’area è uguale alla frequenza, la somma delle aree dei rettangoli è uguale al numero delle osservazioni (nel caso di frequenze assolute) oppure a 1 (nel caso di frequenze relative). Tale i. è chiamato anche i. di densità, poiché l’altezza di ogni rettangolo è una stima della densità nell’intervallo corrispondente, definita come rapporto tra la frequenza e l’ampiezza dell’intervallo stesso. Una valutazione alternativa della funzione di densità è lo stimatore di densità kernel (➔ kernel, density), che utilizza una funzione kernel per ottenere una stima di densità meno ‘frastagliata’.

Istogramma di frequenza

Quando è l’altezza a essere uguale alla frequenza, l’i. è in genere chiamato i. di frequenza. Anche in questo caso, le frequenze possono essere relative o assolute. Se gli intervalli hanno tutti la stessa ampiezza, i due tipi di i. presentano la stessa forma, anche se l’ordine di grandezza delle altezze è diverso. L’i. può anche riportare la somma progressiva delle frequenze, invece che le frequenze di ogni singolo intervallo. Si ha così un i. cumulato.

Composizione di un istogramma

Uno degli aspetti delicati nella costruzione di un i. è la scelta del numero di intervalli e della loro ampiezza. In generale non esiste una scelta ‘ottima’, ampiezze diverse possono mettere in luce differenti aspetti della distribuzione. La letteratura ha comunque proposto alcune ‘regole per una buona scelta’. Tra queste, si può citare la formula di Sturges, per cui gli intervalli hanno ampiezza costante e uguale al primo numero intero maggiore o uguale a 1+log2n, dove n è il numero di osservazioni, e la formula di Freedman-Diaconis, secondo cui l’ampiezza è proporzionale all’intervallo interquartile della variabile X (➔ dispersione).

Esempio di istogramma

Si consideri la distribuzione delle altezze di 82 ragazzi di una scuola media inferiore, esemplificata dalla seguente tabella e dalle figure 1 e 2