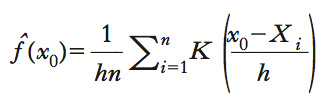kernel density [kernel, stima di densità]
kernel density [kernel, stima di densita]
kernel density (kernel, stima di densità) Metodo nonparametrico di stima della densità di una variabile aleatoria. Questo metodo si basa essenzialmente su una media di funzioni nonnegative, dette funzioni k., centrate attorno a ciascuna osservazione campionaria {X1,...,Xn}. Se la funzione k. è continua o simmetrica , la stima k. di densità è continua o simmetrica. Altre proprietà della funzione k. (momenti e forma funzionale) influiscono sulle proprietà statistiche (distorsione, consistenza ecc.) dello stimatore di densità. Vi sono diverse famiglie di funzioni che possono essere usate come funzioni kernel. Una delle più comuni è la densità gaussiana standardizzata, che gode di proprietà matematiche che la rendono conveniente. Più precisamente, il valore stimato della densità in un punto x0 è ottenuto come
con h>0, cioè come media ponderata dei valori della funzione k. nei punti (x0−X1)/h,...,(x0−Xn)/h. Questa formula assicura che funzione di densità stimata f ̂integri a uno. La quantità h è un parametro chiamato bandwidth, la cui scelta è uno degli aspetti delicati del metodo k.: un valore troppo vicino a zero rende la stima irregolare e con varianza troppo elevata; al contrario, un valore troppo elevato comporta problemi di distorsione. Il metodo k. può essere generalizzato al caso di densità multivariate, ma non è adatto a stimare funzioni di densità di molte variabili, poiché la velocità di convergenza dello stimatore (➔ asintotica, distribuzione) decresce con l’aumentare della dimensione del vettore aleatorio. Questo problema è chiamato curse of dimensionality. La stima k. di una densità condizionata si ottiene dal rapporto tra la stima k. di una densità bivariata e quella della densità marginale della variabile aleatoria condizionante. Tale procedimento è alla base dello stimatore di Nadaraya-Watson (➔ regressione non parametrica, modelli di).