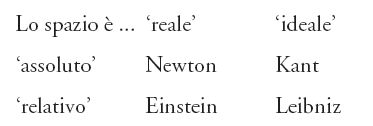L'Età dei Lumi: la fine della conoscenza naturale 1700-1770. Concetti generali di materia e moto

L'Eta dei Lumi: la fine della conoscenza naturale 1700-1770. Concetti generali di materia e moto

Concetti generali di materia e moto

Nel 1726, in seguito ai contrasti con le autorità francesi, François-Marie Arouet comunemente noto come Voltaire (1694-1778) scelse la via dell'esilio volontario in Inghilterra. Qui lo scrittore e uomo d'ingegno, già noto in Francia, frequentò letterati, personaggi politici e scienziati. Più tardi raccolse la sue impressioni sulla vita e sul pensiero degli Inglesi in una serie di brevi saggi, pubblicati nel 1734 con il titolo di Lettres philosophiques, che erano già apparsi l'anno precedente in versione inglese (Letters concerning the English nation). In un celebre brano delle Lettres philosophiques Voltaire scrive:

Un francese che arrivi a Londra trova le cose assai mutate in filosofia come in tutto il resto. Ha lasciato il mondo pieno; lo trova vuoto. A Parigi, si vede l'Universo composto da vortici di materia sottile; a Londra, non si vede niente di tutto questo. Da noi, è la pressione della Luna che causa il flusso del mare; presso gli Inglesi, è il mare che gravita verso la Luna […]. Secondo i vostri Cartesiani, tutto avviene per un impulso assolutamente incomprensibile: secondo Newton, tutto avviene per un'attrazione, di cui non si conosce meglio la causa. A Parigi, vi figurate la Terra fatta come un melone; a Londra essa è appiattita ai due poli. Per un cartesiano, la luce esiste nell'aria; per un newtoniano, giunge dal Sole in sei minuti e mezzo. La chimica francese effettua tutte le sue operazioni con acidi, àlcali e materia sottile; in Inghilterra, l'attrazione domina perfino nella chimica. L'essenza stessa delle cose è totalmente mutata. Non è possibile accordarvi né sulla definizione dell'anima né su quella della materia. Descartes assicura che l'anima s'identifica col pensiero, e Locke gli prova abbastanza bene il contrario. Descartes assicura che l'estensione da sola costituisce la materia, Newton vi aggiunge la solidità. Ecco dei contrasti piuttosto stridenti. (ed. Alatri, p. 85)

Il viaggio di Voltaire attraverso la Manica corrisponde, per certi versi, al viaggio nel tempo compiuto dai pensatori scientifici del XVIII secolo. Il Settecento coincise con un periodo di assestamento e di rielaborazione. Nel 1687, la pubblicazione dei Philosophiae naturalis principia mathematica di Newton aveva segnato l'inizio di una nuova era per la scienza europea; per quanto riguarda le scienze fisiche, quasi tutto il XVIII sec. può essere letto come una reazione a quest'opera e quindi come uno strenuo sforzo per comprenderla a fondo. Fu un processo scandito da dispute e controversie, ma il risultato fu l'assimilazione, seguita da un rapido sviluppo e perfezionamento dei metodi di Newton e dalla correzione definitiva dei suoi errori. La materia e il vuoto, la forza e il moto, lo spazio e il tempo: tutti questi concetti furono attentamente analizzati e discussi.

Le Lettres philosophiques di Voltaire contribuirono a suscitare tra gli intellettuali francesi (e non solo tra gli scienziati) un grande interesse per la filosofia di Newton. In seguito, Voltaire scrisse un'opera divulgativa molto più ampia, gli Élémens de la philosophie de Neuton (1738). Per affrontare in modo corretto i temi scientifici, egli si consultò con i suoi amici scienziati e, in particolare, con Pierre-Louis Moreau de Maupertuis (1698-1759), il primo apostolo del newtonianesimo all'interno dell'Académie Royale des Sciences di Parigi. Negli anni Trenta e Quaranta del XVIII sec., la teoria della gravitazione universale di Newton fu oggetto di un vivace dibattito tra gli scienziati continentali. Verso la metà del secolo le ostilità cessarono e la spiegazione newtoniana dei moti del Sistema solare, così come la sua teoria della luce e dei colori finirono per informare non soltanto la ricerca scientifica, ma anche il dibattito filosofico e le conversazioni erudite dei salon. Il dipinto della fig. 1, Mademoiselle Ferrand medita su Newton, di Maurice-Quentin de la Tour (1704-1788), coglie alla perfezione questo momento della storia intellettuale e sociale. Nel margine superiore della pagina, la seconda parte del titolo del libro, "de Newton", lascia supporre che Mademoiselle Ferrand sia intenta alla lettura degli Élémens de la philosophie de Neuton di Voltaire. Nella nostra analisi dei concetti generali relativi alla materia e al moto del XVIII sec., ci troveremo quindi a riflettere sull'opera di Newton.

Lo spazio e il tempo

All'inizio dei Principia, Newton riflette sulla natura dello spazio e del tempo. Per entrambi i concetti egli operò una distinzione tra assoluto e relativo, secondo la quale noi siamo in grado di percepire solamente le posizioni e i moti relativi dei corpi. Questo fu uno dei più importanti insegnamenti della rivoluzione astronomica. Se fosse stato facile capire quali corpi rimangono effettivamente in stato di quiete e quali si muovono, non sarebbero trascorsi quasi 1400 anni tra la sistematizzazione dell'astronomia matematica geocentrica di Tolomeo e la scoperta copernicana del moto della Terra intorno al Sole. Tuttavia, per Newton, lo 'spazio assoluto' esisteva come entità in sé e per sé.

Analogamente, misuriamo il tempo attraverso l'osservazione dei fenomeni periodici e, dal momento che nessun fenomeno è perfettamente regolare, non si può percepire il tempo assoluto, ma soltanto una sua approssimazione imperfetta. A riprova di ciò, Newton indicò l'irregolarità del tempo solare. La lunghezza del giorno solare, vale a dire dello spazio di tempo che intercorre tra un mezzogiorno e quello successivo, non è costante. Le cause di questa irregolarità sono due: il Sole si muove a una velocità non uniforme lungo l'eclittica, e il piano dell'eclittica è inclinato rispetto a quello dell'equatore. Di conseguenza, se possedessimo un orologio perfetto, in grado di scandire il tempo in modo uniforme, nel corso di un anno si creerebbe uno scarto di ±15 minuti tra il tempo dello strumento e quello solare. Sin dai tempi di Tolomeo, gli astronomi erano a conoscenza della necessità di correggere il tempo solare attraverso l'aggiunta di un termine, chiamato più tardi 'equazione del tempo'. Secondo Newton quindi, il tempo solare, immediatamente percepibile e misurabile, era un'approssimazione imperfetta del tempo assoluto. Ci si può avvicinare al tempo assoluto applicando l'equazione del tempo, ma non si deve pensare che questa consenta di giungere a una misurazione esatta del tempo assoluto: possono esistere, infatti, altre irregolarità ancora non individuate. Tuttavia, per Newton, il tempo assoluto in realtà esisteva e scorreva in modo uniforme, indipendentemente da qualsiasi relazione esterna.

Secondo una celebre massima di Newton, il fardello che grava sulla filosofia della Natura consiste per una buona metà nel problema di dedurre i moti dei corpi dalle forze che agiscono su di essi. Nel caso del moto rotatorio, ritiene Newton, l'applicazione di questa massima consentirebbe la determinazione del moto assoluto ‒ cioè, del moto di un corpo rispetto allo spazio assoluto. Egli immagina di sospendere a una fune un secchio pieno d'acqua. Se si torce la fune per poi lasciarla libera di svolgersi, il secchio inizia a ruotare intorno a un asse verticale. Lentamente anche l'acqua contenuta nel secchio inizia a ruotare, allontanandosi dall'asse di rotazione, e la superficie dell'acqua assume una forma concava. Newton propone anche un esempio analogo, quello di due pesi legati alle estremità di uno spago. Proiettando i due pesi in aria, essi iniziano a ruotare uno intorno all'altro e lo spago, sottoposto a tensione, si tende. Volendo, si potrebbe dire che il secchio è in quiete, mentre il resto dell'Universo ruota intorno a esso; ma, dal punto di vista di Newton, questa posizione rivela un ostinato e cieco relativismo. La forma assunta dalla superficie dell'acqua dimostra che il secchio in realtà ruota rispetto allo spazio assoluto. Analogamente, la tensione dello spago dimostra che i due pesi si muovono realmente lungo un percorso circolare nello spazio assoluto; Ernst Mach, tuttavia, avrebbe in seguito asserito che si trattava di una tesi opinabile, basata su un esperimento che nella realtà non poteva essere sottoposto a verifica: "Si provi a tener fermo il secchio di Newton, a far ruotare il cielo delle stelle fisse e quindi a dimostrare l'assenza di forze centrifughe" (Mach 1960, p. 279).

Nel 1715, Gottfried Wilhelm Leibniz (1646-1716) inviò una lettera a Carolina di Anspach (1683-1737), principessa del Galles. In Germania, Leibniz era stato in contatto con Carolina per molti anni, prima che, nel 1714, alla dinastia degli Hannover fosse riconosciuta la successione al trono d'Inghilterra e che suo suocero divenisse re con il nome di Giorgio I. In questa lettera alla sua antica allieva e protettrice, Leibniz esprimeva la sua inquietudine per i pericolosi esiti che potevano scaturire dalla filosofia di Newton, soprattutto per quanto riguardava la religione naturale in Inghilterra. Carolina mostrò questa lettera a Samuel Clarke (1675-1729), membro della Chiesa anglicana, teologo eterodosso, amico e discepolo di Newton. La sua iniziativa diede luogo a uno scambio di lettere, cinque di Leibniz e cinque di Clarke, in cui si affrontano molte questioni relative alla religione e alla filosofia naturale; l'episolario fu pubblicato da Clarke nel 1717. Il dibattito tra Newton e Leibniz si svolse in forma indiretta, attraverso Carolina che agiva da mediatrice tra Leibniz e Clarke, mentre Newton vigilava silenzioso sull'intera vicenda. Tra le ragioni dell'atteggiamento di Newton, ricorderemo la sua orgogliosa riservatezza e l'avversione per le dispute e il clima di ostilità venutosi a creare tra i due scienziati in seguito alla controversia sulla priorità dell'invenzione del calcolo infinitesimale.

Benché, sin dai tempi di Aristotele, i filosofi abbiano discusso sulla natura del 'tempo', il dibattito svoltosi nel XVIII sec. tra Leibniz e Clarke (dominato sullo sfondo da Newton) può essere considerato il primo serio esame filosofico della natura dello 'spazio'. Bisogna distinguere due questioni: in primo luogo, lo spazio è 'reale' o 'ideale', cioè un prodotto della mente degli esseri umani? In secondo luogo, lo spazio deve essere considerato 'assoluto', vale a dire dotato di proprietà indipendenti da qualsiasi altra condizione, o 'relativo'? Nella seguente tavola, elaborata dal filosofo Paul Loeb, sono illustrate in modo molto chiaro diverse posizioni assunte in relazione a tali questioni:

In relazione alla natura del tempo questi pensatori assunsero le stesse posizioni indicate in questa tavola. Come abbiamo già osservato, Newton credeva nell'esistenza di uno spazio reale, dotato di proprietà assolute. Secondo Leibniz, invece, lo spazio non è che l'ordine di fenomeni coesistenti e il tempo l'ordine di fenomeni successivi. Dipendendo dai corpi, lo spazio e il tempo possono essere definiti 'relativi' o 'relazionali'. Inoltre, per Leibniz, lo spazio e il tempo sono ideali perché non sono sostanze e soltanto le sostanze possono essere veramente reali. Egli stabilisce un'analogia tra le relazioni spaziali e alcuni nozioni matematiche, come, per esempio, il rapporto tra due linee, che non è una sostanza né un accidente inerente alle due linee, ma qualcosa di astratto rispetto ad esse. Quindi un rapporto non è qualcosa di reale, ma qualcosa di ideale, anche se in alcuni casi può rivelarsi estremamente utile.

Clarke obiettò che se Dio avesse deciso di creare l'Universo in un luogo diverso da quello in cui effettivamente lo ha collocato, le relazioni tra i corpi non sarebbero cambiate. La teoria di Leibniz quindi sembrava privare Dio del potere di creare l'Universo in un luogo di sua scelta. Clarke usò lo stesso argomento per la questione della creazione dell'Universo da parte di Dio in un dato momento. Se Dio avesse creato il mondo milioni di anni prima, l'ordine delle cose successive non sarebbe cambiato, e quindi Dio non avrebbe veramente creato il mondo in un momento anteriore. Leibniz ricorse al suo principio dell'identità degli indiscernibili per dimostrare che due cose che non possono in alcun modo essere distinte sono in realtà identiche. Per Leibniz, quindi, non aveva alcun senso dire che l'intero Universo si sarebbe potuto trovare in un altro luogo. Dio in realtà non aveva nulla da scegliere e quindi la sua teoria relazionale non limitava in alcun modo il suo potere.

Nella posizione di Leibniz sono individuabili alcune contraddizioni, mai chiarite dal filosofo. Egli sottolineò, per esempio, l'importanza della 'forza viva' (il prodotto della massa per il quadrato della velocità ‒ che corrisponde al moderno concetto di energia cinetica di un corpo mobile) considerandola una cosa reale. Questo concetto sembra presupporre una distinzione tra moto assoluto e moto relativo, che Leibniz finì per riconoscere, senza tuttavia spiegare in che modo tale distinzione potesse essere conciliata con la sua teoria relazionale dello spazio e del tempo.

La corrispondenza tra Leibniz e Clarke fu letta da un vasto pubblico ed ebbe numerose edizioni, fra cui ricorderemo la celebre raccolta del 1720 curata da Pierre Des Maizeaux (1666-1745). Nel 1740, Gabrielle-Émilie Le Tonnelier de Breteuil (1706-1749), marchesa di Châtelet, riesaminò attentamente l'intero dibattito nelle sue Institutions de physique. In realtà, la marchesa, una volta completata la sua opera di divulgazione, era rimasta affascinata dalla metafisica leibniziana, e ritardò la pubblicazione del testo per quasi due anni, in modo da potervi inserire due nuovi capitoli dedicati alla filosofia di Leibniz e alla sua teoria dello spazio e del tempo.

Inizialmente schieratosi in difesa della teoria di Leibniz, Immanuel Kant abbandonò questa concezione a favore di quella di Newton dopo aver letto il saggio di Leonhard Euler Réflexions sur l'espace et le temps pubblicato nella "Histoire de l'Académie Royale des Sciences et Belles Lettres de Berlin" del 1748. In questo articolo, Euler sottolineava l'importanza delle leggi della meccanica, che erano state verificate dall'esperienza. La validità del principio di inerzia tende a confermare l'esistenza dello spazio assoluto e l'esperienza insegna che lo stato di inerzia deve essere determinato in riferimento alle stelle fisse. Ma se lo spazio è un concetto esclusivamente relazionale, come sosteneva Leibniz, come spiegare l'inerzia dei corpi, se non asserendo che le stelle fisse la dirigono e la regolano? Euler respinge questa possibilità ‒ che sembra anticipare il principio di Mach ‒ considerandola contraria alla tradizionale metafisica ed oltremodo stravagante. Per Euler è impossibile attribuire qualsiasi significato alle leggi della meccanica basandosi su un concetto di spazio ottenuto per astrazione dalle relazioni esistenti tra gli oggetti: adottando questo punto di vista, infatti, si rischia di cadere in un circolo vizioso.

Il richiamo di Euler alle leggi della meccanica esercitò una profonda influenza sul pensiero di Kant. Questi modificò però la sua posizione anche grazie alla riflessione sugli 'opposti incongruenti', di cui la mano destra e la mano sinistra costituiscono un valido esempio. La differenza tra la mano destra e la sinistra non è determinata dalle relazioni esistenti tra le diverse parti della mano, perché il rapporto tra il pollice e le dita della mano sinistra non è diverso da quello esistente tra il pollice e le dita della mano destra. Tale differenza non è determinata neppure dal rapporto tra la mano e il resto dell'Universo, perché anche se fosse il solo oggetto dell'Universo una mano sinistra rimarrebbe sempre una mano sinistra. La spiegazione di questa differenza va invece ricercata nel rapporto esistente tra le mani e lo spazio assoluto in cui sono contenute.

Kant abbandonò ben presto anche questa posizione. Nella sua dissertazione inaugurale del 1770 e poi nella Kritik der reinen Vernunft (Critica della ragion pura) del 1781, egli rifiuta la concezione newtoniana che, a suo parere, fa riferimento a un mondo di pura invenzione. La posizione di Leibniz risulta però ugualmente indifendibile, perché trasforma la geometria in una scienza empirica, privandola della sua universalità. Nel periodo della maturità, Kant giunse alla conclusione che lo spazio e il tempo sono forme della sensibilità umana, vale a dire, intuizioni pure. Ciononostante, le leggi della geometria euclidea conservano il loro statuto di verità necessarie. Kant, in definitiva, adotta la posizione meno plausibile indicata nella tavola: lo spazio e il tempo sono entità ideali e, tuttavia, in qualche modo assolute, in considerazione della loro universalità.

Il dibattito sulla natura dello spazio e del tempo svoltosi nel XVIII sec. non produsse profonde conseguenze nella pratica scientifica. In realtà, lo stesso Newton, dopo aver introdotto le sue idee su questo argomento all'inizio dei Principia, non ne aveva più fatto uso. Nel XX sec., lo spazio e il tempo divennero, come è noto, relativi. Nella teoria della relatività ristretta (1905) di Albert Einstein, lo spazio e il tempo sono relativi, nel senso che la lunghezza di un regolo e il ritmo della marcia di un orologio dipendono dalla velocità con cui essi si muovono rispetto all'osservatore. A causa della relatività della simultaneità, è persino possibile che due osservatori in moto relativo non concordino sull'ordine temporale di due eventi.

La materia

L'Universo materiale del XVII sec. era estremamente variegato. All'inizio del secolo, gli elementi (terra, acqua, aria e fuoco) e le qualità (caldo, freddo, umido, asciutto) aristotelici coesistevano accanto al misticismo chimico dei seguaci di Paracelso, basato sui tre principî del sale, dello zolfo e del mercurio. In contrapposizione a queste tradizioni, che tendevano a considerare la materia attiva, fu riscoperta l'antica teoria atomistica di Epicuro e di Lucrezio. Nel corso di quasi tutta la sua storia, l'atomismo era stato associato all'ateismo, dal momento che nella sua visione materialistica della Natura non vi era spazio per Dio o per l'anima. Tuttavia, grazie a Pierre Gassendi (1592-1655), che dedicò tutta la sua vita alla difesa di questa dottrina, l'atomismo acquisì una nuova rispettabilità e, verso la metà del secolo, le teorie corpuscolari fecero ovunque la loro comparsa.

Contrapponendosi agli scolastici aristotelici, che spiegavano la Natura in termini di cause finali e che di conseguenza attribuivano alla materia inanimata qualità antropomorfiche come, per esempio, la capacità di desiderare e di proporsi uno scopo, René Descartes (1596-1650) adottò una posizione radicalmente dualista. Egli separa il mondo del pensiero e dello spirito da quello della materia, considerandola assolutamente passiva e identificandola con l'estensione. Egli nega l'esistenza del vuoto (in questo, così come in altri casi, dimostra di essere più vicino ad Aristotele di quanto volesse dare a intendere), prendendo le distanze da Gassendi. Inoltre, a differenza di quest'ultimo, Descartes nega l'esistenza degli atomi ‒ gli elementi costitutivi fondamentali e indivisibili della materia. Tuttavia, nel render conto dei fenomeni, Descartes spesso si richiama al moto e alle collisioni delle particelle della materia. Così, nonostante queste divergenze, la visione della Natura di Descartes presentava molti punti di contatto con quella di Gassendi e, alla fine del XVII sec., i due pensatori erano frequentemente associati come esponenti del 'meccanicismo'.

Nei suoi Principia philosophiae (1644) Descartes introdusse nuove regole esplicative nel campo della filosofia della Natura. I filosofi scolastici, secondo i quali il magnete era in grado di attirare il ferro perché aveva un'affinità con esso o perché dotato di un potere d'attrazione, non facevano che incorrere in un circolo vizioso, nascondendo la loro ignoranza dietro ai termini della loro filosofia. Descartes rifiutava le qualità occulte degli scolastici medievali, come, per esempio, la simpatia, l'affinità e l'attrazione, e pensava che tutti i fenomeni naturali potessero essere spiegati in termini d'impatto tra i corpi. Secondo Descartes, i pianeti girano intorno al Sole trasportati da un vortice (tourbillon) di fluido celeste. Anche il peso dei corpi sulla superficie della Terra è determinato da un vortice di fluido celeste. Tentando di allontanarsi dal centro del vortice, questo fluido sottile spinge la materia terrestre nella direzione opposta. In una delle sue lettere, Descartes descrive persino un esperimento volto a dimostrare la sua teoria del peso. Dopo aver riempito un recipiente rotondo di pallini di piombo, s'inseriscono in esso alcuni pezzi di legno, più leggeri e più grandi dei pallini stessi. Quindi, facendo ruotare rapidamente il recipiente "si vedrà che i pallini spingono tutti i pezzi di legno […] verso il centro del recipiente, proprio come la materia sottile spinge i corpi terrestri" (Oeuvres, ed. Adam, IX, pp. 593-594).

Le idee di attrazione e gravità, introdotte da Newton come principî esplicativi dei moti del Sistema solare, naturalmente disorientarono i filosofi continentali, imbevuti delle teorie meccaniciste. Dal loro punto di vista, Newton si basava su un modo di pensare ormai caduto in discredito e sembrava voler reintrodurre le forze occulte degli scolastici. Nei suoi Essais de théodicée (1710), infatti, Leibniz criticò la teoria della gravità di Newton basandosi proprio su questi argomenti. Analoghe accuse furono mosse alla fisica newtoniana dal matematico e fisico francese Joseph Saurin (1659-1737). Nella seconda edizione dei Principia (1713) apparve una nuova prefazione in cui un amico di Newton, l'astronomo Roger Cotes (1682-1716), rispose con chiarezza alle critiche di Leibniz. Una proprietà può dirsi occulta se la sua esistenza non è stata dimostrata, ma solamente immaginata, mentre l'esistenza della gravità è chiaramente dimostrata dall'osservazione; soltanto la 'causa' della gravità rimane occulta. Coloro che intendevano escludere la gravità dalla filosofia soltanto perché la sua causa non era stata ancora scoperta rischiavano di minare i fondamenti stessi della filosofia della Natura.

La forza di persuasione del principio di gravitazione universale di Newton va ricercata nella sua utilità per la spiegazione di numerosi fenomeni, dal moto dei pianeti alle maree. L'universalità di questo principio ‒ secondo cui tutti i corpi esistenti nell'Universo esercitano tra loro un'attrazione reciproca ‒ era dimostrata dal fatto che anche i satelliti di Giove obbediscono alle leggi di Kepler, e cioè che Giove attrae i suoi satelliti con la forza di gravità. I dettagli del complesso moto della Luna intorno alla Terra potevano essere spiegati riconoscendo che non solo la Terra, ma anche il Sole esercita un'azione sulla Luna.

Come dimostra la sua Opticks (1704), Newton applicò l'idea di attrazione anche in altri campi d'indagine. Egli concepì i raggi luminosi come correnti di particelle; secondo Newton, quindi, il fenomeno della rifrazione della luce, che si verifica quando quest'ultima si propaga dall'aria all'acqua, era causato dalla forza d'attrazione che l'acqua esercita sulle particelle della luce. Tuttavia, le particelle della luce di Newton non sono semplici sfere solide, ma corpuscoli complessi e molto attivi. Per spiegare il fatto che, dopo aver colpito la superficie di un vetro, i raggi di luce sono in parte rifratti e in parte riflessi, Newton asserì che essi sono soggetti a una sorta di oscillazione interna. Inoltre, per render conto degli effetti di polarizzazione associati ad alcuni cristalli, come, per esempio, lo spato d'Islanda, Newton finì per supporre che i raggi di luce fossero dotati di lati. La materia inerte e indistinguibile dalla mera estensione descritta da Descartes, riacquistava così proditoriamente un gran numero di proprietà.

L'efficacia del principio di gravità di Newton nello spiegare i moti del Sistema solare favorì la sua applicazione ad altre branche della ricerca scientifica. Come osserva Voltaire nelle Lettres philosophiques, nel campo della chimica, per esempio, si fece ricorso all'idea di attrazione per spiegare le affinità delle sostanze chimiche. Il principio di attrazione fu applicato anche nell'area delle scienze della vita per render conto della generazione e dello sviluppo degli embrioni. Nella Vénus physique (1744), Maupertuis sostenne che soltanto l'attrazione poteva spiegare la progressiva formazione, a partire da piccoli elementi costitutivi invisibili, di oggetti così complessi come gli embrioni.

Oltre all'attrazione, la descrizione della materia imponeva il ricorso a un'altra forza, quella di repulsione. Essa, infatti, era necessaria non soltanto per spiegare la coesione e l'impenetrabilità degli oggetti, ma anche la loro elasticità e la loro espansibilità, come Robert Boyle ed Edme Mariotte avevano dimostrato nel caso dell'aria. Un modello coerente di spiegazione fu in effetti avanzato da Daniel Bernoulli nella Hydrodynamica (1738). Per Bernoulli, infatti, i gas erano costituiti da innumerevoli particelle discrete che si muovevano con grande rapidità e che esercitavano una pressione come risultato della collisione con le pareti del contenitore. Più tardi si fece ricorso ai fluidi elastici (in alcuni casi considerati discreti e in altri continui) per render conto dei nuovi fenomeni dell'elettricità e del calore.

La questione della natura della materia e dell'origine della massa, tuttavia, rimaneva priva di una risposta adeguata. Uno dei più importanti risultati conseguiti da Newton fu l'intuizione che il concetto di massa è in effetti duplice e racchiude in sé un mistero. Newton operò per la prima volta una chiara distinzione tra massa (o quantità di materia) e peso (la forza d'attrazione che la Terra esercita sugli oggetti pesanti). Entrambe le nozioni svolgevano un ruolo nell'analisi del moto del pendolo. La tendenza del pendolo a proseguire il suo moto in avanti dipende dalla sua massa o inerzia, vale a dire dalla m che appare nell'espressione mv della quantità di moto. Ma secondo la legge di gravitazione di Newton, la forza d'attrazione che la Terra esercita su un oggetto è proporzionale alla quantità di materia dell'oggetto. Questa quantità di materia deve dunque essere identificata con la massa inerziale? Sollevando questa questione, Newton compiva un'impresa straordinaria. Per tentare di risolverla, egli eseguì una serie di esperimenti con il pendolo. Prese due scatole di legno rotonde, identiche. Riempì la prima scatola con pezzi di legno. Al centro della seconda scatola pose una quantità d'oro di peso equivalente: "sospendendo le scatole a due corde, entrambe lunghe undici piedi, si avranno due pendoli esattamente identici per quanto riguarda il peso, la forma e la resistenza all'aria" (Principia, ed. Cohen, p. 807). Facendo oscillare le due scatole, constatò che esse si muovevano allo stesso ritmo per un tempo lunghissimo. Lo scienziato quindi giunse alla conclusione che la massa dell'oro stava alla massa del legno come il peso dell'oro al peso del legno. Ripetendo l'esperimento con l'argento, il piombo, il vetro, la sabbia, il sale, l'acqua e il grano, egli ottenne sempre lo stesso risultato, sostenendo di aver riscontrato una differenza di quantità di materia equivalente a una parte su mille. In altre parole, la massa inerziale (la m dell'espressione mv) è essenzialmente uguale alla massa gravitazionale (la m da cui dipende la forza di attrazione gravitazionale). Questa constatazione era strettamente correlata al fatto che la forza di gravitazione agisce con la stessa intensità su ogni particella dei corpi, comprese quelle interne.

La dottrina delle ipotesi

Descartes si rese conto di aver inserito nelle sue spiegazioni dei fenomeni un numero non indifferente di meccanismi invisibili di sua invenzione. Per prevenire eventuali critiche, egli sostenne che questi meccanismi dovevano essere considerati semplici ipotesi. Inoltre, anche nel caso in cui fossero state false, tali ipotesi potevano rivelarsi utili: un'ipotesi falsa che spiega correttamente i fenomeni poteva essere altrettanto utile della verità.

Newton scelse attentamente il titolo della sua opera in modo da non risparmiare una nota di biasimo a Descartes: egli, infatti, decise di chiamarla Philosophiae naturalis principia mathematica, escludendo il vago e impreciso titolo di Principia philosophiae (cioè, genericamente, principî di filosofia) dell'opera cartesiana. Nella prefazione alla prima edizione dei Principia, Newton asserisce che la missione della filosofia è quella di "scoprire le forze della Natura a partire dai fenomeni del moto e di dimostrare gli altri fenomeni a partire da queste forze" (ed. Cohen, p. 382).

Nella seconda edizione dell'opera (1713), egli inserì il celebre Scholium generale, in cui non è formulata alcuna ipotesi sulla causa della gravità: "Perché qualsiasi tesi che non sia dedotta dai fenomeni deve essere chiamata ipotesi e per le ipotesi, metafisiche e fisiche, basate sulle qualità occulte o di tipo meccanico, non vi è spazio nella filosofia sperimentale" (ibidem, p. 943). Rinunciando alle qualità metafisiche e occulte, Newton si limitava a confermare le tesi formulate da Descartes, ma attaccando le ipotesi fisiche e meccaniche, egli attaccava frontalmente Descartes e l'intera scuola del meccanicismo cartesiano.

Newton poté dire di aver rinunciato alle ipotesi meccaniche perché il piano dei suoi Principia corrispondeva, a grandi linee, alla missione stessa della filosofia della Natura come lui la intendeva; esso, infatti, si basava sull'induzione dai fenomeni della legge dell'inverso del quadrato riguardante l'attrazione gravitazionale e sulla deduzione di nuovi fenomeni dalla legge della dinamica. Il rifiuto delle ipotesi formulato nello Scholium generale era però, in parte, un espediente retorico, a cui lo scienziato ricorse per rispondere a coloro che avevano criticato la prima edizione dei Principia (tra cui ricorderemo Leibniz), perché l'autore non aveva indicato la causa della gravità.

Tuttavia, contrariamente al giudizio che di lui hanno dato le generazioni successive, Newton non era affatto un positivista. Nel corso della sua giovinezza egli era rimasto affascinato dai vortici di Descartes, che abbandonò soltanto dopo uno strenuo tentativo di difesa. Nel periodo in cui compose i Principia, Newton pensava ancora che i vortici meritassero almeno di essere confutati come causa meccanica della gravità. Alla fine del secondo libro, infatti, si prese la pena di dimostrare che essi contraddicevano le leggi del moto planetario formulate da Kepler. Anche allora Newton non cessò di speculare sulla causa della gravità. Nell'Opticks, si mostrò incline ad attribuire gli effetti della gravità allo stesso mezzo etereo che provocava la rifrazione della luce. Newton riteneva che l'etere si presentasse in forma estremamente rarefatta all'interno dei corpi e che la sua densità crescesse con l'aumentare della distanza dalla superficie di un corpo. Il mezzo etereo, quindi, era più denso nelle regioni più esterne del Sistema solare che in quelle vicine al Sole. Secondo Newton, se la forza elastica di questo mezzo era abbastanza grande, "essa poteva essere sufficiente a spingere i corpi dalle parti più dense del mezzo verso quelle più rarefatte, con tutto il potere che chiamiamo gravità" (Opticks, ed. 1730, pp. 350-351).

L'eredità intellettuale di Newton, quindi, non era priva di ambiguità. Il Newton dei Principia aveva rinunciato alle ipotesi meccaniche, considerate vane speculazioni, e aveva asserito che era sufficiente riuscire a calcolare gli effetti della gravità. Il Newton dell'Opticks, invece, trovandosi a dover affrontare una serie di nuovi fenomeni ottici, si mostrò più incline alla speculazione: si sapeva così poco sulla natura della luce che egli 'dovette' tentare di trovare delle spiegazioni al di là della superficie dei fenomeni visibili. Come dimostra la voce Hypothèse (1765) dell'Encyclopédie di Diderot e d'Alembert, il Newton dei Principia esercitò un'influenza più profonda di quello dell'Opticks sullo sviluppo dell'epistemologia del XVIII secolo. In questo articolo si tenta con grande saggezza di trovare un compromesso, sostenendo che in fatto di ipotesi è necessario evitare due eccessi: accordare loro troppo credito, come aveva fatto Descartes, o farne del tutto a meno. Secondo l'Encyclopédie, Newton e soprattutto i suoi discepoli erano incorsi nell'errore opposto: "Disgustati dalle congetture e dagli errori di cui traboccavano le opere filosofiche, essi protestarono contro le 'ipotesi' e tentarono di renderle sospette e ridicole, definendole 'veleno della ragione' e 'flagello della filosofia'". L'Encyclopédie precisa scrupolosamente che lo stesso Newton era ricorso a una serie di ipotesi (come definire, del resto, il principio di gravitazione universale?). Ma la questione fondamentale è che 'si è creduto' che Newton fosse risolutamente contrario all'uso delle ipotesi in filosofia naturale. Nel corso del Settecento, si registrò una decisa svolta verso posizioni positivistiche.

A partire dal 1770, la maggior parte degli studiosi di fisica cessarono di tentare di spiegare la gravità e si limitarono ad accettarla e a farne uso come un fatto naturale. La posizione di coloro che erano contrari all'uso delle ipotesi a volte è definita 'laplaciana', dal nome di Pierre-Simon de Laplace (1749-1827) che divenne uno dei suoi principali difensori. In una lettera inviata nel 1797 a Georges-Louis Le Sage (1724-1803), Laplace rifiutò di affrontare la discussione della teoria meccanica della gravità di Le Sage. Secondo Laplace, alcuni filosofi (e tra questi includeva sé stesso) riconoscono la loro ignoranza per quanto riguarda la natura della materia, dello spazio, della forza e dell'estensione e non si curano più di tanto delle cause prime, ravvisando nell'attrazione solo un fenomeno generale che può essere assoggettato a calcoli rigorosi (Evans 2002). La dottrina dell'inutilità delle ipotesi influenzò tuttavia più le discussioni epistemologiche che la pratica scientifica. Come abbiamo già osservato, infatti, gli scienziati del XVIII sec. ipotizzarono continuamente l'esistenza di forze d'attrazione non misurabili che agiscono tra le particelle invisibili. La dottrina dell'inutilità delle ipotesi servì soprattutto a mettere a tacere le speculazioni sul meccanismo che causava l'attrazione o a fornire una valida scusa a chi voleva sottrarsi alla lettura di noiose teorie.

Forza e movimento

Le leggi del movimento di Newton costituirono il fondamento dello studio dei moti e delle forze nel XVIII secolo. Queste leggi sono così formulate nei Principia di Newton:

Prima legge: Ogni corpo persevera nel suo stato di quiete o di moto uniforme in linea retta, a meno che non sia costretto a mutare il proprio stato da forze impresse.

Seconda legge: Il mutamento di moto è proporzionale alla forza motrice impressa, e avviene nella direzione della linea retta in cui quella forza è impressa.

Terza legge: A un'azione corrisponde sempre una reazione uguale e contraria: ossia, le azioni reciproche di due corpi sono sempre uguali e dirette in senso contrario.

Come scrisse Cotes nella prefazione alla seconda edizione dei Principia, la prima era "una legge di Natura, accettata da tutti i filosofi". Nei Principia Newton riconobbe i meriti di Galilei, che aveva adombrato questo principio, ma omise volutamente di menzionare Descartes, che lo aveva formulato in modo molto chiaro nei suoi Principia philosophiae.

La terza legge risultava ragionevole, in quanto asseriva l'equivalenza delle azioni reciproche tra due corpi interagenti. Newton andò oltre, chiarendo che con ciò s'intende che essi esercitano l'uno sull'altro forze uguali.

Una conferma più stringente alla terza legge poteva trovarsi nelle leggi che regolano gli urti elastici e anelastici tra particelle, studiati da Christiaan Huygens (1629-1695), Christopher Wren (1632-1723) e John Wallis (1616-1703), citati da Newton (avevano tutti presentato delle memorie sugli urti agli incontri della Royal Society di Londra, tra il 1668 e il 1669). Quando due sfere elastiche si urtano, se una delle due perde una quantità di moto mv (in cui m è la massa della sfera e v è la velocità persa), l'altra acquisisce esattamente la stessa quantità di moto. Poiché, secondo Newton, le forze si potevano misurare dalla quantità di moto da esse trasmessa, l'osservazione precedente dimostra che le due sfere in collisione agiscono l'una sull'altra con forze uguali e di direzioni opposte.

La seconda legge indica come calcolare il moto di un corpo, prodotto dalle forze che su di esso agiscono, e rappresenta la vera novità della dinamica di Newton. In effetti, però, tra le forze note, Newton era in grado di trattare rigorosamente soltanto le forze di contatto (come quelle in gioco nell'uso di una fune, o negli urti) e la misteriosa forza di attrazione chiamata gravità.

Una caratteristica fondamentale delle forze è che esse si possono comporre e scomporre. Newton applicò abilmente la composizione delle forze ai fenomeni che hanno luogo nel Sistema solare, e in particolare allo studio del sistema a tre corpi costituito da Terra, Sole e Luna.

Quale esempio concreto del metodo di Newton, vediamo come egli utilizza la seconda legge del moto per dimostrare un importante teorema: la legge delle aree di Kepler. Nella fig. 5, S rappresenta un centro di forza statico, come il Sole; nella sua analisi, Newton ipotizza che la forza agente su un corpo in movimento sia sempre diretta verso S, e per semplificare lo studio immagina che la forza non sia applicata in modo continuo, ma attraverso una serie di colpi, o di impulsi. Immaginiamo che un corpo in movimento, per esempio un pianeta, sia posizionato nel punto A. Supponiamo che il corpo possieda una certa velocità e che, se lasciato libero, raggiungerebbe il punto B in un certo tempo. Dopo un ulteriore intervallo di tempo di pari durata, il corpo in moto uniforme arriverebbe quindi al punto c. Grazie a proprietà elementari di geometria, la linea che congiunge S al corpo in movimento spazza aree uguali in tempi uguali; i triangoli SAB e SBc hanno cioè la stessa area (l'area del triangolo è pari al semiprodotto della base per l'altezza; i due triangoli hanno basi uguali ‒ AB per il primo e Bc per il secondo ‒ e le altezze sono identiche, essendo pari alla distanza lungo la perpendicolare tra S e il prolungamento della retta BA).

Cosa succede ora se immaginiamo che il corpo in movimento subisca una serie di colpi, diretti sempre verso S? Supponiamo che, quando il corpo si trova nel punto B, una forza impulsiva fornisca al corpo una velocità tale da causare uno spostamento da B a V, nello stesso tempo necessario al corpo libero per spostarsi da B a c. Mediante la composizione dei moti, il corpo arriverà quindi al punto C (VBcC è un parallelogramma). È ora facile dimostrare che il triangolo SBC ha la stessa area di SBc (che, come abbiamo visto, ha la stessa area di SAB): SBC e SBc hanno la stessa base SB; poiché cC è parallelo a SB, l'altezza del triangolo non cambia nello spostamento da c a C (l'altezza è la distanza di c o C dalla base SB). Newton ha così dimostrato che, purché la forza sia sempre diretta verso un centro fisso, il vettore che descrive la posizione del pianeta spazza aree uguali in tempi uguali, indipendentemente dalla intensità della forza e dalla sua dipendenza dalla distanza. Questa è la seconda legge di Kepler sul moto dei pianeti.

In questa dimostrazione troviamo diverse caratteristiche importanti della meccanica newtoniana. Il percorso del pianeta (ABCDEF) va inteso come una continua deflessione dal moto inerziale lungo la linea retta, determinata dell'azione della forza applicata. Vediamo qui più esplicitamente anche il significato che Newton annette alla seconda legge del moto. Il segmento BV rappresenta la quantità di moto acquisita dal corpo a causa di una forza diretta lungo BS.

Questa semplice dimostrazione della legge delle aree fornisce un esempio del metodo seguito da Newton nei Principia, in cui sono dimostrati anche teoremi molto più complessi. A questo scopo, un elemento chiave fu la dimostrazione che un corpo in movimento con velocità v lungo un cerchio di raggio r subisce un'accelerazione diretta verso il centro del cerchio, e che il suo valore è v²/r (Huygens aveva ricavato lo stesso risultato molto tempo prima, nel 1673, nel suo Horologium oscillatorium).

Newton conosceva anche la terza legge di Kepler (o 'legge armonica'): i quadrati dei periodi di rivoluzione dei pianeti sono proporzionali ai cubi delle loro distanze medie dal Sole. Mettendo insieme la legge armonica di Kepler con il suo teorema sull'accelerazione nel moto circolare uniforme, Newton dimostrò che la forza centripeta con cui il Sole attrae i pianeti deve decadere come l'inverso del quadrato della distanza.

Altri avevano formulato ipotesi in questa direzione, e Newton menzionò, malvolentieri, Christopher Wren, Robert Hooke e Edmond Halley. Questi ultimi avevano in effetti considerato e discusso la possibilità di una forza che seguisse la legge dell'inverso del quadrato della distanza, in un caffè di Londra, nel 1684; fu la conseguente domanda che Halley pose a Newton, sulle orbite che dovrebbero derivare da una tale forza di attrazione, che lo stimolò a scrivere i Principia. Però, anche se altri potevano aver ipotizzato una legge di attrazione basata sull'inverso del quadrato della distanza, Newton fu certamente il primo e il solo a dimostrare matematicamente la sua esistenza a partire dai dati relativi al moto dei pianeti.

Nella sua prima dimostrazione della legge dell'inverso del quadrato, Newton aveva approssimato le orbite dei pianeti con dei cerchi, mentre in seguito passò a un'analisi più dettagliata e realistica del moto dei pianeti. Supponendo valida, oltre alla terza legge di Kepler, anche la prima (secondo la quale l'orbita di un pianeta è una ellissi con il Sole in uno dei fuochi), Newton dimostrò in modo rigoroso che la forza di attrazione deve seguire la legge dell'inverso del quadrato della distanza del pianeta dal Sole. Si trattava di quello che oggi chiamiamo il 'problema diretto'; il 'problema inverso', matematicamente più complesso, consiste nel partire dalla legge dell'inverso del quadrato, e da questa dimostrare che l'orbita è una sezione conica. Nella prima edizione dei Principia, Newton non dimostrò la legge dell'inverso del quadrato. Nella seconda edizione, in risposta alle critiche che ne derivarono, dimostrò il problema inverso. Il lavoro di Newton aveva raggiunto lo scopo che Kepler aveva formulato, ma non realizzato: trovare un fondamento basato sui principî della fisica alle caratteristiche note del moto dei pianeti.

È difficile sovrastimare l'importanza dell'idea, nuova, delle forze centripete (forze cioè dirette verso un centro fisso). Nell'Universo di Descartes i pianeti venivano trascinati dal turbinio della materia celeste che costituiva i vortici; galleggiavano come tappi di sughero in un mulinello, e se era necessaria una forza per mantenerli in movimento, questa veniva fornita da spinte tangenziali, lungo la direzione del moto. Nell'Universo di Newton i pianeti sono permanentemente attratti dal Sole; se dovessero liberarsi della gravità, volerebbero via lungo la tangente all'orbita. Newton dimostrò inoltre che i pianeti devono muoversi in uno spazio quasi completamente privo di materia: se vi fosse una quantità apprezzabile di materia lungo la loro orbita, i pianeti subirebbero l'azione di forze di attrito che provocherebbero il decadimento dell'orbita.

Fu in questo senso che Voltaire, quando scese dalla nave a Dover, lasciò un Universo pieno per entrare in uno vuoto.

Difficoltà con il concetto di forza

La parola 'forza' (vis) aveva diversi significati all'epoca di Newton, e anche nella sua stessa opera. Essa era a volte considerata come contenuta nel corpo in movimento (la forza di inerzia); lo stesso Newton chiamò questa inerzia la vis insita, o 'forza insita', di un corpo. Applicando le leggi del moto, però, Newton rese chiaro che una forza è un'azione esercitata su un corpo dall'esterno, e che provoca una variazione della sua velocità. Quando l'azione della forza cessa, il corpo prosegue il movimento in linea retta, a velocità costante. Newton introdusse tuttavia diverse misure della forza applicata: per esempio, usò a volte la 'quantità motrice' di una forza, proporzionale alla quantità di moto (mv) generata in un tempo dato. Generalmente utilizzava la 'quantità acceleratrice' di una forza, proporzionale alla velocità generata in un tempo dato ossia, in termini moderni, la forza per unità di massa.

Più o meno in coincidenza con la pubblicazione dei Principia, la corretta misura della forza divenne argomento di una disputa che proseguì per metà del XVIII secolo. Nei Principia philosophiae, Descartes aveva affermato che la "quantità di moto" rimane sempre costante nell'Universo, e definì la quantità di moto di un corpo come la quantità di materia moltiplicata per la velocità (mv). Utilizzando questi concetti, Descartes aveva fornito un insieme di regole valide per gli urti tra i corpi, quasi tutte poi dimostratesi sbagliate. Christiaan Huygens diede degli urti una trattazione di chiarezza cristallina, e seppe utilizzare in modo ingegnoso la relatività del moto. Per derivare le regole corrette per gli urti elastici, Huygens li esaminò in due diversi sistemi di riferimento, immaginando degli esperimenti effettuati su una barca in movimento lungo un canale, osservata da un uomo fermo sulla sponda. Questa trattazione fu presentata alla Royal Society nel 1669, come abbiamo già detto, e fu anche pubblicata postuma nel De motu corporum ex percussione (1700). In parte grazie all'opera di Huygens, si chiarì che la quantità di moto si conserva soltanto se intesa come quantità caratterizzata anche da una direzione o, diremmo oggi, come vettore. Newton utilizza il concetto di quantità di moto in questa accezione, trattandola sempre come una quantità direzionale.

Un'altra misura della forza era la 'forza viva' (vis viva), o mv², cioè la massa per il quadrato della velocità iniziale. La forza viva fu introdotta in meccanica nel 1686 da Leibniz, nel suo articolo Brevis demonstratio erroris mirabilis Cartesii. Secondo la legge di Galilei riguardante la caduta dei gravi, l'altezza alla quale arriverà un oggetto lanciato in verticale è proporzionale al quadrato della sua velocità. Era quindi chiaro che la forza viva giocava un ruolo importante in meccanica (si tratta in effetti del doppio della quantità chiamata 'energia cinetica' nella fisica contemporanea). Leibniz ammise la costanza della quantità di moto, a patto d'intenderla come quantità direzionale; negò tuttavia che fosse questo il motore di tutte le cose. A differenza della quantità di moto, la forza viva è sempre una quantità additiva (dipendendo dal quadrato della velocità); la forza viva di diversi corpi è perciò la somma delle forze vive dei singoli. Secondo Leibniz la forza viva è quindi una quantità assoluta; la forza viva inserita da Dio nell'Universo al momento della Creazione rimane sempre conservata. Naturalmente era ben noto che essa svanisce negli urti tra corpi anelastici, come, per esempio, nel caso dei pezzi d'argilla; Leibniz affermava però che in quel caso la forza viva si distribuiva tra i costituenti invisibili dei corpi.

Willem Jacob 'sGravesande (1688-1742) e Giovanni Poleni (1683-1761) effettuarono esperimenti in cui si facevano cadere palle di masse diverse, da diverse altezze, su superfici di argilla, e scoprirono che due palle della stessa dimensione, cadendo, incidono l'argilla nella stessa misura, se vengono lanciate da altezze inversamente proporzionali alle loro masse. In altre parole, ciò che conta è mh, dove m è la massa della palla e h l'altezza dalla quale è lasciata cadere. Poiché, per la legge di Galilei sulla caduta dei gravi, h è proporzionale a v², l'entità dell'incisione dipende chiaramente dalla forza viva mv². Dichiarandosi a favore della forza viva nel 1722, 'sGravesande diede un forte sostegno alla posizione di Leibniz. Quando, nel 1740, apparvero le Institutions de physique di Madame du Châtelet, la forza viva trovò un altro efficace sostenitore. Nel capitolo conclusivo del suo libro, infatti, Madame du Châtelet riassume l'intera disputa, compresi i risultati sperimentali e le diverse opinioni dei vari esperti, prima di esprimersi a favore del punto di vista di Leibniz.

Eppure, gran parte di questo dibattito sul modo di misurare le forze riguardava più le parole che i fatti, come notava nel Traité de dynamique (1758) Jean-Baptiste Le Rond d'Alembert: "Se si propone lo stesso problema di meccanica a due studiosi di geometria, uno avversario e uno fautore della forza viva, le loro soluzioni, se sono bravi, saranno sempre in perfetto accordo" (pp. xxiii-xxiv). In effetti, la forza viva di Leibniz rappresenta il primo uso importante dell'idea di energia, che nel XIX sec. sarebbe diventata un concetto chiave del pensiero fisico.

Matematizzazione e sistematizzazione

La meccanica di Newton fu inventata per determinare il movimento di punti isolati, come nel caso di pianeti orbitanti, o magari di mele in caduta libera. Era molto più difficile utilizzarla per lo studio della dinamica di corpi solidi tridimensionali (come la rotazione di una trottola) o del comportamento dei fluidi (come il flusso dell'acqua da un contenitore forato) o della propagazione di onde (come le onde sonore) attraverso un mezzo elastico. Newton senza dubbio affrontò tutti e tre i problemi nei Principia, anche se con successi parziali. C'erano dunque tre aree applicative in cui rimanevano ampi margini per ulteriori sviluppi.

Inoltre, i metodi matematici di Newton erano di difficile uso e richiedevano notevole finezza per essere applicati con successo. Anche se Newton fu uno degli inventori del calcolo infinitesimale, non ne fece molto uso nei Principia (a eccezione di alcuni teoremi sui limiti). Le sue proposizioni erano formulate piuttosto in termini geometrici e, come abbiamo visto, erano dimostrate mediante procedimenti geometrici e algebrici.

Nel XVIII sec., grazie all'attività ininterrotta e indipendente di vari studiosi, i principî di Newton furono sviluppati in diversi ambiti, migliorandone la chiarezza e la potenzialità di calcolo.

Questo lavoro si sviluppò lungo diverse linee. In primo luogo, l'eliminazione dei metodi geometrici o sintetici di Newton, e la loro sostituzione con il calcolo infinitesimale di Leibniz e dello stesso Newton, portarono la meccanica nell'ambito dell'analisi matematica. Questo rese possibile affrontare problemi più complicati con maggiore sicurezza e minore rischio di errori. In secondo luogo, gli studiosi di meccanica si dedicarono ad argomenti che Newton non aveva trattato, e ad altri che aveva affrontato con successo parziale. Tra questi, il moto dei fluidi, la rotazione dei corpi rigidi, le vibrazioni delle corde e la propagazione delle onde. In terzo luogo si esplorarono formulazioni alternative della meccanica, basate su principî equivalenti alle leggi di Newton, ma espressi in forme molto diverse. Spesso questo implicava uno sforzo volto a organizzare l'argomento in modo più rigoroso dal punto di vista logico, e a ridurre il numero di ipotesi o di principî fondanti.

Un'importante opera del primo tipo fu la Mechanica sive motus scientia analytice exposita di Leonhard Euler (1736), nella quale troviamo per la prima volta la seconda legge del moto di Newton in una forma vicina a quella che oggi vediamo spesso espressa nella forma F_x=ma_x, in cui F_x è la componente della forza applicata lungo uno dei tre assi ortogonali, a_x è la corrispondente componente dell'accelerazione e m è la massa del corpo. Nella Mechanica, Euler scompone la forza e il movimento lungo gli assi ortogonali (in generale non fissi nello spazio), e sceglie tipicamente come assi la tangente alla traiettoria della particella e altri due perpendicolari a questa, uno dei quali giacente nel piano di curvatura. Per una singola direzione, Euler pone dv, cioè la variazione infinitesima della velocità pari a Fdt/m indicando con v la velocità, F la forza, m la massa e t il tempo (alcune delle lettere usate da Euler sono diverse).

Una formulazione ancora più chiara della seconda legge del moto compare nell'articolo di Euler del 1750 Découverte d'un nouveau principe de mécanique, dedicato in gran parte al moto dei corpi rigidi. Un breve capitolo verso l'inizio, però, dedicato alla spiegazione del principio generale e fondamentale di tutta la meccanica, presenta la legge del moto nella forma seguente (riproducendo esattamente la notazione originale): 2Mddx=Pdt², 2Mddy=Qdt² e 2Mddz=Rdt², in cui M è la massa (sia essa finita o infinitesimale) di una particella puntiforme, x, y e z le sue coordinate nello spazio, riferite ora ad assi fissi e perpendicolari, ddx è la maniera in cui Euler indica il differenziale secondo d²x, e P, Q e R sono le forze applicate rispettivamente lungo le direzioni x, y e z. Dunque, a parte il fattore 2, per ognuna delle direzioni nello spazio Euler scrive le equazioni del moto nella forma poi diventata standard: Md²x/dt²=F (massa per accelerazione uguale forza impressa). Euler osserva: "Questa sola formula include tutti i principî della meccanica" (il misterioso fattore 2 dipende dal modo in cui Euler sceglie le unità: la sua M corrisponde alla nostra mg e g, accelerazione dovuta alla gravità, è posta uguale a 1/2). Non fu quindi che verso la metà del XVIII sec. che la seconda legge del moto raggiunse la sua formulazione definitiva, il che indica la difficoltà e la lentezza del processo di maturazione di ciò che Newton aveva iniziato.

Anche l'applicazione della meccanica ad alcune categorie particolari di problemi richiese molto lavoro. Per esempio, la strada per lo studio del moto dei corpi rigidi fu aperta da d'Alembert nelle Recherches sur la précession des équinoxes et sur la nutation de la terre (1749); Euler sistematizzò questo studio e ne ampliò molto la portata nell'opera Theoria motus corporum solidorum seu rigidorum (1760).

Durante tutto il Settecento, si protrasse una disputa su quanto fosse saggio utilizzare la 'forza' tra i concetti fondamentali della meccanica. Alcuni, come d'Alembert, attaccavano questa posizione ritenendo l'idea oscura, anche se poi continuavano a utilizzarla. Altri, fra cui Euler come si è visto, l'abbracciavano più volentieri. Non sorprende il fatto che, durante il XVIII sec., la ricerca di formulazioni alternative della meccanica implicasse spesso un tentativo di fare a meno della forza, focalizzandosi su altri concetti. Un buon esempio ce lo fornisce il Traité de dynamique di d'Alembert, pubblicato nel 1743 e rivisto nel 1758. D'Alembert partì dall'osservazione che c'era un gran numero di principî usati nella statica e nella dinamica, la maggioranza dei quali era oscuro o era formulato in modo oscuro e che di conseguenza, avevano "dato luogo a diverse domande spinose". L'obiettivo di d'Alembert consisteva nell'estendere l'ambito della meccanica riducendo il numero dei suoi principî fondanti. Era convinto di poter ridurre "tutte le leggi della meccanica a tre: quella della forza d'inerzia, quella sulla composizione dei moti e quella sull'equilibrio" (Traité, pp. iv, xxiv).

L'equilibrio, naturalmente, si studia nell'ambito della statica e, in effetti, d'Alembert tentò di ridurre la dinamica alla statica, nel modo seguente. Immaginiamo tre corpi A, B e C, eventualmente soggetti a vincoli mediante legami reciproci realizzati da corde o barre. Supponiamo che in uno stesso istante ognuno dei tre corpi riceva un colpo, e che questi colpi siano tali da imprimere ai tre corpi, se fossero liberi, i movimenti a, b e c. Siccome però i tre corpi si vincolano reciprocamente, i movimenti indotti sono in effetti a′, b′e c′. D'Alembert nota ora che il movimento b che sarebbe impresso al corpo B dal colpo si può pensare composto dal movimento effettivo b′ e da un altro movimento β (e analogamente per gli altri corpi). Il moto effettivo di tutti i corpi sarebbe dunque esattamente lo stesso se i movimenti loro impressi, invece di a, b e c, fossero a′, b′e c′ più α, β e γ. I movimenti α, β e γ perciò non perturbano affatto il moto dei tre corpi. Se cioè a questi corpi fossero stati impressi i movimenti α, β e γ, questi si sarebbero cancellati a vicenda, lasciando il corpo a riposo. L'ingegnoso metodo descritto da d'Alembert, per determinare il movimento di diversi corpi legati l'uno all'altro, e soggetti a forze impulsive, consiste nello scomporre i movimenti impressi ai singoli corpi in quelli che si eliminano, a causa dei vincoli o dei legami, e nella parte residua, che determinerà il moto effettivo. Joseph-Louis Lagrange (1736-1813) osservò che il principio di d'Alembert riduceva la dinamica alla statica, ma questo non è assolutamente vero poiché, in generale, le equazioni del moto che si ottengono sono ancora delle equazioni differenziali (e non algebriche come quelle che si ottengono nel caso statico). Il principio di d'Alembert inoltre è spesso di difficile applicazione.

Un altro tentativo, storicamente più importante, di formulare in modo alternativo la meccanica, derivò dal principio delle velocità virtuali. Si trattava di un vecchio principio della statica, trattato da Galilei, Torricelli e Wallis, ma ripreso e generalizzato da Johann I Bernoulli (1667-1748) nel 1717. Come esempio di applicazione delle velocità virtuali, si consideri un giogo di bilancia a riposo su un fulcro, con i due bracci opposti di lunghezza l e L. Vi siano alle estremità dei due bracci dei pesi w e W, rispettivamente. Il principio delle velocità virtuali fornisce un metodo per la ricerca delle condizioni di equilibrio delle due forze. Immaginiamo di imprimere una rotazione infinitesima al giogo; questo fa sì che i due pesi acquisiscano le velocità di rotazione virtuali v e V rispettivamente. Secondo il principio in questione, le forze saranno in equilibrio se wv+WV=0 (considerando negativa una velocità se diretta in verso opposto a quello della forza corrispondente). Poiché le velocità di rotazione sono proporzionali alla lunghezza dei bracci, ricaviamo immediatamente la consueta legge di equilibrio per le leve: wl=WL.

Lagrange (traendo ispirazione dalla ingegnosa, ma complicata, scomposizione dei movimenti di d'Alembert) estese questo principio delle velocità virtuali dalla statica alla dinamica, definendo in sostanza la forza d'inerzia come il prodotto cambiato di segno della massa per l'accelerazione. La legge del moto F=ma è scritta cioè come F−ma=0. Le forze d'inerzia −ma sono quindi trattate come se agissero in aggiunta alla forza applicata F. Il caso dinamico di un moto accelerato diventa quindi formalmente equivalente a quello dell'equilibrio statico (in cui la somma delle forze è zero), e si può applicare il principio delle velocità virtuali.

L'apice di questi sforzi per generalizzare e sistematizzare la scienza del moto si raggiunse nella Méchanique analitique (1788) di Lagrange. Egli in definitiva fece a meno della nozione di forza, concentrandosi sull'energia cinetica (la forza viva di Leibniz) e su quella che potremmo chiamare la funzione lavoro, risultante da un'estensione naturale del principio delle velocità virtuali. Siano P, Q, R, … le forze che agiscono su diversi punti di un sistema, e siano δp, δq, δr, … gli spostamenti di questi punti lungo le direzioni delle forze impresse. La funzione lavoro è allora Pδp+Qδq+Rδr+… . Se la funzione lavoro è integrabile, il che Lagrange supponeva accadesse tipicamente in Natura, essa diventa quella che oggi chiamiamo energia potenziale. Con l'energia cinetica e l'energia potenziale a disposizione, le equazioni del moto si ottengono calcolando alcune derivate parziali e inserendole nella formula generale di Lagrange.

Come dice Lagrange, "il metodo che espongo non richiede costruzioni né ragionamenti geometrici o meccanici, ma solo operazioni algebriche, secondo una progressione uniforme e regolare" (Mécanique analytique, p. iv).

Il principio di minima azione: un episodio nella 'storia universale dell'ironia'

Tra le formulazioni alternative della meccanica, quella di gran lunga più importante fu il principio di minima azione, enunciato nel 1744 da Pierre-Louis Moreau de Maupertuis in una relazione all'Académie Royale des Sciences di Parigi. Maupertuis chiamò 'azione' il prodotto della massa, della velocità e della distanza, e affermò che in tutti i processi la Natura sceglie il percorso che comporta la minima azione possibile. Con la sua scoperta Maupertuis intendeva porre l'ottica e la meccanica sotto le stesse leggi, e l'applicò sia alla rifrazione della luce sia agli urti tra particelle. Per esaminare le questioni in gioco nella meccanica di Maupertuis, dobbiamo innanzitutto ricostruire lo sviluppo degli studi sull'ottica dei suoi predecessori.

Intorno al 1621, il matematico olandese Willebrord Snel (1580-1626) scoprì per via sperimentale le leggi della rifrazione della luce e benché il suo manoscritto di ottica non fosse stato ancora pubblicato alla sua morte, la sua legge sulla rifrazione era nota a un ristretto circolo di eruditi. Consideriamo in particolare il caso di un raggio luminoso che passa dall'aria all'acqua, e utilizziamo la notazione trigonometrica moderna. Con riferimento alla fig. 6, sia i_a l'angolo di incidenza (usiamo a per aria); analogamente, chiamiamo i_w l'angolo di rifrazione (w, water, per acqua). La legge di Snel si può allora esprimere come seni_a=nseni_w (se volessimo utilizzare i lati dei triangoli invece dei seni degli angoli, scriveremmo AB/AE=nCD/DE). La costante n è chiamata 'indice di rifrazione' dell'acqua, vale approssimativamente 1,3 ed è una proprietà dell'acqua. Il fatto che n>1 riflette il fatto che i_w⟨i_a. Il raggio luminoso è quindi più vicino alla normale in acqua che in aria, come mostrato nella fig. 6.

Anche Descartes ricavò una legge dei seni per la rifrazione, non per via sperimentale, ma deduttivamente, a partire da una teoria meccanica della luce. Nell'opera La dioptrique, pubblicata nel 1637 come supplemento al Discours de la méthode, Descartes tratta un raggio di luce come se fosse costituito da un flusso di palle da tennis, e ipotizza che la componente della velocità parallela all'interfaccia tra i due mezzi rimanga costante quando la luce passa da un mezzo all'altro, mentre invece cambierebbe la componente ortogonale all'interfaccia. Poiché il raggio è più vicino alla normale nell'acqua che nell'aria, ciò significa che la luce viaggia più velocemente nell'acqua. Usando la notazione trigonometrica moderna, la versione di Descartes della legge della rifrazione si potrebbe esprimere come v_a seni_a=v_w seni_w, in cui v_a è la velocità della luce nell'aria e v_w la velocità della luce nell'acqua. Se Descartes è nel giusto nel trattare le particelle di luce come se fossero palle da tennis, potremmo concludere che v_w/v_a=n=1,3. La luce cioè viaggerebbe 1,3 volte più velocemente nell'acqua che nell'aria. L'argomento divenne immediatamente l'oggetto di accese dispute, poiché gli amici di Snel e i critici di Descartes accusarono quest'ultimo di aver plagiato la legge dei seni.

fig. 7

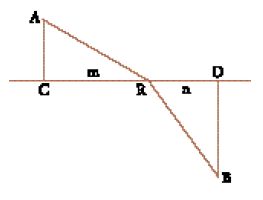
Circa venticinque anni dopo, il matematico e avvocato francese Pierre de Fermat (1601-1665) propose l'ipotesi secondo la quale la luce viaggerebbe da un punto in un mezzo a un punto in un altro mezzo seguendo il percorso che richiede il tempo minimo. A partire dal 1662 ca., Fermat fece conoscere il suo principio di minimo tempo attraverso i suoi scambi epistolari. A questo scopo produsse due brevi scritti, Analysis ad refractiones e Synthesis ad refractiones, che però non vide pubblicati; furono stampati per la prima volta soltanto nell'epistolario di Descartes. Si consideri la fig. 7 (che non è tratta da un'opera di Fermat, ma da un articolo di Maupertuis dal titolo Accord des différentes lois de la nature [...]). Per applicare il principio di Fermat, dobbiamo considerare tutti i percorsi possibili che collegano il punto iniziale A con quello finale B. L'obiettivo è determinare il percorso ARB effettivamente seguito dalla luce, assumendo che la luce segua il percorso di minimo tempo. Se la luce viaggia a velocità v_m nel primo mezzo, e a velocità v_n nel secondo, il tempo totale necessario per andare da A a B è AR/v_m+RB/v_n. Provare percorsi differenti implica semplicemente lo spostamento del punto R a destra o a sinistra. La posizione di R per la quale si ha il tempo minimo dovrebbe fornire il percorso effettivamente seguito dalla luce. A partire da questo principio, Fermat riuscì a ricavare la costanza del rapporto dei seni degli angoli di incidenza e di rifrazione. Usando la notazione moderna, la versione di Fermat della legge della rifrazione risulta (1/v_a)seni_a=(1/v_w)seni_w. Le velocità appaiono ora al denominatore, invece che al numeratore (come nella legge di rifrazione di Descartes). Fermat fu attaccato dai discepoli di Descartes, per aver propugnato un principio secondo il quale la luce viaggerebbe più velocemente nell'aria che nell'acqua, mentre il loro maestro aveva sostenuto la tesi opposta. In effetti, secondo la versione di Fermat della legge della rifrazione, v_a/v_w=n, la luce viaggerebbe nell'aria 1,3 volte più velocemente che nell'acqua. Fermat fu criticato anche per aver reintrodotto argomenti teleologici e finalistici nella filosofia della Natura. Egli rispose aspramente che avrebbe lasciato volentieri a Descartes l'onore di aver spiegato la rifrazione, e che si sarebbe accontentato di fornire un'espressione matematica astratta, senza affermare che essa si applicasse alla luce. Il padre del principio di minimo tempo rinunciò a sostenere che esso avesse qualsiasi significato fisico.

Nel 1690 Christiaan Huygens pubblicò il Traité de la lumière, in cui sviluppava una teoria ondulatoria della luce, e la applicava alla sua propagazione rettilinea, alla riflessione, alla rifrazione e alla rifrazione doppia. Huygens dimostrò anche che, se la luce fosse un'onda, dovrebbe obbedire al principio di minimo tempo di Fermat. Così, sul finire del XVII sec., il principio di Fermat venne associato alla teoria ondulatoria.

Newton, nell'Opticks del 1704, sostenne una teoria corpuscolare della luce. La natura corpuscolare della luce era praticamente l'unica posizione in fisica sulla quale i seguaci di Newton e di Descartes potevano trovarsi d'accordo, e non sorprende che, sotto l'influenza congiunta di Newton e di Descartes, la teoria ondulatoria praticamente si eclissò. Il principio di Fermat cadde in discredito, e quasi nessuno credeva alla sua validità; per esempio, non lo si trova esposto nella maggior parte dei manuali del XVIII secolo. In quel periodo c'erano pochi sostenitori della teoria ondulatoria, tra i quali il più illustre era Euler. La grande maggioranza degli studiosi di fisica però era convinta che luce fosse un flusso di particelle e che, come affermato da Newton e Descartes, essa viaggiasse più velocemente nell'acqua che nell'aria.

Quando nel 1744 Maupertuis enunciò il principio di minima azione, aveva quindi alle spalle una lunga storia. L'articolo che lesse alla Académie Royale des Science di Parigi era intitolato Accord des différentes lois de la nature, qui avoient jusqu'ici paru incompatibles e trattava della rifrazione della luce. In queste pagine Maupertuis definisce l'azione come il prodotto della massa, della velocità e della distanza. Ma nel moto di una singola particella di luce, la massa della particella è sempre la stessa e può essere ignorata. Si consideri la fig. 7: nel trattare la rifrazione della luce, Maupertuis scrisse l'azione come v_mAR+v_nRB, cercando quindi la posizione di R che minimizzasse questa quantità. Si tratta esattamente dello stesso problema affrontato da Fermat, ma qui le velocità si trovano al numeratore. Mentre Fermat aveva impiegato diverse pagine di densi ragionamenti geometrici, Maupertuis poteva avvalersi della nuova matematica del calcolo differenziale per risolvere il problema in poche righe. Maupertuis ricavò la legge della rifrazione nella forma di Descartes: v_m seni_m=v_nseni_n.

Il principio di Maupertuis era coerente con la concezione corpuscolare della luce e con l'opinione condivisa da Newton e Descartes, secondo la quale la velocità della luce è maggiore nei mezzi più densi. Riaffermando questo fatto naturale ‒ esclamò Maupertuis ‒ "l'intero edificio costruito da Fermat viene distrutto: la luce, nell'attraversare mezzi di diversa densità, non segue né il cammino più breve, né quello di minimo tempo […]" (Accord des différentes lois, IV, p. 15). Maupertuis notò anche che per il caso della riflessione e quello della propagazione rettilinea (nei quali la luce rimane nello stesso mezzo e la sua velocità non varia) il cammino di minor tempo coincide con il cammino di minima azione, il che, secondo Maupertuis, dimostrava come Fermat si fosse sbagliato.

Ben presto Maupertuis fu chiamato a Berlino da Federico II di Prussia, per assumere la presidenza della sua Societas Regia Scientiarum. A Berlino, nel 1746 Maupertuis produsse un altro articolo sul principio di minima azione, Recherche des lois du mouvement, in cui tratta con il metodo della minima azione gli urti tra corpi elastici e anelastici. È una delle tante ironie della storia il fatto che Maupertuis abbia applicato il principio di minima azione prima alla luce e soltanto dopo alla meccanica: esso era stato applicato inizialmente in un ambito nel quale non era in realtà valido. Sulla luce, infatti, Fermat e Huygens avevano ragione e Newton e Descartes torto. La luce in effetti viaggia più velocemente nell'aria che nell'acqua, anche se questa idea non fu generalmente accettata fino agli anni 1820-1830.

La definizione dell'azione che Maupertuis aveva dato nel suo articolo sulla rifrazione del 1744, era chiara e applicata in modo chiaro. Sebbene egli effettuasse i suoi calcoli per particelle 'di luce', i suoi argomenti erano validi per 'qualsiasi' particella dotata di massa che cambiasse repentinamente velocità nel passare da un luogo a un altro; per contro, la trattazione svolta da Maupertuis sugli urti tra particelle nell'articolo del 1746, sembrò cambiare la definizione dell'azione. Un'applicazione più generale e molto più rigorosa del principio di minima azione fu data da Euler, residente allora a Berlino come membro dell'Accademia.

Euler aveva lavorato sui problemi di minimo (il calcolo delle variazioni), e nel 1744 pubblicò sull'argomento la Methodus inveniendi lineas curvas maximi minimive proprietate gaudentes, che apparve quindi dopo che Maupertuis aveva presentato il suo primo lavoro sul principio di minima azione, ma ben prima del secondo lavoro di Berlino. Stimolato dall'idea di Maupertuis, Euler inserì una breve trattazione del principio di minima azione come appendice al suo libro. Euler considera una singola particella in moto sotto l'effetto di una forza, cosicché la velocità v della particella è una funzione della posizione. L'integrale d'azione è ∫vds, in cui ds è un elemento infinitesimo della traiettoria tra due punti fissati dello spazio (di nuovo, essendo la massa m una costante, si può ignorare). Effettuando il calcolo variazionale, Euler dimostrò che il principio di minima azione dava esattamente la stessa curvatura per la traiettoria di quella ottenuta con il metodo delle forze.

Poco tempo dopo l'affermazione del principio di minima azione, si levò lo spettro di Leibniz per ingaggiare un'altra aspra disputa sulle priorità, contro la posizione newtoniana di Maupertuis. Nel 1751 Samuel Koenig, professore a L'Aia e membro straniero dell'Accademia di Berlino, in un articolo apparso negli "Acta Eruditorum", pubblicò una lettera, della quale affermava di possedere soltanto una copia, e non l'originale, provocando uno scandalo a Berlino. Questa lettera, apparentemente scritta nel 1707 da Leibniz a Jacob Hermann (1678-1733), conteneva una chiara formulazione del principio di minima azione, sebbene solo in forma discorsiva, e senza illustrare la sua applicazione nei calcoli.

Maupertuis era convinto che la lettera fosse un falso, e chiese a Koenig di produrre l'originale, cosa impossibile, perché Hermann e Leibniz erano entrambi morti da tempo. L'Accademia di Berlino, di cui Maupertuis era presidente, avviò una'inchiesta; Euler, responsabile della sezione matematica dell'Accademia, studiò la lettera, e la dichiarò un falso. Per ordine di Federico II, Euler inviò anche una richiesta a Basilea, dove viveva ancora il fratello del defunto Hermann, e ottenne che Johann II Bernoulli e altre persone di rango si recassero a casa di costui e consultassero le lettere di Hermann. Il comitato di indagine riferì direttamente al re che, sebbene fossero state trovate diverse lettere di Leibniz a Hermann, non c'era nulla che corrispondesse alla misteriosa lettera del 1707. L'Accademia si pronunciò formalmente in favore di Maupertuis e Koenig per protesta restituì il suo attestato di membro dell'Accademia. Euler scrisse una Dissertation sur le principe de la moindre action, in cui sosteneva sia l'originalità di Maupertuis sia la validità del suo principio. Durante lo svolgimento di questa vicenda, Voltaire, allora ospite di Federico II a Berlino, pubblicò un pamphlet satirico, la Diatribe du Dr. Akakia, médecin du Pape, in cui sosteneva la posizione di Koenig e copriva di ridicolo Maupertuis, di cui in passato era stato amico. Offeso da questo affronto fatto al presidente della sua Accademia, Federico cacciò Voltaire da Berlino, fece bruciare in pubblico il suo pamphlet e ne spedì le ceneri a Maupertuis, definendole come "un po' di polvere rinfrescante".

Alla metà del XVIII sec. c'erano quindi due principî variazionali in competizione, il principio di minimo tempo e quello di minima azione. Solamente quest'ultimo poteva fungere da base per la meccanica; in ottica però si poteva scegliere, a seconda che si optasse per la teoria corpuscolare od ondulatoria della luce. Era opinione prevalente che la luce fosse di natura corpuscolare; per i sostenitori di questa teoria, un solo principio (il principio di minima azione di Maupertuis) era in grado di coprire sia l'ottica sia la meccanica. In minoranza c'erano i teorici dell'approccio ondulatorio, che riconoscevano l'esistenza di due principî variazionali, applicabili a due diversi domini della fisica: il principio di minima azione di Maupertuis per la meccanica e il principio di minimo tempo di Fermat per l'ottica.

Sorprendentemente, però, nella pratica dell'ottica non faceva molta differenza quale principio variazionale si utilizzasse. Secondo il principio di minima azione, l'integrale ∫vds è minimo lungo il percorso effettivamente seguito. Secondo il principio di tempo minimo, ∫v⁻¹ds risulta minimo. Nella teoria corpuscolare, l'indice di rifrazione n è proporzionale alla velocità della luce v; nella teoria ondulatoria, n è proporzionale a v⁻¹. Ciò significa che, indipendentemente dalla teoria adottata, l'integrale da minimizzare si può scrivere come ∫nds, che è una forma indifferente rispetto alla teoria scelta. Le due teorie predicono lo stesso percorso per la luce, e si discostano l'una dall'altra soltanto nel prevedere come la luce avanza nel tempo lungo il percorso, il che non era suscettibile di misure nel XVIII secolo.

Il principio di minima azione applicato alla meccanica fu ulteriormente sviluppato da Lagrange nella Mécanique analytique. Lagrange formulò il principio in forma più precisa, estendendolo a sistemi di particelle interagenti, e dimostrò come esso potesse fungere da base della dinamica, fornendo con ciò una gradita alternativa alla fisica di Newton, basata sulle forze e filosoficamente inquietante. Lagrange dimostrò tra l'altro che il principio di minima azione e la conservazione della forza viva (cioè dell'energia), combinati, erano equivalenti alla legge del moto di Newton (F=ma).

Fisica e metafisica

Si dice a volte che se la scienza del XVII sec. lottò per liberarsi dai teologi, nel XVIII sec. dovette lottare per la propria libertà dai metafisici. Si tratta però di un'esagerazione. Ogniqualvolta la scienza si trova immersa in una cultura che considera la religione e la filosofia in modo serio, non è mai totalmente libera da influenze di carattere religioso o filosofico. Tuttavia, il XVIII sec. è stato l'ultimo periodo nel quale le discussioni metafisiche hanno occupato una posizione centrale, imponendosi all'attenzione di molti studiosi di fisica di primo piano.

Nella sua seconda lettera a Samuel Clarke, come pure negli Essais de théodicée, Leibniz affermava di poter fondare tutta la filosofia della Natura su un solo principio. Consideriamo innanzitutto il caso della matematica, a titolo di esempio e di analogia. Il fondamento della matematica è il principio di contraddizione: è impossibile che una proposizione sia al tempo stesso vera e falsa.

Leibniz affermò (anche se con ciò si spinse troppo oltre) che questo solo principio era sufficiente per dimostrare tutto in aritmetica e in geometria. Per passare però dalla matematica al dominio della filosofia (cioè la scienza) della Natura, sarebbero stati necessari anche altri principî, in particolare il 'principio di ragion sufficiente', secondo il quale "Nulla accade senza un motivo per il quale debba essere in quel modo e non in un altro" (Alexander 1956, p. 16). Per Leibniz, la ragione ultima di tutte le cose va ricercata nella bontà di Dio il quale, meditando sulle scelte disponibili al momento della Creazione, scelse di plasmare il migliore dei mondi possibili. Questo è, per esempio, il motivo per il quale l'Universo dev'essere spazialmente infinito (anche se finito nel tempo), e non può esserci spazio vuoto: secondo Leibniz, il migliore dei mondi possibili è un Universo infinito completamente riempito di materia.

Madame du Châtelet meditò attentamente sul principio di ragion sufficiente. Nelle Institutions de physique dedicò alla metafisica di Leibniz la maggior parte del capitolo iniziale, sui principi della conoscenza. Voltaire, d'altra parte, nel romanzo satirico Candide (1759) derise la dottrina leibniziana del migliore dei mondi possibili: il giovane Candide è stato istruito da un maestro sofista di nome Pangloss sulla base di una filosofia riconoscibile come quella di Leibniz. Candide però attraversa in seguito una serie di disavventure (è testimone di stupri, omicidi e persecuzioni, e del terremoto devastante di Lisbona). Alla fine di ogni episodio, Candide scrolla le spalle di fronte alle avversità, dicendo "tutto questo è per il meglio".

Maupertuis rigettava le argomentazioni metafisiche consuete a sostegno dell'esistenza di Dio, come pure l'argomento che muove dalla considerazione della struttura dell'Universo. Vedeva però nel principio di minima azione un segno della saggezza del Creatore, che aveva organizzato la Natura in modo che scegliesse sempre la via più semplice. Nell'opera Essai de cosmologie del 1750, Maupertuis giunse ad affermare che il principio di minima azione fornisce una prova dell'esistenza di Dio. Era, questa, una delle proposizioni ridicolizzate da Voltaire nella Diatribe du docteur Akakia (secondo cui basta l'equazione A+B diviso Z per dimostrare l'esistenza di Dio). Euler sfortunatamente dimostrò che, in una formulazione matematica rigorosa, si poteva soltanto imporre che la variazione dell'integrale d'azione fosse nulla, e questo si può avere sia se l'azione è un 'massimo' sia se è un 'minimo'. È in effetti possibile trovare famiglie di percorsi tra i quali il vero percorso seguito dalla particella dà un valore massimo per l'azione. Ciò sembrava minare la saggezza del Creatore, o almeno ridurlo a un distributore molto poco parsimonioso di azione.

Euler non aveva inclinazione metafisica, anche se aveva una seria considerazione dei metafisici e li trattava con rispetto. Nel 1747, quando l'Accademia di Berlino propose una discussione sulle monadi di Leibniz, teoria molto in voga a Berlino in quel periodo, Euler accettò (per criticarla). Nel suo articolo del 1748 sulla natura dello spazio e del tempo, Euler mise a confronto le teorie dei 'metafisici' (Leibniz e i suoi seguaci) e dei 'matematici' (i newtoniani), scegliendo di allinearsi con questi ultimi. D'Alembert nel suo Discours préliminaire all'Encyclopédie (1751) rigettò completamente la metafisica, e giunse a dire che, sebbene "il titolo di metafisico […] sia ancora abbastanza comune nel nostro secolo […] non dubito che diventerà presto un insulto per le persone intelligenti", e fece allusione al destino del titolo di sofista nella Grecia antica. Per d'Alembert, come per Lagrange, il principio di minima azione era semplicemente un'affermazione di meccanica. Via via che il secolo si consumava, la metafisica andò effettivamente verso il declino, ma non scomparve mai completamente dal pensiero fisico. C'erano inoltre, chiaramente, differenze importanti da nazione a nazione. I Francesi erano decisamente ostili ai metafisici, mentre i Tedeschi, imbevuti della filosofia di Leibniz e poi di Kant, avevano una più seria considerazione della metafisica.

Un altro tema di discussione proposto dall'Accademia di Berlino aprì una nuova disputa: le leggi della meccanica sono delle verità contingenti o necessarie? La maggior parte degli studiosi di meccanica della metà del XVIII sec. era convinta di impegnarsi nella ricerca di verità necessarie. Questo fatto riflette forse un'influenza, non riconosciuta, di Leibniz, che aveva lasciato a Dio così poca libertà nell'organizzare l'Universo. Perfino d'Alembert, l'uomo che aveva rigettato la metafisica, era convinto che le leggi della meccanica fossero delle verità necessarie. Nell'introduzione alla seconda edizione del Traité de dynamique, menzionò la riduzione, da lui operata, delle leggi della meccanica a tre principî fondamentali, che derivano dall'esistenza stessa della materia e del movimento: si trattava, dunque, di verità necessarie e non contingenti.

Un tratto distintivo della scienza moderna consiste nel progressivo abbandono delle assunzioni a priori. Questioni che le generazioni precedenti avevano pensato di poter risolvere mediante il solo uso della ragione, si sono rivelate contingenti. Uno degli esempi più chiari è il destino subito dalla geometria. Kant pensava che, pur essendo lo spazio un'entità ideale, la geometria euclidea fosse ugualmente una verità necessaria e universale. Nel XIX sec., gli studiosi di geometria pura inventarono gli spazi non euclidei per il loro puro diletto; nel XX sec., però, i fisici applicarono queste geometrie non euclidee allo spazio reale in cui viviamo. La questione dell'applicabilità della visione euclidea al nostro Universo si rivelò un problema non di geometria, ma di geografia, definibile soltanto mediante l'osservazione. Dal punto di vista della teoria quantistica, sembra che la Natura ignori con disinvoltura il principio di ragion sufficiente di Leibniz. Secondo l'epistemologia quantistica del XX sec., in un esperimento di fenditure parallele non è possibile distinguere da quale fenditura è passato un determinato elettrone. Anche una proposizione apparentemente ovvia come l'enunciato del principio di ragion sufficiente si rivela un'inferenza empirica (con applicabilità limitata), e non una verità necessaria. Aveva forse ragione Samuel Clarke, quando diceva che è ovviamente vero che ci debba essere sempre una ragione per cui qualcosa è in un certo modo e non in un altro, ma che a volte questa ragione non è altro che il capriccio di Dio.