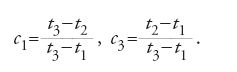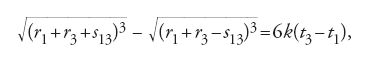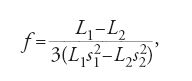L'Età dei Lumi: la fine della conoscenza naturale 1700-1770. Mathematica mixta

L'Eta dei Lumi: la fine della conoscenza naturale 1700-1770. Mathematica mixta

Mathematica mixta

Astronomia

di Curtis Wilson

Nel XVIII sec. l'accuratezza delle misure astronomiche aumentò di circa due ordini di grandezza, dai primi di arco ai secondi di arco. In questo progresso furono di cruciale importanza le scoperte di James Bradley (1693-1762) dell'aberrazione della luce (1729) e della nutazione (1730-1748), che rappresentarono il trionfo della nuova strumentazione e dell'acuta analisi di fenomeni problematici. Ebbero inoltre un ruolo importante la teoria analitica delle perturbazioni, la determinazione analitica delle orbite e l'elaborazione statistica delle osservazioni, tutte sorte negli anni Quaranta e poi perfezionate entro la fine del secolo. Le lenti acromatiche per i telescopi risalgono al 1757 e la graduazione d'interi cerchi piuttosto che di quadranti o settori minori fu introdotta durante gli ultimi due decenni del secolo. In questo paragrafo ci occuperemo essenzialmente delle scoperte di Bradley e dell'introduzione di nuovi metodi di determinazione delle orbite.

fig. 1

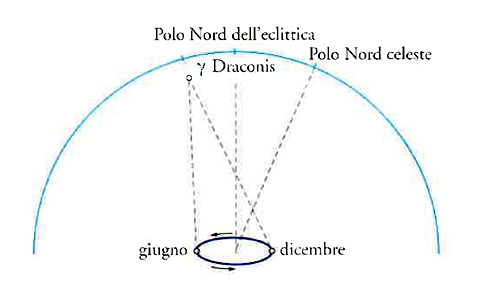
La scoperta dell'aberrazione della luce e quella della nutazione avvennero durante le osservazioni intraprese per verificare la presunta rilevazione della parallasse annua effettuata da Robert Hooke (1635-1702); dal 6 luglio al 21 ottobre del 1669 Hooke osservò che la stella γ Draconis attraversava il meridiano vicino allo zenit di Londra in direzione sud di circa 22-24″ (fig. 1), e questo risultato concordava con l'ipotesi eliocentrica di Niccolò Copernico.

Nel 1725 Samuel Molyneux (1689-1728), con l'aiuto di Bradley, si accinse a cercare conferme della scoperta di Hooke, usando un settore zenitale costruito appositamente da George Graham (1674 ca.-1751). Un tubo di circa 7 m di lunghezza fu sospeso dalla parte superiore in modo che avesse una mobilità di mezzo grado sul piano meridiano; nella parte inferiore un micrometro a vite misurava la deviazione dalla verticale. L'apparato fu completato nel dicembre del 1725 e Molyneux e Bradley misurarono la distanza di γ Draconis dallo zenit al solstizio d'inverno, quando, supponendo che la parallasse annua fosse percettibile, la stella avrebbe dovuto essere nel suo punto più lontano a sud (in questo periodo dell'anno essa attraversa il meridiano a mezzogiorno circa). Osservando nuovamente la stella una settimana dopo, Bradley constatò che si trovava circa 2″ più a sud. Ai transiti successivi γ Draconis continuava a spostarsi verso sud, raggiungendo a marzo una posizione di 20″ più a sud di quando era stata osservata ai primi di dicembre. In seguito si diresse verso nord, ritornando i primi di giugno alla sua posizione di dicembre e arrivando a settembre a 20″ a nord di quella, prima d'iniziare a tornare nuovamente verso sud. I cambiamenti seguivano un ciclo annuale, ma non il ciclo che la parallasse annua avrebbe comportato.

fig. 2

fig. 3

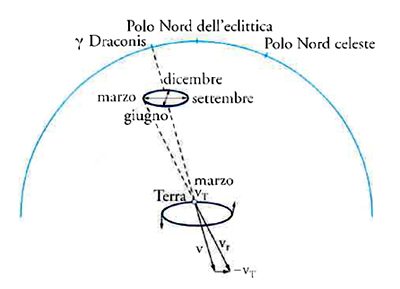
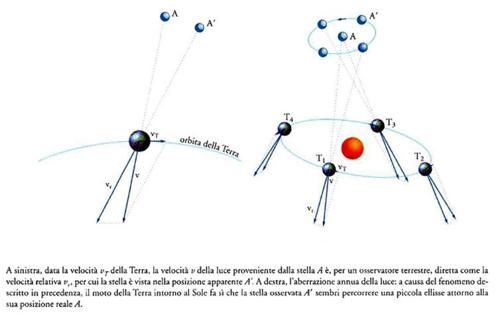
Nessuna delle ipotesi immaginate da Molyneux e Bradley per spiegare tale ciclo sembrava essere soddisfacente. Nell'agosto del 1727 i due astronomi installarono un nuovo settore zenitale a casa della zia di Bradley a Wansted; lungo circa 4 m, esso controllava circa 6°15′ di arco di meridiano da una parte e dall'altra dello zenit, permettendo a Bradley di osservare il transito di 12 stelle abbastanza luminose da poter essere viste al telescopio alla luce del giorno. Molyneux, divenuto nel frattempo ministro della Marina, non poté più seguire le ricerche attivamente e morì prima che il mistero fosse risolto. Durante l'anno successivo, Bradley osservò le 12 stelle, ricostruendo la configurazione dei loro spostamenti, senza però trovarne una spiegazione. Infine, nell'autunno del 1728 ebbe l'intuizione giusta, ossia che gli spostamenti avrebbero potuto essere dovuti alla variazione della differenza tra due vettori, la velocità v della luce proveniente dalla stella e la velocità vT della Terra intorno al Sole. Per un osservatore situato sulla Terra in movimento, bisognava sottrarre vettorialmente vT da v per ottenere la direzione apparente vr della luce proveniente dalla stella (fig. 2, con la situazione nel mese di marzo; per lo schema completo del fenomeno, v. cap. XXIII, fig. 3). I presupposti dell'ipotesi ‒ eliocentrismo e velocità finita della luce ‒ erano perciò confermati in maniera impressionante. Bradley annunciò la sua scoperta nel gennaio del 1729.

All'inizio degli anni Trenta del Settecento Bradley notò che, oltre all'aberrazione, si verificavano ulteriori variazioni nelle posizioni stellari e ben presto fu in grado di spiegare il fenomeno attribuendolo a un'oscillazione del moto di precessione dell'asse della Terra, avente un periodo di 18,6 anni, uguale a quello di rivoluzione dei nodi della Luna. La rotazione del piano orbitale lunare verso ovest intorno all'asse dell'eclittica altera la direzione della forza di attrazione della Luna sul rigonfiamento equatoriale della Terra, causando l''inclinazione', o 'nutazione', dell'asse polare terrestre. Bradley annunciò questa scoperta nel gennaio del 1748, dopo aver seguito le variazioni dovute alla nutazione per un intero ciclo. Dunque gli equinozi, con un periodo di 18,6 anni, subiscono un'oscillazione di circa 17″ in longitudine e l'obliquità dell'eclittica oscilla di circa 9″ attorno al suo valore medio.

Sino ad allora la posizione giornaliera del Sole, della Luna e dei pianeti era determinata confrontando l'orario del loro passaggio con quello delle stelle; se si voleva ottenere una precisione dell'ordine dei secondi di grado queste misure dovevano essere corrette tenendo conto dell'aberrazione e della nutazione. Le Tables astronomiques (1740) di Jacques Cassini (1677-1756) non riportavano ancora tali correzioni, mentre le Tabulae solares di Nicolas-Louis de Lacaille (1713-1762) furono le prime tavole solari (1758) dove queste trovarono piena applicazione.

Il calcolo delle orbite planetarie

Per costruire le tavole astronomiche del Sole, della Luna e dei pianeti sono necessari gli elementi orbitali: sei parametri che determinano la forma e l'orientamento dell'orbita ellittica e che localizzano il pianeta su di essa in quel momento. Questi parametri possono essere ricavati da tre osservazioni, ognuna delle quali determina la longitudine e latitudine geocentriche del pianeta nell'istante dato. Nel 1735 Leonhard Euler (1707-1783) individuò un metodo algebrico per ricavare gli elementi orbitali, riducendo la loro derivazione alla semplice risoluzione di un sistema di equazioni; nel 1740 egli trasformò il metodo in un procedimento di correzione differenziale. Considerando gli elementi orbitali determinati da Thomas Streete (1622-1689) come una buona approssimazione, egli suppose che ognuno di essi dovesse subire una piccola correzione indeterminata, per poi uguagliare la longitudine, calcolata con i valori modificati nell'istante di ciascuna osservazione, con la longitudine osservata; un insieme di 6 equazioni permise di ottenere la soluzione simultanea per le correzioni differenziali.

Nel saggio sulle diseguaglianze di Giove e Saturno del 1749, Recherches sur la question des inégalités du mouvement de Saturne et de Jupiter, Euler applicò lo stesso procedimento, combinandolo con l'uso di 'equazioni di condizione' ridondanti, per correggere sia gli elementi orbitali sia i coefficienti di perturbazione. Johann Tobias Mayer (1723-1762), che studiò attentamente questo saggio, usò molto probabilmente lo stesso procedimento per ricavare gli elementi e i coefficienti di perturbazione per le sue tavole lunari. Laplace lo usò con buoni risultati nella Théorie de Jupiter et de Saturne (1785) e, per Jean-Baptiste-Joseph Delambre (1749-1822) e gli astronomi che seguirono, esso si tradusse in una tecnica standard per accordare la teoria con le osservazioni.

La determinazione delle orbite delle comete è più difficile di quella delle orbite planetarie perché non se ne conosce il periodo orbitale. Isaac Newton (1642-1727), dopo una prolungata ricerca, decise di usare un metodo grafico per adattare una traiettoria parabolica a tre osservazioni. Edmond Halley (1656-1742) usò una versione parzialmente aritmetizzata di tale procedimento ‒ senza però fornire dettagli ‒ e riuscì a determinare gli elementi orbitali di circa 24 comete, come illustrato nel suo Synopsis astronomiae cometicae del 1705.

Il primo tentativo di determinare per via algebrica l'orbita di una cometa fu effettuato da Pierre Bouguer (1698-1758) nel 1733. La sua prima premessa era che il Sole, la Terra e la cometa formano in ogni istante i vertici di un triangolo; la seconda premessa era la condizione dinamica secondo cui i radii vectores dal Sole alla cometa giacciono tutti sul medesimo piano. Tale condizione implica che di tre radii vectores della cometa, il secondo deve essere dato dalla combinazione lineare del primo e del terzo:

[1] r2=c1r1+ c3r3,

dove per c1 e c3 Bouguer utilizza i rapporti temporali:

Queste relazioni non sono affatto corrette, perché non rispettano la legge delle aree di Kepler. In base ai valori di c1 e c3 e alla prima premessa di cui sopra, Bouguer si accinse a ricavare i valori delle tre distanze geocentriche della cometa, ϱ1, ϱ2, ϱ3 (di fatto, con il suo metodo egli poteva ricavare soltanto i rapporti tra ϱ1, ϱ2 e ϱ3); dopo avere determinato ϱ1, ϱ2, ϱ3, poté calcolare gli elementi orbitali. Nel 1743 Euler scoprì una relazione esatta del moto parabolico:

dove r1 e r3 sono le lunghezze dei radii vectores dal Sole alle posizioni sulla parabola, s13 è la corda che congiunge le due ultime posizioni e k è una costante tale che il tempo misurato come kt raggiunge il valore di 2π radianti in un anno sidereo.

Euler stesso, non volendo limitarsi alle sole traiettorie paraboliche, non usò la relazione [3], ma ideò un procedimento algebrico, esposto nella sua Theoria motuum planetarum et cometarum del 1744, che poteva essere applicato a tutte le traiettorie di tipo conico. Egli fissò la seconda di tre osservazioni stimando una distanza ipotetica tra la Terra e la cometa e, per correggere la sua stima, usò la procedura basata sul metodo della falsa posizione. Progressi successivi nella determinazione delle traiettorie delle comete torneranno all'ipotesi newtoniana della traiettoria parabolica.

Johann Heinrich Lambert (1728-1777), avendo riscoperto la relazione [3], nel suo Insigniores orbitae cometarum proprietates (1761) ne fece uso per eliminare qualunque assunzione ipotetica nella determinazione delle orbite paraboliche. Per mezzo di una speciale costruzione mostrò che le quantità r1, r3 e s13 potevano essere espresse in termini di una sola incognita x, ricavabile in linea di principio, anche se l'equazione da risolvere era di grado notevolmente elevato.

Nel 1771 il gesuita Ruggero Giuseppe Boscovich (1711-1787) presentò all'Académie Royale des Sciences di Parigi un metodo per determinare l'orbita di una cometa "mediante tre osservazioni poco distanti tra loro", supponendo che i moti della cometa e della Terra fossero rettilinei e uniformi durante gli intervalli tra le osservazioni. Pierre-Simon de Laplace (1749-1827) obiettò che il procedimento di Boscovich trascurava quantità dello stesso ordine di quelle della supposta soluzione. La controversia s'inasprì a tal punto che la questione fu sottoposta all'esame di una commissione speciale dell'Académie che esortò i due autori a smettere di accusarsi reciprocamente con petizioni di principio.

Nel 1778 e nel 1783 Joseph-Louis Lagrange (1736-1813) presentò alla Königliche Preussische Akademie der Wissenschaften (Accademia Reale Prussiana delle Scienze) di Berlino due dissertazioni, intitolate Sur le problème de la détermination des orbites des comètes, in cui riportava la storia dei tentativi di determinare le traiettorie delle comete e in cui sviluppava un proprio procedimento che dimostrava la non correttezza dell'ipotesi che una qualunque parte della traiettoria di una cometa fosse rettilinea e percorsa in modo uniforme; il suo procedimento non ebbe però una buona accoglienza.

Laplace spiegò per la prima volta il proprio metodo per determinare le orbite delle comete nei "Mémoires de l'Académie Royale des Sciences" di Parigi del 1780, e poi nuovamente nel Traité de mécanique céleste. Iniziando da un insieme di osservazioni a intervalli ravvicinati, usò differenze finite per stabilire valori approssimati per la longitudine e la latitudine della cometa nell'istante centrale tra le osservazioni, servendosi delle loro derivate prime e seconde rispetto al tempo. Da questi valori, essendo note le equazioni del moto della cometa intorno al Sole e del moto eliocentrico della Terra, era possibile determinare sia la distanza della cometa dalla Terra in quell'istante sia i valori delle derivate prima e seconda rispetto al tempo; queste ultime, a loro volta, gli permettevano di ricavare gli elementi parabolici della traiettoria della cometa. Il metodo di Laplace fu in seguito prescelto da Alexandre-Guy Pingré (1711-1796) nel secondo volume della Cométographie (1784).

Il trattato del XVIII sec. sulla determinazione dell'orbita parabolica che raggiunse i risultati più avanzati fu l'Abhandlung über die leichteste und bequemste Methode, die Bahn eines Cometen zu berechnen (Memoria riguardo al metodo più semplice e più conveniente per calcolare la traiettoria di una cometa, 1797) di Heinrich Wilhelm Mathias Olbers (1758-1840). Nel 1779 Achille-Pierre Dionis du Séjour (1734-1794) aveva mostrato che la prima distanza geocentrica della cometa era legata alla seconda e alla terza dalle equazioni approssimate:

[4] ϱ1=M12 ϱ2, ϱ1=M13 ϱ3,

dove M12 e M13 sono i rapporti degli intervalli di tempo moltiplicati per le espressioni contenenti le longitudini e latitudini osservate della cometa e le longitudini del Sole. Olbers usò le [4] per determinare la relazione tra ϱ1 e ϱ3; poi, assegnando un valore arbitrario a ϱ1, e sfruttando il fatto che il Sole, la Terra e la cometa formano a ogni istante un triangolo, ottenne i valori di r1, r3 e s13. Questi valori, sostituiti nella [3], fornivano un valore per l'intervallo di tempo (t3−t1), che poteva essere confrontato con quello derivante dall'osservazione. Per ottenere il valore esatto di ϱ1, Olbers fece un'interpolazione tra diversi valori ipotetici sino a ottenere una concordanza tra gli intervalli di tempo osservati e quelli calcolati. Con questo procedimento si giungeva a determinare i valori di r1 e r3 e quello dell'angolo tra loro, ottenendo gli elementi orbitali. Il procedimento di Olbers, semplice ed efficace, divenne il procedimento standard del XIX secolo.

Nel Settecento i progressi nella determinazione delle orbite non paraboliche furono scarsi; un consistente passo avanti sarebbe stato effettuato soltanto dopo il 1800, quando Carl Friedrich Gauss (1777-1855) calcolò l'orbita del pianetino Cerere, che era appena stato scoperto.

Geodesia: la lunghezza del grado di meridiano

di Curtis Wilson

Le misurazioni geodetiche ebbero inizio in Francia verso la fine degli anni Sessanta del Seicento con propositi cartografici e continuarono nel secolo seguente. L'interrogativo sulla forma della Terra come conseguenza della forza gravitazionale e di quella centrifuga divenne un ulteriore stimolo; ci si domandava, infatti, se si trattasse veramente di un ellissoide schiacciato come avevano suggerito Newton e Christiaan Huygens. L'Académie Royale des Sciences di Parigi inviò spedizioni geodetiche in Lapponia e in Perù e nuove misurazioni furono effettuate anche in altri paesi. Entro il 1740 lo schiacciamento fu confermato, ma la determinazione dei parametri dell'ellissoide non dava risultati coerenti. Entro la fine del secolo, grazie ai progressi nelle procedure e nella strumentazione, la geodesia cominciò a interessarsi a nuove problematiche.

Negli anni dal 1668 al 1670 Jean Picard (1620-1682) misurò il tratto da Parigi ad Amiens del meridiano passante per l'Osservatorio di Parigi. Per definire una lunghezza standard riproducibile con precisione, aveva confrontato la tesa francese (pari a 6 piedi parigini ossia a 1,949 m) con la lunghezza di un pendolo semplice battente i secondi che risultò di 440,5 linee di piede parigino (144 linee a piede). Il risultato ottenuto da Picard per la lunghezza di un grado di latitudine a latitudine 49,5° Nord fu di 57.060 tese, ossia di 111,210 km.

Il tentativo degli anni Ottanta di misurare un arco più ampio, che si estendeva a nord sino a Dunkerque e a sud sino a Perpignan, non fu portato a compimento; fu però ripreso nel Settecento da Gian Domenico Cassini (1625-1712) e da suo figlio Jacques. Dopo la morte del padre nel 1712, fu Jacques Cassini a portare a termine la misurazione nel 1718 e a pubblicare nel 1720 il De la grandeur et de la figure de la Terre.

Nel 1701 i due Cassini avevano trovato un grado medio tra Parigi e Bourges più lungo di quello misurato da Picard tra Parigi e Amiens. Cassini figlio, completando la misurazione sia verso sud sia verso nord trovò che un grado medio di latitudine era di 57.097 tese (111,282 km) a sud di Parigi e di 56.960 tese (111,015 km) a nord di Parigi; dunque, se l'arco di meridiano ampio un grado diventava più corto andando verso nord, la Terra non era schiacciata ai poli ma allungata.

Il padovano Giovanni Poleni (1683-1761) fece notare, in una memoria del 1724, che i risultati di Cassini potevano essere dovuti a errori di osservazione, ma la sua tesi fu pubblicizzata a Parigi soltanto nel 1733 da Pierre-Louis Moreau de Maupertuis (1698-1759). Nel frattempo, negli anni 1733-1734 Cassini figlio misurò un arco del parallelo passante per Parigi che andava da Granville a ovest sino a Strasburgo a est, determinando le differenze di longitudine sulla base dell'eclissi dei satelliti di Giove; da queste misure dedusse nuovamente che la Terra era allungata ai poli.

Le spedizione in Lapponia e in Perù

Quanto potevano essere attendibili le misurazioni di Cassini? I suoi quadranti e settori, come d'altronde anche quelli di Picard, non avevano micrometri; i settori dovevano essere smontati per viaggiare e i triangoli scelti per le triangolazioni non erano certo i più idonei (avevano, per esempio, un angolo ottuso e uno o due angoli di 30° o meno). In queste condizioni, piccoli errori angolari producevano grandi errori nella valutazione delle distanze. Le differenze di latitudine tra gli estremi degli archi meridiani erano determinate in momenti diversi e i cambiamenti delle posizioni delle stelle dovuti all'aberrazione (scoperta soltanto nel 1729) non erano presi in considerazione. Tuttavia, cinque diverse determinazioni dell'ellitticità confermarono tutte il fatto che la Terra era un ellissoide allungato ‒ un risultato comunque poco probabile, se supponiamo che la Terra sia schiacciata ai poli e che gli errori siano stati puramente casuali. Delambre avrebbe in seguito osservato che, quando un'opinione è accettata a priori, "nello scegliere osservazioni nessuna delle quali è sicura, anche l'uomo più onesto è portato inconsapevolmente ad accogliere quelle che vanno a favore della propria opinione e a rifiutare tutte quelle che sembrano contraddirla" (Grandeur et figure de la terre, ed. Bigourdan, p. 28).

Nel 1735 e nel 1736 l'Académie Royale des Sciences di Parigi inviò due sue spedizioni all'equatore e al circolo polare artico; entrambe avevano strumenti di misurazione degli angoli provvisti di micrometri a vite ed erano formate da osservatori che volevano evitare errori a tutti i costi. Il gruppo guidato da Maupertuis in Lapponia fece rientro a Parigi nel 1737, alcuni anni prima rispetto ai membri della spedizione peruviana. Maupertuis era riuscito a procurarsi strumenti inglesi, tra i quali un settore zenitale costruito da Graham, quasi identico a quello usato da Bradley per la scoperta dell'aberrazione. Nella sua relazione, Maupertuis affermò di riportare tutte le osservazioni come erano state inizialmente scritte nei registri della spedizione, prima che fossero apportate correzioni, precauzione, questa, non presa dai Cassini. L'errore nella calibrazione del settore fu accuratamente controllato, a differenza, a quanto sembra, del punto zenitale sull'arco; ciò, secondo Delambre, fu un'omissione imperdonabile, ma questa fu l'unica critica che questi fece sulle misurazioni effettuate in Lapponia. Le posizioni delle stelle usate per determinare l'arco celeste furono corrette tenendo conto dell'aberrazione, secondo le indicazioni inviate da Bradley. La lunghezza di un grado di meridiano a 66,33° di latitudine nord risultò di 57.437,9 tese, ossia maggiore di 377,9 tese (736,53 m ca.) rispetto al grado di Picard. Inoltre, il pendolo a secondi risultò avere una lunghezza di 441,17 linee che, confrontata con le 440,57 linee di Parigi, indicava di nuovo lo schiacciamento polare.

Al rientro in Francia, il gruppo di Maupertuis rideterminò l'ampiezza dell'arco celeste nelle misure di Picard del grado Parigi-Amiens, usando lo stesso settore zenitale e correggendo la posizione delle stelle secondo l'aberrazione. Lo zenit del settore ‒ questa volta finalmente controllato prima e dopo ogni misurazione ‒ variava di circa 1″. Trovarono quindi che il grado era di 57.183 tese (111,4497 km ca.), maggiore dunque di quello ottenuto da Picard. Assumendo che la Terra avesse sezione ellittica, Maupertuis diede per la frazione f, che indica la differenza tra il raggio equatoriale della Terra e quello polare, la seguente formula:

dove L1 e L2 sono due lunghezze corrispondenti a un grado, e s1 e s2 sono i seni delle rispettive latitudini a cui sono state misurate. Le due misure, per il grado al Circolo artico e per quello di Parigi-Amiens, davano come risultato f=1/178.

Il valore esatto di f non era certo, ma lo schiacciamento polare era decisamente confermato. Allora Cassini ordinò di misurare nuovamente il meridiano dell'Osservatorio da Dunkerque a Perpignan. Troppo anziano per intraprendere egli stesso questo compito, lo affidò a Lacaille e a suo figlio César-François Cassini de Thury (1714-1784). Il lavoro fu quasi interamente effettuato da Lacaille, che fu anche l'unico autore della relazione finale. Tuttavia questa, dal titolo La méridienne de l'Observatoire royal de Paris vérifiée dans toute l'étendue du royaume par de nouvelles observations, pour en déduire la vraye grandeur (1744), fu pubblicata con il solo nome di Cassini de Thury, poiché questi era diventato membro dell'Académie pochi mesi prima di Lacaille e il protocollo richiedeva che fosse il membro più anziano della commissione a presentare la relazione; Lacaille restò sgradevolmente sbalordito dall'omissione del proprio nome, come scrisse a Bradley in una lettera del 1744.

Le misurazioni di Lacaille erano state effettuate con grande cura, come poté confermare in seguito Delambre. I triangoli furono scelti in modo da essere il più possibile equilateri; tutti gli angoli furono misurati e non dedotti indirettamente. Fu misurato un arco terrestre del parallelo passante per Rodi; la differenza longitudinale fu determinata in base alla differenza in ora locale tra gli istanti in cui si vedeva il lampo di un'esplosione ai due estremi dell'arco; il risultato confermò lo schiacciamento polare della Terra. Le lunghezze dei gradi di meridiano determinati a diverse latitudini aumentavano da Perpignan a Dunkerque, anche se con una certa irregolarità. Per il grado di Parigi-Amiens, Lacaille ottenne 57.074 tese (105,390 km ca.), allontanandosi di sole 14 tese dal risultato di Picard.

Il valore del grado di Parigi-Amiens, considerabilmente minore di quello ottenuto dal gruppo di Maupertuis, fece aumentare il risentimento di Pierre-Charles Le Monnier (1715-1799), un membro di quel gruppo che nel 1756 ottenne il consenso dell'Académie Royale des Sciences per effettuare di nuovo la misurazione. Due commissioni, lavorando indipendentemente, confermarono, con buona approssimazione, la misura di Lacaille. Nel frattempo erano state pubblicate due relazioni sulle misurazioni effettuate in Perù: quella di Bouguer nel 1749 e quella di Charles-Marie de La Condamine (1701-1774) nel 1751. Le difficoltà di questa spedizione furono enormi, prima fra tutte quella del terreno montagnoso. Spesso le basi di rilevamento per le triangolazioni erano state misurate lungo scarpate e i due settori zenitali, di 6 e 4 m, per essere trasportati avevano dovuto essere smontati e rimontati; essi davano valori per le distanze zenitali delle stelle inspiegabilmente variabili. Bouguer, preoccupato dei possibili effetti dell'attrazione gravitazionale delle montagne, misurò tali distanze a nord e a sud del Chimborazo e trovò una deviazione di 8″. Il luogo, quindi, non era stato ben scelto.

Bisogna inoltre aggiungere a tutto ciò il disaccordo sui procedimenti tra i tre membri della commissione. Louis Godin (1704-1760), il membro più anziano, ritornò in Francia soltanto dopo gli altri due e non scrisse alcuna relazione ufficiale. Bouguer e La Condamine quando erano in Perù non si rivolgevano quasi la parola e più tardi in Francia si attaccarono vicendevolmente per scritto sui rispettivi procedimenti usati. Tuttavia, le diverse misure del grado di meridiano in zona equatoriale concordavano entro un intervallo massimo di 60 tese (117 m ca.); infatti, da un arco celeste di oltre 3° e un arco terrestre di 176.940 tese, Bouguer ricavò per 1 grado (a livello del mare e a temperatura standard) il valore di 56.753 tese (110,612 km), mentre La Condamine trovò il valore di 56.745 tese (110,596 km) e i risultati riportati negli appunti di Godin variavano tra 56.754 e 56.808 tese (tra 110,614 e 110,719 km).

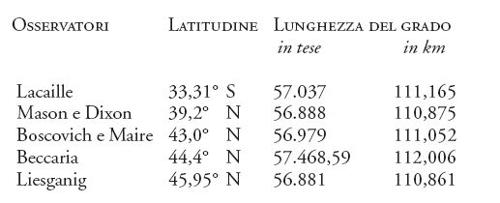
Usando la formula di Maupertuis, che presuppone una forma ellissoidale, il confronto tra il grado equatoriale di Bouguer, quello ricavato in Lapponia e quello di Parigi-Amiens calcolato da Le Monnier, comporta uno schiacciamento f di circa 1/235, laddove il confronto con il valore del grado di Parigi-Amiens di Lacaille dà f=1/321 e con quello della Lapponia f=1/76. Ulteriori misure calcolate in seguito aumentarono la confusione. Altre misurazioni degne di nota effettuate prima dell'ultimo decennio del Settecento furono quelle di Boscovich e Christopher Maire negli Stati pontifici negli anni 1750-1752; di Lacaille al Capo di Buona Speranza nel 1753; dell'astronomo gesuita Joseph Xaver Liesganig in Ungheria agli inizi degli anni Sessanta; di Charles Mason e Jeremiah Dixon in Pennsylvania negli anni 1764-1766 e di Giambattista Beccaria nel montagnoso Piemonte nel 1774. I loro risultati possono essere schematizzati come segue:

I valori dello schiacciamento f ottenuti da questi risultati, confrontati con i gradi della Lapponia e dell'equatore, erano ampiamente discrepanti.

Nuove misurazioni del meridiano di Parigi

Nel 1791 si presentò l'opportunità di misurare nuovamente il meridiano dell'Osservatorio di Parigi. Infatti la Convenzione nazionale ottenne un decreto reale per stabilire un nuovo sistema di pesi e misure con l'auspicio di arrivare in seguito a fissare uno standard internazionale. Per stabilire i criteri del sistema fu designata una commissione dell'Académie Royale des Sciences, formata da Jean-Charles Borda (1733-1799), Marie-Jean-Antoine-Nicolas de Caritat de Condorcet (1743-1794), Lagrange, Laplace e Gaspard Monge (1746-1818). La commissione stabilì come unità di misura per le lunghezze (il 'metro') la decimilionesima parte di un quadrante del meridiano. La lunghezza di tale quadrante doveva essere ottenuta misurando nuovamente il meridiano in Francia e calcolando il valore di f basandosi sul presupposto che la Terra fosse un ellissoide schiacciato.

Quest'ultima ipotesi soddisfaceva i requisiti di equilibrio della meccanica, ma le misure ottenute in precedenza non avevano sciolto i dubbi sull'entità dello schiacciamento. Evidentemente la commissione sperava che una misurazione eseguita con un nuovo strumento di misura per gli angoli, insieme a precauzioni procedurali più raffinate, avrebbero fatto luce sulle discrepanze tra la teoria e le osservazioni. Il nuovo strumento era il 'circolo a riflessione', proposto alcuni anni prima da Mayer. Si trattava di un circolo graduato, che poteva essere ruotato 'sul posto'; dopo aver puntato i due telescopi di cui era dotato su due oggetti e dopo aver annotato la posizione dei loro indici sul circolo, questo era ruotato in modo da mettere la seconda posizione al posto della prima, per poi annotare la posizione del secondo telescopio. Tale operazione era ripetuta più volte e la distanza angolare dei due oggetti era poi registrata come rapporto tra l'arco totale e il numero delle rotazioni; così si riduceva l'errore dovuto a un'errata graduazione del cerchio. Borda diffuse lo strumento, riducendo a uno il numero dei telescopi.

Due abili astronomi, Delambre e Pierre-François-André Méchain (1744-1804), furono incaricati di eseguire nuove misurazioni; la commissione stabilì le regole alle quali si dovevano attenere. La misurazione di ogni angolo doveva essere ripetuta più volte e i dati grezzi dovevano essere trasmessi a Parigi senza correzioni o riduzioni; inoltre, la media di tutte le letture di un determinato angolo doveva essere effettuata senza prendere in considerazione quanto l'osservatore ritenesse attendibile ogni singolo dato ‒ una regola che Delambre considerò sbagliata. Infatti, dopo la morte di Méchain, trovò che il suo collega aveva eliminato le osservazioni che gli erano sembrate 'fuori norma'.

Le operazioni, ritardate dalla guerra civile e da conflitti politici, terminarono finalmente nel 1799. Secondo Delambre, lui e Méchain avevano ridotto l'errore di osservazione approssimativamente di un fattore dieci rispetto a quello delle precedenti operazioni geodetiche. Dividendo in 4 parti l'arco di 9,6734° che era stato misurato e calcolando il valore medio di ciascuna delle parti, Delambre trovò che i valori aumentavano andando verso nord, ma in modo troppo irregolare e non compatibile con la curvatura ellittica. La commissione, supponendo che il meridiano fosse ellittico e confrontando il grado medio trovato in Francia con quello di Bouguer all'equatore, trovò per f il valore 1/334 e calcolò la lunghezza del metro su questa base, ottenendo 443,295936 linee; Delambre, ricalcolando le misure di Bouguer e La Condamine, trovò f=1/308.

Laplace, nel Traité de mécanique céleste, cercò d'individuare l'ellissoide di rotazione che si accordasse meglio con le 7 misure del grado dal Perù alla Lapponia e trovò ‒ usando il metodo di Boscovich, in seguito dimostrato non valido da Gauss ‒ che errori maggiori di quanto lui ritenesse accettabili (ossia 583 piedi parigini per grado, pari a 189,376 m/° ca.) non erano eliminabili. Per questo egli concluse che la Terra si distaccava sensibilmente dalla forma ellissoidale. Eppure, continuò a pensare che un ellissoide di rotazione fosse l'ipotesi più semplice e naturale per poter determinare la lunghezza di un quadrante di meridiano.

Dal 1801 al 1803 una spedizione svedese guidata da Jöns Svanberg (1771-1851) misurò nuovamente l'arco in Lapponia, usando un circolo ripetitore e una tesa standard forniti da Delambre; il risultato fu di 57.196,2 tese/grado (111,475 km/grado) a 66,34° di latitudine nord, ben 242 tese (471,66 m ca.) in meno di Maupertuis. Tuttavia, gli estremi dell'arco di Maupertuis non erano esattamente localizzabili; infatti, sembrava che l'errore nella sua misurazione consistesse nella determinazione della latitudine dell'estremo a nord e che la sua entità fosse di 11″. Ciononostante non si riuscì a individuare con precisione la fonte dell'errore. In seguito, fu rilevato che in genere la deviazione locale del filo a piombo dovuta alla variazione della densità delle falde sottostanti ammontava normalmente a 2″ o 4″ e talvolta a 10″ o più, e questa fu la principale fonte di difficoltà nelle misurazioni geodetiche del XVIII secolo.

Gli sviluppi successivi della geodesia verranno trasformati dal metodo dei minimi quadrati. Nathaniel Bowditch (1773-1838), nel suo commento al secondo volume del Traité de mécanique céleste di Laplace del 1832, rifiutava come non attendibili tutte le misure del XVIII sec., con l'eccezione di quelle di Bouguer, Delambre e Méchain; aggiungendo a queste le nuove misure effettuate in Lapponia da Svanberg e le misure dell'arco meridionale in India e in Inghilterra, ottenne col metodo dei minimi quadrati una forma ellissoidale con f=1/312, per la quale le divergenze delle singole misure erano molto minori di quelle trovate da Laplace.

Ben presto, tuttavia, desumere il valore esatto di f non fu più lo scopo principale delle ricerche. La 'forma matematica della Terra', definita come la superficie del mare, immaginata come se fosse prolungata idealmente sotto i continenti, era soggetta a irregolarità dovute alle variazioni della densità e della conformazione della superficie terrestre. Quello che si poteva trovare era l'ellissoide più vicino a questa forma, sicché, in base a un programma progettato essenzialmente da Friedrich Wilhelm Bessel (1784-1846) nel 1837, il compito dei geodeti divenne quello di determinare le deviazioni verticali dalla forma ellissoidale del cosiddetto 'sferoide di riferimento' (in seguito detto 'geoide').

Cartografia

di Curtis Wilson

Una superficie sferica non può essere riprodotta su una superficie piana senza distorsioni. La dimostrazione formale di ciò fu effettuata per la prima volta nel 1777 da Euler, ma le sue conseguenze pratiche erano già conosciute in precedenza. I disegnatori di carte geografiche e topografiche dovevano scegliere il metodo di proiezione che riproducesse nel miglior modo possibile gli aspetti particolari dei terreni ai quali il cliente era interessato.

Il XVIII sec. ereditò dal periodo ellenistico e rinascimentale una serie di metodi di proiezione cartografica, tuttavia i cartografi del Settecento ne inventarono altri; dal punto di vista matematico, un'innovazione importante di questo secolo fu l'applicazione del calcolo all'analisi delle proiezioni. Fra i metodi ereditati, il più semplice era quello della proiezione cilindrica equidistante attribuito, nella prima metà del II sec. d.C., da Claudio Tolomeo a Marino di Tiro, in base al quale i meridiani e i paralleli formano una griglia rettangolare e sono equidistanti tra loro, con una distorsione che aumenta rapidamente allontanandosi dall'equatore. Questa proiezione fu usata da Matthias Seutter (1678-1757) per le carte regionali e di navigazione, in The English pilot (edizioni dal 1689 al 1794). Tuttavia altri metodi di proiezione offrivano diversi vantaggi.

Nella proiezione 'trapezoidale', i meridiani e i paralleli sono rettilinei ma i meridiani convergono verso il Polo Nord o il Polo Sud per ridurre la distorsione lineare. Philippe de La Hire (1640-1718) usò questo tipo di proiezione per la Carte de France (1693 ed edizioni successive) e John Michell (1724 ca.-1793) per la Map of the British colonies in North America (1755).

Nella proiezione 'stereografica' la sfera terrestre è proiettata da un punto della sua superficie su un piano tangente o secante, con il punto di proiezione allineato con il centro della sfera e il punto di tangenza o il centro del cerchio secante. Tali proiezioni, che erano già usate da tempo per la costruzione dell'astrolabio planisferico, sono conformi, ossia gli angoli attorno a ogni punto sono senza distorsione, come fu dimostrato da Halley nel 1695, e la scala è la stessa in tutte le direzioni. Bradock Mead, nella Construction of maps and globes del 1717, descrisse la costruzione di proiezioni stereografiche polari, equatoriali e oblique. La proiezione stereografica equatoriale fu molto usata per disegnare gli emisferi occidentale e orientale della Terra.

La semplice proiezione conica, già usata nella Geografia di Tolomeo, fu usata per molte carte del XVIII secolo. I paralleli sono archi circolari concentrici equidistanti tra loro e i meridiani sono linee rette che intersecano i paralleli ad angoli retti. Joseph-Nicolas Delisle (1688-1768) ne propose una modifica, individuando due paralleli standard lungo i quali la scala era corretta; i meridiani erano poi disegnati come linee rette passanti per i punti corrispondenti sulla scala dei due paralleli standard. Delisle usò questa proiezione nel 1745 per la sua grande carta della Russia, che si estendeva da 40° a 70° di latitudine nord, con paralleli standard a 47,5° e 62,5°; la distorsione dell'area fu poi ridotta, in base ad altre modifiche introdotte da Patrick Murdoch nel 1758. Un'altra proiezione conica modificata fu quella di Euler del 1777 (De projectione geographica de Lisliana in mappa generali Imperii Russici usitata), nella quale gli errori di scala lungo i due paralleli estremi sono uguali e di segno opposto rispetto all'errore di scala lungo il parallelo centrale.

Del tutto innovativa per il XVIII sec. fu la 'proiezione di Cassini', ideata da Cassini de Thury nel 1745. In questo caso la superficie della carta è un cilindro che avvolge il globo terrestre in modo da risultare tangente lungo un determinato meridiano. I punti del globo sono proiettati sulla superficie cartografica lungo rette che intersecano perpendicolarmente l'asse del cilindro. Cassini de Thury ideò questa proiezione per tenere conto dello schiacciamento del globo terrestre; infatti, il cilindro aveva sezione ellittica. Tale proiezione è stata usata per le carte topografiche ufficiali francesi sino al 1803.

In realtà, la sofisticata cartografia matematica ha inizio con il libro di Lambert Anmerkungen und Zusätze zur Entwerfung der Land- und Himmelscharten (Osservazioni e complementi sul tracciamento di carte terrestri e celesti, 1772), nel quale per la prima volta le condizioni matematiche per la conservazione degli angoli e delle aree sono specificate in termini di calcolo differenziale. Lambert aveva notato che tra le proiezioni conosciute soltanto quella stereografica e quella di Gerardo Mercatore, pur essendo notevolmente diverse tra loro, preservavano gli angoli sul globo. Lambert si chiese quindi se non fosse stato possibile trovare anche altre proiezioni che avessero la stessa proprietà e finì per scoprirne tre.

La prima è la proiezione conica conforme, che è simile a quella conica semplice, ma con i paralleli distanziati in modo da creare conformità. Per ottenerla Lambert impostò un'equazione differenziale dove dp_c/dm_c, rapporto tra la lunghezza differenziale di un parallelo e la lunghezza differenziale di un meridiano in un punto arbitrario sulla proiezione conica, deve essere uguale all'analogo rapporto nei corrispondenti punti sulla sfera. Integrando questa equazione sull'intera carta, Lambert ottenne le regole per disegnare la proiezione.

Anche le altre proiezioni conformi di Lambert sono ricavate in modo analogo per mezzo del calcolo. Una è ottenuta dalla deformazione dell'equatore nella proiezione stereografica ed è normalmente chiamata 'proiezione di Lagrange' perché fu generalizzata da questi. L'altra è una modifica della proiezione di Mercatore ed è normalmente denominata 'proiezione trasversa di Mercatore'.

Lambert, inoltre, ideò un certo numero di proiezioni, chiamate 'equivalenti', che conservavano l'area, le quali peraltro non sono conformi perché la conformità e l'equivalenza sono incompatibili. Nella proiezione cilindrica ad area equivalente, i meridiani e i paralleli formano una griglia rettangolare; i meridiani sono equidistanti tra loro, ma la distanza dei paralleli dall'equatore varia in relazione al seno della latitudine. Lambert ottenne anche le altre proiezioni ad area equivalente, quella azimutale e quella conica, per mezzo dell'integrazione di equazioni differenziali.

Ancora oggi sono frequentemente usate per le carte ufficiali due delle proiezioni di Lambert: quella conforme conica e quella trasversa di Mercatore ‒ quest'ultima con una modifica introdotta da Gauss nel 1822 per poterla applicare a un ellissoide schiacciato. Lo studio del disegno cartografico conforme iniziato da Lambert ebbe in seguito importanti conseguenze nella matematica pura, fornendo uno stimolo allo sviluppo dell'analisi delle variabili complesse.

Meccanica dei corpi solidi e fluidi

di Niccolò Guicciardini

Un'opposizione fra scuola britannica e continentale

Il Settecento è il secolo d'oro di quella disciplina che in Italia è nota come 'meccanica razionale'. I grandi protagonisti che hanno consentito lo sviluppo di questa disciplina nel secolo dei Lumi sono Leonhard Euler, Jean-Baptiste Le Rond d'Alembert, Joseph-Louis Lagrange e Pierre-Simon de Laplace. Isaac Newton parla di "meccanica razionale" nella prefazione ai Principia (1687) per denotare lo studio del moto generato da forze agenti in Natura. La qualifica 'razionale' è impiegata da Newton per distinguere la sua scienza del moto naturale dalla "meccanica pratica" che ha per oggetto le macchine costruite dall'uomo. Nonostante questo illustre battesimo, il termine 'razionale' non venne usato abitualmente nel Settecento in congiunzione a 'meccanica'. Jacob Hermann (1678-1733) propose nel 1716 il termine phoronomia, mentre molti autori continentali, per esempio d'Alembert con il suo Traité de dynamique (1743), identificavano la scienza del moto con il termine leibniziano 'dinamica'. Nel 1736 Euler, nella Mechanica sive motus scientia analytice exposita, introduce il termine 'analitico' che avrà una grande fortuna. La 'meccanica analitica' sarà coltivata da molti illustri matematici del Settecento, primo fra tutti Lagrange che, per l'appunto, intitola la sua opera maggiore Méchanique analitique (1788).

Già queste osservazioni preliminari ci fanno capire quanto sia difficile comprendere la geografia concettuale settecentesca disegnata attorno al termine 'meccanica'. Un luogo classico per orientarci è l'Encyclopédie. La definizione di Dynamique (affidata a d'Alembert) situa la 'dinamica' nell'"ordine enciclopedico" seguente: "Entendement, Raison, Philosophie ou Science, Science de la Nature, Mathématiques Mixtes, Méchanique, Dynamique". Quindi la dinamica viene a dipendere dalla meccanica, che la precede nell'ordine enciclopedico. La dinamica è inoltre definita come "la parte più trascendente della meccanica". Secondo d'Alembert essa è stata coltivata, oltre che da lui stesso, da Johann I (1667-1748) e Daniel Bernoulli (1700-1782), da Euler e da Alexis-Claude Clairaut (1713-1765). L'assenza di Newton in questo elenco è un silenzio clamoroso sul quale vale la pena soffermarsi.

Al livello della scienza 'trascendente' del moto, vale a dire al livello degli studi altamente matematizzati del movimento dei corpi soggetti a forze, si assiste nel Settecento a un'accentuata spaccatura fra le due scuole: quella continentale/leibniziana e quella britannica/newtoniana. Questa spaccatura riguarda il linguaggio matematico utilizzato, i principî base e gli argomenti considerati centrali. L'invettiva di Colin Maclaurin (1698-1746), un convinto newtoniano, contro i leibniziani lega fra loro questi diversi aspetti. Maclaurin infatti accusa i continentali di aver costruito un sistema difettoso tanto nei metodi matematici quanto nei principî fisici e cosmologici. Nel Treatise of fluxions del 1742 egli scrive, riferendosi polemicamente soprattutto a Bernard Le Bovier de Fontenelle:

Dalla geometria gli infiniti e gli infinitesimi hanno dilagato nella filosofia, portando con sé quella oscurità e quella perplessità che non può mancare di accompagnarli. Da alcuni è ammessa una divisione attuale, così come una divisibilità all'infinito della materia. Si immaginano dei fluidi consistenti di particelle infinitamente piccole, che sono composte a loro volta di altre particelle infinitamente più piccole; e si assume che questa suddivisione possa proseguire all'infinito. Si propongono, per la soluzione dei problemi della Natura, dei vortici di gradi indefiniti o infiniti, a imitazione degli infinitesimi della geometria: in modo tale che, quando gli ordini più alti sono considerati insufficienti o si incontra una qualche difficoltà insuperabile, allora un ordine più basso è introdotto per mantenere in vita uno schema così favorito. La Natura è confinata nelle sue operazioni ad agire per passi infinitamente piccoli. I corpi di durezza perfetta sono rifiutati, e la vecchia dottrina degli atomi trattata come frutto di fantasia, dato che nelle loro azioni e collisioni gli atomi potrebbero passare dalla quiete al moto, o dal moto alla quiete, improvvisamente, in violazione a questa legge (di continuità). Così la dottrina degli infiniti è intrecciata alle nostre speculazioni sulla geometria e la Natura. (p. 39)

I leibniziani, secondo Maclaurin, usano un linguaggio matematico non intelligibile, dato che ricorrono a quantità infinitamente piccole. Essi inoltre rifiutano la dottrina degli atomi e accettano la teoria dei vortici per motivi che sono dipendenti dalla loro adesione a una matematica mal fondata.

Inoltre, nelle due scuole erano utilizzati linguaggi matematici differenti (quello differenziale e quello flussionale). Erano anche accettati principî fisici diversi: si pensi alla polemica sulla conservazione della vis viva e della vis mortua, polemica a cui partecipò lo stesso Maclaurin. Si considerino soprattutto le profonde divergenze sui principî base della scienza del moto: da un lato i newtoniani che fanno affidamento sulle tre "leggi o assiomi del moto" con cui si aprono i Principia, dall'altro i continentali che, piuttosto, si rifanno a principî estremali quali quello dei lavori virtuali e quello della minima azione. Non stupisce che d'Alembert, nel suo articolo Dynamique, ricostruisca una genealogia tutta continentale.

Si osservi infine come le due scuole si differenzino anche da un punto di vista contenutistico. Quando uno dei migliori allievi dei Bernoulli, Jacob Hermann, pubblica la sua Phoronomia (1716) suscita la reazione negativa di Newton proprio sul piano degli argomenti omessi dall'autore nel suo trattato. Infatti Newton, dopo una prima lettura della Phoronomia, elenca con ossessiva precisione gli argomenti che Hermann avrebbe dovuto trattare (The mathematical papers, VIII, p. 443).

Per Newton era ovvio che la scienza del moto dovesse trattare le interazioni a distanza (tipicamente gravitazionali) fra 'corpi'. Hermann invece dedicava grande attenzione al comportamento dei corpi estesi, in particolare dei fluidi. Questa è una caratteristica della scuola continentale settecentesca, dove era in genere più vivo l'interesse per i corpi rigidi ed elastici e per il moto dei fluidi. Mentre Euler, Clairaut, Daniel Bernoulli e d'Alembert, per citare soltanto alcuni, costruiscono la dinamica dei corpi estesi, i newtoniani, ritenendola estranea ai loro interessi, si dedicano soprattutto allo studio delle interazioni gravitazionali fra più corpi. L'idea che tutta la 'matematica mista' fosse riducibile al modello newtoniano dell'interazione a distanza fra corpi elementari sarà accettata nel Continente soltanto a partire da Laplace e dalla sua scuola (sostanzialmente, dopo il 1770). Prima di allora, la scuola britannica e quella continentale sono divise anche per quanto riguarda gli argomenti prioritari di studio.

La meccanica

Il fatto che si sia verificata una separazione così accentuata fra le due scuole al livello della dinamica, non deve farci dimenticare che esisteva un ampio terreno di convergenza a un livello teoretico e matematico più basso: quel livello identificato da d'Alembert come 'meccanica', la quale, come sappiamo, è presupposta alle "parti più trascendenti", ossia alla dinamica. Questo terreno comune, toccato marginalmente dalle grandi controversie sulla dinamica, è affrontato in alcuni manuali a uso delle università o indirizzati a un pubblico colto. Oltre agli studenti universitari i lettori di questi testi erano professionisti che, per i motivi più vari, dovevano applicare le conoscenze acquisite sul moto e sull'equilibrio dei corpi solidi e fluidi a campi quali la balistica, l'architettura militare o lo studio del moto delle acque. Il giustificato interesse degli storici per il livello 'trascendente' della scienza del moto (comprendente aspetti avanzati della 'matematica mista' quali l'uso di principî variazionali nella meccanica analitica, o le equazioni alle derivate parziali applicate ai corpi estesi, ecc.) ha fatto dimenticare l'ampia convergenza d'interessi per la meccanica elementare, e la grande, capillare diffusione che si è realizzata nel Settecento di concetti e tecniche propri di un livello più basso nell'ordine enciclopedico: quello, appunto, della 'meccanica'. In questa trattazione parleremo di 'meccanica' per identificare la conoscenza elementare della scienza dell'equilibrio e del moto dei corpi solidi e fluidi (la statica e l'idrostatica rientrano dunque in questa disciplina). È in questa accezione che il termine 'meccanica' è usato in opere come il System of experimental philosophy, prov'd by mechanicks (1719) di Paul Dawson, uno studente di Jean-Théophile Desaguliers (1683-1744), che ‒ senza autorizzazione ‒ anticipava in questo testo molte esperienze condotte nelle lezioni sperimentali del suo maestro.

È quindi opportuno riprendere in mano l'Encyclopédie alla voce Méchanique nella quale d'Alembert traccia gli elementi essenziali di questa disciplina più elementare. Egli osserva che essa si riduce alla statica laddove si prendono in considerazione sistemi in equilibrio; parte della voce è dedicata alla 'meccanica razionale' e ai Principia di Newton. D'Alembert tratta le macchine semplici (prevalentemente la leva) come parti della meccanica, nonché alcuni tentativi di applicare i principî della meccanica al corpo umano. In ogni caso, se prendiamo in considerazione alcuni manuali largamente diffusi nel secolo dei Lumi, si riesce a comprendere meglio che cosa fosse la 'meccanica' nel Settecento.

Uno dei primi manuali dedicati alla nuova scienza del moto è l'Introductio ad veram physicam (1702) di John Keill (1671-1721), scozzese, allievo di David Gregory (1661-1708), che si era trasferito a Oxford alla fine del Seicento per dedicarsi alla diffusione della filosofia newtoniana. La sua fortuna come difensore del newtonianismo, in particolare il ruolo svolto nella polemica con Leibniz, gli consentì di essere eletto nel 1712 professore saviliano di astronomia nell'Università di Oxford. L'Introductio ad veram physicam ebbe un notevole successo editoriale ed è spesso considerata un'opera in difesa della fisica di Newton. Bisogna però osservare che l'opera di Keill è di fatto difficilmente identificabile come un'esposizione della filosofia naturale di Newton. Keill è decisamente critico nei confronti di Descartes, come si evince anche dalla prefazione all'Introductio, e deve la sua fortuna accademica al fatto di essere stato un fedele difensore di Newton, ma questo non fa dell'Introductio un testo newtoniano. Nella prefazione Keill si riferisce, prima che a Newton, ad Archimede, Francis Bacon, Gerolamo Cardano, Galilei, Evangelista Torricelli, Blaise Pascal, Robert Boyle, John Wallis, Edmond Halley, Christiaan Huygens. Nelle sue lezioni egli espone la scienza del moto sviluppata da questi autori. Va subito osservato che la tradizione a cui Keill si riferisce è tanto una tradizione matematica (di cui Archimede sembra essere il capostipite), quanto una tradizione sperimentale (qui evocata dal riferimento a Francis Bacon). Effettivamente Keill inaugurerà uno stile di esposizione della scienza del moto in cui si coniugano dimostrazioni matematiche e dimostrazioni sperimentali. Le leggi e i teoremi relativi al moto dei corpi solidi e fluidi sono illustrati, non soltanto matematicamente come voleva Newton, ma anche sperimentalmente, e spesso con l'ausilio di macchine. Il contenuto delle lezioni di Keill è inoltre notevolmente più elementare rispetto a quanto si può trovare nei Principia di Newton. Egli espone le tre leggi del moto di Newton, tratta le leggi dell'urto dei corpi, si sofferma sui centri di gravità, sul moto lungo piani inclinati, sui moti dei proiettili nel vuoto e in un campo gravitazionale costante, sul moto del pendolo semplice e conclude il suo trattato con lo studio del moto del pendolo cicloidale. In appendice, infine, viene esaminata la dimostrazione della legge di Huygens sull'accelerazione di un corpo in moto circolare uniforme (accelerazione proporzionale al quadrato della velocità e inversamente proporzionale al raggio dell'orbita). Come si vede, a eccezione delle tre leggi del moto (ma si badi che soltanto la terza veniva percepita come genuinamente newtoniana, dato che le prime due erano attribuite da Newton stesso a Galilei), il contenuto delle lezioni di Keill è prenewtoniano. Sostanzialmente egli espone i principali risultati contenuti nei Discorsi e dimostrazioni matematiche intorno a due nuove scienze (1638) di Galilei e nell'Horologium oscillatorium (1673) di Huygens.

Lo stesso si può dire delle lezioni di Desaguliers, un fortunato experimental lecturer che sostituì per un certo periodo Keill a Oxford, prima di diventare membro attivo della Royal Society di Londra, dove eseguì numerose dimostrazioni sperimentali. Fra queste ricordiamo le celebri misurazioni, commissionate da Newton, sui tempi di caduta dei gravi eseguite nella cattedrale di St. Paul a Londra. Il primo volume del suo Course of experimental philosophy apparve nel 1734; qui Desaguliers raccoglieva il contenuto dei suoi fortunati cicli di lezioni, che erano seguiti da un pubblico colto interessato alla nuova scienza. Come nel caso di Keill, Desaguliers espone i teoremi relativi al moto dei corpi solidi e dei fluidi con l'ausilio di macchine costruite appositamente per i suoi corsi. Queste macchine sono "costruite per spiegare e provare sperimentalmente ciò che Sir Isaac Newton ha dimostrato matematicamente", in modo tale che "molte persone acquisiscano una considerevole conoscenza della filosofia naturale come per divertimento". Va osservato che, come nel caso di Keill, queste lezioni, nonostante siano dichiaratamente 'newtoniane', sono basate su teorie acquisite nel corso del Seicento prima della pubblicazione dei Principia di Newton.

Se ci spostiamo sul Continente, troviamo altri divulgatori di successo che seguono l'esempio di Keill e Desaguliers; i più noti sono gli olandesi Willem Jacob 'sGravesande (1688-1742) e Pieter van Musschenbroek (1692-1761). Questi due scienziati di grande levatura si dedicarono alla stesura di manuali che ebbero notevole fortuna. Nei Physices elementa mathematica, experimentis confirmata. Sive, introductio ad philosophiam Newtonianam (1720-1721) 'sGravesande dichiara apertamente la sua adesione al newtonianismo. Nella prefazione egli si definisce "seguace degli Inglesi" per quanto riguarda l'uso di macchine volte a illustrare le conclusioni ottenute dai matematici. In questo fortunato manuale (tradotto immediatamente in inglese da Desaguliers) 'sGravesande descrive le macchine semplici, e tratta del moto uniformemente accelerato (caduta libera e piani inclinati), dell'oscillazione dei pendoli (circolari e cicloidali), del moto parabolico dei proiettili nel vuoto, del moto in un campo di forze centrali, delle collisioni elastiche e anelastiche, dei corpi elastici, della pressione e del moto dei fluidi, del moto in un fluido resistente, della pressione atmosferica, della pompa ad aria, del moto ondulatorio e del suono e, nella parte finale, dei fenomeni ottici. Fatta eccezione per il capitolo sul moto in un campo di forze centrali, sono tutti argomenti ben noti a scienziati del Seicento quali Huygens, Pierre Varignon (1654-1722) o Edme Mariotte (1620 ca.-1684). Non è un caso che proprio Desaguliers sia stato nel 1718 il traduttore in inglese del trattato di Mariotte sul moto delle acque intitolato Traité du mouvement des eaux et des autres corps fluides (1686).

Lo stesso discorso vale per la trattazione del moto e dell'equilibrio dei corpi solidi e fluidi inclusa nell'Introductio ad philosophiam naturalem (1762). L'autore, Pieter van Musschenbroek, aveva avuto rapporti tanto con Desaguliers (che aveva incontrato in Inghilterra) quanto con 'sGravesande, per il quale il fratello, Jan van Musschenbroek (1687-1748), aveva disegnato e costruito le macchine descritte nei Physices elementa mathematica. Anche in questo caso si tratta di un'esposizione di principî e applicazioni di una meccanica in larga misura prenewtoniana.

Keill, Desaguliers, 'sGravesande e Musschenbroek sono fra i più famosi divulgatori della meccanica attivi nella prima metà del XVIII secolo. Il numero di ristampe e traduzioni dei loro manuali fornisce una chiara indicazione della fortuna che essi ebbero nel Settecento.

Sarebbe possibile aggiungere una lunga lista di nomi d'imitatori: itinerant lecturers che, provvisti del loro ingombrante armamentario di macchine sperimentali, organizzavano nelle città e in provincia corsi di filosofia naturale, e che spesso raccoglievano le proprie lezioni in manuali con tirature più che ragguardevoli, come nel caso di A course of lectures in natural philosophy (1739) di Richard Helsham (1682 ca.-1738). Un altro caso esemplare è Benjamin Martin (1704-1782), un autodidatta estraneo al mondo accademico che tuttavia divenne uno dei più prolifici autori di manuali scientifici del Settecento.

La fortuna dell'umile meccanica nel secolo della trascendente dinamica pone allo storico una serie di questioni. A chi interessava questa disciplina? Perché veniva esposta grazie a dimostrazioni sperimentali? Che rapporto aveva con la dinamica matematizzata?

Considerazioni conclusive

Chiaramente gli studenti e i lettori di Keill, Desaguliers, Martin, 'sGravesande e Musschenbroek non avevano alcun bisogno di dotarsi dei faticosi strumenti matematici necessari per seguire gli sviluppi alti della dinamica. Dopo la pubblicazione dell'Horologium (1673) di Huygens, dei Principia (1687) di Newton, e dei lavori di Jakob I e Johann I Bernoulli la scienza matematizzata del moto è accessibile solamente a una ristretta cerchia di specialisti. La convinzione che la scienza del moto sia fondamentale per la comprensione della Natura è però condivisa da pressoché tutti gli uomini di cultura del Settecento. La fortuna di scritti divulgativi come gli élémens de la philosophie de Neuton (1738) di Voltaire, o la View of Sir Isaac Newton's philosophy (1728) di Henry Pemberton è dovuta a questo generale interesse per la filosofia newtoniana. Che cosa si poteva trasmettere della scienza del moto alla base dei Principia newtoniani a un pubblico non preparato matematicamente (o, più semplicemente, non interessato alla matematica)? Poco, oltre alle leggi o assiomi con cui si aprono i Principia e forse un'esposizione del moto di un punto materiale in un campo di forze centrali. Come abbiamo visto, le informazioni trasmesse da Keill e dai suoi imitatori sono limitate a risultati già conseguiti dalla fisica matematica prenewtoniana: una disciplina identificata da d'Alembert come 'meccanica' e che si prestava a un'esposizione sperimentale. Naturalmente, questi risultati venivano inseriti in un contesto concettuale profondamente mutato dalla pubblicazione dei Principia di Newton. I testi di meccanica settecenteschi si potevano qualificare come newtoniani non soltanto per un artificio retorico, per ribadire l'appartenenza a una scuola, ma anche perché portavano a termine l'inserimento della meccanica seicentesca all'interno di un quadro concettuale newtoniano (in quanto basato sulle tre leggi del moto). Il pubblico interessato alla meccanica è formato parzialmente da studenti universitari; le lezioni di Keill e Desaguliers si svolgono in parte all'Università di Oxford, quelle di 'sGravesande e Musschenbroek all'Università di Leida. Lezioni simili erano tenute da William Whiston e Nicholas Saunderson a Cambridge o da Colin Maclaurin a Edimburgo, ma erano seguite anche, e forse soprattutto, da un pubblico esterno all'università. Le motivazioni di questo pubblico sono in gran parte di natura culturale: è l'interesse per la nuova scienza, ma anche il desiderio di assistere a lezioni divertenti e spettacolari, che riempie le aule dove vengono tenuti corsi di filosofia sperimentale.

Infine non va trascurato il fatto che la meccanica insegnata da Keill, Desaguliers, 'sGravesande e Musschenbroek era percepita come una disciplina utile nelle applicazioni ingegneristiche. Nel periodo preso in considerazione in questo capitolo, la meccanica 'trascendente' (la 'dinamica' o la 'meccanica analitica') non si trova ancora a uno stadio così sviluppato da garantire applicazioni efficaci, se non in un ambito molto ristretto. Il matrimonio fra dinamica, o meccanica analitica, e ingegneria è spesso annunciato, ma raramente consumato nella prima metà del Settecento. Infatti, se prendiamo in considerazione la letteratura ingegneristica prodotta in questo periodo troviamo raramente una strumentazione matematica raffinata. Le opere di uno dei più grandi ingegneri francesi della prima metà del Settecento, Bernard Forest de Bélidor (1697-1761), ossia La science des ingénieurs (1729) ‒ un trattato di architettura militare e civile ‒ e l'Architecture hydraulique (1737-1739), sono basate esattamente su quella meccanica prenewtoniana che è trattata nei manuali di filosofia sperimentale. Lo stesso si può dire per le opere dedicate alla balistica di Benjamin Robins (1707-1751) o per le numerose pubblicazioni ingegneristiche di Charles Hutton (1737-1823).

Nonostante la classificazione gerarchica di d'Alembert sarebbe un errore pensare al rapporto fra meccanica e dinamica come a una relazione di semplice inclusione. In alcuni casi la meccanica insegnata nelle lezioni di fisica sperimentale espone con le sue dimostrazioni sperimentali teorie accertate matematicamente, in altri casi le macchine dicono ciò che la matematica non è ancora in grado di calcolare con esattezza.

Ottica: l'eredità di Newton

di Alan E. Shapiro

Lo sviluppo dell'ottica del Settecento appare relativamente stagnante, se lo si confronta con quello dei secoli precedente e successivo. La maggior parte del XVIII sec. fu infatti dominata dalla newtoniana teoria corpuscolare della luce (detta, in genere, 'teoria dell'emissione'), ma questo periodo è in genere giudicato in base ai risultati che andavano in direzione della teoria ondulatoria e al contempo confutavano la teoria dell'emissione, con un approccio che porta inevitabilmente a una valutazione negativa dell'ottica settecentesca. Comunque, anche se teniamo conto di tali considerazioni, non si può certamente considerare questo, nonostante alcuni sviluppi interessanti, come un periodo di grande progresso degli studi; è un dato di fatto che la ricerca sperimentale nell'ottica fisica procedette a singhiozzo fino agli ultimi decenni del secolo. La relativa carenza di ricerche sui fenomeni d'interferenza, di diffrazione e di birifrazione non può essere attribuita al predominio della teoria dell'emissione, ma va ricondotta, più in generale, alla cultura scientifica dell'epoca. Le scienze fisiche avevano, infatti, ancora un carattere prevalentemente qualitativo ed erano legate soprattutto alla filosofia naturale, o alla ricerca di una visione unitaria dell'intero mondo naturale. In ogni caso, fiorirono settori dell'ottica come la fotochimica, la fosforescenza, la fotometria e l'ottica medica. Stabilire la natura della luce fu la questione centrale dell'ottica del XVIII sec., durante il quale si esplorarono le implicazioni della teoria dell'emissione, fu sviluppato l'apparato matematico per la descrizione del moto ondulatorio e si fecero vari tentativi allo scopo di svelare la vera natura della luce.

L'intero secolo è dominato dalla figura di Newton, autore nel 1704 dell'Opticks, l'opera di ottica più autorevole dell'epoca. L'influenza di Newton si esercitò in diversi modi; la sua teoria del colore rivoluzionò il modo di concepire la luce, dovendo essere incorporata in tutte le successive proposte teoriche, e la metodologia da lui impiegata nell'Opticks divenne il modello da seguire per qualsiasi indagine sperimentale; le sue riflessioni generali sulla filosofia naturale costituirono, infine, una preziosa fonte d'ispirazione per gli scienziati. Nel 1672 Newton aveva pubblicato un articolo nel quale dimostrava che la luce del Sole ‒ considerata fino ad allora come pura e omogenea ‒ è in realtà una mescolanza di raggi di tipo diverso, che sono rifratti in modo diverso e mostrano differenti colori. In tal modo i colori spettrali 'elementari' sono distinti da quelli che risultano dal loro mescolamento, essendo il colore più complesso quello della luce del Sole, formato dalla composizione degl'innumerevoli colori spettrali.

In un primo momento la teoria di Newton incontrò qualche obiezione, tuttavia già all'inizio del Settecento essa era ampiamente accettata in Gran Bretagna. La pubblicazione dell'Opticks, che ne conteneva un'esposizione più approfondita rispetto a quella dell'articolo del 1672, suscitò un generale entusiasmo in Gran Bretagna, ma soprattutto ebbe un ruolo decisivo nel Continente, dove il lavoro precedente era quasi caduto nell'oblio. Nel giro di un decennio gli esperimenti di Newton furono ripetuti, e la sua teoria fu adottata in Olanda, Italia, Germania e Francia. Quando, nel 1714, un articolo degli "Acta Eruditorum" lo sfidò a dimostrare che raggi semplici di colore immutabile esistevano realmente, Newton chiese a Desaguliers di provarlo al cospetto della Royal Society. Il successo della dimostrazione di Desaguliers segna l'unanime riconoscimento della teoria dei colori di Newton.

Sin dai suoi primi studi di ottica degli anni Sessanta, Newton aveva adottato la teoria emissiva della luce e si era opposto alle teorie basate sull'idea di continuità, vale a dire alle teorie nelle quali si supponeva che la luce consistesse nella propagazione attraverso un mezzo di una pressione, di una vibrazione o di un'onda, a partire da una sorgente luminosa. L'obiezione di principio che Newton faceva alla teoria del continuo era che essa avrebbe violato la legge della propagazione rettilinea della luce, in quanto ogni pressione o vibrazione in un mezzo fluido come l'etere, se fatta passare attraverso un piccolo foro, si sarebbe diffusa in tutte le direzioni, proprio come accade alle onde sonore oppure alle onde nell'acqua, mentre la luce si propaga comunque in linea retta. Egli presentò una giustificazione teorica di tale affermazione nei suoi Principia del 1687 e, in seguito, la elaborò ulteriormente nell'Opticks.

Newton pubblicò le sue riflessioni sulla natura della luce in una serie di Queries poste in appendice all'Opticks. In esse egli sviluppò i suoi ragionamenti sulla propagazione rettilinea e mostrò che il tipo di etere richiesto dalle teorie della propagazione continua avrebbe rallentato il moto dei pianeti e delle comete. Rivolse anche altre critiche alle teorie ondulatorie, tra le quali, per esempio, la loro incapacità di giustificare la polarizzazione della luce; tali obiezioni, tuttavia, furono in gran parte ignorate nel XVIII secolo.

L'idea più audace proposta da Newton fu quella di ricondurre i fenomeni di rifrazione, riflessione e diffrazione all'esistenza di forze a corto raggio d'azione, sia attrattive sia repulsive, tra le particelle della materia e i corpuscoli di luce; egli ipotizzò per il mondo microscopico l'esistenza di forze a corto raggio per analogia con l'esistenza della forza di gravità per l'intero Universo. Nei Principia Newton aveva ricavato la legge di rifrazione assumendo che i corpuscoli luminosi fossero attratti da forze esercitate dalla superficie rifrangente. Ipotizzò che tali forze agissero perpendicolarmente sul corpo a piccole distanze dalla superficie; le traiettorie dei corpuscoli luminosi erano così del tutto analoghe a quelle di proiettili che si muovono in un campo gravitazionale uniforme. Newton precisò che tale modello era soltanto il frutto di un'analogia e che egli non intendeva sostenere che i raggi luminosi fossero veramente corpi molto piccoli. Tuttavia, la possibilità di trattare il moto della luce con la meccanica newtoniana esercitò un certo fascino sugli scienziati amanti della matematica, dal momento che andava nella direzione di una possibile unificazione della fisica.

La teoria ondulatoria

di Alan E. Shapiro

Nel 1746 Leonhard Euler pubblicò quella che sarebbe stata la versione della teoria ondulatoria più sofisticata del secolo. Quando nel XIX sec. cominciò a essere sviluppata la moderna teoria ondulatoria, il suo progenitore era considerato Christiaan Huygens; in realtà il suo Traité de la lumière (1690) fu in gran parte ignorato nel XVIII secolo. In quel periodo, infatti, i sostenitori delle ipotesi ondulatorie cercavano soprattutto di spiegare la teoria dei colori di Newton e di elaborare una trattazione dinamica della propagazione ondulatoria, mentre Huygens non toccò alcuno di questi argomenti.

René Descartes (1596-1650) non poteva essere certamente considerato un sostenitore della teoria ondulatoria, ma aveva comunque adottato una teoria della propagazione continua; data l'influenza che le sue opere ancora esercitavano all'inizio del Settecento, può essere ritenuto quindi un punto di partenza significativo per analizzare i primi sviluppi delle teorie ondulatorie. Descartes pensava che la luce consistesse in una forma di pressione che si propagava istantaneamente attraverso i corpuscoli perfettamente rigidi di cui era composto il fluido etereo che riempiva tutto lo spazio. Per lui era scontato che la luce si propagasse in linea retta, e per questo motivo non aveva mai cercato una spiegazione di tale fenomeno, né si era mai occupato dei fronti d'onda: in definitiva, egli aveva una concezione statica della luce che non prevedeva oscillazioni o vibrazioni.

Partendo dall'ipotesi che la luce si propagava con una velocità finita, Huygens aveva invece proposto quello che oggi chiamiamo 'principio di Huygens' per descrivere la propagazione di un'onda o di un impulso attraverso le particelle elastiche dell'etere; tuttavia egli non parlava di onde periodiche, perché rifiutava l'idea che gl'impulsi si succedessero a intervalli regolari. Per spiegare la produzione di fronti d'onda Huygens aveva ipotizzato che tutti i punti di un fronte generassero a loro volta piccole onde e che il nuovo fronte si formasse lungo la tangente comune a queste ultime. Per Huygens i fronti d'onda erano entità reali, mentre i raggi luminosi rappresentavano la direzione di propagazione lungo rette perpendicolari ai fronti; per salvaguardare il principio della propagazione rettilinea egli aveva ipotizzato che le onde elementari che nascevano da ciascun punto del fronte d'onda fossero troppo deboli per essere rilevate in punti lontani dalla tangente comune, ma questa spiegazione non fu ritenuta convincente nel Settecento. Tuttavia, in base al suo principio e alla sfericità delle onde elementari, egli poteva spiegare in modo elegante la riflessione e la rifrazione, nonché, introducendo onde elementari di forma sferoidale, il fenomeno della doppia rifrazione, nel quale i raggi luminosi non sono perpendicolari ai fronti d'onda. In ogni caso, Huygens non provò neppure a spiegare i colori, l'interferenza, la polarizzazione o la diffrazione.

Nel 1699 Nicolas Malebranche (1638-1715) pubblicò una teoria neocartesiana della luce, che l'anno successivo incluse nella quinta edizione della Recherche de la vérité. Egli supponeva che la luce consistesse di vibrazioni che si propagano attraverso un etere elastico composto di vortici microscopici, ma, come Descartes, ragionava in termini di raggi e non di fronti d'onda, finendo per attribuire ai raggi stessi un moto vibratorio longitudinale. Nel 1699 Malebranche non aveva ancora accettato la teoria dei colori di Newton; ciò avvenne nel 1712 in una nuova edizione della Recherche de la vérité, dove ipotizzò che ciascun colore corrispondesse a una particolare frequenza di vibrazione; poiché è la luce rossa ad avere maggiore 'forza' e a essere la meno rifratta, gli sembrò ragionevole attribuirle la frequenza più piccola, mentre al 'debole' violetto andava assegnata la frequenza massima. Questa corretta attribuzione deve però essere considerata soltanto come l'effetto di una fortunosa congettura. Malebranche assunse inoltre che soltanto sette frequenze o colori si propagassero attraverso i vortici eterei, in quanto soltanto vortici di particolari dimensioni erano in grado di entrare in risonanza tra loro.

Molte delle idee di Malebranche furono riprese da Johann II Bernoulli (1710-1790) in un apprezzato articolo del 1736 sulla propagazione della luce. Come Malebranche, egli concepì un etere elastico che consisteva di minuscoli vortici, ma in più immaginava che in esso fossero disseminati corpuscoli rigidi ancora più piccoli e di svariate dimensioni. Quando una sorgente luminosa, come il Sole, fa vibrare l'etere, i corpuscoli di una certa dimensione dispersi in esso entrano in risonanza (come nella teoria di Malebranche) e si allineano per formare un raggio vibrante, o 'fibra luminosa', con una frequenza, caratteristica di ciascun corpuscolo, corrispondente a un particolare colore. Bernoulli considerò il suo punto di vista come una soluzione al problema della propagazione rettilinea della luce, e rifiutò esplicitamente il principio di Huygens, considerandolo inadeguato a spiegare quella proprietà fondamentale. La maggior parte dell'articolo è dedicata alla derivazione analitica delle proprietà delle suddette vibrazioni, fornendo un esempio significativo del nuovo approccio all'ottica basato sulla meccanica razionale. Bernoulli fece anche notare che le sue fibre vibranti erano in grado di spiegare i fenomeni cromatici periodici che si presentavano nel caso di strati sottili meglio di quanto Newton stesso aveva fatto nell'Opticks, ma non attribuì valori numerici alle frequenze dei colori. Non facendo uso del concetto di fronte d'onda, le sue spiegazioni della riflessione e della rifrazione erano basate su modelli di meccanica della particella singola.

Era trascorso più di un terzo del XVIII sec. e gli elementi fondamentali della teoria ondulatoria non erano stati ancora accorpati a formare una teoria unitaria; ciò valeva, in particolare, per la relazione fra il concetto di fronte d'onda e quello di raggio luminoso, per la spiegazione della riflessione e della rifrazione basata sui fronti d'onda piuttosto che sui raggi o corpuscoli, e per l'attribuzione ai colori di frequenze determinate.

Nel 1746 Euler pubblicò la Nova theoria lucis et colorum, in cui era presentata quella che appare la descrizione più coerente della teoria ondulatoria dell'intero secolo. Egli iniziò il suo saggio con un paragrafo di carattere polemico nel quale replicava alle critiche mosse alla teoria ondulatoria e metteva in evidenza i tre problemi fondamentali della teoria dell'emissione: (a) in primo luogo, il Sole avrebbe dovuto consumarsi a causa dell'emissione di così tante particelle luminose nel corso dei millenni; (b) in secondo luogo, i raggi non avrebbero potuto incrociarsi senza urtarsi vicendevolmente; (c) infine, i corpi trasparenti, per consentire ai corpuscoli luminosi di passare, avrebbero dovuto contenere soltanto pori, e non materia. Anche se, nella parte successiva dell'articolo, Euler procedeva all'elaborazione della teoria ondulatoria, la maggior parte dei filosofi naturali preferì occuparsi di questi tre problemi, senza sviluppare e applicare i suoi risultati teorici.

Euler, come Bernoulli, aveva basato la teoria della luce sulla meccanica razionale dei corpi vibranti; tuttavia, il suo etere era del tutto omogeneo e privo di corpuscoli risonanti, il che gli consentì di attribuire ai colori una gamma continua di frequenze. Egli considerava il fronte d'onda come un'entità fisica reale, mentre i raggi erano soltanto le rette perpendicolari al fronte stesso. Il concetto di fronte d'onda gli consentiva di spiegare in quale modo la rifrazione dipendesse unicamente dalle diverse velocità di propagazione della luce in mezzi diversi. Egli riuscì a dare questa semplice spiegazione anche perché non aveva preso in considerazione il fenomeno della doppia rifrazione e quindi aveva potuto ignorare il principio di Huygens. La sua teoria non risolveva, tuttavia, il problema della propagazione rettilinea della luce e quindi Euler non fu mai in grado di superare l'obiezione più seria che Newton aveva sollevato contro la teoria ondulatoria.

Euler identificò ciascuna frequenza del suo spettro continuo con uno dei colori elementari di Newton, ma i suoi raggi composti non erano ‒ come Newton aveva stabilito ‒ un miscuglio di raggi di tutti i colori semplici, ma singoli raggi nei quali gl'impulsi, o le vibrazioni, variavano gradualmente da una frequenza più alta a una più bassa. Poiché anche per Euler una mescolanza di raggi semplici dava origine a luce bianca, egli aveva di fatto introdotto, senza alcuna giustificazione, due tipi di luce bianca. Partendo da un'analisi teorica della dispersione Euler giunse alla conclusione che i raggi di colore rosso corrispondevano alle frequenze più alte, ma in seguito cambiò più volte parere su tale questione, sinché alla fine dichiarò che il problema restava irrisolto, senza accorgersi che lo studio dei colori prodotti da strati sottili poteva fornirne la soluzione.

Euler, come d'altronde tutti i sostenitori delle teorie ondulatorie che lo avevano preceduto nel XVIII sec., non effettuò alcun esperimento. Egli aveva elaborato la sua teoria come parte di una filosofia naturale di portata generale e quindi come tentativo di estendere all'ottica la meccanica razionale dei corpi vibranti. L'importanza del suo lavoro sta soprattutto nella trattazione dinamica della teoria ondulatoria, nell'identificazione dei colori con le frequenze e nella reintroduzione del concetto di fronte d'onda. Questi aspetti delineavano uno schema ragionevole per la teoria ondulatoria. La 'nuova teoria' di Euler esercitò un'influenza considerevole nei paesi di lingua tedesca, incontrando molte adesioni, anche se non produsse ulteriori sviluppi nella trattazione fisico-matematica della teoria ondulatoria della luce.

Al centro dell'interesse restava comunque la scelta tra una concezione ondulatoria e una concezione corpuscolare; soltanto le nuove ricerche sperimentali e le analisi condotte da Thomas Young (1773-1829) alla fine del secolo avrebbero determinato ulteriori progressi.

La teoria dell'emissione

di Alan E. Shapiro

La teoria dell'emissione di Newton dominò tutto il Settecento, tuttavia non mancarono altre versioni della teoria corpuscolare, come quelle, per esempio, in cui si assumeva che le particelle di luce sgorgassero dai corpi luminosi come un fluido. La caratteristica essenziale che distingueva la teoria dell'emissione di Newton dalle altre teorie corpuscolari era l'ipotesi che sulle particelle luminose agissero forze a corto raggio; ciò permetteva di trattare l'ottica analiticamente, per mezzo della meccanica newtoniana, e per questo la versione della teoria dell'emissione di Newton fu la sola che consentiva di effettuare previsioni e verifiche e di porre le basi di un programma di ricerca.

Dato che Newton aveva appena abbozzato la sua teoria corpuscolare della luce, peraltro in brani dispersi all'interno della sua opera, il compito di presentare una teoria coerente toccò ai suoi successori. I manuali di filosofia naturale di Willem Jacob 'sGravesande e Pieter van Musschenbroek ebbero, a tale proposito, un ruolo importante. In una serie di testi didattici pubblicati tra il 1720 e il 1762 i due autori presentarono un'ampia rassegna sull'ottica, riconducendo le proprietà della luce all'azione di forze a corto raggio. I loro lavori furono tradotti in inglese e in francese, ma anche la versione originale in latino circolò ampiamente. In Inghilterra, Robert Smith (1689-1768) dedicò la prima parte del suo A compleat system of opticks (1738) a un progetto analogo, anche se il suo testo era sostanzialmente un trattato di ottica geometrica, con un approccio più matematico che sperimentale.

Così come avvenne per la teoria ondulatoria, la meccanica razionale fu applicata anche alla teoria corpuscolare. Nel 1739 Alexis-Claude Clairaut presentò all'Académie Royale des Sciences di Parigi una memoria dal titolo Sur les explications cartesienne et newtonienne de la réfraction de la lumière, importante per diverse ragioni; infatti, essa introduceva la teoria corpuscolare di Newton nell'ambiente francese, ribadendo la supremazia della fisica newtoniana, basata sul concetto di forza, sulla filosofia naturale di Descartes, e dando origine a una tradizione di ricerca nell'ambito della concezione balistica. In quella memoria Clairaut espose dettagliatamente, in forma analitica, la derivazione newtoniana della legge di rifrazione, presentata nei Principia e basata su forze a corto raggio d'azione, sebbene qui la teoria di Newton non fosse più trattata come una semplice analogia ma come la spiegazione più realistica. Nel modello newtoniano l'ipotesi più naturale per giustificare l'origine dei colori e le differenze nella rifrazione dei raggi di diverso colore consisteva nell'assegnare a ciascun colore una differente velocità, attribuendo al rosso la velocità maggiore e al violetto quella minore. Nel 1740 Jean-Jacques Dortous de Mairan (1678-1771) fu il primo a indicare la possibilità di controllare la veridicità di quell'ipotesi osservando se i satelliti di Giove cambiavano colore durante un'eclissi; infatti, quando un satellite scompare dietro un pianeta il colore più lento, il violetto, dovrebbe essere visto per ultimo, mentre quando il satellite riemerge il colore più veloce, il rosso, dovrebbe apparire per primo.

Questa possibilità di verifica fu discussa, poco dopo il 1750, da diversi scienziati, tra i quali Clairaut stesso, Thomas Melvill (1726-1753) e Gaspard de Courtivron (1715-1785). Anche da calcoli approssimativi e da osservazioni occasionali, sembrava che le eclissi non fossero colorate e che la velocità non potesse essere la causa del colore. Nel 1753 Melvill propose l'esperimento alla Royal Society di Londra, e l'astronomo James Short (1710-1768) riferì di non aver osservato alcun mutamento. Questa evidenza sperimentale fece escludere l'interpretazione più naturale dell'origine del colore che poteva accordarsi col modello newtoniano della rifrazione.

Nel corso del XVIII sec., all'interno del modello balistico furono prese in considerazione tre possibili spiegazioni del colore: che esso dipendesse dalla massa dei corpuscoli, dalla loro velocità, oppure da una forza che variava a seconda della natura delle particelle luminose e della materia. La dipendenza del colore dalla massa, come sosteneva Courtivron nel 1752, violava i principî della dinamica, in quanto il moto delle particelle non dipendeva dalla loro massa. Nonostante l'evidenza sperimentale contraria, l'ipotesi della dipendenza dalla velocità non fu del tutto esclusa dai fondamenti della teoria balistica; piuttosto, essa fu in seguito limitata alla trattazione di raggi con una sola velocità e un solo colore, cioè raggi monocromatici. La terza ipotesi, quella delle forze selettive, divenne un'opzione praticabile soltanto verso la fine del secolo, con il sorgere della chimica della luce.

Mentre la teoria balistica continuava a essere usata dai matematici, per esempio da John Michell nel suo calcolo della deviazione dei corpuscoli luminosi a causa dell'azione gravitazionale delle stelle, tra il 1780 e il 1820 essa assunse un ruolo centrale nella fisica e nella chimica francesi, allorché gli scienziati, guidati da Pierre-Simon de Laplace diedero un nuovo impulso al programma newtoniano basato sulle forze a corto raggio. Laplace applicò il modello balistico alla rifrazione atmosferica nel quarto volume (1805) del suo Traité de mécanique céleste; negli anni successivi, insieme a Jean-Baptiste Biot (1774-1862) ed Étienne-Louis Malus (1775-1812), lo estese alla doppia rifrazione e alla polarizzazione. Nonostante questo apparente successo, il modello balistico di Laplace non era ancora in grado di spiegare i colori, per cui questi erano accuratamente evitati. Comunque, nel giro di un decennio anche quest'ultima fioritura della teoria dell'emissione avrebbe dovuto soccombere di fronte all'affermazione della teoria ondulatoria.

La chimica della luce

Nel 1758 l'ottico londinese John Dollond (1706-1761) annunciò di avere costruito, incollando tra loro due lenti di curvatura opportuna e tratte da due diversi tipi di vetro, una lente 'acromatica', cioè capace di rifrangere allo stesso modo luci di colore differente; con tale invenzione si risolse l'annosa questione dell'eliminazione dei colori che distorcevano le immagini osservate attraverso una lente semplice. Egli trovò che la dispersione di una delle due lenti poteva compensare quella dell'altra, senza peraltro eliminare la rifrazione dei raggi, e ciò in contrasto con quanto affermato da Newton nell'Opticks. La scoperta di Dollond portò a significativi miglioramenti degli strumenti, ma ebbe anche conseguenze importanti per le teorie ottiche.

Molti interpretarono la scoperta di Dollond come conferma del fatto che la 'forza di rifrazione' non fosse di natura meccanica. Infatti, diversamente dalla forza gravitazionale, essa dipendeva dalla natura della sostanza rifrangente e non agiva allo stesso modo su tutte le particelle luminose; si trattava cioè di una forza selettiva che dipendeva dalle proprietà dei due mezzi. In base a questo molti giunsero alla conclusione che le 'forze ottiche' fossero di natura chimica. Nell'Optics (1797) il filosofo naturale scozzese John Robison formulò esplicitamente tale deduzione, affermando che l'ipotesi di Newton sulla proporzionalità tra rifrazione e dispersione "era infondata; e Newton stesso avrebbe potuto dubitarne, in quanto aveva già notato l'analogia tra il carattere selettivo delle attrazioni e repulsioni chimiche dei corpi e le azioni simili sulla luce [...]. Le recenti scoperte della chimica ci mostrano delle prove evidenti che la luce non è estranea alle leggi dell'azione chimica, essendo suscettibile di combinazioni chimiche" (p. 286).

La cosiddetta 'chimica della luce', ossia l'idea che la luce sia una sostanza chimicamente attiva che possiede affinità elettive con la materia e può combinarsi chimicamente con essa proprio come una qualsiasi altra sostanza, fu ampiamente adottata nell'ultimo quarto del XVIII secolo. Forse il motivo principale del suo successo furono le ricerche sui processi fotochimici, soprattutto la fotosintesi e l'annerimento dei sali d'argento prodotto dalla luce (fenomeno che nel secolo successivo avrebbe condotto alla fotografia). Nel 1782, attingendo al precedente lavoro di Joseph Priestley e Jan Ingen-Housz, Jean Senebier (1742-1809) stabilì che le piante esposte alla luce solare estraevano dall'atmosfera biossido di carbonio rilasciando ossigeno, il che era anche la causa del loro colore verde; si era dunque di fronte a un prodigioso effetto chimico della luce.

Anche se la chimica della luce non era una teoria meccanica, tuttavia in essa si continuava a concepire la luce come il prodotto dell'emissione di corpuscoli. Il numero crescente di fatti sperimentali che dimostravano come la luce si combinasse chimicamente con la materia fu considerato una prova definitiva in favore della teoria dell'emissione, dato che, a quel tempo, nessuno era in grado d'immaginare in quale modo un'onda potesse alterare le proprietà chimiche dei corpi; così, lo sviluppo della chimica della luce fece crollare il consenso verso la teoria ondulatoria. Ciononostante, nel primo ventennio del XIX sec. la teoria ondulatoria avrebbe ripreso vigore grazie a nuove ricerche sperimentali e a importanti innovazioni teoriche.