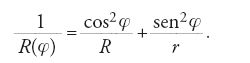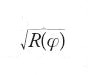L'Età dei Lumi: matematica. Geometria analitica, delle curve e delle superfici. Il problema delle parallele
L'Eta dei Lumi: matematica. Geometria analitica, delle curve e delle superfici. Il problema delle parallele
Geometria analitica, delle curve e delle superfici. Il problema delle parallele
A prima vista può sembrare poco interessante considerare lo sviluppo del metodo delle coordinate nel XVIII sec. poiché storicamente gli sviluppi più importanti di questa branca della matematica si ebbero nel secolo precedente e in quello successivo. Infatti, se nel XVII sec. si assiste alla nascita di questo metodo, che doveva porre le premesse per lo sviluppo della matematica moderna, nel XIX sec. la possibilità, che il metodo delle coordinate aveva implicita fin dall'inizio, di estendere tutti i concetti geometrici bi- e tridimensionali al caso di una dimensione qualunque e dal caso euclideo a quello di spazi a metrica non euclidea portò all'enorme estensione del dominio della geometria, al punto da far meritare a giusto titolo al XIX sec. il nome di 'secolo della geometria'.
Una riflessione più attenta ci mostra invece come fu proprio nel corso del XVIII sec. che il metodo delle coordinate, a partire da uno stadio che oggi definiamo elementare perché legato all'evidenza geometrica, si sviluppò raggiungendo un livello ancora sufficientemente valido per le applicazioni. Furono pubblicate raccolte di enormi quantità di problemi, soluzioni ed esempi che avevano un ruolo importantissimo nella preparazione di matematici non professionisti. Affascinante sarà la ricerca dei primi embrioni di quelle idee e concetti fecondi per gli sviluppi del XIX sec., dei quali abbiamo detto. La potenza dei nuovi metodi algebrici e analitici portò i matematici, con rare eccezioni, a escludere ciò che non si conformava a questi nuovi metodi, a porre cioè i problemi e, in caso, a modificarli in modo che si potessero trattare con il metodo allora in auge. Sarà allora anche più interessante riscoprire quei pochi tentativi dai quali già allora avrebbe potuto svilupparsi una concezione meno rigida del metodo delle coordinate, se lo spirito del tempo non fosse stato così duramente contrario.
In breve, per noi che viviamo in un mondo dominato dai computer, il metodo geometrico delle coordinate è soltanto un caso particolare del metodo generale di descrivere oggetti attraverso 'strutture di dati' e di applicare a queste ultime algoritmi originariamente pensati per tali oggetti. Di ciò fa parte naturalmente l'intero apparato concettuale degli insiemi ordinati e non ordinati, costruito inizialmente per la logica e la teoria degli insiemi, e cioè delle 'liste' di insiemi i cui elementi sono ancora liste di operazioni, relazioni, grafi, matrici, ecc. In questo senso i matematici del XVIII sec. si sono limitati in sostanza a considerare oggetti geometrici che si lasciano descrivere mediante equazioni o sistemi di equazioni; l'analoga descrizione che fa uso di disequazioni vedrà la luce solamente all'inizio del XIX sec. con Augustin-Louis Cauchy (1789-1857). Nel XVIII sec. si attribuiscono delle coordinate ai punti, senza andare oltre. È ancora di là da venire il punto di vista che considera i coefficienti di un'equazione o di un sistema di equazioni algebriche come coordinate dell'insieme di punti che queste descrivono, e le equazioni come una traduzione delle relazioni di incidenza nel linguaggio delle coordinate, due fatti che si riveleranno essere estremamente fecondi. L'unica sortita da questo quadro puramente algebrico furono le funzioni definite da serie. Tuttavia, soltanto una piccola minoranza di matematici, avversari dei metodi infinitesimali o scettici nei confronti di questi, considerava le serie estranee all'algebra. La maggioranza vedeva, per esempio, le serie di potenze semplicemente come polinomi di grado infinito, e perciò le manipolava senza porsi troppi problemi.
Premettiamo un'ultima considerazione. Il metodo delle coordinate non soltanto rende possibile affrontare problemi geometrici utilizzando il 'calcolo' (in senso lato), ma permette anche, viceversa, d'interpretare geometricamente e rappresentare concretamente, almeno in due e tre dimensioni, relazioni che in origine non hanno nulla a che vedere con la geometria. Si parte dalla rappresentazione grafica di funzioni che esprimono, per esempio, un legame tra due variabili di natura fisica o economica, per finire come oggi con modelli che hanno poco a che vedere con quelli in gesso così in voga soprattutto nel XIX secolo. Questi 'modelli' (da intendersi in senso molto lato) di fatti aritmetico-algebrici permettono spesso di cogliere intuitivamente dati di natura non algebrica, fungendo soprattutto nei secc. XVII e XVIII da dimostrazioni euristiche di numerosi teoremi la cui dimostrazione rigorosa nel senso dei criteri attuali non sarebbe stata possibile. Questa duplice funzione del metodo delle coordinate, cioè dell'algebra come ausilio della geometria e della geometria come ausilio dell'algebra, si avverte già nei fondatori del metodo, Pierre de Fermat (1607-1665) e René Descartes (1596-1650), anche se soltanto implicitamente e in alcuni esempi. All'epoca, tuttavia, non fu oggetto di riflessione. Per esempio Descartes, dal fatto geometricamente evidente che la circonferenza di raggio q/2 e con il centro nel punto O di coordinate (q/2,0) interseca la parabola x2=py esattamente una volta nel primo quadrante, aveva concluso che l'equazione cubica x3+p2x=p2q, che si incontra nel calcolo dei punti di intersezione, ha sempre esattamente una radice positiva. D'altra parte, poiché, assegnati due numeri positivi a, b qualunque, se ne possono calcolare altri due p,q>0 tali che p2=a e p2q=b, il risultato vale per tutte le equazioni del tipo x3+ax=b (con a,b>0).
Preistoria
Riassumiamo brevemente la situazione creatasi a opera di Fermat e Descartes intorno al 1637, che ha favorito la creazione del metodo delle coordinate, e lo status del metodo alla fine del XVII secolo. Grazie all'introduzione, dovuta a Descartes, di un'unità di misura, l'applicazione dell'algebra alla geometria si affranca dalle limitazioni alle quali era soggetta in precedenza: (a) il prodotto è possibile soltanto tra due o al massimo tre segmenti (da intendersi quindi come aree di rettangoli o rispettivamente volumi di parallelepipedi rettangoli); (b) si possono addizionare o sottrarre solamente grandezze della stessa dimensione (nel senso del punto a).
Descartes rappresenta inoltre ogni grandezza, costruita con operazioni algebriche (comprese le estrazioni di radici) a partire da segmenti assegnati, a,b,c,…,x,y,…, ancora con un segmento. Tuttavia non enuncia esplicitamente quella corrispondenza biunivoca tra i numeri reali e i punti di una retta (o di un 'asse', sul quale sono fissati due punti O e U), che oggi ci è così familiare. Fino a un certo punto le sue trasformazioni algebriche appartengono, per usare il linguaggio informatico moderno, alla 'manipolazione formale'; il resto, cioè l'applicazione numerica, per dirla ancora nel linguaggio di oggi, va pensato come costruzione geometrica.
Fermat si attiene alle vecchie limitazioni (a) e (b) ma chiarisce, in modo più esplicito di quanto non faccia Descartes, che ogni equazione a due incognite x e y rappresenta, una volta scelto un sistema di coordinate, una curva del piano, indipendentemente dal fatto che la curva venga costruita con uno strumento meccanico, per punti o in altro modo. Spiega anche come, dalla classificazione algebrica delle equazioni, segua una classificazione delle curve e come proprietà geometriche di una curva possano essere dedotte dall'equazione di questa, anche senza aver mai visto concretamente la curva. In particolare, risultato del quale andava molto fiero, le curve descritte da equazioni algebriche di secondo grado ‒ nel rispetto dei punti (a) e (b) ‒ sono esattamente quelle definite geometricamente in modo interamente diverso, e cioè attraverso le sezioni coniche. Noi abbiamo ormai perso la capacità di stupirci davanti a questa coincidenza che ha effettivamente del meraviglioso, ed è un vero peccato. Il fatto che la geometria, con le sezioni coniche e lo strumento della proiezione centrale, permetta di scoprire che curve apparentemente così diverse sia per la forma geometrica sia per quella algebrica sono invece in relazione tra loro e possono essere trasformate una nell'altra va considerato come un modello metodologico dal quale discendono campi come la geometria algebrica e la moderna teoria di Lie delle equazioni differenziali.
Newton e la nascita della geometria algebrica
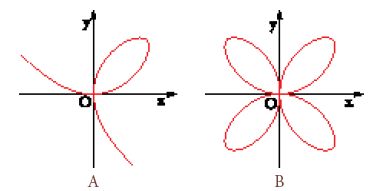
Non è nostro compito in questo capitolo parlare di come l'impulso dato da Descartes e le linee generali di una geometria delle coordinate da lui tracciate si siano diffusi e abbiano raggiunto il successo grazie alla traduzione in latino e alle elaborazioni, integrazioni e numerose applicazioni dovute, nel Seicento, soprattutto a matematici olandesi. Leibniz utilizzò per la prima volta i termini "ascissa" e "ordinata" nel 1676 e, dal 1692, quello collettivo di "coordinate", al quale i fratelli Jakob I (1654-1705) e Johann I (1667-1748) Bernoulli aggiunsero l'aggettivo di "cartesiane". È nel XVIII sec. tuttavia che si ha il contributo maggiore a un ulteriore sviluppo del metodo delle coordinate, e ciò a opera di Newton. Se è vero che Newton aveva cominciato a occuparsi della questione già nel 1665, e i suoi contributi risalgono a prima del 1700, la pubblicazione dei risultati avvenne però soltanto nel corso del XVIII sec. e per molti di questi solamente dopo la sua morte. In uno dei suoi lavori postumi (1736) si trova per la prima volta, nel titolo, l'espressione "geometria analitica". Newton fu influenzato da Descartes e Fermat più di quanto non fosse disposto ad ammettere, ma nella percezione oggi diffusa i suoi contributi fondamentali allo sviluppo del metodo delle coordinate sono oscurati dagli altri suoi risultati. Se già John Wallis (1616-1703) nel 1655 e Jan Hudde (1628-1704) nel 1659 avevano ammesso, in casi particolari, valori negativi delle variabili, è soltanto con Newton che si giunge a una sistematica geometria delle coordinate in tutti e quattro i quadranti (nell'Enumeratio linearum tertii ordinis del 1668, di cui parleremo più avanti, e nell'Arithmetica universalis, che è del 1673 ma fu pubblicata nel 1707). Quanta confusione e perplessità si siano avute in un primo momento sull'interpretazione da dare alle coordinate negative è bene illustrato dall'immagine completamente arbitraria che si era fatto Descartes del cosiddetto folium x3+y3=3axy per valori negativi di x e y, una curva che dopo tutto prendeva il nome dallo stesso Descartes (fig. 1).
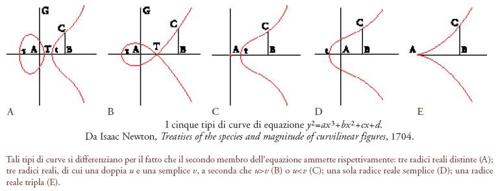
Nell'Enumeratio Newton proseguiva il programma di classificazione già iniziato da Fermat, riducendo le curve rappresentate da equazioni di terzo grado a 78 tipi, ottenuti per proiezione centrale da cinque forme base (fig. 2). Questa ricerca fu pubblicata per la prima volta nel 1704 con il titolo Treatises of the species and magnitude of curvilinear figures, e come appendice dell'Opticks (i tipi di curve di terzo grado considerati sono però soltanto 72). Solamente nel XVIII sec., l'opera conobbe sette ristampe, la prima delle quali vide la luce negli anni 1708-1710 e fu inclusa nel Lexicon technologicum, edito dal segretario della Royal Society di Londra (e ciò contraddice l'opinione, di tanto in tanto riproposta, di una presunta scarsa reazione del mondo scientifico al lavoro di Newton). Mentre i disegni delle curve non giocano un ruolo essenziale nella geometria di Descartes, l'Enumeratio di Newton è un vero e proprio atlante di tutte le possibili forme delle curve di terzo grado.
Newton, stranamente, non riconosceva tutto ciò come geometria. Il suo punto di vista, che limitava il contenuto della geometria (ma non i metodi) a quanto conoscevano già i Greci, sopravvive ancora nel fatto che si riserva la denominazione di 'geometria analitica' a quella parte della geometria delle coordinate che non va oltre le forme del secondo ordine (e dunque, nel piano, oltre le coniche). Di fatto, i seguaci di Newton in Gran Bretagna hanno sviluppato i suoi risultati soprattutto nella direzione che oggi va sotto il nome di 'geometria algebrica' e che, malgrado il nome, è più algebra studiata con l'ausilio di strumenti geometrici che geometria affrontata con strumenti algebrici. James Stirling (1692-1770) pubblicò nel 1717 un libro sulle curve algebriche piane ‒ Lineae tertii ordinis neutonianae ‒, con particolare riguardo a quelle di terzo grado, nel quale tra l'altro riporta i sei tipi tralasciati da Newton. Dal numero dei coefficienti dell'equazione generale di grado n in x e y egli conclude che una tale curva è individuata in generale dal passaggio per n(n+3)/2 punti. Nel 1720 seguiva un testo di Colin Maclaurin (1698-1746) sullo stesso tema ‒ la Geometria organica sive descriptio linearum curvarum universalis ‒, nel quale l'autore osservava che una curva di ordine n e una di ordine m hanno in generale nm punti in comune, chiedendosi poi come mai, visto che questa regola applicata a due curve di terzo grado fornisce nove punti di intersezione, il risultato di Stirling affermasse invece che una curva di terzo grado è univocamente determinata da nove punti. Dopo che Gabriel Cramer (1704-1752) ebbe ripreso questa osservazione nel suo libro ‒ molto influente e autorevole ‒ Introduction à l'analyse des lignes courbes algébriques (1750), questo 'fenomeno' divenne noto con il nome di 'paradosso di Cramer', trovando dopo lunghe discussioni una soluzione definitiva soltanto nel 1828 con la teoria dei sistemi indipendenti di punti di Julius Plücker (1801-1868).
Rappresentazione parametrica di curve e superfici
Prima di abbandonare definitivamente Newton occorre menzionare due suoi notevoli contributi. Come diremmo oggi, egli ragionava da fisico e, pertanto, riteneva che a rigore esistesse una sola variabile effettivamente indipendente, il tempo t. Nei suoi studi di fisica le coordinate x, y di un punto della curva erano perciò date come funzioni del parametro t. L'equazione F(x,y)=0 si otteneva soltanto secondariamente eliminando la variabile t.
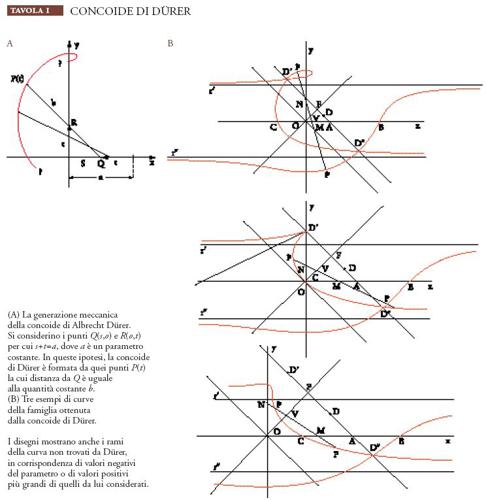
È singolare che ci sia voluto molto tempo prima che i matematici si accorgessero che le rappresentazioni parametriche di tale tipo sono più generali, o si prestano a essere generalizzate, sotto tre aspetti. In primo luogo, una rappresentazione parametrica permette, mediante una restrizione dell'intervallo di variazione del parametro, di restringere lo studio della curva alla parte di questa che di volta in volta interessa o alla parte prodotta, per esempio, con mezzi meccanici, mentre l'equazione di una curva racchiude spesso rami di cui è difficile sospettare, o almeno rivelare, l'esistenza sulla base dei suddetti sistemi meccanici o di altri mezzi (Tav. I). Per esempio, è solo attraverso la rappresentazione algebrica delle sezioni coniche che si è riconosciuto come il cono sia in realtà un doppio cono, e che l'iperbole consta perciò di due rami separati.
In secondo luogo, la descrizione di una curva mediante una rappresentazione nella forma x=f(t), y=g(t) si può estendere senza difficoltà a tre o più coordinate, mentre con le equazioni già una curva dello spazio si può rappresentare solo come intersezione di due superfici, cioè come soluzione di un sistema di più equazioni. Infine, in un'altra direzione, è indispensabile la generalizzazione a due parametri indipendenti che fornisce la rappresentazione parametrica di una superficie, oppure, ancor più in generale, la descrizione di una varietà in uno spazio di dimensione n mediante k parametri indipendenti (k⟨n). Il caso della superficie nello spazio si presentò la prima volta quando si stabilì la corrispondenza tra i punti della superficie terrestre e i punti di una carta geografica mediante 'coordinate geografiche', cioè tramite latitudine e longitudine. Una cartografia matematica generale ha inizio con l'opera di Johann Heinrich Lambert (1728-1777) Anmerkungen und Zusätze zur Entwerfung der Land- und Himmelscharten (Note e complementi per la compilazione di carte della terra e del cielo, 1772). Partendo da esempi concreti Lambert giunse per la prima volta al concetto di carta geografica soggetta unicamente alle condizioni della conservazione degli angoli o delle aree, esprimendo queste condizioni per mezzo di equazioni differenziali. Tuttavia, soltanto nel 1827, con Carl Friedrich Gauss (1777-1855), si giunse all'idea ‒ oggi considerata naturale ‒ di estendere a una superficie qualunque la rappresentazione nella forma x=f(u,v), y=g(u,v), z=h(u,v), mentre ancora nel 1825 lo stesso Gauss lavorava con rappresentazioni del tipo F(x,y,z)=0 o z=f(x,y).
Trasformazioni di coordinate e coordinate non cartesiane
La trasformazione di sistemi di coordinate cartesiane del piano in altri dello stesso tipo si trova in casi particolari già in Johann I Bernoulli e Philippe de La Hire (1640-1718), e in forma più in generale in Leonhard Euler, nel 1748, e in Cramer nel 1750. Bernoulli utilizzò coordinate polari nel 1691, denotando tuttavia con x la coordinata angolare concepita come lunghezza dell'arco, e con y il relativo raggio vettore. Anche Euler, nel 1748, nel capitolo 17 dell'Introductio in analysin infinitorum, rappresentò in coordinate polari curve qualunque e non soltanto le spirali, com'era costume. Nella Methodus fluxionum et serierum infinitarum (del 1671, ma pubblicata nel 1736) Newton considera le coordinate polari del piano e anche quelle bipolari solamente come due 'modi' tra molti sistemi di coordinate piane, e determina le formule di passaggio dalle coordinate cartesiane a questi altri sistemi. Da un punto di vista storico ciò può sembrare un passo indietro. Infatti i 'sintomi' (equazioni locali), per mezzo dei quali i Greci caratterizzavano alcune particolari curve, erano riferiti a sistemi di coordinate utilizzati liberamente e implicitamente, e scelti di volta in volta a seconda del problema, mentre uno dei progressi raggiunti da Descartes consisteva proprio nell'assunzione di un sistema di coordinate fisso, stabilito una volta per tutte. Il ritorno a un concetto più generale di coordinate era però inevitabile, se si voleva applicare il metodo anche alla geometria non euclidea (da intendersi nel senso più lato, per esempio alla geometria intrinseca delle superfici curve), come si cominciò effettivamente a fare verso la fine del XVIII secolo. Newton, inoltre, con le formule di trasformazione delle coordinate aveva lasciato alle generazioni successive uno strumento paradigmatico: si utilizzino le coordinate più convenienti per il problema, quelle che permettono di descrivere nel modo più semplice l'oggetto geometrico in questione, e per lavorare ulteriormente sul problema si passi quindi, utilizzando l'algoritmo universale di conversione, a una rappresentazione alla quale siano applicabili altri strumenti come, per esempio, il calcolo differenziale e integrale. L'analogia con quanto accade in informatica è evidente: si formula un problema nel linguaggio più comodo per l'utente del computer, lasciando poi al compilatore il compito di tradurlo in un linguaggio che il computer comprende o in quello utilizzato dal software a disposizione.
Geometria cartesiana tridimensionale
È quasi impossibile, oggi, capire il perché del ritardo e delle esitazioni che hanno accompagnato il passaggio dalle coordinate nel piano a quelle nello spazio. In Descartes e Fermat si trovano soltanto brevi e vaghi cenni in proposito, che non lasciano intravedere alcun particolare interesse per la geometria dello spazio. La Hire descrive nel 1679, nei Nouveaux élémens des sections coniques, il luogo di un punto P dello spazio per mezzo della lunghezza del segmento di perpendicolare condotta da P a un piano e delle coordinate del piede della perpendicolare in questo piano, ma il modo in cui è situato il sistema di coordinate è tale che i punti che lo interessano giacciono tutti da una stessa parte del piano. Pioniere di una geometria generale cartesiana tridimensionale fu il francese Antoine Parent (1666-1716), oggi quasi dimenticato. Tra il 1700 e il 1713 egli descrisse l'elica e altre curve dello spazio, come pure le superfici sferiche, coniche e cilindriche, nel modo oggi usuale, cioè mediante tre coordinate cartesiane, anche se considerava soltanto le coordinate positive. Ritrovò inoltre ‒ dopo Christopher Wren (1632-1723) ‒ le rette generatrici dell'iperboloide a una falda. Parent non sembra avere problemi a esprimere la distanza tra due punti in termini delle loro coordinate nello spazio; se ne può dedurre che questo modo di esprimere la distanza era già noto, anche se non ve ne è traccia nella letteratura del tempo. Julian Lowell Coolidge, dalle ricerche metodologicamente avanzate ma di scarso contenuto di Parent trae la conclusione ‒ nella sua A history of geometrical methods (1940) ‒ che a quel tempo dovevano già esistere molti lavori di geometria analitica tridimensionale, oggi non più reperibili. Tra i matematici più famosi, tuttavia, nessuno parla di geometria analitica dello spazio prima del 1715, anno in cui Johann I Bernoulli scrive a Leibniz: "I punti di una superficie curva come quelli di una curva sghemba sono individuati da tre coordinate x,y,z le cui mutue relazioni sono espresse da certe equazioni. Queste tre coordinate altro non sono che le perpendicolari condotte dal dato punto a tre piani mutuamente ortogonali e che si trovano in una data posizione dello spazio" (Opera, III, p. 938).
Joseph-Louis Lagrange (1736-1813) utilizzò le coordinate polari dello spazio r, φ e λ (vale a dire le "coordinate geografiche" a distanza r dall'origine), ma prendendo, invece della latitudine, la distanza dal polo, cosa che accentua l'analogia tra le coordinate sferiche e quelle piane. Anche gli angoli introdotti in meccanica da Euler nel 1776 per descrivere il moto dei corpi rigidi si possono considerare una sorta di coordinate polari dello spazio. La variante più utile per i calcoli, quella dei tre coseni direttori degli angoli α, β, γ, tre quantità non più indipendenti ma legate dalla relazione cos2α+cos2β+cos2γ=1, si trova per la prima volta alla fine del XVIII sec. in Gaspard Monge (1746-1818).
Origini della geometria differenziale
Abbiamo cercato fin qui di tenere il più possibile separati dal calcolo infinitesimale gli aspetti geometrici e algebrici del metodo cartesiano. È quanto avevano cercato di fare Descartes, Christiaan Huygens (1629-1695), Ehrenfried Walther von Tschirnhaus (1651-1708) e pochi altri che si opponevano ai metodi infinitesimali senza tuttavia riuscire a imporsi, tanto più che il metodo così fecondo introdotto da Newton, per trattare gli infinitesimi utilizzando serie infinite, aveva abolito nella coscienza di molti matematici dell'epoca la separazione tra soluzioni algebriche e soluzioni analitiche. Newton aveva definito il centro di curvatura di una curva piana come punto d'intersezione di normali alla curva infinitamente vicine, e proposto formule per il raggio di curvatura e per il suo reciproco, la curvatura. Il fatto che il cerchio osculatore, tra tutti i cerchi che in un dato punto hanno la tangente in comune con la curva, sia quello che approssima meglio quest'ultima, non aveva per Newton bisogno di dimostrazione. Il calcolo differenziale e quello integrale permettevano di risolvere, spesso in modo elegante, problemi riguardanti la direzione di tangenti, la curvatura, la lunghezza di archi, il volume della superficie generata, ecc., per intere classi di curve e anche per molte curve particolari da poco scoperte. Denis Diderot (1713-1784), il letterato, redattore dal 1751, della grande Encyclopédie francese, è un esempio di quanto fosse diffuso nel XVIII sec., anche in ambienti intellettuali di non professionisti della matematica, l'interesse per la geometria e soprattutto per le nuove curve. Nel 1748 egli dimostrò, in un piccolo scritto a carattere divulgativo dal titolo Examen de la dévelopante du cercle, che mediante un'evolvente del cerchio (costruita in modo concreto e molto espressivo con un filo) si può tagliare un angolo o arco di cerchio in un qualunque rapporto razionale, si può quadrare un settore circolare e anche rettificare l'evolvente stessa. Ma in generale, per quanto riguarda l'interesse per le curve nel XVIII sec., vale ancora quanto scrisse Immanuel Kant a proposito dei matematici dell'Antichità: "È una vera gioia considerare lo zelo con il quale gli antichi geometri indagavano queste proprietà delle linee di tale tipo [le sezioni coniche] senza lasciarsi sconcertare dalla domanda di menti ristrette: a che dovrebbe poi servire questa conoscenza?" (Wieleitner 1908, p. 1).
I problemi sulle curve piane dei quali oggi si occupano l'analisi o la geometria differenziale, e non tanto quelli più generali quanto invece i numerosi problemi particolari, avevano prodotto nel tempo una mole enorme di materiale, tanto che il trattamento generale e geometrico-differenziale di curve sghembe e superfici curve ebbe inizio lentamente e con difficoltà. Lo studio delle superfici curve ha preceduto storicamente quello delle curve sghembe, e ciò per due motivi. Per cominciare, nel XVIII sec. erano in primo piano nella matematica applicata i problemi posti dalla geodesia e dalla cartografia. I problemi della meccanica dell'epoca, come la traiettoria di una massa puntiforme sotto l'effetto della forza di gravità, il moto del pendolo, la brachistocrona o la catenaria portavano quasi sempre alla considerazione di curve piane. Le curve sghembe compaiono invece, nel quadro di problemi pratici, innanzitutto come linee su una superficie curva: nella determinazione della via più breve tra due punti della superficie, come lossodromiche (il percorso di una nave che forma un angolo costante con i meridiani terrestri), o come controimmagini di curve semplici disegnate su una carta. L'altro motivo è che queste curve, dette anche 'a doppia curvatura', potevano all'inizio essere descritte soltanto come intersezione di due superfici curve. Il concetto di 'curvatura doppia' (double courbure) compare per la prima volta nel 1724 in Henri Pitot (1695-1771). Non si tratta però della 'seconda curvatura', cioè della torsione, ma soltanto del fatto che una curva nello spazio viene descritta mediante le proiezioni su due piani ortogonali, proiezioni che sono curve piane con una propria curvatura nel senso ordinario. Con la doppia curvatura così intesa comincia anche il primo libro dedicato alle curve sghembe, Recherches sur les courbes à double courbure, presentato all'Académie Royale des Sciences di Parigi nel 1729 dall'allora soltanto sedicenne Alexis-Claude Clairaut (1713-1765), e pubblicato nel 1731. Dopo un'accurata, anche se elementare, introduzione alla rappresentazione analitica delle superfici (sfera, cono circolare, superfici di rotazione generate da curve piane qualunque, coni aventi per base una qualsiasi curva chiusa) Clairaut passa alla descrizione analitica di una curva sghemba utilizzando un sistema di due equazioni, la prima delle quali descrive la superficie mediante la curva che giace perpendicolarmente nel piano x−y, mentre la seconda fornisce la dipendenza della coordinata z dalla y, e quindi rappresenta l'analoga curva nel piano y−z. Soltanto nella seconda parte del libro comincia l'"usage du calcul differentiel". Anche nel titolo di questo agile volumetto, all'epoca molto apprezzato, si fa riferimento alla doppia curvatura, sebbene vi si parli solamente del primo quoziente differenziale, e non siano trattati, né potevano esserlo, problemi relativi alla torsione.
I manuali di Euler, di Cramer e di Maria Gaetana Agnesi
Già tra il XVII e il XVIII sec. Guillaume-François-Antoine de L'Hôpital (1661-1704) aveva esposto in due manuali, Analyse des infiniment petits (1696) e Traité analytique des sections coniques (postumo, 1720), tutti i risultati di Leibniz, Bernoulli e dei loro collaboratori. In questi manuali, tuttavia, il metodo delle coordinate entra soltanto occasionalmente come strumento dell'analisi. Anche negli articoli dell'Encyclopédie curati da Jean-Baptiste Le Rond d'Alembert (1717-1783) che riguardano la matematica e che sono spesso molto dettagliati, il metodo delle coordinate è trattato sbrigativamente come una delle possibilità di applicazione dell'algebra alla geometria. Alla voce Coordonnées si dice soltanto che si tratta di una denominazione che comprende le ascisse e le ordinate dei punti di una curva, e che non devono necessariamente formare un angolo retto. Alla voce Surface si afferma però che una superficie è data da un'equazione nella quale intervengono le tre coordinate mutuamente ortogonali x, y e z. Nei lavori ingegnosi di Diderot, di Giovanni Francesco Castillon (1704-1791) e di molti altri geometri non professionisti, il metodo delle coordinate non gioca in generale alcun ruolo.
L'organizzazione del metodo delle coordinate dello spazio euclideo a due e tre dimensioni in una teoria unitaria, che per la prima volta vede uniti metodi e risultati dei matematici della Gran Bretagna e dell'Europa continentale, è dovuta soprattutto a Euler. Il secondo volume della sua Introductio in analysin infinitorum è il primo vero manuale europeo di geometria cartesiana. Le applicazioni alla matematica infinitesimale, che indubbiamente anche per Euler costituivano un argomento di importanza centrale, si trovano però soltanto nelle sue opere successive (due volumi sul calcolo differenziale e tre su quello integrale). La parte principale della Theoria linearum curvarum (così recita il sottotitolo del secondo volume dell'Introductio) riguarda la nuova ricerca con tecniche algebriche sulle curve di secondo e terzo grado e la loro classificazione, con estensione alle curve di quarto grado. Euler distingue 146 tipi di curve e sottolinea, a questo proposito, che la classificazione di curve secondo il grado dell'equazione algebrica che le rappresenta ha un significato geometrico, perché il grado non varia per una trasformazione lineare delle coordinate, anche oblique. Egli introduce inoltre quella che oggi si chiama 'trasformazione delle coniche secondo gli assi principali'. Negli ultimi capitoli definisce i diversi gradi di contatto tra curve piane e, in particolare, i cerchi tangenti (osculatori), la curvatura e il centro di curvatura, il tutto senza ancora utilizzare esplicitamente il calcolo differenziale. Eppure in Euler la geometria piana mantiene una posizione di privilegio: della rappresentazione delle superfici dello spazio per mezzo di coordinate (con riferimenti ed elogi a Clairaut) si parla infatti soltanto in un'appendice di 78 pagine; essa dapprima riassume alcuni fatti fondamentali, per poi trattare le superfici del secondo ordine in analogia con le curve del secondo ordine, e in particolare la loro classificazione completa e la trasformazione a 'forma normale' che permette di stabilire a quale tipo (ellissoide a due o tre assi, iperboloide a una o due falde, ecc.) una data superficie appartenga.
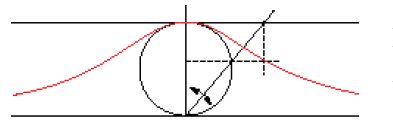
Appena due anni dopo, nel 1750, usciva a Ginevra la già citata Introduction à l'analyse des lignes courbes algébriques di Cramer, un autore che conosceva personalmente quasi tutti i matematici importanti del suo tempo e che aveva tra l'altro curato la pubblicazione delle opere complete di Johann I e Jakob I Bernoulli, come pure il carteggio di quest'ultimo con Leibniz. Nella detta opera di Cramer si trova la prima presentazione sistematica di quanto avevano pubblicato originariamente i Bernoulli, Maclaurin ed Euler, il paradosso di Stirling-Maclaurin (noto poi come 'paradosso di Cramer'), trasformazioni di coordinate e punti notevoli di curve piane, come punti di flesso, cuspidi e punti multipli. Stranamente anche Cramer si muove tra questo materiale senza utilizzare esplicitamente il calcolo differenziale, con il quale peraltro aveva grande familiarità. Nella prefazione egli scrive di aver scoperto e apprezzato l'Introductio di Euler, che per molti versi è molto simile alla sua Introduction, soltanto dopo aver completato il proprio manoscritto. Occorre aggiungere tuttavia che Cramer intendeva soprattutto scrivere un manuale che fosse di più facile lettura di quello di Euler, che tra l'altro era scritto in latino. Quasi contemporaneamente, nel 1749, usciva in italiano un manuale di matematica in due volumi, che fu molto apprezzato sia dal punto di vista dell'organizzazione del materiale sia da quello didattico, tanto da essere subito tradotto in francese, nello stesso anno, e ancora nel 1801 in inglese. L'autrice, Maria Gaetana Agnesi (1718-1799), figlia di un professore di matematica dell'Università di Bologna, fu la prima donna in Europa a entrare nella ristretta cerchia dei matematici famosi del tempo. Il primo volume delle sue Instituzioni analitiche ad uso della gioventù italiana è dedicato alla matematica elementare (nel senso di matematica non infinitesimale) e comprende anche il metodo delle coordinate. Il secondo riguarda il calcolo differenziale e integrale. Alla Agnesi si devono molti contributi originali, ma il suo nome è legato soprattutto a una curva particolare, la "versiera" (fig. 4), che però prima di lei già Fermat e, nel 1717, Guido Grandi (1671-1742) avevano studiato.
Concetto di curva e modo di generarla
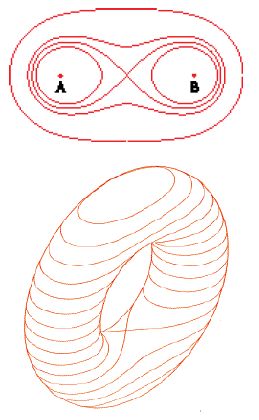
è stato dimostrato in modo convincente che Descartes non possedeva un'idea precisa di come definire una curva in modo da poterla considerare un oggetto geometrico legittimo. L'oscillazione tra i diversi modi di concepire una curva (come immagine geometrica di un'equazione algebrica; come prodotta da un mezzo meccanico o da un movimento; oppure definita da una costruzione per punti) ha attraversato tutto il Settecento, causando una notevole confusione e non permettendo di arrivare a un concetto generale di curva o di funzione. Le tre concezioni prima elencate non soltanto portano a gerarchie e principî di classificazione tra loro diversi, ma soprattutto producono classi di curve non confrontabili. Si trovano già in Descartes, ma anche in Maclaurin e altri, contributi sempre nuovi, nella direzione di una diversa classificazione delle curve piane nella quale le curve di classe n+1 si possano ottenere in modo puramente geometrico da quelle di classe n. Per esempio, Maclaurin scoprì nel 1720 il seguente risultato, in seguito attribuito a Jakob Steiner (1796-1863), che permette di costruire una conica: se due angoli si muovono in modo che il punto d'intersezione di un lato dell'uno con uno dell'altro scorra su una retta, il punto d'intersezione degli altri due lati descrive una conica. Seguì una profusione di nuovi metodi per generare singole curve o intere famiglie. Descartes ed Ehrenfried Walther von Tschirnhaus, suo seguace, considerarono una generalizzazione del 'metodo del giardiniere' di costruzione dell'ellisse per generare, mediante un filo, curve con più di due fuochi. Louis Carré (1663-1711) nel 1705 e Castillon nel 1740 si interessarono alla generalizzazione delle curve descritte da un punto appartenente a un oggetto che rotola, scoprendo in particolare interessanti proprietà della cardioide. Guido Grandi fece conoscere in due articoli (1723 e 1728) fasci di curve nel piano e sulla superficie della sfera, a cui diede nomi di fiori: rodonee (dal greco ϱ̔όδον, 'rosa') nel piano, e clelie (in onore della contessa Clelia Borromeo) sulla sfera. Huygens aveva scoperto nel 1659 il principio generale evolvente-evoluta sul problema concreto di determinare il moto di un pendolo di orologio in modo che fosse isocrono (ossia tale che il periodo di oscillazione fosse indipendente dall'ampiezza): il peso deve percorrere un arco di cicloide avendo l'evoluta della curva, anch'essa una cicloide, come guida. Si deve a Maclaurin il metodo per determinare la curva podaria di una curva. Entrambi questi risultati stimolarono nella seconda metà dell'Ottocento la ricerca, allora in primo piano, di metodi per costruire, a partire da superfici con date proprietà di curvatura, altre superfici dello stesso tipo (Bour, Ribaucour, Bianchi, Bäcklund, Lie, ecc.). Gian Domenico Cassini (1625-1712) generalizzò nel 1694 la lemniscata di Jakob I Bernoulli a curve ottenute come sezioni della superficie di un toro con piani paralleli all'asse ('ovali di Cassini'), sottolineando che si trattava di casi particolari di curve già note nell'Antichità come 'spiriche di Perseo' (fig. 5).
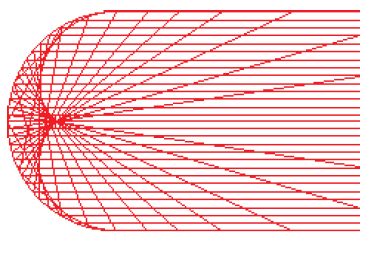
Si cercarono occasionalmente anche applicazioni di queste nuove curve. Cassini vedeva, per esempio, le sue ovali come possibili orbite astronomiche. Tschirnhaus si interessava alle evolute come curve catacaustiche (inviluppi dei raggi riflessi da uno specchio curvo, fig. 6), deducendo in modo affrettato ed erroneo dall'approssimativa costruzione per punti che l'evoluta di un arco di cerchio per raggi incidenti paralleli consta di due archi di cerchio.
Geometria differenziale delle curve
La strada per una geometria differenziale delle curve effettivamente tridimensionale, cioè delle curve non pensate come appartenenti a una superficie, fu aperta da Monge negli anni 1769-1771 (i suoi lavori, con tutti i particolari, furono però pubblicati più tardi, nel 1785, per cui spesso la sua priorità in materia non è riconosciuta). Egli si esprimeva in modo intuitivo e didatticamente molto efficace. In ogni punto P della curva, la tangente determina un piano normale per P a essa ortogonale. Due piani normali infinitamente vicini si intersecano in generale (cioè quando la curva non è una retta) in una retta, che a sua volta ha come piano normale in P il piano osculatore della curva. La velocità di variazione dell'inclinazione di questo piano osculatore è la torsione della curva in P. La direzione della tangente, la normale principale nel piano osculatore a essa ortogonale e la retta normale al piano osculatore (binormale) formano il sistema locale di coordinate della curva nel punto P. La prima curvatura è relativa al piano osculatore, nel quale la curva è infinitamente vicina a una curva piana, ed è in questo piano che si considerano il centro e il raggio di curvatura, e la curvatura come reciproco del raggio. I punti di flesso vengono caratterizzati da Monge come quelli nei quali la curvatura è nulla. Egli non parla ancora esplicitamente di torsione, ma è chiaro che egli considera la variazione dell'inclinazione del piano osculatore come misura di una seconda curvatura. Ulteriori precisazioni, e in una terminologia più vicina a quella attuale, si ebbero soltanto nel 1806 a opera di Michel-Ange Lancret (1774-1807), uno studente di Monge.
Geometria differenziale delle superfici
Come abbiamo già osservato, la geometria differenziale delle superfici nasce da problemi di geodesia e di cartografia. Il concetto di piano tangente a una sfera risale all'astronomia e alla cartografia dell'Antichità. Equazioni per piani tangenti a una superficie a partire dall'equazione di questa furono determinate in casi semplici già nel 1715 da Parent. Egli fa muovere piani secanti in una data direzione finché l'intersezione non degenera in un punto (o, nel caso di un cono, in una retta). Il problema della curva più breve tra due punti su una superficie curva fu formulato da Johann I Bernoulli già nel 1697. È interessante il fatto che egli si limitava a superfici convesse, immaginando evidentemente che altrimenti il percorso più breve avrebbe potuto passare in qualche punto per lo spazio circostante. Sebbene anche Leibniz avesse discusso a lungo con i fratelli Bernoulli di questo problema, formulazioni in termini di equazioni differenziali si ebbero soltanto nel 1728 a opera di Johann I Bernoulli e di Euler con De linea brevissima in superficie quacumque, in cui Euler risolse il problema impostandolo come problema di calcolo differenziale, trasformando la disuguaglianza triangolare fra tre punti vicini in un'equazione differenziale. Nel 1732 egli formulò per la prima volta il problema come caso particolare del problema generale del calcolo delle variazioni: trovare, in un insieme di curve o di funzioni caratterizzate da particolari condizioni, quella che massimizza o minimizza una certa quantità. Negli anni 1735-1737 l'Académie di Parigi organizzò in grande stile due spedizioni, una in Lapponia e una nell'America Meridionale, allo scopo di confermare (e in tal caso misurare) o smentire lo schiacciamento della Terra al Polo Nord e all'equatore, e ciò mediante la misurazione della curvatura della meridiana. Clairaut, che partecipava alla spedizione in Lapponia, applicò in quel contesto i metodi di Euler, in particolare alle superfici di rotazione, dimostrando tra l'altro che su una tale superficie le curve geodetiche, cioè le più brevi, sono caratterizzate dal fatto che il prodotto del raggio del parallelo di latitudine e il seno dell'angolo tra la tangente alla curva e il meridiano è in ogni punto costante. Nei suoi due volumi sul calcolo differenziale del 1775 e in numerosi articoli dell'anno successivo, Euler diede alla teoria delle superfici un indirizzo più generale: in ogni punto P di una superficie liscia, ogni piano passante per la normale alla superficie taglia la superficie secondo una curva piana, il cui raggio di curvatura R è perciò una funzione di P e della direzione di questa curva, espressa da un angolo φ. La curvatura è quindi dotata di segno, a seconda della parte della superficie in cui si trova il centro di curvatura della curva. Euler stabilì che questa funzione R(P,φ) assume il valore massimo R (sempre positivo) e minimo r (eventualmente negativo) in due direzioni tra loro ortogonali, e che per ogni fissato φ essa è determinata dall'equazione:
Conoscendo i due raggi di curvatura principali R e r si può calcolare la curvatura in ogni direzione. Soltanto nel 1813 fu introdotta, da Charles Dupin (1784-1873), quella che egli chiamò "indicatrice": sostituendo R(φ) con
la [1] si scrive in una forma più chiara. Riportando nel piano tangente in P i valori di
nelle varie direzioni si ottiene, se la curvatura gaussiana è positiva, un'ellisse, e se è negativa una coppia di iperboli con gli stessi asintoti. Jean-Baptiste Meusnier (1754-1793) e Monge si dedicarono subito alla [1]. Monge studiò nel 1784 le curve sulla superficie che, in ogni punto, hanno la direzione della massima (o rispettivamente minima) curvatura e stabilì che si determinano due fasci di curve che si tagliano ortogonalmente in ogni punto della curva. Il contributo di Meusnier del 1776 (pubblicato però nel 1785) va in un'altra direzione: per il problema variazionale posto da Lagrange nel 1760, e cioè determinare la superficie minima avente un assegnato contorno sghembo semplice chiuso, egli trovò come condizione necessaria che in una tale superficie minima le curvature principali devono soddisfare la condizione R=−r (come si osservò più tardi, ciò ha anche la conseguenza che la curvatura gaussiana deve essere ovunque negativa). Come primi esempi non banali di queste superfici Meusnier trovò la catenoide, ottenuta per rotazione di una catenaria, e la superficie elicoidale.
Dopo il già menzionato volumetto Anmerkungen und Zusätze zur Entwerfung der Land- und Himmelscharten di Johann Heinrich Lambert, si sviluppò presto una cartografia improntata alla geometria differenziale. Euler scrisse nel 1777 tre articoli dedicati all'argomento per i "Commentarii" dell'Academia Scientiarum Imperialis Petropolitana. Il primo cominciava con la seguente dichiarazione: "In questo lavoro le proiezioni che io considero non sono soltanto quelle dell'ottica, per mezzo delle quali i vari punti di una superficie sferica vengono rappresentati su un piano così come appaiono ad un osservatore che si trova in un determinato punto […]; con la parola 'rappresentazione' io intendo invece più in generale una qualunque legge che faccia corrispondere ad ogni punto della sfera un ben determinato punto del piano, e viceversa" (Drei Abhandlungen über Kartenprojection, ed. Wangerin, p. 1).
Euler caratterizza poi, come già aveva fatto Lambert, le proprietà di conservazione dell'area e della "similitudine nelle parti più piccole" (cioè la conservazione degli angoli; il concetto di 'rappresentazione conforme' fu coniato soltanto più tardi da Gauss) per mezzo di equazioni differenziali alle derivate parziali, dando la soluzione generale del problema della rappresentazione conforme della superficie sferica sul piano. Nel 1779 Lagrange estese questo risultato a una qualunque superficie di rotazione.
Concludendo, vogliamo ricordare che fino alla fine del periodo preso in esame le superfici sono sempre state considerate oggetti dello spazio a tre dimensioni e, di conseguenza, descritte mediante tre coordinate. A una 'geometria intrinseca' delle superfici, suggerita dalla geodesia, si arriverà solamente con Gauss a partire dal 1828.
Il problema delle parallele
Il problema della dimostrabilità, a partire dagli altri assiomi, del quinto postulato di Euclide (in sostanza l'affermazione dell'unicità della retta parallela a una retta assegnata e passante per un dato punto), o più precisamente se questo postulato si potesse invece considerare 'evidente', problema già discusso nell'Antichità, si ripropose in Europa soprattutto attraverso l'edizione di Euclide del 1574 a opera di Cristoforo Clavio (1538-1612). Egli non parla soltanto degli sforzi fatti in proposito dai matematici dell'Antichità, ma affronta anche il problema dimostrando il quinto postulato sotto l'ipotesi che una linea che ha distanza costante da una retta è essa stessa una retta. Anche dopo Clavio, ci si dedicò alla questione, soprattutto da parte di gesuiti (gli Elementi di Euclide rivestivano infatti un ruolo notevole nella loro formazione). Tra gli altri si ricordano Pietro Antonio Cataldi nel 1603, Paul Guldin nel 1641, Giovanni Alfonso Borelli nel 1658, Giordano da Bitonto nel 1680 e Girolamo Saccheri nel 1733.
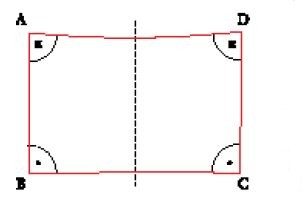
Il titolo del voluminoso scritto di Saccheri pubblicato nel 1733, anno della sua morte, Euclides ab omni naevo vindicatus, si riferisce al fatto che Sir Henry Savile (1549-1622), professore di matematica a Oxford, aveva definito naevi (cioè "nei") il problema delle parallele e alcuni punti non molto chiari della teoria delle proporzioni e aveva istituito sempre a Oxford una cattedra, con l'obbligo di non insegnare più gli Elementi ma di occuparsi invece soprattutto di questi naevi. Saccheri introdusse la figura, oggi nota come 'quadrilatero di Saccheri', nella quale AB=CD e gli angoli in B e in C sono retti (fig. 7). Per l'angolo α vi sono tre possibilità: acuto, ottuso o retto. Saccheri dimostrò, correttamente, che l'ultimo caso è equivalente al postulato delle parallele (si riconosce subito il rapporto con l'ipotesi di Clavio, che le curve a distanza costante da una retta sono rette). Il secondo caso si verifica sulla superficie di una sfera, ma ovviamente non nel piano euclideo. Saccheri fece due tentativi, mal riusciti, di dimostrare che l'ipotesi dell'angolo acuto portava a una contraddizione, ma scoprì in tal modo una serie di teoremi di quella che sarà poi chiamata 'geometria assoluta'. Questa consta dei teoremi che valgono sia nella geometria euclidea sia in quella non euclidea, che sono cioè indipendenti dall'accettare o meno il postulato delle parallele. Tra le altre cose si trova già in Saccheri il teorema, noto più tardi come 'teorema di Legendre' da Adrien-Marie Legendre (1752-1833), secondo il quale, indipendentemente dall'assioma delle parallele, la somma degli angoli di un triangolo non può superare 180°; l'assioma delle parallele segue come teorema se anche in un solo triangolo la somma degli angoli è uguale a 180°.
Alla fine del XIX sec., i matematici tedeschi Friedrich Engel (1861-1941) e Paul Stäckel (1862-1919) hanno il grande merito di portare all'attenzione generale la lunga preistoria, largamente dimenticata, di quella geometria non euclidea che è finalmente riconosciuta. Essi riportarono alla luce gli scritti più importanti di Wallis, di Saccheri soprattutto, e di Lambert; scritti che furono resi accessibili in traduzione al pubblico tedesco nel 1895. La bibliografia curata da Engel e Stäckel nel 1895 sul problema delle parallele copre gli anni che vanno dal 1680 al 1800 e contiene oltre 80 voci (che però si distribuiscono molto irregolarmente lungo il periodo, addensandosi verso la fine). Vi si trovano gli autori menzionati, ma non, per esempio, i manoscritti di Euler sull'argomento, allora ancora sconosciuti.
Un considerevole studio preliminare fu la tesi di dottorato di Georg Simon Klügel (1739-1812) sulla storia del problema delle parallele, redatta sotto la direzione di Abraham Gotthelf Kästner (1719-1800), del quale Gauss fu allievo all'università. Il lavoro più importante, quello di Lambert del 1766 (pubblicato postumo nel 1786), non era ancora stato scritto, mentre Lambert non soltanto aveva letto lo studio di Klügel, ma fu probabilmente a causa di questo che s'interessò al problema.
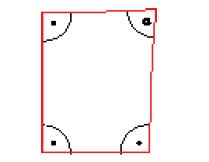
Lambert richiama l'attenzione su una figura simile a quella di Saccheri, ma più semplice (fig. 8). Anche qui si dimostra che l'ipotesi che l'angolo α sia ottuso è incompatibile con gli altri assiomi euclidei, mentre è soddisfatta sulla sfera, e che l'ipotesi che α sia retto è equivalente al postulato delle parallele. Anche Lambert cerca in vari modi di ricavare una contraddizione dall'ipotesi dell'angolo acuto, ma a differenza dei suoi predecessori non si accontenta dei risultati. Spinge le conseguenze di questa ipotesi fino a riconoscere che l'area di un triangolo deve allora essere proporzionale alla differenza tra la somma degli angoli e 180° (il cosiddetto 'difetto del triangolo') e confronta questo fatto con quello secondo il quale, sulla sfera, l'area di un triangolo è uguale al quadrato del raggio moltiplicato per l'eccesso sferico (l'eccedenza della somma degli angoli rispetto a 180°). Successivamente scrive: "Ne dovrei concludere che la terza ipotesi si verifica su una sfera immaginaria [cioè prendendo il raggio r della sfera puramente immaginario, di modo che r2 risulti negativo e compensando il cambiamento di segno tra eccesso e difetto]. Deve pur esserci un motivo perché essa [l'ipotesi degli angoli acuti] non si riesca da tempo ad invalidarla così facilmente, come invece è accaduto con la seconda [ipotesi degli angoli ottusi]" (Engel 1895, p. 203).
Con l'osservazione sulla validità dell'ipotesi degli angoli acuti sulla superficie di una sfera di raggio immaginario, Lambert era arrivato più vicino a concepire la geometria non euclidea di quanto non abbiano fatto Janos Bolyai (1802-1860) e Nikolaj Ivanovič Lobačevskij (1792-1856), che oggi sono ritenuti esserne stati i fondatori. Essi invece, contrariamente a Lambert, non avevano da offrire altro che conseguenze più o meno profondamente elaborate della negazione del postulato delle parallele, assieme all'intima convinzione che questa teoria non presentava contraddizioni logiche, ma urtava soltanto contro l'esperienza comune e soprattutto contro radicati pregiudizi. Lambert avrebbe invece fornito un modello per questa teoria qualora fosse stato assolutamente sicuro del fatto suo, ed è chiaro che non lo era, perché limitò i suoi sforzi a cercare una contraddizione, lasciando il tutto inedito. Johann III Bernoulli (1774-1807) pubblicò nel 1786 il manoscritto, come prima di una serie di opere postume di Lambert, sul "Magazin für Reine und Angewandte Mathematik", da poco fondato. La pubblicazione non destò apparentemente alcuna attenzione e finì completamente dimenticata nel successivo sviluppo della questione. Il curatore del "Magazin", Carl Friedrich Hindenburg (1741-1808), fece da parte sua un commento in questi termini:
L'esperienza mi ha insegnato che non bisogna credere a ciò che si dice a proposito della dimostrazione del postulato di Euclide, e cioè che essa si può portare avanti fino ad un punto tale che ciò che rimane da dimostrare è evidente, e che ad una sua dimostrazione si può provvedere volendo in un secondo tempo. Se quanto resta da dimostrare sembra infatti all'inizio poca cosa, quando lo si affronta rigorosamente ci si accorge che si tratta invece proprio della cosa fondamentale; in generale essa presuppone il teorema o una sua forma logicamente equivalente. (Engel 1895, p. 143)
Le parole di Hindenburg lasciano indovinare il travaglio psicologico di chi si occupava di questi problemi, impensabile prima dell'Ottocento. Nel 1741 Clairaut aveva scritto negli Éléments de géométrie: "Ogni ragionamento a proposito di qualcosa che si può stabilire già con il buon senso è oggi del tutto inutile, serve solo a oscurare la verità e a far passare la voglia a chi legge" (p. X).
Molti matematici del XVIII sec., che lavoravano in sintonia con lo spirito del tempo, si spinsero fino ad affermare che il problema delle parallele era un divertimento per dilettanti, profani e gente stravagante. Uno sguardo più attento alla delicata battaglia condotta da questi 'strani' personaggi mostra invece che c'è qualcosa di fondamentalmente nuovo che viene alla luce, e cioè una comprensione più profonda dell'essenza della dimostrazione matematica, che, soltanto verso la fine del XIX sec., portò al riconoscimento del carattere formale della matematica, alla chiarificazione delle nozioni di sistema di assiomi, teoria, struttura, modello, conseguenza, indipendenza, ecc., e anche allora in modo incompleto e non da tutti ben capito. Citiamo ancora Lambert, che come logico ed epistemologo vide più lontano dei suoi contemporanei:
E poiché il postulato di Euclide e gli altri assiomi sono enunciati in parole, si può e si deve pretendere che in nessun punto della dimostrazione si faccia ricorso al tema in questione, ma che la dimostrazione venga condotta se possibile in modo completamente simbolico. In questo senso i postulati di Euclide sono come altrettante equazioni algebriche, che vogliamo risolvere rispetto a x,y e z, senza preoccuparci del problema in discussione. (Engel 1895, p. 162)