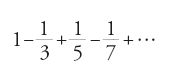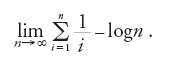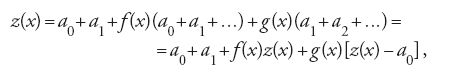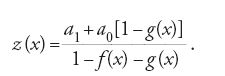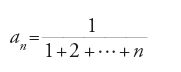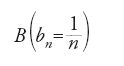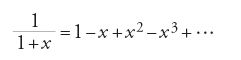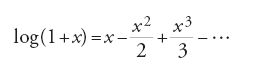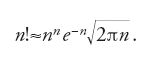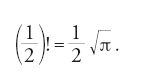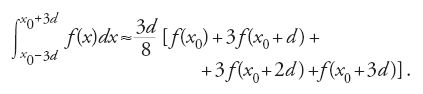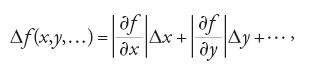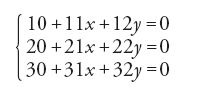L'Età dei Lumi: matematica. I metodi numerici

L'Eta dei Lumi: matematica. I metodi numerici

I metodi numerici

Il XVII sec. è stato in generale un 'secolo geometrico'. A parte alcune considerazioni di carattere puramente numerico, le grandezze erano rappresentate come grandezze geometriche e le operazioni su di esse erano effettuate mediante costruzioni, a volte anche solo concettuali. Per questo motivo occupano una posizione dominante, come precursori del futuro concetto aritmetico-algebrico di funzione e di numero, i concetti di punto, curva e superficie. Nel XVII sec. l'odierna funzione reale di una o più variabili era una curva o una superficie e questo punto di vista si riflette nella terminologia, in modo particolare in Inghilterra fino al XVIII sec. inoltrato. James Stirling (1692-1770) chiama y=P(x) "curva di tipo parabolico", in riferimento all'ordinaria parabola y=ax²+bx+c, per distinguerla dalle curve del tipo yⁿ=P(x) o P(x,y)=0, che in generale non si lasciano esprimere come funzioni univoche di x. Newton scrive nella Methodus differentialis: "Trovare l'area approssimata di una curva qualunque" (The mathematical works, II, p. 172) e descrive il problema dell'interpolazione con le seguenti parole: "Dato un numero qualsivoglia di punti, descrivere una curva che passi per questi punti" (The mathematical papers, IV, p. 61). Questa tradizione non impedisce però che nell'analisi numerica del XVIII sec. si sviluppino algoritmi che hanno come risultato numeri o funzioni. Nei problemi per i quali il risultato può essere espresso esattamente rispetto a un dato sistema di notazioni, questi algoritmi permettono di distinguere tra quelli nei quali si vuole determinare, per esempio, un numero intero o un numero razionale e quelli nei quali si richiede un risultato approssimato, eventualmente prescrivendo il grado di precisione.

Il concetto di funzione compare per la prima volta, e con un significato geometrico-operazionale ancora piuttosto oscuro, in una delle prime memorie di Gottfried Wilhelm Leibniz (1646-1716) del 1673, Methodus tangentium inversa, seu de functionibus, e va via via precisandosi nella corrispondenza tra Leibniz e i fratelli Bernoulli, Jakob I (1654-1705) e Johann I (1667-1748), negli anni Novanta del Seicento. Nel 1718 Johann Bernoulli ne dà la prima 'definizione': "Si dice funzione di una quantità variabile una quantità costituita in un modo qualunque a partire da questa variabile e da costanti" (Opera, II, p. 241). Una definizione che tende già a dare del concetto di funzione un'interpretazione 'sintattica', che avrà una grande influenza sulla forma che assumerà in seguito l'analisi numerica. Questo punto di vista si consoliderà con Leonhard Euler (1707-1783). Nella Introductio in analysin infinitorum del 1748, dopo aver chiarito la nozione di quantità variabile (nel senso che i valori che una variabile può assumere sono soltanto numeri, ivi compresi i numeri complessi), Euler scrive: "Una funzione di una quantità variabile è un'espressione analitica, composta in un modo qualunque a partire da questa variabile e da numeri o quantità costanti" (II, p. 18). Le funzioni sono perciò considerate come oggetti dati 'sintatticamente' attraverso una formula o un'espressione. Si manifesta allora una profonda frattura tra la soluzione algoritmica dei problemi mediante manipolazioni formali e i procedimenti dell'analisi numerica vera e propria. Per fare un esempio, per trovare le soluzioni di una classe di equazioni differenziali, si può procedere in due modi: (a) determinare la funzione soluzione sotto forma di una formula, a partire da una data equazione e mediante un algoritmo i cui passi sono manipolazioni formali; (b) dare un algoritmo che per un valore w della variabile indipendente x fornisca il valore f(w) della funzione soluzione con una data precisione.

Le relazioni tra questi due metodi di soluzione sono state fino a oggi difficili. Analizziamo qui brevemente soltanto alcuni dei problemi più importanti e maggiormente rilevanti per il periodo in esame.

1) La soluzione, e anche la risolubilità nel senso (a), dipende dalla sintassi scelta. Nel XVIII sec. si pensava a formule che facevano intervenire polinomi P(x) o funzioni razionali fratte P(x)/Q(x). Sul fatto che si potessero accettare come soluzioni serie di potenze, considerate ancora all'epoca come polinomi di grado infinito, l'accordo non era affatto unanime.

2) Nel corso dei secc. XVII e XVIII la sintassi, considerata nel senso delineato sopra, fu gradualmente ampliata inserendo simboli per funzioni particolari come i logaritmi naturali, le funzioni trigonometriche e le relative funzioni inverse. A queste si aggiunsero presto le funzioni gamma e beta introdotte da Euler nel 1731; le funzioni cilindriche o di Bessel, come soluzioni di equazioni differenziali motivate da problemi fisici introdotte da Daniel Bernoulli (1700-1782) nel 1732 e da Euler nel 1759; infine le funzioni che attualmente chiamiamo non elementari. Sovrapponendo nomi di funzioni base era possibile generare nuove funzioni, tramite l'uso di parentesi. Fu Euler a utilizzare per la prima volta, nel 1734, la scrittura f( ) ‒ in precedenza l'argomento compariva senza parentesi ‒, in un contesto nel quale si doveva sostituire una funzione con un'altra, operazione che non si può descrivere univocamente senza parentesi:

(Additamentum ad dissertationem de infinitis curvis ejusdem generis, p. 186).

Soltanto dalla fine del XX sec. risulterà chiaro come il concetto di soluzione di un problema nel senso (a) possa diventare banale, semplicemente introducendo simboli che rappresentano la soluzione del problema (occorre ovviamente considerare prima sotto quali condizioni la soluzione esiste e sotto quali è unica). I recenti sviluppi dell'algebra computazionale hanno riproposto questo ordine di problemi in un contesto diverso e più complesso.

3) Nella pratica solo una soluzione nel senso (b) è effettivamente utilizzabile. Una tale soluzione è inoltre in stretta relazione con il moderno punto di vista estensionale, secondo il quale le funzioni sono coppie ordinate: un punto di vista accolto con estrema difficoltà nel XVII sec. perché prescinde radicalmente dal calcolo concreto e dall'effettiva descrizione della relazione funzionale. Accettare una soluzione della forma (a) significa supporre tacitamente che con essa si ottenga anche una soluzione di tipo (b), mentre il viceversa, come oggi sappiamo, non è possibile. Questa accettazione presuppone inoltre che le funzioni alle quali la sintassi assegna nomi simbolici siano date o sotto forma di tabelle, oppure di prescrizioni di calcoli, cioè nella forma (b), per cui si richiede anche che sia possibile determinare il valore di una funzione per un dato argomento con una certa facilità (per es., nel caso di funzioni già tabulate). Euler fu il primo a enunciare le condizioni sotto le quali una serie infinita si può considerare soluzione di un problema. Essa deve rispondere a due criteri: deve convergere rapidamente e i singoli termini devono potersi calcolare con facilità. Come esempio di serie che soddisfa il secondo criterio ma non il primo egli fornì la serie di Leibniz per π/4:

4) I matematici del XVIII sec. preferivano evidentemente le soluzioni di tipo (a). Il paradigma delle soluzioni in 'forma chiusa' che allora si stabilì spinse in secondo piano lo stile numerico-algoritmico del tipo (b), uno stile che aveva caratterizzato la matematica europea dei secc. XV e XVI (e ancor più le varie culture matematiche dell'Estremo Oriente). La matematica che si insegna oggi nelle scuole, e che si basa ancora largamente su quella del XVIII sec., è talmente influenzata da quest'ultima che la comprensione dell'aspetto algoritmico ne è fortemente ostacolata. A parte il fatto che la maggior parte dei problemi non si lascia risolvere ‒ o almeno non soltanto, 'formalmente' ‒ nel senso banale sopra delineato, questa forma di matematica esclude per esempio questioni riguardanti l'efficienza di un algoritmo (numero di passi, spazio di memoria, precisione, ecc.), che sono oggi al centro dell'analisi numerica e hanno da tempo dato origine a nuove teorie. Una ragione in più per rivolgere il nostro interesse ai rari tentativi che in questa direzione si sono manifestati nel XVIII secolo.

Quanto detto sopra a proposito delle funzioni si applica anche, con poche modifiche, ai problemi che richiedono di determinare dei numeri: (a) fornisce il numero cercato sotto forma di radice, o in altra forma, non necessariamente algebrica. Una soluzione di questo tipo è utile nel senso di (b) soltanto se le operazioni che intervengono sono facili da realizzare mediante calcoli non troppo complicati, semplici costruzioni o l'uso di tavole. Quale sia la sintassi appropriata per denotare i numeri dipende molto dalle successive elaborazioni e dalle applicazioni dei numeri stessi. Se si cercano oggetti costruibili con riga e compasso è preferibile una rappresentazione con radicali quadratici, perché questa si può ottenere costruttivamente passo dopo passo. Euler, per descrivere i numeri reali mediante successioni infinite di cifre, introdusse in uno dei suoi primi lavori (1737, pubblicato nel 1744) il metodo delle frazioni continue, come alternativa alle frazioni decimali. Diede la rappresentazione del numero e e di √e in frazioni continue, e dimostrò che una frazione continua periodica si può anche rappresentare con un radicale quadratico. Il viceversa di quest'ultimo risultato fu ottenuto soltanto nel 1769 da Joseph-Louis Lagrange (1736-1813). Nel corso del XVIII sec. la diffusione delle tavole logaritmiche, trigonometriche e di altre funzioni in forma decimale, come pure l'invenzione di macchine calcolatrici che operavano con decimali, può aver avuto un influsso decisivo nell'imporsi delle frazioni decimali infinite come metodo standard di scrittura di quantità reali, a eccezione di qualche campo particolare. Vale forse la pena di ricordare che questa rappresentazione non è sempre la più conveniente. Se, per esempio, si vogliono rappresentare graficamente dei segmenti determinati con riga e compasso, un valore approssimato sotto forma di un radicale quadratico 'semplice' è certamente più appropriato.

Anche in problemi che richiedono di determinare un numero la 'sintassi delle soluzioni' si può ampliare introducendo nomi per costanti non determinabili esattamente. Sappiamo che intorno al 1728 Euler introdusse il simbolo e per la base dei logaritmi naturali (esso comparve per la prima volta in stampa nel 1736, insieme all'espressione "logaritmo naturale", anch'essa usata per la prima volta) e nel 1734 la "costante di Euler" C per indicare il limite

L'introduzione del simbolo π, attribuito a Euler e la cui diffusione si deve all'uso che egli ne fece a partire dal 1736, ebbe invece un precursore in William Jones (1675-1749), che l'aveva tratto dalla parola greca πεϱιφεϱῶϚ per indicare la circonferenza.

Prima di addentrarci in un'analisi più propriamente storica, premettiamo alcune considerazioni sull'idea intuitiva che nel XVIII sec. si aveva degli algoritmi. Analogamente a quanto detto sopra a proposito dei primi timidi tentativi di ripensare il concetto di funzione, non bisogna aspettarsi riflessioni di carattere generale per quanto riguarda il concetto e la natura di un algoritmo. Un algoritmo si applica per risolvere un problema concreto, cercando eventualmente di migliorarne uno già noto per accrescerne velocità e precisione. Numerosi errori sono commessi riguardo alla struttura algoritmica delle soluzioni, sorprendentemente anche da parte di grandi matematici. Vediamone qualche esempio.

1) Contrariamente agli autori di testi matematici del Rinascimento, che spesso si rivolgevano a un pubblico non qualificato, e quindi dovevano spiegare tutti i dettagli e dare le dimostrazioni basate su esempi, i matematici del XVIII sec. si rivolgevano a colleghi che non avevano bisogno di molte spiegazioni per capire un nuovo metodo e metterlo in pratica. Questi matematici erano inoltre in forte competizione tra loro e tendevano perciò a tenere nascosti i dettagli dei propri procedimenti risolutivi piuttosto che a divulgarli. In molti casi, però, questo atteggiamento portava a non rendersi conto di certe difficoltà o a sottovalutarle. Un esempio è il modo in cui Euler nella Vollständige Anleitung zur Algebra (Introduzione generale all'algebra, 1770), che doveva essere un libro di divulgazione, descrive la soluzione dei sistemi di equazioni lineari in n incognite. Dopo essersi soffermato a lungo sui casi n=2, 3, Euler scrive: "Se vi sono più di tre incognite ed equazioni la soluzione si può determinare in modo analogo, in generale con calcoli noiosi. Si possono però utilizzare metodi che facilitano notevolmente la soluzione, e ciò accade quando si introduce arbitrariamente nel calcolo una nuova incognita, per esempio la somma di tutte le incognite. Chi ha esperienza di questo genere di calcoli lo potrà testimoniare facilmente" (p. 45 e segg.).

Euler parla di calcoli "noiosi", svelando con ciò di aver affrontato la risoluzione numerica di sistemi lineari con molte equazioni senza seguire un metodo preciso. È anche evidente che egli era lontano dall'elaborazione di un algoritmo sistematico di eliminazione, anche se questo è piuttosto naturale. Ignorava ciò che oggi sa uno studente del primo anno d'università, e cioè il caso di sistemi di equazioni lineari per i quali o non esistono soluzioni oppure una soluzione esiste ma non è univocamente determinata, anche se il numero delle equazioni è uguale al numero delle incognite.

2) Come per i sistemi di equazioni lineari, si presenta spesso in matematica la distinzione tra un caso 'generale' e uno o più casi 'particolari'. Il pensiero matematico del XVIII sec., d'ispirazione naturalistica, spingeva a concentrarsi sul caso che aveva maggiori probabilità di essere 'normale', lasciando da parte i possibili casi degeneri. Non si sviluppò perciò la coscienza che la variabilità tipica dei processi algoritmici e la varietà di casi particolari che ne discende sono componenti legittime del processo, e che quindi occorre prestare attenzione anche alla loro effettiva possibilità di esecuzione.

3) Procedimenti che si ripetono ciclicamente compaiono nella matematica del XVIII sec., soprattutto quando si tratta di iterazioni volte a ottenere una data precisione; in questi casi ci si limita alla descrizione della successione di passi da ripetere. L'idea che il test di precisione e l'iterazione dei passi facciano anch'essi parte del procedimento non si sviluppò. Nel XVIII sec. il concetto intuitivo di procedimento racchiudeva l'idea errata che un 'procedimento regolare' termina dopo un dato numero di passi di calcolo noto in anticipo. Citiamo di nuovo, a testimonianza di ciò, la Vollständige Anleitung di Euler. Descrivendo il procedimento per trovare soluzioni intere n, m dell'equazione an²+1=m² (dove a non è un quadrato) egli scrive: "A questo proposito uno studioso inglese di nome Pell ha trovato in passato un metodo molto ingegnoso che vogliamo qui spiegare. Esso però non si presta a essere applicato in modo generale per un qualunque numero a, ma solo in ogni singolo caso particolare" (ibidem, pp. 313-329).

Segue la descrizione di un algoritmo che si ripete ciclicamente. Il suo mondo concettuale e la sua terminologia permettevano a Euler di trattare soltanto i casi a=2, 3, 5, 6, 7, 8. Egli poi continua: "A volte si raggiunge rapidamente lo scopo, altre volte sono necessarie molte operazioni, e ciò a seconda della natura del numero a, del quale però non si possono indicare a priori le proprietà" (ibidem). E dopo un ulteriore esempio (a=13): "Da questo esempio risulta chiaro quanto lungo e complicato possa risultare un simile calcolo […]. E non si può nemmeno prevedere per quali numeri sia inevitabile una tale fatica" (ibidem). Segue una tabella dei risultati ottenuti per valori di a fino a 100. Dal testo risulta chiaro che Euler non accettava l'idea di un procedimento che richiedesse un numero di passi di calcolo che poteva variare in modo imprevedibile a seconda dei dati, anche se egli stesso aveva incontrato procedimenti di questo genere.

Contrasta con questo atteggiamento nei confronti degli algoritmi ciclici l'introduzione del concetto di successione ricorrente, a opera di Abraham de Moivre (1667-1754). Casi particolari erano noti da tempo; molto popolare è oggi la successione di Fibonacci (1202), definita dalla legge a_n+2= a_n+a_n+1 e dalle condizioni iniziali a₀=a₁=1. Newton aveva introdotto la tecnica di descrivere funzioni mediante serie di potenze, ottenendo in particolare soluzioni di equazioni differenziali. Posto

come soluzione, la data equazione differenziale diventa un sistema infinito di equazioni nelle incognite a_n, che si può risolvere in passi successivi e che in molti casi fortunati porta a una formula ricorsiva per le a_n. In questo modo si ottenevano in un sol colpo moltissime successioni ricorrenti di interesse pratico. De Moivre afferma che una serie si può definire ricorrente se i suoi termini dipendono, secondo una ben determinata legge, da un numero fissato di termini precedenti. Nel 1730 lo stesso de Moivre approfondisce lo studio in una vasta opera, Miscellanea analytica, nella quale dimostra che una funzione razionale fratta con numeratore 1 si può sviluppare in una serie ricorrente e mostra, viceversa, come trovare la somma di una tale serie. Se per esempio (in notazione moderna) z(x)=a₀+a₁+a₂+…, dove le a_n sono funzioni di x, e la legge di ricorrenza è a_n+2=f(x)a_n+g(x)a_n+1, allora

cioè

Già nel 1728 Daniel Bernoulli faceva uso del nuovo concetto in una memoria, Observationes de seriebus recurrentibus, descrivendo, senza giustificarlo, un procedimento ciclico approssimato piuttosto oscuro per la risoluzione di equazioni polinomiali del tipo P(x)=1 e di grado qualunque, fornendo però soltanto esempi nei quali il procedimento certamente non funzionava. Nel 1748, nel capitolo 17 dell'Introductio intitolato Sull'utilizzazione delle serie ricorrenti per il calcolo delle radici delle equazioni, Euler presenta una ricerca sul modo di operare di questo procedimento, fino ad allora misterioso, e della sua validità. Citiamo questo lavoro solo per sottolineare la rapidità con cui l'espressione 'ricorrente' diventa, dopo il 1720, di dominio pubblico.

Cercheremo di concentrare in sei paragrafi una discussione più approfondita dei vari argomenti ai quali abbiamo accennato. Altre questioni di analisi numerica riguardano la soluzione approssimata di equazioni differenziali, la tabulazione di funzioni speciali (integrali ellittici e loro funzioni inverse, funzioni ellittiche, denominate più tardi funzioni di Bessel, funzioni ipergeometriche), che nel Settecento fanno la loro comparsa nella soluzione di particolari problemi spesso di natura fisica, e algoritmi per la soluzione di problemi di teoria dei numeri.

Soluzioni di equazioni e di sistemi di equazioni

Il dualismo tra manipolazione formale e soluzione propriamente numerica si riscontra anche nella soluzione di equazioni e di sistemi di equazioni fin dall'Antichità. Da un lato, mediante manipolazioni formali, si 'elimina' un'incognita, in modo che in un membro dell'equazione o delle equazioni del sistema ne compaia una sola. Dall'altro, si sviluppano metodi iterativi per la determinazione effettiva delle radici quadrate o cubiche. Non è facile stabilire quali metodi fossero effettivamente algebrici: ancora nel XX sec. si trovano numerosi testi di algebra che trattano di procedimenti numerici per la soluzione di equazioni. Se si lascia da parte tutto ciò che oggi definiamo 'algebrico', ci si trova davanti alla soluzione numerica di un'equazione in un'incognita, cioè in linguaggio moderno alla ricerca degli zeri di una funzione f di una variabile x e alla soluzione di sistemi di equazioni in più incognite. Il primo problema diventa a sua volta, già per equazioni polinomiali di grado qualunque, quello della 'localizzazione approssimata' degli zeri, che contiene a sua volta il problema del numero degli zeri e di una loro determinazione numerica che sia sufficientemente esatta. Un motivo importante della scomposizione del polinomio in fattori lineari e quadratici, che oggi è facile sottovalutare, era la scomposizione in frazioni parziali delle funzioni razionali fratte, passo indispensabile per l'integrazione formale di queste funzioni: un'ulteriore dimostrazione di quanto siano reciprocamente legati in maniera complessa manipolazione formale e procedimenti numerici.

I primi passi verso la localizzazione degli zeri dei polinomi erano stati compiuti nel XVII sec. da Descartes con la 'regola dei segni' e, nel 1690, da Michel Rolle (1652-1719). Rolle considerava la successione (da lui detta "cascade") delle derivate di un polinomio f, determinate in modo puramente algebrico, e concludeva geometricamente che tra un minimo negativo e un massimo positivo doveva necessariamente trovarsi uno zero di f. Quello che oggi va sotto il nome di 'teorema di Rolle' non si riferisce a questa formulazione originaria del teorema del valor medio, bensì al lemma che serve a dimostrarla, secondo il quale tra due zeri della derivata k-esima si trova sempre uno zero della derivata (k+1)-esima. Del numero degli zeri di un polinomio, della loro localizzazione e realtà, e in particolare della dimostrazione e precisazione della regola dei segni di Descartes, si sono occupati tra gli altri anche Newton (Arithmetica universalis, 1707), Jean-Paul de Gua (1712-1786) negli anni 1740-1742, Euler nel 1742 ed Edward Waring (1734-1798) nel 1759.

Seguendo Rolle, la precisa determinazione di uno zero tra un valore positivo e uno negativo della funzione (in questo contesto Rolle chiama "ipotesi" un valore della funzione) si ottiene costruendo una nuova ipotesi a partire da una x che giace tra i due valori: si tratta quindi di un avvicinamento allo zero cercato ottenuto per iterazione. Il metodo di approssimazione di Newton rappresenta tuttora il perfezionamento più importante di questo procedimento piuttosto rozzo; esso viene oggi generalizzato a problemi astratti e studiato a fondo dal punto di vista della teoria della complessità. Tutti i procedimenti conosciuti si basavano essenzialmente sulla rappresentazione geometrica del comportamento della funzione (e quindi sulla curva o la superficie e sulle loro proprietà di continuità e differenziabilità) quando Waring, nel 1770, cominciò ad affrontare il problema in modo completamente diverso, con un metodo che se alla fine porta anch'esso a un algoritmo numerico fa però appello a proprietà dei polinomi e a loro trasformazioni algebriche. Supponiamo che il polinomio abbia uno zero molto più grande degli altri; il teorema di Viète ci dice che questo zero coincide in prima approssimazione con il valore di −a_n−1, il coefficiente cambiato di segno della potenza xⁿ⁻¹ dell'incognita. Si passa allora dal dato polinomio P a uno le cui radici sono i quadrati delle radici di P e si itera questo procedimento, fino a che le radici non sono sufficientemente distanti l'una dall'altra. Questo procedimento non funziona sempre, ma in molti casi porta rapidamente al risultato. È stato riscoperto più volte da vari matematici del XIX sec. ed è noto come 'metodo di Gräffe', dal nome del suo ultimo scopritore Carl Heinrich Gräffe (1799-1873). La situazione riguardo ai vari metodi di soluzione conosciuti alla fine del XVIII sec. fu riassunta da Lagrange nel Traité de la résolution des équations numériques de tous les degrés (1798).

Alla risoluzione numerica dei sistemi di equazioni appartengono: la cosiddetta 'regola di Cramer' (1750) per sistemi di equazioni lineari, ideata appunto da Gabriel Cramer (1704-1752); i metodi di eliminazione delle incognite, dovuti a Étienne Bézout (1730-1783) ed Euler (1760); infine l'estensione, dovuta a Euler, del metodo di Newton a funzioni di più variabili. La regola di Cramer, all'inizio di carattere essenzialmente algoritmico, aveva poco in comune con la nota formula esplicita del rapporto di due determinanti che conosciamo.

Serie e prodotti infiniti; accelerazione della convergenza

Durante tutto il Settecento per le serie e i prodotti infiniti si usavano notazioni del tipo a+b+c+etc. oppure a+b+c+&c. Euler scrive a volte 1+x+x²+…+x^∞ e anche 1−3+5−7+9−…+ +(2∞+1); nel 1755 egli utilizza per la prima volta il simbolo Σ per indicare la somma, anche se non sistematicamente come si usa oggi. Se ne deduce che la pratica con successioni e serie doveva avere in quell'epoca un carattere piuttosto sperimentale e che calcoli numerici elaborati giocavano un ruolo molto importante anche in riflessioni di carattere teorico. Dalla verifica di un numero sufficientemente grande di passi si deduceva la validità di un risultato, mentre dimostrazioni come le intendiamo oggi, cioè sintatticamente corrette e che trattano il caso generale, sono quasi impossibili da trovare nel Settecento. È vero però, come si può constatare anche oggi, che l'espressione esplicita di 4 o 5 addendi di una serie stimola l'inventiva e favorisce la comprensione, più di quanto non faccia una dimostrazione generale vera e propria. Si potrebbe perciò riflettere sul ruolo che una notazione ancora primitiva può aver avuto nella scoperta di risultati così profondi come quelli del XVIII secolo.

La rappresentazione sistematica di costanti e funzioni note mediante somme infinite (serie) o prodotti infiniti, come pure la determinazione con questi metodi di funzioni incognite, risale principalmente all'Arithmetica infinitorum (1655) di John Wallis (1616-1703). Nei cento anni successivi si farà sempre più spesso riferimento a serie a coefficienti costanti e a serie di potenze in termini essenzialmente algebrici (trattando cioè le serie come somme di infiniti termini). L'Ars conjectandi di Jakob I Bernoulli, pubblicata postuma nel 1713, contiene il metodo generale per determinare da uno sviluppo in serie di potenze di una funzione lo sviluppo della funzione inversa. Nel 1715 Brook Taylor (1685-1731) unificò i numerosi sviluppi in serie per funzioni elementari fino ad allora conosciuti, ottenendoli tutti come applicazione della formula che sarà in seguito chiamata 'formula di Taylor' e che fornisce un metodo generale basato su derivazioni successive. Una nuova dimostrazione della formula di Taylor, insieme a numerose altre applicazioni e varianti, fu proposta nel 1742 da Colin Maclaurin (1698-1746) in A treatise of fluxions, in due volumi, nel quale si riconosce a Taylor il dovuto credito.

Fino alla fine del XVIII sec. la convergenza della serie ottenuta come sviluppo di una funzione alla funzione stessa era data per scontata. Anche per Lagrange, che nel 1797 darà la prima formula per il resto interrompendo lo sviluppo di Taylor dopo un numero finito di termini, questa convergenza era ovvia. La possibilità che la serie potesse non convergere, o convergere verso un valore 'errato', non era presa in considerazione. Il fenomeno della divergenza era noto da tempo (la divergenza della serie armonica 1+1/2+1/3+… era stata osservata già nel XIV sec. da Nicola Oresme) e, per fortuna o grazie all'intuito, i calcoli che consideravano anche serie divergenti davano, nella maggior parte dei casi, risultati giusti. Per esempio Leibniz aveva 'sommato', nel 1672, la serie A dei reciproci dei numeri triangolari

utilizzando la serie armonica B di termine generico

e operazioni termine a termine su

ottenendo il risultato (giusto) A=2. Guido Grandi (1671-1742) concludeva, a partire dalla serie

e ponendo x=1, che 1−1+1−1+…=1/2 e inoltre notava che 1/2=(1−1)+(1−1)+(1−1)+…=0+0+0+…, uguaglianza che egli interpretava come la capacità che Dio ha di creare qualcosa dal nulla. Leibniz scriveva nel 1693:

In questo modo (cioè mediante una serie di potenze per la funzione cercata) non soltanto quando una proprietà di una curva è determinata con un calcolo ordinario, ma anche con una formula integrale, differenziale, o differenziale di ordine superiore che si può sviluppare a piacere, è sempre possibile pervenire a una serie che permette di rappresentare quanto cercato esattamente, se si considera l'intera serie, con un'approssimazione a piacere se se ne considera solo una parte. (über die Analysis des Unendlichen, ed. Kowalewski, p. 19)

L'espressione "se si considera l'intera serie" presuppone che sia possibile trovare una legge ricorsiva di costruzione dei termini della serie. Leibniz sembra darlo per scontato. Egli tendeva, come i suoi seguaci, a generalizzare anche affrettatamente sottovalutando le difficoltà, molto più di quanto non facessero gli studiosi britannici del tempo. Anche il problema di trovare una formula per esprimere le somme parziali, problema che naturalmente ha senso anche per le serie divergenti, era affrontato spesso. Leibniz lavorò invano per anni alla ricerca di una formula per la serie armonica.

Già nel 1666 Newton aveva trovato con metodi complessi l'estensione della formula del binomio

al caso di un esponente n frazionario; la somma finita del secondo membro diventa una serie infinita. Questa serie, che più tardi fu scelta tra tutti i risultati di Newton per adornare la tomba dello scienziato, giocò in tutto il XVIII sec. un ruolo molto particolare. Fu utilizzata sia per ricerche di carattere teorico sia per calcoli pratici ‒ James Gregory, per esempio, calcola l'interesse giornaliero al tasso annuale del 6% come 100(1+0,06)^1/365 ‒ e in particolare per passare da un valore noto di una funzione a valori vicini. Nel corso del secolo si ebbero oltre cinquanta tentativi di dimostrazione, tutti basati però su risultati logicamente equivalenti alla formula stessa. È possibile che Euler fosse consapevole di questo fatto, perché nel 1748 cita la formula senza dimostrarla. Fu solo nel 1826 che Niels Henrik Abel (1802-1829) riuscì a dimostrarla, nel caso di esponenti anche irrazionali.

Dopo Leibniz, il quale aveva dimostrato la convergenza solamente delle serie a segni alterni e a termini decrescenti in valore assoluto, il primo a riflettere sul problema generale della convergenza di serie infinite e integrali impropri fu a quanto pare Maclaurin nel Treatise of fluxions. Le sue conclusioni hanno spesso una motivazione geometrica. Per esempio, sommare una serie infinita corrisponde a integrare una funzione a gradini tra zero e infinito, e seguendo un'idea di Stirling si può poi sostituire la n nella formula che dà l'espressione del termine generale a_n in funzione di n con una variabile continua e vedere se l'integrale improprio che ne risulta esiste. Di ciò tratteremo più diffusamente quando parleremo dell'interpolazione.

L'utilizzazione delle serie per calcoli numerici portò alla nozione, all'inizio soltanto intuitiva, di maggiore o minore velocità di convergenza. Edmond Halley (1656-1742) deduce dalla serie di Mercatore

la serie per

che oggi si trova in tutte le raccolte di formule, osservando che la velocità di convergenza di quest'ultima è doppia della precedente. Intorno al 1730 anche Euler cominciò a occuparsi della somma di una serie e di accelerazione della convergenza. Se in parte considerava, e in modo analogo a quanto visto sopra per Leibniz, anche serie notoriamente divergenti, Euler conseguì un gran numero di risultati particolari, come quello secondo il quale la somma di tutti i numeri 1/m, con m della forma n^k−1, dove n e k sono interi maggiori di 1, è uguale a 1:

Nel 1736 egli trovò che la somma degli inversi dei quadrati degli interi, che invano i fratelli Bernoulli avevano cercato, valeva π²/6.

Il passaggio che abbiamo delineato dal modo di pensare geometrico a quello aritmetico-algebrico appare chiaro in particolare nei tentativi effettuati per determinare il numero π con una precisione sempre maggiore. Dopo che fin dall'Antichità i matematici avevano utilizzato poligoni inscritti e circoscritti a un cerchio con un numero di lati via via crescente, la nuova rappresentazione delle funzioni trigonometriche e delle loro funzioni inverse mediante serie permetteva ora metodi di calcolo del tutto scissi da una visione geometrica. Jacques Ozanam (1640-1717) e Thomas de Lagny (1660-1734), che intorno al 1700 cercavano di precisare il valore di π, stabilirono che la serie per π/4

ottenuta ponendo x=1 nella serie di Leibniz per la funzione arcotangente, fornisce il valore 3,14 per π soltanto dopo più di 300 termini. L'astronomo inglese John Machin (1680-1751) ottenne intorno al 1706 mediante ingegnose trasformazioni la serie, anch'essa ben nota,

che gli permise di calcolare π con 100 cifre decimali; altre 27 cifre furono aggiunte nel 1717 da de Lagny.

Riassumendo, si può affermare che nel XVIII sec. a fronte di una grande abilità nel 'calcolo con formule infinitamente lunghe' e una notevole quantità di risultati particolari, l'impostazione di teorie e risultati generali su somme infinite e convergenza è piuttosto scarna.

Tavole di funzioni, interpolazione, calcolo delle differenze

La compilazione di tavole per le funzioni di uso più comune (all'inizio soprattutto logaritmi e funzioni trigonometriche) è stata fin dal Rinascimento una delle occupazioni più laboriose e noiose dei matematici. È significativo che a questo compito si siano dedicati nel XVII e nel XVIII sec., insieme a numerosi dilettanti, molti matematici di valore. Le ricerche su come migliorare e semplificare la compilazione delle tavole portarono anche a importanti progressi sul piano teorico. Se per valori di x equidistanti, x₀, x₁,…, x_n, e un polinomio f di grado m si formano le differenze f(x_i+1)−f(x_i), quindi le differenze di queste, e così via (in modo da formare una disposizione a triangolo), si osserva subito empiricamente che le differenze di ordine m+1 si annullano, come d'altra parte segue da un semplice ragionamento algebrico. È molto probabile che l'osservazione empirica del fatto che questo fenomeno si presenta, con poche eccezioni, anche nel caso di logaritmi e funzioni trigonometriche sia all'origine della rappresentazione delle funzioni (analitiche) mediante serie di potenze, dell'approssimazione mediante polinomi e del teorema di Taylor-Maclaurin. Il metodo delle differenze fornisce poi lo strumento più importante per tabulare funzioni analitiche a partire da un numero limitato di valori iniziali, e per scoprire errori di calcolo in tavole già compilate.

Contrariamente al metodo delle tavole, il problema dell'interpolazione è in origine di natura geometrica: tracciare una 'curva' di un dato ordine passante per un numero di punti assegnato. Il problema ha una motivazione concreta: determinare la traiettoria di un corpo celeste a partire da un numero finito di osservazioni. Rispetto al metodo di Lagrange, proposto nel 1778 e nel 1779 indipendentemente da quello di Waring, nel metodo di Newton si ha il vantaggio di ottenere nuove coppie (x,y) in modo ricorsivo e di poter utilizzare i calcoli già svolti per un nuovo caso, mentre la formula di Lagrange-Waring fornisce esplicitamente il polinomio cercato e s'inserisce nella tendenza moderna di dedurre la soluzione di un problema generale da quella di un certo numero di problemi particolari (in questo caso lineari). A proposito della formula d'interpolazione di Lagrange, della sua pubblicazione si parla di solito nella letteratura dell'anno 1795; secondo alcuni però già nel 1778 Lagrange ne aveva fatto menzione in una seduta della Königliche Preussische Akademie der Wissenschaften (Accademia Reale Prussiana delle Scienze) di Berlino. Per le applicazioni pratiche la formula di Lagrange era poco utile, ma malgrado ciò per lungo tempo essa comparirà nei manuali di matematica più spesso del metodo di Newton, un chiaro segno dello spostamento di interesse dei principali campi della matematica proprio del XIX sec. a favore del punto di vista teorico e a danno degli aspetti numerici.

Stirling aveva mostrato su numerosi esempi nell'opera Methodus differentialis (1730, in due parti) come estendere una successione discreta a(n) a una funzione reale, sostituendo la variabile n con una variabile continua (chiameremo interpolazione anche questo procedimento). Tra i risultati che si sperava di raggiungere in questo modo c'era quello di ottenere valori approssimati per la somma di serie finite e infinite, calcolando, invece della somma, l'integrale delle funzioni risultanti dall'interpolazione. Si intravede qui di nuovo la relazione sopra menzionata tra la serie armonica, il logaritmo naturale e la costante C. Naturalmente questo metodo porta a risultati utili solamente quando la funzione da interpolare in un dato intervallo ha un andamento non troppo particolare (per es., quando tra due valori di una successione monotona crescente essa è del pari monotona). Ricerche di questo tipo non vengono però proposte in modo esplicito. Stirling mostra come passare, mediante successioni che crescono molto rapidamente, dapprima al logaritmo per poi interpolare e tornare indietro trasformando la funzione f così ottenuta in e^f. Applicando questo metodo alla successione a_n=n! egli determinò la famosa forma asintotica per il fattoriale:

Non sappiamo se Euler fosse a conoscenza del lavoro di Stirling, ma egli affrontò nel 1731 con lo stesso metodo il problema dell'interpolazione del fattoriale mediante una funzione analitica. Trasformò dapprima n!=1∙2∙3∙…∙n nel prodotto infinito

nel quale ora n può assumere anche valori non interi, e osservò che dalla formula di Wallis

segue

Ciò lo portò per complicate vie euristiche a quella che sarà chiamata 'funzione β', di due variabili, e infine alla funzione

che ha la proprietà richiesta per valori interi positivi dell'esponente n di fornire il valore 1∙2∙…∙n.

A cavallo tra il XVIII e il XIX sec. nei manuali di Sylvestre-François Lacroix (1765-1843) furono raccolti per la prima volta, in capitoli a essi appositamente dedicati, gli aspetti numerici dell'algebra e dell'analisi. Il suo Traité du calcul différentiel et du calcul intégral (1797-1800), ristampato più volte e tradotto in inglese e tedesco subito dopo la pubblicazione, e i successivi Traité des différences et séries (1800) e Traité élémentaire (1802) trattano, tra l'altro, del calcolo differenziale e delle sue applicazioni all'interpolazione, all'inversione numerica di funzioni e alla soluzione di equazioni differenziali in una e due variabili.

Quadratura e rettificazione

Il contrasto e la dipendenza reciproca, sopra menzionati, tra manipolazioni formali e algoritmi numerici si ritrovano anche nei problemi di misura (lunghezze, superfici, volumi, ecc.), affrontati con il calcolo integrale e che risalgono ai più antichi problemi posti alla matematica dalle attività pratiche. Il calcolo differenziale elaborato da Leibniz e Newton, insieme a quello che oggi si chiama 'teorema fondamentale del calcolo' ‒ dovuto agli studi di Gregory nel 1668 e di Isaac Barrow nel 1670 ‒ avevano favorito l'illusione che si fosse trovata una soluzione generale a questi problemi, e che la soluzione si potesse determinare numericamente. Già nel 1702 Leibniz e Johann I Bernoulli avevano stabilito, con il metodo della decomposizione in frazioni parziali, la formula per l'integrale delle funzioni razionali. L'integrazione termine a termine di una serie di potenze, che veniva effettuata in modo non rigoroso, sembrava poter risolvere definitivamente il problema. Parallelamente già dal 1676 si era affrontato (con Newton) il problema di integrare in modo approssimato una curva (data eventualmente in modo empirico) a partire da un numero finito di valori. La regola più semplice, che consiste nell'integrare la funzione quadratica determinata di volta in volta da tre punti di interpolazione equidistanti (x_i, y_i), era già stata utilizzata da Kepler nella Nova stereometria doliorum vinariorum (1615), e fu riscoperta indipendentemente da Bonaventura Cavalieri nel 1639, da Gregory intorno al 1670 e da Thomas Simpson (1710-1761) nel 1743. Essa oggi viene ricordata soprattutto sotto il nome di quest'ultimo (regola di Simpson). Per determinare questa formula Newton estende il metodo (che risale al 1671, e che si trova nella Methodus fluxionum pubblicata per la prima volta nel 1711) a quattro punti, ottenendo la cosiddetta 'regola dei 3/8':

Il risultato fu generalizzato da Roger Cotes (1682-1716) nello stesso anno 1711 fino al caso di undici coppie di valori equidistanti, e Stirling sperimentò l'efficacia della formula nel 1719 utilizzandola con nove coppie di valori per calcolare π/4 con sei decimali. In seguito risultò chiaro che aumentare il numero dei valori non forniva risultati migliori dell'applicazione della regola di Simpson o di quella dei 3/8.

Problemi numerici d'integrazione nascevano anche in questioni relative alla rettificazione delle curve: le funzioni integrande che vi compaiono non sono elementarmente integrabili. Pionieri in questo campo furono Giulio Carlo Fagnano (1682-1766) e il figlio Giovanni (1715-1797). Il primo aveva rettificato, tra altre curve, la lemniscata di Bernoulli, parabole di ordine superiore e l'arco di ellisse, introducendo in questo contesto la nozione di integrale ellittico. I suoi risultati sulla possibilità di suddividere, sotto determinate condizioni, archi di queste funzioni in n parti uguali con riga e compasso furono il punto di partenza della scoperta di Euler dei teoremi di addizione per gli integrali ellittici e della teoria delle funzioni ellittiche, studiata a fondo nel XIX secolo. Giovanni Fagnano trovò tra l'altro numerose formule integrali ricorsive utilizzando l'integrazione per parti, per esempio per le primitive di xⁿsenx e xⁿcosx.

Calcolo degli errori

Esempi isolati di determinazione dei limiti inferiore e superiore dell'errore di una misurazione e di ricerche su come questo errore si ripercuote sui calcoli si trovano già nell'Antichità. Basta pensare alla misura approssimata delle dimensioni del Sole e della Luna e della loro distanza, dovuta ad Aristarco di Samo o al calcolo dei granelli di sabbia di Archimede. Seguirono però in Europa molti secoli di netta separazione in matematica tra teoria e applicazioni. In ambito teorico non c'era posto per grandezze affette da errori, mentre nelle applicazioni lo studio degli errori non poteva essere un tema di ricerca, perché nella raccolta e nell'elaborazione dei dati ci si accontentava di metodi rozzi e spesso scorretti. Dopo che Kepler e Galilei ebbero discusso, nel quadro della fondazione della scienza moderna basata sull'osservazione e sugli esperimenti, i problemi degli errori di misura e di osservazione, c'era da attendersi che grandi imprese scientifiche ‒ come la ricognizione e la mappatura della gran parte del mondo fino ad allora inesplorato (non solo per mare ma anche per terra), le spedizioni per misurare la declinazione in vari punti della Terra organizzate dall'Académie Royale des Sciences di Parigi nell'America Meridionale e in Lapponia, o la ricerca, all'epoca ancora vana, della parallasse delle stelle fisse da parte degli astronomi ‒ stimolassero l'interesse per una sistematica teoria degli errori. Così fu, ma l'interesse rimase circoscritto a un numero sorprendentemente esiguo di studiosi. Inoltre, fino a oggi l'argomento non è stato molto considerato e approfondito dalla storiografia matematica. Il quadro che ora cercheremo di delineare ha quindi valore solamente provvisorio.

La teoria matematica degli errori si suddivide fin quasi dagli inizi nella teoria dell'errore massimo ‒ che si occupa della massima deviazione Δf del valore di una funzione f, in generale di più variabili, dal valore nominale f(x,y,…) dipendente dalla variazione dell'errore delle variabili entro determinati limiti Δx, Δy,… ‒ e nella teoria del valore più probabile di una funzione, a partire da una serie di valori misurati e dal loro grado di precisione. La teoria dell'errore massimo doveva prendere, nel XX sec., la direzione che nell'analisi numerica va sotto il nome di 'matematica degli intervalli di fiducia'; la teoria del valore più probabile di una funzione condusse al metodo dei minimi quadrati, formulato agli inizi del XIX sec. indipendentemente da Adrien-Marie Legendre (1752-1833) e da Carl Friedrich Gauss (1777-1855), e alla cui fondazione e giustificazione si dedicarono numerosi autori durante tutto il secolo. Le due teorie sono legate dal fatto che la seconda provvede a fornire i valori approssimati e i limiti di errore con i quali la prima lavora. Inizieremo con l'affrontare lo sviluppo storico della teoria dell'errore massimo che è precedente e più elementare.

Tra i pionieri degli studi sulla propagazione dell'errore merita di essere ricordato Cotes. In un'appendice alla Harmonia mensurarum, pubblicato postumo nel 1722, egli si occupò del problema di determinare la variazione dei lati e degli angoli di un triangolo piano o sferico, definiti secondo una formula trigonometrica, quando i termini che intervengono nella formula e che sono risultati di misurazioni variano di una data quantità. Egli suppone però dapprima che due dei sei elementi da determinare siano invariabili, cioè esatti, per poter formulare il problema rispetto a una variabile. In uno scolio successivo, egli esprime a parole la legge generale di propagazione dell'errore, che noi oggi scriviamo come

sottolineando l'analogia delle formule ottenute con quelle del calcolo differenziale. Scrive Cotes:

Supponiamo che l'errore cercato di una grandezza A sia dovuto agli errori delle quantità B, C e D. Si determini allora il valore di A a partire dai valori di B, C e D, e la sua derivata con il metodo di Newton. Sostituendo alle derivate gli errori di B, C e D col segno positivo o negativo si ottiene l'errore della quantità A. Gli errori di cui parliamo sono infatti tanto più vicini alle loro derivate quanto più sono piccoli. (Kaunzner 1987, p. 442)

Cotes passa poi a determinare su alcuni esempi di trigonometria i valori delle variabili indipendenti B, C e D per i quali il valore della quantità dipendente A, per date variazioni degli errori di B, C e D, è massimo. In un altro scolio si trovano anche i primi tentativi di determinare il valore più probabile di una serie di osservazioni.

Questi tentativi, che anticipavano di molto i tempi, restarono a lungo poco conosciuti. Unicamente Nicolas-Louis de Lacaille (1713-1762) fa riferimento ai risultati di Cotes, in un lavoro di trigonometria sferica del 1741 pubblicato nei "Mémoires de l'Académie Royale des Sciences". Il problema della propagazione degli errori fu ripreso nel caso particolare della trigonometria, e a quanto pare indipendentemente da Cotes, da Pierre Bouguer nel 1749, da Johann Jacob Marinoni nel 1751, e da Abraham Gotthelf Kästner nel 1753. Soltanto ora, e dopo che Euler aveva stabilito nell'Introductio in analysin infinitorum (1748) il concetto generale di funzione, facendovi rientrare le funzioni trigonometriche, si poteva prescindere dalle complicazioni che nascevano dal considerare queste ultime come rapporti tra segmenti e dai conseguenti problemi dimensionali. Osserviamo per inciso che, riguardo alla stima degli errori, anche la fisica dovette affrontare fino alla fine del XIX sec. analoghe difficoltà e alcuni paradossi dovuti all'associazione tra le grandezze fisiche e le diverse unità di misura. Un'opera sistematica di chiarificazione in questo campo si è avuta per la prima volta grazie al matematico russo Aleksej Nikolaevič Krylov (1863-1945) con le sue Lezioni di calcolo approssimato, pubblicate postume nel 1946.

Alla riflessione sul valore più probabile di una serie di osservazioni si accompagnava la convinzione che l'espressione matematica delle leggi naturali doveva essere semplice: una volta che una legge è stata prevista o dedotta, una conferma sommaria è sufficiente. Differenze nelle misure non giustificavano dubbi sulla validità della legge, in quanto mettevano soltanto in discussione l'esattezza delle misure. Come precursori di una teoria degli errori di osservazione, in contraddizione con questo spirito newtoniano, vanno ricordati i lavori di Simpson del 1755 e 1757, di Johann Tobias Mayer, Johann Heinrich Lambert, Pierre Bouguer, Daniel Bernoulli del 1777 e Ruggero Giuseppe Boscovich. Simpson, Mayer, Daniel Bernoulli e Boscovich erano motivati da problemi di carattere astronomico, Bouguer (nello scritto del 1729, e nell'Optical treatise del 1761, postumo) e Lambert (Photometria, 1760) da ricerche sull'intensità della luce. Lambert, in contrasto con la propria visione metodologico-filosofica, finì con l'elaborare una teoria della compensazione degli errori per tutte le osservazioni della Natura. Le sue idee sul valore 'più probabile' di una serie di osservazioni erano condivise tra gli altri da Mayer, astronomo a Gottinga. Egli adduce buone ragioni per spiegare perché non sempre la media aritmetica è il valore più probabile, cosa che né Gauss né i sostenitori del metodo dei minimi quadrati faranno. Lambert, come pure Mayer, si occuperanno presto del problema della regressione lineare, di trovare cioè, dato un insieme finito di coppie di valori (x_i, y_i), 'la migliore' funzione lineare y=f(x) che esprime la legge in esso latente.

Strumenti di calcolo

L'effettiva funzione dei numeri con molti decimali e il motivo per cui si cercava di determinarne sempre nuove cifre rimangono attualmente piuttosto oscuri al grande pubblico. La funzione di questi numeri, che si esplica oggi nelle calcolatrici tascabili, nei computer e in molti altri strumenti, la loro utilizzazione nei contesti più diversi, come pure la determinazione di nuovi decimali, hanno avuto nel tempo un ruolo molto importante, non solo nel campo della matematica ma anche nella vita quotidiana. Non c'è dunque da meravigliarsi se, accanto a matematici e astronomi, si trovano anche molti studiosi non professionisti impegnati a calcolare tavole numeriche, a inventare o a migliorare strumenti per il calcolo meccanico. Dopo i primi timidi tentativi, di scarso successo, di Wilhelm Schickhardt (1592-1635), macchine calcolatrici furono costruite da Blaise Pascal (1623-1662) e da Leibniz. Tra gli altri si ricordano, nel 1726, il costruttore di strumenti musicali Antoni Braun, austriaco, e il commissario alle miniere della Sassonia, Jacob Leupold; dopo il 1768 il parroco svevo Philipp Matthäus Hahn, che fu il primo ad avviare una produzione in serie, e già nel 1709 Giovanni Poleni, professore di astronomia, matematica e fisica nell'Università di Padova. La macchina di quest'ultimo non era molto migliore di quella di Leibniz, ma è storicamente importante per via dell'invenzione del principio tecnico della ruota a pioli. Vanno anche ricordati i notevoli miglioramenti apportati al regolo calcolatore da James Watt (1736-1819) e l'impegno di questi affinché questo strumento, allora volgarmente detto Soho-rule, venisse utilizzato in modo massiccio.

Un ruolo più importante di quello degli apparecchi e delle macchine ebbero le tavole: più precisamente, accanto a quelle di carattere puramente matematico (logaritmiche, trigonometriche), le tavole astronomiche e nautiche e, in misura crescente, quelle relative a importanti funzioni della fisica. La maggior parte di esse era piena di errori, e non poca fatica costò correggerle con i metodi del calcolo differenziale e migliorarle con l'interpolazione. Le tavole logaritmiche più famose furono quelle di Georg von Vega (1754-1802), un ufficiale austriaco di origine slovena. Il suo manuale logaritmico-trigonometrico, che ebbe circa cento edizioni, era ancora in uso in molti paesi alla metà del XX secolo. Devono essere menzionate anche le tavole lunari di Mayer: la vedova ricevette il premio del concorso indetto dalla Royal Society per il problema della longitudine.

Attualmente non c'è differenza tra l'elaborazione algoritmica delle successioni di cifre e quella di altre serie di simboli (un computer elabora soltanto serie di 0 e 1; non sa se queste codificano numeri, formule o poesie d'amore). Una presentazione della storia degli aspetti pratici della matematica, delle procedure e degli algoritmi non deve però trascurare i progressi raggiunti nel corso del XIX sec. nella scrittura e nella simbologia. Alle novità già ricordate di quel secolo aggiungiamo l'invenzione degli indici semplici e multipli, che ha reso possibile l'odierno modo di scrivere somme e prodotti, l'utilizzazione di alfabeti diversi per denotare oggetti di natura diversa, e l'abbandono, estremamente utile per certi scopi, della scrittura lineare.

Leibniz aveva usato per la prima volta nel 1693, in una lettera al marchese Guillaume-François-Antoine de L'Hôpital (1661-1704), la scrittura

per un sistema di equazioni lineari, dove 20 indica il coefficiente che si trova nella seconda riga e nella prima colonna (il nostro a₂₁; come si vede, la numerazione delle colonne comincia con 0). Questa notazione non fu però utilizzata per molto tempo. Nel 1750 Cramer scriveva i coefficienti di un sistema nella forma Z²,Yⁿ, ecc., dove Z² indicava il coefficiente della variabile z nella seconda equazione, un modo di scrivere i coefficienti seguito principalmente da Alexandre-Théophile Vandermonde (1735-1796) nel 1772 e da Bézout nel 1779. Nel 1708 gli "Acta Eruditorum", fondati da Leibniz, suggerivano agli autori l'uso di esponenti frazionari invece del segno di radice, ma prescrivevano ancora le pesanti notazioni aa invece di a², aaa invece di a³, e così via. L'uso sistematico delle parentesi per le espressioni aritmetiche, che mediante il segno ':' per la divisione permette di scrivere con chiarezza anche frazioni di frazioni, fu diffuso da Leibniz nel 1710. Euler espresse, per la prima volta nel 1778, i coefficienti binomiali nella forma oggi in uso in lavori pubblicati soltanto nel 1784 e anche più tardi.