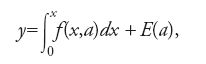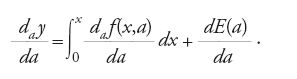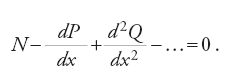L'Età dei Lumi: matematica. Il calcolo delle variazioni
L'Eta dei Lumi: matematica. Il calcolo delle variazioni
Il calcolo delle variazioni
Il calcolo in una e più variabili
Una volta sviluppata la teoria della differenziazione e integrazione delle funzioni y=f(x) di una variabile x, nei termini di una relazione fra x e y nel piano, un modo naturale di estendere il calcolo differenziale, che tenga conto del fatto che molti problemi sono tridimensionali invece che bidimensionali, è quello di considerare una funzione z=F(x, y) di due variabili, di applicare la teoria nota a ciascuna delle variabili x e y e infine di analizzare la corrispondente superficie nei termini delle sue sezioni con i piani xz e yz. Tuttavia, lo sviluppo storico dell'estensione del calcolo non ha affatto seguito questo percorso; infatti la generalizzazione da f(x) a F(x, y) fu preceduta da una transizione da f(x) a f(x, a), dove a è una variabile parametrica che distingue l'una dall'altra le curve di una stessa famiglia. Il motivo di questo sviluppo risiede nell'interesse, che risale all'Antichità, per i problemi o le proprietà dell'ottimizzazione, per esempio i problemi della determinazione della distanza minima fra due punti in un particolare ambiente, o dell'area massima delimitata da una curva chiusa di lunghezza data (notiamo di passaggio che le soluzioni a questi problemi nell'ambiente del piano sono rispettivamente la retta e il cerchio).
Durante il XVII sec., i problemi posti dalla meccanica, che fu una fondamentale fonte di ispirazione per il calcolo, condussero a un raffinamento di tali questioni. La prima applicazione significativa fu il tentativo, riuscito, condotto da Newton, a partire dal Libro II dei Principia mathematica (1687), di determinare la forma che consenta a un corpo di incontrare resistenza minima attraversando un mezzo non viscoso. Anche l'ottica fu fonte di nuovi temi, come l'analisi dei cammini dei raggi luminosi sotto varie condizioni: il principio di Pierre de Fermat del tempo minimo per individuare il percorso del raggio riflesso è una legge di grande importanza.
Sebbene Christiaan Huygens (1629-1695) operasse generalmente in un contesto strettamente geometrico, parte del suo lavoro è connessa a questioni di natura variazionale, in particolare per via del suo interesse per le evolute e le evolventi delle curve. Tuttavia l'impulso principale venne dagli studiosi del calcolo, in special modo quando Johann I Bernoulli (1667-1748) riesaminò nel 1696 un problema che era stato posto da Galilei ma risolto in maniera inesatta: la curva descritta, nel vuoto e sotto l'azione della gravità, da una particella che si sposti nel tempo minimo da un punto dato a un altro (situato più in basso). Newton, Leibniz, lo stesso Johann e suo fratello maggiore Jakob I (1654-1705) proposero alcune soluzioni. Jakob Bernoulli, nella sua tesi dottorale nel 1701 usò, forse per la prima volta, l'aggettivo 'isoperimetrico', poiché il problema imponeva qualche tipo di uguaglianza o di identità, e tale termine fu gradualmente adottato. La soluzione di questo problema era la cicloide, già definita come la linea tracciata da un punto posto sulla circonferenza di un cerchio che rotoli su una retta orizzontale. Gli studiosi erano particolarmente colpiti dal fatto che, come nel caso ora esaminato, le soluzioni a questa tipologia di problemi erano spesso curve note in altro contesto. Secondo lo stile caratteristico di Johann I Bernoulli, la discussione sulla correttezza della soluzione diventò una questione di famiglia, e fu portata avanti anche dopo la morte di Jakob I.
Entrambi i fratelli studiarono vari problemi più o meno collegati al precedente. Per esempio, Johann determinò anche la forma di un filo flessibile e inestensibile, soggetto al solo peso proprio, che sia sospeso in due punti e trovò che si trattava della catenaria. Nel 1730 esaminò una versione complessa del problema della determinazione della tautocrona, nel caso in cui si ammetta la resistenza dell'aria e si supponga che sia proporzionale al quadrato della velocità.
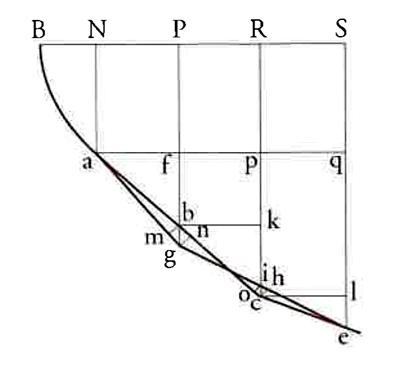
In questa fase non era ancora emersa l'idea di utilizzare variabili parametriche. I metodi consistevano principalmente nel confrontare la curva desiderata C con una curva a essa prossima, analizzando in particolare le corrispondenti sotto-aree, e cercando di individuare i criteri per cui quella sottesa a C fosse ottimale, oppure attingendo a proprietà specifiche della curva in oggetto. La disputa fra i fratelli Bernoulli riguardava non solamente i dettagli di queste tecniche, ma anche questioni generali e di metodo. Per esempio, l'inserimento di una condizione di ottimalità introduceva nell'analisi un ulteriore grado di libertà, cosa che fu compresa meglio da Jakob che da Johann. D'altra parte, Johann si rese conto che questa condizione richiedeva che si dovesse normalmente considerare la variazione di due punti dalla curva desiderata; un esempio del suo modo di procedere è mostrato nella fig. 2. Ragionamenti di questo tipo erano nuovi nella giovane scienza del calcolo e giovarono anche alla geometria differenziale delle curve e delle superfici. Altri problemi riguardanti le famiglie di curve divennero molto diffusi, sebbene non tutti comportassero procedure di ottimizzazione. Un problema comune, introdotto anch'esso da Johann I Bernoulli e da suo nipote Nikolaus I (1687-1759), era la determinazione delle curve ortogonali a una data famiglia. Per esempio, le curve di decadimento esponenziale y=Kexp[−x/(2a)] sono ortogonali alle parabole y2=−4ax. Un importante problema correlato era determinare i cosiddetti 'sincroni', ossia la curva piana tracciata collettivamente da un insieme di particelle che in un dato istante sono rilasciate dallo stesso punto: essi risultano essere le curve ortogonali alle rispettive cicloidi.
Nel secondo decennio del Settecento altri matematici francesi si interessarono al problema originale dei Bernoulli e cercarono di risolverlo. Essi, essendo seguaci di Leibniz, si adoperavano a mostrare la potenza del sistema di calcolo di quest'ultimo, con un atteggiamento reso più aspro dalla ridicola contesa sulla priorità del calcolo fomentata da Newton presso la Royal Society. I contributi newtoniani al nostro argomento furono relativamente modesti, sebbene Brook Taylor (1685-1731) avesse studiato le traiettorie ortogonali nella sua Methodus incrementorum directa et inversa (1715), che contiene anche il teorema sulle serie di potenze, al quale venne erroneamente accostato il suo nome. Il responsabile di questo errore storico fu Colin Maclaurin (1698-1746), che lo riportò nel suo A treatise of fluxions (1742), il quale contiene anche alcune tecniche variazionali implicite ‒ esposte nell'ambito della determinazione per via geometrica, a partire dalle leggi di Newton ‒ delle superfici equipotenziali per punti esterni. Tuttavia, la gran parte della storia del calcolo del Settecento si svolse nel Continente, sebbene, come vedremo presto, vi abbia fatto una curiosa apparizione la notazione 'a puntini' usata da Newton.
Fontaine, Euler e il calcolo in più variabili
In tutti i problemi affrontati dai matematici, si trovava un'equazione differenziale di qualche tipo, di cui si cercava poi la soluzione (o le soluzioni). Quando fu riconosciuto l'uso delle variabili parametriche, venne messa in atto nell'analisi la procedura importante di invertire l'ordine dei differenziali misti:
[1] dadxƒ(x,a)=dxdaƒ (x,a).
Tuttavia, ci si può chiedere se era sempre legittimo assumere la verità dell'uguaglianza [1]; allo stesso modo, se era corretto asserire che il differenziale parziale di
dove E(a) era una funzione d'integrazione, fosse necessariamente dato da
In questo caso è stata usata una notazione moderna per il differenziale parziale, basata sulla tradizione leibniziana: all'epoca la scelta dei simboli non era univoca. Un metodo simile a questo impiegava in tale ambito i differenziali totali delle funzioni. Per esempio, esso veniva usato per trovare una funzione q tale che per una data funzione p
[4] dy = p(x,a)dx + q(x,a)da.
All'epoca si riteneva che le curve fossero per la maggior parte differenziabili. I casi anomali venivano accantonati ammettendo che il differenziale potesse occasionalmente assumere infiniti valori positivi o negativi. Anche in questo campo, tali tecniche non potevano essere utilizzate incondizionatamente, e la dipendenza sensibile dai valori dei parametri appariva talora con evidenza.
Un protagonista sconosciuto di questa fase storica del calcolo fu Alexis Fontaine des Bertins (1704-1771). Egli scrisse diffusamente sul calcolo in molte variabili, in particolare negli anni Trenta; tuttavia pubblicò relativamente poco, e spesso dopo che altri avevano già reso noti i risultati a cui egli era pervenuto. Una ragione che rende conto dell'esiguità dei suoi interlocutori fu la sfortunata scelta dei simboli: egli infatti rappresentava il differenziale rispetto alla curva con la notazione 'a puntini' newtoniana invece che con quella leibniziana, e indicava con 'dx' la distanza infinitesima tra due punti corrispondenti a uno stesso valore di x, ma appartenenti a curve vicine (ossia, una differenziazione parametrica in cui il parametro non appariva esplicitamente). Così, nei suoi scritti il teorema (o ipotesi) di inversione [1] prendeva la forma seguente, tutt'altro che chiara:
Tuttavia, la sua opera era di notevole portata e perspicacia, e affrontava gran parte dei problemi studiati al suo tempo. Egli cercava condizioni sufficienti che fossero soddisfatte dalle curve estremali generalmente basate sull'equazione [5]. Come alcuni suoi predecessori, fra cui Johann I Bernoulli, egli considerò versioni più complesse di alcuni problemi, ammettendo per esempio che il punto finale della curva ricercata potesse essere variabile invece che costante, oppure trovando la curva che rappresentasse la caduta più rapida nell'aria invece che nel vuoto.
I contributi di Fontaine, nonostante la sua opera fosse di notevole livello, sarebbero stati eclissati da quelli del pupillo di Bernoulli, Leonhard Euler (1707-1783), che scrisse diffusamente su questo argomento nei primi anni Trenta. Egli sviluppò il problema estendendo innanzitutto il metodo di Bernoulli descritto nella fig. 2, ossia adottando la procedura di uno spostamento infinitesimo del singolo punto dalla curva ricercata e poi supponendo che il differenziale dello spostamento fosse zero. Sembra anche che egli sia stato influenzato da Taylor nell'espressione in forma analitica delle condizioni isoperimetriche.
In uno scritto pubblicato nel 1740, Euler fece un passo in avanti di tipo concettuale, trattando la variabile parametrica a, che egli chiamava il 'modulo', non come un parametro ma come una variabile alla pari di x, y, … . Respingendo il modo tradizionale di trattare gli integrali e i differenziali, in cui a giocava solo il ruolo di un parametro, egli cercò varie condizioni necessarie perché il differenziale fosse totale. Alcune di queste condizioni erano simili a quelle della teoria delle equazioni differenziali. Il differenziale degli integrali della forma [2] era la cosiddetta 'equazione modulare'
[6] dy = ƒ(x,a)dx+Q(x,a)da
e Q poteva essere trovato in vari modi: per esempio, mediante manipolazioni algebriche, oppure ponendo a zero i differenziali di y di ordine maggiore, o ancora formando equazioni differenziali ordinarie ausiliarie che Q doveva soddisfare. Un esempio assai efficace di quest'ultima opzione era di assumere che ƒ fosse una funzione omogenea delle sue variabili, nel qual caso era possibile formare immediatamente un'equazione del primo ordine a partire dalla [6]. Con questi espedienti egli fu in grado di risolvere molti tipi di equazioni e conseguentemente anche i problemi corrispondenti.
Il trattato principale che Euler scrisse su questo argomento è la Methodus inveniendi lineas curvas (1744). Qui egli impiegò ed estese i metodi precedenti al fine di trovare e classificare curve che soddisfacessero alcune condizioni ottimali; per esempio, per trovare la curva che, ruotando attorno a un asse, generi il solido di resistenza minima. Egli fu stimolato da un suggerimento del suo amico Daniel Bernoulli (1700-1782), figlio di Johann I, secondo il quale una linea elastica assume la propria curva di equilibrio C quando l'integrale ∫Cds/R2 raggiunge il valore minimo. Egli, andando oltre il metodo delle equazioni modulari, comprese che molti problemi potevano essere formulati nei termini di un integrale della forma
[7] ∫baƒ (x,y,p)dx
in cui p è uguale a dy/dx e fy=d(fp)/dx è una condizione del primo ordine necessaria per l'ottimalità. Manipolando una funzione dZ con coefficienti differenziali di ordine superiore p, q (uguale a dp/dx), r, s, … ossia
[8] dZ=M(x,y)dx+N(x,y)dy+P(x,y)dp+Q(x,y)dq+…,
egli trovò la seguente condizione più generale per l'ottimalità di ∫Zdx:
In analoghe situazioni Euler considerò Z come una funzione di variabili addizionali, risolvendo in questa maniera problemi più complessi. Per esempio, trovò la curva che una particella uscente da un punto segue per passare attraverso un altro analogo punto raggiungendo la velocità massima a una data altezza più bassa. In due voluminose appendici egli applicò i suoi risultati allo studio delle condizioni di equilibrio delle linee flessibili e delle vibrazioni alle quali queste erano sottoposte sotto l'azione di forze esterne. Queste analisi lo spinsero a coltivare i suoi interessi nell'ambito della teoria dell'elasticità.
Poco dopo, un altro aspetto più generale della meccanica trasse vantaggio dal ricorso ai metodi variazionali. Pierre-Louis Moreau de Maupertuis (1698-1759), collega di Euler alla Königliche Preussische Akademie der Wissenschaften (Accademia Reale Prussiana delle Scienze) di Berlino, probabilmente ispirato da un'idea di Daniel Bernoulli, propose negli anni Quaranta il 'principio della minima quantità di azione', il quale suggeriva che la forma di equilibrio assunta da una linea era determinata dalla minima azione delle forze esterne centrali. Dalla fine degli anni Quaranta Euler gli fece seguito con un'analisi assai più approfondita della teoria e delle sue principali conseguenze: se le forze V agiscono con spostamenti infinitesimi dv, è possibile determinare l'equilibrio minimizzando gli integrali del tipo ∫ds∫(∑Vdv) calcolati lungo una curva conveniente per una data configurazione, ossia, imponendo che le variazioni fossero uguali a zero.
Questo periodo ricco di eventi vide anche l'introduzione delle equazioni differenziali alle derivate parziali, frutto dell'opera di Jean-Baptiste Le Rond d'Alembert (1717-1783), e la loro immediata adozione ed estensione da parte di Euler. Il problema delle corde vibranti fu il primo e famoso banco di prova sia per la formulazione sia per l'estensione del problema fisico relativo, ed ebbe importanti sviluppi nel campo dell'idrodinamica. Questa estensione, nell'ambito della quale fu introdotta la formulazione descritta all'inizio di questo capitolo, arricchì enormemente la portata del calcolo in generale, e in particolare del calcolo delle variazioni. La contiguità dei due argomenti si manifestò ancora più apertamente per effetto del processo di algebrizzazione messo in pratica dall'ultima figura di rilievo che prenderemo in considerazione.
Lagrange e l'algebrizzazione della matematica
Nel 1755, il diciannovenne Joseph-Louis Lagrange (1736-1813) ‒ o, come allora si firmava, Louis de la Grange Tournier ‒ mostrando una precocità superiore persino a quella di Euler nella carriera matematica, scrisse a quest'ultimo suggerendo che la teoria degli spostamenti individuali potesse essere generalizzata e semplificata ammettendo che tutti i punti su una data curva si potessero muovere simultaneamente, e inoltre che questa operazione complessiva potesse essere indicata mediante un operatore al quale egli assegnò, in uno scritto del 1762, il simbolo 'δ'. La possibilità d'invertire le variabili si trasformava così nella relazione operazionale 'δd=dδ', che veniva ancora ritenuta normalmente valida. Euler rimase entusiasta dell'approccio, e segnalò l'importanza della teoria di Lagrange e il suo futuro promettente assegnandole il nome di 'calcolo delle variazioni': il suo metodo delle equazioni modulari divenne quindi superato. Il suo trattato sul calcolo integrale in tre volumi (1768-1770) terminava con un'appendice dedicata a quest'argomento, nella quale egli cercava le condizioni necessarie e/o sufficienti che la funzione Z(x) doveva soddisfare affinché ∫Z(x)dx fosse integrabile. I risultati che egli ottenne erano incompleti; alcuni progressi concernenti le condizioni necessarie vennero realizzati verso la fine del decennio da Marie-Jean-Antoine-Nicolas Caritat de Condorcet (1743-1794), in parte per via dell'entusiasmo che egli provava nel trovare soluzioni in forma chiusa alle equazioni differenziali.
Tuttavia, fu Lagrange ad assegnare un ruolo di cruciale importanza ai metodi variazionali, come parte del suo sforzo per algebrizzare tutte le parti della matematica che egli affrontava. Egli tentò di fondare il calcolo differenziale e integrale sulle serie di Taylor, ottenendo le 'funzioni derivate' esclusivamente mediante metodi algebrici; i metodi variazionali ne derivano naturalmente, come un terzo argomento. Il suo primo manuale sul calcolo, la Théorie des fonctions analytiques (1797), includeva una dimostrazione dell'integrabilità di ƒ(x) nei termini della versione corrispondente della [9]. Egli estese notevolmente la portata dei suoi risultati nel suo lavoro sul calcolo, le Leçons sur le calcul des fonctions (1806).
In maniera analoga, nel campo della meccanica Lagrange preferiva esprimere il principio di minima azione in una forma più generale di quella di Euler che abbiamo indicato in precedenza, tuttavia sempre in termini delle variazioni nulle di integrali appropriatamente definiti. Egli sviluppò il calcolo in molte applicazioni, trovando formule che mettevano in relazione i differenziali di ordine superiore e le variazioni. Un'estensione assai importante concerneva il movimento di insiemi di masse sottoposte sia a forze P con spostamenti dp sia a vincoli di vario tipo, espressi come equazioni della forma L=0. La condizione di equilibrio era espressa dall'equazione
[10] ∑Pδp+∑λ δL=0,
dove i fattori λ divennero noti come 'moltiplicatori di Lagrange'. Il suo approccio alla meccanica rappresentava un'alternativa formidabile alla tradizione newtoniana e a quelle basate sull'energia, sebbene i suoi punti di forza fossero soprattutto le situazioni di equilibrio. Euler adottò questo approccio, riassumendo le caratteristiche principali della teoria in una lunga appendice all'ultimo volume delle sue Institutiones calculi integralis (1768-1770).
Lagrange sviluppò gradualmente la sua teoria in vari articoli a partire dal 1760; alcuni erano dedicati alla soluzione di problemi particolari, come quello della librazione della Luna. Egli formulò definitivamente il suo approccio alla meccanica in un trattato intitolato Méchanique analitique (1788), nel quale l'aggettivo fin troppo usato, analitique, scritto nella grafia arcaica, faceva riferimento al primato dell'algebra. Questo testo, completato nei primi anni Ottanta, mentre egli era all'Accademia di Berlino, fu pubblicato solo sei anni dopo a Parigi, in un periodo di poco successivo al suo trasferimento in questa città (anche se non in seguito a tale trasferimento). Fra i nuovi colleghi di Lagrange, Adrien-Marie Legendre (1752-1833), che nel 1786 ebbe modo di vedere il trattato in corso di stampa, aveva da poco attirato l'attenzione sulla variazione totale del secondo ordine, cercando di trovare le condizioni che distinguevano le situazioni di massimo da quelle di minimo. Pierre-Simon de Laplace (1749-1827) sviluppò la teoria delle equazioni differenziali, in particolare per applicarle all'astronomia matematica, e utilizzò su qualche caso metodi variazionali per stabilire le equazioni del moto, o per determinare situazioni di equilibrio. Essi compaiono occasionalmente nei primi due volumi del suo Traité de mécanique céleste (1798-1799), un lavoro che sarebbe stato considerato un classico nel secolo successivo.
In quel periodo Sylvestre-François Lacroix (1765-1843), autore di diversi manuali, scrisse la prima edizione della sua grande oeuvre, il gigantesco Traité du calcul différentiel et du calcul intégral (1797-1800). Il secondo volume si concludeva con un capitolo di 70 pagine 'sul metodo delle variazioni', che offriva una buona panoramica sia dei principî sia delle applicazioni. Egli riportava le formule conosciute per le variazioni degli integrali ed esponeva l'importanza dell'inversione. Tuttavia, egli commise un errore grave e sistematico relativo alla variazione di un integrale doppio; lo stesso errore venne ripetuto anche nella seconda edizione del 1814. La correzione dell'errore non fu cosa di poco conto, anzi costituì un importante indicatore dei progressi del settore nel corso del XIX secolo. Tuttavia, era stato fatto abbastanza perché si potesse iniziare a scrivere la storia dello sviluppo del calcolo delle variazioni. Già Lacroix aveva indicato opere di riferimento e fornito alcuni commenti. Un resoconto più sistematico è contenuto in un breve libro del 1810, intitolato A treatise on isoperimetrical problems and calculus of variations, scritto da Robert Woodhouse (1773-1827), un'autorevole figura all'interno della comunità, allora piuttosto insignificante, dei matematici britannici, che tuttavia cominciava ad abbandonare la notazione newtoniana, accingendosi a svolgere un ruolo più rilevante nello sviluppo della matematica.