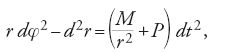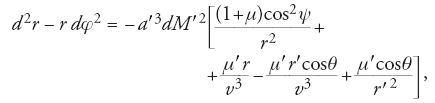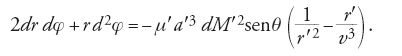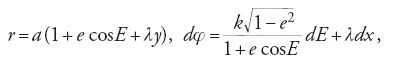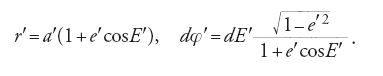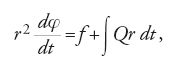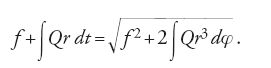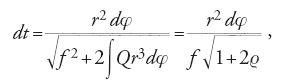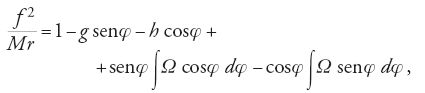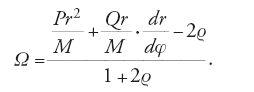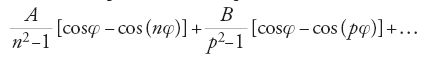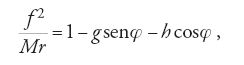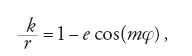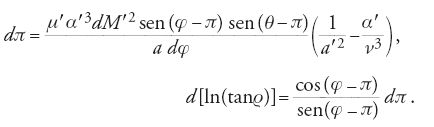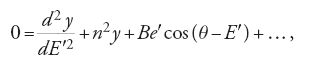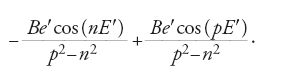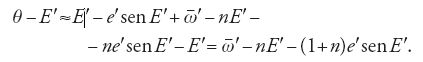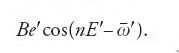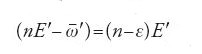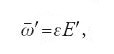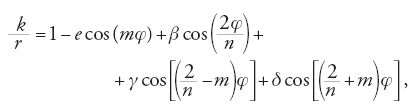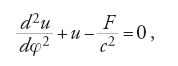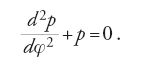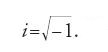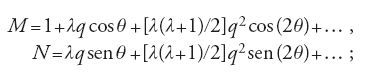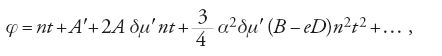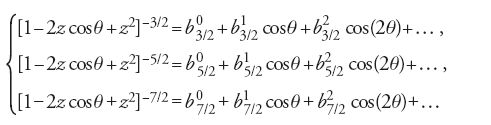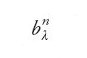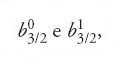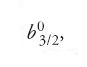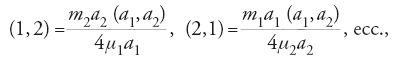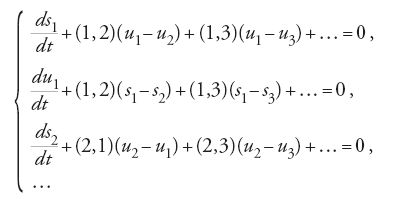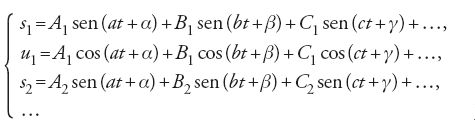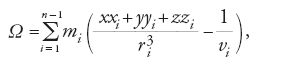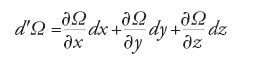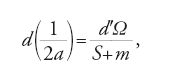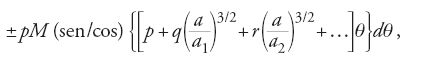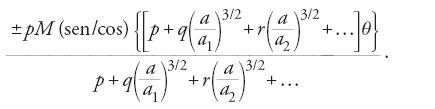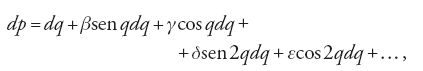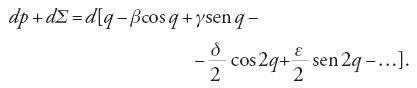L'Età dei Lumi: matematica. La matematica della teoria delle perturbazioni da Euler a Laplace

L'Eta dei Lumi: matematica. La matematica della teoria delle perturbazioni da Euler a Laplace

La matematica della teoria delle perturbazioni da Euler a Laplace

Accanto allo sviluppo dei mezzi di osservazione, nell'astronomia del Settecento ebbe un ruolo importante anche quello della meccanica dei corpi celesti. In questo capitolo ci si propone di focalizzare le questioni matematiche presenti in tale disciplina, cercando di dare una risposta a domande del tipo: quali furono le difficoltà che i matematici del Settecento incontrarono nel trattare analiticamente il problema dei tre corpi e nello sviluppare la teoria delle perturbazioni dei moti celesti? E quali furono i metodi escogitati per ovviare a tali difficoltà?

Formulazione e soluzione delle equazioni del moto dei corpi celesti: Euler e Clairaut

I primi lavori a stampa sulle equazioni differenziali del moto per un corpo celeste soggetto a perturbazioni gravitazionali furono due memorie di Leonhard Euler (1707-1783), entrambe completate nel giugno 1747 e pubblicate nel 1749 ‒ una indirizzata alla Königliche Preussische Akademie der Wissenschaften (Accademia Reale Prussiana delle Scienze) di Berlino, l'altra all'Académie Royale des Sciences di Parigi per il concorso bandito per il 1748 ‒, e la Théorie de la lune di Alexis-Claude Clairaut (1713-1765), che apparve nel 1752.

All'inizio della memoria presentata all'Accademia di Berlino, Euler formulò le equazioni del moto di un corpo di massa m in coordinate cartesiane ortogonali (O,x,y,z):

[1] md²x = (1/2)Xdt², md²y = (1/2)Ydt², md²z  = (1/2)Zdt²,

dove X, Y, Z sono le componenti della forza motrice (fu forse la prima volta in cui la seconda legge newtoniana del moto fu espressa in coordinate cartesiane ortogonali) e il fattore (1/2) deriva dalle particolari unità usate da Euler per esprimere l'accelerazione. Passando in coordinate cilindriche, egli ottenne tre equazioni che possiamo scrivere così:

[2] d²r-r dφ² =-(1/2)P dt²

[3] 2 dr dφ+r d²φ =- (1/2)Q dt²,

[4] d²z =- (1/2)R dt2,

dove P, Q, R sono le componenti della forza acceleratrice (termine utilizzato da Newton per indicare l'accelerazione in un campo gravitazionale), la cui direzione positiva è tale da fare diminuire r, φ, z; se φ è l'angolo tra l'asse x e r, allora

Occorre notare che le variabili r e φ sono le proiezioni del raggio vettore e della longitudine del corpo perturbato su un piano di riferimento scelto, come raccomanda Euler, in modo tale che z resti sufficientemente piccola.

Clairaut derivò equazioni molto simili alle [2] e [3], ma inizialmente fece la supposizione che il corpo soggetto alla perturbazione e le forze che lo perturbano fossero confinati a stare su un piano. Senza far uso di coordinate ortogonali egli derivò allora, direttamente dalla geometria del problema, le equazioni del moto in coordinate polari (r,φ):

[7] r d²φ+2dr dφ=Q dt ²,

dove M è la somma delle masse del corpo perturbante e di quello perturbato, mentre P e Q sono rispettivamente l'aggiuntiva accelerazione radiale e l'accelerazione trasversale dovute alla perturbazione. Soltanto in seguito, e in maniera insoddisfacente, Clairaut introdusse il problema della latitudine.

Euler formulò le equazioni [2], [3] e [4] allo scopo di risolvere il problema posto dall'Académie di Parigi per il concorso del 1748, relativo alla "spiegazione delle anomalie che [Giove e Saturno] appaiono causarsi reciprocamente […]" (Sur les inégalités du mouvement de Saturne et de Jupiter, in Opera, p. 45). Egli circoscrisse la sua analisi, tuttavia, alle perturbazioni del moto di Saturno causate da Giove e questa, come vedremo, fu una limitazione foriera di problemi. Euler considerò il moto di Giove intorno al Sole non soggetto a perturbazioni e confinato nel piano di riferimento xy o rφ. Siano r′ e φ′ il raggio vettore e la longitudine di Giove e siano r e φ le proiezioni del raggio vettore e della longitudine di Saturno sul piano rφ (al posto dei complicati simboli euleriani viene utilizzata qui la notazione con indici, introdotta da Lagrange negli anni Sessanta del Settecento).

Il passo successivo di Euler fu di esprimere P, Q, R mediante la legge dell'inverso del quadrato della distanza. Siano Θ, J e S le masse, rispettivamente, del Sole, di Giove e di Saturno; sia ψ=arctan(z/r) la latitudine di Saturno sul piano rφ a un istante qualsiasi; sia, infine, φ′−φ=θ. Le 'forze' cui Saturno è soggetto sono l'attrazione solare, ossia Θ/[r²+z²]=Θcos²ψ/r², e l'attrazione esercitata da Giove, J/v², dove v è la distanza tra i due pianeti. Inoltre, per far sì che il moto di Saturno possa essere riferito al Sole considerato immobile, le forze con cui Giove e Saturno attraggono il Sole debbono essere considerate applicate a Saturno, ma con il verso opposto. La prima di queste è J/r′² e agisce su Saturno in direzione parallela alla congiungente le masse JΘ; la seconda è Scos²ψ/r² ed è diretta lungo SΘ. Ciascuna di queste quattro forze deve essere scomposta secondo le tre direzioni individuate, rispettivamente, da r, dalla direzione ortogonale a r nel piano rφ e da z.

Per eliminare il fattore dt²/2 dalle equazioni [2], [3] e [4] Euler usò l'anomalia media di Giove, che designeremo con M′; per un corpo che si muove di moto circolare uniforme alla distanza media Sole-Giove a′, l'equazione [2] implica che, con buona approssimazione, sia dt²/2=a′³dM′²/Θ. Ponendo S/Θ=μ, J/Θ=μ′, egli ottenne per le equazioni [2] e [3] le seguenti espressioni (per la trasformazione della [4] si veda più avanti):

Le equazioni [8] e [9] contengono nei membri di destra le variabili r, r′, v, θ e ψ. Con il proposito di ridurre a due il numero di variabili indipendenti, Euler pose tre problemi, ciascuno dei quali costituiva una diversa approssimazione alla situazione implicata dalla teoria newtoniana.

Nel primo problema suppose che, in assenza di perturbazioni, i due pianeti avrebbero dovuto muoversi intorno al Sole lungo orbite circolari. Egli scrisse per Giove r′=a′, φ′=M′ e per Saturno r=a(1+λy), dφ=n dM′+λdx, dove n è il rapporto tra il moto medio di Saturno e quello di Giove, a la distanza media Sole-Saturno, λ≪1, e y e x sono nuove variabili.

Nel secondo problema Euler introdusse l'ellitticità dell'orbita di Saturno, non alterando le altre ipotesi. Dalle equazioni [8] e [9], rimuovendo la forza perturbatrice di Giove e ponendo la latitudine ψ pari a zero, egli ricavò:

dove e è l'eccentricità della sua orbita, E l'anomalia eccentrica, legata all'anomalia media M dall'equazione di Kepler M=E+esenE, e φ ha ora il significato dell'anomalia vera (la longitudine misurata dall'afelio). A partire dalla situazione descritta nel secondo problema, le equazioni [10] si devono modificare per rendere conto della perturbazione. Euler scrisse:

dove k può differire di poco da 1 per descrivere il moto dell'afelio e dove, come prima, λ≪1.

Nel suo terzo problema Euler introdusse l'eccentricità e′ dell'orbita di Giove, mantenendo, per il resto, le ipotesi fatte nel primo problema. Così, per Saturno egli pose

[12] r = a(1+y), dφ  = n dM' + λdx,

e per Giove

Per mezzo delle sostituzioni proposte nei tre problemi precedenti Euler eliminò r, r′, φ e θ=φ′−φ dalle equazioni [8] e [9], per passare a x e y come variabili dipendenti e a M′ ed E′ come variabili indipendenti, e uguagliò a zero la latitudine ψ, considerato il suo valore trascurabile. Nei membri di destra delle equazioni [8] e [9] restava però la variabile v, che varia cospicuamente allorché i due pianeti passano dalla congiunzione all'opposizione e viceversa, e questa variazione rendeva la risoluzione delle equazioni particolarmente complessa; vedremo in seguito come Euler risolse questa difficoltà.

La procedura adottata da Clairaut per risolvere le equazioni [6] e [7] fu molto differente. Egli dapprima moltiplicò la [7] per la variabile r e successivamente effettuò un'integrazione, ottenendo:

dove f è una costante d'integrazione. Moltiplicò poi la [14] per Qr dt, integrò, completò il quadrato ed estrasse la radice, ottenendo:

Sostituendo con la [15] il secondo membro della [14], Clairaut ottenne:

dove ϱ=(1/f ²)∫Qr³dφ. Per mezzo della [16] Clairaut eliminò dt dalla [6] e, integrando due volte quest'ultima relazione così modificata, ottenne un'equazione per r in termini di φ:

dove g e h sono costanti, e

Per calcolare gli integrali che compaiono nella [17], Ω doveva essere esprimibile nella forma Acos(nφ)+Bcos(pφ)+..., dove n, p, ecc. sono fattori numerici. Gli ultimi due termini presenti nella [17] prendevano in questo modo la forma:

Per ridurre Ω alla forma desiderata, nella [18] occorreva rimpiazzare r con una funzione di φ. Così, come Euler, anche Clairaut entrò qui in un circolo vizioso del problema perturbativo e l'unica via d'uscita era ricorrere a un'approssimazione. Se Ω è nulla, la [17] fornisce

che può essere considerata come l'equazione di una fissata ellisse con parametro f²/M, eccentricità (g²+h²)^1/2 e afelio arctan(g/h). Clairaut osservò tuttavia che usare questo risultato per rimpiazzare r in Ω sarebbe stato un errore, poiché dalle osservazioni risultava la mobilità dell'apside lunare e perciò propose di utilizzare l'equazione per una 'ellisse rotante':

dove k, e, m sono costanti indeterminate. Se i termini più grandi della teoria che sarebbe seguita avessero avuto la forma della [21], queste costanti avrebbero potuto essere determinate e così l'introduzione di tale equazione sarebbe risultata giustificata.

La soluzione costituita dalle equazioni [17], [18], [19] e [21] fu applicata da Clairaut per la prima volta al problema del moto lunare (a questo riguardo si veda il par. 2). Nel 1757 egli dedusse da questa soluzione le perturbazioni relative alla teoria solare, da usarsi nelle Tabulae solares di Lacaille, e nel periodo 1757-1758 se ne servì per dedurre le perturbazioni esercitate da Giove e Saturno sul moto della cometa di Halley; ciò comportò l'esecuzione della prima integrazione numerica su vasta scala. Il metodo di Clairaut per l'analisi delle perturbazioni fu l'unico descritto nell'Astronomie di Lalande (le cui edizioni apparvero nel 1764, nel 1771 e nel 1792), il più importante testo di astronomia della seconda metà del Settecento. Lagrange meditò su di esso e quindi riuscì a comprendere in quale modo le variazioni dell'eccentricità orbitale e dell'apside orbitale fossero connesse. L'Ω di Clairaut può aver contribuito a ispirare in Lagrange l'invenzione della funzione perturbatrice negli ultimi anni Settanta del Settecento, da lui indicata, appunto, con il simbolo Ω. Analogamente, nello sviluppo delle equazioni del moto Laplace emulò la concisione delle relazioni di Clairaut [17] e [18] e giunse a relazioni per alcuni versi simili a quelle di quest'ultimo.

Tav. I

I problemi perturbazionali relativi alla Luna differiscono da quelli planetari soprattutto perché v ‒ la distanza tra il corpo celeste perturbante e quello perturbato ‒ è, nel caso lunare, soggetta solamente a piccole variazioni ed è facilmente esprimibile mediante uno sviluppo in serie di Taylor con pochi termini, mentre nel caso planetario fluttua enormemente. Nel caso di Giove e Saturno, v varia per un fattore maggiore di 5 e v⁻³ varia per un fattore maggiore di 150. Per esprimere queste variazioni in modo da poter eseguire le integrazioni necessarie, Euler introdusse le serie trigonometriche (Tav. I).

Tale introduzione a questo punto si rivelò cruciale; se Euler non avesse preso questa strada, è da dubitare che lo avrebbe fatto qualcuno dei matematici suoi contemporanei. Il problema delle perturbazioni dei moti planetari non avrebbe potuto così essere affrontato se non attraverso laboriosi processi basati su integrazioni numeriche.

Torniamo ora all'equazione del secondo ordine [4] del moto di Saturno al di fuori del piano rφ. Euler s'ingegnò di rimpiazzarla con due equazioni del primo ordine nei parametri dell'astronomia tradizionale ‒ ossia l'inclinazione ϱ del piano dell'orbita rispetto al piano di riferimento e la longitudine π del nodo ascendente in tale piano ‒, parametri che, se soggetti a una perturbazione, divengono variabili.

In termini dell'inclinazione ϱ e della longitudine π del nodo ascendente, abbiamo z=rsen(φ−π)tanϱ. Da questa equazione Euler derivò dz, ipotizzando dapprima che π e ϱ fossero costanti e poi che fossero variabili, e uguagliò alla fine i due risultati. Questo passo, apparentemente illogico, fu da lui giustificato dicendo che π e ϱ variano molto più lentamente di r e φ, cosicché π e ϱ possono essere considerati costanti quando r e φ variano rispettivamente di dr e dφ. Procedendo poi a calcolare d²z sotto l'ipotesi che r e φ siano le uniche variabili e operando alcune sostituzioni a partire dalle [2], [3] e [4], egli ottenne equazioni per dπ e d[ln(tanϱ)]. Sostituendo poi P, Q, R e dt²/2 con i loro valori dati dalle [8] e [9], e con l'ulteriore ipotesi che l'orbita di Giove e la proiezione dell'orbita di Saturno sul piano rφ potessero essere considerate circolari, queste equazioni divengono:

Con tali equazioni si compì un primo passo sulla strada del metodo della variazione dei parametri orbitali. Esse erano soltanto approssimate ed Euler non affrontò la loro integrazione esatta. Considerando π come una costante nei membri di destra, egli dimostrò, integrando su θ (qui pari a M′−M), che la linea dei nodi si muove di moto retrogrado a una velocità media e con piccole oscillazioni, mentre l'inclinazione è costante, se si eccettuano alcune fluttuazioni minori.

Nell'integrazione delle equazioni del suo terzo problema, Euler incontrò un termine, arc de cercle, crescente con il tempo. Ciò spiegava, egli ritenne, perché nessuna teoria sul moto di Saturno si fosse rivelata soddisfacente. Per mostrare come questo termine si manifesta, esprimiamo la parte relativa a y dell'equazione differenziale:

dove E′ è l'anomalia eccentrica di Giove, n è il rapporto dei moti medi e θ=φ′−φ. Se (θ−E′) può essere espresso nella forma pE′, dove p è un coefficiente numerico, allora la soluzione della [23] conterrà i due termini:

Per mettere (θ−E′) nella forma richiesta osserviamo che dφ′=dE′(1−e′cosE′) è al primo ordine in e′, cosicché

dove

è una costante d'integrazione. Inoltre, abbiamo che

[25] dφ≈n(dM')=n(dE'+e'dE' cosE')

cosicché φ≈n(E′+e′senE′) e quindi:

Qui (1+n)e′senE′ è abbastanza piccolo affinché, indicandolo con α, si possa porre cosα≈1 e senα≈α; allora

Al primo ordine in e′, il termine Be′cos(θ−E′) nella [23] diviene

Quando la [23] è integrata, i denominatori dei due termini risultanti della [24] diventano entrambi del tipo n²−n²=0, e anche la somma dei numeratori è zero. Euler evitò questo risultato indeterminato supponendo che nella [24] p differisca da n per una quantità ε abbastanza piccola da far sì che il suo quadrato possa essere trascurato, cosicché cos(εE′)≈1 e sen(εE′)≈εE′. I due termini della [24] si riducono allora a −[Be′E′/2n]sen(nE′). Questo termine aumenta con E′, e quindi con il tempo; Euler ne concluse che in ciò andava ricercata "la causa principale delle anomalie del moto di Saturno […]" (Recherches sur la question des inégalités, in Opera, p. 98).

La supposizione di Euler concernente p implica però che

vari, poiché se

allora occorre che sia

e

cresce con il tempo

(

è la longitudine dell'apside orbitale di Giove). Euler aveva già trovato che l'afelio di Saturno si muove se è soggetto a una perturbazione; perché non ammettere, come Jean-Baptiste Le Rond d'Alembert (1717-1783) lo spingeva a fare, che anche l'afelio di Giove si muova nelle stesse circostanze? In una memoria che meritò il premio dell'Académie di Parigi per l'anno 1752, Euler fece esattamente in questo modo, trattando simultaneamente le reciproche perturbazioni dell'afelio e dell'eccentricità di Giove e di Saturno. Egli trovò che il moto di ognuno dei due pianeti dipendeva dalla distanza angolare tra il proprio afelio e quello dell'altro pianeta e possedeva un'eccentricità propria e un'eccentricità temporanea. Combinati insieme, questi risultati fornivano per ogni pianeta un afelio mobile e un'eccentricità variabile. I calcoli di Euler, purtroppo, contenevano diversi errori e le conclusioni numeriche che egli aveva tratto erano sbagliate; i relativi lavori non furono pubblicati sino al 1769. Nel frattempo, Lagrange aveva scoperto indipendentemente ciò di cui Euler si era reso conto, cioè che le lente variazioni che Giove e Saturno inducono ciascuno nell'eccentricità orbitale e nell'afelio dell'altro devono essere prese in considerazione simultaneamente.

Il moto degli apsidi lunari: Clairaut, Euler e d'Alembert

Sostituendo la [21] nella [18] e risolvendo per mezzo di quest'ultima la [17], Clairaut trovò che la prima fra queste doveva essere modificata con l'aggiunta di tre termini:

dove, per il sistema Sole-Terra-Luna, n è il moto medio giornaliero della Luna diviso per la differenza tra questo e il moto medio solare e β, γ e δ hanno i valori numerici, rispettivamente, di 0,007090988, −0,00949705 e 0,00018361. Nella soluzione della [17] il coefficiente di cos(mφ) conteneva il fattore e/(m²−1); ponendo tale coefficiente pari a e, Clairaut trovò per m il valore 0,9958036, la qual cosa implicava per il moto medio mensile degli apsidi lunari il valore di 1°30′39″, meno della metà del valore osservato, che egli assumeva pari a 3°4′11″.

Euler e d'Alembert erano pervenuti a un risultato simile attraverso procedure alquanto differenti. A entrambi sembrava impossibile che la legge gravitazionale dell'inverso del quadrato della distanza potesse essere rigorosamente vera e che al tempo stesso potesse fornire una prima approssimazione così poco accurata del moto apsidale. D'Alembert riteneva più probabile che la legge gravitazionale fosse davvero di proporzionalità inversa al quadrato della distanza, ma che nel caso lunare essa dovesse essere modificata a causa dell'esistenza di una forza non gravitazionale come, per esempio, una forza d'origine magnetica.

Clairaut si rese conto che per costruire tavole accurate era richiesta un'approssimazione del secondo ordine e infine riuscì a venirne a capo, attraverso un lavoro tedioso. Si trattò di sostituire la [28] in Ω, lasciando indeterminati β‚ γ e δ, di risolvere di nuovo la [17] e di ricalcolare le costanti. I contributi al coefficiente di cos(mφ) dei termini con coefficienti γ e δ ‒ essendo entrambi questi termini proporzionali alla componente trasversale della forza perturbatrice ‒ si rivelarono di considerevoli dimensioni. Per il nuovo valore di m Clairaut trovò 0,99156 e ciò implicava un moto medio apsidale mensile di 3°2′18″, soltanto 2′ in meno del valore osservato. Spronato dai risultati di Clairaut, Euler capì infine qual era il difetto della propria precedente derivazione. Egli aveva inizialmente posto m pari al valore osservato, ma nella sua equazione aveva inserito una grandezza μ che rappresentava una possibile deviazione dalla legge dell'inverso del quadrato. Aumentando l'ordine dell'approssimazione, trovò che μ era trascurabile.

La teoria della Luna di d'Alembert comparve nel 1754 (Recherches sur différents points importants du système du monde), dopo quelle di Clairaut e di Euler. Come approssimazione iniziale d'Alembert aveva considerato circolare l'orbita della Luna. La sua soluzione procedette per stadi, definiti dall'ordine di grandezza delle quantità prese in considerazione (procedura che successivamente anche Laplace avrebbe seguito). Svolgendo i calcoli sino al sesto ordine, per il moto apsidale egli trovò quattro termini: 1°30′39″+ 1°3′34″+23′30″+5′5″=3°2′48″, un risultato che si discostava di circa 1′ rispetto al valore osservato. Alla metà degli anni Cinquanta del Settecento, dunque, era ormai chiaro che l'ipotesi con la quale si doveva procedere era la validità della legge gravitazionale dell'inverso del quadrato della distanza.

I lavori di Lagrange del 1766

Per il concorso del 1766 l'Académie di Parigi propose il problema delle anomalie nel moto dei satelliti di Giove causate dalle loro mutue interazioni. La memoria che si aggiudicò il premio fu quella di Joseph-Louis Lagrange (1736-1813), il quale, in un'altra derivazione, determinò poi le reciproche perturbazioni secolari di Giove e Saturno. In queste memorie apparve per la prima volta la notazione con indici: ad una lettera per una determinata variabile (per es. 'r' per il raggio vettore), erano affiancati un certo numero di segni o apici scritti a esponente per riferirsi a un determinato satellite o pianeta.

Lagrange sviluppò formalmente equazioni parallele per l'inverso del raggio vettore u e per la tangente p della latitudine in assenza di perturbazioni:

Integrando queste equazioni e variando poi le costanti d'integrazione, egli mostrò che le risultanti variazioni secolari dell'eccentricità e dell'afelio erano formalmente analoghe a quelle dell'inclinazione e del nodo.

Una delle innovazioni introdotte da Lagrange nelle memorie del 1766 concerne il calcolo di v⁻³, l'inverso del cubo della distanza tra il pianeta o satellite perturbante e quello perturbato. Lo sviluppo in serie di Taylor per v⁻³ è esprimibile in termini di (1−2qcosθ+q²)^−λ, dove q=a′/a⟨1 e λ assume i valori 3/2, 5/2, 7/2, … Lagrange scrisse la precedente espressione nel prodotto di due fattori complessi:

[31] [1q(cosθ+i senθ)]^-λ[1-q(cosθ-i senθ)]^-λ,

dove

Usando il teorema di de Moivre nella forma

[32] [cosθ ± i senθ)]ⁿ=cos(nθ) ± i sen(nθ),

egli ottenne:

dove

da cui seguiva:

[35] [1-2q cosθ+q²]^-λ=M²+N².

Questo metodo di sviluppo della serie sarebbe stato adottato anche da Laplace.

Un altro risultato della memoria di Lagrange sui satelliti di Giove fu di dimostrare che il metodo standard delle approssimazioni successive nella teoria delle perturbazioni, nella versione data per esempio da Clairaut, porta inevitabilmente a termini di n-esimo ordine nell'approssimazione d'ordine (n+1) e genera un numero infinito di termini aventi denominatore nullo. Con un metodo indiretto, Lagrange dimostrò che questi termini che creavano difficoltà non erano in realtà inerenti al problema, ma piuttosto prodotti collaterali del metodo stesso: di conseguenza, egli si dedicò esclusivamente al metodo della variazione delle costanti d'integrazione.

Nella memoria sui satelliti di Giove, Lagrange dimostrò che la soluzione del primo ordine per la longitudine e il raggio vettore di ciascun satellite contiene quattro termini, ciascuno riferibile a uno dei satelliti. Così, ciascun satellite ha un'eccentricità e un apocentro 'propri', e tre eccentricità e tre apocentri 'accidentali', prodotti dall'attrazione di uno degli altri satelliti; gli apocentri si muovono lentamente, facendo variare l'eccentricità e l'apocentro complessivi. Una situazione del tutto simile si ha nel caso delle inclinazioni orbitali e dei nodi. Paragonando tra loro i moti medi n₁, n₂, n₃ dei primi tre satelliti, Lagrange trovò che essi erano quasi commensurabili: n₁/n₂=2,0073 e n₂/n₃=2,0147. Per il secondo satellite risultavano due grandi anomalie, una di argomento (n₁−n₂)t e l'altra di argomento 2(n₂−n₃)t, ma le osservazioni indicavano che entrambe dovevano avere lo stesso periodo, e precisamente n₁−n₂=2(n₂−n₃) ossia n₁−3n₂+2n₃=0. Anche dalle osservazioni Lagrange derivò che, indicando con λ la longitudine di un satellite, λ₁−3λ₂+2λ₃=180°. La spiegazione di queste relazioni sarebbe rimasta nascosta per altri due decenni.

Laplace sull'immunità dei moti medi dalla variazione secolare

Pierre-Simon de Laplace (1749-1827) entra nella nostra storia con una memoria completata nel 1773 ma apparsa per la prima volta nel 1776. Nella prima metà di questa si discute in generale su questioni concernenti la gravitazione universale e l'accelerazione secolare della Luna. La seconda metà è dedicata alle variazioni secolari degli elementi orbitali dei pianeti; in particolare, vi si trova la dimostrazione che, con ottima approssimazione, i moti medi dei pianeti (o, equivalentemente, le loro distanze medie dal Sole) non sono affetti dalla variazione secolare.

Nelle equazioni differenziali del moto perturbato, Laplace indicò le masse dei corpi perturbati e perturbanti rispettivamente con δm e δm′; i termini con effetti perturbativi in queste equazioni contenevano pertanto il fattore δm′. Tornando alle equazioni per il moto imperturbato, egli le derivò rispetto all'operatore 'δ', aggiunse loro i termini perturbativi precedentemente identificati e così ‒ sfruttando la commutabilità tra 'δ' e l'operatore 'd' della derivazione ordinaria ‒ ottenne equazioni differenziali sia per δφ sia per δr, ossia per le variazioni, rispettivamente, della longitudine e del raggio vettore prodotte dalla perturbazione.

Laplace risolse queste equazioni col metodo dei coefficienti indeterminati, limitandosi a calcolare i contributi principali alle variazioni secolari. Aggiungendo il valore risultante δφ al valore di φ ricavato per il moto imperturbato, egli ottenne:

dove δμ′=δm′/S, con S massa solare, n è il valore che il moto medio per unità di tempo avrebbe in assenza del pianeta perturbatore, αe l'eccentricità dell'orbita del pianeta perturbato, A, B e D sono costanti che dipendono dai coefficienti della serie trigonometrica che esprime v⁻³ e, infine, il coefficiente di t² dà la variazione secolare del moto medio. Assumendo a′/a=z e indicando con θ l'angolo eliocentrico tra i due pianeti, Laplace scelse, per i coefficienti della serie trigonometrica che esprime v⁻³, una notazione con due indici che diamo qui nella forma finale con cui apparve nella Mécanique céleste (Oeuvres, I, p. 292 e segg.):

Egli fu il primo a estendere lo sviluppo in serie di v⁻³ fino all'ordine dei quadrati delle eccentricità, e dunque a calcolare i coefficienti b nella terza riga della [37]. Calcolando numericamente (B−eD) nella [36], egli ottenne un valore prossimo a zero; usando allora le formule euleriane per esprimere tutte le

in termini di

Laplace dimostrò che (B−eD) si riduce identicamente a zero. Ne concluse che l'accelerazione secolare di Giove e la decelerazione secolare di Saturno (da lui a questo punto accettate come un dato di fatto) non potevano essere causate dalla loro mutua interazione e avanzò l'ipotesi che esse potessero essere causate da attrazioni esercitate dalle comete.

Lagrange e Laplace sulle perturbazioni planetarie, 1774-1785

In una memoria inviata all'Académie di Parigi nell'ottobre del 1774, Lagrange ridusse il problema delle variazioni secolari delle inclinazioni orbitali e dei nodi dei pianeti a quello di risolvere un sistema di equazioni differenziali lineari del primo ordine. Qui l'intuizione geniale fu di rimpiazzare la tangente dell'inclinazione orbitale θ e la longitudine ω del nodo ascendente con le nuove variabili:

[38] u=θsenω, s=θcosω.

Indicate con a₁, a₂, ecc. le distanze medie dei pianeti dal Sole e con (a₁, a₂), (a₁, a₃), ecc. le costanti delle serie trigonometriche per gli inversi dei cubi delle distanze tra i pianeti prese a due per volta (ossia ciò che nella notazione laplaciana è rappresentato dalle costanti

differenti per ogni coppia di pianeti) e indicando inoltre con μ₁, μ₂, ecc. i moti medi di questi pianeti e con m₁, m₂, ecc. le loro masse relative alla massa solare, per mezzo delle abbreviazioni

Lagrange ottenne le equazioni differenziali per s₁, u₁, s₂, u₂, … nella forma:

Le soluzioni di queste equazioni erano della forma:

In tali soluzioni le costanti a, b, c, … rappresentavano le radici di un'equazione di grado n incontrata nella soluzione della [40] e A₁, B₁, C₁, …, A₂, B₂, C₂, …, α, β, γ, … erano costanti arbitrarie, determinabili dai valori empirici di s₁, u₁, s₂, … a un istante assegnato.

Determinare le costanti nella [41] è difficile e nell'applicare questa equazione ai pianeti Lagrange considerò Giove e Saturno come un sistema separato, ottenendo così quattro equazioni molto più semplici. Dopo averle risolte, dimostrò che i nodi e le inclinazioni orbitali di questi pianeti oscillano tra limiti fissi con un periodo di 51.150 anni. Egli tralasciò questa volta di occuparsi della questione se una simile condizione valesse anche per i pianeti più piccoli.

Laplace lesse il lavoro di Lagrange al suo arrivo a Parigi, prima che fosse pubblicato, e subito si accorse che un'analoga procedura poteva essere applicata agli afeli e alle eccentricità orbitali. Ciò vuol dire che, introducendo nuove variabili h, k, del tipo h=e senL, k=e cosL, dove e è l'eccentricità e L la longitudine dell'afelio, sarebbe stato possibile ottenere e risolvere equazioni differenziali lineari del primo ordine in dh/dt e dk/dt per i vari pianeti del Sistema solare. Lagrange stesso aveva previsto questa possibilità, ma un'applicazione completa dell'idea fu pubblicata per la prima volta da Laplace, sia pure con il dovuto riconoscimento dell'ispirazione che Lagrange gli aveva dato (Recherches sur le calcul intégral et sur le système du monde, 1772-1776).

A questo punto Laplace era apparentemente pronto per l'assalto al problema delle variazioni secolari. Il suo silenzio su questo argomento durò invece per dieci anni; egli si dedicò alle attrazioni degli sferoidi, alle maree e a problemi correlati con questi argomenti. Come spiegò in seguito a Lagrange in una lettera del 10 febbraio 1783, egli si era trovato in difficoltà per le incertezze sui valori delle masse dei pianeti più piccoli e sulla misura dell'influsso delle comete sui moti planetari. Nel corso di questo decennio Lagrange continuò a dedicare i suoi sforzi al problema delle perturbazioni planetarie, alla continua ricerca di formulazioni che avessero caratteristiche sia di eleganza sia di generalità. In una memoria presentata all'Accademia di Berlino nel 1776 e pubblicata nel 1779, egli diede una nuova dimostrazione dell'immunità dei moti medi planetari dalla variazione secolare. Questa memoria contiene la formulazione classica della variazione degli elementi orbitali e introduce la 'funzione perturbatrice' (secondo la denominazione di Laplace), ossia una funzione potenziale da cui è possibile ricavare, per derivazione parziale, le forze perturbative lungo differenti direzioni. Nella sua memoria del 1774 ‒ vincitrice del premio di detta Accademia ‒ sull'equazione secolare della Luna, Lagrange aveva già usato una funzione potenziale per derivare la forza di gravità esercitata da un corpo esteso, come la Terra, su una particella; la memoria del 1776 fu la prima nella quale egli introdusse una funzione potenziale per le forze tra punti materiali che si attraggono l'un l'altro. Egli definì questa funzione mediante l'espressione:

dove x, y, z sono le coordinate del pianeta soggetto alla perturbazione, m_i è la massa dell' i-esimo pianeta perturbante, le cui coordinate sono x_i, y_i e z_i, r_i il modulo del suo raggio vettore e v_i la sua distanza dal pianeta perturbato.

Indicando con d′ la differenziazione rispetto alle coordinate del pianeta perturbato, Lagrange scrisse:

e dimostrò che

dove a è il semiasse trasverso dell'orbita del pianeta perturbato, S è la massa del Sole e m è la massa del pianeta perturbato. Il membro di destra della [44] può essere rappresentato da una serie i cui termini hanno la forma:

dove la scrittura (sen/cos) significa che si prende a seconda dei casi la funzione seno oppure la funzione coseno; M è una funzione degli elementi orbitali del pianeta; p, q, r, … assumono valori interi positivi, negativi o nulli e le a che compaiono nei denominatori sono i semiassi trasversi dei vari pianeti. L'integrale della [45] ha la forma:

La conclusione di Lagrange fu che poiché il termine 1/(2a) contenuto nella [44] era dato da una serie i cui termini hanno la forma [46], esso era soggetto soltanto ad anomalie periodiche, posto che il denominatore della [46] non fosse mai nullo per ogni insieme particolare di valori di p, q, r, ... "Ma ‒ scrisse Lagrange ‒ è facile convincersi che questo caso non può verificarsi nel nostro sistema, in cui i valori di a^3/2, a₁^3/2, a₂^3/2, ... sono tra loro incommensurabili" (Sur l'altération des moyens mouvements des planètes, in Oeuvres, p. 270). Per quanto probabile, l'asserita incommensurabilità non fu dimostrata ed egli, come aveva fatto Laplace, la diede per scontata. Nel 1783 Lagrange riconobbe che la dimostrazione precedente non esclude la possibilità di variazioni secolari di 1/(2a), che traggono origine da variazioni secolari degli elementi orbitali di cui M è funzione.

In una memoria presentata all'Accademia di Berlino nel 1777 e pubblicata nel 1779, egli usò la funzione perturbatrice per dimostrare che, in un sistema di corpi che si attraggono con la legge dell'inverso del quadrato della distanza, il momento angolare e le 'forze vive' si conservano e il centro di gravità si muove di moto uniforme. Questa è la prima derivazione sistematica, per un sistema del genere, di tutti gli integrali del moto conosciuti.

Negli anni 1781 e 1782 Lagrange completò le due parti di un lungo trattato sulle diseguaglianze secolari; esse furono pubblicate nel 1783 e nel 1784 e Laplace espresse a Lagrange, in una lettera del febbraio 1784, la sua felicità nel vedere che i loro risultati erano in accordo. Per tutti i sei pianeti conosciuti, le variazioni annuali degli afeli, delle eccentricità, dei nodi e delle inclinazioni (determinate dalle equazioni differenziali, senza integrazione) erano piccole. L'incertezza maggiore traeva origine dal valore sconosciuto delle masse di Marte, Venere e Mercurio, che Lagrange ipotizzò essere inversamente proporzionali alle distanze dal Sole; supposizione che, come sappiamo oggi, era sbagliata.

Per risultati validi sul lungo termine, occorreva integrare le equazioni differenziali. Come aveva fatto già nella memoria del 1774, Lagrange considerò Giove e Saturno come un sistema isolato e di nuovo trovò un'oscillazione delle inclinazioni e dei nodi di questi pianeti; ora, in aggiunta, ottenne un'oscillazione simile anche per gli afeli e per le eccentricità. Nel caso dei pianeti minori ‒ Mercurio, Venere, Terra e Marte ‒ egli ottenne per ciascuna delle variabili s, u, h, k espressioni formate da sei termini sinusoidali; aggiungendo i valori assoluti dei coefficienti di questi termini, ricavò alcuni limiti superiori per le inclinazioni e le eccentricità, che si rivelarono essere tutti piuttosto piccoli. Lagrange osservò tuttavia che sarebbe stato desiderabile ottenere una dimostrazione della stabilità indipendente dai valori, non noti, delle masse.

Alle diseguaglianze periodiche ‒ distinte dalle variazioni secolari in quanto dipendenti dalla posizione dei pianeti nelle loro orbite ‒ Lagrange dedicò un trattato a parte, sempre basato sul metodo della variazione degli elementi orbitali. Nella Théorie des variations séculaires egli aveva derivato la variazione dp del moto medio, espressa mediante il moto vero:

dove β, γ, δ, ε, ecc. sono funzioni degli elementi orbitali. Essendosi reso conto che p avrebbe potuto essere soggetto a variazioni secolari apparenti a causa delle variazioni degli elementi orbitali, egli separò la variazione del moto medio in due parti: una parte periodica dp che varia in funzione del semiasse trasverso in base alla relazione dp∝dt/a^3/2, e un'altra parte dΣ che dipende soltanto dalle variazioni secolari degli altri elementi orbitali. La [47] pertanto diviene:

La variazione dΣ dipende da dβ, dγ, dδ, ecc. e deve essere messa in relazione, come ci dice Lagrange, con l'epoca, "la quale nelle orbite non soggette a variazioni contiene la sesta costante arbitraria di integrazione […]" (Théorie des variations périodiques, in Oeuvres, p. 350). Qui, per la prima volta, tutti e sei gli elementi dell'orbita furono condotti alla portata del metodo della variazione analitica degli elementi orbitali.

Lagrange proseguì mostrando che un'espressione per Σ accurata al primo ordine nelle potenze delle eccentricità, delle inclinazioni e delle forze perturbatrici è immune dalla variazione secolare, ma che se l'approssimazione è portata al secondo ordine nelle eccentricità e nelle inclinazioni, allora emergono termini in dΣ proporzionali al tempo. In una speciale aggiunta al lavoro egli mostrò che per quanto riguarda Giove e Saturno questi termini secolari erano troppo piccoli per rendere conto delle anomale accelerazione di Giove e decelerazione di Saturno. Lagrange osservò che tra i termini di ordine superiore in dΣ sarebbe bastato prendere in considerazione quelli che erano grandemente accresciuti sotto l'operazione d'integrazione; questi sarebbero stati i termini contenenti seni o coseni di angoli variabili lentamente rispetto a p. Così, se un angolo π varia in modo tale che dπ=λdp, dove λ è molto piccolo, allora la prima integrazione produce un fattore λ⁻¹ e la seconda integrazione introduce un fattore λ⁻²; i termini risultanti sarebbero dunque molto grandi. L'angolo π deve però essere una combinazione lineare degli angoli p, p₁, p₂, ... per i vari pianeti. Di qui un esame delle possibili combinazioni lineari rivela quali di esse, una volta integrate, conducono a termini particolarmente grandi. Questa osservazione può aver giocato un ruolo importante nella scoperta di Laplace della 'grande anomalia' di Giove e Saturno.

La soluzione di Laplace delle grandi anomalie, 1785-1787

Dal punto di vista della teoria newtoniana della gravitazione, le principali anomalie nei moti del Sistema solare ancora insolute nel XVIII sec. e fino al 1785 erano due: un continuo incremento del moto medio lunare apparente, scoperto da Halley negli anni Novanta del Seicento e valutato da Richard Dunthorne nel 1749 pari a 10″/secolo, e un'apparente accelerazione di Giove e decelerazione di Saturno, che Halley, nelle sue Tabulas astronomicas pubblicate postume nel 1749, stimò essere, in 2000 anni, pari a 3°49′ per Giove e −9°16′ per Saturno. Per la spiegazione dell'accelerazione lunare era stato indetto due volte un premio dall'Académie Royale des Sciences di Parigi, nel 1770 e 1772, ma nessuna causa gravitazionale era stata trovata per questo effetto.

Il 23 novembre 1785 Laplace annunciò all'Académie di aver risolto l'anomalia dei moti medi di Giove e di Saturno. Due erano gli argomenti che suggerivano che l'anomalia fosse periodica e causata dall'interazione gravitazionale. Johann Heinrich Lambert aveva scoperto che, dalla metà del XVII sec., Giove era andato rallentando e Saturno accelerando, invertendo così il precedente andamento. Lo stesso Laplace, partendo dalla conservazione delle forces vives per un sistema di punti materiali interagenti (senza dubbio presa da Lagrange) mostrò che, in buona approssimazione, la quantità ∑ⁿ_i=1(m_i/a_i) era pari a una costante. Considerando Giove e Saturno (indici rispettivamente J e S per le relative grandezze) come un sistema isolato, egli notò che le loro distanze medie a_J e a_S erano, in unità astronomiche, rispettivamente pari a 1/n_J^2/3 e a 1/n_S^2/3, dove n_J e n_S sono i moti medi espressi in cicli per anno; egli poté allora scrivere m_Jn_J^2/3+m_Sn_S^2/3=costante, concludendo che δn_J/δn_S=−(m_S/m_J)(n_J/n_S)^1/3=−1/2,33. Questo rapporto era quasi uguale a quello trovato da Halley per le accelerazioni secolari, ossia 3°49′/(−9°16′)=−1/2,43 (laddove le osservazioni recenti forniscono il valore −1/2,48). Le variazioni potevano pertanto essere attribuite all'interazione gravitazionale.

Come se stesse seguendo le istruzioni dello stesso Lagrange, Laplace cercò ora una combinazione lineare dei moti medi di Giove e Saturno la cui variazione, nell'intervallo di tempo dt, fosse piccola rispetto a n_Jdt o n_Sdt. Di fatto, il periodo dell'orbita di Giove è poco meno di 12 anni e quello di Saturno è di poco inferiore a 30 anni; ne segue che (2n_J−5n_S)dt è piccolo. Dal calcolo dei termini perturbativi, Laplace sapeva già che il coefficiente di ogni termine nella longitudine proporzionale a sen[(2n_J−5n_S)t] doveva contenere uno dei seguenti fattori di ordine tre nelle eccentricità e_J, e_S e nella tangente γ dell'inclinazione dei due piani orbitali: e_J³, e_S³, e_J²e_S, e_Je_S², e_Jγ² o e_Sγ². A causa della piccolezza di questi fattori, si era ritenuto che il termine risultante fosse trascurabile. Tuttavia, poiché le equazioni differenziali sono del secondo ordine, è richiesta un doppia integrazione, per cui l'integrale del termine in questione conterrà nel suo coefficiente il fattore (2n_J−5n_S)⁻², che è molto grande, facendo sì che tale termine risulti rilevante. Calcolando e sommando l'uno all'altro i vari contributi che entrano a far parte dei due coefficienti, Laplace trovò per Giove l'anomalia +(20′49,5″)sen[(2n_J−5n_S)t+costante] e per Saturno −(48′44)sen[(2n_J−5n_S)t+costante]. Queste anomalie hanno un periodo di circa 900 anni.

La spiegazione completa di Laplace della teoria di Giove e Saturno apparve nel 1785: in essa si mostrava che tale teoria era in accordo sia con le osservazioni antiche sia con quelle recenti. Laplace ne dedusse che le masse delle comete erano troppo piccole per perturbare i moti planetari in maniera percettibile. Risultava così risolta la 'grande anomalia' di Giove e Saturno, la più consistente fra quelle del Sistema solare.

La memoria di Laplace del 23 novembre 1785 conteneva altri due argomenti. Uno riguardava le caratteristiche risonanze tra i primi tre satelliti galileiani di Giove; Lagrange le aveva scoperte ma non ne aveva dato una spiegazione. Da un esame delle interazioni tra questi satelliti, dipendenti dai quadrati delle distanze e dai prodotti delle loro masse, Laplace derivò un'equazione differenziale del secondo ordine per V=λ₁−3λ₂+2λ₃, il cui integrale primo dV/dt si mostrò suscettibile d'una soluzione oscillante attorno a V=180°, il che spiegava le risonanze studiate da Lagrange. La soluzione conteneva una stretta analogia con quella che Lagrange aveva trovato per il moto di librazione della Luna. In entrambi i casi fu mostrato che l'equilibrio attuale non doveva necessariamente essere sempre esistito ma, per condizioni iniziali non troppo differenti da quelle attuali, sarebbe stato causato dall'azione delle forze. Infine, nella memoria del novembre 1785 Laplace fornì una nuova dimostrazione della stabilità del Sistema solare, basata sulla conservazione del momento angolare, nella quale mostrò esplicitamente che tutte le eccentricità e le inclinazioni dovevano restare piccole. Il suo sviluppo in serie del momento angolare, però, era soltanto approssimato, poiché era troncato al secondo ordine nelle eccentricità e nelle inclinazioni, e così ‒ come Le Verrier osservò in seguito ‒ la conseguenza tratta da Laplace sarebbe stata valida soltanto nel caso in cui tutte le masse planetarie fossero state approssimativamente uguali; ciò è evidentemente falso per pianeti come Mercurio, Venere, Terra e Marte, così piccoli in confronto a giganti come Giove e Saturno. Laplace tuttavia non si accorse di questo difetto della sua dimostrazione.

Laplace presentò all'Académie di Parigi la sua spiegazione dell'apparente accelerazione secolare della Luna il 19 dicembre 1787 e questa memoria fu pubblicata l'anno seguente. L'eccentricità orbitale della Terra, come era stato dimostrato anni prima, diminuisce lentamente a causa della perturbazione dei pianeti; la sua diminuzione causa un lieve decremento della componente radiale della forza perturbatrice che il Sole esercita sulla Luna e, da ciò, segue che l'attrazione esercitata dalla Terra sulla Luna è relativamente più efficace, per cui la Luna si sposta su un'orbita più bassa e si muove attorno alla Terra con velocità angolare maggiore. I valori calcolati da Laplace dell'incremento di velocità angolare, corrispondenti a 10″/secolo ca., erano in accordo coi valori empirici generalmente accettati. Era possibile aspettarsi che in futuro l'accelerazione lunare avrebbe cambiato segno allorché, dopo milioni di anni, l'eccentricità dell'orbita della Terra avrebbe ricominciato a crescere.

Come John Couch Adams avrebbe osservato nel 1854, anche se i calcoli di Laplace erano esatti, egli aveva omesso di prendere in considerazione la componente trasversale della forza perturbatrice dovuta al Sole. Allorché fu fatto il calcolo in cui si teneva conto anche di tale forza, si vide che solamente 6″ dell'accelerazione secolare osservata erano giustificati teoricamente. La spiegazione sulla quale si sarebbe finalmente trovato accordo nel XX sec. contiene due termini aggiuntivi: uno che Laplace aveva scartato e uno che egli non aveva neppure immaginato, ossia un'irregolare diminuzione della velocità diurna di rotazione della Terra, dovuta all'attrito delle maree e a un trasferimento di energia mareale alla Luna; tale diminuzione faceva sì che quest'ultima si portasse su un'orbita più alta, con un movimento medio angolare più lento. Il valore attuale osservato del movimento medio della Luna è il risultato netto di tutti questi effetti.

Le prospettive alla fine del XVIII secolo

I procedimenti di Laplace per il calcolo delle perturbazioni furono presentati nella loro forma definitiva nella Mécanique céleste, i primi quattro volumi della quale uscirono tra il 1798 e il 1805 e contenevano anche una dettagliata applicazione della teoria ai pianeti e alla Luna. L'opera era caratterizzata da un esprit di fiducioso ottimismo, dal momento che tutte le anomalie dei moti planetari potevano essere spiegate e, di fatto, lo sarebbero state; la teoria lunare era stata sviluppata fin quasi al punto in cui tutte le anomalie avrebbero potuto essere dedotte con il grado di accuratezza voluto dalla sola gravitazione universale, fatte salve le indispensabili condizioni iniziali. La Mécanique céleste (soprattutto quando fu accompagnata dal commento di Nathaniel Bowditch) sarebbe stata per molti decenni il libro di testo dal quale gli astronomi matematici avrebbero appreso la loro arte. Tuttavia, è da notare un certo opportunismo nelle deduzioni effettuate da Laplace; egli, infatti, si servì di un insieme di metodi diversi, scegliendo l'uno o l'altro a seconda di quale offriva la strada più veloce verso lo scopo da raggiungere. Così, nel caso di Giove e Saturno, Laplace derivò le perturbazioni di breve periodo mediante una modifica del procedimento di Clairaut e le aggiunse poi all'anomalia vera; per calcolare le anomalie di lungo periodo usò invece un procedimento diverso, addizionandole poi all'anomalia media. Ci si può chiedere se questi diversi procedimenti siano coerenti tra loro. E ancora: nel caso della Luna egli ipotizzò che l'inclinazione dell'orbita rispetto all'eclittica fosse costante, sebbene ciò valesse soltanto approssimativamente. Correggere questi difetti avrebbe significato ricominciare tutto dal principio.

Il punto di partenza per il nuovo inizio sarebbe stato la Méchanique analitique di Lagrange (la prima edizione è del 1788; la seconda, con importanti aggiunte, è del 1814), un'opera che è stata definita "a fondamento della moderna fisica teorica" (Gutzwiller 1998, p. 613). Qui la soluzione delle equazioni differenziali per i problemi perturbativi era ottenuta sempre con il metodo di variazione delle costanti arbitrarie. Tale metodo, dagli anni Trenta dell'Ottocento in poi, ricevette importanti contributi innovativi da parte di Peter Andreas Hansen, William Rowan Hamilton, Carl Gustav Jacob Jacobi e Charles-Eugène Delaunay, tramite un approfondimento delle nozioni fondamentali e un'estensione delle applicazioni, con procedure strettamente rigorose, a perturbazioni d'ordine più elevato.