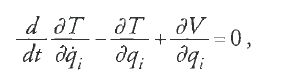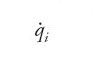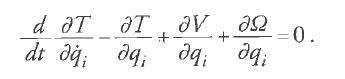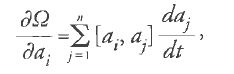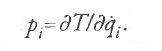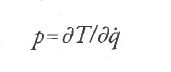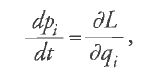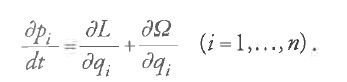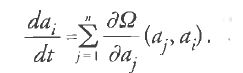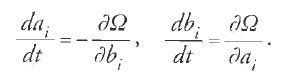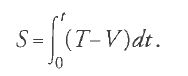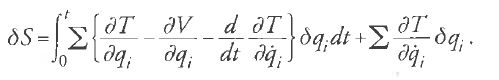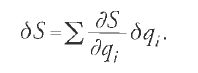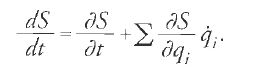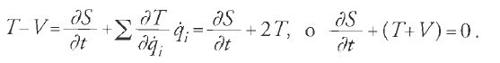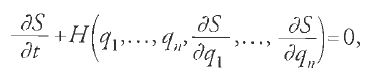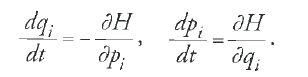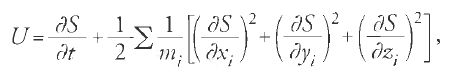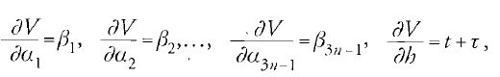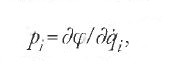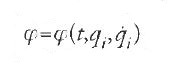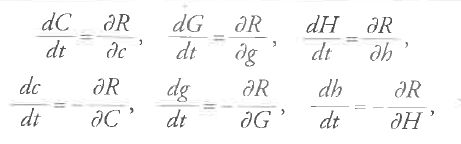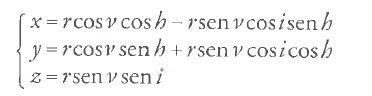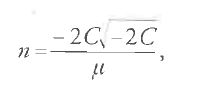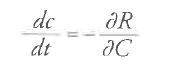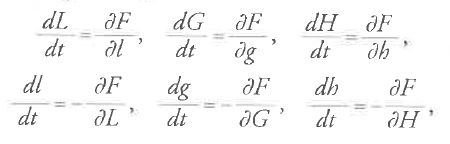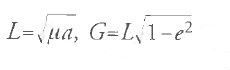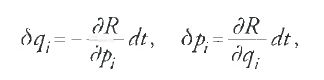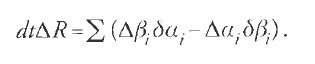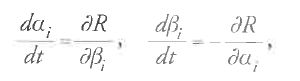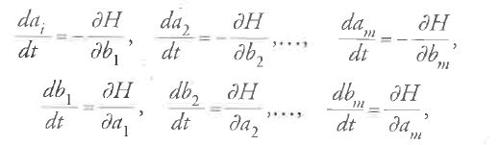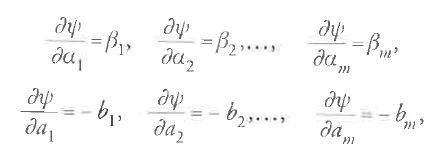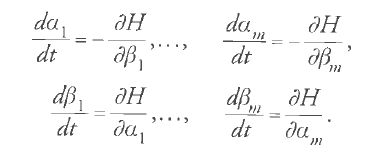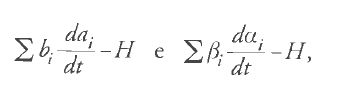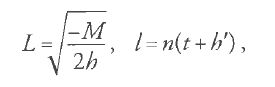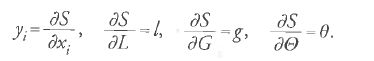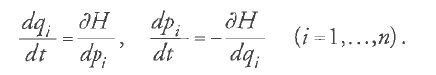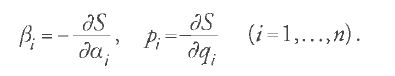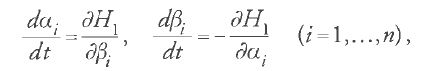L'Ottocento: astronomia. La meccanica celeste dopo Laplace: la teoria di Hamilton-Jacobi

L'Ottocento: astronomia. La meccanica celeste dopo Laplace: la teoria di Hamilton-Jacobi

La meccanica celeste dopo Laplace: la teoria di Hamilton-Jacobi

La teoria di Hamilton-Jacobi, così come si trova esposta nei manuali odierni, non comprende soltanto i risultati di tutto rilievo ottenuti da William R. Hamilton e Carl Gustav Jacob Jacobi, ma anche contributi molto importanti di Joseph-Louis Lagrange, Siméon-Denis Poisson, Michail Vasil´evič Ostrogradskij, Jules-Henri Poincaré e altri ancora. Su un piano strettamente matematico, essa può essere intesa come un'interessante sintesi di argomenti diversi, quali il calcolo delle variazioni, le equazioni differenziali ordinarie e alle derivate parziali, la geometria differenziale e la meccanica analitica. Storicamente la teoria di Hamilton-Jacobi si è sviluppata nel tentativo di analizzare il moto dei sistemi di corpi nell'ambito della meccanica celeste e quest'ultima ha continuato a essere il suo principale stimolo e campo di applicazione per tutto il XIX secolo. Qui di seguito esamineremo gli eventi più significativi che accompagnarono lo sviluppo della teoria nel corso dell'Ottocento, occupandoci sia delle sue caratteristiche e del suo significato in quanto teoria matematica, sia delle sue applicazioni allo studio delle perturbazioni nella meccanica celeste.

La teoria delle perturbazioni di Lagrange e Poisson

Il matematico italiano Joseph-Louis Lagrange (1736-1813) completò la sua opera principale, la Méchanique analitique, nei primi anni Ottanta del XVIII sec., quando era direttore della classe di matematica della Königliche Preussische Akademie der Wissenschaften (Accademia Reale Prussiana delle Scienze) di Berlino; egli ne seguì poi personalmente la pubblicazione in Francia nel 1788, poco dopo il suo trasferimento a Parigi.

Il trattato è un ampio manuale sulla statica e sulla dinamica, basato su una formulazione generale del principio dei lavori virtuali. Tale principio era enunciato nonché applicato ricorrendo al δ-formalismo del calcolo delle variazioni. Il risultato fondamentale di Lagrange fu la derivazione della forma cosiddetta 'lagrangiana' delle equazioni differenziali del moto:

per un sistema con n gradi di libertà e coordinate generalizzate q_i (i=1,...,n) le cui derivate rispetto al tempo sono indicate come

Le quantità T, funzione scalare di q_i e

e V, funzione di q_i, rappresentano rispettivamente, secondo la terminologia adottata successivamente in fisica, l'energia cinetica e l'energia potenziale del sistema.

I vantaggi di tali equazioni sono ben noti: la loro applicabilità a un'ampia varietà di sistemi fisici, la possibilità di scegliere liberamente le coordinate più appropriate per la descrizione del sistema, l'eliminazione di forze vincolari, la loro semplicità ed eleganza.

La teoria di Lagrange-Poisson

Siméon-Denis Poisson (1781-1840) nacque in una città di provincia, da una famiglia appartenente al ceto medio e raggiunse una posizione di prestigio nella vita scientifica parigina durante uno dei periodi più vitali nella storia della scienza francese. Nel giugno del 1808 presentò una memoria all'Académie des Sciences di Parigi sul tema delle diseguaglianze secolari nel moto planetario, nella quale studiava il problema delle perturbazioni seguendo i dettami della dinamica analitica lagrangiana. Stimolato dalle idee di Poisson, Lagrange, che era stato uno dei recensori dello scritto, nei dodici mesi successivi sviluppò personalmente una serie di ricerche sulla teoria delle perturbazioni. Nell'ottobre del 1809, Poisson integrò la sua memoria dell'anno precedente con un lungo trattato sul problema della variazione di costanti arbitrarie in meccanica analitica; Lagrange perfezionò i risultati che aveva ottenuto in precedenza e ne fornì una presentazione sistematica nella seconda edizione della Méchanique analitique, il cui primo volume fu pubblicato nel 1811, seguito nel 1815 dal secondo.

All'origine della teoria di Lagrange-Poisson vi era un approccio analitico alla risoluzione di equazioni differenziali, rappresentato dal metodo della variazione delle costanti arbitrarie. Lagrange enunciò in due lavori scritti nel 1774 e nel 1775 tale metodo generale che fu alla base della riuscita analisi delle anomalie nel sistema Giove-Saturno-Sole sviluppata da lui stesso e da Laplace in seguito.

Si consideri un'equazione differenziale ordinaria di ordine n:

[2] x⁽ⁿ⁾=P(t,x,x',x⁽²⁾,...x^(n-1);

si assuma di conoscerne una soluzione completa

x=F(t, a₁,…,a_n)

che contenga n costanti arbitrarie a_i. Se si aggiunge a P una perturbazione Q=Q (t,x,x′,x⁽²⁾,…, x⁽ⁿ⁻¹⁾), l'equazione [2] diventa:

[3] x⁽ⁿ⁾(t)=P+Q.

Consideriamo ora soluzioni della [3] che abbiano la forma

y=F[t, a₁(t),…,a_n(t)],

dove le a_i, prima costanti, sono ora da considerare variabili. Il problema si riduce a quello di determinare le a_i come funzioni del tempo. Una condizione da imporre per la soluzione è che le derivate della x abbiano la stessa espressione in entrambi i casi: a_i costanti e a_i(t) variabili. Una seconda condizione deriva dal fatto che la porzione dell'equazione perturbata che contiene le parti non perturbate delle x e delle loro derivate è, in base alla [2], uguale a zero. Il metodo di integrazione che ne risulta è noto come metodo di variazione delle costanti arbitrarie.

Nei lavori del 1808 e del 1809, Poisson e Lagrange svilupparono questo metodo nel quadro del formalismo lagrangiano della Méchanique analitique. Sebbene la teoria finale sia stata ottenuta con il contributo di entrambi, e la formulazione data da Lagrange nella seconda edizione dell'opera appena citata abbia avuto maggiore influenza, alcune delle più importanti innovazioni concettuali sembrano dovute proprio a Poisson. Stimolato dal lavoro del giugno 1808 del suo giovane collega, Lagrange pubblicò immediatamente una memoria sulle perturbazioni del moto planetario, da lui generalizzata, sette mesi più tardi, a tutta la meccanica. Lagrange assunse che un termine perturbativo Ω(q₁,…, q_n) andasse ad aggiungersi al potenziale V delle equazioni del moto [1]:

Sia q_i=q_i (t,a₁,…,a_2n), con i=1,…,n, una soluzione completa delle equazioni di Lagrange in assenza di perturbazione, contenente le 2n costanti arbitrarie a_i. Possiamo considerare il termine perturbativo Ω come una funzione di tali costanti. Lagrange assunse che le coordinate q_i, in cui le a_i sono funzioni variabili di t, fossero soluzioni dell'equazione [4] e quindi derivò l'uguaglianza generale

nella quale compare la cosiddetta 'parentesi di Lagrange', definita come segue:

dove la nuova variabile p_i è definita come

Lagrange dimostrò che [a,b] è indipendente dal tempo, un importante teorema che avrebbe poi provato anche in maniera esplicita nella seconda edizione della Méchanique analitique.

Si noti che l'idea di porre

e di usare p come una nuova variabile era un'innovazione di un certo rilievo, già introdotta da Poisson nel suo scritto dell'ottobre 1809. Il concetto di tale 'momento coniugato' sarebbe diventato una delle nozioni fondamentali della teoria di Hamilton-Jacobi.

Poisson scrisse le equazioni lagrangiane nella forma

dove L=T−V. A differenza di Lagrange, che era interessato soprattutto alle q_i in quanto funzioni delle costanti arbitrarie che figurano nella soluzione della [1], Poisson assunse che gli integrali della [7] avessero la forma:

[8]  a=a(t,q₁,...,q_n,p₁,...,p_n),  b=b(t,q₁,...,q_n,p1,...,p_n)

e studiò le 2n costanti a e b come funzioni di p_i e q_i. Quindi definì quelle che sarebbero poi diventate note come 'parentesi di Poisson' di a e b nel modo seguente:

Poisson mostrò che se a e b sono integrali del sistema, la quantità (a,b) è indipendente dal tempo, sicché si ottiene un terzo integrale del moto nella forma (a,b)=cost. Nel 1866 Jacobi, riferendosi a quest'ultimo risultato, avrebbe scritto che Poisson aveva "compiuto il maggiore passo in avanti nella trasformazione delle equazioni del moto dopo la prima edizione della Méchanique analitique".

Poisson riscrisse l'equazione di Lagrange perturbata come segue:

Se q_i=q_i[t,a₁(t),…,a_n(t)] è un sistema di soluzioni della [10], allora le a_i(t) soddisfano le equazioni

Poiché la matrice {(a_i,a_j)} è l'inversa di {[a_i,a_j]}, si può affermare che la [11] è l'inversa della [5].

Un'altra importante innovazione introdotta da Poisson è la derivazione di equazioni differenziali del primo ordine per le funzioni dei parametri in forma simmetrica e tale da contenere le derivate parziali della funzione perturbatrice rispetto a tali parametri. Questo risultato fu ottenuto da Poisson nel lavoro dell'ottobre 1809, anche se egli non ne fornì alcuna dimostrazione o deduzione e considerò le equazioni stesse come prive di "grande utilità". Lagrange, viceversa, riconobbe la simmetria e l'utilità di tali equazioni, delle quali fornì una derivazione dettagliata nel Second mémoire del 1810 e nel primo volume della seconda edizione della Méchanique analitique (parte 2, sez.5). Imponendo che a₁,…,a_n rappresentassero i valori di q₁,…,q_n per t=0, e b₁,…,b_n i valori di p₁,…,p_n per t=0, Lagrange ottenne le equazioni differenziali del moto perturbato nella forma seguente:

Tav. I

In letteratura è invalsa l'abitudine di chiamare 'canonica' ogni equazione che presenti tale forma generale, sebbene il termine, introdotto da Jacobi, si possa associare più propriamente solo alle equazioni del moto derivate da Hamilton nel 1835. Le equazioni [12] sono connesse intimamente con le relazioni fondamentali [5] e [11] e costituiscono la pietra angolare della teoria delle perturbazioni di Lagrange e Poisson. Nella trattazione contemporanea esse sono ottenute in tutt'altro modo e il procedimento esposto da Lagrange nella Méchanique è pressoché sconosciuto, nonostante nella derivazione originaria delle [12] ci siano dettagli tecnici meritevoli di attenzione (Tav. I).

Hamilton

In due lavori pubblicati nel 1834 e nel 1835 nelle "Philosophical Transactions" della Royal Society di Londra, il matematico irlandese William R. Hamilton (1805-1865) poneva le basi di una nuova teoria dinamica. Dopo aver studiato al Trinity College di Dublino, Hamilton proseguì la sua carriera come astronomo reale d'Irlanda e direttore dell'Osservatorio di Dunsink. Oltre che per i suoi lavori di dinamica, è ricordato per l'invenzione di una nuova struttura algebrica: i quaternioni. Alcune delle sue idee fisiche traggono origine dagli studi giovanili di ottica e la loro applicazione alla dinamica fu motivata dallo studio da lui condotto sui problemi delle perturbazioni nei moti planetari.

Gli studi di ottica

A partire dal 1828, Hamilton pubblicò una serie di lavori sulla teoria dei raggi in ottica geometrica. Egli definiva un sistema di raggi come un fascio di raggi che possiedono qualche proprietà in comune, come l'essere stati tutti emessi da una sola sorgente puntiforme o tutti riflessi da uno specchio, sicché diventa possibile costruire rispetto a essi una superficie comune, o 'congruenza normale'. Hamilton estese le ricerche di Étienne-Louis Malus su questo argomento introducendo un nuovo strumento matematico, la cosiddetta 'funzione caratteristica', che descrive il comportamento dei raggi allorché passano attraverso uno strumento ottico. Mostrò che la funzione caratteristica soddisfa un'equazione differenziale alle derivate parziali del primo ordine non lineare e che, una volta trovata la soluzione di quest'equazione, si può descrivere completamente il comportamento globale del sistema.

Hamilton, inoltre, mostrò che un raggio di luce segue un percorso determinato da una legge variazionale, che risulta essere valida nell'ambito sia della teoria ondulatoria della luce sia di quella corpuscolare, ma che è interpretata diversamente nei due contesti: nella teoria corpuscolare, essa assume la forma del principio di minima azione di Lagrange valido per la dinamica; nel contesto della teoria ondulatoria, invece, si riduce al principio del tempo minimo di Fermat, che vale per l'ottica. La funzione caratteristica descrive le proprietà di raggi di luce governati da tale legge. Le ricerche di Hamilton dimostrarono l'esistenza di una più profonda connessione matematica tra il calcolo delle variazioni ‒ la branca tradizionale dell'analisi superiore che si occupa dei massimi e dei minimi ‒ e la teoria delle equazioni differenziali alle derivate parziali.

Hamilton indagò sui fenomeni ottici avvalendosi della sua nuova teoria e, così facendo, formulò un'importante previsione circa un fenomeno poi noto come rifrazione conica. Sulla base della teoria ondulatoria della luce, congetturò che un singolo raggio incidente secondo un particolare angolo avrebbe formato un cono cavo all'interno di un cristallo biassiale, emergendone poi sotto forma di cilindro cavo. Oppure che, facendo incidere sul cristallo un cono di raggi (focalizzato da una semplice lente) esso sarebbe divenuto un singolo raggio che viaggiava all'interno del cristallo nella direzione del centro della cuspide e sarebbe emerso come un cono cavo. Humphrey Lloyd (1800-1881), l'ideatore del programma di matematica adottato al Trinity College, riuscì a verificare sperimentalmente le ipotesi di Hamilton. Sebbene la previsione e la scoperta della rifrazione conica appartengano all'ottica geometrica, tale risultato offriva un forte elemento a sostegno della teoria ondulatoria della luce. Per questo lavoro a Hamilton fu assegnata la Royal Medal.

Dinamica

Nelle sue ricerche di ottica geometrica, Hamilton fu colpito dalla somiglianza tra ottica e dinamica. Oltre all'analogia fisica tra il percorso di un raggio curvo in ottica e la traiettoria di un punto materiale, vi era anche parallelismo matematico tra il principio ottico variazionale di Hamilton e il principio di minima azione di Lagrange e tra la funzione caratteristica in ottica e l'integrale d'azione in dinamica. Hamilton si rese conto che si poteva dimostrare che l'integrale d'azione soddisfaceva un'equazione differenziale alle derivate parziali e che questo fatto poteva essere usato nell'analisi di sistemi legati di particelle soggette a forze gravitazionali. Nel 1833 applicò tale idea al sistema dei tre corpi costituito dal Sole, da Giove e da Saturno e scoprì alcune relazioni che non avevano alcun corrispettivo in ottica.

La prima fase di tale ricerca culminò nel lavoro pubblicato nel 1834 sulle "Philosophical Transactions", un articolo il cui scopo principale appare manifesto già nel titolo: On a general method employed in dynamics, by which the study of motions of all free systems of attracting or repelling points is reduced to the search and differentiation of one central solution, or characteristic function.

Per quanto riguarda l'evoluzione successiva della meccanica analitica, gli elementi essenziali della nuova teoria dinamica di Hamilton sono contenuti alla fine dell'articolo del 1834 e, più compiutamente, nel Second essay on a general method in dynamics, del 1835. Sebbene fosse fortemente influenzato dall'approccio di Lagrange alla meccanica, la straordinaria originalità delle sue idee derivava dal fatto che esse traevano origine dalle ricerche di ottica. La sua prima e più importante innovazione fu quella di collegare le equazioni differenziali ordinarie della dinamica a un'equazione differenziale alle derivate parziali che conteneva ciò che egli chiamava 'funzione principale'. L'equazione differenziale alle derivate parziali che ne risultava sarebbe poi diventata nota in dinamica come 'equazione di Hamilton-Jacobi'.

L'idea matematica generale alla base del suo lavoro ‒ della quale Hamilton, non avendola mai specificata in modo chiaro, potrebbe essere stato non del tutto consapevole ‒ è quella di considerare un integrale definito come una quantità che viene calcolata lungo una delle curve che rappresentano le soluzioni delle corrispondenti equazioni differenziali dinamiche. L'integrale che ne segue può essere considerato come una funzione di t e dei valori estremi delle coordinate. Considerando le variazioni di tale integrale, otteniamo un'espressione priva di componenti integrali e contenente soltanto quantità che sono calcolate nei punti estremi (tale idea è stata poi sviluppata nel calcolo delle variazioni e ha dato origine all'importante concetto di integrale di campo).

Supponiamo che la funzione da integrare sia T−V, ossia la lagrangiana del problema. Allora la funzione principale S viene definita così:

S va considerata come funzione del valore iniziale e finale di t e delle coordinate generalizzate q₁,…,q_n. In quanto segue, restringiamo per comodità le nostre considerazioni al caso in cui i valori iniziali delle q_i siano fissati, sicché S dipende solamente dai loro valori finali. Se consideriamo la variazione di S, con una procedura tipica del calcolo delle variazioni otteniamo:

Poiché S è calcolata lungo una curva che è soluzione delle equazioni dinamiche, il termine integrale nell'equazione [14] si riduce a zero e otteniamo quindi l'equazione:

Dato che S è funzione delle q_i, vale l'identità:

Confrontando i coefficienti delle δq_i nella [15] e nella [16], otteniamo infine le equazioni seguenti:

Derivando S rispetto al tempo abbiamo

Dalla [13] è evidente che dS/dt=T−V. Avvalendoci di tale uguaglianza e dell'equazione [17], dalla [18] otteniamo

Se teniamo conto che, grazie alla [17], ciascun

può essere espresso in termini di ∂S/∂q_i, ricaviamo infine l'equazione differenziale alle derivate parziali di Hamilton-Jacobi:

dove H=T+V, l'energia totale, è detta 'hamiltoniana' del sistema. La [20] è un'equazione differenziale alle derivate parziali non lineare del primo ordine nelle variabili q₁,…,q_n,t e S, in cui S non figura esplicitamente.

La seconda idea fondamentale di Hamilton fu che le equazioni di Lagrange potevano essere formulate diversamente, in una forma 'canonica'. Avvalendosi di un'idea che egli aveva trovato probabilmente in Poisson (di cui aveva consultato la memoria del 1809), pose la derivata parziale di T rispetto a ^.q_i uguale a una nuova variabile p_i e quindi mostrò che le n equazioni di Lagrange del secondo ordine [1] sono equivalenti alle 2n equazioni del primo ordine:

Sebbene le equazioni [21], chiamate da Jacobi 'canoniche', abbiano la stessa forma matematica di quelle con perturbazione di Lagrange-Poisson [12], esse sono equazioni del moto e occupano un posto fondamentale nell'intera teoria dinamica.

Una volta stabiliti i fondamenti della sua nuova teoria, Hamilton dimostrò come essa potesse essere applicata all'analisi delle perturbazioni nella meccanica delle particelle; anche se si trattò di un primo passo importante, il valore di questi risultati non era paragonabile a quello delle innovazioni teoriche introdotte da Hamilton. Egli divise S o H in una parte non perturbata (S₁ o H₁) e in una perturbata (S₂ o H₂), dopo averle calcolate separatamente, sommò il risultato al fine di ottenere un valore di S o H per l'intero sistema. Sebbene avesse dimostrato l'importanza, in linea di principio, della riduzione di un problema dinamico allo studio di una sola funzione, non ottenne progressi di particolare valore pratico, al punto che, nei due articoli citati, fornì la soluzione dell'equazione di Hamilton-Jacobi in un solo caso; d'altra parte, la sua analisi del problema dei due corpi era complicata quanto la soluzione tradizionale. Alla fine degli anni Trenta del XIX sec., il suo interesse si spostò dalla dinamica all'algebra, nel tentativo di trovare un analogo tridimensionale dei numeri complessi, un'indagine che culminò nel 1843 con la scoperta dei quaternioni. Lo studio di questo nuovo sistema algebrico assorbì le sue energie fino alla morte, avvenuta nel 1865.

Jacobi

Gli articoli pubblicati da Hamilton nelle "Philosophical Transactions" ebbero grande risonanza non soltanto in Gran Bretagna, ma anche tra i ricercatori continentali, tra i quali il matematico tedesco Carl Gustav Jacob Jacobi (1804-1851). Nato da una famiglia ebrea, Jacobi si convertì al cristianesimo con l'intento di proseguire in quella che si sarebbe rivelata una splendida carriera di matematico presso le università di Königsberg e di Berlino. Dopo la morte, avvenuta nel 1851 a causa delle conseguenze del diabete di cui soffriva, le sue lezioni sulla dinamica tenute a Königsberg nel 1842-1843 furono raccolte e pubblicate da Alfred Clebsch. Nelle Vorlesungen über Dynamik (Lezioni sulla dinamica, 1866), Jacobi riuscì a fare proprie le scoperte di Hamilton e a svilupparle in una teoria dinamica più generale, di grande bellezza e potenza matematica.

L'elaborazione di Jacobi della teoria di Hamilton

Laddove Hamilton si avvicinava alla dinamica partendo da idee tratte dall'ottica, Jacobi seguiva un percorso più convenzionale nell'ambito della meccanica analitica. Le sue doti di ricercatore e studioso risiedevano nell'insuperabile padronanza dell'analisi e nell'abilità creativa nello sviluppare nuovi algoritmi e nuove soluzioni tecniche. Il suo primo importante risultato in dinamica fu la scoperta, nel 1836, di un altro integrale per il problema dei tre corpi. Egli prese in considerazione un sistema fisico costituito dal Sole, da un pianeta e da un punto materiale e tale che, mentre il Sole e il pianeta interagiscono vicendevolmente e attraggono il punto, l'influenza di quest'ultimo sui due corpi principali risulti trascurabile. Jacobi considerò per il punto una funzione potenziale che contenesse esplicitamente il tempo e giunse così a un integrale del sistema. Quando venne a conoscenza degli articoli di Hamilton, Jacobi si rese conto che i risultati di quest'ultimo potevano essere estesi in modo del tutto naturale a sistemi non conservativi con potenziali dipendenti dal tempo. Hamilton, infatti, aveva concentrato l'attenzione su sistemi conservativi e, apparentemente, non era nemmeno consapevole della possibilità di trattare sistemi di tipo più generale; ciononostante, il ragionamento effettuato nella derivazione dell'equazione [20] è valido anche se il potenziale U dipende dal tempo, come notò Jacobi in Über die Reduktion der Integration der partiellen Differentialgleichungen (Sulla riduzione dell'integrazione delle equazioni differenziali parziali), pubblicato sul "Journal für die reine und angewandte Mathematik" nel 1837. Jacobi si rese conto inoltre che la teoria dinamica di Hamilton poteva essere sviluppata, entro un quadro matematico più generale, come parte del calcolo delle variazioni.

In Über die Reduktion, Jacobi presentò un risultato che da allora è diventato classico. La grande idea di Hamilton era stata quella di dimostrare che il problema dinamico ‒ tradizionalmente trattato in termini matematici come un problema di equazioni differenziali ordinarie ‒ poteva essere ricondotto all'analisi di un'equazione differenziale alle derivate parziali, la cosiddetta equazione di Hamilton-Jacobi. Jacobi mostrò come ottenere una soluzione delle equazioni dinamiche del moto a partire da una soluzione completa della corrispondente equazione di Hamilton-Jacobi. Quest'ultima può essere scritta in coordinate cartesiane come segue:

dove S è la funzione principale, U è il potenziale cambiato di segno con H=T−U. Una soluzione completa della [22] conterrà 3n costanti arbitrarie α₁,…,α_3n. Jacobi affermò, dimostrandolo, che il sistema di equazioni espresso nella forma

in cui si fa uso di un nuovo insieme di costanti arbitrarie β₁,…,β_3n, fornisce una soluzione completa delle equazioni differenziali del moto per il problema considerato.

Una volta ricavato tale risultato, Jacobi prese in esame il caso di una funzione potenziale che non dipende esplicitamente dal tempo; il sistema è dunque conservativo e quindi vale la legge di conservazione delle forze vive, o dell'energia meccanica. Sia la funzione V=V(x_i,y_i,z_i) definita come V=S+ht, dove h è l'energia totale. Se sostituiamo V−ht al posto di S nell'equazione [22], otteniamo l'equazione differenziale alle derivate parziali

Se V è una soluzione completa di quest'equazione che contiene le costanti arbitrarie α₁,…,α_3n−1, allora, invece della [23], la soluzione delle equazioni dinamiche si può scrivere nella forma

dove β₁, β₂, …, β_3n−1 e τ sono nuove costanti arbitrarie.

Nelle Vorlesungen del 1866 Jacobi estese tali risultati dalla dinamica al contesto molto più generale del calcolo delle variazioni. Hamilton, nel suo lavoro, si era avvalso del fatto che T è una funzione omogenea del secondo ordine nelle variabili

e che U dipende solamente dalle variabili q_i, condizioni particolari nel contesto dinamico. Jacobi si rese conto che la teoria avrebbe potuto essere sviluppata in termini più generali se si fosse posto

là dove φ è un integrando variazionale di tipo generale,

che nella teoria di Hamilton corrisponde a T−U. Egli chiarì così la relazione matematica tra il problema variazionale, l'equazione differenziale alle derivate parziali che comprende l'integrale di campo S e le equazioni di Euler in forma canonica. Il formalismo che ne seguì divenne la base della teoria di Hamilton-Jacobi così come è presentata nei manuali odierni di dinamica e matematica.

Il problema dell'attrazione verso due centri fissi

Il principale vantaggio pratico dell'affrontare il problema dinamico avvalendosi dell'equazione differenziale alle derivate parziali di Hamilton-Jacobi consiste nel fatto che, se le variabili sono completamente separate, l'equazione può essere risolta per quadrature. Diventa perciò indispensabile trovare, per ciascun problema, una sostituzione appropriata che permetta di separare le variabili. Sebbene Jacobi riconoscesse che non esiste una regola generale per effettuare tale riduzione, addusse alcuni esempi in cui le variabili potevano essere separate introducendo coordinate ellittiche. Egli, tra l'altro, determinò le curve geodetiche su un ellissoide a tre assi e fornì un'altra dimostrazione del teorema di Abel, un risultato puramente matematico che riguarda la soluzione di un sistema di equazioni differenziali ordinarie. Tuttavia il suo risultato più importante fu la soluzione del problema dell'attrazione da parte di due centri fissi.

Tale problema, proposto per la prima volta da Euler, è un caso particolare del problema dei tre corpi e prevede che due centri, pur non influenzandosi l'un l'altro, esercitino entrambi un'attrazione su un punto materiale. Euler aveva considerato il caso in cui il sistema giace su un piano, mentre Lagrange ‒ ricorrendo a particolari ipotesi sulla soluzione ‒ estese il problema allo spazio tridimensionale e ottenne equazioni che si risolvono in termini di integrali ellittici; Jacobi, nelle Vorlesungen, risolse completamente il problema, avvalendosi dell'equazione di Hamilton-Jacobi. Dopo aver introdotto coordinate ellittiche, mostrò che le variabili sono separabili e fornì una soluzione per quadrature. Dato che il problema non era risolvibile in altro modo, esso fornì un esempio notevole della potenza della teoria di Hamilton-Jacobi nell'analisi dinamica.

La teoria della Luna

Le notevoli teorie lunari sviluppate nella prima parte del XIX sec. dal barone Marie-Charles-Théodore Damoiseau e da Giovanni Antonio Amedeo Plana assumevano come punto di partenza le formule di Laplace. Nel 1835 Poisson tentò un approccio differente basandosi sul metodo della variazione delle costanti, sviluppato da lui e da Lagrange, ma non conseguì risultati di rilevanza pratica. Anche l'astronomo tedesco Peter Andreas Hansen (1795-1874), in un lavoro condotto tra il 1825 e il 1850 e coronato da maggiore successo, basò la sua analisi del moto della Luna sulla teoria delle perturbazioni di Lagrange e Poisson, così come era presentata nella seconda edizione della Méchanique analitique. Partendo dalle formule [9] e [11], nelle quali le quantità q_i e p_i sono sostituite dai loro valori a_i e b_i in un determinato istante, Hansen trovò le espressioni per le derivate rispetto al tempo degli elementi ellittici in termini delle derivate parziali della funzione di perturbazione. A tale fine espresse gli elementi ellittici come funzioni delle a_i e delle b_i, derivò rispetto al tempo ed espresse le derivate delle a_i e delle b_i così ottenute avvalendosi dell'equazione [11].

Le idee di Poisson e Lagrange furono inglobate più profondamente nell'approccio alla teoria lunare sviluppato da Charles-Eugène Delaunay (1816-1872). Questi cominciò la sua carriera a Parigi, con una dissertazione matematica che rappresentava un'ulteriore elaborazione di alcune delle nuove idee che Jacobi aveva introdotto nel calcolo delle variazioni, con l'articolo Zur Theorie der Variations-Rechnung (Sulla teoria del calcolo delle variazioni) pubblicato nel "Journal für die reine und angewandte Mathematik" del 1837. Delaunay proseguì la sua carriera diventando professore di meccanica e matematica a Parigi e poi direttore dell'Observatoire nel 1871.

Come Lagrange aveva predetto nel 1811, le equazioni canoniche [12], dette anche di Poisson-Lagrange, potevano essere utilizzate con efficacia in meccanica celeste. Nel 1860 e nel 1867 Delaunay sintetizzò venti anni di lavoro pubblicando due ampi scritti sul moto lunare basati su una formulazione modificata di queste equazioni. L'ispirazione teorica di Delaunay si basava su un articolo pubblicato nel 1841 da Jacques-Philippe-Marie Binet (1786-1856) sul "Journal de l'École Polytechnique". Binet, professore di astronomia al Collège de France, volle dimostrare che la teoria delle perturbazioni di Poisson e Lagrange poteva essere estesa dall'ambito della dinamica a quello di problemi matematici più generali riguardanti il calcolo delle variazioni. Egli fornì anche un'analisi molto dettagliata del moto ellittico perturbato e dimostrò che la derivazione da parte di Lagrange delle equazioni di Poisson-Lagrange poteva essere modificata in modo da consentire una più ampia scelta dei dati orbitali iniziali. In quest'opera, Binet attinse a un lavoro non pubblicato di Augustin-Louis Cauchy, che questi aveva realizzato nel 1831 durante il suo soggiorno a Torino e del quale era stato diffuso soltanto un numero limitato di copie litografate.

Binet scrisse le equazioni di Lagrange per il moto ellittico non perturbato (R=0) in coordinate polari e derivò le costanti arbitrarie del moto C, G, H, c, g, h, quantità che sarebbero divenute variabili nel caso di moto perturbato (R≠0). Applicando in modo innovativo la teoria di Lagrange del 1811, Binet riuscì quindi a dedurre le equazioni canoniche per il moto perturbato:

dove le variabili arbitrarie possono essere interpretate come elementi che determinano la posizione dell'orbita del pianeta. Le [26] vanno confrontate con le equazioni originali di Poisson-Lagrange [12], nelle quali gli elementi arbitrari erano semplicemente i valori iniziali delle coordinate e delle variabili coniugate.

Delaunay basò le sue indagini sulle equazioni newtoniane del moto che comprendevano la funzione perturbatrice. Egli trattò il moto della Luna come un problema tridimensionale ellittico ristretto ed espresse le coordinate rettangolari x,y,z della Luna rispetto alla Terra in termini delle quantità polari h,i,ν:

Qui h rappresenta la longitudine del nodo ascendente della Luna, i l'inclinazione dell'orbita lunare e ν l'angolo tra la linea nodale e il raggio congiungente la Luna alla Terra. Delaunay riportò le equazioni [26] di Binet, citandone la dimostrazione nella memoria apparsa nel 1841 sul "Journal de l'École Polytechnique". Egli richiamò l'attenzione su un 'grave inconveniente', che si manifesta ogni qualvolta si tenti di integrare le equazioni [26] scegliendo un valore appropriato per R. In generale R contiene un termine periodico della forma sen[n(t+c)] oppure cos[n(t+c)], ove la quantità n ha la seguente espressione:

dove μ è la somma delle masse dei corpi di cui si prende in considerazione il moto relativo.

Ne consegue che la soluzione dell'equazione

contiene un termine che ha la forma tcos[n(t+c)] oppure la forma tsen[n(t+c)], il cosiddetto termine secolare, nel quale t appare come coefficiente di una quantità trigonometrica. In tale caso c assume valori che crescono o decrescono indefinitamente nel tempo, conseguenza estremamente imbarazzante (extrêmement gênante), dal momento che si era fatta l'ipotesi che gli effetti della perturbazione restassero modesti. Delaunay modificò pertanto le equazioni di Binet e introdusse una sostituzione che eliminasse tali termini e preservasse al tempo stesso la forma canonica delle equazioni, ottenendo le seguenti equazioni:

con

e H=Gcosi, dove a rappresenta il semiasse maggiore dell'orbita, e l'eccentricità, i l'inclinazione dell'orbita rispetto a un piano fisso, l l'anomalia media, g la distanza angolare dell'apside inferiore dal nodo ascendente e h la longitudine del nodo ascendente; la funzione perturbatrice modificata F, uguale a R+μ2/(2L2), fu sviluppata da Delaunay come una serie infinita.

Nel 1876 l'astronomo americano George W. Hill (1838-1914) pubblicò su "Analyst" un lavoro sul metodo di Delaunay, in cui dichiarava che "tra gli innumerevoli insiemi di elementi canonici non sembra possibile trovarne uno migliore" (Hill 1876, p. 227). Egli inoltre richiamò l'attenzione su alcuni aspetti peculiari delle equazioni [30], quali il ricorso all'anomalia media l (che non è una costante nel moto ellittico) come elemento e l'aggiunta di un termine ulteriore alla funzione perturbatrice, un'innovazione introdotta da Delaunay al fine di impedire che nelle derivate parziali di F comparissero termini secolari dipendenti da t.

Delaunay sviluppò la funzione di perturbazione F fino al settimo ordine di piccoli parametri. Lo sviluppo in serie che ne derivava era composto di 320 termini, in cui comparivano termini moltiplicati per il coseno di una funzione lineare. Allo scopo di eliminare questi termini da F, egli impiegò un metodo specifico, la cui procedura, piuttosto complicata, fu ripetuta cinquantasette volte termine per termine, riuscendo infine a eliminare quelli periodici significativi e a integrare le equazioni ottenute. Le coordinate della Luna, la sua longitudine, latitudine e parallasse furono quindi espresse come serie infinite nelle quali il tempo compariva soltanto come argomento dei termini periodici. Sebbene l'utilizzazione pratica dei suoi risultati fosse limitata dalla debole convergenza delle serie, era comunque importante l'aver mostrato la possibilità di eliminare i termini secolari.

Affinché il metodo di Delaunay funzioni, è essenziale che la sua tecnica di approssimazione preservi a ogni passo la forma canonica delle equazioni del moto perturbato. Il successo del metodo costituì una dimostrazione dei notevoli vantaggi che si ottenevano nello scrivere le equazioni in forma canonica. Sebbene egli avesse descritto a grandi linee il suo metodo già nel 1846, i risultati finali non furono pubblicati prima degli anni Sessanta, in alcune lunghe memorie dell'Académie des Sciences. Poincaré definì l'uso da parte di Delaunay degli elementi canonici nella teoria delle perturbazioni come il più grande contributo alla meccanica celeste dai tempi di Laplace; un'opinione analoga fu espressa anche da Hill nel suo articolo del 1876. Dal punto di vista storico, la rilevanza pratica della sua teoria sembra essere stata più modesta; le effemeridi pubblicate in Gran Bretagna e negli Stati Uniti negli anni Venti del Novecento sono basate infatti su una diversa teoria lunare, quella di Hill e di Ernest W. Brown (1866-1938). I metodi di Delaunay hanno goduto tuttavia di un rinnovato interesse in meccanica celeste applicata (satelliti artificiali, perturbazioni planetarie) sin dagli anni Cinquanta del XX sec. grazie all'uso di elaboratori elettronici.

Tisserand

Jacobi aveva ottenuto per le equazioni canoniche del moto soluzioni della forma ∂S/∂α_i=β_i, dove la funzione principale S è una soluzione dell'equazione differenziale alle derivate parziali di Hamilton-Jacobi. In un suo scritto del 1837 egli asserì, senza tuttavia dimostrarlo, che, se un sistema conservativo viene perturbato, gli elementi arbitrari α_i, β_i ‒ costanti nel caso di moto non perturbato ‒ soddisfano le equazioni canoniche di Poisson-Lagrange per il moto perturbato. Ne diede una dimostrazione esplicita nella trentaseiesima delle Vorlesungen über Dynamik, anche se prese in considerazione soltanto sistemi conservativi e non discusse né indagò sul significato del suo risultato.

L'astronomo e matematico francese François Tisserand (1845-1896), nella sua dissertazione dottorale del 1868, formulò il teorema in questione per sistemi di tipo più generale e dimostrò come potesse essere usato per derivare le equazioni canoniche di Delaunay per il problema lunare. Tisserand fu incoraggiato nelle sue ricerche da Urbain-Jean-Joseph Le Verrier (1811-1877), che, non amando il metodo di Delaunay, cercava di criticarne la teoria lunare. Nel primo volume del Traité de mécanique céleste (1889-96) Tisserand fornì una dimostrazione dettagliata del teorema e lo utilizzò per ricavare le equazioni per le derivate rispetto al tempo degli elementi orbitali; tali equazioni sarebbero diventate successivamente di uso comune nelle ricerche sulle perturbazioni dei moti planetari.

Nel suo libro del 1896 sulla teoria lunare, Brown fornì una succinta derivazione del teorema di Tisserand che si riporta qui di seguito. Dalle equazioni p_i=∂S/∂q_i e β_i=∂S/∂α_i per sistemi non perturbati consegue che per la variazione ΔS di S=S(t,q_i,α_i) si può scrivere:

[31] ΔS=∑(p_iδq_i+β_iδα_i).

Se δq_i e δp_i rappresentano gli incrementi rispettivamente di q_i e p_i causati, durante il tempo dt, dalla presenza di una forza di perturbazione R, applicando il metodo delle variazioni delle costanti alle equazioni canoniche del moto per i sistemi perturbati, otteniamo le relazioni

dalle quali consegue l'identità

[33] dtΔR=∑(δp_iΔq_i-δq_iΔp_i).

Partendo dalle equazioni [31] e [33], utilizzando le proprietà delle operazioni δ e Δ ed effettuando alcuni calcoli, possiamo ricavare l'equazione:

Poiché δα_i=(dα_i/dt)dt e δβ_i=(dβ_i/dt)dt, si possono dedurre dalla [34] le equazioni

ossia le equazioni di Poisson-Lagrange del moto perturbato, espresse in termini delle costanti che appaiono nella soluzione dell'equazione di Hamilton-Jacobi.

Lo scopo del lavoro di Tisserand del 1868 era mostrare che gli elementi canonici di Delaunay potevano essere ottenuti dalle α_i e β_i mediante un procedimento efficace, superiore al metodo ben diverso impiegato da Binet e Delaunay. In questo scritto e in quelli successivi Tisserand si rivelava un convinto sostenitore della teoria di Hamilton-Jacobi e ne raccomandava l'uso, preferendola ai primi metodi sviluppati da Lagrange e Poisson. Benché, stando alle apparenze, egli avesse fornito un resoconto del procedimento di Lagrange nel primo volume del Traité de mécanique céleste, nella sua esposizione erano inserite in vari punti idee introdotte da Hamilton, un segno della considerevole influenza che gli sviluppi successivi della teoria dinamica avevano esercitato sul suo pensiero.

Poincaré

Nella teoria moderna di Hamilton-Jacobi è data grande enfasi allo studio delle trasformazioni che preservano il carattere canonico delle equazioni del moto. Tale punto di vista si affermò in modo sistematico, alla fine del XIX sec., negli scritti di Henri Poincaré (1854-1912), figura guida nella matematica francese e al quale si devono contributi fondamentali alla teoria qualitativa delle equazioni differenziali. Le sue ricerche di meccanica celeste, incentrate sullo studio del problema dei tre corpi, nacquero da una memoria ‒ scritta nel 1889 per una competizione scientifica indetta per celebrare il sessantesimo compleanno del re Oscar di Svezia ‒ e culminarono in due ampi trattati sulla meccanica celeste, Les méthodes nouvelles de la mécanique céleste (1892-1899) e le Leçons de mécanique céleste professées à la Sorbonne (1905-1910).

Nei suoi trattati di meccanica, Poincaré impiegò i metodi di Hamilton e Jacobi. Sebbene né Lagrange né Jacobi avessero usato metodi canonici nelle loro famose risoluzioni del problema dei tre corpi, a partire dagli anni Cinquanta del XIX sec. la tendenza dei ricercatori a ricorrere alla teoria di Hamilton-Jacobi nell'analisi di tale problema era divenuta sempre più usuale. Da questo punto di vista, notevole importanza ebbero le ricerche di Edmond Bour, Wilhelm Scheibner e Rodolphe Radau, i quali scrissero le equazioni del moto in forma canonica e tentarono di sviluppare metodi che semplificassero la descrizione analitica del sistema. Questi studiosi sembravano riconoscere alcuni dei vantaggi dell'approccio di Hamilton: l'ordine del sistema, ossia il numero di integrali indipendenti o di costanti d'integrazione, coincide con il numero di equazioni canoniche del primo ordine; tali equazioni possono essere scritte usando coordinate generalizzate, scelte in modo tale da facilitare la riduzione del problema; il secondo membro di ogni equazione presenta la stessa funzione H, la quantità costante di energia totale, che è indipendente dal cambiamento di coordinate del sistema.

Nel 1868 Radau introdusse un nuovo punto di vista, definendo sostituzioni di tipo generale che preservano la forma canonica delle equazioni. Egli considerò gli effetti di una trasformazione ortogonale delle variabili canoniche e applicò quest'idea al problema dei tre corpi per ottenere le soluzioni di Jacobi e di Scheibner. Il tema delle trasformazioni considerato in una prospettiva puramente matematica diede peraltro origine, negli anni Settanta del XIX sec., alla teoria di Sophus Lie delle trasformazioni di contatto. Nel suo articolo del 1887 sugli integrali algebrici del problema dei tre corpi, Ernst Heinrich Bruns impiegò variabili e trasformazioni canoniche al fine di ridurre l'ordine del sistema. La tendenza a fare delle equazioni canoniche del moto la base della dinamica fu rafforzata dal ruolo speciale assunto da tali equazioni nella nascente teoria delle trasformazioni. Simili sviluppi ebbero come effetto complessivo quello di introdurre metodi matematici sempre più raffinati e astratti nell'affrontare un problema tradizionale e piuttosto concreto della meccanica celeste.

Al pari di Tisserand, Poincaré era un difensore dei metodi di Jacobi, sebbene a suo avviso questi includessero non soltanto l'equazione differenziale alle derivate parziali di Hamilton-Jacobi ma, più in generale, la teoria delle trasformazioni. In un articolo breve ma significativo, pubblicato nel 1837 nei "Comptes Rendus de l'Académie des Sciences", Jacobi aveva formulato un teorema fondamentale su quella che oggi è chiamata 'funzione generatrice' delle trasformazioni di contatto. Si consideri il sistema di equazioni canoniche

dove le a_i e b_i sono funzioni di t e H=H(t,a1,…,a_m,b1,…,b_m). Si supponga che le variabili a1,…,a_m, b1,…,b_m siano collegate a un nuovo insieme di variabili α1,…,α_m, β1,…,β_m tramite equazioni della forma seguente:

dove ψ è una funzione di α1,…,α_m, a1,…,a_m. Allora le nuove variabili soddisfano le seguenti equazioni canoniche:

Sebbene Jacobi non avesse dimostrato tale risultato, il suo ragionamento era chiaramente basato su considerazioni tratte dal calcolo delle variazioni, come Poincaré avrebbe spiegato in dettaglio nel terzo volume delle sue Méthodes nouvelles. Si noti che la [36] e la [38] sono le equazioni di Euler corrispondenti rispettivamente agli integrandi variazionali

dove i due sistemi di 2m variabili indipendenti sono a_i,b_i e α_i,β_i. Si assuma ora che le equazioni [36] e [38] definiscano il medesimo problema variazionale. Ciò accadrebbe se la differenza tra le due espressioni [39] fosse uguale a un differenziale esatto di forma dψ, una condizione che è garantita se sono valide le equazioni di trasformazione [37]. Nel caso in cui la funzione generatrice ψ contenga la variabile t, la quantità H nella [38] è sostituita da H*, dove

Si noti che, identificando la funzione generatrice ψ con la soluzione S(t,q1,…,q_n,a1,…,a_n) dell'equazione di Hamilton-Jacobi, si giunge a un'altra dimostrazione del teorema fondamentale (v. l'equazione [23]) relativo alla soluzione β_i=∂S/∂α_i delle equazioni canoniche del moto. Nel paragrafo otto del capitolo introduttivo del primo volume delle Méthodes nouvelles, Poincaré adottò il teorema delle trasformazioni di Jacobi nell'analisi di alcuni esempi che comprendevano gli elementi di Delaunay o 'kepleriani' per il moto ellittico. Si consideri il moto di un singolo punto di coordinate (x1,x2,x3), attratto da una massa M posta nell'origine del sistema di coordinate. Poincaré ottenne una soluzione completa S=(x1,x2,x3,G,θ,h) dell'equazione di Hamilton-Jacobi associata, dove G, θ e h (che rappresenta l'energia totale) sono costanti arbitrarie. La soluzione delle equazioni canoniche del moto è data nella forma usuale:

dove g, Θ e h′ sono altre costanti arbitrarie. Se si pone

dove n è il moto medio, allora la seconda delle equazioni [41] è sostituita da ∂S/∂L=l. Poincaré interpretò quindi le costanti in termini degli elementi che convenzionalmente definiscono il moto ellittico.

Lo scienziato francese osservò che, se la massa in movimento è sottoposta a forze addizionali (perturbative), è possibile considerare S ‒ la soluzione dell'equazione di Hamilton-Jacobi ‒ come una funzione generatrice e definire quindi sei nuove variabili, L,G,Θ,l,g,θ come funzioni delle x_i e dei momenti y_i (i=1, 2, 3) per mezzo delle equazioni

Tali quantità non sono più costanti, bensì variabili che definiscono il moto perturbato. In molti esempi successivi Poincaré derivò le equazioni canoniche usando le variabili di Delaunay e le derivate parziali della forza perturbante.

Il procedimento impiegato da Poincaré in questi esempi era basato sull'intuizione implicita che il teorema delle trasformazioni di Jacobi poteva essere utilizzato allo scopo di fornire un'ulteriore derivazione delle equazioni canoniche con perturbazione, che si aggiungeva alle soluzioni di Lagrange e Tisserand. Il ragionamento che era alla base fu sintetizzato da Carl Wilhelm Ludwig Charlier (1862-1934), professore di astronomia all'Università di Lund in Svezia, nel secondo volume (1907) dell'opera Die Mechanik des Himmels (La meccanica del cielo). Si assuma che H0 sia l'hamiltoniana del sistema senza perturbazione e che S(t,q_i,α_i) sia una soluzione della corrispondente equazione di Hamilton-Jacobi; una soluzione delle equazioni del moto del sistema imperturbato è data nella forma ∂S/∂α_i=β_i. Si consideri ora il sistema perturbato, con un'hamiltoniana H=H0+H1 ed equazioni canoniche

Si definisca ora una trasformazione dalle variabili q_i, p_i al nuovo insieme di variabili α_i, β_i, usando S come funzione generatrice:

Le equazioni canoniche nelle nuove variabili sono:

dove K=H+∂S/∂t. Poiché H=H0+H1 e H0+∂S/∂t=0, ne consegue che K=H1 e quindi che le [46] si riducono a:

dove H1 è la parte di hamiltoniana dovuta all'azione di una forza perturbatrice. Se si interpretano le quantità α_i, β_i come arbitrarie nel moto non perturbato, ne consegue che le [47] sono semplicemente le equazioni canoniche perturbate nella forma ottenuta da Tisserand. La derivazione di Charlier è stata da allora universalmente accettata e figura nei manuali di Theodore E. Sterne (1960) e Yusuke Hagihara (1970).

L'uso delle trasformazioni nella teoria di Hamilton-Jacobi è diventato oggi così dominante che sarebbe impossibile seguire l'argomento senza una qualche conoscenza dei principî associati. Sebbene la precedente derivazione delle equazioni canoniche con perturbazione sia elegante, essa comprende diversi elementi tecnici ‒ le soluzioni delle equazioni differenziali alle derivate parziali, le trasformazioni di contatto, le funzioni generatrici ‒ che richiedono una trattazione matematica di livello elevato.

Come mostra la ricostruzione storica fin qui delineata, molte delle applicazioni significative all'astronomia lunare e planetaria del XIX sec. furono sviluppate usando metodi meno astratti di quelli utilizzati da Poincaré. In realtà, anche se il concetto di trasformazione di contatto ebbe origine negli anni Trenta del XIX sec. con Jacobi, un numero considerevole di studiosi di meccanica celeste del XIX sec. non sembrava averne colto l'utilità, come avvenne del resto anche nel caso di un matematico molto abile come Delaunay. Perfino Charlier, nel primo volume (1902) del testo Die Mechanik des Himmels, riprodusse la vecchia derivazione delle equazioni canoniche con perturbazione di Tisserand, preferendola ai metodi più sofisticati basati sulle trasformazioni, che egli avrebbe invece impiegato cinque anni più tardi. La scelta di adottare l'approccio della teoria delle trasformazioni nel secondo volume della sua opera è il segno del suo riconoscimento della versatilità e della superiorità dei metodi di trasformazione nell'indagine condotta in settori tecnicamente avanzati della meccanica celeste.

Bibliografia

Barrow-Green 1997: Barrow-Green, June, Poincaré and the three body problem, Providence (R.I.), American Mathematical Society; London, London Mathematical Society, 1997.

Cook 1988: Cook, Alan, The motion of the moon, Bristol-Philadelphia, Hilger, 1988.

Costabel 1978: Costabel, Pierre, Poisson, Siméon-Denis, in: Dictionary of scientific biography, edited by Charles Coulston Gillispie, New York, Scribner's Sons, 1970-1990, 18 v.; v. XV: Supplement 1, 1978, pp. 480-490.

Hagihara 1970: Hagihara, Yusuke, Celestial mechanics, Cambridge (Mass.), MIT Press, 1970-1976, 5 v.; v. I: Dynamical principles and transformation theory, 1970.

Hankins 1980: Hankins, Thomas L., Sir William Rowan Hamilton, Baltimore, Johns Hopkins University Press, 1980.

Hawkins 1992: Hawkins, Thomas W., Jacobi and the birth of Lie's theory of groups, "Archive for history of exact sciences", 42, 1992, pp. 187-278.

Lévy 1976: Lévy, Jacques R., Tisserand, François Félix, in: Dictionary of scientific biography, edited by Charles Coulston Gillispie, New York, Scribner's Sons, 1970-1990, 18 v.; v. XIII, 1976, pp. 422-424.

Lützen 1990: Lützen, Jesper, Joseph Liouville, 1809-1882. Master of pure and applied mathematics, New York-Berlin, Springer, 1990.

Nakane 1991: Nakane, Michiyo, The role of the three-body problem in construction of characteristic function for mechanics by W.R. Hamilton, "Historia scientiarum", s. 2, 1, 1991, pp. 27-38.

Sterne 1960: Sterne, Theodore E., An introduction to celestial mechanics, New York, John Wiley & Sons, 1960.