L'Ottocento: fisica. L'elettromagnetismo e il campo
L'Ottocento: fisica. L'elettromagnetismo e il campo
L'elettromagnetismo e il campo
William Thomson e Michael Faraday
Nel corso degli anni Trenta del XIX sec., Michael Faraday (1791-1867) ottenne risultati senza precedenti studiando in laboratorio l'azione diretta esercitata da un mezzo sui fenomeni elettrici e giunse a scoprire quella che in seguito sarebbe stata chiamata 'capacità dielettrica'. Il risultato ottenuto da Faraday suscitò grandi perplessità tra i contemporanei, soprattutto perché era descritto con il linguaggio di una proto-teoria di campo. Faraday aveva introdotto una distinzione fondamentale, che da allora in poi avrebbe permeato tutta la fisica dei campi, tra l'intensità di una linea di forza e la quantità totale (o il numero) di linee, e queste due proprietà erano (in un dato mezzo) proporzionali tra loro. Egli riteneva inoltre che la quantità di linee si conservasse sempre quando, connettendo tra loro conduttori carichi, le linee di forza erano ridistribuite e che le linee di forza elettriche dovessero iniziare e terminare su una superficie conduttrice. A partire da queste affermazioni, Faraday poté calcolare il valore della capacità di un dielettrico ‒ il fattore di proporzionalità tra la quantità e l'intensità ‒ e dimostrare che essa rimaneva la stessa indipendentemente dal modo in cui i conduttori del suo apparato fossero caricati.
Questa scoperta segnò la vera e propria nascita della teoria di campo, poiché indicò un nuovo modo di trattare, sia concettualmente sia quantitativamente, i fenomeni elettrici. Secondo Faraday l'universo elettrico si divideva (quantomeno) in oggetti che incidevano sullo stato locale del campo, da un lato, e sul campo stesso, dall'altro lato. I primi potevano essere di due tipi: conduttori, all'interno dei quali lo stato del campo era in qualche modo completamente distrutto, oppure dielettrici, che sostenevano il campo, anche alterandolo. Faraday pensava che lo stato del campo variasse da un punto all'altro, a seconda della presenza di materia nelle vicinanze: la condizione elettrica di un oggetto ‒ si trattasse di un conduttore o di un dielettrico ‒ dipendeva quindi soltanto dallo stato del campo nella posizione in cui l'oggetto si trovava, e tale stato dipendeva a sua volta dalla distribuzione spaziale di oggetti vicini.
L'introduzione della costante dielettrica da parte di Faraday simboleggiava dunque la creazione di una nuova fisica del campo, o indicava piuttosto un nuovo modo di affrontare l'induzione elettrica. Fin qui essa non offriva una spiegazione esauriente dei sistemi magnetici oppure del modo in cui analizzare le forze moventi originate dai corpi elettrizzati. In questa fase, la teoria di campo era priva di un qualche elemento che potesse svolgere, al suo interno, un ruolo analogo a quello rivestito dalle leggi di Newton nell'ambito della dinamica e che mettesse in relazione reciproca lo stato del campo e i movimenti degli oggetti dai quali esso dipendeva. Tale elemento mancante emerse ben presto sotto forma di conservazione dell'energia.
Quando si imbatté per la prima volta nella teoria analitica del calore di Jean-Baptiste-Joseph Fourier (1768-1830), William Thomson (1824-1907) aveva solamente quindici anni. Profondamente colpito da quello che egli considerava l'approccio geometrico di Fourier al flusso di calore, e dal fatto che tale approccio fosse fondato su quantità sperimentalmente significative, un anno più tardi Thomson redasse uno studio in cui mise in luce le analogie esistenti tra la teoria matematica del calore di Fourier e la struttura dell'elettrostatica basata sulla funzione potenziale. Egli dimostrò, tra l'altro, che allo stato stazionario si potevano sostituire semplicemente la temperatura con il potenziale elettrico e il flusso di calore con la forza elettrica (il gradiente di potenziale), senza alterare la struttura matematica. Fin qui, Thomson non prese in alcuna considerazione la possibilità di stabilire una connessione con le indagini di Faraday. Dopo essersi laureato a Cambridge, dove le sue concezioni geometriche e antiipotetiche furono probabilmente rafforzate dal suo tutor William Hopkins (1793-1866), Thomson soggiornò per un certo periodo a Parigi, dove ebbe l'opportunità di lavorare nel laboratorio di Henri-Victor Regnault (1810-1878) e di apprendere, così, una grande quantità di conoscenze sulla misurazione e sulla sperimentazione di precisione, aspetti della ricerca che gli erano mancati durante gli intensi studi di matematica a Cambridge.
Durante il suo soggiorno a Parigi, Thomson conobbe il matematico Joseph Liouville (1809-1882), che gli chiese informazioni circa i recenti lavori di Faraday sull'elettrostatica e, in particolare, sul fatto che questi ultimi sembravano contraddire la teoria sviluppata da Charles-Augustin Coulomb (1736-1806) e poi da Siméon-Denis Poisson (1781-1840), apparentemente molto efficace dal punto di vista empirico. A quel tempo, Thomson non teneva in alta considerazione le concezioni di Faraday ma, ben presto, cambiò opinione. Educato a Cambridge, dove si insegnava a pensare agli oggetti matematici in termini di strutture geometriche, e in particolare di superfici e di linee, e influenzato dalla tradizione scozzese che attribuiva una grande importanza alla sperimentazione e all'autonomia nei confronti di ipotesi e credenze specifiche, Thomson tentò in modo naturale di individuare una connessione tra la versione di Faraday dell'elettrostatica e quella di Coulomb e Poisson. Dopo aver stabilito una relazione tra la teoria matematica di Fourier del calore da una parte, e la struttura analitica dell'elettrostatica dall'altra, egli mise quest'ultima in rapporto con le concezioni di Faraday, che in tal modo erano ricondotte anche alla teoria del flusso di calore.
Thomson osservò che esisteva una stretta analogia tra le linee di Fourier del flusso di calore e le linee di Faraday della forza elettrica e che il gradiente termico di Fourier era analogo alla nozione di intensità di una linea di forza, introdotta da Faraday. Inoltre, le sorgenti e i pozzi di calore di Fourier corrispondevano, rispettivamente, ai punti iniziali e terminali delle linee elettriche di Faraday. Come Thomson aveva già precedentemente intuito, questo modello matematico si adattava anche all'elettrostatica, purché ci si astraesse dall'idea di sostanza elettrica e ci si basasse, piuttosto, sul comportamento del potenziale elettrico ‒ a condizione che (seguendo l'analogia con il modello termico) la conducibilità termica del mezzo interposto fosse sempre unitaria, in modo da mantenere fisso il rapporto tra il gradiente termico e il flusso di calore (ossia a condizione che la componente normale alla superficie del gradiente termico rimanesse ovunque continua). Thomson, di conseguenza, dimostrò che era possibile escludere qualsiasi contraddizione tra l'elettrostatica di Faraday e quella di Coulomb e Poisson, per ciò che riguardava il comportamento elettrico di corpi conduttori separati dal vuoto o dall'aria.
Le tesi di Faraday, però, si basavano soprattutto sul comportamento dei corpi dielettrici e a questo proposito la sfida più impegnativa per Thomson fu senza dubbio quella di estendere anche a questi ultimi il suo parallelismo matematico. In tale fase egli dovette misurarsi, se non con vere e proprie difficoltà, almeno con le profonde differenze esistenti tra una teoria di campo quale era quella di Faraday e una teoria, come quella di Coulomb e Poisson, che si basava sul comportamento di fluidi elettrici che interagivano a distanza. Faraday aveva dimostrato sperimentalmente che i dielettrici modificano l'intensità delle linee di forza poste tra conduttori caricati con una data quantità di elettricità. Secondo Faraday, la quantità di elettricità era ricondotta al numero totale delle linee di forza che attraversavano una superficie e che, quindi, fuoriuscivano da un conduttore oppure vi entravano; tale numero si conservava sempre quando i conduttori erano collegati l'uno all'altro da altri corpi conduttori. Quando, tra i conduttori carichi, si trovavano invece alcuni dielettrici, l'intensità di ogni linea di forza era alterata; tale intensità, affermava lo studioso, variava in misura inversa alla capacità del dielettrico di 'trasportare' le linee di forza: una volta assegnata la loro quantità totale, all'aumentare di questa attitudine ogni linea diminuiva la propria intensità. Nell'elettrostatica di Coulomb e Poisson non vi era nulla che corrispondesse al potere di 'trasportare' le linee posseduto dai dielettrici di Faraday. Si poteva, tuttavia, includere l'effetto dei dielettrici in un'elettrostatica basata sul potenziale se si presupponeva che la derivata normale (ovvero il gradiente) del potenziale fosse discontinua lungo la superficie di separazione tra diversi dielettrici: una tale superficie avrebbe avuto un potenziale costante e avrebbe di conseguenza potuto essere rappresentata matematicamente attraverso una distribuzione, lungo i bordi, di sorgenti oppure di pozzi di elettricità. Per quanto riguardava il loro effetto sul potenziale elettrico, in questo caso tali sorgenti o pozzi avrebbero agito dunque esattamente come sulle superfici conduttrici, rivestendosi così di tutte le nuove e originali proprietà richieste da Faraday per i dielettrici.
Thomson era consapevole del fatto che le proprietà conduttive del dielettrico di Faraday corrispondevano alla conducibilità termica della teoria della propagazione del calore elaborata da Fourier. Tuttavia, egli non si spinse oltre nell'analogia tra il calore e i dielettrici; anzi, ignorò del tutto quello che per Faraday era un aspetto duplice e fondamentale delle forze che, come Faraday stesso si era reso conto, si manifestava in modo evidente negli esperimenti condotti in presenza di superfici che delimitavano diversi dielettrici, o i dielettrici e l'aria. Più in particolare, nella struttura analogica adottata da Thomson, non vi erano regioni con conducibilità differente, termica o elettrica che fosse, e gli effetti delle diverse conducibilità erano rappresentati piuttosto, formalmente, attraverso la discontinuità dei gradienti di potenziale o di temperatura. Ciò significava che il flusso termico rimaneva in realtà identico al gradiente di temperatura e la forza elettrica al gradiente di potenziale. In questo modo, però, Thomson non colse la principale novità dello schema di Faraday, vale a dire la sua idea che i dielettrici avessero il potere di 'portare', o condurre, le linee di forza. Tale nozione, infatti, implicava una duplice interpretazione del concetto di forza nei fenomeni elettrici: da un lato, forza intesa come qualcosa che attraversa una superficie e che si conserva (quello che oggi si chiama 'flusso elettrico' o, nella terminologia di Maxwell, 'spostamento'); dall'altro, forza valutata lungo una linea e che determina l'intensità di un'interazione elettrostatica per un dato flusso totale (quella che oggi è detta semplicemente 'intensità del campo elettrico').
Nel 1845 Thomson era interessato non tanto a cogliere determinati concetti di Faraday, quanto a dimostrare come le tesi di quest'ultimo sul comportamento dei dielettrici potessero essere inquadrate in uno schema tradizionale attraverso l'introduzione di un modello opportuno con cui rappresentare il dielettrico. Tra la metà e la fine degli anni Quaranta, le concezioni di Thomson subirono un notevole sviluppo, soprattutto grazie alla scoperta del diamagnetismo e del paramagnetismo da parte di Faraday. Nell'estendere il dominio di applicazione della sua fisica di campo dall'elettrostatica alla 'magnetostatica', come la si definisce oggi, Faraday introdusse, per analogia con la costante dielettrica, la 'capacità magnetica'. Inizialmente Faraday non ritenne possibile considerare i due tipi di comportamento magnetico come il semplice risultato di differenze tra le capacità magnetiche dei corpi rispetto alla capacità del loro ambiente circostante, sia per ragioni sperimentali sia per motivi teorici (dal momento che era poco incline ad ammettere l'esistenza di un etere). Tuttavia nel 1847, dopo aver condotto ulteriori indagini, egli si era ormai convinto che le due classi di corpi magnetici ‒ ossia quelli diamagnetici e quelli paramagnetici ‒ formassero un'unica categoria e che le loro differenze fossero riconducibili esclusivamente alla maggiore o minore capacità, rispetto all'ambiente circostante, di condurre le linee di forza. Faraday poté perciò sviluppare in senso più ampio rispetto a prima il concetto di campo.
Nel 1847 Thomson enunciò un principio essenziale che, due anni più tardi, avrebbe portato all'unificazione delle interpretazioni che Faraday aveva fornito dell'elettrostatica e della magnetostatica (sulla base di quella che, ben presto, sarebbe divenuta una vera e propria scienza dell'energia). Thomson aveva già osservato che l'integrale del quadrato della forza, calcolato all'interno di un dato volume, era proporzionale all'integrale del prodotto tra la densità elettrica e il potenziale.
Nel 1845 Carl Friedrich Gauss aveva dimostrato che questo secondo integrale avrebbe dovuto essere un minimo, per fare in modo che la condizione di equilibrio elettrostatico fosse univocamente definita. Thomson, quindi, concluse che la condizione di minimo di Gauss poteva essere applicata a una funzione ‒ l'integrale del quadrato della forza ‒ che rappresentava l''effetto meccanico', o 'lavoro', necessario a costituire il sistema elettrico; la forza meccanica, per esempio quella agente tra conduttori carichi, era il gradiente di questa espressione. In altre parole, la forza che causava il movimento poteva essere determinata analiticamente derivando un'espressione che rappresentava, per così dire, il 'valore meccanico' totale immagazzinato nel sistema, senza tener conto delle interazioni reciproche tra le diverse parti del sistema stesso.
Era questa la chiave che avrebbe consentito di stabilire su solide basi l'interpretazione che Faraday aveva fornito del magnetismo e, ipso facto, di elaborare una spiegazione del moto dei corpi basata su una teoria di campo. Thomson, infatti, aveva compreso che l'integrale di volume del prodotto tra la capacità induttiva (elettrica o magnetica) e il quadrato del gradiente di potenziale (ancora una volta elettrico o magnetico) avrebbe dovuto essere minimizzato per poter determinare il modo in cui i corpi si sarebbero mossi: ciò significava che, almeno formalmente, si poteva trattare il valore meccanico di un sistema come se fosse distribuito nello spazio e avesse una densità espressa dal prodotto della capacità per il quadrato del gradiente di potenziale.
A partire dal 1849, allorché in merito al movimento dei corpi magnetici Faraday adottò e sviluppò per le linee di forza il concetto di potere differenziale di conduzione, Thomson fu in grado di interpretare l'idea di Faraday secondo il proprio principio di riduzione al minimo.
Nei termini in cui la forza, in accordo con l'idea originale di Faraday, era dotata di quantità e di intensità, Thomson aveva dimostrato, di fatto, che il prodotto delle quantità per le intensità rappresenta la densità di volume del valore meccanico del campo e che i corpi si muovevano nella direzione individuata dal gradiente dell'energia del campo. Molto probabilmente egli era consapevole di tutto ciò, ma non compì il passo successivo di identificare i due diversi aspetti e quello di forza. Secondo Thomson la forza rimaneva ancora, semplicemente, un gradiente di potenziale e ciò, nel caso dei corpi magnetici, lo obbligava a introdurre una descrizione particolareggiata del modo in cui misurare la forza, che rendeva necessaria una forma appropriata delle cavità di prova all'interno dei corpi.
Queste diverse rappresentazioni si sarebbero ben presto sviluppate grazie all'operato di un altro giovane ricercatore scozzese, James C. Maxwell (1831-1879), in una direzione che lo stesso Thomson rifiutò di seguire.
James C. Maxwell
Benché la distinzione tra 'quantità' e 'intensità' ‒ o tra quelli che oggi si definiscono 'flusso' e 'forza' ‒ sia presente nella tendenza a fondere la teoria di campo con la nozione di conservazione dell'energia operata da Thomson, quest'ultimo, tuttavia, non ne approfondì ulteriormente il significato. I successivi sviluppi si devono al giovane Maxwell che, come Thomson, era uno scozzese laureato a Cambridge, esperto in matematica e decisamente incline a ragionare seguendo termini geometrici.
Già nel 1842 Thomson aveva fatto ampio ricorso a un metodo fondato sull'analogia tra argomenti diversi della fisica, con lo scopo di applicare teoremi, che fossero facilmente dimostrabili in un'area, ad altri campi, nei quali gli enunciati analoghi avrebbero potuto non essere altrettanto evidenti. Per esempio, nella teoria del flusso del calore di Fourier è immediatamente evidente che tutti gli effetti termici che si producono al di fuori di una superficie isoterma chiusa dipendono solamente dalla sua temperatura, dal momento che ogni reale distribuzione delle sorgenti di calore nella superficie stessa non influisce sulle condizioni esterne. Per analogia (identificando la temperatura con il potenziale elettrostatico), nell'ambito dei fenomeni elettrici era sufficiente conoscere il potenziale della superficie chiusa, senza tener conto delle sorgenti elettriche presenti al suo interno. Thomson si era ampiamente servito del metodo dell'analogia per sviluppare la propria interpretazione della teoria di Faraday e le connessioni con quella di Poisson, ma fu Maxwell che vi ricorse nel modo più sistematico e approfondito.
Nel 1854 il giovane Maxwell inviò a Thomson una lettera, divenuta celebre, in cui delineava le proprie idee sulle linee di forza e, in particolare, sul loro possibile impiego nell'analisi delle connessioni esistenti tra la forza magnetica e la corrente elettrica. Thomson non aveva trattato pubblicamente quest'ultimo argomento, sul quale Maxwell decise di elaborare una serie di 'idee geometriche'. Nei mesi seguenti egli modificò e sviluppò le nozioni di base abbozzate nella lettera a Thomson, rendendole note nella sua prima grande opera, On Faraday's lines of force, divisa in due parti e pubblicata nel 1856. In essa Maxwell ricorre senza riserve al metodo dell'analogia usato da Thomson e riconduce le proprietà geometriche di un fluido viscoso e incompressibile a quelle dei campi elettrici, magnetici e di corrente.
Maxwell si spinse oltre Thomson non soltanto nell'uso dell'analogia ma anche nell'approfondire la fondamentale distinzione, introdotta da Faraday, tra quantità e intensità di un campo. A grandi linee, si può dire che Maxwell cercò di sviluppare una serie di connessioni geometriche tra questi due aspetti del campo. A tal fine, egli si basò soprattutto sull'analogia tra il flusso di un fluido, da un lato, e le proprietà dei campi elettrici, magnetici e di corrente, dall'altro lato. Nel caso dell'elettricità, la struttura elaborata era del tutto simile a quella ideata da Faraday per i corpi dielettrici, dal momento che la quantità del campo elettrico, o quello che il fisico alla fine avrebbe chiamato il suo 'spostamento', era semplicemente proporzionale alla sua intensità o, precisamente, all'intensità del campo, proprio come la portata del liquido è semplicemente proporzionale al gradiente di pressione che gli consente di vincere la resistenza. Allo stesso modo, nella magnetostatica vi era un rapporto di proporzionalità diretta tra una quantità magnetica (l'induzione) e l'intensità del campo magnetico. La quantità di corrente elettrica, infine, era a sua volta proporzionale alla sua intensità, ossia alla forza elettrica (il che equivaleva alla legge di Ohm).
L'aspetto più originale dello schema di Maxwell risiede nel tentativo di stabilire una serie di relazioni tra le proprietà elettriche e quelle magnetiche. Ispirandosi con ogni probabilità all'immagine ideata da Faraday di circui-ti magnetici ed elettrici collegati tra loro, Maxwell sviluppò un sistema in cui un'intensità considerata lungo una curva doveva essere connessa a una quantità che attraversava l'area da essa racchiusa. L'intensità (forza) magnetica considerata lungo una curva era dunque uguale alla quantità di corrente che attraversava l'area da questa racchiusa: si trattava della prima versione, nei termini di una teoria di campo, di quella che sarebbe divenuta nota come 'legge di Ampère'. Non era facile stabilire un'analoga connessione riguardo la quantità magnetica che attraversava un'area, poiché non sembrava esservi alcuna grandezza che fornisse, lungo il bordo di tale area, la corrispondente intensità. Faraday, tuttavia, aveva preso in considerazione una cosiddetta 'intensità elettrotonica', la cui velocità di variazione, nel tempo, nel luogo di una corrente avrebbe dovuto rappresentare l'intensità della corrente stessa (vale a dire la forza elettrica associata). Basandosi su questa analisi, Maxwell identificò l'intensità elettrotonica di Faraday con la grandezza corrispondente alla quantità magnetica; in questo modo l'intensità elettrotonica lungo una curva forniva la misura dell'induzione magnetica nell'area da essa racchiusa.
Maxwell aveva così elaborato per l'elettromagnetismo una struttura che era interamente espressa nei termini di una teoria di campo, era connessa per analogia al flusso di un fluido viscoso e incompressibile ed era fondata sullo schema quantità-intensità proposto da Faraday. Nel corso dei sei anni successivi, Maxwell si orientò in un'altra direzione, verso una vera e propria analogia fisica basata su un modello del campo elettromagnetico di tipo meccanico. Questo tentativo va ricondotto almeno in parte all'influenza di Thomson che, dopo aver accettato all'inizio degli anni Cinquanta dell'Ottocento la teoria dinamica del calore, si era sforzato di elaborare modelli fisici concreti. In realtà, già nel 1846 Thomson aveva delineato un'analogia matematica tra la deformazione di un solido elastico e le forze elettriche e magnetiche, in questo caso accennando per la prima volta in termini quantitativi al potenziale vettore magnetico, che in seguito Maxwell avrebbe usato nel trattare lo stato elettrotonico di Faraday. Nel 1845, inoltre, Faraday aveva scoperto che il piano di polarizzazione della luce ruota quando un fascio di luce attraversa una determinata sostanza immersa in un campo magnetico. Nel 1856, anno in cui, come già detto, Maxwell pubblicò On Faraday's lines of force, Thomson aveva avanzato l'ipotesi secondo la quale l'effetto scoperto da Faraday rifletteva l'esistenza di vortici molecolari magnetici. A questo punto, anche Maxwell si applicò alla costruzione di modelli fisici, sviluppando tale metodo molto più di quanto avesse fatto lo stesso Thomson, il quale aveva lasciato parzialmente incompiute le proprie riflessioni sui vortici; questa fase della sua attività vide, infatti, l'introduzione di una quantità fisica di grande importanza, che derivava dal modello sviluppato dallo stesso Maxwell e che venne impiegata da tutte le successive teorie di campo: la 'corrente di spostamento'.
L'introduzione della corrente di spostamento nella fisica di campo non fu un'operazione semplice, dal momento che non derivava direttamente, come si è invece più volte sostenuto, dall'aver percepito un'incoerenza matematica nelle equazioni del campo delle quali Maxwell disponeva all'inizio degli anni Sessanta. In particolare, la relazione differenziale parziale che legava la corrente di conduzione alla forza magnetica (la legge di Ampère) implicava che tutte le correnti di quel tipo fossero rientranti, o chiuse, cosa che ovviamente non si verificava. Si sarebbe potuto risolvere tale problema inserendo nella versione della legge di Ampère che ricorreva al concetto di campo un termine aggiuntivo rispetto alla corrente di conduzione che consistesse nel tasso di variazione in funzione del tempo della quantità elettrica: ciò equivaleva ad aggiungere la corrente di spostamento a quella di conduzione.
Maxwell, tuttavia, pervenne alla nozione di corrente di spostamento non tanto attraverso la matematica o più ampie concezioni della teoria di campo, quanto grazie al suo modello fisico dell'etere (benché un tale concetto abbia indubbiamente le sue radici anche nei tentativi di Faraday di comprendere le relazioni che legavano l'induzione e la conduzione elettrica). Emerge quindi un legame molto stretto tra la teoria di campo e un modello di etere che fu adottato per cinque anni circa e che si sarebbe rivelato ben presto di grande utilità nello sviluppo dell'elettrodinamica maxwelliana.
La prima versione del modello di Maxwell raffigurava la corrente elettrica (che in quella fase esisteva ancora solamente nei conduttori) mediante oggetti simili a cuscinetti a sfera, in rotazione tra celle rotanti che immagazzinavano il momento della quantità di moto e l'energia cinetica. Questi 'cuscinetti' si muovevano vincendo la resistenza dell'attrito all'interno dei conduttori, ma non potevano fare lo stesso in altri corpi. Tale circostanza costituiva un problema per Maxwell, poiché implicava la possibilità che il modello non fosse compatibile con una situazione di assenza di corrente in una zona in cui un conduttore presentasse una frattura: se le particelle non potevano inserirsi nella fessura, il meccanismo con ogni probabilità si sarebbe interrotto. Per risolvere questo problema Maxwell introdusse la corrente di spostamento. Egli sostenne che le celle rotanti dovevano essere considerate elastiche, in modo da poter cedere alla sollecitazione. Ciò consentiva ai cuscinetti situati tra le celle di spostarsi leggermente anche all'interno di un materiale non conduttore; questo, a sua volta, consentiva al meccanismo di rimanere inalterato e di evitare che vi fosse una corrente ‒ intesa come una traslazione di cuscinetti che, vincendo l'attrito, si spostavano da una cella all'altra ‒ all'interno della lacuna. In altre parole, lo scopo originario della corrente di spostamento era proprio quello di impedire il prodursi di correnti, in senso stretto, nei corpi dielettrici. Indubbiamente il più importante risultato ottenuto da Maxwell attraverso la costruzione di modelli fu il calcolo non del tutto rigoroso in base a cui l'elasticità delle sue celle rotanti avrebbe dato luogo a vibrazioni trasversali, dotate di una velocità pari a quella della luce; egli stabilì così per la prima volta un legame diretto tra elettromagnetismo e ottica. Nel corso del decennio successivo Maxwell iniziò a concepire la sua teoria in termini di rappresentazione molto astratta dei processi del campo, piuttosto che prestare attenzione ai dettagli del proprio modello, e iniziò così a erigere un nuovo edificio teorico, portato a compimento con la pubblicazione di un'opera di grande importanza, A treatise on electricity and magnetism.
L'elettrodinamica maxwelliana
Il Treatise di Maxwell fu dato alle stampe nel 1873, a sei anni di distanza dalla pubblicazione del Treatise on natural philosophy di William Thomson e Peter Guthrie Tait (1831-1901). Le due opere erano strettamente legate, anche se il 'Thomson and Tait', così come era chiamato a quell'epoca, aveva come oggetto la meccanica mentre il testo di Maxwell riguardava l'elettrodinamica. Entrambi i trattati, infatti, esprimevano l'immagine di un mondo in cui tutto era ridotto a materia in movimento. Si pensava che esistesse una materia nascosta, costituita di una sostanza, o 'etere', ovunque presente ma percepibile solo indirettamente, attraverso i suoi complicati effetti. L'elettricità, il magnetismo e persino la chimica ‒ come Joseph J. Thomson (1856-1940) avrebbe tentato di dimostrare in seguito ‒ dovevano essere assoggettati alle leggi dell'etere meccanico. Thomson e Tait fornirono un accurato resoconto su come ciò avvenisse e il Treatise di Maxwell esemplificava questo metodo in molti dei suoi più importanti capitoli.
L'idea fondamentale era quella di basare ogni cosa, per quanto fosse possibile, direttamente sulle espressioni dell'energia dell'etere, alcune delle quali avrebbero rappresentato la materia in movimento e altre l'energia accumulata, o potenziale; anche quest'ultima fu considerata, in ultima analisi, riconducibile alla materia in movimento. Dopo aver espresso in forma appropriata l'energia associata a un certo fenomeno, il passo successivo sarebbe stato quello di utilizzarla attraverso procedimenti matematici tratti dalla meccanica. Esistevano due modi principali per farlo. Il primo si basava sull'utilizzazione di alcune equazioni, in origine stabilite da Joseph-Louis Lagrange (1736-1813), come rappresentazioni generali delle equazioni del moto, in cui le espressioni dell'energia avrebbero potuto essere inserite direttamente; in tal modo si sarebbero ottenute, per così dire, analoghe 'equazioni del moto' per il fenomeno in questione. Similmente si sarebbero, per esempio, potute inserire nelle equazioni di Lagrange opportune espressioni tratte dall'elettrodinamica e ottenere le leggi che governavano le interazioni di due circuiti percorsi da corrente. Il secondo metodo era più generale ma anche di più difficile applicazione, perché richiedeva l'esecuzione di un'integrazione che avrebbe potuto rivelarsi complessa. Questo metodo si basava su un procedimento sviluppato da William R. Hamilton (1805-1865) per la meccanica; in questo caso l'espressione dell'energia era usata per ottenere, attraverso un processo che fissava i valori estremi di un certo integrale, sia le 'equazioni del moto' del fenomeno in questione, sia le espressioni di ciò che accadeva in corrispondenza delle superfici presso le quali i valori di certe grandezze, come per esempio la costante elettrica o quella magnetica, subivano una variazione. Nel corso del successivo quarto di secolo questo schema guidò la ricerca dei 'maxwelliani' esperti di matematica di Cambridge, i quali tentarono di elaborare teorie a partire dall'individuazione di espressioni appropriate per l'energia dell'etere che, inserite nell'apparato di Lagrange o di Hamilton, consentissero di ottenere risultati empiricamente verificabili. Come si vedrà, questo modo di concepire la fisica, esclusivamente britannico, fu abbandonato in seguito all'introduzione dell'elettrone.
Il Treatise di Maxwell, così come i numerosi articoli e libri scritti fin quasi alla fine del secolo dai sostenitori del campo elettromagnetico, è poco conosciuto per quattro ragioni: (1) i concetti e i procedimenti fisici impiegati sono differenti da quelli moderni; (2) le quattro equazioni differenziali oggi chiamate 'di Maxwell' e studiate in tutti i corsi universitari di elettrodinamica non sono formulate in modo chiaramente riconoscibile in questo testo; (3) sono molto usati in tutto il Treatise, a livello di grandezze fondamentali, quelli che sono stati poi definiti 'potenziale vettore' e 'potenziale scalare' e che non sono più considerati, a stretto rigor di termini, nozioni fisiche fondamentali (eccetto che in meccanica quantistica); (4) il calcolo vettoriale, che attualmente è alla base di tutte le trattazioni dell'elettrodinamica, in gran parte dell'opera non è affatto impiegato con lo scopo di svolgere calcoli, benché alcuni suoi aspetti appaiano sotto la forma più generale dei tipici quaternioni di Hamilton, oggetti matematici che combinano i moderni calcoli scalare e vettoriale.
Queste caratteristiche erano legate tra loro. Si consideri il problema dei 'potenziali', grandezze usate per ottenere il campo elettrico (dal potenziale scalare) e il campo magnetico (dal potenziale vettore) utilizzando appropriate combinazioni di derivate; sotto certi aspetti, rispetto ai campi essi presentavano determinati vantaggi per quanto riguardava il calcolo, ma alcuni pensavano che potessero avere anche un significato fisico: il potenziale vettore, per esempio, avrebbe potuto essere associato a una sorta di 'quantità di moto' posseduta dall'etere, mentre il potenziale scalare avrebbe potuto essere posto in relazione con una sua 'pressione' interna. Proprio perché i 'potenziali' (che hanno poi acquisito una funzione essenzialmente ausiliaria) svolgono un ruolo decisivo nel Treatise di Maxwell, il campo elettrico e quello magnetico ‒ che per noi costituiscono gli oggetti fisici di riferimento ‒ non sempre sono al centro dell'analisi maxwelliana. Di conseguenza, l'insieme di relazioni che Maxwell effettivamente stabilì è molto più elaborato delle quattro leggi compatte che da lui prendono il nome: le equazioni alle quali Maxwell pervenne, infatti, spezzano le connessioni tra i campi elettrici e quelli magnetici in legami in seguito considerati non importanti, a un livello fisico fondamentale, tra questi medesimi campi e i corrispondenti potenziali. Non tutti gli studiosi della fisica dei campi, tuttavia, attribuivano una così grande importanza ai potenziali; Oliver Heaviside, George F. Fitzgerald (dopo il 1879) e Oliver J. Lodge erano decisamente riluttanti a ricorrervi; dal loro punto di vista, infatti, le sole quantità veramente fisiche erano proprio i campi elettrici e magnetici.
Dal punto di vista dei maxwelliani, le funzioni dell'energia dell'etere avrebbero potuto essere specificate senza che, di quest'ultimo, si conoscesse la vera struttura, né era necessario sapere in che modo i cambiamenti di energia si producessero. Si pensava che l'etere possedesse alcune proprietà che potevano subire alterazioni in presenza di materia e, in particolare, se ne distinguevano due di immediata importanza: la capacità induttiva specifica e la permeabilità magnetica. Per i maxwelliani, queste due proprietà erano rappresentate da funzioni continue della posizione: i loro valori potevano cambiare (e, in effetti, in presenza di materia cambiavano) ma con continuità. I maxwelliani ammettevano che tali variazioni fossero causate dagli effetti di particelle materiali e che i valori usati nelle equazioni macroscopiche dovessero, di conseguenza, considerarsi medie di effetti microscopici; tuttavia, secondo la loro concezione, ogni molecola materiale avrebbe prodotto un'alterazione continua delle proprietà dell'etere e, pertanto, anche a livello microscopico la continuità non sarebbe stata mai interrotta.
Il nucleo della teoria di campo maxwelliana era costituito dalla rinuncia alla nozione di conservazione della carica così come la si era intesa in precedenza. Invece di considerare la carica come una particolare sostanza elettrica che poteva accumularsi nei corpi, Maxwell la presentò come un epifenomeno del campo: nella sua concezione era implicita l'idea della trasformazione dell'energia, che era immagazzinata nell'etere, in una forma materiale (come, per es., il calore), attraverso un processo piuttosto simile a quello del rilassamento elastico; ciò poteva accadere ovunque vi fosse materia, benché né Maxwell né i maxwelliani avessero tentato di spiegare perché la materia potesse produrre questo effetto, rappresentato a livello macroscopico dalla conducibilità elettrica.
Per capire le implicazioni di questa concezione, s'immagini una regione dell'etere priva di materia, ma in cui sia presente un campo elettrico che immagazzina energia potenziale nell'etere; si inserisca poi un frammento di materia in questa regione. Dal momento che, secondo i maxwelliani, tutte le sostanze materiali possiedono un certo grado di conduttività, la regione dell'etere ora occupata dalla materia inizierà a perdere l'energia immagazzinata nel campo elettrico, la quale si manifesterà nella materia sotto forma di calore. Il risultato di tutto ciò è l'emergere di una differenza nei valori di una certa quantità ‒ lo spostamento elettrico, che è il prodotto della capacità induttiva per l'intensità del campo elettrico ‒ in corrispondenza della superficie di separazione tra la materia e l'etere libero; tale differenza rappresenta, in ogni istante, la 'carica' elettrica su tale superficie. Le 'cariche' positive e negative maxwelliane, dunque, non si conservano singolarmente perché, in base a questi principî, potrebbe non esistere alcuna carica nell'Universo. Questa teoria entrava in contrasto con quelle del fluido elettrico, che si limitavano ad asserire che nell'Universo avrebbe potuto non esserci alcuna carica complessiva ma che naturalmente seguitavano a esistere le singole particelle positive e negative. Nonostante questa differenza la teoria maxwelliana, grazie alla sua concezione di corrente elettrica, soddisfaceva la stessa equazione della conservazione della carica soddisfatta dalle teorie particellari.
Nella teoria maxwelliana la 'corrente' elettrica è la velocità con cui una parte dell'etere si muove; se l'etere è in quiete, non si ha alcuna corrente. La 'carica' elettrica si produce perché l'etere si è mosso, o si muove, attraversando regioni in cui il rapporto tra la conducibilità e la capacità induttiva varia da un punto all'altro. Per collegare tra loro i due processi ‒ carica e corrente ‒ si presume che la corrente generi un campo magnetico oppure che un cambiamento del campo magnetico causi uno spostamento dell'etere. Entrambe le ipotesi ben formulate, insieme ad altre equazioni del campo portano alla stessa equazione della conservazione della carica che deriva dalle teorie particellari. Il punto è che, nonostante questa concordanza, la corrente maxwelliana in senso proprio non è la velocità con la quale varia la carica nel tempo e può soltanto indurre tale variazione.
Tutte queste idee sono presenti in embrione nel Treatise di Maxwell, anche se messe in ombra dalla novità e dalla vastità del testo. Questi e altri concetti fondamentali appaiono con chiarezza negli scritti dei suoi seguaci che operavano a Cambridge, così come in quelli di altri studiosi che non si erano formati in quella stessa università (anche se tra le rispettive posizioni sono rilevabili alcune divergenze). In realtà, la struttura concreta del 'maxwellismo' cantabrigense fu in gran parte elaborata durante i corsi in cui gli studenti analizzavano i diversi problemi sotto la guida dei loro tutors. Ai fini della presente analisi è opportuno elencare le nozioni che si erano andate definendo in questo modo e che erano in gran parte accettate dai maxwelliani: la 'carica' non è altro che una discontinuità nello spostamento e la 'corrente' non è che etere in movimento; per formulare una nuova teoria, è necessario modificare la funzione di energia dell'etere (cosa che equivale a dire che bisogna modificare la struttura dell'etere stesso); l'effetto prodotto dalla materia sull'etere è misterioso e non deve essere preso in considerazione fin quando tutti i problemi non siano stati risolti attraverso i metodi relativi all'energia; la conduttività elettrica è un fenomeno particolarmente misterioso e implica in qualche modo la struttura parcellizzata della materia; le condizioni al contorno sono strumenti analitici cruciali; i modelli meccanici dell'etere sono un mezzo importante per illustrare scambi di energia, ma è poco probabile che riflettano la vera struttura dell'etere.
La crisi delle concezioni maxwelliane
La dimostrazione più chiara dell'influenza che ebbe l'elettrodinamica maxwelliana e della sua distanza dalle successive teorie va forse ricercata nella storia dell'effetto Hall. Questo effetto, scoperto nel 1879 da Edwin H. Hall (1855-1938), dimostra che la corrente elettrica è costituita da particelle in movimento dotate di carica negativa. Il relativo esperimento può essere facilmente eseguito con un'apparecchiatura moderna, ricorrendo a una tecnica non troppo diversa da quella impiegata da Hall. Si prenda una lamina metallica ‒ per esempio di rame ‒ e si invii una corrente nella direzione della sua lunghezza; si applichi poi alla lamina un sensibile galvanometro nella direzione della sua larghezza e si ponga l'intero apparato tra i poli di un elettromagnete, in modo che il campo magnetico sia perpendicolare al piano della lamina. Il galvanometro rileverà una corrente se, e soltanto se, l'elettromagnete è in funzione. Secondo la teoria moderna, questo effetto è la prova diretta della deflessione degli elettroni in movimento all'interno di un campo magnetico e la direzione della deflessione rivela il loro segno.
I maxwelliani, compreso lo stesso Hall, interpretarono in un altro modo questo effetto. Essi ipotizzarono che, quando in presenza di un campo magnetico si produce una corrente elettrica, l'esistenza di questi due oggetti (corrente e campo) nello stesso luogo e nello stesso tempo crei un campo elettrico sussidiario; questo nuovo campo forma sempre un angolo retto sia con la corrente sia con il campo magnetico. Dal momento che per i maxwelliani la 'corrente' elettrica era un flusso di qualche tipo attraverso l'etere ‒ all'interno del quale si verificavano tutti i processi elettrici e magnetici ‒, ciò significava che l'effetto osservato da Hall dovrebbe esistere anche nei corpi non conduttori, poiché in questi ultimi i campi elettrici muovono sempre l'etere per piccole distanze (mentre nei conduttori l'etere può fluire). Come si è già osservato, in base alla convinzione maxwelliana qualsiasi cosa accada in un dato fenomeno deve riflettere in realtà le caratteristiche energetiche dell'etere. Se tali proprietà energetiche subiscono un cambiamento, allora anche le equazioni del campo devono essere modificate, e viceversa.
Hall aveva scoperto un effetto che implicava l'esistenza di un nuovo tipo di campo elettrico. Ciò significava che le equazioni dell'elettromagnetismo dovevano essere modificate nei casi in cui si era in presenza di questo nuovo campo, in modo da tener conto della sua esistenza. Dal momento che non è possibile modificare le equazioni senza modificare le energie, si rendeva necessario anche alterare le espressioni dell'elettromagnetismo in cui compariva l'energia, in modo da renderle coerenti con il nuovo campo di Hall. Una volta portato a termine tale compito si scoprì che, dal punto di vista matematico, queste energie modificate, se riferite a corpi non conduttori, producevano le equazioni relative a un importante effetto scoperto nel 1845 da Faraday: la rotazione del piano di polarizzazione di un raggio di luce che attraversa un corpo non conduttore immerso in un campo magnetico. Nel corso degli anni Ottanta la fisica maxwelliana registrò così un'intricata serie di sviluppi derivanti dalle implicazioni dei nuovi termini relativi all'energia, in particolare per quanto riguardava il difficile problema della riflessione della luce in superfici metalliche magnetizzate, che rappresentava la situazione più generale con cui si potesse avere a che fare e tale da riassumere in sé le altre: risolverla avrebbe significato chiarire tutti i problemi concernenti la riflessione e la rifrazione delle onde elettromagnetiche. All'inizio degli anni Novanta sembrò (tra gli altri, a Joseph J. Thomson) che persino in questo campo si sarebbero ottenuti risultati interessanti.
Tuttavia, ci si rese conto che le nuove equazioni non potevano inglobare realmente tutte le proprietà sperimentali perché, come si fece notare, erano prive di una costante necessaria che avrebbe potuto essere ricavata da una teoria microfisica e che chiamasse in causa meccanismi nascosti come, per esempio, l'elettrone; le equazioni del campo dei maxwelliani, però, non erano apparentemente in grado di assimilare una tale teoria. Ciononostante, la conclusione che la fisica maxwelliana si fosse ormai irreparabilmente incrinata e che fosse costretta a invocare qualche genere di microfisica in grado di completare le equazioni fondamentali del campo, non emerse dai progressi compiuti nella sperimentazione (benché, alla fine, ciò sarebbe potuto accadere), ma dall'approfondimento teorico sulla natura della conduzione elettrica.
Nel corso degli anni Ottanta, i maxwelliani avevano ritenuto che il fenomeno della conduzione non costituisse un problema per i loro procedimenti non perché fossero effettivamente in grado di incorporarlo nella loro teoria, ma perché, in realtà, essi non potevano effettuare questa operazione; all'inizio degli anni Novanta, Oliver Heaviside dimostrò persino che la conduzione elettrica non poteva essere direttamente inserita nelle equazioni dell'energia allora utilizzate, perché (come in ogni effetto che aveva a che fare con la produzione di calore) nella conduzione elettrica l'energia sembrava sfuggire alla trattazione matematica. Così i maxwelliani decisero di evitare del tutto la questione, relegandola in un'area che ammettevano apertamente di non conoscere a sufficienza, ossia quella dell'ignoto meccanismo che legava la materia all'etere. A tal fine, essi ricorsero a un teorema formulato da John H. Poynting (1852-1914), che aveva come oggetto il trasporto di energia da parte del campo elettromagnetico. Questo teorema poteva essere utilizzato per tracciare la disposizione dell'energia intorno a una corrente e sembrava dimostrare che l'energia non scorre lungo il filo elettrico, ma si trasferisce radialmente dall'esterno verso il suo interno. Tale enunciato sembrava fissare efficacemente l'immagine della corrente elettrica quale processo che coinvolgeva l'etere, dal momento che il filo elettrico ora appariva agire come una sorta di pozzo che assorbiva l'energia elettromagnetica dall'etere esterno, e non come un tubo di conduzione.
Poynting e altri impiegarono queste immagini in modo tale da permettere ai maxwelliani di eludere le questioni concernenti la natura della conduzione e le loro tecniche si dimostrarono all'altezza delle aspettative della comunità per un decennio circa. In realtà, questa interpretazione non fu posta in discussione all'interno del gruppo dei maxwelliani, bensì da uno studioso formatosi a Cambridge, Joseph Larmor (1857-1942), che certamente conosceva la teoria di campo, ma che non aveva condotto ricerche su questo argomento fino alla metà degli anni Novanta; fu soltanto allora che egli tentò di dare una risposta proprio a quel genere di questioni che i più esperti maxwelliani, come per esempio Poynting e Thomson, avevano a lungo evitato, finendo così per mettersi in una situazione complicata.
Su suggerimento di Fitzgerald, Larmor si districò da tali difficoltà inventando l'elettrone. Inizialmente egli concepiva questa particella non tanto come un sostituto dei tradizionali metodi maxwelliani, quanto come un modo di evitare certi problemi all'interno di questi ultimi. Tuttavia, in breve egli fu in grado di riorganizzare completamente la fisica del campo: separò l'elettrone, come unica sorgente del campo, dal campo stesso e relegò decisamente l'etere in una posizione di secondo piano. Larmor fu tanto persuasivo che molti maxwelliani alla fine giunsero alla conclusione che non era più il caso di continuare a perdere tempo con le energie del campo dell'etere, perché la forma assunta da tali energie poteva ormai essere considerata come stabilita una volta per tutte. Il nuovo metodo che essi adottarono richiedeva l'invenzione di modelli che fossero in grado di descrivere questa microstruttura materiale, e non nuove forme di energia del campo.
L'elettrodinamica di Helmholtz
Nel 1870 Hermann von Helmholtz, da poco nominato professore di fisica presso l'Università di Berlino, sviluppò una forma di elettrodinamica che si discostava nettamente sia dalla teoria basata sulle particelle formulata da Wilhelm Weber ‒ che godeva di un largo seguito in Germania ‒ sia dalla fisica del campo britannica. Helmholtz tentò di formulare un insieme del tutto generale di equazioni, basate su considerazioni relative all'energia e in grado di conciliare ogni possibile variante dell'elettrodinamica attraverso l'elaborazione di una funzione 'potenziale', che rivestisse un significato energetico e dalla quale fosse possibile dedurre le forze con metodi variazionali: la variazione con coordinate spaziali fisse avrebbe prodotto un effetto elettromotore, mentre la variazione con un tempo fisso avrebbe prodotto un effetto meccanico. Le equazioni così ottenute contenevano una costante indeterminata k e Helmholtz sostenne che, assegnandole valori diversi, si sarebbero riottenute le rispettive teorie che all'epoca descrivevano le correnti che attraversavano i conduttori.
Nonostante le affermazioni di Helmholtz, il suo potenziale elettrodinamico non portava né alla teoria di Weber (in cui le forze agivano in modo istantaneo tra particelle elettriche) né alla teoria di campo (che sostituiva le particelle con i campi e in cui le forze si propagavano). Una delle ragioni di questa mancata corrispondenza consisteva nel fatto che l'elettrodinamica di Helmholtz si basava su una concezione delle relazioni tra oggetti considerati sorgenti diversa da quella delle altre due teorie. Al contrario dei suoi concorrenti, nel descrivere i fenomeni Helmholtz si arrestava ai corpi (senza introdurre nozioni come quelle di particelle o campi) e spiegava tutte le azioni come se fossero determinate immediatamente ed esclusivamente dagli stati degli oggetti interagenti e dalle loro reciproche distanze. In realtà, nella sua fisica, nemmeno la forza propriamente detta esisteva quale entità indipendente, giacché essa emergeva soltanto attraverso il calcolo dell'energia (come accadeva anche nella teoria di campo, benché con un significato notevolmente diverso).
Per ottenere una riproduzione dell'elettrodinamica di Maxwell, Helmholtz avrebbe dovuto introdurre nel suo sistema un oggetto elettrodinamico invisibile, vale a dire una forma di etere. Tra i fisici britannici, l'etere era considerato un'entità sui generis alla base di tutte le cose e non semplicemente una forma di materia. Il punto di vista di Helmholtz era sostanzialmente diverso, in quanto egli pensava che l'etere (ammettendo che fosse elettricamente attivo) dovesse essere visto come un oggetto onnipresente, suscettibile di essere polarizzato elettricamente (come i dielettrici) e magneticamente (come i corpi paramagnetici). Ciò significa che qualsiasi fossero le proprietà dell'etere, non sarebbero state di un genere diverso rispetto alle proprietà elettriche e magnetiche dei corpi, così come esse si manifestano nel mondo che ci circonda. Tuttavia, l'etere di Helmholtz si distingueva dai corpi ordinari almeno per la sua onnipresenza e intangibilità. Ben presto questo modo di pensare condusse a concrete conseguenze pratiche: per sviluppare un sistema elettrodinamico che incorporasse l'etere, si doveva aggiungere, a ogni interazione elettrica o magnetica tra una coppia di corpi ordinari, un terzo e un quarto corpo, entrambi invisibili, che andavano collocati tra ognuno dei due corpi ordinari e l'etere stesso. Nel 1870 Helmholtz analizzò diversi aspetti di tale tipo di sistema, nel duplice presupposto che l'etere fosse polarizzabile sia elettricamente sia magneticamente, esattamente allo stesso modo dei corpi ordinari. Tuttavia, a causa della sua intangibilità, l'etere rimaneva per Helmholtz un'entità ipotetica e quindi sospetta.
Nelle indagini elettrodinamiche condotte nel laboratorio di Helmholtz nel corso degli anni Settanta dell'Ottocento, si possono distinguere due componenti connesse tra loro. In primo luogo, vi erano gli effetti primitivi ‒ le nuove forze indipendenti da considerazioni relative all'etere ‒ che erano associati alla funzione potenziale di Helmholtz. Se queste forze fossero esistite (nelle forme stabilite semplicemente dall'analisi delle interazioni reciproche tra corpi ordinari), allora, qualsiasi fosse stato l'effetto provocato dall'etere stesso, si sarebbe necessariamente trovato al di fuori del dominio delle forze rilevabili che agiscono tra i corpi del mondo su cui abbiamo, per così dire, un accesso strumentale diretto. Se, invece, queste forze non fossero esistite, o se le loro intensità fossero state diverse da quelle indicate dalla pura teoria, allora sarebbe stato necessario quantomeno prendere in considerazione l'azione di un altro corpo di natura intangibile. Questo corpo, ossia l'etere, avrebbe inciso sulle forze misurate in un modo che sarebbe dipeso direttamente dalla grandezza delle proprie suscettibilità, elettrica e magnetica. Se, in particolare, la suscettibilità elettrica dell'etere fosse stata tanto grande da dover essere considerata infinita per gli strumenti di misura disponibili, allora le nuove forze di Helmholtz (che si manifestavano solamente in presenza di circuiti aperti) avrebbero potuto essere mascherate dalle azioni compensatrici delle grandi cariche di polarizzazione che si generavano in corrispondenza della separazione tra i conduttori carichi e l'etere stesso. Ciò non escludeva l'esistenza delle nuove forze ‒ che, in effetti, dovevano esistere ‒, ma in questo caso bisognava aggiungere loro le forze compensatrici derivanti dalla polarizzazione dell'etere (ciò sollevava una serie di questioni concernenti il bilanciamento della quantità di moto, poiché l'etere che esercitava una forza doveva ora essere considerato un corpo a sua volta suscettibile di subire la forza ponderomotrice, o almeno di trasmettere la quantità di moto).
Nessun esperimento eseguito negli anni Settanta nel laboratorio di Helmholtz fornì la prova che esistessero le nuove forze elettromotrici presupposte dalla sua teoria pura. Sfortunatamente sembra che non siano sopravvissuti né appunti manoscritti, né relazioni di laboratorio, né frammenti di calcolo relativi a tali esperimenti, forse proprio perché questi ultimi non diedero i risultati positivi sperati. Di alcuni esperimenti sono disponibili, tuttavia, resoconti che furono dati alle stampe. Questi ultimi, e in particolare quelli redatti dallo stesso Helmholtz, sono molto approssimativi, non forniscono cioè alcun dettaglio circa il previsto grado di accuratezza degli esperimenti, i loro limiti strumentali e così via; essi indicavano, tuttavia, che per Helmholtz le prove raccolte dimostravano quantomeno la necessità di inserire alla base della sua teoria una forma di etere polarizzabile, anche se le sue proprietà non erano ancora definite con precisione e sicurezza.
Però non era tutto; se si fosse dovuto tener conto dell'etere nel misurare le forze elettrodinamiche, allora la sua presenza avrebbe sollevato la questione se questa entità avesse anche altri effetti, come quelli che erano stati attribuiti all'etere dai seguaci di Maxwell e studiati analiticamente dallo stesso Helmholtz. Emersero così nuovi problemi, indubbiamente pertinenti al contesto del laboratorio di Helmholtz, ma non nella Gran Bretagna maxwelliana. Come già osservato, i fisici britannici non consideravano affatto l'etere simile a un dielettrico con una struttura magnetizzabile; dal loro punto di vista, esso era la sede in cui avevano luogo tutti i processi elettromagnetici. I corpi materiali, gli oggetti del mondo circostante, non erano in realtà dotati di proprietà elettromagnetiche specifiche, ma modificavano i valori delle proprietà dell'etere nelle regioni in cui erano situati (in realtà, molti fisici britannici, quando ricorrevano a un linguaggio speculativo, concepivano la materia stessa come una modificazione dell'etere, e quindi non pensavano a quest'ultimo come a un'entità semplicemente simile alla materia). Proprio perché lo concepivano come un'entità diversa dai corpi ordinari, i maxwelliani non pensavano di dover dividere le proprietà dell'etere in diversi compartimenti. Avevano già combinato le proprietà elettriche e magnetiche dell'etere nella complessa, e piuttosto eterogenea, struttura di una teoria di campo e quindi non erano particolarmente interessati a chiedersi se, per esempio, un flusso elettrico variabile nell'etere fosse in grado di dar luogo a un campo magnetico e viceversa. Il punto di vista di Helmholtz era diverso, perché nella sua concezione l'etere non era il principio essenziale dell'elettrodinamica, ma un elemento ‒ forse necessario ‒ che avrebbe potuto essere aggiunto o meno, a seconda del responso del laboratorio. Di conseguenza, Helmholtz era profondamente interessato a scoprire se i corpi che dovevano comportarsi nello stesso modo dell'etere ‒ quali i dielettrici ‒ potessero, per esempio, essere polarizzati elettricamente da una corrente variabile in un conduttore o, viceversa, se un dielettrico con una polarizzazione variabile potesse esercitare una forza magnetica, come un conduttore di corrente. Scoprire questo genere di cose era tutt'altro che facile.
Hertz e le onde elettriche
Per collocare nella giusta prospettiva il fisico tedesco Heinrich Rudolf Hertz (1857-1894), che per primo produsse e rilevò le onde elettriche, è essenziale ricordare che anteriormente al 1887, anno in cui egli costruì un dispositivo a dipolo oscillante ('oscillatore di Hertz') e il risonatore che, rispettivamente, generavano e rilevavano la radiazione elettromagnetica, nessun fisico sapeva come produrre onde elettriche che si propagassero liberamente. In Gran Bretagna la radiazione ottica era considerata il solo esempio conosciuto di questo genere di onde, che erano quindi quasi sempre associate a strumentazioni ottiche. Inoltre, almeno fino alla metà degli anni Ottanta, alcuni maxwelliani, e in particolare Fitzgerald, escludevano che fosse possibile produrre tali onde attraverso dispositivi elettromagnetici.
A Berlino, dove Hertz aveva appreso le tecniche della ricerca elettromagnetica come assistente di Helmholtz, la situazione era persino più confusa di quanto non fosse in Gran Bretagna, dal momento che le implicazioni della teoria di Maxwell rimanevano inesplorate per la maggior parte dei fisici tedeschi che, del resto, erano schierati su posizioni molto diverse tra loro. Helmholtz era pervenuto personalmente a uno schema che prevedeva l'esistenza di onde in strutture suscettibili di polarizzazione elettrica e magnetica; ma né lui, né altri in Germania si erano chiesti se fosse possibile produrle artificialmente e, tanto meno, come. Evidentemente Helmholtz, così come i suoi contemporanei britannici, riteneva che la radiazione ottica fosse il modello paradigmatico, e forse l'unico appropriato esempio, del fenomeno delle onde elettriche, a eccezione dei processi che si verificavano esclusivamente nei mezzi conduttori o su di essi. Inoltre, l'ipotesi della presenza di radiazione elettrica nei mezzi non conduttori (prevista dal sistema di Helmholtz) sollevò questioni alle quali, negli anni in cui Hertz lavorava a Berlino, non erano state ancora date risposte sufficientemente chiare. In realtà, fu Helmholtz che tentò di convincere il suo giovane allievo a dedicarsi a una loro verifica sul piano sperimentale.
Un nuovo apparato sperimentale
Non c'è da meravigliarsi che la strada seguita da Hertz per produrre onde elettriche artificiali sia stata tutt'altro che semplice. Nel 1886, anno in cui iniziò a lavorare intensamente sulle oscillazioni assai rapide nei fili metallici, che alla fine lo condussero a effettuare i suoi esperimenti sulla propagazione delle onde elettriche nell'aria, Hertz pensava che le interazioni tra i fili si basassero sull'azione diretta di un oggetto sull'altro. Egli riuscì a produrre effetti stabili di accoppiamento tra il dispositivo che generava l'oscillazione ‒ il suo dipolo ‒ e il rilevatore di risonanza, costruito per rilevare le oscillazioni. Si convinse così di avere a che fare con oscillazioni sincrone dell'ordine di decine di milioni di cicli al secondo. La produzione di un nuovo regime delle oscillazioni elettriche era un risultato di per sé estremamente importante, che Hertz fu fiero di annunciare a Helmholtz. L'effetto di accoppiamento prodotto non suggeriva nulla riguardo alla propagazione, perché, dal suo punto di vista, esso operava conformemente alle leggi dell'induzione previste da tutte le teorie dell'elettrodinamica allora correnti, da quella basata sulle particelle elettriche di Weber al potenziale elettrodinamico di Helmholtz, alla teoria del campo di Maxwell. Data la straordinaria rapidità delle oscillazioni, tuttavia, Hertz si convinse di essere riuscito a ideare un dispositivo che poteva essere usato per produrre correnti di polarizzazione altrettanto rapide nei dielettrici e, quindi, per risolvere la seconda delle due questioni che premevano a Helmholtz: se, cioè, i dielettrici potessero essere polarizzati da correnti variabili nei conduttori e se la polarizzazione dielettrica variabile potesse esercitare una forza elettromotrice. In realtà Helmholtz aveva tentato di spingere il suo giovane allievo a effettuare esperimenti che avessero come oggetto questi argomenti, ma in un primo momento Hertz si era sottratto a tale compito perché, dopo una lunga analisi, era giunto alla conclusione che quei problemi non fossero risolvibili con gli apparecchi in uso all'epoca. Da allora in poi Hertz aveva tenuto a mente tali questioni come singole 'icone' che rappresentavano questioni centrali nella fisica promulgata dal suo mentore.
Nell'autunno del 1887 Hertz aveva compreso come si comportavano le scintille emesse dal suo risonatore quando gli si collocava accanto una grande lamina conduttrice. Le enormi cariche rapidamente variabili che fluttuavano avanti e indietro sull'oscillatore si configuravano elettrostaticamente in quel conduttore che, come l'oscillatore stesso, era sede di potenti correnti di conduzione. Ciò dava modo a Hertz di calibrare il comportamento di un dielettrico sotto l'effetto di un fenomeno assolutamente non problematico: l'induzione elettrodinamica di una corrente variabile di conduzione. Esaminare le correnti dielettriche era estremamente semplice: era sufficiente rimuovere la lamina conduttrice e collocare al suo posto un blocco di pece. L'oscillatore di nuovo si configurò elettricamente, questa volta sotto l'effetto della polarizzazione dielettrica, e di conseguenza generò correnti di polarizzazione. Per rispondere alla seconda questione sollevata da Helmholtz sui dielettrici, Hertz doveva limitarsi a osservare se le scintille del risonatore si comportassero, con il dielettrico, nello stesso modo in cui si erano comportate in presenza della lamina conduttrice. Il responso fu positivo. L'esperimento diede risultati pressoché stabili e Hertz si affrettò a pubblicarli.
Con ciò abbiamo posto le premesse per capire perché e in che modo Hertz affrontò il fenomeno della propagazione e il motivo per cui è ragionevole dire che egli scoprì qualcosa sulle forze e non sui campi. A Hertz non venne subito in mente di usare il suo dispositivo per effettuare esperimenti relativi alla propagazione, del resto non ne aveva motivo. In quel periodo era profondamente concentrato sulle due questioni, relative ai dielettrici, sollevate molto tempo prima da Helmholtz, ma fino ad allora ne aveva chiarita solamente una. A dire il vero nel 1886 aveva tentato, senza successo, di utilizzare il suo dispositivo per verificare l'azione di polarizzazione elettrica di correnti di conduzione variabili, ossia di dare una risposta alla prima questione berlinese, e ancora non intravedeva la strada da percorrere per ottenere tale verifica. Improvvisamente egli intuì la chiave della risoluzione del problema che a posteriori potrebbe sembrare ovvia; comprese cioè di poter rispondere simultaneamente ai due quesiti considerando la propagazione nell'aria: supponendo che quest'ultima si comportasse a tutti gli effetti come un dielettrico, tale propagazione avrebbe implicato una risposta positiva per entrambe le questioni. Nell'autunno del 1887, quindi, le ricerche di Hertz non erano volte tanto a dimostrare la propagazione nell'aria di per sé, quanto a esaudire la richiesta formulata quasi un decennio prima dal suo mentore. La propagazione era, per così dire, uno strumento e non un fine.
La propagazione dei fenomeni elettrici
Adottando lo stesso schema utilizzato nei suoi esperimenti sui dielettrici, Hertz decise di mettere a confronto la propagazione nell'aria con un effetto che non poneva problemi di interpretazione, ma che fino ad allora non era mai stato prodotto in laboratorio: le onde ad altissima frequenza nei fili metallici. A tal fine bisognava fornire prove convincenti che dimostrassero l'esistenza di queste onde e Hertz dedicò molto tempo al tentativo di documentarla in modo inoppugnabile. Una volta assicurato lo status di fenomeno reale alle onde nei metalli ‒ che erano già facilmente interpretabili ‒, Hertz dovette in qualche modo raffrontarle all'azione diretta dell'oscillatore. Egli decise di far agire insieme la forza del filo metallico e quella dell'oscillatore in modo da azionare il risonatore. L'esperimento di Hertz, in definitiva, faceva affidamento proprio sull'interferenza tra forze motrici e non, per esempio, sulla composizione dei campi. In questa fase, le sue forze non erano in alcun modo diverse, in quanto al genere, dalle forze che agivano tra conduttori percorsi da correnti variabili; dal punto di vista di Hertz, esse presentavano tutte le proprietà delle forze studiate nel precedente decennio di ricerca, e nessun'altra. Anzi, per la precisione, possedevano un solo attributo in più, ossia la forza esercitata dall'oscillatore poteva impiegare un certo tempo per raggiungere il risonatore, proprio come l'onda trasmessa lungo il filo metallico impiegava un certo tempo per compiere il suo percorso. A questo stadio, secondo Hertz, tale intervallo temporale si limitava semplicemente a complicare una situazione per altri versi ben conosciuta ed estremamente semplice, quella in cui due forze agivano nello stesso tempo e sul medesimo oggetto per produrre un effetto complessivo. L'esperimento era stato progettato per rilevare questa somma delle forze punto per punto lungo il filo. Per quanto lo riguardava, Hertz ricercava un nuovo tipo di forza elettromotrice in grado di propagarsi e non una struttura elettromagnetica del tutto nuova. Nella prima fase del suo lavoro, quindi tenne conto di tutte le caratteristiche della forza elettromotrice così come egli la concepiva.
Facendo scorrere il risonatore lungo il filo e prendendo nota di come cambiava la scintillazione tra due posizioni scelte in modo canonico, Hertz pensò di riuscire in breve a trarre conclusioni sulla propagazione. Egli sapeva che la forza esercitata dal filo si 'muoveva', per così dire, lungo il filo stesso, perché aveva già rilevato le onde interne a esso. Nel caso in cui la forza dell'oscillatore non si fosse propagata, ma semplicemente fosse variata la sua intensità con la distanza, il carattere della scintillazione avrebbe chiaramente seguito l'onda del filo stesso, perché soltanto quest'ultima avrebbe viaggiato. Se, per contra, la forza si fosse propagata nell'aria esattamente alla stessa velocità dell'onda del filo, allora la scintillazione avrebbe dovuto essere esattamente dello stesso tipo di quella che si propagava nel filo (di quale tipo, sarebbe stato determinato dalla differenza di fase iniziale tra le due propagazioni). Qualsiasi altra situazione avrebbe prodotto variazioni della scintillazione, calcolabili in base al rapporto tra le due velocità. Tutte le tavole elaborate da Hertz nel corso di questi primi esperimenti indicavano lo stesso risultato, infatti pochi giorni prima di Natale, non era ancora in possesso di un chiaro indizio o di una traccia in grado di suggerire che la variazione della scintilla non seguiva l'onda del filo; ciò significava stabilire che la propagazione nell'aria non avveniva con velocità finita. Pur tenendo conto di un ampio margine di errore ‒ e Hertz non aveva esplicitamente preso in considerazione niente di simile ‒ l'esperimento non poteva assolutamente essere usato per indurre gli scettici a riconoscere la scoperta della propagazione nell'aria, e questo Hertz lo sapeva.
Nel corso di quelle settimane egli cercò di convincersi ad accettare un risultato che sembrava inesorabilmente negativo. Egli doveva però essere in grado di sostenere in modo persuasivo che l'apparato del tutto originale che aveva appena ideato, e con cui aveva già prodotto effetti nuovi e complessi, avrebbe potuto essere impiegato come uno strumento dotato di un'affidabilità tale da individuare qualche cosa che si trovava agli estremi confini della speculazione teorica contemporanea e che certamente andava oltre i limiti della sperimentazione corrente. Hertz, quindi, tentò di convertire il suo dispositivo in un congegno utilizzabile per rilevare l'interferenza: il 17 dicembre 1887 decise di effettuare una serie di trentacinque esperimenti numerati destinati a stabilizzare l'apparato e il 21 dicembre li condusse a termine. Nei due giorni successivi esaminò ancora una volta l'interferenza tra la forza del filo e quella dell'oscillatore, allo scopo di confermare che, come aveva precedentemente già concluso, la forza non si propagava nell'aria. Il risonatore era disposto, anche in questo caso, nel piano perpendicolare a quello formato dal filo e dall'oscillatore e la sua apertura era verticale. Questa posizione era la più adatta a osservare l'interferenza, ma non l'unica possibile e, in effetti, non era stata adottata da Hertz per rilevare l'onda del filo: in quel caso il piano del risonatore includeva sia il filo sia l'oscillatore, e l'apertura per la scintilla era collocata di fronte al filo. Il motivo per cui Hertz non aveva usato già in precedenza la posizione di cui abbiamo detto per rilevare l'interferenza era soprattutto di carattere pratico; non era facile, infatti, invertire l'interferenza delle forze del filo e dell'oscillatore.
Tuttavia, il 24 dicembre egli decise di verificare l'interferenza ricorrendo a tale scomoda disposizione e collocò il risonatore a 3 m di distanza dal punto dove, in un esperimento precedente, lo scintillio era apparso più intenso. Operando nel solito modo, a questo punto la scintilla avrebbe dovuto decisamente indebolirsi e non rafforzarsi, ma ciò non accadde. Hertz tentò immediatamente di approfondire questa scoperta nell'esperimento numero 52: l'effetto rimaneva dello stesso tipo a 1, 2, 3 e persino 4 m di distanza, benché tendesse a indebolirsi a 4 e 5 m, al punto che la situazione divenne 'dubbia'. In base alla concezione di Hertz dell'interferenza delle forze, questa incontrovertibile e, prima di quel giorno, del tutto inaspettata scoperta poteva essere interpretata in un solo modo, ossia la forza dell'oscillatore doveva propagarsi a una velocità percettibilmente differente da quella dell'onda del filo. Tale conclusione costringeva naturalmente a chiedersi che cosa non avesse funzionato negli esperimenti precedenti. Hertz, ovviamente, pensò che la forza elettrostatica si propaga molto più rapidamente di quella elettrodinamica; in prossimità dell'oscillatore, dove i primi esperimenti avevano indicato una velocità infinita dell'azione elettrodinamica, la forza elettrostatica era decisamente più intensa. In quel punto, essa soverchiava l'azione elettrodinamica e falsava la situazione inducendo ad attribuire anche a quest'ultima una velocità infinita; ciò significava che, se i primi esperimenti fornivano la prova presunta dell'alta e forse infinita velocità della forza elettrostatica, i nuovi dimostravano la velocità finita dell'azione elettrodinamica: le due forze si manifestavano in modi diretti e decisamente diversi.
L'interpretazione in termini di propagazione di onde nell'aria
Hertz era consapevole del fatto che, nella teoria di Maxwell, le velocità della propagazione nell'aria e nel filo dovessero coincidere, mentre avrebbero potuto essere diverse in base ai principî di Helmholtz, benché quest'ultimo non avesse analizzato a fondo, almeno in termini espliciti, tale punto; gli esperimenti di Hertz potevano essere combinati in modo da dedurre il rapporto delle due velocità. Hertz aveva osservato che a 7,5 m ca. l'interferenza cambiava di segno; considerando di 2,8 m la metà della lunghezza dell'onda del filo, egli asserì, in un lavoro dato alle stampe, che il rapporto tra la velocità dell'azione elettrodinamica dell'oscillatore e quella dell'onda del filo era di 75:47, o di circa 1,6:1. Hertz, naturalmente, più tardi sarebbe ritornato sui propri passi per quanto riguardava questi primi risultati; tuttavia sul momento non esitò a pubblicarli e a scrivere una trilogia, strutturata ad arte, per persuadere i propri colleghi tedeschi che, dal punto di vista sperimentale, si trattava di conclusioni attendibili. Le sue argomentazioni non gli procurarono i risultati sperati, per due ragioni: in primo luogo, apparentemente Hertz non godeva di grande credito, almeno in certi ambienti, e non aveva ancora consolidato la propria reputazione; in secondo luogo, i suoi esperimenti richiedevano un profondo lavoro di interpretazione e, in effetti, furono capiti meglio soltanto quando fu lo stesso Hertz a darne una personale spiegazione. Egli prese atto quanto meno di questa seconda motivazione e, nel corso di quella primavera, cercò di giustificare la propagazione ricorrendo ad argomentazioni più convincenti. Pur avendo incontrato molte difficoltà, ideò la nozione secondo cui la forza nell'aria è paragonabile a un'onda nel senso più stretto del termine; d'improvviso gli venne in mente che forse avrebbe potuto produrre, per riflessione, onde stazionarie nell'aria, proprio come le aveva prodotte nei fili metallici. Eseguì così una serie di esperimenti estremamente più chiari di quelli che lo avevano portato a ipotizzare per la prima volta la propagazione. Al contrario dei primi, questi nuovi esperimenti esercitarono ben presto una profonda influenza, perché le caratteristiche d'insieme delle onde stazionarie erano spiegate nei dettagli sia dall'ottica sia dalla meccanica e perché Hertz aveva già prodotto le onde elettriche nei fili metallici.
Dopo essere giunto alla conclusione che la forza si comporta nell'aria esattamente come un'onda, nell'estate del 1888 Hertz tentò di pervenire a una matematica appropriata, che non si fondasse esclusivamente sulla composizione delle forze (operazione che aveva costituito il punto di partenza delle sue indagini); tale composizione avrebbe dovuto tuttavia sopravvivere, come approssimazione del fenomeno reale. Hertz, quindi, decise esplicitamente di risolvere la propria versione delle equazioni di Maxwell per il dipolo oscillante: il suo scopo era soltanto quello di capire quali conseguenze prevedessero queste equazioni per i suoi esperimenti, aspettandosi nell'ipotesi più sfavorevole minime variazioni rispetto alle conclusioni che aveva tratto in precedenza dalla composizione delle forze.
Con grande sorpresa, Hertz constatò che la sua iniziale scoperta della propagazione era in contraddizione con i calcoli eseguiti a partire dalle equazioni di Maxwell; ne concluse che le proprie osservazioni erano comunque degne di fede, ma che la sua soluzione delle equazioni del dipolo era resa imprecisa dall'approssimazione del filo come infinitamente sottile e da valori forse errati della lunghezza dell'onda del filo. Tra l'inverno del 1887 e la primavera successiva, quella che sembrava una trionfale conferma si era trasformata in un problema tormentoso. Questo cambiamento coincise con il primo tentativo da parte di Hertz di sostituire le forze di Helmholtz che si propagavano con la trasmissione delle onde attraverso i campi.
Non si può dire che Hertz abbia del tutto sostituito con campi unitari le forze che interferivano tra loro, finché non fu persuaso che le onde nei fili non esistevano affatto, se non come casi speciali di onde nell'aria, e che gli esperimenti che sembravano dimostrare il contrario non dovevano essere presi in considerazione, o dovevano essere reinterpretati. Hertz pensava cioè che la propagazione nell'aria implicasse un tipo speciale di forza elettromotrice e che la propagazione nei metalli fosse un processo a sé. Nel 1890, invece, egli iniziò a pensare che la propagazione nell'aria fosse basata sul solo tipo di campo elettrico esistente e che la propagazione nei metalli fosse un caso speciale di propagazione nell'aria.
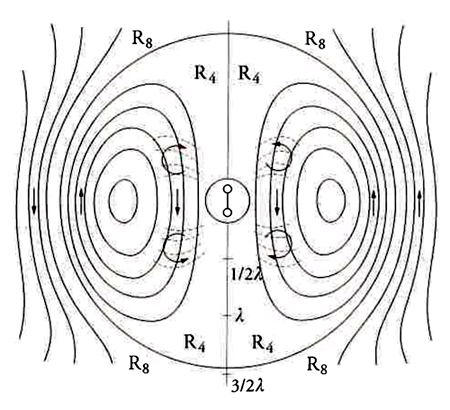
Nel corso di quell'anno, Hertz pubblicò due lavori dedicati alle equazioni fondamentali dell'elettromagnetismo che furono letti da un vasto pubblico, non soltanto in Germania. I numerosi rimandi a questi due articoli, contenuti in opere contemporanee, dimostrano il profondo impatto che esercitarono sui fisici tedeschi; la qual cosa non sorprende dal momento che, con questi lavori, Hertz introdusse molti colleghi alla comprensione dell'ampia gamma dei processi elettromagnetici dal punto di vista di una teoria di campo. Già nel 1889 egli aveva presentato le quattro equazioni del campo, nonché la loro soluzione per il dipolo; tuttavia, mentre gli articoli del 1890 non contenevano diagrammi di alcun tipo, in questo lavoro del 1889 ne furono inseriti molti, incluso quello che indicava una sequenza temporale di mappe che rappresentavano il campo del dipolo radiante; la fig. 9 mostra la mappa per t=0 (R4 e R8 indicano gli spazi sferici riempiti dalle linee di forza, λ la lunghezza d'onda). Nel periodo immediatamente successivo alla scoperta di Hertz, questo articolo servì spesso da base per la comprensione dell'opera dello scienziato e fu usato per sviluppare un'interpretazione pragmatica di un nuovo oggetto scientifico, ossia il campo di radiazione.
Hertz poté costruire un dispositivo multivalente come il dipolo radiante perché, unico tra i suoi contemporanei, combinava all'approccio helmholtziano alla fisica un superbo acume sperimentale e una straordinaria ricercatezza analitica, ai quali, infine, si aggiungeva un forte desiderio di riconoscimento professionale. Hertz aveva imparato da Helmholtz a ricercare in laboratorio nuove interazioni tra oggetti, senza preoccuparsi in modo particolare dei processi nascosti che spiegassero la capacità di tali oggetti di produrre effetti; il suo dipolo e il suo rivelatore di risonanza furono sviluppati nel tentativo di indagare questa sorta di interazioni. Hertz non riteneva neppure di dover analizzare tali dispositivi, perché aveva imparato da Helmholtz a esplorare il carattere delle interazioni tra i dispositivi, piuttosto che la loro intrinseca, e forse profondamente nascosta, natura. I maxwelliani della Gran Bretagna si interessavano a ciò che accadeva sulle superfici dei conduttori, lasciati liberi di raggiungere il loro equilibrio elettrico. Alcuni fisici tedeschi, stretti nella morsa dell'ethos della misurazione esatta, non avrebbero trattato con la stessa disinvoltura mostrata da Hertz i valori numerici ricavati dagli esperimenti; altri, convinti del fatto che i conduttori fossero meri contenitori di entità attive nascoste, si sarebbero mostrati maggiormente interessati di Hertz a comprendere il più rapidamente possibile i processi che dovevano aver luogo nel dipolo e nel risonatore stessi.
Nel corso degli anni Novanta, il dipolo di Hertz rappresentò un'entità nuova, assente nella struttura analitica dell'effetto che produceva (la radiazione elettromagnetica), ma fisicamente presente, come dispositivo reale, nei laboratori. Tra i fisici, il dipolo di Hertz non fu mai considerato un oggetto di grande interesse, perché, dal loro punto di vista, non produceva nulla di davvero nuovo, ma si limitava a generare per così dire un tipo di luce artificiale. Tuttavia, divenne un utile modello, una sorgente canonica di radiazione elettromagnetica e, negli anni Novanta del XIX sec. e nel primo decennio del XX, fu spesso utilizzato senza troppe discussioni nei calcoli riguardanti la radiazione. è per questo che, mentre l'elettrone assumeva sempre più frequentemente una posizione di primo piano, si sviluppò un'inquietante relazione tra il dipolo radiante e l'elettrone oscillante.
L'elettrone e il periodo successivo
Fu soprattutto grazie all'opera del fisico olandese Hendrik Antoon Lorentz (1853-1928) che sorgenti e microfisica furono ampiamente introdotti nello studio dell'elettromagnetismo. Almeno a partire dalla fine degli anni Settanta del XIX sec., la posizione di Lorentz si era discostata da quelle di quasi tutti i suoi contemporanei per un aspetto tutt'altro che trascurabile: soltanto Lorentz, infatti, aveva distinto la materia dall'etere nella formulazione delle equazioni elettromagnetiche, anche se il metodo utilizzato per compiere questa operazione era stato introdotto molti anni prima da Helmholtz. La prima opera dedicata da Lorentz all'elettromagnetismo (1875) non si allontanava dai principî essenziali su cui si fondavano le idee più diffuse al di fuori della Gran Bretagna, anche se Lorentz operava alle frontiere di queste idee, poiché, sull'esempio di Helmholtz, trattava l'etere come un corpo polarizzabile magneticamente ed elettricamente. Quest'approccio non era affatto comune neppure in Germania, dove erano ancora privilegiate le varianti della vecchia elettrodinamica weberiana (basata su particelle elettriche confinate nei corpi materiali) e l'etere era ancora concepito come una struttura meccanica.
Nel 1878 Lorentz, unificando due teorie di Helmholtz, compì un passo decisivo oltre il punto in cui si era arrestato quest'ultimo: egli combinò la teoria elettromagnetica dell'etere formulata nel 1870, alla quale egli stesso aveva fatto ricorso già nel 1875, con una teoria ‒ del tutto non elettromagnetica ‒ enunciata da Helmholtz per spiegare il fenomeno recentemente scoperto della dispersione anomala; questa seconda teoria si basava su due equazioni meccaniche distinte, destinate rispettivamente all'etere e alla materia, che avevano alcuni termini in comune. Lorentz si appropriò dell'idea implicita in questo lavoro, ossia che per spiegare i fenomeni sulle interazioni tra l'etere e la materia erano necessarie due equazioni legate tra loro; la combinò inoltre con quella di Helmholtz dell'etere polarizzabile e, nel 1878, enunciò la propria teoria elettromagnetica della dispersione. Si trattava di una teoria che richiedeva che le particelle di materia possedessero allo stesso tempo carica e massa mentre quelle dell'etere fossero dotate soltanto di carica.
A partire da queste premesse, Lorentz riuscì a mettere a punto una tecnica che permetteva di trattare il rapporto esistente tra l'etere e la materia, e della quale i maxwelliani non erano a conoscenza, poiché si basava proprio su quel concetto di sostanzialità della carica che essi avevano negato ostinatamente; fino a questo momento (1878) Lorentz aveva applicato tale tecnica soltanto per enunciare una formula della dispersione, tuttavia anche così aveva compiuto un'operazione che nessun maxwelliano avrebbe mai intrapreso o potuto intraprendere. Si potrebbe dire che l'approccio di Lorentz alla teoria della dispersione del 1878 equivaleva a un'inversione del metodo maxwelliano: invece di ignorare la materia e di modificare l'etere, come accadeva nel metodo maxwelliano, egli ignorò l'etere e alterò la materia.
La teoria della dispersione non fu l'unico lavoro dedicato da Lorentz prima del 1892 alle connessioni esistenti tra l'elettromagnetismo e l'ottica. Egli aveva analizzato anche le implicazioni dell'effetto Hall, per quanto riguardava l'azione della materia sulla luce in presenza di campi magnetici (gli effetti Faraday e Kerr), seguendo una linea di condotta decisamente nuova. Al contrario della propria precedente teoria della dispersione, che non alterava l'etere, nella sua analisi delle implicazioni ottiche dell'effetto Hall l'etere era modificato. Nel contesto della teoria di Helmholtz, questo significava che il fenomeno della dispersione non obbligava Lorentz a modificare le costanti che governavano le proprietà dell'etere, mentre ciò accadeva per gli effetti Hall, Faraday e Kerr: entrambi i fenomeni riguardavano, ovviamente, gli effetti della materia sull'etere. Lorentz, probabilmente, iniziò a capire a fondo le implicazioni di questa contraddizione soltanto nel 1886, quando si ripresentarono nel tentativo di comprendere le ragioni dell'esistenza del coefficiente di trascinamento di Fresnel per l'aberrazione stellare.
Nel 1886 Lorentz si trovò di fronte a due possibili scelte, dal momento che, come tutto lascerebbe credere, egli riteneva che il coefficiente di resistenza dovesse avere un'interpretazione elettromagnetica, così come la dispersione e gli effetti Faraday, Hall e Kerr: o tale coefficiente traeva origine, al pari di questi ultimi tre effetti, da un cambiamento imposto dalla materia all'etere, oppure, come nel caso della dispersione, derivava dal modo in cui la materia produceva effetti elettromagnetici nell'etere stesso. Per Lorentz questa alternativa rifletteva la differenza esistente tra la teoria di Fresnel e quella di Stokes sugli effetti ottici del movimento attraverso l'etere: la teoria di Stokes, analiticamente scorretta, era analoga all'analisi degli effetti Faraday, Hall e Kerr offerta da Lorentz, perché entrambe alteravano l'etere (giacché la prima prevedeva che quest'ultimo fosse trascinato da un grande corpo opaco e la seconda che si modificassero le equazioni fondamentali del campo elettromagnetico); la teoria di Fresnel aveva tradizionalmente preso in esame un etere parzialmente trascinato, ma in questo caso soltanto una minima quantità di etere doveva muoversi rispetto a quella richiesta da Stokes. Di conseguenza, la teoria di Fresnel era molto vicina allo spirito con cui Lorentz aveva spiegato la dispersione.
Lorentz si rese conto che queste differenze evocavano un problema di carattere estremamente generale, vale a dire se l'etere dovesse mai essere modificato. Compiendo un passo radicale e senza precedenti, tra il 1886 e il 1892 Lorentz stabilì che non si dovesse modificare l'etere in alcun modo per quanto riguardava i fenomeni ottici ed elettromagnetici, prefiggendosi così un nuovo compito, ossia la formulazione di una teoria in cui il coefficiente di Fresnel fosse causato esclusivamente dal modo di organizzarsi della materia. Si trattava di un problema straordinariamente difficile, perché Lorentz non era disposto ad accontentarsi di soluzioni parziali. Egli insistette sul fatto che la dispersione e il coefficiente di Fresnel dovessero emergere da un calcolo dettagliato degli effetti che le particelle materiali radianti producevano l'una sull'altra. Se Lorentz non avesse insistito sull'importanza di una teoria tanto precisa e approfondita, forse avrebbe conseguito gli stessi risultati finali per una via molto più semplice. In realtà, egli avrebbe potuto ideare proprio lo schema che, diversamente dal suo, avrebbe esercitato un'influenza piuttosto profonda in Germania durante gli anni Novanta dell'Ottocento, soprattutto in seguito alle pubblicazioni di Paul Karl Ludwig Drude (1863-1906); secondo tale schema, all'insieme delle equazioni del campo ‒ il 'limite di Maxwell' delle relazioni di Helmholtz, come spesso si usava dire ‒ era aggiunta un'equazione relativa alla materia, dalla cui manipolazione si deducevano vari effetti. Si sarebbe trattato, a grandi linee, di ciò che lo stesso Lorentz aveva già realizzato nel 1878 per la teoria della dispersione, ma egli ora non scelse questo approccio perché senza dubbio non lo considerava sufficientemente rigoroso.
La teoria che Lorentz pubblicò nel 1892 spiegava tutti gli effetti elettromagnetici, e in particolare il coefficiente di trascinamento, attraverso quelle che a partire da quel momento sarebbero state chiamate 'forze ritardate'. In questo schema le particelle cariche accelerano e perciò irradiano emettendo onde che si propagano attraverso l'etere, eternamente invariante; quando queste onde colpiscono altre particelle, le costringono a muoversi e quindi a irradiare a loro volta. Il modello delle interazioni risultante determinava le proprietà ottiche del sistema e Lorentz riuscì a dimostrare, in modo chiaro ma complicato, che un sistema di particelle che si muovono attraverso l'etere si comporterà, al primo ordine, nel modo richiesto dal coefficiente di trascinamento. Nel 1895, appena tre anni dopo aver riformulato l'elettromagnetismo sulla base delle azioni ritardate, egli offrì un resoconto unitario della propria teoria, un'interpretazione che è ancora oggi alla base dell'elettrodinamica classica.
Nel corso dei cinque anni successivi alla formulazione della teoria degli elettroni da parte di Lorentz e di Larmor, la sperimentazione evidenziò in modo sempre più chiaro questa nuova entità fisica. Durante quegli anni lo status del campo elettromagnetico fu soggetto a frequenti mutamenti soprattutto per due ragioni: in primo luogo, l'attenzione si era cristallizzata intorno alla natura dell'elettrone stesso quale fondamento di tutto ciò che riguardasse la materia; in secondo luogo, non era chiaro come legare profondamente le forze ritardate di Lorentz al campo, vale a dire, come concetti fondamentali quali quelli di energia e quantità di moto potessero essere recuperati nel contesto delle azioni propagate. Queste ultime difficoltà resistettero a una soddisfacente soluzione per parecchi anni, agendo, tuttavia, più come ispirazione di studi specialistici ‒ in particolare da parte di Léon Rosenfeld (1904-1974) ‒ che come ostacoli alla piena accettazione della teoria degli elettroni.
In ogni caso, la concentrazione teorica e sperimentale sulla fisica dell'elettrone iniziò a subire un profondo mutamento verso il 1910. In questo periodo, infatti, cominciarono a essere assimilate le implicazioni della teoria della relatività speciale, pubblicata nel 1905 da Albert Einstein (1879-1955). In un primo momento la maggior parte dei fisici non scorse rilevanti differenze tra l'opera di Einstein e la versione compiuta della teoria dell'elettrone di Lorentz, ma cinque anni più tardi essi mutarono opinione. Ciò produsse l'effetto di marginalizzare ulteriormente la teoria di campo in senso proprio, poiché la relatività introduceva concezioni applicabili in tutte le teorie fisiche, concezioni che rendevano superflua la vecchia idea di un sostrato (l'etere) il cui stato osservabile s'identificava con il campo.
Bibliografia
Anderson 1964: Anderson, David Leonard, The discovery of the electron. The development of the electronic concept of electricity, Princeton, Van Nostrand, 1964.
Buchwald 1985: Buchwald, Jed Z., From Maxwell to microphysics. Aspects of electromagnetic theory in the last quarter of the nineteenth century, Chicago, University of Chicago Press, 1985.
‒ 1994: Buchwald, Jed Z., The creation of scientific effects, Chicago, University of Chicago Press, 1994.
‒ 2001: Histories of the electron. The birth of microphysics, edited by Jed Z. Buchwald and Andrew Warwick, Cambridge, MIT Press, 2001.
Darrigol 1991: Darrigol, Olivier, The electrodynamic revolution in Germany as documented by early German expositions of 'Maxwell's theory', "Archive for history of exact sciences", 45, 1991, pp. 189-280.
Einstein 1957: Einstein, Albert, H.A. Lorentz, his creative genius and his personality, in: H.A. Lorentz. Impressions of his life and work, edited by Geertruida L. de Haas-Lorentz, Amsterdam, North-Holland, 1957, pp. 5-9.
Falconer 1987: Falconer, Isobel, Corpuscles, electrons and cathode rays. J.J. Thomson and the 'Discovery of the electron', "British journal for the history of science", 20, 1987, pp. 241-276.
Heilbron 1964: Heilbron, John L., A history of the problem of atomic structure from the discovery of the electron to the beginning of quantum mechanics, (Diss.), Berkeley, University of California, University Microfilms Inc., 1964.
Hunt 1991: Hunt, Bruce J., The Maxwellians, Ithaca (N.Y.), Cornell University Press, 1991.
Smith 1989: Smith, Crosbie - Wise, M. Norton, Energy and empire. A biographical study of Lord Kelvin, Cambridge, Cambridge University Press, 1989.
Springford 1997: Electron. A centenary volume, edited by Michael Springford, Cambridge, Cambridge University Press, 1997.
Warwick 1994: Warwick, Andrew, The worlds of Cambridge physics, in: The physics of empire. Public lectures, edited by Richard Staley, Cambridge, Whipple Museum of the History of Science, 1994, pp. 57-86.
Weinberg 1983: Weinberg, Steven, The discovery of subatomic particles, New York, Scientific American Library, 1983.
Whittaker 1973: Whittaker, Edmund Taylor, A history of the theories of aether and electricity, New York, Humanities, 1973, 2 v. (1. ed.: London-New York, Nelson, 1951-1953).
Wise 1979: Wise, M. Norton, The mutual embrace of electricity and magnetism, "Science", 203, 1979, pp. 1310-1318.