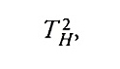L'Ottocento: fisica. La teoria cinetica dei gas

L'Ottocento: fisica. La teoria cinetica dei gas

La teoria cinetica dei gas

Le prime teorie dei gas

Le origini della teoria cinetica dei gas vanno ricercate nell'antica concezione secondo la quale la materia è costituita da piccoli e invisibili atomi in rapido movimento. Questa idea fu ripresa nel XVII sec. e usata per spiegare vari fenomeni, in particolare, le proprietà dei gas.

Il filosofo naturale Robert Boyle (1627-1691), basandosi sul lavoro di alcuni scienziati suoi contemporanei, mise in evidenza che l'aria è 'elastica': essa, cioè, resiste alla compressione e si espande fino a occupare tutto lo spazio a disposizione. Allo scienziato inglese si deve l'enunciazione della legge, che oggi porta il suo nome, secondo la quale, a una temperatura data, la pressione meccanica P esercitata da una determinata quantità di gas è inversamente proporzionale al volume V da esso occupato.

Boyle accenna a due spiegazioni atomistiche alternative della pressione dell'aria: secondo la prima, l'aria sarebbe composta di particelle che si respingono reciprocamente, come piccole molle o fili di lana arrotolati; nella seconda si ipotizza, invece, che essa sia costituita da particelle in moto vorticoso che si respingono reciprocamente quando urtano tra loro. La prima ipotesi fu adottata da Isaac Newton, il quale dimostrò matematicamente che se la pressione dell'aria è dovuta alla repulsione reciproca tra particelle vicine, allora la forza repulsiva deve essere inversamente proporzionale alla distanza fra esse. La seconda ipotesi, che Boyle aveva messo in relazione con la teoria cartesiana dei vortici di etere, nel XVII sec. mancava di una base quantitativa, anche se era sostenuta da un punto di vista qualitativo dall'idea, largamente condivisa, che il calore fosse legato al moto degli atomi e dall'osservazione del fatto che la pressione dell'aria aumenta con il crescere della temperatura.

La prima formulazione quantitativa della teoria cinetica dei gas compare nel 1738 nel trattato Hydrodynamica, sive de viribus et motibus fluidorum commentarii del fisico matematico svizzero Daniel Bernoulli (1700-1782). Questi derivò la legge di Boyle per la pressione dei gas calcolando la forza esercitata su un pistone mobile dagli urti di n particelle in moto con velocità v, racchiuse in una porzione di spazio di volume V. Se V viene ridotto, la pressione aumenta in virtù del fatto che le particelle urtano il pistone con frequenza maggiore. Se lo spazio occupato dalle stesse particelle è piccolo rispetto a V, la pressione P risulta inversamente proporzionale a V; in tal modo, come asserito dalla legge di Boyle, il prodotto PV è costante (ovviamente a temperatura costante).

Bernoulli mostrò anche che la pressione è proporzionale all'energia cinetica delle particelle (mv²/2, dove m è la massa della singola particella), dato che la frequenza degli urti è proporzionale alla velocità v e l'efficacia della forza esercitata da ciascun urto è proporzionale alla quantità di moto mv. Egli, inoltre, sottolineò come ciò spiegasse il fatto che gli aumenti di pressione prodotti da aumenti di temperatura uguali tra loro sono proporzionali alla densità; suggerì inoltre che la temperatura stessa potesse essere definita in termini di pressione dell'aria in condizioni standard di densità. Benché altri scienziati non avessero ancora accettato il concetto di scala assoluta di temperatura, la teoria di Bernoulli introduceva l'idea che il calore o la temperatura potessero essere identificati con l'energia cinetica delle particelle di un gas ideale.

Agli inizi dell'Ottocento la ricerca sperimentale sui gas confermò la relazione semplice tra pressione, volume e temperatura sostenuta da Bernoulli. Il chimico francese Joseph-Louis Gay-Lussac (1778-1850) e altri studiosi mostrarono che, mantenendo costante la pressione, il volume cresceva con la temperatura. In generale si poteva scrivere l'equazione PV=NR(T+273), dove N è proporzionale alla massa totale del gas, T è la temperatura in gradi Celsius e R è una costante universale. Tuttavia, non era ancora noto se l'equazione fosse valida fino a temperature così basse tali che T+273=0, o se tutti i gas si sarebbero condensati prima di raggiungere il punto di 'freddo assoluto', rendendo inapplicabile tale relazione.

Nel XVIII sec. la teoria cinetica non era comunemente accettata, poiché la maggioranza degli scienziati preferiva la teoria repulsiva di Newton, compatibile con l'ipotesi che il calore fosse un fluido ‒ il cosiddetto 'calorico' ‒ piuttosto che l'energia dei movimenti atomici. In genere il calorico era concepito come un insieme di particelle che si respingevano reciprocamente ed erano attratte dagli atomi della materia ordinaria. La pressione, quindi, doveva crescere con l'aumento della temperatura, essendo tale aumento prodotto dall'immissione di fluido calorico autorepulsivo. La temperatura stessa poteva essere definita come la densità del calorico, ossia come rapporto tra quantità di calorico e volume.

Con questa definizione di temperatura, mediante la teoria del calorico si poteva spiegare perché la compressione di un gas producesse un aumento della sua temperatura, anche quando non veniva assorbito calore dall'esterno (la stessa quantità di calorico era concentrata in un volume più piccolo), oppure, viceversa, perché un'espansione provocasse una diminuzione di temperatura anche senza emissione di calore (la stessa quantità di calorico si diffondeva in un volume più grande). Esisteva, tuttavia, un fenomeno anomalo, il cui significato non fu apprezzato se non molto tempo dopo: nel 1809, infatti, nel Premier essai pour déterminer les variations de température qu'éprouvent les gaz en changeant de densité, et considérations sur leur capacité pour le calorique, Gay-Lussac aveva asserito che nell'espansione libera di un gas, cioè in un'espansione che avviene nel vuoto e non sollevando un pistone, non si assisteva ad alcun cambiamento sensibile di temperatura.

La teoria del calorico poteva spiegare anche fenomeni come quelli legati al calore latente delle transizioni di fase ‒ dalla fase solida a quella liquida, e da questa a quella gassosa ‒ oppure come quelli legati al calore emesso o assorbito nelle reazioni chimiche, postulando che il calorico fosse in parte 'legato' ai composti o ai singoli atomi. Le normali relazioni pressione-volume, invece, erano determinate dal calorico 'libero' che riempiva lo spazio tra le particelle. La teoria cinetica non sembrava in grado di fornire spiegazioni plausibili di questi fenomeni; inoltre l'ipotesi che gli atomi si muovessero con velocità costante tra una collisione e l'altra sembrava incompatibile con l'idea generalmente accettata che tutto lo spazio fosse riempito da un fluido etereo.

La teoria del calorico acquistò credibilità all'inizio del XIX sec. grazie a Pierre-Simon de Laplace (1749-1827), che se ne servì per calcolare la velocità del suono nei gas, eliminando una vecchia discrepanza tra teoria e osservazione. A ciò va aggiunto il fatto che essa era indirettamente sostenuta dalla diffusa accettazione di una teoria corpuscolare della luce, dal momento che i fenomeni ottici e termici erano considerati qualitativamente identici.

La teoria atomica in chimica

Un aspetto essenziale della moderna teoria cinetica dei gas è che le particelle (atomi o molecole) di un gas occupano una parte relativamente piccola del volume totale a disposizione; possono quindi muoversi per la maggior parte del tempo in linea retta attraverso lo spazio vuoto, senza essere ostacolate dalla presenza di altre particelle o dalla resistenza di un qualsivoglia tipo di fluido etereo. Questo modello è radicalmente differente da quello proposto all'inizio del XIX sec. dal chimico inglese John Dalton (1766-1844), il fondatore della moderna teoria dell'atomo chimico. Dalton adottò esplicitamente l'ipotesi di Newton secondo cui la pressione dei gas è dovuta a forze repulsive a corto raggio agenti tra le particelle, immaginando queste ultime circondate da atmosfere di calorico in contatto con quelle delle particelle vicine. Le particelle dei vari elementi chimici, inoltre, avrebbero dovuto avere differenti dimensioni in modo tale che, a parità di numero, avrebbero occupato spazi di dimensione diversa.

Dalton integrò le tesi di Newton con un'ipotesi supplementare, forse ispirata dalle teorie elettrostatiche settecentesche: gli atomi di elementi diversi non si respingono gli uni con gli altri, ma possono anche attrarsi. Egli utilizzò quest'idea per spiegare perché l'aria, ormai nota come miscela di ossigeno e di azoto, non si separava nei suoi componenti sotto l'influenza della gravità (in questo caso l'ossigeno, più denso, avrebbe dovuto 'affondare' verso il basso): la mutua repulsione agente tra atomi della stessa specie tendeva a disperderli tra quelli di specie diversa, piuttosto che ad aggregarli tra loro. Un'altra conseguenza di questa concezione è la legge delle pressioni parziali, dovuta sempre a Dalton: la pressione totale di una miscela di gas è semplicemente la somma delle pressioni che ciascun gas eserciterebbe se occupasse da solo l'intero spazio a disposizione. Tale legge ovviamente può essere dedotta anche dalla teoria cinetica senza fare appello a una differenza fra la forza agente tra particelle simili e quella tra particelle diverse.

Quando Dalton approntò la famosa tavola dei 'pesi atomici', ipotizzò per ciascun composto chimico la formula più semplice possibile. In questo modo si assumeva che una molecola d'acqua fosse costituita da un atomo di ossigeno e uno di idrogeno. Se ciò fosse stato vero, dato che, usando dati moderni, 1 g di idrogeno reagisce con 8 g di ossigeno per formare 9 g d'acqua, il peso atomico dell'ossigeno relativo all'idrogeno sarebbe stato pari a 8.

La scoperta di Gay-Lussac della legge della combinazione dei volumi non si accordava con le idee di Dalton. Tale legge, infatti, stabilisce che nelle reazioni gassose i volumi dei reagenti sono legati ai volumi dei prodotti di reazione secondo rapporti tra numeri interi piccoli; così, per esempio, 2 litri di idrogeno si combinano con 1 litro di ossigeno per formare 2 litri d'acqua. Dal punto di vista atomistico l'interpretazione più plausibile di questa legge è che il volume di ciascun gas sia proporzionale al numero di particelle in esso contenute. Dunque, 2 particelle di idrogeno dovrebbero combinarsi con 1 particella di ossigeno per formare 2 particelle d'acqua. Ciò, però, implicherebbe che 1 particella di ossigeno possa suddividersi in 2 parti, 1 per ciascuna particella d'acqua e che quindi le particelle dei gas possano essere composte da due o più atomi; inoltre, il peso atomico dell'ossigeno sarebbe in tal caso 16 e non 8.

Dalton respinse le conclusioni di Gay-Lussac, criticandone anche l'accuratezza delle misure; appare tuttavia evidente che la principale obiezione nasceva dal fatto che i risultati contraddicevano la sua teoria. Come si è detto, il volume di un gas non poteva essere proporzionale al numero di particelle daltoniane, dato che queste avevano dimensioni diverse ed erano in contatto reciproco; inoltre, l'idea di una molecola composta da due atomi di ossigeno violava il principio secondo cui atomi della stessa specie si respingevano reciprocamente.

Il fisico italiano Amedeo Avogadro (1776-1856) fu il primo a esplorare e sviluppare tutte le conseguenze dei risultati di Gay-Lussac e a dare alla teoria dell'atomo chimico la sua forma attuale. Le particelle ultime con cui la teoria cinetica ha a che fare non sono atomi ma molecole, ciascuna delle quali può essere composta da uno o più atomi di specie uguali o diverse. L'ipotesi di Avogadro stabilisce che in un dato volume, nelle stesse condizioni di temperatura e pressione, ogni specie di gas contiene lo stesso numero di molecole. Questa ipotesi, che fu generalmente adottata dai chimici dopo il 1860, permise di calcolare in modo definitivo i pesi atomici degli elementi quando essi potevano dar luogo a composti gassosi. Le forme gassose di molti elementi comuni, come l'idrogeno, l'azoto, l'ossigeno e il cloro sono composte da molecole biatomiche, mentre altri elementi, come il mercurio, si sarebbero rivelati più tardi monoatomici.

L'ipotesi di Avogadro è a favore della teoria cinetica dei gas nella misura in cui essa implica che il volume occupato da un certo numero di molecole è indipendente dalle loro forme e dimensioni, il che suggerisce che normalmente esse non siano a contatto fra loro. Solamente nel 1859 James C. Maxwell (1831-1879) mostrò che l'ipotesi poteva essere dedotta dalla teoria cinetica; le precedenti versioni di tale teoria, che ora prenderemo in esame, sono di fatto in contraddizione con essa. Ciò potrebbe provare, se non altro, che forse il rapporto tra fisica e chimica nel XIX sec. non era così stretto come avrebbe potuto essere.

Herapath e Waterston

John Herapath (1790-1868) potrebbe essere considerato uno scienziato dilettante se non fosse che all'epoca la distinzione tra dilettante e professionista non era molto significativa. Tuttavia egli era decisamente un outsider, eccentrico e brillante, che non ebbe mai alcun riconoscimento dalla comunità scientifica anche se visse abbastanza da vedere confermate le proprie idee. Inizialmente Herapath era interessato a sviluppare una teoria della gravità basata sugli urti delle particelle di un fluido etereo per alcuni aspetti simile alla teoria cinetica della gravità proposta da Georges-Louis Le Sage (1724-1803) e da molti altri. La versione di Herapath presentava, però, significative differenze: egli proponeva di tener conto dell'effetto delle alte temperature, nello spazio vicino al Sole, sulle particelle che producevano la gravità, arrivando in tal modo a considerare la relazione tra la temperatura e la velocità delle particelle. La concezione della struttura dei gas che egli sosteneva era per certi versi simile a quella di Dalton.

Herapath doveva risolvere dapprima il vecchio paradosso della collisione tra atomi, consistente nell'osservare che se essi si urtano frontalmente devono fermarsi almeno per un istante prima di rimbalzare, ponendo la questione se la collisione fosse elastica o anelastica. Essa non poteva essere elastica, poiché un atomo non poteva per definizione essere costituito di parti più piccole e non poteva cambiare la sua forma, il che rendeva problematica la possibilità di immagazzinare la sua energia cinetica durante l'istante in cui si fosse fermato. Tuttavia, se la collisione fosse stata anelastica, entrambi gli atomi avrebbero dovuto fermarsi e si sarebbe, in tal caso, dovuto risolvere il problema di cosa fosse accaduto alla loro energia. Per evitare tale paradosso, Herapath decise di considerare come misura fondamentale del movimento la quantità di moto invece dell'energia. Questa infatti si conserva sempre, sia per gli urti elastici, sia per quelli anelastici. Herapath formulò la semplice ipotesi che la quantità di moto scalare mv di una particella fosse una misura della sua temperatura assoluta e che la quantità di moto totale del sistema si conservasse durante gli urti, mentre quelle individuali tendevano a eguagliarsi. Una conseguenza di questa definizione poco ortodossa era che la temperatura di una miscela di fluidi freddi e caldi avrebbe dovuto essere un po' più bassa di quanto ci si sarebbe aspettato in base alla definizione usuale di temperatura. Egli giunse in tal modo alla stessa relazione tra pressione, volume e velocità delle particelle che Bernoulli aveva derivato in precedenza (anche se non sembra che egli conoscesse il lavoro di Bernoulli). Herapath però la formulò in maniera leggermente diversa: PV risulta infatti proporzionale a

dato che T_H, da lui chiamata 'temperatura vera', è proporzionale a mv e non a mv² (il deponente H alla temperatura di Herapath è stato aggiunto per non confonderla con la temperatura assoluta T ). Herapath sottopose il suo primo lavoro sulla teoria cinetica alla Royal Society di Londra nel 1820, sperando che fosse pubblicato nelle "Philosophical Transactions".

Humphry Davy (1778-1829), un chimico molto noto, divenne presidente della Royal Society poco dopo l'arrivo del lavoro di Herapath. Davy in precedenza aveva sostenuto la concezione secondo la quale il calore consisteva in un movimento molecolare piuttosto che in una sostanza; sarebbe stato dunque lecito attendersi da lui una buona accoglienza verso una teoria che dava alle sue idee un formulazione matematica rigorosa. La sua reazione fu invece negativa e per diverse ragioni. L'unica che egli manifestò esplicitamente a Herapath fu la propria riluttanza a considerare il calore come una semplice proprietà quantitativa, che poteva essere completamente estratta da un corpo annichilendo il moto delle sue molecole, e quindi ad ammettere l'esistenza di un minimo assoluto per la temperatura (lo 'zero assoluto'). È anche evidente che egli trovava difficili da seguire i calcoli di Herapath e che avrebbe preferito un approccio meno astratto e meno matematico, ossia tale da mettere in luce a ogni passo la corrispondenza tra concetti e osservazioni, secondo un atteggiamento tipico dei chimici più che dei fisici.

Herapath fu dunque informato che il suo lavoro non sarebbe stato pubblicato sulle "Philosophical Transactions" e gli fu consigliato di ritirarlo, poiché, secondo le consuetudini della Royal Society, una volta 'letto' (ossia presentato formalmente, anche se soltanto come titolo o come riassunto, a una riunione) sarebbe divenuto proprietà della Società e non avrebbe potuto essere restituito al suo autore. Herapath accettò il consiglio e inviò l'articolo a una rivista scientifica indipendente, gli "Annals of philosophy", dove fu pubblicato nel 1821. Più tardi attaccò Davy e la Royal Society in una serie di lettere pubblicate sul "Times" di Londra.

Tuttavia non è possibile imputare soltanto a Davy e alla Royal Society il fatto che la teoria di Herapath sia stata in quegli anni ignorata dalla maggioranza degli scienziati. Occorre riconoscere che una simile teoria non si accordava con le idee prevalenti sulla natura dei gas e del calore e che Herapath non riuscì a convincere i suoi lettori che quelle idee dovevano essere riviste. Successivamente egli divenne redattore del "Railway Magazine" ed ebbe l'opportunità di pubblicare i suoi lavori scientifici, anche se per un pubblico ristretto e forse incapace di apprezzarli. Nel 1836 presentò un calcolo della velocità del suono, che aveva completato quattro anni prima: fu il primo calcolo della velocità media di una molecola derivato dalla teoria cinetica dei gas. James P. Joule (1818-1889), al quale viene abitualmente attribuito tale risultato, seguì semplicemente il metodo di Herapath, il quale aveva calcolato che la velocità del suono nell'aria a 32° F (0° C) avrebbe dovuto essere circa 1090 piedi al secondo (330 m/s ca.), in accordo con i risultati disponibili a quell'epoca.

Negli anni Quaranta dell'Ottocento, stimolato dai lavori di Thomas Graham sulla diffusione dei gas e da quelli di Henri-Victor Regnault sulla loro compressibilità, Herapath rielaborò la sua teoria cinetica, che pubblicò nel 1847 nel trattato in due volumi Mathematical physics; or the mathematical principles of natural philosophy. Egli sostenne che, sin dal 1844, aveva derivato da questa teoria una formula per stabilire il tempo impiegato da un dato volume di gas per espandersi nel vuoto attraverso una piccola apertura e che tale formula fosse stata successivamente confermata mediante i risultati sperimentali ottenuti da Graham. Herapath, inoltre, asserì di aver anticipato la scoperta di Regnault secondo cui la pressione di un gas molto denso è più grande di quella deducibile dalla legge di Boyle. In effetti, il modello che considerava gli atomi alla stregua di sfere impenetrabili avrebbe portato a questo risultato se fossero state ignorate le forze attrattive a corto raggio. Tuttavia esperimenti precedenti avevano indicato possibili soluzioni opposte, suggerendo che le forze attrattive fossero più importanti di quelle repulsive (le teorie cinetiche successive sarebbero riuscite a spiegare il fatto che le forze attrattive prevalgono a temperature basse e quelle repulsive a temperature elevate). Joule, uno degli scopritori della legge di conservazione dell'energia, è probabilmente l'unico scienziato ad aver letto il libro di Herapath del 1847 durante i cinque anni successivi alla pubblicazione. Egli presentò un breve articolo sulla teoria cinetica, basato sulle teorie esposte da Herapath, in convegni scientifici cui partecipò durante il corso dell'anno 1848, ma pochi colleghi ne vennero a conoscenza.

Come si è accennato, la versione di Herapath della teoria cinetica era in contraddizione con l'ipotesi di Avogadro, un fatto passato inosservato negli anni Venti del secolo, ma che avrebbe richiesto una revisione della teoria di Herapath se qualcuno avesse voluto integrarla con la teoria atomica chimica, così come questa era stata recepita dopo il 1860.

L'altro dimenticato pioniere della teoria cinetica dei gas è lo scienziato scozzese John James Waterston (1811-1883). La sua formulazione era più corretta di quella di Herapath, ma non ebbe alcuna influenza poiché rimase sconosciuta fino a molto dopo l'esposizione della teoria cinetica moderna da parte di Rudolf Clausius (1822-1888) e Maxwell. Come Herapath, Waterston cercava una spiegazione per la gravità in termini di urti fra particelle e i suoi tentativi in questa direzione lo portarono a sviluppare una teoria cinetica dei gas. Nel 1843 pubblicò il volume Thoughts on the mental functions, che comprendeva alcuni dei suoi primi risultati. La conclusione più significativa alla quale era pervenuto consisteva nel sostenere che l'equilibrio della temperatura dipendeva dalle molecole, per quanto diverse fossero le loro dimensioni, purché animate dalla stessa energia cinetica. Questa asserzione delineava un caso particolare di quello che più tardi sarebbe stato indicato come 'teorema di equipartizione'.

Due anni più tardi Waterston sottopose alla Royal Society un lungo manoscritto in cui veniva presentato un resoconto dettagliato della teoria cinetica dei gas. Due membri della Società, a cui era stato richiesto di giudicare il lavoro, gli consigliarono di non pubblicarlo, soprattutto perché non condividevano le sue premesse fondamentali. Tuttavia nessuno aveva detto a Waterston, ancora in India, dove era impiegato come istruttore navale per i cadetti della Compagnia delle Indie orientali a Bombay, che il suo articolo, una volta 'letto' alla Società, non gli sarebbe stato più restituito; Waterston non ne aveva conservato una copia. Di conseguenza egli non poté seguire la strada di Herapath, cioè quella di pubblicare l'articolo originale su una rivista indipendente, anche se provò a richiamare l'attenzione sulla sua teoria facendone circolare versioni abbreviate e citandola quando pubblicava articoli su argomenti a essa connessi.

Nel 1851 Waterston presentò un breve articolo sulla sua teoria cinetica al convegno annuale della British Association for the Advancement of Science. Il riassunto pubblicato di quel lavoro asseriva con chiarezza che nelle miscele gassose l'energia cinetica media di una molecola era la stessa per ogni specie di gas; in questo modo egli stabiliva la sua priorità per la prima enunciazione del teorema di equipartizione. In questo riassunto si segnalava, inoltre, che l'ipotesi di Avogadro era una conseguenza della teoria cinetica. Il chimico e fisico tedesco August Karl Krönig (1822-1879), che propose una teoria cinetica dei gas in un breve articolo dal titolo Grundzüge einer Theorie der Gase (Fondamenti di una teoria dei gas) pubblicato nel 1856, era probabilmente a conoscenza del riassunto di Waterston e potrebbe esserne stato influenzato.

Waterston tentò anche di calcolare il rapporto dei due calori specifici (c_p, a pressione costante, e c_v, a volume costante) ma, per un errore di calcolo, ottenne per un gas monoatomico il valore c_p/c_v=4/3 invece del valore teorico corretto 5/3. Tuttavia, dato che il suo rapporto era abbastanza vicino a quelli misurati per l'aria e per altri gas, Waterson non si accorse dell'errore. Nel 1858 lo scienziato scozzese pubblicò un articolo nel quale sosteneva che la derivazione della velocità del suono effettuata da Laplace, in base alla teoria della compressione e dell'espansione adiabatica fondata sull'ipotesi del calorico, poteva essere ottenuta altrettanto bene dalla propria teoria cinetica e quindi non la si poteva considerare una prova a favore di quella precedente ipotesi.

Nel 1891 il fisico inglese John W. Strutt (lord Rayleigh, 1842-1919), ripercorrendo la letteratura riguardante argomenti di acustica per il suo trattato generale sulla disciplina, lesse il lavoro di Waterston del 1858 e in questo trovò il riferimento al manoscritto non pubblicato che giaceva negli archivi della Royal Society. Lord Rayleigh era a quel tempo segretario della Royal Society e non ebbe difficoltà a ritrovare il manoscritto e a farlo pubblicare sulle "Philosophical Transactions". Nella sua introduzione a questa ritardata pubblicazione lord Rayleigh sottolineava che indagini altamente speculative, in particolare se condotte da autori ignoti, erano presentate al mondo attraverso canali diversi da una società scientifica, per la quale è naturale esitare ad accogliere nei suoi testi a stampa argomenti di valore incerto: un autore giovane che si fosse ritenuto capace di grandi cose avrebbe fatto meglio ad assicurarsi il riconoscimento del mondo scientifico con lavori su argomenti ben circoscritti, prima di imbarcarsi in voli più grandiosi.

Queste osservazioni di lord Rayleigh non giustificano il rifiuto da parte della Royal Society di pubblicare il brillante manoscritto di Waterston, ma mettono in evidenza una delle carenze di questa istituzione come organismo volto al progresso della conoscenza scientifica. Rifiutando lavori di autori privi di una reputazione riconosciuta o teorie che erano in conflitto con le idee stabilite, la società scientifica si sottraeva a una delle sue funzioni più importanti. Nel caso della teoria cinetica dei gas, l'esito finale del rifiuto della Royal Society di pubblicare i lavori di Herapath e di Waterston fu quello di ritardare il progresso della fisica molecolare di uno o due decenni nonché di danneggiare la reputazione della stessa Società, facendo sì che scienziati tedeschi come Krönig e Clausius ottenessero i maggiori riconoscimenti come scopritori della nuova teoria.

La rinascita della teoria cinetica a opera di Clausius

La 'teoria cinetica del calore', cioè la vecchia idea secondo la quale il calore è legato direttamente all'energia cinetica del movimento degli atomi, sarebbe stata presa in seria considerazione alla metà del XIX sec., non appena furono introdotti il principio della conservazione dell'energia e le leggi della termodinamica. Ulteriori prove del fatto che la pressione dei gas non è dovuta alle forze repulsive intermolecolari (precedentemente associate al fluido calorico) vennero dagli esperimenti sull'espansione libera dei gas effettuati da Joule e da William Thomson (lord Kelvin, 1824-1907). Essi confermarono che, come aveva già sostenuto Gay-Lussac, durante l'espansione non si verifica alcuna variazione di temperatura; esperimenti più accurati avrebbero poi indicato che le forze a lungo raggio sono di carattere attrattivo piuttosto che repulsivo. Un altro elemento a favore della teoria cinetica del calore fu l'adozione generalizzata della teoria ondulatoria della luce, la quale, collegata alla convinzione che calore e luce fossero qualitativamente lo stesso fenomeno, suggeriva immediatamente che entrambi fossero una forma di movimento e non una sostanza. Tuttavia, era ancora logicamente possibile respingere la teoria cinetica del calore, come fecero Julius Robert von Mayer (1814-1878) e più tardi Ernst Mach (1838-1916), e negare la necessità di ridurre il calore a una qualche altra forma di energia. Questa posizione antiriduzionista o positivista fu alla base del movimento 'energetista' della fine del XIX sec., ma non incontrò il favore della maggior parte degli scienziati.

Anche accettando la teoria cinetica del calore, si poteva scegliere tra molte possibili ipotesi. I moti molecolari potevano essere di tipo traslatorio, rotatorio o vibratorio, oppure una combinazione di questi tre; le molecole potevano essere piccole rispetto allo spazio in cui si muovevano, oppure grandi e quindi densamente raggruppate; il moto poteva avere caratteristiche simili per ogni molecola del sistema, oppure avere una particolare configurazione per ogni molecola. I fisici credevano ancora nell'esistenza di un etere come mezzo di trasmissione dell'energia tra corpi distanti sotto forma di luce o di calore radiante; e se l'etere riempiva lo spazio tra le molecole all'interno di un corpo, allora esso avrebbe dovuto avere un qualche effetto sul loro moto. Infatti, ancora non era stata del tutto abbandonata la vecchia idea che le molecole 'nuotassero' nell'etere, o che fossero sospese al suo interno in punti definiti di equilibrio attorno ai quali potevano oscillare. Tra queste possibilità la teoria cinetica dei gas era forse la più semplice, ma certamente non la più plausibile. In realtà essa sembrava troppo semplice per essere vera, in quanto richiedeva di ignorare l'etere e di asserire che le molecole si muovevano nello spazio a velocità costante, non incontrando alcuna resistenza se non quando si urtavano tra loro o con le pareti del recipiente.

Il primo scienziato in grado di superare la diffusa riluttanza a prendere seriamente in considerazione la teoria cinetica fu il fisico tedesco Rudolf Clausius (1822-1888). Nel primo articolo che vi dedicò, pubblicato nel 1857 e intitolato über die Art der Bewegung, welche wir Wärme nennen (Sulla natura del movimento che chiamiamo calore), Clausius asserì di aver riflettuto sui moti molecolari anche prima del primo lavoro sulla termodinamica del 1850, ma di essersi astenuto dal pubblicare le sue idee dal momento che desiderava formulare le leggi empiriche del calore senza farle apparire dipendenti da una qualsiasi ipotesi molecolare. Ora che Krönig aveva aperto la strada con l'articolo del 1856, non sussistevano più problemi di priorità e i tempi sembravano favorevoli per tentare una descrizione unificata di diversi fenomeni da un punto di vista cinetico. Krönig aveva ipotizzato che le molecole avessero solo un moto traslatorio e, cosa che Clausius evitò educatamente di sottolineare, neppure per questo semplice caso era riuscito a ricavare il valore corretto del fattore numerico nell'equazione della pressione. Clausius arrivò alla conclusione che fosse necessario tener conto anche degli altri tipi di moto molecolare, per esempio di quello rotatorio, e mostrò come, partendo dalla conoscenza delle proprietà termiche del gas, si potesse stimare la frazione dell'energia totale che doveva essere attribuita ai soli moti traslatori.

Includendo nella sua teoria cinetica i moti rotatori, Clausius non scendeva a compromessi né con le teorie alternative né con le conoscenze sperimentali riguardanti le proprietà dei gas. Il risultato di un simile compromesso si sarebbe comunque rivelato dannoso per la teoria cinetica: infatti il rapporto tra l'energia di traslazione e l'energia totale risultava pari a 0,6315 per i gas il cui rapporto tra i calori specifici a pressione costante e a volume costante, c_p/c_v, è 1,421. Maxwell e altri ne dedussero che la teoria cinetica prevedeva un valore significativamente errato per il rapporto tra i calori specifici. Clausius cercò di superare il problema riprendendo l'ipotesi di Avogadro secondo la quale le molecole gassose potevano contenere due o più atomi della stessa specie (come accade effettivamente) e, sebbene alcuni chimici fossero già pervenuti alla stessa conclusione, tuttavia fu probabilmente Clausius il primo a introdurla nella fisica della metà del XIX secolo.

Un'altra ipotesi dettata dai dati sperimentali fu quella relativa alle dimensioni estremamente piccole delle molecole. Sempre nella memoria del 1857 Clausius postulò che "lo spazio effettivamente occupato dalle molecole del gas deve essere infinitesimo rispetto all'intero spazio occupato dal gas stesso", e che "l'influenza delle forze intermolecolari deve essere molto piccola" (Clausius 1857 [1965, p. 116]). Ciò significava non soltanto che erano trascurabili le forze che si esercitavano tra le molecole poste a distanze di media entità, ma anche che le forze repulsive a corto raggio che facevano rimbalzare le molecole in seguito a una collisione dovevano agire nel corso di una frazione molto piccola della loro traiettoria. Se queste condizioni non fossero state soddisfatte, il gas non avrebbe obbedito alle leggi del gas ideale. È vero che a quel tempo, in base agli esperimenti di Regnault, era già noto che i gas reali non rispettavano le leggi valide per il gas ideale, ma nel 1857 Clausius non fu in grado di eseguire i difficili calcoli necessari per ricavare le suddette deviazioni in base a un modello molecolare, e per tale motivo egli limitò la sua teoria al caso del gas ideale.

Mentre le deduzioni matematiche in senso stretto della teoria si limitavano al caso del gas ideale, ossia del gas che obbedisce alle leggi di Boyle e di Gay-Lussac ‒ ovvero in condizioni di temperatura e di pressione non molto diverse da quelle dell'atmosfera ‒, Clausius non esitò a proporre una descrizione qualitativa dei moti molecolari negli altri stati della materia. Nei solidi le molecole oscillano attorno a posizioni fisse di equilibrio, mentre i loro atomi costituenti oscillano e ruotano all'interno di ciascuna molecola. Nei liquidi, le molecole non oscillano più attorno a posizioni fisse di equilibrio, ma si spostano, pur non separandosi completamente dalle molecole vicine. Nello stato gassoso, infine, le molecole si muovono in linea retta al di fuori della portata delle forze attrattive delle altre molecole e subiscono di tanto in tanto collisioni elastiche con queste.

Partendo da questa rappresentazione qualitativa, Clausius riuscì a sviluppare una teoria dei cambiamenti di stato. Infatti, per spiegare l'evaporazione di un liquido anche quando la velocità media delle molecole non era sufficiente a portarle fuori dal campo di azione delle forze attrattive delle molecole vicine, si doveva "supporre che le velocità di parecchie molecole deviano entro ampi limiti in entrambe le direzioni da questi valori medi" (ibidem, p. 118) e che quindi alcune molecole si muovevano abbastanza rapidamente da sfuggire dalla superficie del liquido anche a temperature inferiori a quella di ebollizione. Se si adottava la descrizione di Clausius dei tre stati di aggregazione della materia, la teoria cinetica era in grado di spiegare anche il fenomeno del calore latente: "Nel passaggio dallo stato solido allo stato liquido, di fatto le molecole non vanno al di là della loro reciproca sfera d'azione; ma, secondo le ipotesi di cui si è detto, esse passano da una posizione definita in base alle forze molecolari, ad altre posizioni irregolari: nel fare ciò devono superare le forze che tendono a trattenere le molecole nelle posizioni originarie" (ibidem, p. 121). Ora, un corpo che si muove contro l'azione di una forza effettua lavoro meccanico e quindi, secondo la legge di conservazione dell'energia, deve ricevere energia sotto forma di calore: "Anche nell'evaporazione, la completa separazione tra le molecole che evaporano e il resto della sostanza richiede evidentemente il superamento di forze contrastanti" (ibidem), e così occorre fornire di nuovo calore (il cosiddetto 'calore latente di evaporazione').

Alla fine dell'articolo del 1857 Clausius calcolò le velocità medie delle molecole dell'ossigeno, dell'azoto e dell'idrogeno alla temperatura del ghiaccio fondente, trovando rispettivamente i valori di 461 m/s, 492 m/s e 1844 m/s. Un meteorologo olandese, Christoph Hendrik Diederik Buys-Ballot (1817-1890), leggendo questi valori si accorse di una loro conseguenza che era sfuggita all'attenzione di Herapath, Joule, Waterston e Clausius: se le molecole del gas si fossero mosse veramente in maniera così veloce, il mescolamento dei gas per interdiffusione avrebbe dovuto essere molto più rapido di quanto veniva osservato. Se per esempio si liberava un gas come l'ammoniaca o l'anidride solforosa in un angolo di una stanza, ci voleva almeno un minuto prima di avvertirne l'odore nell'angolo opposto; laddove, secondo la teoria cinetica, nello stesso intervallo di tempo le molecole avrebbero dovuto attraversare la stanza per parecchie volte.

Buys-Ballot pensava di aver avanzato un'obiezione fatale alla nuova teoria e di aver messo in evidenza un'ovvia contraddizione tra le sue predizioni e i fenomeni reali. Fu così che, per superare questa obiezione, Clausius fu costretto a introdurre un cambiamento importante nelle proprie ipotesi. Avendo abbandonato il postulato originale che le molecole gassose possedessero dimensioni infinitesime, ora egli suppose che esse avessero un diametro, o una 'sfera d'azione', abbastanza grande da non potersi spostare molto senza urtare un'altra molecola. Questa revisione, tra l'altro, comportò l'introduzione nella teoria cinetica del metodo statistico.

A questo punto, Clausius definì un nuovo parametro, il 'cammino libero medio' L di una molecola gassosa, calcolabile come distanza media percorsa da una molecola prima di interagire con un'altra. Egli sostenne che L doveva essere presumibilmente grande rispetto ai diametri molecolari, sicché le ipotesi basilari della teoria cinetica, necessarie per derivare la legge dei gas ideali, potevano essere mantenute; tuttavia L doveva essere abbastanza piccolo da far sì che una molecola cambiasse direzione molte volte in ogni secondo e quindi impiegasse un tempo abbastanza lungo per sfuggire da una regione macroscopica di spazio. In questo modo poteva essere spiegata la relativa lentezza, rispetto alle velocità molecolari, della normale diffusione dei gas.

Il cammino libero medio era inversamente proporzionale alla probabilità di collisione di una molecola che si muoveva all'interno del gas. Per sfere di diametro d, questa probabilità è proporzionale alla sezione d'urto geometrica πd² e al numero di molecole per unità di volume N/V. Cosicché il cammino libero medio è determinato dalla relazione L=kV/(N d²), dove k è una costante numerica di ordine di grandezza pari a 1, anche se va precisato che per un certo periodo il suo valore esatto fu oggetto di dibattito.

Quando nel 1858 Clausius introdusse il cammino libero medio, la sua poteva essere considerata come un'ipotesi ad hoc, inserita soltanto per salvare la teoria, dato che esisteva un metodo indipendente per stimare i parametri N e d nella relazione di cui sopra. Tuttavia, prima che qualcuno potesse fare una critica di questo tipo, Maxwell inserì il cammino libero medio nella sua teoria cinetica, mostrando che esso poteva essere messo in relazione con altre proprietà dei gas come, per esempio, la viscosità. Esso, dunque, divenne un concetto importante, non solo per interpretare dati sperimentali, ma anche per determinare le dimensioni delle molecole e quindi avvalorare l'ipotesi della loro esistenza.

La teoria dei fenomeni di trasporto di Maxwell e le dimensioni degli atomi

Ben presto la teoria cinetica di Clausius venne ripresa da Maxwell e trasformata in un importante strumento di ricerca matematica. Se Clausius aveva adoperato concetti probabilistici nella derivazione della formula del cammino libero medio, fu Maxwell a trasformare la teoria cinetica dei gas in una dottrina pienamente statistica. Clausius, come peraltro i suoi predecessori, aveva ipotizzato che tutte le molecole di un gas omogeneo a una data temperatura avessero la stessa velocità, anche se, come abbiamo osservato, nella sua spiegazione dell'evaporazione egli supponeva che alcune molecole si muovessero più rapidamente rispetto a tale velocità media. Maxwell, invece, affermò che gli urti tra le molecole avrebbero prodotto una distribuzione casuale delle velocità e per descrivere tale distribuzione importò una formula matematica dalle scienze sociali. Il passo cruciale fu la sua trasformazione della 'legge di distribuzione normale' detta anche 'legge degli errori' ‒ scoperta indipendentemente da Robert Adrain (1775-1843) e Carl Friedrich Gauss (1777-1855) e applicata estesamente da Lambert-Adolphe-Jacques Quételet (1796-1874) ‒ in una legge di distribuzione delle velocità molecolari, come vedremo meglio in seguito. Per il momento è sufficiente osservare che, secondo la legge di Maxwell, la velocità media è proporzionale a √T come nelle precedenti teorie cinetiche, tuttavia un gas a temperatura elevata contiene molecole che si muovono con tutte le velocità, quindi anche con velocità molto basse, e un gas a bassa temperatura contiene pure (in proporzione diversa) molecole che si muovono con velocità assai elevate.

Maxwell estese molto la portata della teoria cinetica mostrando come potesse essere usata non soltanto per derivare le proprietà termiche e meccaniche di un gas in condizioni di equilibrio, ma anche per derivare le sue 'proprietà di trasporto': diffusione, viscosità e conduzione termica. Nel suo primo articolo, Illustrations of the dynamical theory of gases, pubblicato nel 1860, egli usò il concetto di cammino libero medio di Clausius ottenendo risultati inattesi riguardo alla viscosità di un gas; inoltre analizzò le collisioni tra sistemi di molecole sferiche e non sferiche, cercando di trovare un modello teorico che potesse render conto del valore osservato per il rapporto tra i calori specifici dei gas.

Maxwell calcolò la viscosità di un gas stimando l'attrito reciproco tra due strati adiacenti di esso che si fossero mossi a diverse velocità. Sulla base dell'esperienza con i liquidi ci si sarebbe potuti aspettare che un qualsiasi fluido avrebbe avuto una maggiore viscosità a temperature più basse e che un fluido più denso sarebbe stato più viscoso di uno meno denso, dato che in entrambi i casi il moto sarebbe stato ostacolato più intensamente dalle forze intermolecolari. Maxwell mostrò che, se la teoria cinetica dei gas fosse stata corretta, entrambe le previsioni sarebbero risultate errate, in quanto il meccanismo che produceva la viscosità era diverso da quello ipotizzato. In un gas le forze di attrito interno non sono prodotte dalle forze tra molecole vicine, ma dal trasferimento di quantità di moto, che avviene quando una molecola appartenente a una corrente più veloce entra in contatto con una corrente più lenta e urta con una delle sue molecole. La rapidità di trasferimento della quantità di moto cresce con la velocità molecolare media, cosicché la viscosità aumenta con la temperatura.

La quantità di moto trasferita in ogni collisione inoltre risulta essere proporzionale alla differenza di velocità tra i due strati e, se supponiamo che tale differenza sia semplicemente proporzionale alla distanza tra i due strati (ossia che il gradiente della velocità sia lineare), essa risulta proporzionale anche al cammino libero medio tra due collisioni. La frequenza delle collisioni è proporzionale alla densità, ma, secondo la formula di Clausius, il cammino libero medio è inversamente proporzionale alla densità; ne deriva che scompare il termine di densità, dalla quale la viscosità risulta quindi indipendente, mentre, come il cammino libero medio, quest'ultima è inversamente proporzionale al quadrato del diametro delle molecole.

In quel periodo i soli dati sperimentali sulla viscosità dei gas sembravano indicare che essa crescesse con la densità e quando nel 1859 rese pubblici i suoi calcoli teorici, Maxwell si aspettava quindi che essi avrebbero portato a rigettare la teoria cinetica. Egli ottenne risultati deludenti pure dalla sua analisi della distribuzione di energia in sistemi di particelle non sferiche, poiché trovò che anche in questo caso doveva valere un teorema generale di equipartizione: l'energia cinetica media dei moti traslatori delle particelle avrebbe dovuto eguagliare l'energia cinetica media dei moti rotatori attorno a ciascuno dei tre assi principali della particella. Ciò portava a un rapporto tra i calori specifici pari a 4/3, chiaramente diverso dal valore osservato, di circa 1,4 per i gas più comuni. Quindi Maxwell, in Illustrations of the dynamical theory of gases, concluse che "un sistema di tali particelle non potrebbe soddisfare in alcun modo la relazione nota tra i due calori specifici di tutti i gas" (1860 [1986, p. 318]).

Secondo la teoria cinetica, assumendo l'equipartizione dell'energia, il rapporto tra i calori specifici avrebbe dovuto essere c_p/c_v =(2+n)/n, dove n è il numero dei 'gradi di libertà' meccanici. Un punto materiale ha 3 gradi di libertà, dato che si può muovere in una qualsiasi delle 3 direzioni spaziali, e pertanto il suo rapporto tra i calori specifici avrebbe dovuto essere 5/3; i rapporti per gas monoatomici quali il mercurio e l'argon hanno effettivamente questo valore. Un corpo non sferico, o una molecola biatomica composta da due punti materiali legati tra loro da forze conservative, ha 3 gradi di libertà in più, e quindi il suo rapporto avrebbe dovuto essere 4/3, laddove le molecole biatomiche di gas come l'idrogeno e l'ossigeno hanno il rapporto di 1,4 o 1,41.

Più tardi Ludwig Boltzmann (1844-1906) suggerì che in realtà una molecola biatomica può possedere solo 5 gradi di libertà effettivi, dato che la rotazione attorno all'asse di simmetria (la retta che congiunge i due atomi) non viene alterata dalle collisioni tra le molecole e quindi non contribuisce al calore specifico (con ciò il rapporto risulterebbe essere pari a 1,4). Maxwell non accettò questa ipotesi e continuò a considerare il problema irrisolto; fortunatamente la confutazione delle sue previsioni iniziali sui calori specifici e la viscosità non lo scoraggiò dal portare avanti l'elaborazione della teoria cinetica, mentre la questione dei calori specifici fu risolta in maniera soddisfacente solamente nel XX sec., quando furono introdotte considerazioni di tipo quantistico.

Maxwell stesso diede avvio alla verifica sperimentale delle sue previsioni per l'effetto della temperatura e della densità sulla viscosità. In effetti, egli trovò che il coefficiente di viscosità dell'aria si manteneva costante per ampie variazioni della densità, in contraddizione con i fatti sperimentali prima citati. In seguito, Oskar Emil Meyer (1834-1909) e altri misero per esempio in evidenza come l'interpretazione dei dati relativi al pendolo smorzato fosse basata sull'ipotesi ‒ abbastanza naturale prima della teoria di Maxwell ‒ che il coefficiente di viscosità tendesse lentamente a zero quando la densità tendeva a zero. Tuttavia, mentre è vero che il suo valore deve essere nullo quando la densità è nulla (il gas, se non c'è, non può esercitare alcuna resistenza viscosa sull'oscillazione del pendolo), la sua diminuzione avviene piuttosto rapidamente soltanto a densità più basse di quelle raggiunte nella maggior parte degli esperimenti effettuati prima del 1850.

In questo caso fu la teoria a confutare l'esperienza. Si può forse sostenere che a essere smentito non fu l'esperimento in sé ma la sua interpretazione. Tuttavia nel discorso scientifico ordinario il termine 'fatto sperimentale' viene normalmente applicato ai dati inferiti dall'esperimento con l'aiuto di qualche interpretazione o di ipotesi teoriche. Come avrebbe osservato Albert Einstein, sono le nostre teorie che determinano ciò che osserviamo e quindi gli esperimenti non possono mai fornire un controllo del tutto imparziale di una teoria.

L'indagine sulla dipendenza della viscosità dalla temperatura non diede risultati inequivocabili. Secondo il modello originale 'a palle di biliardo' (sfere elastiche che non interagiscono con forze se non durante la collisione), il coefficiente di viscosità μ avrebbe dovuto essere proporzionale alla radice quadrata della temperatura, ma Maxwell e altri trovarono una dipendenza più accentuata, del tipo μ∝T^x, dove x varia circa da 0,75 a 1.

Nello stesso periodo ‒ ossia i primi anni Sessanta dell'Ottocento ‒ Maxwell sviluppò una formulazione migliore della teoria dei fenomeni di trasporto, che evitava l'approssimazione del cammino libero medio. Tutti i risultati della nuova teoria dipendevano dalla funzione di distribuzione delle velocità per un gas in condizioni diverse da quelle di equilibrio termico, funzione che Maxwell non fu in grado di ricavare se non per il caso particolare di forze repulsive inversamente proporzionali alla quinta potenza della distanza tra le particelle. In questo caso, infatti, non era necessario conoscere la funzione di distribuzione delle velocità, e Maxwell trovò che il coefficiente di viscosità era direttamente proporzionale alla temperatura assoluta, ossia μ∝T. I risultati sperimentali da lui stesso ottenuti si accordavano con questa previsione; sicché, a partire dal 1866, egli concluse che la teoria cinetica forniva predizioni del tutto accurate circa la viscosità dei gas. Nel caso di forze inversamente proporzionali alla quinta potenza della distanza intermolecolare, il coefficiente di viscosità era ancora indipendente dalla densità, almeno finché questa non diveniva così alta o così bassa da far sì che le proprietà dei gas non dipendessero più, in modo prevalente, dalle sole collisioni binarie tra le particelle; infatti, a densità molto basse, il flusso del gas cominciava a dipendere in maniera sostanziale dalle interazioni con la superficie del recipiente, mentre a densità molto alte bisognava tener conto delle collisioni simultanee fra tre o più particelle.

Pochi anni più tardi, Boltzmann sviluppò una versione diversa della teoria dei fenomeni di trasporto, equivalente a quella di Maxwell nella misura in cui portava alle stesse formule per i coefficienti di diffusione, viscosità e conduzione termica, ma più conveniente per altre applicazioni. Piuttosto che tentare di eliminare la funzione di distribuzione delle velocità di non equilibrio scegliendo una particolare legge della forza, Boltzmann prese quella funzione come principale oggetto di studio. La scriveremo nella forma f (x,v,t) per indicare che essa dipende non solo dalle velocità molecolari v, ma anche dalla posizione spaziale x e dal tempo t. Boltzmann derivò la variazione di f (x,v,t) come effetto di tutti i processi fisici rilevanti, in particolare delle collisioni, le quali facevano variare i numeri di particelle aventi velocità specificate. Il risultato, pubblicato nel 1872, si tradusse in un'equazione integro-differenziale per f (x,v,t), ora chiamata 'equazione di trasporto di Boltzmann' o semplicemente 'equazione di Boltzmann'. Essa avrebbe giocato un ruolo di primaria importanza nella teoria cinetica del XX sec., poiché sarebbe stata utilizzata anche nelle teorie dei gas ionizzati (fisica dei plasmi) e nel calcolo del flusso di neutroni nei reattori nucleari.

Il calcolo delle proprietà di trasporto di Maxwell e Boltzmann generò una grande quantità di lavoro teorico e sperimentale sulla diffusione, sulla conduzione termica e sulla viscosità. Stimolati dal diffuso interesse verso il radiometro di William Crookes, nel corso degli anni Settanta dell'Ottocento Maxwell e Osborne Reynolds estesero la teoria cinetica al caso di gas rarefatti, nel quale è necessario tener conto delle interazioni gas-superfici.

Negli anni Dieci del Novecento, il fisico svedese David Enskog (1884-1947) elaborò una soluzione generale dell'equazione di trasporto di Boltzmann, mentre il geofisico inglese Sydney Chapman (1880-1970) ottenne una soluzione generale equivalente per le equazioni di trasporto di Maxwell. Enskog e Chapman furono in grado allora di derivare formule per i coefficienti di trasporto per un'ampia varietà di leggi della forza; inoltre essi scoprirono un nuovo processo di trasporto, la 'diffusione termica', previsto dalla teoria cinetica e utilizzato più tardi come uno dei processi di separazione degli isotopi nella realizzazione della bomba atomica. La determinazione sperimentale della dipendenza dalla temperatura dei coefficienti di trasporto può ancora essere utilizzata per trarre conclusioni su quale legge rappresenti in modo più adeguato la forza effettiva tra gli atomi.

Tuttavia negli anni Sessanta dell'Ottocento, quando la stessa esistenza di una struttura atomica della materia non era altro che un'ipotesi, la teoria di Maxwell fu utilizzata per compiere un progresso decisivo: la prima stima affidabile delle dimensioni di un atomo. A questo fine la prima formula che legava μ al diametro d delle particelle risultò la più utile: μ∝L∝V/Nd² (dove L è il cammino libero medio di Clausius, e N il numero di molecole nel volume V). Joseph Loschmidt (1821-1895), un chimico-fisico austriaco, sottolineò nella memoria del 1865, Zur Grösse der Luftmolecule (Sulla dimensione della molecola dell'aria), come questa relazione avrebbe potuto essere utilizzata per determinare d se fossero state note altre relazioni per N e L. In particolare, egli suggerì che il volume occupato dalle molecole del gas, se esse fossero state raggruppate l'una vicino all'altra, sarebbe stato più o meno quello della sostanza condensata nello stato liquido, ossia V_liq≈Nd³. Se la densità di una sostanza è nota sia per lo stato gassoso, sia per lo stato liquido, il 'coefficiente di condensazione' V/V_liq=V/Nd³ poteva essere combinato con il cammino libero medio L≈V/Nd² per ottenere un valore per d.

In questo modo Loschmidt concluse che il diametro d di una 'molecola d'aria' era circa 10⁻⁷ cm. Questo valore è circa quattro volte più grande delle stime attuali, ma notevolmente migliore di tutte quelle disponibili a quel tempo. Il valore corrispondente per il numero di molecole in 1 cm³ di un gas ideale in condizioni standard (0° C, 1 atmosfera di pressione) sarebbe dunque stato N_L≈2·10¹⁸ atm⁻¹ cm⁻³.

Anche se Loschmidt non riportò questo risultato nell'articolo del 1865, esso poteva essere facilmente dedotto dalla sua formula e così oggi viene talvolta chiamato 'numero di Loschmidt'; il suo valore attuale è 2,687·10¹⁹ atm⁻¹ cm⁻³. Il 'numero di Loschmidt' non deve però essere confuso con l'altra costante a esso collegata che è il 'numero di Avogadro', definito come numero di molecole gassose per mole di gas, e che risulta essere N_A=N_L/V₀=6,02·10²³ mole⁻¹ (V₀=22.420,7 cm³ atm mole⁻¹). Anche Avogadro non aveva fornito una stima di tale valore, ma solo ipotizzato che esso dovesse essere lo stesso per tutti i gas.

Nel corso degli anni successivi altri scienziati (il più influente dei quali era lord Kelvin) fecero stime analoghe delle dimensioni e di altri parametri atomici usando la teoria cinetica dei gas. A seguito di questi sviluppi l'atomo, che inizialmente era un concetto meramente ipotetico, cominciò a essere considerato un'entità fisica reale che poteva essere sottoposta a misure quantitative anche se non poteva essere 'vista'. Fu questo uno dei contributi più importanti della teoria cinetica alla fisica del XIX sec.; eppure questa fu criticata da scettici come Mach e Friedrich Wilhelm Ostwald (1853-1932), i quali ancora alla fine dell'Ottocento sostenevano che non fossero emersi fatti sperimentali convincenti a favore dell'esistenza degli atomi e che quindi la teoria cinetica non potesse essere ammessa nell'élite delle teorie fisiche stabilite.

L'equazione di van der Waals e il punto critico

La maggior parte delle previsioni quantitative della teoria cinetica a cui finora abbiamo fatto riferimento è valida soltanto per gas che sono approssimativamente 'ideali', ossia la cui densità è abbastanza bassa da far sì che le dimensioni di ciascuna molecola siano piccole rispetto allo spazio tra le molecole stesse. In questo caso sono valide le leggi di Boyle e di Gay-Lussac, normalmente combinate nella cosiddetta 'equazione di stato del gas ideale' PV=RT. Inoltre, per derivare le equazioni di trasporto di Maxwell e Boltzmann e le formule per i coefficienti di trasporto, occorre ammettere che le molecole subiscano solo collisioni binarie.

Già nel 1738 Daniel Bernoulli si era accorto che ci si sarebbe dovuti aspettare violazioni della legge del gas ideale se lo spazio occupato dalle molecole non fosse stato infinitamente più piccolo del volume occupato dall'intero gas, ma solamente nel 1873 il fisico olandese Johannes Diderik van der Waals (1837-1923) fece una valutazione accurata delle correzioni teoriche da apportare, mostrando come, in base anche a una stima degli effetti delle forze attrattive a lungo raggio, si potevano spiegare alcune delle proprietà tipiche dei gas con densità elevata. Van der Waals sostenne che, se una molecola occupa una regione finita di spazio, il volume V nell'equazione di stato deve essere sostituito da (V−b), dove b rappresenta un piccolo multiplo dello spazio occupato da sfere di diametro d.

Le forze attrattive intermolecolari erano state introdotte in precedenza da Laplace e da altri per spiegare la capillarità e la tensione superficiale nei liquidi; tuttavia, prima del 1850, si pensava che esse agissero soprattutto a distanze brevi e che nei gas ci dovessero essere forze repulsive a lungo raggio (associate alla presenza del fluido calorico) per spiegare la resistenza dei gas alla pressione esterna. Nella teoria di van der Waals si ipotizza che le forze attrattive siano più influenti a grandi distanze tra le molecole e che le forze repulsive agiscano con efficacia soltanto quando le particelle sono quasi a contatto tra loro. Van der Waals non specificò la forma di queste forze e si limitò a ipotizzare che l'effetto netto dell'attrazione sarebbe stato quello di aumentare la pressione esterna per una quantità proporzionale al quadrato della densità (ossia inversamente proporzionale al quadrato del volume). Combinando queste due correzioni, van der Waals pervenne all'equazione di stato [P+(a/V²)](V−b)=RT, dove a e b sono costanti caratteristiche di ciascun gas.

La proprietà più interessante dell'equazione di van der Waals non è tanto quella di accordarsi con le piccole deviazioni osservate dalla legge del gas ideale, quanto il fatto che essa fornisce una descrizione notevolmente efficace del comportamento del sistema vicino al punto critico gas-liquido scoperto nel 1822 dallo scienziato francese Charles Cagniard de la Tour (1777-1859). Questi aveva trovato che, quando l'alcol liquido veniva racchiuso in un tubo a vuoto insieme al suo vapore (in assenza di aria) e poi veniva riscaldato, a un certo punto scompariva il menisco che separava la fase liquida da quella gassosa. Cagniard de la Tour e altri scienziati mostrarono poi che per ciascuna sostanza esisteva un particolare valore della pressione, della temperatura e del volume, chiamato 'punto critico', raggiunto il quale svaniva la distinzione tra liquido e gas (per un grammo di acqua tale punto corrisponde ai seguenti valori: P_c=218 atm; V_c=3,2 cm³, T_c=374 °C). Inizialmente si suppose che sopra il punto critico il liquido si trasformasse semplicemente in gas, ma nel 1863 il chimico-fisico irlandese Thomas Andrews dimostrò che una sostanza in condizioni supercritiche può passare con continuità tanto allo stato liquido quanto allo stato gassoso in seguito a variazioni opportune della temperatura e della pressione.

Fornendo la prima spiegazione efficace delle transizioni di fase, la teoria di van der Waals dimostrò la fecondità dell'approccio atomistico e, nell'ultimo quarto dell'Ottocento, specialmente in Olanda, diede avvio a intense ricerche sui fenomeni critici. La novità principale stava nella dimostrazione che lo stesso modello molecolare poteva essere adottato allo scopo di spiegare due diversi stati della materia, dal momento che in precedenza alcuni scienziati avevano attribuito proprietà diverse alle 'molecole gassose' e alle 'molecole liquide'. Anche se nel XX sec. la teoria dei fenomeni critici di van der Waals sarebbe stata soppiantata da teorie più sofisticate, essa giocò un ruolo importante nel rilevare che cambiamenti qualitativi a livello macroscopico, come i passaggi di stato, potevano essere ricondotti a cambiamenti quantitativi a livello microscopico.

Maxwell e Boltzmann su irreversibilità e determinismo

Subito dopo aver fornito un'interpretazione molecolare soddisfacente della prima legge della termodinamica, i sostenitori della teoria cinetica rivolsero la loro attenzione alla seconda legge. Così come era stata formulata da Clausius, la seconda legge della termodinamica implica che: (1) non si può ottenere lavoro meccanico utile dal calore se non quando una data quantità di quest'ultimo fluisce da un corpo a temperatura elevata a uno a temperatura più bassa, come ipotizzato da Sadi Carnot; (2) il calore fluisce spontaneamente dal caldo al freddo e non viceversa; (3) una grandezza allora misteriosa, chiamata da Clausius 'entropia', tende sempre a crescere fino a raggiungere un valore massimo. Lo stato di massima entropia riferito all'intero Universo era stato chiamato da Clausius 'morte termica': in questo stato, infatti, tutta l'energia sarebbe distribuita uniformemente nello spazio e la temperatura sarebbe uniformemente bassa, sicché non potrebbe essere effettuato lavoro meccanico e la vita non potrebbe esistere.

Mentre si interrogavano sul significato dell'entropia, alcuni fisici riflettevano anche sulle conseguenze dell'approccio statistico della teoria cinetica. Spesso si dice che tale approccio fosse usato solo per comodità, dato che si aveva a che fare con grandi quantità di particelle le cui posizioni e velocità esatte a ogni istante non potevano essere conosciute o che, anche se fossero state note, sarebbe stato praticamente impossibile usare per calcolare il comportamento complessivo del gas. Sembra infatti che, almeno fino a Maxwell, i fisici del XIX sec. avessero sempre supposto che il gas fosse un sistema meccanico deterministico; così, se l'intelligenza superiore immaginata da Laplace avesse posseduto tutte le informazioni necessarie circa lo stato di moto di tutti gli atomi a un istante dato, avrebbe potuto calcolare le loro posizioni e le loro velocità per ogni altro istante, derivando al contempo le proprietà macroscopiche del gas. Per questo motivo, l'approccio statistico di cui si è parlato deve essere nettamente distinto, secondo i resoconti abituali della storia della fisica moderna, dai postulati riguardanti il carattere casuale e indeterminato dei movimenti atomici che sarebbero stati introdotti soltanto negli anni Venti del Novecento in relazione allo sviluppo della meccanica quantistica. D'altra parte si sostiene anche che un aspetto saliente della 'rivoluzione scientifica' avvenuta nei primi decenni del XX sec. sarebbe stato il passaggio repentino dal determinismo classico all'indeterminismo quantistico. Tuttavia, come vedremo, i dibattiti sull'irreversibilità sorti riaguardo alla teoria cinetica dei gas portarono a mettere in dubbio il determinismo molti decenni prima della formulazione del principio di Heisenberg.

Alla fine del 1867, negli stessi anni in cui Clausius prevedeva la 'morte termica' dell'Universo, Peter Guthrie Tait (1831-1901) scriveva al suo vecchio amico Maxwell chiedendogli aiuto per un'esposizione della termodinamica che stava preparando per un libro di testo. Maxwell propose l'immagine di un piccolo guardiano che poteva dar luogo a violazioni della seconda legge: il 'demone di Maxwell'.

Oltre a invertire un processo irreversibile, il demone di Maxwell indicava un nuovo modello per il processo irreversibile fondamentale: il flusso di calore poteva essere concepito come un semplice processo di mescolamento. Il fenomeno ordinario del passaggio di calore da un corpo caldo a uno freddo ora poteva essere considerato equivalente, anche se non sempre identico, alla transizione da uno stato parzialmente ordinato (più molecole veloci da una parte, più molecole lente dall'altra) a uno stato meno ordinato. Da allora in poi i concetti di 'ordine' e 'disordine' molecolari furono associati al flusso di calore e all'entropia, anche se Maxwell non rese mai esplicita tale connessione.

La conclusione di Maxwell fu che la validità della seconda legge della termodinamica non è assoluta, ma dipende dall'inesistenza di un demone capace di selezionare le molecole, vale a dire dalla nostra incapacità di seguire il moto delle singole molecole e individuarne le velocità; per questo essa è una legge statistica, valida solamente per i fenomeni macroscopici. Definire tale legge come 'statistica' non equivaleva però ad asserire che essa si basasse su eventi casuali, anzi questa definizione sembrava implicare il contrario. Se non avesse potuto prevedere il comportamento futuro delle molecole, osservandole mentre si avvicinano alla porta, il demone di Maxwell non avrebbe nemmeno potuto intervenire in maniera efficace. Eppure, a un livello più superficiale, attribuire un carattere 'statistico' a una legge o a un fenomeno dava l'impressione che in essi fosse implicato un qualche elemento di casualità o di disordine. Più tardi fu Boltzmann a fornire una versione quantitativa dell'argomentazione di Maxwell servendosi della sua equazione di trasporto per la funzione di distribuzione delle velocità in condizioni di non equilibrio. Egli mostrò che le collisioni spingono sempre la f (x,v,t) verso la distribuzione di equilibrio di Maxwell. In particolare, la grandezza H=f (x,v,t) log f (x,v,t) diminuisce costantemente nel tempo fino a che la f non diviene la distribuzione di Maxwell, nel qual caso H mantiene un valore minimo stabile. Tale dimostrazione è universalmente nota come 'teorema H di Boltzmann'.

Per un gas in condizioni di equilibrio termico, la funzione H di Boltzmann è proporzionale a −S, dove S è l'entropia così come nel 1865 era stata definita da Clausius. Mentre la grandezza 'entropia' ha in termodinamica un valore definito soltanto per gli stati di equilibrio, Boltzmann suggeriva tuttavia che la sua funzione H potesse essere considerata come un'entropia generalizzata, con un valore definito per qualsiasi stato. Quindi il teorema H equivale all'asserzione che l'entropia non può che aumentare o tutt'al più restare costante; asserzione che può essere considerata come una diversa versione della seconda legge della termodinamica. La giustificazione della legge di distribuzione di Maxwell è quindi basata sul riconoscimento della tendenza generale dei sistemi fisici a evolvere irreversibilmente verso l'equilibrio termico.

Tuttavia, nel 1876, Loschmidt, il collega viennese di Boltzmann, fece la seguente osservazione: un sistema che segue le leggi di Newton deve tornare nel suo stato iniziale se, in un qualsiasi stato successivo, vengono cambiate di segno le velocità di tutte le sue molecole. Apparentemente, quindi, vi è una contraddizione fondamentale tra la reversibilità delle leggi di Newton e l'irreversibilità che osserviamo in Natura. Questa contraddizione, in seguito chiamata 'paradosso della reversibilità', era stata già discussa due anni prima da lord Kelvin in un articolo al quale però non era stata rivolta una grande attenzione.

Boltzmann replicò sostenendo che l'entropia non è altro che una misura della probabilità di uno stato definito in termini macroscopici. Mentre si può supporre che ciascuno stato microscopico (individuato da determinati valori delle posizioni e delle velocità di tutte le molecole) abbia la stessa probabilità, lo stato macroscopico di equilibrio termico è compatibile con un insieme molto vasto di stati microscopici e quindi possiede una grande probabilità. Gli stati macroscopici sensibilmente lontani dall'equilibrio sono invece compatibili solo con pochi stati microscopici e quindi hanno una probabilità molto più bassa. In un tipico processo irreversibile il sistema passa da uno stato di non equilibrio (per es., uno stato in cui la temperatura non è uniforme) a uno stato di equilibrio (temperatura uniforme): questo equivale a dire che passa da uno stato meno probabile (o di entropia minore) a uno stato più probabile (di entropia maggiore).

Per invertire tale processo non basta partire dallo stato di equilibrio e cambiare il segno delle velocità molecolari, dato che questa operazione riporterebbe quasi certamente il sistema al suo stato di equilibrio; per allontanare il sistema dall'equilibrio bisognerebbe invece individuare (nella sterminata moltitudine degli stati microscopici corrispondenti all'equilibrio) uno di quei pochissimi stati microscopici molto particolari, che sono il risultato di un'evoluzione a partire da uno stato di non equilibrio, e invertire le velocità molecolari. Ne deriva che una diminuzione di entropia è possibile, ma estremamente improbabile.

Nella teoria di Boltzmann la distinzione tra macrostati e microstati è di importanza cruciale. Allo stesso modo del demone di Maxwell, un osservatore che potesse accedere direttamente ai microstati non percepirebbe l'irreversibilità come proprietà immutabile dei fenomeni naturali. È solo quando si decide di raggruppare tra loro certi microstati, chiamandoli collettivamente 'disordinati' o 'di equilibrio', che è possibile parlare di passaggio da stati 'più probabili' a stati 'meno probabili'. Da questo punto di vista, un processo è irreversibile nello stesso senso in cui mischiare le carte dopo aver distribuito una mano da 'grande slam' nel gioco del bridge è un processo irreversibile; sono le regole del gioco che 'selezionano' certe distribuzioni di carte come 'ordinate' (tutte quelle dello stesso colore, o tutti gli assi, i re e le regine nella stessa mano), e siamo noi a considerare 'rare' queste distribuzioni, anche se di fatto tutte le possibili distribuzioni di cinquantadue carte tra quattro giocatori hanno esattamente la stessa probabilità. Se si gioca a bridge abbastanza a lungo si avrà una mano da 'grande slam' non una ma numerose volte. Lo stesso vale per i sistemi meccanici governati dalle leggi di Newton, come dimostrò nel 1890 con il suo 'teorema di ricorrenza' il matematico francese Jules-Henri Poincaré (1854-1912): un sistema con energia totale fissata e racchiuso in un volume finito tornerà prima o poi arbitrariamente vicino allo stato microscopico preso come stato iniziale. Se l'entropia fosse determinata dalle velocità e dalle posizioni delle molecole, allora anch'essa dovrebbe tornare al suo valore iniziale, sicché come aumenta in un certo intervallo di tempo, così dovrebbe diminuire in un altro intervallo.

Questa apparente contraddizione tra il comportamento di un sistema meccanico deterministico e la seconda legge della termodinamica è nota come 'paradosso della ricorrenza'. Essa fu usata nel 1896 dal matematico tedesco Ernst Zermelo (1871-1953) per attaccare la concezione meccanicistica del mondo. Egli sosteneva che la seconda legge è una verità assoluta, sicché ogni teoria che porta a previsioni in contraddizione con essa deve essere necessariamente falsa. Questa confutazione non varrebbe soltanto per la teoria cinetica dei gas ma per ogni teoria basata sull'ipotesi che la materia è composta da particelle che si muovono secondo le leggi della meccanica.

Boltzmann aveva precedentemente negato la possibilità di tali ricorrenze e avrebbe potuto continuare a negare il loro carattere necessario, respingendo la visione determinista che era alla base dell'argomento di Poincaré e Zermelo. Invece, egli ammise con franchezza che le ricorrenze sono del tutto coerenti con il punto di vista statistico, come suggerisce l'analogia con il gioco delle carte; esse sono fluttuazioni che devono quasi certamente verificarsi se si aspetta abbastanza a lungo. In questo modo la visione deterministica porta alla stessa conseguenza qualitativa che ci si aspetterebbe da una successione puramente casuale di stati. In entrambi i casi, tuttavia, il tempo di ricorrenza è così inconcepibilmente lungo che il fatto che non si riesca a osservare il ritorno alle condizioni iniziali non costituisce certo un'obiezione alla teoria.

Mentre riuscì ad aggirare il problema del determinismo nella discussione del paradosso della ricorrenza e a mantenere un ambiguo punto di vista 'statistico', Boltzmann dovette invece affrontarlo direttamente nel corso di un altro dibattito che si sviluppò pressappoco nello stesso periodo. Nel 1890, a Dublino, Edward P. Culverwell aveva sollevato quella che sarebbe stata chiamata 'l'obiezione di reversibilità al teorema H', da non confondersi con il 'paradosso della reversibilità' discusso da lord Kelvin, da Loschmidt e da Boltzmann negli anni Settanta dell'Ottocento. Culverwell si chiedeva come potesse valere il teorema H essendo questo basato sull'ipotesi che la dinamica delle collisioni molecolari fosse reversibile e suggeriva che l'irreversibilità potesse subentrare a livello molecolare forse a causa delle interazioni con l'etere. Va detto, per inciso, che l'etere era spesso alla base di ipotesi per spiegare proprietà della materia e dell'energia che non si accordavano con lo schema della fisica newtoniana, anche se alcuni fisici cominciavano a nutrire sospetti sulla tendenza dei loro colleghi a risolvere in questo modo le loro difficoltà teoriche.

Negli anni immediatamente successivi, l'obiezione di Culverwell fu discussa ai congressi della British Association for the Advancement of Science e sulle colonne della rivista "Nature". Fu il fisico londinese Samuel Burbury (1831-1911) a sottolineare, nel 1894, che la dimostrazione del teorema H dipendeva dall'ipotesi di Maxwell e di Boltzmann secondo la quale le molecole che prendono parte a una collisione non sono tra loro correlate. Mentre ciò sembrava plausibile se ci si riferiva a una situazione precedente la collisione, si poteva invece supporre che la collisione stessa introducesse una correlazione tra le molecole appena urtate, sicché l'ipotesi non sarebbe stata più valida per le collisioni successive. Burbury, allora, in un articolo del 1894 intitolato Boltzmann's minimum function, propose che l'ipotesi potesse essere giustificata chiamando in causa una sorta di "perturbazione esterna che agisce in maniera casuale" (p. 78).

Prendendo parte in prima persona al dibattito inglese sul teorema H, Boltzmann finì per accettare la conclusione di Burbury circa la necessità di un'ipotesi aggiuntiva che nelle Vorlesungen über Gastheorie (Lezioni sulla teoria dei gas, 1896-1898), chiamò 'ipotesi del disordine molecolare'. Secondo l'autore, questa ipotesi poteva essere giustificata dal fatto che in un gas il cammino libero medio è grande rispetto alla distanza media tra due molecole vicine, cosicché una data molecola non avrebbe quasi mai incontrato di nuovo una delle molecole che aveva urtato in precedenza e con la quale, quindi, essa sarebbe stata correlata.

L'ipotesi del 'disordine molecolare' non prevede soltanto che gli stati delle molecole individuali si presentino in maniera completamente casuale; essa, piuttosto, esclude quei particolari stati ordinati del gas che porterebbero a violazioni della seconda legge della termodinamica. In realtà, questi stati ordinati sarebbero generati anche da un processo casuale, cosa che Boltzmann riconobbe nella sua discussione del paradosso della ricorrenza. Usando una terminologia moderna, la distinzione introdotta da Boltzmann equivale a quella tra 'numeri casuali' e 'numeri generati da processi casuali': in effetti, nel preparare una sequenza di numeri casuali da usare in analisi statistiche, si escludono sempre certe sottosequenze che, pur essendo possibili, risultano un prodotto troppo 'ordinato' del processo di generazione dei numeri stessi. Boltzmann riconobbe che l'ipotesi del disordine molecolare era necessaria per dedurre l'irreversibilità, tuttavia ammise anche che l'ipotesi avrebbe potuto non essere sempre valida per i gas reali, in particolare per quelli ad alta densità, dove avrebbero potuto verificarsi fenomeni di ricorrenza.

Alla luce di questo parziale abbandono del determinismo a livello molecolare, è necessario rivedere la tesi secondo la quale i fisici del XIX sec. erano tutti deterministi e usavano i metodi statistici solo per motivi di convenienza. Non c'è dubbio che alcuni pensatori del XIX sec. sostenessero ipotesi fortemente deterministe, considerando il determinismo la vera essenza della scienza. Così, per esempio, scriveva in The principles of science (1874) il filosofo della scienza William S. Jevons:

Possiamo tranquillamente accettare come ipotesi scientifica soddisfacente la dottrina che Laplace ha esposto in maniera così grandiosa e cioè che la conoscenza perfetta dello stato dell'Universo a un istante dato ci darebbe una conoscenza perfetta di ciò che avverrà da allora in poi in ogni istante futuro. L'inferenza scientifica sarebbe impossibile se non potessimo considerare il presente come un prodotto del passato e come causa del futuro. Per una intelligenza perfetta non vi è nulla di incerto. (Jevons 1874 [1877, pp. 738-739])

Come lo stesso Laplace aveva sottolineato nel 1783, la causa degli eventi naturali non può essere attribuita a qualcosa come la 'sorte'; questa è solo l'espressione della nostra ignoranza, sicché "la probabilità appartiene esclusivamente alla mente" (ibidem, p. 198).

C'è da chiedersi, però, se questa concezione fosse effettivamente condivisa anche dagli scienziati. Nel periodo in cui Jevons scriveva il sostegno a favore del determinismo assoluto cominciava a vacillare. Non si intende con questo sopravvalutare gli elementi di continuità tra la fisica del XIX e quella del XX sec.: furono senza dubbio le scoperte del Novecento (compresa quella del decadimento radioattivo, anche se avvenne di fatto prima dell'inizio del secolo) a dare l'impulso decisivo all'affermazione della casualità a livello atomico. Tuttavia le discussioni sulla casualità e sull'irreversibilità, legate alla teoria cinetica e alla seconda legge della termodinamica, erano molto familiari ai fisici dei primi decenni del Novecento.

L'affermazione che la teoria cinetica del XIX sec. era fondata sul determinismo molecolare deve basarsi fortemente sugli scritti di Maxwell e Boltzmann, anche se in assenza di ammissioni esplicite si può legittimamente inferire che essi accettassero tacitamente il punto di vista dei loro colleghi contemporanei. In realtà, come abbiamo appena visto nel caso di Boltzmann, la situazione è un po' più complessa: le parole erano ambigue ma i problemi affrontati spingevano la teoria fisica in maniera decisiva in direzione dell'indeterminismo. Come in altre svolte della scienza fisica ‒ possiamo citare i casi di Johannes Kepler, Augustin-Jean Fresnel, Max Planck e Werner Heisenberg ‒, furono i risultati matematici che costrinsero ad accettare profondi cambiamenti concettuali a livello qualitativo.

I primi lavori di Maxwell nel campo della teoria cinetica, in particolare la sua introduzione della legge di distribuzione delle velocità molecolari, sembrano derivare più dalla tradizione della teoria generale della probabilità e dalla statistica sociale (quale era stata sviluppata da Quételet) che dall'analisi in termini meccanici dei moti molecolari. Tale legge asserisce che ogni componente della velocità di ciascuna molecola è una variabile casuale, che è statisticamente indipendente da ogni altra componente della molecola considerata e delle altre molecole. Solamente nei suoi articoli più tardi Maxwell tentò di giustificare la legge collegandola alle collisioni molecolari e anche allora fu costretto a supporre che le velocità di due molecole collidenti fossero statisticamente indipendenti. D'altra parte, la derivazione matematica di proprietà dei gas quali la viscosità e la conducibilità termica, il cui confronto con i dati sperimentali diede una conferma sostanziale alla teoria, implicava un'accurata analisi dinamica delle collisioni tra particelle con specifiche velocità, posizioni e leggi di forza. Senza adottare un punto di vista deterministico, in questa parte della teoria Maxwell non sarebbe riuscito a ottenere il suo sorprendente successo nel collegare le proprietà macroscopiche con le grandezze molecolari.

Maxwell non sostenne in maniera coerente la concezione deterministica a livello molecolare, anche se occasionalmente si schierò per questa posizione, come per esempio nella conferenza dal titolo Molecules tenuta nel 1873 al convegno della British Association for the Advancement of Science. Eppure, nello stesso anno, nelle discussioni e nella corrispondenza private, egli cominciò a ripudiare il determinismo come dottrina filosofica. Un'esposizione dettagliata delle sue idee può essere trovata in un saggio dal titolo Does the progress of physical science tend to give any advantage to the opinion of necessity (or determinism) over that of the contingency of events and the freddom of the will?, presentato a un gruppo informale dell'Università di Cambridge. La risposta a questa domanda fu negativa: essa si basava sul riferimento all'esistenza di punti singolari nella traiettoria di sistemi dinamici, punti nei quali una forza infinitesima produce effetti finiti (argomentazioni come queste hanno portato alcuni scienziati contemporanei a includere Maxwell nell'elenco dei precursori della 'teoria del caos'). La conclusione era che "può darsi che lo sviluppo della conoscenza della Natura tenderà a rimuovere quel pregiudizio a favore del determinismo che sembra nascere dall'idea che la scienza fisica del futuro non sarà altro che un'immagine ingrandita della scienza del passato" (in Campbell 1882, p. 434).

Dal 1875 in poi, come nel caso dell'articolo pubblicato su "Nature", On the dynamical evidence of the molecular constitution of bodies, Maxwell continuò ad asserire che il moto molecolare è "perfettamente irregolare; il che equivale a dire che la direzione e la grandezza della velocità di una molecola a un dato istante non può essere espressa come dipendente dalla posizione della molecola e dal tempo" (Maxwell 1875a, p. 235). Nella voce Atom dell'Encyclopaedia Britannica egli affermò anche che questa irregolarità è condizione necessaria perché il sistema si comporti in maniera irreversibile.

Due decenni dopo, come si è detto, Boltzmann sembrò raggiungere la stessa conclusione. Tuttavia egli non era così sicuro che la sua ipotesi del disordine molecolare risolvesse i paradossi della reversibilità e della ricorrenza. In risposta alle ulteriori critiche da parte di Zermelo egli propose quindi una nuova ipotesi: immaginiamo di prendere in considerazione la curva descritta dalla grandezza H in funzione del tempo per l'intero Universo o per una parte dell'Universo isolata dal resto. Un valore elevato di H corrisponderà a uno stato molto ordinato di bassa entropia, stato in cui, per esempio, può esistere la vita. Se il teorema di ricorrenza è corretto, allora possiamo considerare tale stato come uno degli infiniti massimi di una curva oscillante. Se seguiamo l'andamento di H dopo che essa ha raggiunto uno di questi picchi, noteremo che il suo valore decrescerà in accordo con il teorema H; ma, prima o poi, la curva dovrà risalire e raggiungere un picco successivo. Durante quest'ultima epoca (in cui l'entropia è decrescente) la seconda legge della termodinamica sarà dunque violata. Tuttavia, ipotizzò Boltzmann, se i processi irreversibili nel nostro ambiente e all'interno del nostro corpo 'vanno a ritroso', allora deve avvenire un'inversione anche del nostro senso della direzione del tempo. E quindi, per ogni essere cosciente che si trovasse a esistere nell'era suddetta, la grandezza H dovrebbe apparire decrescente se misurata rispetto alla propria cognizione dell'evoluzione temporale in modo tale che, per lui, la seconda legge continuerebbe a essere valida.

Sebbene la considerasse poco più che un'ipotesi speculativa, in un articolo del 1897, Zu Hrn. Zermelo's Abhandlung über die mechanische Erklärung irreversibler Vorgänge (Sullo scritto di Zermelo 'Sulla spiegazione meccanica dei processi irreversibili'), Boltzmann giustificò tale proposta descrivendola nei termini seguenti:

Possiamo scegliere tra due tipi di rappresentazione. Si può supporre che l'intero Universo si trovi nel periodo attuale in uno stato altamente improbabile. Viceversa, si può invece supporre che sia gli eoni durante i quali tale stato improbabile perdura, sia la distanza tra la Terra e Sirio, siano poca cosa rispetto all'età e alle dimensioni dell'Universo. Vi devono quindi essere, in un Universo che è globalmente in equilibrio e quindi termicamente 'morto', piccole regioni sparse qui e là delle dimensioni della nostra galassia (regioni che chiamiamo 'mondi') che per eoni di tempo relativamente piccoli si allontanano in maniera significativa dall'equilibrio termico. La probabilità dello stato di questi mondi cresce e altrettanto spesso diminuisce. Per l'intero Universo le due direzioni del tempo sono indistinguibili, così come nello spazio non si può distinguere il basso dall'alto. Tuttavia, proprio come sulla superficie terrestre possiamo indicare come rivolta verso il 'basso' qualsiasi direzione orientata verso il centro della Terra, così un essere vivente che si trova in uno dei mondi suddetti in un certo periodo di tempo potrà definire la direzione del tempo come quella diretta dagli stati meno probabili agli stati più probabili (i primi saranno il 'passato' e i secondi il 'futuro') e in virtù di questa definizione troverà che questa piccola regione, isolata dal resto dell'Universo, si trova 'inizialmente' in uno stato improbabile. Questo punto di vista mi appare come il solo modo in cui si possa comprendere la validità della seconda legge e della 'morte termica' per ciascun mondo individuale senza fare appello a un'evoluzione unidirezionale dell'intero Universo da un definito stato iniziale a uno stato finale. (pp. 392-398)

L'ipotesi di Boltzmann afferma dunque che l'irreversibilità, ossia l'asserzione che 'l'entropia cresce con il tempo', non è una legge di Natura ma una tautologia: la direzione del tempo è determinata dalla direzione di crescita dell'entropia. Si può notare, peraltro, che curiosamente la stessa idea era stata appena proposta da Mach, il critico più famoso delle teorie atomistico-cinetiche di Boltzmann. Da un altro punto di vista si può sostenere che tale ipotesi preluda a quella di Einstein sulla non assolutezza del tempo e sulla sua relatività rispetto all'osservatore.

Nel corso del XIX sec. la teoria cinetica dei gas risolse vecchi problemi, anticipò fatti inaspettati e generò difficili paradossi. Essa lasciò alla scienza del Novecento una ricca eredità di conoscenze utili sulle molecole e sui gas e alcune stimolanti congetture sull'irreversibilità e sull'indeterminismo.

Bibliografia

Achinstein 1987: Achinstein, Peter, Scientific discovery and Maxwell's kinetic theory, "Philosophy of science", 54, 1987, pp. 409-434.

‒ 1991: Achinstein, Peter, Particles and waves. Historical essays in the philosophy of science, New York-Oxford, Oxford University Press, 1991.

Battimelli 1993: Proceedings of the International Symposium on Ludwig Boltzmann (Rome, february 9-11, 1989), edited by Giovanni Battimelli, Maria Grazia Ianniello and Otto Kresten, Wien, Verlag der Österreichischen Akademie der Wissenschaften, 1993.

Baucia 1973: Baucia, Giovanni, Microfenomeni e macrofenomeni secondo Maxwell in relazione alla 'Teoria dinamica del calore', "Physis", 15, 1973, pp. 333-350.

Bellone 1972: Bellone, Enrico, Aspetti dell'approccio statistico alla meccanica, 1849-1905. Saggio sull'uso di parametri probabilistici nella fisica teorica della seconda metà dell'Ottocento, Firenze, Barbera, 1972.

‒ 1978: Bellone, Enrico, Le leggi della termodinamica da Boyle a Boltzmann, Torino, Loescher, 1978.

‒ 1989: Bellone, Enrico, I nomi del tempo. La seconda rivoluzione scientifica e il mito della freccia temporale, Torino, Bollati Boringhieri, 1989.

Blackmore 1995: Ludwig Boltzmann. His later life and philosophy, 1900-1906, edited by John Blackmore, Dordrecht-Boston, Kluwer Academic, 1995, 2 v.

Broda 1955: Broda, Engelbert, Ludwig Boltzmann. Mensch, Physiker, Philosoph, Wien, Deuticke, 1955 (trad. ingl.: Ludwig Boltzmann. Man, physicist, philosopher, translated by Larry Gay and Engelbert Broda, Woodbridge (Conn.), Ox Bow, 1983).

Brush 1965-72: Brush, Stephen G., Kinetic theory, Oxford-New York, Pergamon, 1965-1972, 3 v.; v. I: The nature of gases and of heat, 1965; v. II: Irreversible processes, 1966; v. III: The Chapman-Enskog solution of the transport equation for moderately dense gases, 1972.

‒ 1976: Brush, Stephen G., The kind of motion we call heat. A history of the kinetic theory of gases in the 19th century, Amsterdam, North Holland, 1976, 2 v.

‒ 2003: Brush, Stephen G., The kinetic theory of gases: an anthology of classic papers with historical commentary, London, Imperial College, 2003.

Cahan 1990: Cahan, David, From dust figures to the kinetic theory of gases. August Kundt and the changing nature of experimental physics in the 1860s and 1870s, "Annals of science", 40, 1990, pp. 151-172.

Cardoso Dias 1994: Cardoso Dias, Penha Maria, Clausius and Maxwell. The statistics of molecular collisions, "Annals of science", 51, 1994, pp. 249-261.

Daub 1969: Daub, Edward E., Probability and thermodynamics. The reduction of the second law, "Isis", 60, 1969, pp. 318-330.

‒ 1970: Daub, Edward E., Maxwell's demon, "Studies in history and philosophy of science", 1, 1970, pp. 213-227.

‒ 1971: Daub, Edward E., Waterston's influence on Krönig's kinetic theory of gases, "Isis", 62, 1971, pp. 512-515.

Dorling 1970: Dorling, Jon, Maxwell's attempts to arrive at non-speculative foundations for kinetic theory, "Studies in history and philosophy of science", 1, 1970, pp. 229-248.

Dugas 1959: Dugas, René, La théorie physique au sens de Boltzmann et ses prolongements modernes, Paris, Éditions du Griffon, 1959.

Ehrenfest 1911: Ehrenfest, Paul - Ehrenfest, Tatiana, Begriffliche Grundlagen der statistichen Auffassung in der Mechanik, in: Enzyklopädie der mathematischen Wissenschaften, mit Einschluss ihrer Anwendungen, redigiert von Wilhelm F. Meyer [et al.], Leipzig, Teubner, 1898-1935, 6 v. in 24 tomi; v. IV/2.2: Mechanik, redigiert von Felix Klein und Conrad Müller, 1911, pp. 1-90 (trad. ingl.: The conceptual foundations of the statistical approach in mechanics, translated by Michael J. Moravcsik, Ithaca (N.Y.), Cornell University Press, 1959).

Everitt 1975: Everitt, C.W. Francis, James Clerk Maxwell. Physicist and natural philosopher, Cambridge, Scribner's Sons, 1975 (rist. in: Maxwell, James Clerk, in: Dictionary of scientific biography, edited by Charles Coulston Gillispie, New York, Scribner's Sons, 1970-1990, 18 v.; v. IX, 1981, pp. 198-230).

Fox 1971: Fox, Robert, The caloric theory of gases. From Lavoisier to Regnault, Oxford, Clarendon, 1971.

Garber 1970: Garber, Elizabeth, Clausius and Maxwell's kinetic theory of gases, "Historical studies in the physical sciences", 2, 1970, pp. 299-319.

‒ 1972: Garber, Elizabeth, Aspects of the introduction of probability into physics, "Centaurus", 17, 1972, pp. 11-39.

‒ 1995: Maxwell, James Clerk, Maxwell on heat and statistical mechanics: on 'avoiding all personal enquiries' of molecules, edited by Elizabeth Garber, Stephen G. Brush and C.W. Francis Everitt, Bethlehem (Penn.), Lehigh University Press, 1995.

Gillispie 1963: Gillispie, Charles Coulston, Intellectual factors in the background of analysis by probabilities, in: Scientific change. Historical studies in the intellectual, social, and technical conditions for scientific discovery and technical invention, from antiquity to the present, edited by Alistair C. Crombie, New York, Basic Books, 1963, pp. 431-453.

Harman 1970: Harman, Peter M., Molecular forces, statistical representation and Maxwell's demon, "Studies in history and philosophy of science", 1, 1970, pp. 189-211.

Heisenberg 1971: Heisenberg, Werner, Physics and beyond. Encounters and conversations, New York, Harper and Row, 1971.

Kipnis 1996: Kipnis, Alexandr Ya. - Yavelov, Boris E. - Rowlinson, John S., Van der Waals and molecular science, Oxford, Clarendon, 1996.

Kirschke 1987: Ludwig Boltzmanns Werk in naturwissenschaftlicher und philosophischer Sicht, hrsg. von Siegfried Kirschke und Wolfgang Eisenberg, Halle, Martin-Luther-Universität, 1987.

Klein 1970: Klein, Martin J., Maxwell, his demon, and the second law of thermodynamics, "American scientist", 58, 1970, pp. 84-97.

‒ 1973a: Klein, Martin J., The development of Boltzmann's statistical ideas, in: The Boltzmann equation. Theory and applications, edited by Ezechiel G.D. Cohen and Walter Thirring, Wien-New York, Springer, 1973, pp. 53-106.

‒ 1973b: Klein, Martin J., The Maxwell-Boltzmann relationship, in: Transport phenomena. 1973, edited by Joseph Kestin, New York, American Institute of Physics, 1973, pp. 297-308.

‒ 1974: Klein, Martin J., The historical origins of the van der Waals equation, "Physica", 73, 1974, pp. 28-47.

Kox 1990: Kox, Anne J., H.A. Lorentz's contributions to kinetic gas theory, "Annals of science", 47, 1990, pp. 591-606.

Leff 1990: Maxwell's demon. Entropy, information, computing, edited by Harvey S. Leff and Andrew F. Rex, Princeton, Princeton University Press, 1990.

Levelt Sengers 1979: Levelt Sengers, Johanna M.H., Liquidons and gasons. Controversies about the continuity of states, "Physica", 90A, 1979, pp. 363-402.

Locqueneux 1983: Locqueneux, Robert - Maitte, Bernard - Pourprix, Bernard, Les statuts épistémologiques des modèles de la théorie des gaz dans les oeuvres de Maxwell et Boltzmann, "Fundamenta scientiae", 4, 1983, pp. 29-54.

Mendoza 1962-63: Mendoza, Eric, The surprising history of the kinetic theory of gases, "Memoirs and proceedings of the Manchester literary and philosophical society", 105, 1962-1963, pp. 1-14.

‒ 1975: Mendoza, Eric, A critical examination of Herapath's dynamical theory of gases, "The British journal for the history of science", 8, 1975, pp. 155-165.

‒ 1982: Mendoza, Eric, The kinetic theory of matter. 1845-1855, "Archives internationales d'histoire des sciences", 32, 1982, pp. 184-220.

Nyhoff 1988: Nyhoff, John, Philosophical objections to the kinetic theory, "The British journal for the philosophy of science", 39, 1988, pp. 81-109.

Porter 1986: Porter, Theodore M., The rise of statistical thinking, 1820-1900, Princeton, Princeton University Press, 1986.

Porterfield 1996: Porterfield, William W. - Kruse, Walter, Loschmidt and the discovery of the small, "Journal of chemical education", 72, 1996, pp. 870-875.

Pourprix 1988: Pourprix, Bernard - Locqueneux, Robert, Josef Stefan (1835-1893) et les phénomènes de transport dans les fluids. La jonction entre l'hydrodynamique continuiste et la théorie cinétique des gaz, "Archives internationales d'histoire des sciences", 38, 1988, pp. 86-118.

de Regt 1996: Regt, Henk W. de, Philosophy and the kinetic theory of gases, "British journal for the philosophy of science", 47, 1996, pp. 31-62.

Rocke 1984: Rocke, Alan J., Chemical atomism in the nineteenth century. From Dalton to Cannizzaro, Columbus, Ohio State University Press, 1984.

Schneider 1975: Schneider, Ivo, Rudolph Clausius. Beitrag zur Einführung wahrscheinlichkeitstheoretischer Methoden in die Physik der Gase nach 1856, "Archive for history of exact sciences", 14, 1975, pp. 137-161.

Sebastiani 1981: Sebastiani, Fabio, Le teorie caloricistiche di Laplace, Poisson, Sadi Carnot, Clapeyron e la teoria dei fenomeni termici nei gas formulata da Clausius nel 1850, "Physis", 23, 1981, pp. 397-438.

‒ 1982: Sebastiani, Fabio, Le teorie microscopico-caloricistiche dei gas di Laplace, Ampère, Poisson e Prévost, "Physis", 24, 1982, pp. 197-236.

Stiller 1988: Stiller, Wolfgang, Ludwig Boltzmann. Altmeister der klassischen Physik und Wegbereiter der Quantenphysik und Evolutionstheorie, Leipzig, Barth, 1988.

Talbot 1966: Talbot, G.R. - Pacey, A.J., Some early kinetic theories of gases: Herapath and his predecessors, "British journal for the history of science", 3, 1966, pp. 133-149.

Truesdell 1968: Truesdell, Clifford A., Early kinetic theories of gases, in: Truesdell, Clifford A., Essays in the history of mechanics, New York-Berlin, Springer, 1968, pp. 272-304.

‒ 1980: Truesdell, Clifford A. - Muncaster, Robert G., Fundamentals of Maxwell's kinetic theory of a simple monatomic gas. Treated as a branch of rational mechanics, New York, Academic Press, 1980.

Wilson 1981: Wilson, David B., Kinetic atom, "American journal of physics", 49, 1981, pp. 217-222.

Wolff 1992: Wolff, Stefan L., August Kundt (1839-1894). Die Karriere eines Experimentalphysikers, "Physis", 29, 1992, pp. 403-446.

‒ 1994: Wolff, Stefan L., Von der Hydrodynamik zur kinetischen Gastheorie - Oskar Emil Meyer, "Centaurus", 37, 1994, pp. 321-348.

‒ 1995: Wolff, Stefan L., Clausius' Weg zur kinetischen Gastheorie, "Sudhoffs Archiv für Geschichte der Medizin und der Naturwissenschaften", 79, 1995, pp. 54-72.