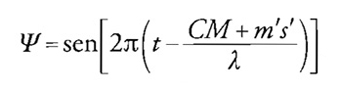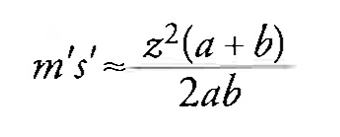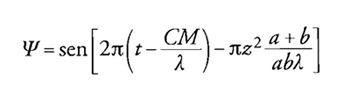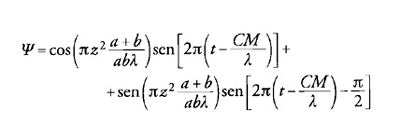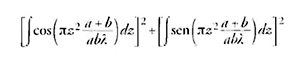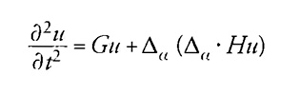L'Ottocento: fisica. Raggi e onde luminosi
L'Ottocento: fisica. Raggi e onde luminosi
Raggi e onde luminosi
Dal XVII al XIX sec., due immagini fisiche fondamentali dominarono la speculazione e, talvolta, persino la matematizzazione negli studi di ottica: ricorrendo a un'estrema semplificazione, tali immagini si riducono all'interpretazione della luce, rispettivamente, come sequenza di particelle materiali che si muovono nel vuoto e come perturbazione meccanica che si propaga in un mezzo materiale che permea tutto lo spazio. Quest'ultima immagine, che affonda le radici nel sistema filosofico di Descartes, ebbe di gran lunga il più elevato numero di sostenitori fino a quasi tutto il XVIII sec., sia pure in una miriade di forme diverse. Nel 1690 l'ipotetico mezzo materiale dell'ottica cartesiana acquisì un nuovo carattere, allorché la perturbazione che si supponeva esso trasportasse fu di fatto ricondotta entro i confini di una trattazione matematica dall'olandese Christiaan Huygens: a tale scopo, nel suo Traité de la lumière egli introdusse una legge fisico-matematica, indicata in seguito come 'principio di Huygens', per descrivere la propagazione delle perturbazioni ottiche. In sostanza, egli pensava che tali disturbi fossero, usando il linguaggio odierno, impulsi longitudinali, ossia singole perturbazioni, parallele alla loro direzione di propagazione. Questi impulsi non possedevano alcuna proprietà periodica e, infatti, la teoria di Huygens non era in grado di spiegare né i colori né certi curiosi fenomeni, che egli stesso aveva scoperto facendo passare due volte la medesima luce attraverso un tipo di cristallo, lo spato d'Islanda. In ogni caso Huygens, per le particolari immagini doppie generate da questo cristallo, riuscì a formulare una teoria geometrica particolareggiata, corroborata da accurati esperimenti. Tuttavia è importante sottolineare che gli strumenti di calcolo dell'epoca non consentivano di esplorare i lati più oscuri delle affermazioni di Huygens e la sua interpretazione della doppia rifrazione rimase controversa fino all'inizio del XIX sec., quando, come vedremo, la conferma di essa a Parigi mise in moto un'importante catena di eventi.
Nel corso del XVIII sec. apparvero numerosi lavori nell'ambito della filosofia naturale speculativa, ma ciononostante l'ottica matematica restò in gran parte legata al concetto di 'raggio luminoso', che il sistema di Huygens aveva privato, di fatto, della profonda importanza di cui aveva goduto fino ad allora in fisica. Tale concetto, in effetti, era stato a lungo il fondamento dell'ottica geometrica e, nel XVII sec., aveva acquisito il significato di una nuova realtà fisica all'interno del primo dei due sistemi che abbiamo citato precedentemente, in quanto indicava il percorso delle particelle che, secondo Newton, costituivano la luce. Questa concezione della struttura fisica della luce esercitò una straordinaria influenza, essendo parte essenziale della filosofia naturale newtoniana, se non anche dell'ottica matematica elaborata dallo stesso Newton. Durante il XVIII sec., però, lo studio dell'ottica matematica non fu proseguito in modo esauriente né seguendo percorsi originali e l'ottica non pervenne ad alcun risultato di rilievo, sperimentale o matematico, sebbene fossero stati compiuti progressi importanti nella strumentazione. Inoltre, per gran parte del Settecento, in numerose situazioni le differenze tra la teoria dell'emissione e le teorie basate sul moto attraverso un mezzo materiale non furono affatto chiarite, non da ultimo perché, comparendo elementi di entrambi i sistemi nell'Opticks (1704) di Newton, molti lettori rimanevano disorientati.
Oltre a quanto abbiamo ora brevemente ricordato, nel ricostruire il clima culturale del Settecento non va peraltro dimenticato che, a causa (o forse a dispetto) della particolare attenzione posta a quell'epoca sui principî fisici, fino all'ultimo quarto del XVIII sec. soltanto una piccola parte dell'attività svolta in ogni settore che avesse attinenza con il laboratorio era di tipo quantitativo; uno spazio ancora minore inoltre era riservato al tentativo di integrare il dettaglio quantitativo con precise situazioni sperimentali la cui accuratezza potesse essere specificata. Ciò era particolarmente vero sia per le ricerche sull'elettricità e sul calore sia in campi relativamente oscuri, come l'ottica dei cristalli. La situazione cominciò a cambiare radicalmente in Francia, appunto nel corso dell'ultimo quarto del secolo. Tanto gli studi di Charles-Augustin Coulomb (1736-1806) sui fenomeni elettrici quanto la collaborazione tra Antoine-Laurent Lavoisier (1743-1794) e Pierre-Simon de Laplace (1749-1827) nelle indagini sui fenomeni termici costituiscono un esempio di questo cambiamento: si nota un crescente interesse per l'aspetto quantitativo associato a esperimenti accurati e spesso sofisticati, progettati con l'esplicito intento di compiere misurazioni. In Francia, in effetti, alla fine del secolo un lavoro che non fornisse valori numerici o un esperimento che non fosse attentamente progettato e matematicamente analizzato avevano scarse possibilità di ricevere qualche attenzione. Una sede dove questa nuova aspirazione poté essere coltivata al meglio fu l'École Polytechnique a Parigi: tutti e quattro i principali protagonisti francesi delle controversie sull'ottica, che riformarono la disciplina in modo decisivo ‒ Jean-Baptiste Biot, Étienne-Louis Malus, Dominique-François Arago e Augustin-Jean Fresnel ‒, frequentarono l'École negli anni Novanta del XVIII sec. e nei primi anni del XIX. Malus, Biot e Fresnel fecero interamente proprio il nuovo spirito quantitativo, mentre non fu così per Arago.
L'ottica dei raggi, la scoperta della polarizzazione e la controversia Biot-Arago
In Francia, durante il primo decennio del XIX sec. l'interesse per l'ottica, e in particolare per i nuovi esperimenti, divenne piuttosto forte. Infatti, grazie in parte allo stimolo proveniente dalla chiara conferma dell'interpretazione di Huygens per la doppia rifrazione‒ fornita dal chimico inglese William H. Wollaston nel suo lavoro del 1802 A method of examining refractive and dispersive powers by prismatic refraction‒, Laplace affidò a Étienne-Louis Malus (1775-1812), un laureato dell'École Polytechnique, il compito di intraprendere un'indagine sperimentale approfondita su tali argomenti; Laplace riponeva grande fiducia in Malus grazie alle ricerche già compiute da questi nell'elaborazione di una matematica che descrivesse i sistemi di raggi luminosi. Dopo aver completato ‒ sempre su invito di Laplace ‒ un'enorme mole di lavoro matematico, che gli aveva permesso di tradurre in termini algebrici l'interpretazione di Huygens, Malus portò a termine un'attenta indagine sperimentale che dimostrava inequivocabilmente come la costruzione di Huygens fosse estremamente accurata. Né Malus, né Laplace, tuttavia, trassero la conclusione che la teoria di Huygens degli impulsi di luce, che essi distinguevano in modo attento e completo dalla teoria dell'emissione, dovesse per questo essere accettata. Entrambi sottolinearono invece, in modi diversi, ma altrettanto singolari, che le formule risultanti erano in realtà compatibili (e forse persino unicamente compatibili, se volessimo attenerci fedelmente a Laplace) con la matematica che descriveva forze e particelle. Questa affermazione assai discutibile era sufficientemente convincente per i collaboratori e per gli allievi di Laplace e anche per certi ambienti scientifici britannici, e per oltre quindici anni l'ottica rimase strettamente legata, come vedremo, alla teoria dell'emissione.
Le affermazioni persuasive su cui si fondava l'ottica dell'emissione furono favorite, in misura tutt'altro che trascurabile, dalla scoperta, dovuta allo stesso Malus ‒ la prima di un certo rilievo dopo quelle del XVII sec. ‒, di un processo ottico completamente nuovo. Già Huygens aveva notato come la luce che emerge dai cristalli birifrangenti sembri possedere una sorta di asimmetria intrinseca, poiché nell'entrare in un secondo cristallo non è ulteriormente divisa perfettamente in due. Nel 1809 Malus scoprì che questa proprietà intrinseca, che nel 1811 avrebbe chiamato 'polarizzazione', per manifestarsi non richiedeva necessariamente un cristallo, ma poteva anche essere prodotta per riflessione secondo un particolare angolo da un qualunque corpo trasparente. Malus descrisse questa scoperta in tre importanti lavori del 1809: Sur une propriété de la lumière réfléchie; Sur une propriété des forces répulsives qui agissent sur la lumière; Sur une propriété de la lumière réfléchie par les corps diaphanes.
Nel corso del decennio successivo, questa scoperta stimolò un'eccezionale quantità di lavoro sperimentale e teorico, svolto soprattutto da Arago e Biot in Francia e da David Brewster e, poco più tardi, John Herschel in Gran Bretagna. In effetti, durante il primo decennio del XIX sec., il settore dell'ottica sul quale si concentrò maggiormente la ricerca sperimentale e quantitativa gravitava attorno alle molte novità strumentali e alle conseguenti opportunità di ricerca aperte dalla scoperta di Malus; in particolare, fu posta molta attenzione al passaggio della nuova forma di luce attraverso sottili lamine cristalline, che generava belle e complesse immagini colorate. Questo studio aveva carattere profondamente matematico, ma non si fondava affatto sulla teoria dell'emissione né poteva essere definito come semplicemente strumentale: esso, in realtà, aveva una natura estremamente teorica.
In questo schema la nozione teorica fondamentale era quella di raggio luminoso e non di particella ottica. Gli esperti di ottica dei raggi ritenevano che ogni singolo raggio esistesse come oggetto a sé stante che poteva essere numerato e che i fasci luminosi fossero costituiti di raggi riuniti in gruppi; gli oggetti fisici basilari erano proprio i raggi e la matematica più appropriata per descriverli ne comportava il conteggio o metodi che si traducevano in una sorta di statistica dei raggi. Il carattere del sistema è straordinariamente evidente nella concezione che Malus aveva della polarizzazione: l'intensità di un fascio luminoso era misurata dal numero dei raggi che conteneva e, a differenza di un raggio singolo, troppo debole per essere rilevato, un fascio poteva essere osservato. Ogni raggio, insiste Malus, possiede un'asimmetria intrinseca per tutta la sua lunghezza; in un certo senso, lo si potrebbe immaginare come un bastoncino lungo il quale si inchiodi ad angolo retto un'asticella, la cui orientazione in un piano perpendicolare al raggio ne determini l'asimmetria. Malus aveva ben compreso che, a rigor di termini, il concetto di polarizzazione non si applicava al singolo raggio componente il fascio, ma soltanto al fascio stesso come insieme di raggi. Un fascio poteva essere polarizzato in un certo modo, ma non si poteva affermare altrettanto dei singoli raggi che lo componevano, sebbene ciascuno di essi presentasse una certa asimmetria. Se le asimmetrie dei raggi in un dato fascio erano dirette casualmente in più direzioni, allora, nella descrizione di Malus, il fascio poteva essere considerato 'non polarizzato'; se, invece, tali raggi potevano essere raggruppati in insiemi tali che gli elementi di ciascuno presentavano la medesima asimmetria, o anche se fosse stato possibile raggruppare solamente una certa porzione dei raggi, allora il fascio era definito 'parzialmente polarizzato'; se, infine, tutti i raggi presentavano la stessa asimmetria, il fascio era semplicemente considerato 'polarizzato'.
D'ora in avanti si farà riferimento a Malus e a coloro che seguivano le sue teorie come ai 'selezionisti' ‒ nome attribuito loro da Thomas Young (1773-1829) ‒, poiché ritenevano la polarizzazione un processo nel quale, dopo che i raggi di un fascio erano stati selezionati, le direzioni delle loro asimmetrie venivano modificate. Il 'selezionismo', da un lato, non coincideva affatto con la teoria dell'emissione, tant'è vero che gli stessi 'selezionisti' sostennero tale distinzione nella controversia con i loro oppositori, difensori della teoria ondulatoria; d'altro canto, esso non fu neanche considerato ipotetico, proprio perché, come è facile comprendere, dal punto di vista dei principî della teoria ondulatoria esso era del tutto errato. Più precisamente, i principî dei 'selezionisti' poterono essere usati per sviluppare leggi matematiche di immediata applicazione negli esperimenti. Queste leggi non rappresentavano né mere sintesi di risultati sperimentali (sebbene direttamente legate all'uso di particolari tipi di strumenti), né erano ricavate semplicemente dal nulla; al contrario, esse erano dedotte direttamente dai principî fondamentali del 'selezionismo' ed erano incompatibili con le leggi che, per lo stesso genere di fenomeni, erano implicate dai principî dell'ottica ondulatoria. Tuttavia, all'epoca, i due dispositivi che permettevano di esaminare la polarizzazione ‒ il cristallo e lo specchio ‒ dipendevano in modo critico dall'occhio per valutare la presenza, l'assenza o addirittura l'intensità della luce, ma l'occhio, se non aiutato da ausili tecnici, poneva alcune restrizioni in questo genere di esperimenti. In effetti, sino alla fine degli anni Quaranta del XIX sec., tali limitazioni furono sufficienti a precludere qualsiasi esperimento che potesse mostrare la differenza tra le formule ottenute dai 'selezionisti' e quelle ottenute da quanti consideravano la teoria ondulatoria adatta a descrivere i fenomeni più importanti, ossia la riflessione parziale e la rifrazione della luce sulla superficie dei mezzi trasparenti. Del resto, non fu questo l'unico campo nel quale non si riuscì a mettere in evidenza tale differenza.
Malus non visse abbastanza per sviluppare la sua nuova idea, sebbene le sue linee guida fossero abbastanza evidenti a molti suoi contemporanei. Dominique-François Arago (1786-1853), per esempio, capì chiaramente che il lavoro di Malus si basava sulla divisione e sul raggruppamento dei raggi luminosi in insiemi e ciò lo aiutò a interpretare un fenomeno relativo agli anelli di Newton che egli stesso aveva scoperto poco prima della morte di Malus, come è testimoniato da due memorie del 1811: Mémoire sur les couleurs des lames minces e Mémoire sur la polarisation colorée. Arago aveva soltanto 23 anni quando, nel 1809, era stato nominato membro della sezione di astronomia dell'Académie des Sciences dell'Institut de France e, due anni più tardi, il suo lavoro sugli anelli di Newton rappresentava l'unica ricerca della quale potesse ritenersi l'unico artefice. Egli aveva motivo di essere fiero dei propri risultati, dei quali andava geloso. Sin dal suo esordio, infatti, Arago adottò la terminologia e la descrizione della polarizzazione di Malus e, forte di queste idee, decise di farsi strada esaminando la polarizzazione degli anelli di Newton. Scoprì subito un'evidente eccezione alle regole che Malus aveva fornito per la polarizzazione della luce riflessa; eccezione che Malus stesso trovò problematica quando gli fu comunicata da Arago. Nell'analizzare la propria scoperta, comunque, quest'ultimo non abbandonò la descrizione di Malus, ma invece, secondo una normale prassi scientifica, la arricchì operando una nuova distinzione tra la formazione degli anelli e il prodursi della loro polarizzazione. Tutto ciò, come si vedrà fra breve, lo assorbì quasi completamente. Tuttavia, l'11 agosto 1811 egli annunciò un'altra scoperta, riguardante un fenomeno che successivamente sarebbe stato chiamato 'polarizzazione cromatica'; esso consiste nella generazione di figure colorate al passaggio della luce polarizzata attraverso sezioni di cristallo.
Ciò che successe in seguito si dimostrò d'importanza cruciale per l'andamento della rivoluzione all'interno dell'ottica. Tra l'11 agosto del 1811 e l'autunno successivo, Arago continuò a indagare sulle sue nuove ed entusiasmanti scoperte, anche se non sappiamo esattamente quale fosse la sua occupazione in questo periodo.
Gravato da pesanti impegni nell'insegnamento e nell'amministrazione, Malus non ebbe il tempo di riunire i risultati del proprio lavoro per una conferenza pubblica, prima che accadesse un serio imprevisto. All'improvviso Jean-Baptiste Biot (1774-1862) irruppe nel campo di ricerca di Arago e lesse all'Institut una nota sulla polarizzazione cromatica che immediatamente privò quest'ultimo del primato di cui aveva goduto in questo nuovo settore. Arago chiese che fossero esaminate le Notes sur les phénomènes de la polarisation de la lumière (1812) che aveva depositato in precedenza, per dimostrare la sua paternità riguardo a ciò che Biot reclamava come propria scoperta. L'Institut incaricò Burckhardt e Alexis Bouvard (1767-1843) di indagare sulla controversa questione e ad aprile i due annunciarono che la dichiarazione resa da Arago era certamente attendibile. In realtà le note furono pubblicate soltanto quarant'anni dopo, nella raccolta delle opere complete di Arago (Oeuvres de François Arago, 1854-1858), il quale non presentò più relazioni all'Institut fino al dicembre successivo, otto mesi dopo la sfortunata disputa. Nel frattempo, l'attivo Biot lesse all'Institut una memoria straordinariamente lunga sulla depolarizzazione cromatica, seguita sei mesi dopo da una discussione ancora più estesa che ebbe un notevole impatto su molti suoi contemporanei, sia in Francia sia in Inghilterra.
Arago perse il controllo del settore di ricerca che egli stesso aveva inaugurato. A questo proposito vi è qualcosa di sorprendente: le note che egli aveva depositato, e che costrinse a far esaminare dall'Institut, non citavano, se non di sfuggita, la polarizzazione cromatica, che era l'argomento trattato da Biot. Inoltre, le due successive memorie di Arago riguardanti questo campo, così come le sue note inedite dello stesso periodo, presentavano caratteristiche molto diverse dalle memorie di Biot. Infatti, differentemente dal lavoro di quest'ultimo, il materiale di Arago era interamente qualitativo e privo di ogni riferimento ai principî della teoria dell'emissione ed era dedicato quasi del tutto alle caratteristiche generali di ciò che succede ai raggi, piuttosto che alla spiegazione del perché questo accade o, seguendo l'esempio di Malus, alle spiegazioni matematiche del fenomeno. Il contenuto principale delle note, sebbene ancora in forma molto poco sviluppata, consisteva in una teoria generale che cercava di unificare gli effetti di polarizzazione della doppia rifrazione con quelli del passaggio della luce attraverso cristalli sottili con gli effetti dovuti alla riflessione. La teoria era piuttosto vaga e per nulla quantitativa, ma cercava di unificare fenomeni molto differenti e si prefiggeva uno scopo assai generale. Arago non provò mai a ricavarne formule e il suo lavoro non conteneva alcun tipo di dato numerico, né tabelle. Biot, al contrario, nonostante non potesse disporre di alcuno strumento paragonabile alla teoria unificante di Arago, nel suo lavoro sugli effetti cromatici presentò subito alcune formule e i suoi lunghi scritti erano pieni di minuziose tabelle. Arago stava procedendo in modo più tradizionale e qualitativo, cercando principî generali che comprendessero molte classi di fenomeni: formule e tabelle di dati non si adattavano a questo genere di discussioni. Biot, invece, ricorreva a ipotesi assai restrittive, dalle quali cercava con acume di ottenere formule che descrivessero casi specifici: nei suoi primi lavori egli non fece alcuno sforzo per collegare saldamente questi risultati quantitativi a più ampie classi di fenomeni.
Il primo lavoro di Biot in questo campo seguiva dunque il nuovo metodo tipico del tardo Settecento, che nell'ottica era stato solidamente stabilito da Malus. Tale schema, che stava rapidamente diventando un modello di riferimento dell'epoca, si basava sull'attenta presentazione di dati numerici mediante tabelle e sulla conseguente produzione di formule in grado di sintetizzare l'informazione disponibile, con scarso interesse immediato per l'estensione dei risultati ottenuti ad altri fenomeni, anche strettamente correlati. Le differenze tra il lavoro di Biot e quello di Arago, quindi, dipendevano dal mutamento dei canoni della ricerca sperimentale e del modo di esporre i risultati, canoni che erano apparsi per la prima volta e con nettissima evidenza in ottica nel lavoro di Malus.
In seguito, per parecchio tempo, Biot non soltanto giunse a una completa padronanza dell'argomento che Arago aveva introdotto, ma pubblicò anche lunghe e complesse memorie che lo collegavano alla teoria dell'emissione. Il rapido progresso di Biot nel campo della polarizzazione cromatica culminò, nel 1814, nella pubblicazione delle Recherches expérimentales et mathématiques sur les mouvements des molécules de la lumière autour de leur centre de gravité, un libro straordinariamente dettagliato che simboleggiava in modo concreto il sorprendente successo dei suoi sforzi. Per molte persone, quindi, Biot divenne l'esponente più autorevole di quella teoria. Arago non poteva essere entusiasta di una simile situazione: anche prima di questi eventi, egli aveva espresso qualche dubbio sulla teoria dell'emissione, o almeno su numerosi suoi aspetti, e non c'è da stupirsi se iniziò ad avversarlo violentemente. Arago era quindi ben preparato a reagire quando, nel settembre del 1815, ricevette una lunga lettera da parte di Augustin-Jean Fresnel (1788-1827), che gli sottopose proprio il tipo di lavoro che avrebbe potuto eseguire Biot ma che lui, Arago, non era stato capace di realizzare.
Fresnel, laureatosi anch'egli dieci anni prima all'École Polytechnique, aveva reso una breve visita ad Arago a Parigi nel precedente mese di luglio, mentre si stava recando in esilio volontario a casa di sua madre per aver contestato il ritorno dall'Elba di Napoleone Bonaparte, unendosi alla resistenza del duca d'Angoulême. Già da allora egli si stava occupando di ottica e aveva chiesto informazioni sulla diffrazione ad Arago, il quale gli aveva suggerito una lista di autori inglesi, che Fresnel non poté leggere. La lettera di Fresnel ad Arago dell'autunno successivo proponeva una teoria ottica simile a quella che era già stata discussa da Young e conteneva esperimenti precisi, dettagli numerici e formule interessanti. Inoltre, elemento ancora più importante, per Arago essa sembrava illustrare qualcosa che né Biot (né lo stesso Arago) avrebbe potuto assolutamente predire e neanche spiegare: vale a dire che le frange colorate prodotte dalla luce che passava sul bordo di un oggetto sottile ‒ ossia le cosiddette 'frange di diffrazione' ‒, nell'allontanarsi dall'oggetto medesimo, seguivano una traiettoria iperbolica. Sebbene, nella lettera ad Arago, Fresnel stesso non enfatizzasse affatto questa scoperta, Arago ne fece invece tesoro e, allo stesso tempo, incoraggiò Fresnel a migliorare le osservazioni, per rendere la scoperta inattaccabile. Egli tra l'altro notò che la teoria di Fresnel era essenzialmente la stessa di quella sostenuta da Young, anche se non si rese conto che quest'ultimo aveva già messo in evidenza l'andamento iperbolico (che peraltro era stato già considerato come una proprietà empirica generale da Newton nell'Opticks). Ciò che colpì maggiormente Arago non fu tanto l'euforia per una nuova scoperta, quanto l'opportunità di farne uso per riparare ai torti recenti che aveva subito per mano di Biot; Fresnel era invece profondamente turbato dalla priorità di Young e questo, tutto sommato, lo stimolò a sforzi ancora maggiori: le loro rispettive inquietudini, per una volta, si erano felicemente incontrate.
L'interferenza e la diffrazione
Nel 1799, in Inghilterra, Young aveva dato inizio a una serie di pubblicazioni mediante le quali si ampliava la capacità predittiva di teorie quantitative che trattavano la luce come perturbazione di un mezzo materiale. Come Leonhard Euler (1707-1783) prima di lui, egli associava il colore della luce alla frequenza dell'onda luminosa, ma si spinse ben oltre nell'applicare tale assunzione. Medico di formazione, nel corso dei suoi studi Young si era profondamente interessato all'acustica, specialmente ai fenomeni di sovrapposizione, arrivando a enunciare il 'principio d'interferenza', secondo il quale onde della stessa frequenza generate dalla medesima sorgente producono, incontrandosi, figure spaziali regolari di intensità variabile. Questo principio non era stato concepito per ogni genere d'onda e si può affermare che lo studio generale dell'interferenza delle onde ebbe inizio proprio grazie a Young, anche se questi non lo affrontò estesamente al di fuori dell'ottica. Egli dovette risolvere molti problemi difficili, compreso quello delle condizioni di coerenza che rendevano possibile l'esistenza stessa di interferenza spaziale rilevabile. Anche il 'principio di sovrapposizione', secondo il quale le onde si combinano linearmente ‒ presupposto necessario per il principio di interferenza‒, all'epoca si presentava abbastanza problematico e dovette essere sviluppato e appoggiato da Young.
Lo scienziato inglese applicò il principio d'interferenza sia alla diffrazione della luce da parte di un corpo sottile sia alla luce che attraversa due fenditure, sebbene in quest'ultimo caso sembra che non avesse eseguito misurazioni accurate. Egli spiegò la struttura delle frange che si osservano in questi fenomeni calcolando la differenza di cammino tra una coppia di raggi originati da un'unica sorgente, ma non eseguì i calcoli utilizzando le onde vere e proprie, bensì assegnando una periodicità al raggio luminoso, che in tal modo mantenne un ruolo molto importante nell'ottica di Young. Benché egli avesse sufficiente familiarità con il lavoro di Huygens, non fece ricorso alla sua riduzione dei raggi ad artifici puramente matematici, in quanto tale concezione era legata al principio di Huygens, che Young considerava difficile da accettare.
In ogni caso l'ottica di Young non ebbe alcun riscontro immediato e generale; in effetti, il suo principio di interferenza era tanto difficile da assimilare che non fu subito applicato allo studio di nuovi fenomeni (famosa fu la reazione di Henry Brougham, che si oppose con veemenza al sistema basato sulle onde di Young come alternativa al sistema delle particelle ottiche di Newton e rifiutò lo stesso principio di interferenza, anche solanto come legge matematica applicata ai raggi). Gli scienziati che studiavano l'ottica erano, per la maggior parte, più interessati alla fisica che alla matematica dei fenomeni luminosi e in questo campo l'etere di Young non poneva meno problemi qualitativi del sistema delle particelle.
In Francia il lavoro di Young, sebbene non avesse stimolato un'ampia discussione, era comunque sufficientemente conosciuto, tanto da far sì che Arago nominasse Young, tra gli altri studiosi di ottica, in una lettera a Fresnel dell'estate del 1815. Arago accompagnò Fresnel a Parigi e partecipò con lui alla realizzazione di nuovi esperimenti che sembravano mettere in dubbio alcuni aspetti della teoria dell'emissione, e dunque il valore degli studi di Biot. Questa fu l'origine di un famoso esperimento condotto con l'ausilio di uno specchio: l'interferenza si manifestò anche tra raggi che non passavano vicino al bordo di oggetti e che, quindi, presumibilmente non potevano essere soggetti alle forze che, altrimenti, avrebbero potuto spiegare la formazione delle frange. Il punto di vista di Fresnel conobbe notevoli sviluppi nei tre anni successivi; il 17 marzo 1817, quando l'Académie des Sciences di Parigi annunciò pubblicamente che aveva deciso di istituire un premio sul problema della diffrazione, Fresnel aveva ormai modificato profondamente la sua concezione originaria, ed era passato da una teoria basata sul confronto di coppie di raggi, a una teoria che si fondava sui fronti d'onda, sul principio di Huygens e su elaborati metodi di integrazione.
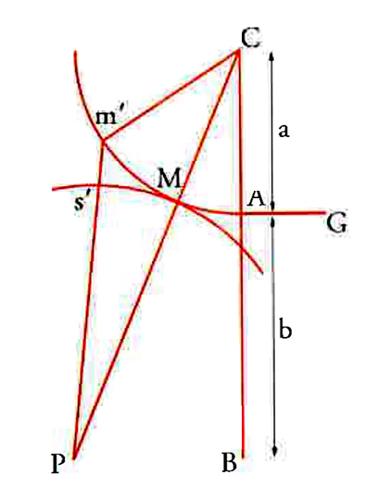
La fig. 3 è ricavata da un diagramma disegnato dallo stesso Fresnel per illustrare il procedimento con cui studiare l'illuminazione prodotta su uno schermo posto al di là di un diffrattore; C rappresenta la sorgente di un fronte a simmetria sferica AMm′, parzialmente intercettato da uno schermo AG. Riadattando il principio di Huygens, Fresnel pensava che ogni punto del fronte emettesse un'onda sferica, ma con un'ampiezza che decresceva all'aumentare dell'inclinazione della linea che congiunge il punto stesso alla sorgente C. Chiamando z la distanza da M lungo AMm′, Fresnel riuscì a rappresentare l'ampiezza Ψ di una perturbazione di lunghezza d'onda λ, che arrivava al generico punto P di un altro schermo, nella seguente forma:
dove
da cui
che si decompone in
Da ciò Fresnel riuscì a dimostrare che il quadrato della risultante di tutte le onde secondarie generate lungo il fronte AMm′, raccogliendo i termini in coseno e in seno, poteva essere ricondotto alla seguente somma:
dove compaiono i cosiddetti 'integrali di Fresnel'.
Due furono le difficoltà principali che Fresnel incontrò a proposito di questo risultato. Una riguardava il problema di come stabilire un sistema di coordinate sufficientemente generale per poter effettuare il calcolo. Nel caso più semplice, la questione si poneva quando l'oggetto diffrattivo o l'apertura avevano due bordi, circostanza che, in pratica, rendeva necessario estendere il calcolo a tutti i punti di una superficie. L'altra difficoltà, che si presentava in ogni caso compreso quello del piano seminfinito ‒ dove era presente soltanto un bordo e dove, di conseguenza, la superficie appena menzionata si riduceva a una linea ‒, consisteva semplicemente nel problema di come calcolare meglio i valori degli integrali. Fresnel tentò la strada più rapida, ossia l'integrazione numerica, invece che ricorrere, per esempio, alle serie, anche se in seguito Augustin-Louis Cauchy (1789-1857) ottenne serie divergenti per questi integrali. Mediante una quantità sbalorditiva di calcoli, egli riuscì a tabulare gli integrali da 0 a 5 in passi di 0,1, con un metodo che sarà scoperto nelle sue lettere pubblicate postume (i suoi errori di calcolo erano, in media, soltanto di 0,0003 e le differenze tra i suoi valori e quelli più accurati calcolati con le serie ottenute in seguito da Cauchy erano solamente di 0,0006).
All'epoca non era affatto inusuale, nelle equazioni che descrivevano fenomeni fisici, la comparsa di soluzioni che potevano essere calcolate soltanto per mezzo di sviluppi in serie o attraverso integrazioni numeriche. Queste tecniche erano state introdotte nei problemi di astronomia e presto furono estese a questioni riguardanti l'elasticità e il flusso di calore. Nondimeno, nel caso che stiamo esaminando risultava del tutto insolita la loro presenza come espressione, a livello fondamentale, della fisica sottostante: gli integrali di Fresnel, a differenza dei polinomi di Legendre in astronomia o delle serie di Fourier nei processi termici, non erano stati affatto ottenuti come soluzioni di particolari equazioni differenziali; al contrario, erano stati introdotti da Fresnel senza che egli avesse trattato né equazioni alle derivate parziali né meno che mai i metodi e le tecniche per risolverle partendo da opportuni insiemi di condizioni al contorno. Si potrebbe affermare che Fresnel abbia trovato la soluzione di quella che in seguito sarebbe stata chiamata l''equazione d'onda ridotta' o, dopo il 1860, 'equazione di Helmholtz', senza avere alcuna idea di quale fosse l'equazione. Questo aspetto dell'ottica ondulatoria di Fresnel era in netto contrasto con un'ottica in cui le immagini fisiche erano fondate su forze e particelle, perché in quel caso le equazioni differenziali fondamentali erano ben conosciute e, per di più, si trattava di equazioni ordinarie.
Naturalmente, in quest'ultimo caso, non vi era alcun modo di affrontare quello che, in sostanza, non era altro che un problema a n corpi; di conseguenza, in modo paradossale, l'unica via per trattare matematicamente la diffrazione richiedeva un metodo nel quale la fisica sottostante e la matematica fondamentale collegata rimanevano completamente sconosciute, mentre lo schema alternativo, nel quale la fisica era invece compresa benissimo, non conduceva ad alcuna matematica utilizzabile. Eppure fu proprio questa notevole differenza a favorire l'assimilazione dei metodi matematici di Fresnel, e successivamente dei concetti fisici che a questi si accompagnavano, giacché nessun membro della commissione che assegnò il premio sulla diffrazione‒ comprendente Laplace e Siméon-Denis Poisson, tra i massimi sostenitori della teoria corpuscolare ‒ obiettò che gli integrali di Fresnel non dovessero essere sfruttati come espressioni fenomenologiche di ciò che avveniva empiricamente. Nella restante parte del secolo, scienziati come Cauchy, George Green, George G. Stokes, Hermann von Helmholtz, John W. Strutt (lord Rayleigh), Gustav Robert Kirchhoff e Arnold Sommerfeld, per ricordarne solamente alcuni, si sarebbero cimentati nella creazione di una teoria fisica, sia per il suono sia per la luce, basata sull'equazione delle onde alle derivate parziali in tre dimensioni e sulle sue utili soluzioni, proprio nel tentativo, potremmo dire, di scoprire di quale equazione fossero soluzioni le formule originali di Fresnel e come, a posteriori, potessero essere giustificate o modificate.
Laplace, Poisson e persino Biot non furono eccessivamente disturbati dal successo ottenuto da Fresnel nello sviluppo delle formule per la diffrazione, principalmente perché non la consideravano un argomento fondamentale nell'ottica: benché importante, ai loro occhi le sue applicazioni erano limitate a casi piuttosto marginali, come ciò che succede in prossimità dei bordi di un oggetto oppure ai raggi luminosi che, in particolari situazioni, interagiscono tra loro. Essi non ritenevano necessario ricostituire su nuove basi tutta l'ottica, perché continuavano a trattare il raggio luminoso come un elemento fondamentale e irriducibile e a rifiutare le onde: sino alla fine degli anni Trenta del XIX sec., fu abbastanza comune che si accettassero le formule di Fresnel per la diffrazione ‒ almeno per una coppia di raggi interagenti ‒, ma se ne respingesse, allo stesso tempo, la teoria ondulatoria. Ciò, tuttavia, non significa che la teoria dell'emissione conservasse di per sé la sua forza, ma piuttosto che era stata tracciata una tacita distinzione tra la teoria dell'emissione e l'ipotesi che i raggi fossero singoli oggetti numerabili. Sicuramente il lavoro di Fresnel aveva sollevato molti dubbi sulle particelle di luce, ma, per parecchio tempo, non causò altrettante incertezze sulla realtà fisica dei raggi luminosi.
Una nuova ottica matematica e i dibattiti onda-particella
Per la maggior parte degli anni Dieci del XIX sec., la diffrazione non era stata un argomento particolarmente stimolante nel panorama della ricerca ottica. L'attenzione degli studiosi si era concentrata prevalentemente sulla polarizzazione, e in particolare sulla polarizzazione cromatica, che era stata alla base della fama scientifica di Biot dopo che quest'ultimo l'aveva, per così dire, sottratta dalle mani di Arago nel 1811. Pare che sia stato Arago, a metà luglio del 1816, a suggerire a Fresnel di esaminare le frange prodotte dall'interferenza dei due fasci polarizzati che emergono da un cristallo. Il primo lavoro di Fresnel sulla polarizzazione cromatica, basato sul principio di interferenza, non apportava alcun miglioramento alla teoria di Biot, principalmente perché, all'epoca, lo stesso Fresnel non sapeva come calcolare la risultante di più di due raggi che interferivano; sebbene avesse proposto questo studio per la pubblicazione, per cinque anni non ebbe alcuna risposta da parte di Arago e André-Marie Ampère (1775-1836), ai quali era stato richiesto un parere.
La relazione di Arago, quando finalmente apparve, si rivelò una polemica nei confronti di Biot; forse Arago ne aveva ritardato di cinque anni la stesura proprio per studiare come il lavoro di Fresnel potesse essere utilizzato per screditare Biot, il quale, a sua volta, appena ebbe modo di leggere gli articoli su cui si presumeva che Arago avesse basato il proprio resoconto, capì subito che la manovra era stata attuata da quest'ultimo. Biot notò che Fresnel non si era proposto come obiettivo di fondo del suo lavoro di dimostrare che ciò che egli chiamava "la mia teoria della polarizzazione mobile" è, in molti punti, insufficiente e inesatta, e lamentò che la relazione di Arago "devia dalle regole generalmente stabilite dalle società scientifiche per garantire l'equità dei loro giudizi". La spiacevole, e a tratti molto aspra, controversia che seguì coinvolse in parte lo stesso Fresnel, che aveva scritto le sue memorie originali non per attaccare Biot, ma piuttosto per presentare la propria teoria. Sebbene consapevole della strumentalizzazione operata da Arago, nella foga della sua replica Biot mise in dubbio alcuni aspetti del lavoro di Fresnel, offrendo in tal modo il fianco a un potente attacco da parte di quest'ultimo. La disputa con Arago e, successivamente, l'incapacità di Biot di chiarire la natura della sua teoria negli scambi di opinioni con Fresnel segneranno un'epoca nella storia dell'ottica. Appena due anni dopo l'assegnazione del premio a Fresnel per la sua memoria sulla diffrazione, l'Académie des Sciences ordinò che fosse stampato lo studio di Fresnel sulla polarizzazione cromatica, nonostante le obiezioni pubbliche ed esplicite di Biot. I membri dell'Académie non accettarono la relazione di Arago, ma, apparentemente, soltanto perché egli non insistette; in ogni caso fu pubblicata quasi subito nelle "Annales de chimie et de physique" dirette da Arago stesso.
Più che la sua spiegazione della diffrazione, fu la teoria finale di Fresnel sulla polarizzazione a rompere in maniera radicale con l'ottica 'selezionista'. Come si è osservato in precedenza, in Francia si considerava la polarizzazione un processo spaziale essenzialmente statico, nel quale i raggi di ciascun gruppo presentavano le loro asimmetrie allineate tra loro. Il tempo non rientrava in questo schema e, di conseguenza, un fascio osservabile di luce non polarizzata era sempre semplicemente non polarizzato, a prescindere da quanto piccolo fosse l'intervallo di tempo nel quale avveniva l'osservazione. Per parecchi anni Fresnel aveva trovato estremamente difficile rinunciare alla nozione secondo la quale la luce comune non dovesse presentare alcun segno di asimmetria, benché non potesse ricorrere al conteggio di raggi per spiegare perché questo avvenisse. Egli, dunque, si sforzò di costruire uno schema nel quale la polarizzazione era dovuta a una combinazione, fissa nel tempo, di oscillazioni orientate: una lungo la normale al fronte, l'altra perpendicolare a essa. Nella luce comune la componente trasversale scompariva totalmente, nella luce completamente polarizzata spariva la componente longitudinale. Questa, come la sua controparte basata sui raggi, era un'immagine spaziale intrinsecamente statica. Fresnel non riuscì a costruire una struttura quantitativa su simili basi e quindi, nel 1821, mise in movimento questa immagine statica.
Il nocciolo della nuova concezione di Fresnel della polarizzazione riconduceva il fenomeno alla variazione (o all'immutabilità) nel tempo di una grandezza orientata, il cui quadrato determinava l'intensità ottica. Questa grandezza deve sempre giacere sul fronte d'onda (e perciò nei mezzi otticamente isotropi è trasversale al raggio); nella riflessione e nella rifrazione essa può subire una scomposizione, con le componenti che sono sottoposte a effetti differenti, a seconda che appartengano al piano di riflessione oppure siano a questo perpendicolari. La luce comune consiste in una rotazione più o meno casuale e in un cambiamento di ampiezza di questa oscillazione orientata che avvengono nel tempo, e non, come originariamente credeva Fresnel, in una perturbazione (longitudinale) spazialmente fissa. I raggi luminosi sono astrazioni matematiche: essi sono semplicemente le direzioni che uniscono il centro dell'onda al fronte. In un senso puramente analitico, è possibile collegare un raggio all'asimmetria del fronte nel punto che contiene il raggio stesso. Si può quindi sostenere, se si vuole, che nella teoria ondulatoria un raggio singolo è polarizzato, perché la polarizzazione si riferisce all'asimmetria in un punto del fronte e a ognuno di questi punti corrisponde un solo raggio; tuttavia ‒ e questo è un tratto distintivo della teoria ondulatoria ‒ poiché i raggi sono considerati semplicemente come linee rette, non è possibile contarli: un fascio luminoso non è un insieme di raggi discreti, e perciò non lo si può dividere alla maniera di Malus. L'ampia divergenza tra le due concezioni rendeva particolarmente difficile, a persone che avevano una diversa concezione della polarizzazione, comunicare i rispettivi risultati sperimentali senza un inevitabile residuo di ambiguità che poteva portare a controversie.
Fresnel derivò immediatamente sensazionali implicazioni dalla sua nuova teoria sulla polarizzazione. Egli produsse, per cristalli birifrangenti, nuove superfici che collegavano la polarizzazione alle velocità dell'onda, e quindi alle direzioni dei raggi. Queste superfici, che Fresnel ottenne soltanto dopo parecchi tentativi e molto lavoro, aprirono un nuovo e inesplorato dominio per l'analisi fisica e matematica, subito avidamente esplorato in Inghilterra, Irlanda e Francia. Per esempio, Humphrey Lloyd (1800-1881), in Irlanda, confermò l'esistenza del sorprendente fenomeno della rifrazione conica, che William R. Hamilton (1805-1865) aveva previsto teoricamente; in Inghilterra, George B. Airy (1801-1892) esaminò matematicamente il particolare tipo di doppia rifrazione che si produce quando la luce passa attraverso un quarzo inclinato rispetto al suo asse ottico, rielaborando con finezza la nuova matematica di Fresnel per la polarizzazione. Nei tardi anni Trenta e negli anni Quaranta del XIX sec. si assistette inoltre ad accesi dibattiti tra i sostenitori della vecchia e della nuova ottica, che spesso sollevavano questioni concernenti i fondamenti fisici delle due teorie.
La maggior parte dei sostenitori dell'ottica ondulatoria nel criticare la teoria avversaria prendeva di mira direttamente le forze e le particelle che ne erano a fondamento. Lloyd, per esempio, nel Report on the progress and present state of physical optics (1834) sosteneva che la teoria dell'emissione fosse essenzialmente priva di utilità perché "è un aggregato di principî separati" che riguardano il comportamento delle particelle ottiche. Secondo Lloyd, l'ottica ondulatoria era invece in grado di generare una nuova fisica, comprendente la riflessione e la rifrazione parziali, nelle quali parte della luce che investe un corpo trasparente lo attraversa, mentre l'altra parte è riflessa. In questo caso, Lloyd spiegò che la fisica di Biot delle particelle ottiche, che egli stesso aveva sviluppato in modo abbastanza dettagliato, semplicemente non era in grado di fornire alcuna formula, né alcunché di utile. Fresnel, secondo Lloyd, si trovava invece in una situazione migliore: a differenza dei teorici dell'emissione, che dalle loro forze e dalle loro particelle non potevano dedurre formule, Fresnel poteva ricavarne dalle proprietà del mezzo materiale, o etere, nel quale si supponeva esistessero le onde.
La sintesi con la quale Lloyd intendeva spiegare la potenza della teoria ondulatoria e la sagacia intuitiva dei suoi sostenitori non convinse alcun rappresentante dell'opposto schieramento che si fosse lungamente impegnato nella ricerca. Neppure le simili osservazioni di William Whewell, contenute nell'History of the inductive sciences from the earliest to the present time del 1837, produssero alcuna conversione, perché, negli anni in cui l'ottica ondulatoria prendeva forma, era ancora possibile pensare nella vecchia maniera basata sui raggi luminosi, dato che il nuovo sistema doveva essere adeguatamente elaborato in pubblicazioni e prove di laboratorio. Durante gli anni Trenta del XIX sec., i fautori della teoria ondulatoria produssero strumenti, sia teorici sia pratici, che permisero loro di stabilire una dinamica tradizione di ricerca comprendente la fisica dell'etere. Per ragioni che non avevano molto a che fare con un'astratta superiorità della loro teoria, essi controllavano anche importanti riviste e costruirono una rete organizzata nelle università e, in particolar modo, nelle associazioni professionali. I sostenitori dei raggi, invece, non si dimostrarono altrettanto intraprendenti. A partire dagli anni Quaranta, erano stati realizzati innummerevoli dispositivi per lo studio delle onde e la stessa strumentazione basava sempre più il proprio funzionamento sul comportamento di fronti e di fasi. Tutte queste dotazioni di laboratorio non offrivano spazi di ingresso ai fisici dei raggi, per i quali fronti e fasi non possedevano un significato particolare. La maggior parte delle ricerche nel campo dell'ottica andò progressivamente concentrandosi sui metodi ondulatori, tanto che si sarebbe potuto affermare che la fisica dei raggi era obiettivamente debole rispetto a quella delle onde.
La struttura fisica dell'ottica ondulatoria alla metà del XIX secolo
Nell'ottica dei raggi, i concetti di 'forza' e 'particella' non servirono tanto a dar vita a una nuova matematica e a nuovi esperimenti, quanto piuttosto a garantirle un fondamento fisico. In maniera simile, nell'ottica ondulatoria l'etere servì più che altro a discernere e a giustificare anziché a produrre nuova fisica. Per esempio, Fresnel, nell'elaborare una matematica adatta allo studio della diffrazione, utilizzò l'etere in un primo tempo soltanto per convincersi del fatto che la luce non dovesse essere pensata come un insieme di raggi fisicamente distinti. Si potrebbe facilmente mostrare persino che lo scarso uso che egli fece allora dell'etere gli impedì di accettare, per circa cinque anni, il fatto che il principio di Huygens potesse tornare utile per interpretare la diffrazione. Quando sviluppò la sua teoria finale, si servì dell'etere principalmente per controbattere quelle che, a lui, apparivano come assurdità fisiche conseguenti all'uso del concetto di 'particella ottica', ma quasi certamente non se ne servì per ricavare una teoria matematica che, almeno in questo campo, poté nascere nonostante l'immagine fisica che Fresnel aveva dell'etere.
Considerazioni analoghe valgono a maggior ragione per il lavoro di Fresnel sulla polarizzazione. Per oltre cinque anni, egli fu ostacolato dall'incapacità di distinguere differenti tipi di propagazione di onde associandone soltanto uno alla polarizzazione. Il vecchio modo di concepire la polarizzazione ‒ che Fresnel faticò ad abbandonare ‒ portava a immaginare onde di pressione nell'etere, ma le asimmetrie dei fenomeni di polarizzazione richiedevano soluzioni diverse: l'unica possibilità, come Fresnel presto capì, era l'ipotesi di un'onda trasversale. Tutto ciò sollevava problemi ora ben noti (per es., come i pianeti potessero attraversare una sostanza che permettesse tale genere di onde), tuttavia in questi primi anni tali istanze non ebbero effetto su Fresnel, che non capiva ancora come produrre una teoria unificata per la polarizzazione nemmeno considerando onde di pressione. Soltanto dopo aver concepito l'idea, del tutto nuova, che l'asimmetria del fronte d'onda potesse cambiare direzione mentre il fronte si propagava liberamente, Fresnel pervenne a una descrizione davvero originale. E in questo sviluppo ‒ come era avvenuto nel caso della diffrazione ‒ l'etere risultò essere più una pietra d'inciampo che un aiuto alla costruzione.
Si potrebbe obiettare che almeno in un caso Fresnel fece ricorso all'etere come a un modello per produrre una nuova teoria matematica, vale a dire nell'introduzione della superficie d'onda per cristalli biassici: nel resoconto finale, scritto da Fresnel nel 1824, si può leggere di un'elaborata struttura per l'etere, che, a quanto sembra, permetteva di generare le complesse serie di superfici che condussero Fresnel a generalizzare la costruzione di Huygens. Dopo tutto, fu questa generalizzazione a portare Hamilton e Lloyd alla scoperta della rifrazione conica, che Whewell e altri celebrarono come evidente dimostrazione della potenza della teoria ondulatoria.
Persino in questo caso, tuttavia, ci si sbaglierebbe nel considerare creativa la dinamica dell'etere, perché Fresnel usò l'immagine di un etere elastico soltanto per giustificare fisicamente l'asserzione che le velocità d'onda che corrispondevano all'oscillazione in una data direzione potessero dipendere da tale direzione. Su questa asserzione, ma soltanto su questa, egli costruì poi la sua teoria della doppia rifrazione, che lo condusse, dopo parecchi passi falsi e intenso lavoro, a introdurre la 'superficie di elasticità' (sostanzialmente, con linguaggio moderno, l''indicatrice ottica'); da questa seguì la cosiddetta 'superficie normale' per le velocità del fronte e quindi la 'superficie d'onda', in una sequenza nella quale, come si vede, l'etere non appare in alcun modo.
Comunque, nella versione finale pubblicata, Fresnel suggerì un fondamento per la dinamica dell'etere che, sebbene carente, come certamente egli sapeva, sembrava almeno fornire una base fisica per la complicata serie di passaggi derivanti dalla superficie di elasticità, basata, dopo tutto, essa stessa sull'etere. Qual era, dunque, questo fondamento? L'etere, per Fresnel (ma anche per molti di coloro che si occuparono in seguito di ottica), era un sistema di masse puntiformi che esercitavano forze repulsive centrali le une sulle altre. Quasi certamente questa idea era stata presente per molti anni nella mente di Fresnel, il quale, nel fornire gli elementi per dotare di fondamento le proprietà ondulatorie di tale sistema, seguì una strada che avrebbe rappresentato un'utile alternativa alle teorie che avrebbe elaborato Cauchy negli anni Trenta del XIX secolo.
Fresnel sviluppò la sua dinamica dell'etere su due livelli, uno strettamente legato alle richieste immediate della teoria ottica e l'altro con il compito di fornire al precedente un fondamento. Quest'ultimo livello della trattazione permetteva a sua volta due affermazioni: la reazione vettoriale allo spostamento di ogni dato punto era una funzione lineare delle componenti dello spostamento stesso; i coefficienti che regolavano la reazione erano costanti. Da ciò Fresnel riuscì a introdurre la superficie di elasticità e tuttavia per dimostrarne l'esistenza adottò l'ipotesi piuttosto dubbia che la reazione generata dallo spostamento di un punto dato potesse essere calcolata mantenendo fisso ogni altro punto. Egli stesso dubitava fortemente che questa assunzione fosse ragionevole, tuttavia era l'unica che gli permise di ottenere la superficie di elasticità mediante una qualche sorta di dinamica dell'etere.
Ciò mostra nuovamente come, secondo Fresnel, non fosse necessaria la conoscenza del comportamento dell'etere per formulare la sua teoria ottica, compresa la parte che più direttamente si ripercuoteva sulle proprietà dell'etere, vale a dire quella relativa alla doppia rifrazione. Tuttavia, da ciò non si devono trarre conclusioni affrettate: senza l'etere, per gli scienziati dell'epoca sarebbe stato estremamente difficile ricorrere alla teoria ondulatoria e non avvertire l'assenza di un fondamento fisico solido, mentre l'alternativa basata su insiemi di raggi possedeva, se non altro, una base fisica solida nell'immagine della particella ottica governata da forze. Anzi, una delle critiche che spesso i teorici delle onde muovevano ai loro predecessori era che l'etere avrebbe potuto rappresentare un fondamento fisico molto più valido di quanto non lo fosse la particella ottica; in parte perché, come Fresnel aveva cominciato a mostrare e come Cauchy avrebbe provato con molto maggior rigore, dalla struttura meccanica dell'etere si potevano trarre teoremi e formule, non soltanto nel caso della doppia rifrazione.
Non è lecito pensare che, se anche fosse vissuto più a lungo, Fresnel avrebbe continuato a lavorare grosso modo come aveva fatto nella costruzione della teoria ondulatoria tra il 1815 e il 1827, anno della sua morte. Al contrario, sia il lavoro pubblicato, sia il manoscritto testimoniano quanto per lui l'etere stesse diventando importante per l'elaborazione della teoria: egli aveva cominciato a guardare all'etere come a un'ipotesi per fornire spiegazioni e formule per quei fenomeni che sfuggivano ai principî fondamentali della teoria ondulatoria. Secondo Fresnel, un fenomeno in particolare sembrava richiedere un'accurata conoscenza del comportamento dell'etere: la dispersione della luce. Nel 1823, infatti, egli avanzò una spiegazione qualitativa della dispersione, che si basava sulla dinamica dell'etere e che avrebbe avuto enorme influenza negli anni Trenta, soprattutto su Cauchy. La dispersione, secondo tale spiegazione, dipendeva dalle distanze e dalle forze di mutua repulsione esistenti tra le particelle dell'etere, con la chiara implicazione che, per trattare quantitativamente la dispersione, la teoria dovesse dare una sistemazione conveniente ai due fattori in questione ‒ distanza e forza. Nel 1827 Cauchy, in un diverso contesto, iniziò a occuparsi esattamente di tale questione. La matematica per la dispersione che egli mise a punto permise lo sviluppo di un programma di ricerca che fu seguito in Francia, Gran Bretagna e Germania a partire dagli anni Trenta ‒ e, in Germania e in Francia, sino agli anni Cinquanta dell'Ottocento‒, al punto che, in quegli anni, la teoria ottica divenne per qualche tempo quasi sinonimo di dinamica dell'etere di Cauchy.
I contributi di Cauchy
La prima formulazione di una dinamica dell'etere in ottica da parte di Cauchy risale al 1830; all'epoca, egli era ben preparato a capire le potenzialità dei suggerimenti di Fresnel e provvide immediatamente a correggere la grave lacuna che la dinamica di quest'ultimo presentava, ossia l'assunzione che il reticolo dell'etere rimanesse essenzialmente rigido, anche quando uno dei suoi elementi fosse stato spostato. Assumendo soltanto che lo spostamento u fosse piccolo in confronto alle distanze tra i punti del reticolo, Cauchy pervenne piuttosto facilmente a un'equazione differenziale alle differenze finite per il moto di un arbitrario elemento del reticolo, in funzione delle differenze tra i suoi spostamenti e quelli di ogni altro elemento nel reticolo stesso. Questa equazione, che incontrò una tale diffusione negli articoli e nei testi di ottica del decennio successivo che dovrebbe essere chiamata 'canonica', può essere riscritta nel seguente modo:
trattando l'operatore gradiente come una variabile.
In questa equazione G e H sono operatori formati da serie di potenze dell'operatore gradiente, mentre Δα è un operatore vettoriale le cui componenti sono le derivate parziali rispetto alle componenti del gradiente stesso. Elaborare una teoria della dispersione a partire da equazioni simili non fu un compito facile, come attesta l'enorme mole di calcoli e di approssimazioni che Cauchy pubblicò nel 1836. In sostanza, dapprima egli impose condizioni di simmetria al reticolo, calcolò quindi le differenze negli spostamenti servendosi di una serie di Fourier. Dopo un'immensa e noiosa quantità di lavoro, la montagna di calcoli elefantiaci partorì qualcosa che alcuni tra i suoi contemporanei considerarono un topolino: la serie per l'indice di rifrazione, che da allora sarà conosciuta come 'serie di Cauchy'. Sebbene tale serie sembrasse funzionare empiricamente, cosa questo significasse precisamente rimaneva una questione aperta, poiché le costanti libere erano così numerose che il fisico Samuel Earnshaw (1805-1888) riteneva che essa rappresentasse in fondo soltanto un'identità. Inoltre vi era più di un modo per ricavare una formula di dispersione dalla struttura generale di Cauchy e non erano nemmeno chiare le implicazioni fisiche di tutta quella manipolazione di costanti. Tuttavia, non c'è alcun dubbio sul fatto che molti fra i contemporanei di Cauchy ‒ compreso Hamilton ‒ rimasero profondamente impressionati dal fatto che quest'ultimo fosse riuscito a ottenere una formula di dispersione.
Gli articoli sulla teoria di Cauchy furono oggetto di attente analisi e riflessioni, particolarmente in Gran Bretagna. La struttura teorica che egli aveva elaborato, seppure avesse permesso di ricavare ‒ a fatica ‒ la legge per la dispersione, da altri punti di vista era quasi completamente priva di interesse e addirittura estranea a tutto ciò che riguardava la sperimentazione: Cauchy utilizzò la superficie d'onda di Fresnel come una sorta di laboratorio intellettuale, per mezzo del quale sottoporre a verifica i propri risultati, ma relativamente all'aspetto sperimentale non emerse nulla di nuovo. Il tutto rimase un esercizio al più alto livello di costruzione di modelli astratti, e la situazione rimase immutata fino a quando James MacCullagh (1809-1847) ne individuò il punto debole.
Molti anni prima, Arago aveva scoperto il fenomeno della rotazione ottica, che aveva contribuito allo sviluppo di una nuova comprensione della polarizzazione da parte di Fresnel. In linea di principio, il reticolo di Cauchy per l'etere avrebbe dovuto abbracciare tutti i fenomeni ottici, compreso questo, ricorrendo a opportune scelte delle costanti che descrivevano il reticolo in equilibrio. Le equazioni della struttura matematica erano così complicate e difficili che sembrò verosimile che la loro validità si estendesse a tutta l'ottica, visti in particolare i successi ottenuti da Cauchy sia nel caso della dispersione sia in quello della doppia rifrazione. Tuttavia nel 1841 MacCullagh dimostrò in modo inequivocabile che la struttura stessa delle equazioni era in contraddizione con la rotazione ottica: il tipo di reticolo ‒ o meglio, il tipo di matematica creata da Cauchy per il reticolo ‒ falliva dunque inesorabilmente nella descrizione di un fenomeno che aveva una grande importanza.
Dal punto di vista di MacCullagh ciò rappresentava l'atto conclusivo di quello che, in ogni caso, egli riteneva fosse un argomento di ricerca molto poco opportuno: la costruzione di immaginarie strutture in grado di inquadrare fenomeni che erano già perfettamente conosciuti (al pari di Earnshaw, MacCullagh non riteneva che la legge di dispersione fosse molto di più di un'interpolazione e la considerava qualcosa che aveva quasi lo stesso valore empirico di uno sviluppo in serie di Taylor). In Gran Bretagna, la struttura di Cauchy sparì dunque rapidamente dalla scena, ma non soltanto a causa del colpo infertogli da MacCullagh. In effetti Cauchy stesso, e con lui molti suoi sostenitori francesi (e più tardi tedeschi), riteneva che essa potesse essere salvata; e nel 1847, sei anni dopo l'invettiva matematica di MacCullagh, François-Napoléon Moigno (1804-1884) scrisse infatti un imponente Répertoire d'optique moderne (1840-1861) che, in sintesi, era una lunga difesa delle meraviglie che Cauchy aveva realizzato, nella quale la rotazione ottica era trattata semplicemente come un piccolo e fastidioso problema, che poteva essere rimosso. Effettivamente il problema fu superato, ma soltanto creando una nuova struttura matematica per il reticolo, che al confronto faceva apparire le precedenti equazioni di Cauchy come l'essenza della semplicità.
Fu proprio per risolvere questo problema che Cauchy creò la teoria matematica delle strutture periodiche, utilizzando concetti che erano stati da poco introdotti nella cristallografia da Auguste Bravais (1811-1863). In termini delle sue vecchie equazioni, ciò significava che le costanti dovevano essere trattate come funzioni periodiche della posizione. Cauchy fu molto abile a dimostrare, trattando con grande perizia il vasto insieme di relazioni implicate dalla periodicità, che ora comparivano termini di ordine inferiore che permettevano di descrivere la rotazione ottica. Ciò avvenne nel 1850, quasi un decennio dopo la critica di MacCullagh, quando ormai la profonda influenza esercitata in passato dalla concezione di Cauchy del reticolo dell'etere era completamente venuta a mancare in Gran Bretagna, in Francia stava diventando meno popolare, mentre continuava a esserlo in Germania, paese nel quale soltanto allora si iniziava a dare un contributo sostanziale all'ottica matematica.
Come già detto in precedenza, i modelli fisici che interessavano i teorici dell'etere ottico, così come i problemi che questi ultimi affrontavano, avevano le loro origini nel lavoro di Fresnel; ma per la prima volta si tentò di risolvere in maniera quantitativa i modelli stessi piuttosto che interessarsi esclusivamente dei principî fondamentali per la cui comprensione tali modelli erano stati ideati. A questo proposito, gli anni Trenta, durante i quali la struttura di Cauchy fu maggiormente studiata, somigliano all'ultimo decennio dell'Ottocento e al primo del Novecento, periodi in cui furono costruiti i modelli della materia in grado di fornire formule di ottica confrontabili con gli esperimenti. Questo rappresentò il primo tentativo di sviluppare su così vasta scala le conseguenze di un modello dettagliato per fenomeni che non era possibile osservare direttamente e, fino all'avvento dell'elettrone, tale genere di indagini continuò a essere insolito e anche fortemente controverso.
Almeno fino agli inizi degli anni Quaranta dell'Ottocento, furono pochi i fisici o i matematici che si occuparono dei principî fondamentali della teoria ondulatoria e, fatto altrettanto importante, a quell'epoca molti di essi erano in grado di applicarla all'elevato livello di dettaglio matematico richiesto. Durante questo periodo, le indagini basate sulla teoria ondulatoria cominciarono a evolvere verso due settori collegati, ma distinti. Continuò il lavoro teso ad approfondire, come già aveva fatto Cauchy, le implicazioni della meccanica dell'etere, ma dall'inizio del decennio successivo ben pochi dei lavori pubblicati riguardavano direttamente deduzioni di meccanica; la grande maggioranza concerneva piuttosto lo sviluppo dei principî matematici della teoria ondulatoria e le sue applicazioni.
La meccanica dell'etere, giustamente, ha ricevuto le attenzioni maggiori da parte della ricerca storica, nonostante la sua scarsa importanza sia per quanto riguarda la nascita e gli sviluppi dell'ottica dell'epoca sia per quanto riguarda la durata dei suoi risultati. La relatività ha pervaso così diffusamente la concezione moderna dell'ottica che, per la maggior parte del XX sec., praticamente tutta l'età vittoriana, è stata considerata una sorta di suo preludio. Il motivo per cui, inoltre, la meccanica dell'etere di Cauchy fu considerata una sorta di aberrazione, più che una parte centrale dell'ottica, è che essa non era per nulla affine al nucleo della maggior parte dei lavori di ottica dell'epoca: l'attività di ricerca riguardava prevalentemente questioni quali la forma più appropriata per le soluzioni dell'equazione d'onda, le equazioni per vari tipi di mezzi, e così via; se è pur vero che alcune avevano a che fare con la meccanica dell'etere, la maggior parte di tali questioni ne era sostanzialmente indipendente.
Comunque non v'è alcun dubbio che, specialmente prima del 1870, alcuni lavori fossero rivolti alla meccanica dell'etere, nonostante la nascita, dopo i primi anni Quaranta, di una seconda tendenza che si discostava notevolmente da quella di Cauchy. Essa emerse in primo luogo nei lavori di MacCullagh e di George Green, cui seguirono negli anni Cinquanta e Sessanta dell'Ottocento quelli di George G. Stokes e di altri. In questo caso le equazioni del reticolo non svolgevano alcun ruolo ed erano, perciò, attentamente evitate; le equazioni dell'etere, invece, erano ottenute manipolando una funzione potenziale macroscopica, che dopo gli anni Cinquanta acquisì un significato energetico. Questi due metodi ‒ che potremmo chiamare molecolare e macroscopico ‒ condividevano l'ipotesi che la materia modificasse l'etere, alterando i coefficienti che ne determinavano le equazioni del moto (sebbene le teorie macroscopiche differissero tra loro nello stabilire se l'alterazione riguardasse i coefficienti di densità o, invece, quelli di elasticità). Anche durante gli anni Quaranta, comunque, alcuni fisici pensavano che questa ipotesi non fosse adeguata e ritenevano piuttosto che l'etere e la materia dovessero essere trattate come sistemi distinti, ma dinamicamente connessi l'uno all'altro. Questa linea di pensiero scomparve, o almeno divenne una convinzione piuttosto che un programma, fino alla scoperta della dispersione anomala nel 1870.
Il principio di Huygens, l'integrale di diffrazione e la natura della luce non polarizzata
Sebbene Fresnel avesse approfondito notevolmente sia i principî dell'ottica ondulatoria sia i suoi fondamenti matematici, rimanevano aperte molte questioni, che andavano dai problemi riguardanti la fisica dell'etere in quanto tale, affrontati in vari modi nel corso del XIX sec., a difficoltà ancora più fondamentali, che stimolarono una considerevole attività di ricerca. Forse il più importante problema sui fondamenti stessi dell'ottica lasciato insoluto da Fresnel riguardava il principio di Huygens, che egli aveva utilizzato, come già abbiamo detto, per ottenere gli integrali che oggi portano il suo nome. Tali integrali, tuttavia, non erano stati elaborati come soluzioni di equazioni differenziali date. Al contrario, essi erano stati introdotti senza che egli avesse avuto a disposizione le equazioni differenziali alle derivate parziali di cui si pensava fossero soluzione e meno che mai i metodi e le tecniche necessari a risolverle con un opportuno insieme di condizioni al contorno. Un aspetto ancora peggiore era che Fresnel era stato costretto a congetturare, più che a dedurre, la forma del fattore che regolava il contributo al fronte d'onda lungo una specifica direzione apportato da una piccola onda secondaria (chiamato in seguito 'fattore d'inclinazione'). Siméon-Denis Poisson, in due memorie del 1823 ‒ Extrait d'un mémoire sur la propagation du mouvement dans les fluides élastiques ed Extrait d'une lettre de M. Poisson à M. A. Fresnel ‒, aveva criticato il fondamento stesso degli integrali di Fresnel, ossia il particolare uso che era fatto del principio di Huygens. Tutte queste difficoltà dipendevano dal fatto che Fresnel non poteva disporre di un'equazione differenziale alle derivate parziali per l'ottica ondulatoria, tantomeno di un metodo per ottenerne la soluzione generale.
Va senz'altro tenuto presente che il problema con cui si confrontò Fresnel traeva origine dalle incerte fondamenta fisiche dell'ottica ondulatoria, ma in realtà le difficoltà maggiori erano essenzialmente matematiche. Nonostante l'equazione d'onda tridimensionale fosse stata sviluppata nel XVIII sec., le sue soluzioni erano state elaborate in una forma che non si adattava al comportamento generale di interi fronti d'onda. Poisson fu il primo ad analizzare questo genere di questioni: partendo da una superficie chiusa a un istante dato e da una data distribuzione di velocità e condensazione, dall'equazione d'onda egli ricavò la perturbazione in ogni punto dello spazio e in ogni istante di tempo, in funzione di un integrale calcolato sulla superficie di partenza. In effetti, Poisson esaminò il caso di un impulso isolato a simmetria sferica e specificò che esso doveva soddisfare particolari condizioni, che a suo parere difficilmente sarebbero state soddisfatte dalle richieste che Fresnel aveva posto al principio di Huygens. Poisson ammise l'efficacia empirica degli integrali di Fresnel per la diffrazione, ma rifiutò la giustificazione che quest'ultimo ne aveva dato.
Il lavoro di Poisson sull'equazione d'onda sembrava quindi porre alcuni problemi all'ottica ondulatoria, non da ultimo attraverso la constatazione dell'alto grado di problematicità legato al fattore di inclinazione di Fresnel. Nel 1849 Stokes si dedicò a tale questione ricorrendo proprio alla soluzione che Poisson stesso aveva elaborato. Egli tentò di sviluppare una teoria per la diffrazione di un'onda vettoriale partendo dalle cosiddette 'equazioni di Navier-Stokes' per un mezzo elastico continuo, dalle quali riuscì a dedurre proprio quel fattore di inclinazione che Fresnel aveva a lungo ipotizzato e Poisson criticato. La soluzione di Poisson, comunque, non era adatta ad affrontare le questioni generali sollevate dall'uso che Fresnel aveva fatto del principio di Huygens: partendo da un fronte non periodico, essa permetteva di ottenere i fronti successivi per integrazione di quello iniziale; il principio di Huygens invece, così come era utilizzato nella teoria della diffrazione, richiedeva che si considerasse una perturbazione infinitamente lunga e periodica. Le argomentazioni basate sulla periodicità, da una parte, costituivano l'essenza stessa dell'analisi di Fresnel, dall'altra erano precisamente ciò che Poisson si rifiutava di accettare.
Un metodo utile e generale di integrazione, basato sulle proprietà di cui godeva la soluzione dell'equazione d'onda, fu sviluppato per la prima volta da Helmholtz nel 1860. Analizzando il comportamento delle canne d'organo, egli ipotizzò l'esistenza di una periodicità e ridusse l'equazione d'onda alla forma ∇2w+k2w=0 (dove k rappresenta 2π diviso per la lunghezza d'onda). Il passo critico nell'analisi di Helmholtz riguardava l'uso che egli faceva del teorema di Green, che gli permise di esprimere la perturbazione in un punto attraverso il calcolo di integrali su una superficie che racchiudeva il punto stesso; tali integrali contenevano i valori assunti sulla superficie dalla funzione e dalle sue derivate normali alla superficie stessa. L'analisi di Helmholtz si limitò a onde armoniche sferiche e non fu estesa alla diffrazione poiché egli non stava considerando perturbazioni ottiche; le questioni problematiche che riguardavano le condizioni al contorno non furono perciò sollevate.
Kirchhoff, nell'articolo Zur Theorie der Lichtstrahlen (La teoria dei raggi luminosi) del 1833, ampliò l'uso che Helmholtz aveva fatto del teorema di Green in ottica ondulatoria al caso generale di una perturbazione arbitraria e infinitamente estesa, sviluppando gli integrali di superficie adatti alla teoria della diffrazione; successivamente egli si concentrò sul caso di un'onda armonica. Le formule di Kirchhoff, però, richiedevano condizioni al contorno non coerenti tra loro sulla superficie diffrangente; tale incoerenza dette vita a una discussione che, nel 1896, culminò in un completo riesame del problema, da parte di Sommerfeld, sulla base della teoria elettromagnetica.
La teoria di Sommerfeld, che faceva uso degli spazi riemanniani, raggiunse il suo scopo per la diffrazione da schermi perfettamente riflettenti, ma lasciava ancora irrisolti i problemi riguardanti gli schermi neri perfettamente assorbenti. Queste numerose analisi, così come altre condotte in quel periodo, riducevano il principio di Huygens, tutt'al più, a un enunciato sui termini differenziali che comparivano negli integrali generali della diffrazione, privandolo quasi completamente di un chiaro significato fisico. Alla fine degli anni Trenta del Novecento, Bevan B. Baker, all'Università di Londra, e Edward T. Copson, all'Università di St. Andrews, pubblicarono The mathematical theory of Huygens' principle, un'ampia dissertazione che tentava di recuperare, per quanto possibile, il contenuto fisico del principio.
Il principio di Huygens e gli integrali di diffrazione non erano le uniche questioni che preoccupavano coloro che, sostenitori della teoria ondulatoria, intendevano svilupparne ed espanderne il dominio. La stessa polarizzazione poneva problemi particolarmente ostici. Nella nuova ottica di Fresnel, la luce polarizzata consisteva in una grandezza orientata, localizzata proprio sul fronte d'onda, il cui modulo e la cui direzione cambiavano nel tempo, e in modo calcolabile, mentre il fronte avanzava nello spazio. Per ottenere una matematica appropriata, Fresnel impiegò un metodo di decomposizione ortogonale: ogni perturbazione poteva essere specificata fornendo i parametri che caratterizzavano le sue componenti lungo una data coppia di assi ortogonali. In generale ogni componente possedeva la forma acos(ωt+φ), dove a indicava l'ampiezza della componente e φ la sua fase. Questo metodo si rivelò di straordinaria efficacia sia nel trattare tutte le forme di luce polarizzata note all'epoca di Fresnel, sia nel predire le caratteristiche di una forma di luce che non era ancora stata scoperta (vale a dire la luce polarizzata ellitticamente).
Il sistema, nella forma in cui era stato introdotto da Fresnel, non poteva essere utilizzato facilmente con la luce non polarizzata o polarizzata parzialmente, perché in quei casi l'ampiezza e la fase della polarizzazione non hanno valori fissati. Infatti, nell'ottica di Fresnel, la luce non polarizzata ha ampiezza e fase che variano casualmente nel corso del tempo, mentre nel caso di luce parzialmente polarizzata le variazioni in ampiezza e in fase sono limitate. In nessuno dei due casi si può condurre l'analisi a partire dalla decomposizione che Fresnel aveva introdotto per la luce polarizzata.
Fresnel, in termini moderni, aveva costruito l'ottica ondulatoria sulla base di una formulazione in ampiezza, nella quale l'analisi era ricondotta all'ampiezza e alla fase dell'onda. Poiché tali grandezze non potevano essere osservate direttamente, di fatto andavano dedotte sperimentalmente da ciò che si poteva misurare, ossia intensità e angoli. D'altra parte, la luce non polarizzata e quella parzialmente polarizzata non avevano affatto un'ampiezza e una fase stabili e, per questo motivo, qualsiasi sistema che avesse voluto incorporarle in uno schema generale coerente avrebbe dovuto basarsi sull'intensità e sugli angoli, e non sull'ampiezza e sulla fase, con quella che potremmo chiamare una 'formulazione in intensità'. Sviluppato da Stokes nel 1852, questo nuovo sistema caratterizzò la polarizzazione in termini di quattro parametri, ognuno dei quali poteva essere direttamente osservato. All'epoca, ai parametri di Stokes non si attribuivano particolari significati ‒ e per questo motivo non furono analizzati a fondo nemmeno dallo stesso Stokes ‒, perché non vi erano pressanti problemi fisici da risolvere ai quali si potessero applicare.
L'interpretazione ottica delle grandezze complesse
Le rappresentazioni geometriche dei numeri complessi erano state sviluppate nel 1797 dal norvegese Caspar Wessel e nel 1806 dallo svizzero Jean-Robert Argand, ma non avevano trovato un'applicazione immediata ai problemi di fisica. Fu l'ottica ondulatoria, infatti, il primo settore della fisica in cui i numeri complessi fornirono un ausilio che non avrebbe potuto essere ottenuto altrimenti: essi apparvero per la prima volta nell'analisi condotta nel 1823 da Fresnel sulla riflessione interna. Quando la luce incide, per esempio, all'interno di un prisma sulla superficie di separazione con l'aria secondo angoli maggiori di un particolare valore, essa è totalmente riflessa. D'altra parte, le equazioni di Fresnel per il rapporto tra grandezze riguardanti la luce riflessa e quella incidente fornivano numeri complessi proprio a partire da tale valore dell'angolo: nel cercare d'interpretare questo apparente fallimento di espressioni che sembravano prive di significato fisico, Fresnel sviluppò la prima utilizzazione pratica dei numeri complessi (sebbene non del tutto rigorosa).
Egli ragionò nel modo seguente. Prima di tutto, la caratteristica dell'espressione complessa che si otteneva in questi casi era che la somma dei quadrati della parte reale e di quella immaginaria uguagliava il quadrato dell'intensità incidente. Questo suggeriva a Fresnel la seguente interpretazione: la luce doveva essere totalmente riflessa e subire anche un cambiamento di fase; esso poteva essere interpretato scomponendo l'onda risultante in due parti, le cui fasi differivano di 90° l'una dall'altra e una coincideva con quella dell'onda incidente ‒ secondo la decomposizione generale che Fresnel aveva originariamente eseguito per la diffrazione. L'ampiezza relativa di ciascuna delle due parti doveva essere data, rispettivamente, dal coseno e dal seno della fase della risultante. Poiché nel caso di riflessione interna totale si presentavano effettivamente due termini la cui somma dei quadrati era pari a uno, Fresnel ipotizzò che ognuno di questi termini rappresentasse l'ampiezza di una delle parti dell'usuale scomposizione dell'onda. La fase della luce completamente riflessa si sarebbe spostata di un angolo la cui tangente era il rapporto tra la parte reale e la parte immaginaria dell'ampiezza riflessa, assumendo come parte reale quella che aveva la stessa fase dell'onda incidente.
Negli anni successivi, l'interpretazione di Fresnel fu ripresa e ulteriormente sviluppata, tra gli altri, da Cauchy, il quale apportò personalmente contributi fondamentali alla teoria delle funzioni complesse. Nella memoria del 1839, Sur la quantité de lumière réfléchie, sous diverses incidences, par les surfaces des corps opaques, et spécialement des métaux, egli analizzò la riflessione nei metalli ipotizzando che in essi l'indice di rifrazione stesso diventasse complesso, ma che la forma delle usuali espressioni di Fresnel per le ampiezze riflesse rimanesse la medesima (MacCullagh escogitò indipendentemente la stessa idea). Jules-Célestin Jamin, nella Memoir on metallic reflection (1852), fu il primo a compilare tabelle di costanti metalliche per diversi metalli e per differenti lunghezze d'onda. Tale approccio raggiunse la sua forma matematica più elevata nel 1858 nella trattazione di Friedrich Eisenlohr nell'Ableitung der Formeln für die Intensität des an der Oberfläche zweier isotropen Mittel gespiegelten, gebrochenen und gebeugten Lichtes (Derivazione delle formule per l'intensità della luce riflessa, rifratta e diffratta sulla superficie di due mezzi isotropi): le sue equazioni furono ampiamente utilizzate durante l'ultima parte del XIX secolo.
La dispersione prima dell'ottica elettromagnetica
L'argomento della riflessione nei metalli sollevò numerose questioni che coinvolsero molti scienziati durante l'ultimo quarto del XIX secolo. Un vasto lavoro sperimentale, condotto, tra gli altri, da Georg Hermann Quincke (1834-1924) dal titolo Optische Experimental-Untersuchungen (Ricerche sperimentali di ottica, 1866-1872), aveva evidenziato che, per tutti i metalli conosciuti, la parte reale dell'indice di rifrazione doveva diminuire all'aumentare della frequenza, con la conseguenza che i metalli avrebbero mostrato (se fosse stato possibile osservarla) una dispersione esattamente opposta rispetto a quella manifestata da corpi trasparenti ordinari. Questa non era l'unica difficoltà, perché le stesse misurazioni indicavano anche che nei metalli la velocità dell'onda avrebbe dovuto essere oltre cinque volte più grande della velocità della luce nel vuoto. La conseguente dispersione inversa dei metalli fu associata a questioni riguardanti la dispersione nei corpi trasparenti, per i quali gli scienziati delle onde non erano mai riusciti a fornire un resoconto che riscuotesse ampio consenso, sebbene, come già detto, Cauchy avesse ottenuto una formula che funzionava.
Per quanto riguarda l'ottica ondulatoria, grandi cambiamenti incominciarono a verificarsi negli anni Settanta e Ottanta del XIX sec., quando in Germania gli scienziati spostarono la loro attenzione dal comportamento dell'etere ottico di per sé stesso a questioni riguardanti piuttosto le interazioni tra l'etere e la materia.
Nel 1870 lo scienziato danese Christian Christiansen (1843-1917) osservò in modo incontrovertibile un fenomeno che divenne noto come 'dispersione anomala'. Usando un colorante magenta all'anilina disciolto in alcol, egli stabilì che l'indice di rifrazione della soluzione cresceva dalla linea spettrale B a quella D, decresceva dalla D alla G e cresceva di nuovo dopo la G. L'interesse suscitato in Germania dallo studio dei metalli fu incrementato dalla scoperta di Christiansen, poiché le proprietà ottiche dei metalli potevano essere ricondotte a tale dispersione anomala. Infatti, circa due anni dopo la sua scoperta, il tedesco Wolfgang Sellmeier, in una serie di lavori intitolati Über die durch Aetherschwingungen erregten Körpertheilchen und deren Rückwirkung auf die ersten, besonders zur Erklärung der Dispersion und ihrer Anomalien (Sulle molecole eccitate dalle vibrazioni dell'etere e sulle loro ripercussioni sulle prime, soprattutto per spiegare la dispersione e le sue anomalie, 1872), sviluppò per questo fenomeno una teoria meccanica quantitativa, secondo la quale tutte le forme di dispersione erano dovute all'interazione delle vibrazioni dell'etere con le naturali oscillazioni delle molecole. L'idea guida di questa spiegazione consisteva nel ritenere che l'equazione d'onda per l'etere non fosse di per sé influenzata dalla presenza delle particelle di materia, ma che per spostare una particella materiale dotata di massa legata elasticamente a una posizione fissa dovesse essere estratta una data quantità di energia da un'onda nell'etere. Utilizzando un'analisi basata solamente su considerazioni energetiche, Sellmeier dedusse una formula per la dispersione che spiegava le principali caratteristiche del fenomeno.
Gli aspetti cruciali della teoria di Sellmeier erano innanzitutto la sua tacita assunzione che né l'elasticità né la densità dell'etere dovessero essere manipolate, in modo che le proprietà dell'etere rimanessero sostanzialmente fisse (sebbene Sellmeier non fosse intransigente su questo punto: per lo studioso tedesco queste assunzioni erano prima di tutto convenzioni, perché riteneva che l'etere e la materia insieme costituissero realmente un reticolo duale di masse puntiformi); da ciò seguiva, inoltre, che tutti i fenomeni di rifrazione implicassero un'azione di risonanza meccanica, nella quale le onde nell'etere mettessero in moto sia le particelle materiali dotate di massa sia la sostanza della quale era fatto l'etere stesso. Alla teoria di Sellmeier mancava una rappresentazione matematica di ciò che avviene nel caso di risonanza, ossia quando la frequenza di un'onda nell'etere coincide con la frequenza propria di una particella materiale, che è esattamente la condizione perché avvenga l'assorbimento (anche se Sellmeier presentò un'intrigata e difficile spiegazione qualitativa per questa situazione).
Nel 1875 Helmholtz fece proprie le idee alla base dell'interpretazione di Sellmeier e le riformulò matematicamente in equazioni meccaniche del moto che permettevano di trattare sia l'assorbimento sia la dispersione. Le equazioni di Helmholtz erano basate sull'idea, comunemente accettata, che l'assorbimento ottico comportasse la trasformazione di energia luminosa in un movimento interno e irregolare delle molecole di materia, in altre parole in calore. Questa trasformazione rendeva necessaria l'azione di una forza, che però mancava nella teoria di Sellmeier. La trattazione di Helmholtz formò la base di una gran quantità di teorie ottiche che furono sviluppate successivamente e comparve (in forma mutata) anche nella prima ottica elettromagnetica.
Helmholtz era ben consapevole del fatto che il fenomeno dell'assorbimento ‒ la diminuzione esponenziale dell'ampiezza all'aumentare della distanza percorsa dall'onda luminosa in un mezzo materiale ‒ richiedesse la presenza di un termine proporzionale alla velocità nelle equazioni differenziali, ma egli sapeva anche che tale termine non sarebbe potuto comparire nell'equazione del moto dell'etere, poiché nel vuoto non vi è assorbimento. La soluzione che Helmholtz dette al problema fu a un tempo semplice e originale: egli stabilì un'equazione del moto distinta per la materia, che conteneva essa stessa una forza dipendente dalla velocità. L'idea consisteva nell'ipotizzare che le particelle materiali, spinte dalle onde presenti nell'etere, fossero soggette ad altre due forze, una elastica di richiamo e una di attrito che avevano origine dalle particelle materiali circostanti. Quando le particelle materiali assorbono energia dall'onda nell'etere, l'energia ottica diminuisce e l'energia assorbita è convertita in agitazione termica dalla forza di attrito (come possa avvenire quest'ultima trasformazione è una questione completamente estranea alla teoria di Helmholtz). Non si pensava che le due forze materiali agissero su una molecola intera, ma piuttosto che ogni molecola fosse costituita di un nucleo centrale pesante, che si muoveva pochissimo se investito da un'onda di etere, e da una particella mobile più leggera; è quest'ultima a essere frenata nel suo moto dall'attrito, mentre le forze armoniche la vincolano elasticamente al nucleo (lo scopo della distinzione nucleo-particella era quello di spiegare le proprietà di assorbimento e di dispersione da parte dei gas).
Secondo Helmholtz le mutue azioni dell'etere e della materia, che causano scambi di energia tra essi, soddisfano il principio di azione e reazione: qualunque forza rappresenti, nell'equazione del moto dell'etere, l'azione esercitata su quest'ultimo dalla materia, deve comparire con segno opposto nell'equazione del moto della materia. Helmholtz ipotizzò su basi meccaniche che questa mutua azione fosse direttamente proporzionale alla differenza tra gli spostamenti, dalle rispettive posizioni di equilibrio, dell'etere e delle particelle leggere e mobili di materia. Egli trattò inoltre entrambi i mezzi come continui e impenetrabili, in modo tale che gli spostamenti dell'etere e della materia fossero, in realtà, funzioni continue del tempo e della distanza. Tutto ciò gli permise di ricavare equazioni differenziali alle derivate parziali. L'equazione del moto dell'etere era così ricondotta alla consueta equazione per un mezzo continuo incomprimibile, isotropo ed elastico, alla quale si aggiungeva un termine per rappresentare l'azione della materia sull'etere. L'equazione del moto della materia contemplava tre forze: il termine che descriveva l'interazione con l'etere (di segno opposto rispetto al caso precedente), la forza di attrito e l'azione armonica. Queste equazioni 'gemelle' costituivano la struttura matematica della teoria di Helmholtz, poiché esse conducevano immediatamente a un'equazione d'onda che, oltre a essere facilmente applicabile a tutte le forme di dispersione e di assorbimento, era in buon accordo con i risultati di laboratorio, a patto di scegliere opportunamente le varie costanti, come Helmholtz mostrò in maniera abbastanza dettagliata.
La teoria di Helmholtz ebbe enorme influenza, non soltanto in Germania, e durante i successivi quindici anni numerosi fisici tedeschi, fra i quali Eduard Ketteler, Eugen Lommel e Woldemar Voigt, la utilizzarono variamente in ottica fisica per ottenere teorie meccaniche dei fenomeni. Generalmente queste teorie, come quella di Helmholtz, prestavano scarsa attenzione all'effettiva struttura molecolare della materia, preferendo invece ricorrere a termini semplici, e solitamente a priori, nelle equazioni della materia stessa. Tra i britannici, William Thomson (lord Kelvin), nelle Baltimore lectures (1884), che ebbero grande successo, basò la maggior parte dei complessi modelli meccanici, per i quali sarebbe presto divenuto famoso, direttamente sul modello di Helmholtz-Sellmeier. Il suo lavoro, tuttavia, differiva in modo sostanziale dalle descrizioni dei contemporanei tedeschi perché il suo scopo era costruire una rappresentazione continua per l'etere e per la materia.
Le due equazioni di Helmholtz, e le loro rielaborazioni tedesche e britanniche precedenti l'ultimo decennio dell'Ottocento, erano puramente meccaniche. Intorno al 1878, l'idea su cui esse si basavano era già stata utilizzata nella teoria elettromagnetica: Hendrik Antoon Lorentz, nel suo lavoro del 1875 Over de theorie der terugkaatsing en breking van het licht (Sulla teoria della riflessione e rifrazione della luce), aveva ipotizzato che le proprietà dell'etere fossero intrinsecamente invarianti e che gli effetti ottici fossero dovuti alle conseguenze del moto interno di particelle materiali. Egli rafforzò quest'idea quando dedusse per la prima volta una formula per la dispersione da due insiemi di equazioni tra loro collegati: uno per la polarizzazione dell'etere e l'altro per il moto di una carica all'interno di una molecola con un nucleo centrale fisso. I legami esistenti tra le equazioni erano, da un lato, la polarizzazione nell'etere invariante causata dalle cariche in moto e, dall'altro, la forza motrice esercitata dalla polarizzazione dell'etere sulla carica.
Le corrispondenze tra questa teoria e quella meccanica di Helmholtz, contenute nell'articolo Zur Theorie der anomalen Dispersionen (Sulla teoria delle dispersioni anomale, 1875), sono manifeste. Lorentz, comunque, trattava l'etere come una sostanza, essa stessa polarizzabile e non operò, quindi, una chiara distinzione tra la polarizzazione della materia e quella dell'etere. In ogni caso, la teoria di Lorentz del 1878 ebbe in apparenza un'influenza relativamente scarsa, eccetto forse in Olanda, perché coinvolgeva quel tipo di ipotesi e calcoli dettagliati di fisica microscopica che, ancora alla metà degli anni Novanta dell'Ottocento, pochi fisici tedeschi amavano utilizzare. Affinché l'approccio di Helmholtz alle due equazioni gemelle acquistasse un significato elettromagnetico che la maggior parte dei fisici tedeschi potesse facilmente comprendere e approvare, le equazioni dovevano essere reinterpretate in modo tale da preservare sia la loro struttura formale come sistemi collegati, sia la loro relativa indipendenza dal punto di vista dei calcoli dettagliati di fisica microscopica. Tutto ciò fu realizzato da Helmholtz stesso nella Electromagnetische Theorie der Farbenzerstreuung (Teoria elettromagnetica della dispersione dei colori) del 1893; la nuova interpretazione, abbinata a quella esposta nel 1892 da Lorentz in La théorie électromagnétique de Maxwell et son application aux corps mouvants, riuscì a stimolare una radicale trasformazione dei fondamenti della scienza ottica, nella quale sempre maggiore importanza rivestiva la struttura delle molecole e, in definitiva, degli stessi atomi.
Bibliografia
Atzema 1993: Atzema, Eisso J., The structure of systems of lines in 19th century geometrical optics. Malus' theorem and the description of the infinitely thin pencil, (Diss.), Utrecht, Rijksuniversiteit, 1993.
‒ 1994: Atzema, Eisso J., A theory of caustics. The contribution of Dupin, Quetelet, and Gergonne to geometrical optics, in: Ad radices. Festband zum fünfzigjährigen Bestehen des Instituts für Geschichte der Naturwissenschaften der Johann Wolfgang Goethe-Universität Frankfurt am Main, hrsg. von Anton von Gotstedter, Stuttgart, Steiner, 1994, pp. 331-354.
Baker 1939: Baker, Bevan B. - Copson, Edward T., The mathematical theory of Huygens' principle, Oxford, Clarendon, 1939.
Bauschinger 1921: Bauschinger, Johan, Necrolog Heinrich Bruns, "Vierteljahresschrift der Astronomischen Gesellschaft", 56, 1921, pp. 159-169.
Buchwald 1985: Buchwald, Jed Z., From Maxwell to microphysics. Aspects of electromagnetic theory in the last quarter of the nineteenth century, Chicago, University of Chicago Press, 1985.
‒ 1989: Buchwald, Jed Z., The rise of the wave theory of light. Optical theory and experiment in the early nineteenth century, Chicago, University of Chicago Press, 1989.
Collett 1993: Collett, Edward, Polarized light. Fundamentals and applications, New York, Dekker, 1993.
Elfving 1981: Elfving, Gustav, The history of mathematics in Finland, 1828-1918, Helsinki, Societas Scientiarum Fennica, 1981.
Fellmann 1973: Fellmann, Emil, Leonard Eulers Stellung in der Geschichte der Optik, in: Euler, Leonhard, Opera omnia, ser. III, v. 9, 1973, pp. 297-322.
Hakfoort 1995: Hakfoort, Casper, Optics in the age of Euler. Conceptions of the nature of light, 1700-1795, Cambridge (Mass.), Cambridge University Press, 1995.
Herzberger 1931: Herzberger, Max, Geschichtliche Bemerkungen, in: Herzberger, Max, Strahlenoptik, Berlin, Springer, 1931, pp. 179-190.
‒ 1932: Herzberger, Max, Geschichtlicher Abriß der Strahlenoptik, "Zeitschrift für Instrumentkunde", 52, 1932, pp. 429-435, 485-493, 534-542.
Hiroshige 1969: Hiroshige, Tetsu, Origins of Lorentz theory of electrons and the concept of the electromagnetic field, "Historical studies in the physical sciences", 1, 1969, pp. 151-209.
Kipnis 1991: Kipnis, Nahum, History of the principle of interference of light, Boston, Birkhäuser, 1991.
Kline 1972: Kline, Morris, Mathematical thought from ancient to modern times, Oxford-New York, Oxford University Press, 1972 (trad. it.: Storia del pensiero matematico, a cura di Alberto Conte, Torino, Einaudi, 1991, 2 v.).
Mahnke 1991: Mahnke, Reinhard, Ludwig Matthiessen. Erster ordentlicher Professor der Physik an der Universität Rostock, "Beiträge zur Geschichte der Universität Rostock", 17, 1991, pp. 19-33.
Oseen 1937: Oseen, Carl W., Allvar Gullstrand, "Kungliga Svenska Vetenskapsakademiens Årsbok", 35, 1937, pp. 249-273.