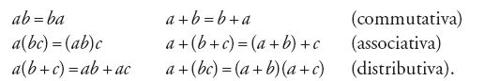L'Ottocento: matematica. Algebra della logica

L'Ottocento: matematica. Algebra della logica

Algebra della logica

Logica e matematica: pensare e calcolare

Sia nell'Antichità sia durante il Medioevo, la logica e la matematica si configurano come due discipline che si sviluppano in modo sostanzialmente indipendente l'una rispetto all'altra, con pochi scambi e rapporti reciproci. Nei secc. XV e XVI, la reazione contro la logica scolastica e la progressiva riscoperta degli Elementi di Euclide (e di commenti antichi a questo testo) fanno sì che si affermi la convinzione secondo la quale la vera tecnica dimostrativa debba essere ricercata nello scritto euclideo, anziché nella logica della tradizione aristotelica. Al tempo stesso, in tale periodo, viene posto in modo esplicito il problema dei rapporti tra la dottrina logica tramandata e la dimostrazione quale viene svolta in ambito matematico-geometrico. Così, a partire dal XVI sec., da un lato ci si interroga sulla possibilità che la logica tradizionale sia davvero capace di render conto delle dimostrazioni euclidee, dall'altro si comincia a pensare di sviluppare una logica che ricorra a strumenti e metodi matematici. Questa seconda tendenza si afferma soprattutto con la scoperta dell'algebra, negli anni 1591-1593, da parte di François Viète e si rafforza durante il Seicento. Leibniz è il primo a proporre in maniera esplicita (e a tentare di attuare) un programma di 'matematizzazione della logica', che trae diretta ispirazione dall'algebra. Nella seconda metà del XVIII sec., Étienne Bonnot de Condillac considera l'algebra come la lingua migliore di cui dispongano gli uomini per dare forma alle loro argomentazioni. Nello stesso periodo, in Germania, il matematico tedesco Johann Heinrich Lambert (1728-1777) si propone di dare una forma matematica alle inferenze sillogistiche. Nella medesima direzione si muovono Johann Andreas von Segner (1704-1777), Gottfried Ploucquet (1716-1790) e Georg J. von Holland (1742-1784), che si ingegnano per la realizzazione di calcoli logici sul modello di quelli aritmetici. Agli inizi del XIX sec. il matematico Joseph-Diez Gergonne (1771-1859), fondatore delle "Annales des mathématiques pures et appliquées", nell'Essai de dialectique rationnelle (1817) espone chiaramente la tradizionale teoria del sillogismo, espressa nei termini del rapporto estensionale tra classi di oggetti qualunque.

Il periodo compreso tra il XVI e la prima metà del XIX sec. è di solito considerato un periodo di decadenza della logica, rispetto alle epoche precedenti (Antichità e Medioevo). La principale motivazione per un giudizio così severo risiede nella sostanziale identificazione dell'intera logica con la teoria del sillogismo. Tale valutazione trascura tuttavia il fatto che, proprio in questo periodo, nell'ambito della cultura europea, si afferma l'idea di stabilire uno stretto rapporto tra logica e matematica: un'idea che, giudicata nella prospettiva degli sviluppi successivi, costituisce un risultato di gran lunga più importante di quanto fosse stato concepito, riguardo alla logica, in epoche precedenti. Ciononostante, se si eccettua il caso di Leibniz (i cui scritti logici rimasero perlopiù sconosciuti fino agli inizi del XX sec.), coloro che, in quest'epoca, si cimentano nel tentativo di trasformare il ragionamento logico in calcolo si limitano a stabilire analogie fra operazioni logiche e operazioni aritmetiche, senza dare la dovuta importanza alle proprietà che caratterizzano tali operazioni. Nella seconda metà del XIX sec., la matematizzazione della logica diviene possibile in quanto si fonda su una concezione dell'algebra (in definitiva, della stessa matematica) che si estende al di là dell'orizzonte offerto dall'algebra di Viète. L'algebrizzazione della logica diviene un fatto compiuto con la pubblicazione, nel 1847, di The mathematical analysis of logic di George Boole. Il terreno sul quale questi si muove è la tradizione matematica del Regno Unito, rivitalizzata da un forte desiderio di mutamento e animata da un rinato interesse per la logica.

Algebra e logica in Gran Bretagna nella prima metà dell'Ottocento

Agli inizi dell'Ottocento, Robert Woodhouse (1773-1827) ebbe un ruolo non trascurabile nel modificare l'insegnamento della matematica a Cambridge. Egli nei Principles of analytical calculation (1803) illustrò e difese il sistema notazionale leibniziano in analisi e pose l'accento sull'importanza che assumono le dimostrazioni formali nel giustificare la validità dei procedimenti matematici. In polemica con John Playfair (1748-1819), che in un articolo pubblicato sulle "Philosophical Transactions" aveva teorizzato il ricorso alla nozione di 'analogia' per render conto della validità delle operazioni con numeri complessi, Woodhouse sottolineò l'intrinseca indeterminatezza cui è sottoposto l'impiego di tale nozione e contrappose a essa il ricorso a una distinta e rigorosa dimostrazione. L'esistenza di tale dimostrazione era garantita, secondo Woodhouse, dalla fondamentale convenzionalità della matematica: se il sistema dei simboli con i quali opera il matematico è di sua invenzione, allora non possono esserci in esso né paradossi né misteri inesplicabili. Questa concezione del carattere convenzionale della matematica venne espressa da Woodhouse in varie occasioni ed è ribadita nel saggio del 1801, On the independence of the analytical and geometrical methods of investigation; and on the advantages to be derived from their separation, concernente la reciproca indipendenza dei metodi 'geometrico' e 'analitico'. In tale saggio Woodhouse sembra ammettere una maggiore 'naturalezza' del 'metodo geometrico', rispetto a quelli dell'algebra e dell'analisi. Proprio questa naturalezza, tuttavia, può costituire uno dei limiti del metodo geometrico, soprattutto quando la complessità delle operazioni e dei procedimenti matematici rende vano l'appello alla rappresentazione visiva. Egli conclude che il metodo geometrico ha superiore evidenza in indagini 'di natura semplice', mentre il metodo analitico è preferibile quando si renda necessaria una rapida deduzione della verità. La distinzione tra metodo geometrico e metodo analitico svincola l'analisi dal riferimento obbligato all'interpretazione geometrica e prepara altresì il terreno al punto di vista che porterà in seguito a distinguere un sistema di regole e procedimenti puramente formali dalle sue possibili interpretazioni.

Un passo ulteriore in quest'ultima direzione viene compiuto, negli anni compresi tra il 1830 e il 1845, da George Peacock (1791-1858). Fermo difensore, come Woodhouse, della nozione di dimostrazione formale nell'indagine matematica, Peacock tenta, nel Treatise on algebra (1830; seconda edizione ampliata in due volumi: 1842-1845) di fornire una sistemazione della teoria dei numeri complessi e di quelli negativi, ricorrendo a una trattazione rigorosamente logica, di tipo assiomatico, che gli valse l'appellativo di 'Euclide dell'algebra'. Nel Treatise Peacock distingue due tipi di algebra: la aritmetica e la simbolica. L'algebra aritmetica è una trattazione astratta dell'aritmetica, nella quale i segni di operazione denotano le consuete operazioni aritmetiche e le lettere designano numeri naturali. L'algebra simbolica è invece un'algebra nella quale i simboli di operazione indicano le medesime operazioni dell'algebra aritmetica, senza però tener conto delle restrizioni sotto le quali le operazioni sono valide nell'algebra aritmetica. Così, la sottrazione a−b, mentre vale nell'algebra aritmetica sotto la condizione a≥b, nell'algebra simbolica vale senza questa restrizione e diventa perciò sempre eseguibile.

L'estensione delle operazioni dell'algebra aritmetica all'algebra simbolica è attribuita da Peacock al cosiddetto 'principio di permanenza delle forme equivalenti': in algebra sussiste una fondamentale uniformità delle operazioni, indipendentemente dal dominio di enti matematici ai quali le operazioni sono applicate. Alla base dell'applicazione del 'principio di permanenza', lo studioso pone una distinzione tra l'assunzione di una regola di operazione e la definizione dell'operazione stessa. I risultati dell'addizione e della sottrazione nell'algebra simbolica, per esempio, sono ottenuti prescrivendo certe regole di esecuzione delle operazioni, non ricavandoli dalla definizione delle operazioni, che per Peacock hanno il significato attribuito loro nell'algebra aritmetica.

Il 'principio di permanenza' risultò decisamente ridimensionato dalla scoperta, compiuta nel 1843 da William R. Hamilton (1805-1865), di un'algebra di quadruple di numeri (i 'quaternioni'), nella quale non vale la proprietà commutativa della moltiplicazione. Il risultato di Hamilton venne reso pubblico l'anno successivo; tuttavia l'idea che potesse esistere una pluralità di algebre tra loro differenti era stata avanzata anche da Augustus De Morgan (1806-1871) nel saggio On the foundations of algebra del 1843. Ciò mostra che la scoperta hamiltoniana si situa in un clima culturale piuttosto diverso rispetto a quello che dominava nel Regno Unito agli inizi dell'Ottocento, vale a dire meno chiuso e più disposto ad accogliere contributi innovatori. Ad avviare siffatto mutamento, oltre ai già menzionati Woodhouse, Peacock e De Morgan, contribuirono in maniera sostanziale anche Charles Babbage (1792-1871) e John Herschel (1792-1871). Nel 1812 Babbage e Herschel avevano fondato, con Peacock e altri colleghi, l'Analytical Society, che si era proposta, tra vari compiti, quello di diffondere nel Regno Unito l'uso della notazione leibniziana per il calcolo differenziale, più comoda di quella newtoniana e ormai affermatasi tra i matematici e i fisici del Continente. L'Analytical Society promosse incontri fra i soci, conferenze pubbliche e discussioni su argomenti di matematica e si incaricò della traduzione (avvenuta a opera degli stessi Babbage, Herschel e Peacock) del Traité du calcul différentiel et du calcul intégral (1799), un testo introduttivo al calcolo differenziale e integrale del matematico francese Sylvestre-François Lacroix (1763-1843). Grazie anche all'attività dell'Analytical Society, in poco meno di un ventennio nelle università inglesi la notazione differenziale sostituì progressivamente quella newtoniana e intorno alla metà del secolo si poteva affermare che i matematici europei fossero tornati a parlare una medesima lingua.

Sebbene Hamilton non appartenesse alla scuola di Cambridge e sostenesse una concezione personale dell'algebra, che risentiva di influenze kantiane (l'algebra era da lui considerata la "scienza del tempo puro"), è indubbio che anche le sue scoperte si connettono a una situazione determinata in gran parte dall'attività dei matematici di Cambridge. Tra questi un ruolo preminente rivestì, intorno agli anni Quaranta, Duncan Gregory (1813-1844), fondatore nel 1838, con Richard Ellis, del "Cambridge mathematical journal". Gregory elaborò una concezione dell'algebra intesa come "la scienza che tratta delle combinazioni di operazioni definite non dalla loro natura, vale a dire da ciò che esse sono o fanno, ma dalle leggi di combinazione alle quali le operazioni sono soggette". Uno dei punti centrali di questa concezione era il cosiddetto 'principio di separazione dei simboli di operazione da quelli di quantità', già usato dal matematico francese François-Joseph Servois (1767-1847) e da Herschel. La separazione dei simboli esprimenti quantità da quelli esprimenti operazioni consentiva una considerazione astratta delle operazioni e delle loro proprietà, indipendentemente dal particolare dominio di enti ai quali le operazioni si applicavano. Ricorrendo a tale principio, Gregory riuscì a isolare le proprietà commutativa e distributiva in algebra, fornendo in tal modo una base per le ulteriori speculazioni di Boole.

La nascita dell'algebra della logica: George Boole

George Boole (1815-1864) insegnò matematica al Queen's College di Cork, in Irlanda, dal 1849 al 1864 e pubblicò due testi fondamentali per lo sviluppo dell'algebra della logica: The mathematical analysis of logic (1847) e The laws of thought (1854). Egli stesso dichiara di essersi deciso a scrivere The mathematical analysis of logic sollecitato dalla disputa sulla 'quantificazione del predicato' che era divampata tra De Morgan e il filosofo scozzese William Hamilton (1788-1856). Si deve interpretare tuttavia siffatta sollecitazione come una sorta di 'causa occasionale', che spinse Boole a riprendere il filo di vecchi pensieri, anziché come un evento che abbia avuto un rilevante impatto teorico sulle meditazioni booleane. La disputa concerneva una questione di priorità: chi per primo, tra De Morgan e Hamilton, avesse affermato che, contrariamente al parere di Aristotele, nei tradizionali enunciati categorici fosse legittimo esprimere la quantità non soltanto del soggetto, ma anche del predicato. Ciò portava ad accettare come logicamente corretti enunciati del tipo: "Tutti gli uomini sono alcuni animali". Sebbene una concezione analoga si trovasse già in autori del passato (tra cui Leibniz) e contemporanei (per es., nel testo di George Bentham: Outline of a new system of logic, 1827); e nonostante fosse evidente che De Morgan era giunto a essa per vie indipendenti rispetto a Hamilton, questi accusò De Morgan di plagio, dando luogo a una controversia che assunse ben presto toni aspri. Si creò di conseguenza un caso intorno a una questione di logica e ciò contribuì ad accrescere l'interesse per la disciplina. Da tale clima fu sicuramente stimolato l'ingegno di Boole.

Nell'Analysis Boole distingue l'interpretazione dei simboli impiegati nel calcolo dalle leggi che, di quegli stessi simboli, regolano la combinazione; e afferma che l'interpretazione quantitativa dei simboli (come numeri o grandezze geometriche) non è l'unica possibile. I simboli possono essere usati per designare in modo altrettanto legittimo operazioni logiche e concetti generali (classi di oggetti qualsiasi). Ciò, sostiene Boole, sanziona l'avvenuta evoluzione della matematica da 'scienza della quantità' a 'scienza della qualità'. Il fatto che l'interpretazione quantitativa si sia imposta così a lungo nell'ambito dell'algebra è soltanto una contingenza storica, che non possiede alcuna necessità intrinseca. La riconduzione della logica nell'ambito di una trattazione algebrica estende la sfera delle applicazioni della matematica: il calcolo logico diventa un particolare settore della matematica applicata. Coerentemente con questa impostazione Boole, anche nella successiva opera del 1854, tiene distinte 'logica' e 'matematica': rispetto all'Analysis, tuttavia, sottolinea con maggior enfasi il ruolo del linguaggio nella determinazione delle leggi logiche. La matematica, secondo l'impostazione di The laws of thought, offre gli strumenti d'indagine e l'apparato simbolico per studiare le leggi logiche fondamentali, ossia quelle che regolano le operazioni in virtù delle quali si attua il ragionamento. In primo luogo viene il 'ragionamento', il naturale svolgersi di processi razionali; il 'linguaggio' e l''introspezione' sono i due mezzi che consentono di scoprire e far venire alla luce distintamente le operazioni eseguite nel corso del ragionamento; la struttura matematica fornisce, infine, la possibilità di indicare con simboli alcuni processi mentali e di definire il comportamento dei simboli in base a leggi che presiedono allo svolgersi delle operazioni mentali. La logica è perciò una scienza descrittiva: fondandosi, al pari di ogni altra scienza empirica, sull'osservazione analizza le forme e i meccanismi del ragionamento, e studia le forme attraverso l'applicazione di strumenti matematici. L'osservazione, tuttavia, non conduce alle leggi logiche mediante generalizzazione induttiva, come accade nel caso di altre scienze empiriche (per es., la fisica). Ciascuna legge logica viene colta dall'osservatore con un singolo atto di riconoscimento: basta un unico esempio affinché l'intelletto ricavi la legge nella sua generalità. Boole considera le leggi logiche come 'leggi del pensiero': esse hanno a che fare con il modo in cui è costituita la nostra 'mente'; il fatto però che non vengano determinate mediante induzione non le espone al rischio di fallire e ne garantisce la necessità. Gli errori di ragionamento sono dovuti alle nostre limitate capacità, all'applicazione delle leggi, non alla natura intrinseca di queste. D'altra parte, proprio la possibilità di dare forma matematica alle 'leggi del pensiero' permette, se non altro in linea di principio, uno studio astratto di logiche diverse da quella che possediamo: tali logiche sarebbero per noi non concepibili, nel senso che non potremmo immaginare come operano; possiamo tuttavia studiarle come meri oggetti matematici.

Boole indica con i simboli x, y, z… singoli atti di scelta con i quali la mente seleziona da un dato universo la classe degli oggetti che sono x, quella degli oggetti che sono y, ecc. Definisce quindi una serie di relazioni e operazioni che si applicano a tali simboli. Le due principali operazioni sono quella di prodotto: xy, indicante la classe degli oggetti che sono sia x sia y; e quella di somma: x+y, indicante la classe degli oggetti che sono x oppure y, ma non entrambi. La somma corrisponde all'uso esclusivo della disgiunzione e ammette un'operazione inversa: la sottrazione, che Boole designa con il consueto segno '−'. Con '1' egli indica l'universo di discorso e con '1−x' il complemento di x (la classe di tutte le cose che non sono x). Con il segno '=' designa l'uguaglianza tra classi; 'x=y' indica perciò che le classi x e y sono uguali (hanno gli stessi elementi). L'atto di selezione al quale corrisponde la classe vuota è indicato con '0'. Boole fissa quindi i seguenti tre principî del calcolo: (1) x(u+v)=xu+xv; (2) xy=yx; (3) xⁿ=x.

Il principio 3 è chiamato da Boole 'legge degli indici' ed è considerato il principio caratteristico su cui poggia l'intero sistema (in The laws of thought è presentato semplicemente come 'xx=x'). La struttura algebrica così costruita è un sistema matematico astratto, suscettibile di differenti piani di lettura: da un lato i 'simboli elettivi' del sistema (le variabili) possono essere interpretati come classi logiche; dall'altro si può assegnare loro un valore numerico. In quest'ultimo caso, date le restrizioni imposte dalla 'legge degli indici', gli unici valori che possono essere impiegati sono 0 e 1. Tipico del sistema booleano è il procedimento per sviluppare una data funzione logica f(x), f(x,y), ecc., sviluppo che Boole concepisce in analogia con la serie di Maclaurin per lo sviluppo di f(x) secondo potenze crescenti di x. In tal caso, l'analogia ha un valore meramente euristico: data, per esempio, la funzione logica f(x,y), se si interpretano x e y come classi, lo sviluppo dà luogo a una disgiunzione delle quattro classi che esauriscono l'universo di discorso e che si possono descrivere affermando e negando x e y (in The laws of thought l'Universo, come aveva indicato De Morgan, viene assunto variabile). Se invece x e y sono interpretati come enunciati, lo sviluppo dà luogo a una disgiunzione di membri che esaurisce tutti i possibili stati di verità e falsità in cui si può trovare una coppia di enunciati: xy+x(1−y)+(1−x)y+(1−x)(1−y)=1.

Il complesso sistema al quale Boole aveva dato vita nelle sue due opere maggiori possedeva alcune caratteristiche che lo rendevano difficilmente accettabile a molti tra i contemporanei e tra gli immediati successori. In particolare accadeva che, in talune circostanze, la macchina dimostrativa si mettesse in moto usando regole e procedure matematiche, senza che tutti i passi del processo fossero interpretabili in termini logici evidenti. Il compito di rendere meno artificioso l'impianto generale booleano e di migliorarlo nei punti essenziali fu assolto da William S. Jevons e da Charles S. Peirce (e dalla sua scuola).

William S. Jevons e Charles S. Peirce

William S. Jevons (1835-1882), allievo di De Morgan, logico ed economista, nel saggio intitolato Pure logic, or logic of quality apart from quantity (1864), sebbene contrario all'approccio eccessivamente 'matematizzante' di Boole, introdusse nel calcolo booleano alcuni cambiamenti che ne semplificano le procedure. Due tra le modifiche più rilevanti sono l'eliminazione dell'operazione inversa rispetto alla somma e l'interpretazione della somma come 'non esclusiva'. Tale modifica permette in primo luogo di estendere il principio di idempotenza alla somma logica, in modo da ottenere che valga non soltanto: aa=a, ma anche: a+a=a; consente inoltre di derivare importanti teoremi che rendono più agevole il calcolo, come le cosiddette 'leggi di assorbimento': 'a+(ab)=a' e 'a(+b)=a'.

Qualche anno dopo la pubblicazione della Pure logic di Jevons, Charles S. Peirce (1839-1914) proponeva in un saggio sull'algebra di Boole (On an improvement in Boole's calculus of logic, 1867) l'adozione della somma logica non esclusiva e avanzava l'esigenza di 'depurare' il calcolo booleano dal ricorso a un uso non sempre motivato di strumenti e metodi desunti dalla matematica. Tra il 1867 e i primi anni del Novecento, Peirce si occupò intensamente di logica, sviluppando una trattazione algebrica dei 'termini relativi' e individuando una nutrita serie di teoremi per il calcolo delle classi, che Friedrich Wilhelm Karl Ernst Schröder riprenderà nelle Vorlesungen.

Già De Morgan, al quale Peirce si rifà consapevolmente, aveva sviluppato una trattazione sistematica della logica delle relazioni in On the syllogism (edito negli anni compresi tra il 1846 e il 1862). Con l'abbozzo di un calcolo logico delle relazioni, De Morgan aveva inteso andare oltre le ristrette possibilità della tradizionale logica aristotelica; adesso Peirce cercava di progredire ulteriormente, trattando le relazioni in maniera sistematica in rapporto alla quantificazione. Come Boole aveva considerato le proprietà alla stregua di classi di oggetti, analogamente Peirce, nel calcolo dei relativi, concepisce le relazioni quali classi di coppie, di terne, di quadruple, ecc., di oggetti tra i quali sussistono quelle determinate relazioni. Ricorrendo alle matrici, egli definisce le nozioni di somma relativa e di prodotto relativo e sviluppa una trattazione sistematica dei quantificatori universale (che rappresenta con il simbolo 'Π') e particolare (che rappresenta con il simbolo '∑'). Per esempio, ponendo l=amante, b=benefattore e i, j essendo variabili su individui nell'ambito degli esseri umani, gli enunciati 'i è un amante di j' e 'i è un benefattore di j' vengono espressi nel simbolismo di Peirce, rispettivamente come: 'l_ij' e 'b^ij'. Di conseguenza, Πⁱ ∑^j l^ij b^ij significherà che ogni i è un amante e un benefattore di qualche j; mentre Πⁱ ∑^j l^ij b^ji significherà che ogni i è un amante di un benefattore di sé stesso. Con le risorse del proprio simbolismo, Peirce riesce a determinare i rapporti reciproci tra quantificatori e a individuare le regole che ne governano l'uso anche nel caso di quantificazioni reiterate e tra loro intrecciate. Egli prescrive inoltre una serie di regole comprendenti quella che, in seguito, verrà chiamata la 'forma normale premessa': in una formula in cui compaiono quantificatori, questi devono essere disposti all'inizio, e i quantificatori esistenziali devono essere disposti quanto più a sinistra di quelli universali.

Fin dal 1870, Peirce introduce nei suoi saggi sul calcolo logico il segno

per indicare la relazione di inclusione tra classi. Circa un decennio più tardi adopererà il medesimo segno per indicare sia l'inclusione tra classi sia l'implicazione tra proposizioni, in modo da sviluppare, contemporaneamente al calcolo delle classi, un vero e proprio 'calcolo degli enunciati'. In rapporto a tale sviluppo, Peirce fissa un insieme di assiomi per la logica enunciativa e propone di valutare gli enunciati composti attribuendo in maniera puramente combinatoria i valori 'vero' e 'falso' agli enunciati componenti.

Non tutti gli scritti logici di Peirce vennero editi mentre questi era in vita. Tra i saggi pubblicati postumi, merita di essere ricordato un breve scritto (1880), nel quale vengono espressi mediante un unico connettivo tutti i connettivi del calcolo enunciativo classico; lo stesso risultato sarà ottenuto nel 1913 da Henry M. Sheffer. Peirce si impegnerà inoltre con notevole intensità nella costruzione e nello studio di grafi per rappresentare enunciati, inferenze e operazioni logiche complesse, che impiegano anche quantificatori.

Lo sviluppo algebrico della logica raggiunge con l'opera di Peirce un punto di svolta: il sistema booleano infatti, sia pure con i miglioramenti apportati da Jevons, era sufficientemente potente per poter esprimere la logica tradizionale di origine aristotelico-scolastica, ma non si spingeva molto oltre. Con Peirce si ha un potenziamento radicale delle capacità espressive della logica algebrica, che ingloba una raffinata teoria della quantificazione, estranea alla dottrina della tradizione.

La sistemazione dell'algebra della logica: la tradizione tedesca e Schröder

Friedrich Wilhelm Karl Ernst Schröder (1841-1902), matematico tedesco, insegnante dal 1876 al 1902 presso la Technische Hochschule di Karlsruhe, è colui che sistema e porta a compimento l'algebra della logica del XIX secolo. I tre volumi delle sue Vorlesungen über die Algebra der Logik (Lezioni sull'algebra della logica), pubblicati a Lipsia, rispettivamente, nel 1890 (calcolo delle classi), nel 1891 (calcolo enunciativo) e nel 1895 (calcolo dei relativi; ma la pubblicazione di parti inedite proseguì dopo la morte dell'autore, fino al 1905), costituiscono una vera e propria summa dei principali risultati ottenuti dall'algebra della logica nei circa cinquant'anni successivi alla comparsa di The mathematical analysis of logic di Boole. Animato dal desiderio di conferire un solido fondamento alla fisica e all'intero ambito delle scienze della Natura, Schröder vede nella logica e in quella che chiama 'algebra assoluta', intesa come una teoria generale delle connessioni, la base di tutte queste discipline. La logica, secondo Schröder, ha il compito di indagare le regole la cui applicazione ci permette di conoscere la verità. Oggetto della logica è il pensiero in quanto ha come fine la conoscenza; l'algebra, a sua volta, ha tra i propri compiti quello di indagare le proprietà strutturali della logica: sotto questo aspetto, la logica risulta subordinata all'algebra.

In Über die formalen Elemente der absoluten Algebra (Sugli elementi formali dell'algebra assoluta, 1874), la concezione dell'algebra assoluta di Schröder risente dell'influenza che su di lui aveva esercitato la prospettiva combinatoria proposta da Carl Friedrich Hindenburg (1741-1808). Altri autori che ebbero un ruolo importante nella formazione delle idee di Schröder sull'algebra della logica sono Martin Ohm (1792-1872) e i due fratelli Grassmann: Hermann Günther (1809-1877) e Robert (1815-1901). Ohm, nel primo volume del Versuch eines vollkommen consequenten Systems der Mathematik (Ipotesi per un sistema matematico perfettamente coerente, 1822) aveva distinto, come più tardi farà Boole, l'aspetto quantitativo da quello qualitativo della matematica e aveva usato nel calcolo simboli che designavano operazioni mentali. Inoltre, nella seconda parte del saggio Der Geist der mathematischen Analysis (Lo spirito dell'analisi matematica, 1846) aveva legato strettamente l'analisi matematica alla logica, presentando l'attività di calcolo come fondata non su grandezze o numeri, bensì su 'forme', ovvero su operazioni. Schröder aveva stretti rapporti personali con Hermann Grassmann e aveva familiarità con le prospettive filosofiche e con i risultati presenti sia nell'Ausdehnungslehre (Teoria dell'estensione, 1862) sia nel Lehrbuch der Arithmetik (Manuale di aritmetica, 1861; scritto in collaborazione con Robert). In Hermann Grassmann, Schröder trovava una distinzione delle scienze in 'reali', concernenti l'essere, e 'formali', che studiano i principî generali del pensiero; trovava inoltre l'elaborazione di una teoria astratta delle connessioni e delle loro proprietà. Attraverso Robert Grassmann, Schröder veniva a contatto con un vasto e ambizioso progetto per la costruzione di una dottrina del pensiero capace di determinare le leggi, o forme, del ragionamento scientifico che rimangono identiche per tutti gli uomini. Nel tentativo di realizzare questo progetto, Robert Grassmann aveva costruito, per vie completamente indipendenti, un sistema logico del tutto analogo a quello booleano.

Nel primo volume delle Vorlesungen, Schröder sviluppa il calcolo delle classi sulla base della 'relazione di sussunzione' (inclusione). Date due classi qualunque a e b, 'a=(=b' significa: la classe a è sussunta o identica alla classe b. Di tale relazione fissa quindi le proprietà caratteristiche: 'a=(=a' [riflessività]; 'se a=(=b e b=(=c, allora a=(=c' [transitività]; 'se a=(=b e b=(=a, allora a=b' [antisimmetria]. Sulla base della sussunzione, dopo aver definito il significato dei simboli '1' [l'universo] e '0' [la classe vuota], introduce la negazione a₁ di una classe a:

[1]  aa₁=(=0   1=(=a+a₁.

Indipendentemente dall'inclusione, egli introduce le operazioni di prodotto e di somma, che rappresenta, rispettivamente, con la giustapposizione di lettere e con il segno '+'; e ne descrive le relative proprietà:

Un'importante acquisizione che risalta nelle Vorlesungen (ma era già presente nel breve saggio Der Operationskreis des Logikkalkuls, Le operazioni del calcolo logico, 1877) è la consapevolezza del carattere duale delle operazioni di prodotto e di somma logica. La dualità si basa sull'osservazione del comportamento simmetrico della somma e del prodotto logici: date due formule f e g nelle quali le sole operazioni che compaiono sono la somma, il prodotto logico e la negazione, se in entrambe si scambiano tra loro simultaneamente le occorrenze del prodotto con quelle della somma, si ottengono due formule f′ e g′ che sono 'duali' rispetto a f e g. Se f implica g, f′ (il duale di f) implica g′ (il duale di g), ecc. Le cosiddette 'leggi De Morgan' (note almeno fin dal Medioevo, ma così chiamate in onore di De Morgan, al quale si deve un'applicazione sistematica di esse) sono un tipico esempio di comportamento duale di congiunzione e disgiunzione: 'non(p e q)' equivale a 'non-p o non-q'; 'non(p o q)' equivale a 'non-p e non-q' (per 'p' e 'q' enunciati qualsiasi).

All'algebra delle relazioni Schröder attribuisce un ruolo fondante in rapporto al progetto di una lingua universale ('pasigrafia'), mutuato direttamente da Leibniz. Per costruire una lingua scientifica che fosse al di sopra delle peculiarità linguistiche nazionali, Schröder riteneva indispensabile la costituzione di una 'filosofia esatta' che avesse come momento essenziale lo studio dei relativi. Nel terzo volume delle Vorlesungen, Schröder introduce le operazioni sulle relazioni e ne studia le proprietà più rilevanti. L'inserimento della dottrina delle relazioni nel programma per la costruzione della lingua universale fa sì, tuttavia, che Schröder abbia scarso interesse per la definizione di una struttura assiomatica per il calcolo dei relativi. Ciò comporta una scarsa selettività: come osserverà Peirce, nel terzo volume delle Vorlesungen Schröder deriva una gran quantità di teoremi e svolge dimostrazioni assai complesse, senza un criterio che ne specifichi l'importanza e i reciproci rapporti all'interno del sistema.

Come figure di rilievo nel panorama degli algebristi della logica del secondo Ottocento, sono da ricordare infine John Venn (1834-1923) e Hugh McColl (1837-1909). Venn, insegnante di logica e scienze naturali presso l'Università di Cambridge, elaborò un metodo diagrammatico che, estendendo i metodi di Euler, consente di dare una rappresentazione geometrica delle relazioni tra classi e tra enunciati. Nella Symbolic logic (1881) egli fornì inoltre un'interessante traccia storica degli sviluppi della logica fino alla seconda metà dell'Ottocento. McColl, laureatosi presso l'Università di Londra, insegnò per lungo tempo in una scuola francese a Boulogne-sur-Mer. Riteneva che la logica dovesse trovare il proprio fondamento nella teoria degli enunciati piuttosto che nella teoria delle classi e, a partire dalla fine degli anni Settanta, sviluppò un sistema logico nel quale teorizzava il ricorso a un condizionale non materiale.

Bibliografia

Ferriani 1999: Ferriani, Maurizio, Logica e filosofia della logica. Studi su Boole e Peirce, Bologna, Clueb, 1999.

Freguglia 1978: Freguglia, Paolo, L'algebra della logica. Un profilo storico, Roma, Editori Riuniti, 1978.

Grattan-Guinness 1991: Grattan-Guinness, Ivor, The correspondence between George Boole and Stanley Jevons, 1863-1864, "History and philosophy of logic", 12, 1991, pp. 15-35.

Hailperin 1981: Hailperin, Theodore, Boole's algebra isn't Boolean algebra, "Mathematics magazine", 54, 1981, pp. 172-184.

‒ 1986: Hailperin, Theodore, Boole's logic and probability. A critical exposition from the standpoint of contemporary algebra, logic and probability theory, 2. revised and enlarged edition, Amsterdam-London, North-Holland, 1986 (1. ed.: 1976).

Koppelmann 1971-72: Koppelmann, Elaine, The calculus of operation and the rise of abstract algebra, "Archive for history of exact sciences", 8, 1971-1972, pp. 155-242.

Peckhaus 1997: Peckhaus, Volker, Logik, Mathesis universalis und allgemeine Wissenschaft. Leibniz und die Wiederentdeckung der formalen Logik im 19. Jahrhundert, Berlin, Akademie Verlag, 1997.

Pycior 1981: Pycior, Helena, George Peacock and the British origins of symbolical algebra, "Historia mathematica", 8, 1981, pp. 23-45.

‒ 1983: Pycior, Helena, Augustus De Morgan's algebraic work: the three stages, "Isis", 74, 1983, pp. 211-226.

Schubring 1996: Hermann Günther Grassmann (1809-1977). Visionary mathematician, scientist and neohumanist scholar. Papers from a sesquicentennial conference, edited by Gert Schubring, Dordrecht-Boston-London, Kluwer Academic, 1996.

Thibaud 1975: Thibaud, Pierre, La logique de Charles Sanders Peirce. De l'algèbre aux graphes, Aix-en-Provence, Éditions de l'Université de Provence, 1975.