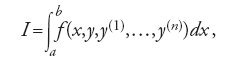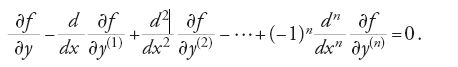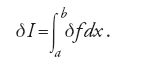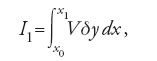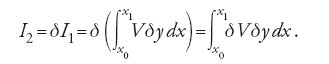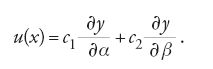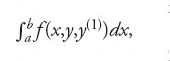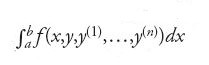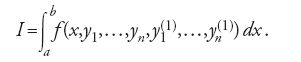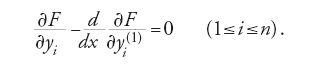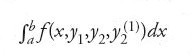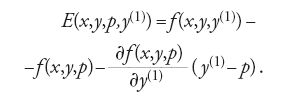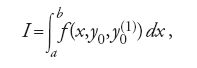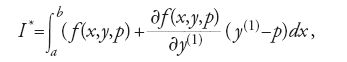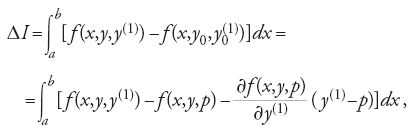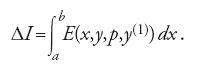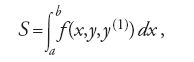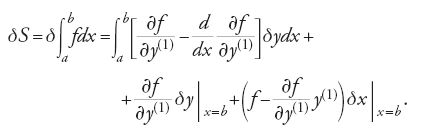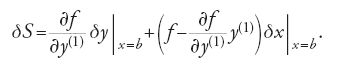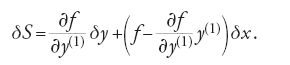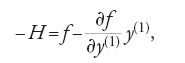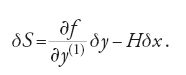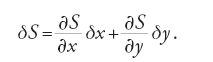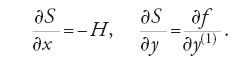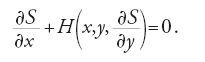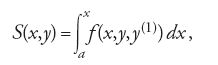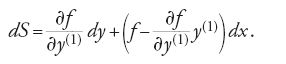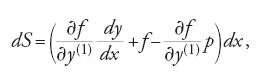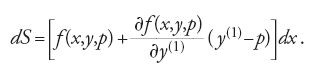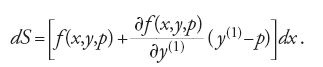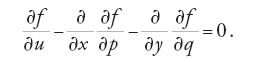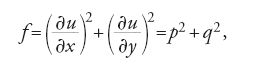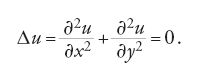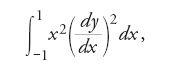L'Ottocento: matematica. Calcolo delle variazioni
L'Ottocento: matematica. Calcolo delle variazioni
Calcolo delle variazioni
Il problema di Euler
Nel 1744 Leonhard Euler formulò il problema principale del calcolo delle variazioni nei seguenti termini: determinare, in un opportuno insieme di curve, quella particolare curva y=y(x), detta in seguito da Adolf Kneser 'curva estremale', che rende massimo o minimo l'integrale definito:
ove x varia nell'intervallo [a,b] e y(k) (1≤k≤n) è la derivata di ordine k della funzione y. In questa formulazione si parte dal presupposto che le suddette curve assumano tutte gli stessi valori negli estremi a e b: per questa ragione la [1] rappresenta quello che si è soliti chiamare un 'problema a estremi fissi'. Euler arrivò alla conclusione che la soluzione y=y(x), se esiste, deve soddisfare la seguente equazione differenziale:
Egli ottenne la [2] calcolando l'integrale [1] prima lungo la curva y(x), poi lungo un'altra curva passante ‒ come la y(x) ‒ per uno stesso numero finito di punti, valutando la differenza fra i due valori dell'integrale e ponendo infine tale differenza uguale a zero.
Nel 1762 il giovane matematico torinese Joseph-Louis Lagrange introdusse un nuovo e migliore metodo per ottenere la [2], basato sul suo 'algoritmo δ'. Egli identificò l'insieme delle curve che intervengono nella [1] con le curve del tipo y+δy, dove l'operatore δ soddisfa algoritmicamente la relazione dδ=δd. In questo nuovo 'processo variazionale' la curva di confronto y+δy, detta anche 'curva campione', può assumere, in ciascuno degli infiniti punti x dell'intervallo [a,b], valori diversi da quelli della curva soluzione y. L'algoritmo δ di Lagrange consente la derivazione sistematica delle equazioni variazionali e agevola, inoltre, il trattamento delle condizioni che la curva soluzione deve soddisfare nei punti estremi a e b. Euler adottò immediatamente il metodo di Lagrange e introdusse il termine 'calcolo delle variazioni' per indicare la nuova disciplina basata su quel metodo. In onore del contributo fondamentale dato dai due matematici, l'equazione [2] è nota come equazione di Euler-Lagrange, o semplicemente come equazione differenziale di Euler; essa indica le condizioni fondamentali che deve soddisfare qualsiasi soluzione del problema variazionale.
In una memoria pubblicata nel 1788, Adrien-Marie Legendre ampliò la teoria di Lagrange avviando lo studio della 'variazione seconda' dell'integrale [1]. La variazione seconda è il termine di secondo ordine nello sviluppo di
Per curve che soddisfino l'equazione di Euler esso domina lo sviluppo dell'integrale [3] ‒ costituendone il primo termine non nullo ‒ cosicché lo studio del suo segno può indicare se la soluzione proposta per la [1] sia in effetti ottimale (ossia se effettivamente renda massimo o minimo l'integrale [1]). Le conclusioni di Legendre erano basate sulla possibilità di ottenere la variazione seconda come integrale di un'espressione in forma definita positiva (ossia a segno costante). Per compiere tale trasformazione è necessario integrare una equazione differenziale non lineare, ma Legendre non propose alcun metodo che consentisse, in generale, di ottenere tale integrazione.
Successivamente Lagrange fornì esempi particolari, con i quali mostrava che il suddetto integrale può non esistere nell'intervallo considerato. Egli inoltre dimostrò che se non si limita opportunamente l'ampiezza dell'intervallo [a,b], è possibile determinare, in corrispondenza di una curva y che soddisfi l'equazione di Euler e la condizione di Legendre, altre curve campione y+δy sulle quali l'integrale [1] assuma valori sia maggiori sia minori del valore assunto su y. Lagrange, che pure aveva approfondito questi problemi, non sviluppò però alcuna teoria sulla variazione seconda che indicasse quando poterla trasformare nell'espressione di Legendre.
Jacobi
Nel 1837 il matematico tedesco Carl Gustav Jacob Jacobi pubblicò, un articolo molto originale e di grande rilievo sul "Journal" diretto da Crelle. In effetti fu proprio nel periodo trascorso all'Università di Königsberg, tra il 1826 e il 1843, che Jacobi produsse i lavori migliori. Nel 1843 egli si trasferì a Berlino, ove tenne seminari e continuò le sue ricerche fino alla morte, avvenuta nel 1851. Nell'articolo del 1837 Jacobi riuscì a definire un insieme organico di condizioni che assicurano l'esistenza di un massimo o di un minimo come soluzione di un problema generale variazionale. Il suo contributo, denso di risultati, diede origine a un vasto programma di ricerche matematiche, anche perché in esso non erano fornite dimostrazioni e giustificazioni dettagliate. L'idea nuova di Jacobi era di esprimere, in maniera opportuna, la relazione tra variazione prima e variazione seconda facendo uso dell'operatore variazionale δ. Nel caso più semplice, nel quale l'integranda della [1] ha la forma f=f(x,y,y(1)), le relazioni tra l'integrale I della [1] e le sue variazioni prima (I1) e seconda (I2) sono:
[4] I1=δI , I2=δI1.
Pertanto, esprimendo I1 nella forma
dove V=(∂f/∂y)−(∂f/∂y(1))d/dx è la trasformata di Euler, la variazione seconda I2 assume la seguente espressione:
La soluzione y=y(x) del problema variazionale deve soddisfare l'equazione di Euler, che è un'equazione differenziale del secondo ordine la cui soluzione dipende da due costanti arbitrarie α e β. Affinché una soluzione sia un 'buon estremale' (o, come anche si dice, sia 'non degenere'), nessuna variazione δy deve rendere nulla I2. È pertanto naturale studiare le condizioni nelle quali I2=0. Dalla [6] appare evidente che I2=0 se δV=0. Indicata con y=y(x,α) una funzione della quale è resa esplicita la dipendenza da α (una delle due costanti arbitrarie), il fatto che la y sia la soluzione dell'equazione di Euler implica che essa soddisfi anche l'equazione V(α)=0. Considerata, allora, la costante α come un parametro, aggiungendole un incremento δα si ottiene anche che V(α+δα)=0; se si considera un processo variazionale nel quale δy=(∂y/∂α)δα, sottraendo V(α)=0 da V(α+δα)=0 si perviene alla conclusione che (∂y/∂α)δα è soluzione dell'equazione δV=0. Analogo risultato si ottiene per β, l'altra costante arbitraria da cui dipende la soluzione y del problema variazionale: ossia δy=(∂y/∂β)δβ è soluzione dell'equazione δV=0; ma δV=0 è un'equazione differenziale lineare del secondo ordine nell'incognita δy, la cui soluzione generale ha pertanto la forma δy=εu(x), dove u(x) è la funzione in [7] con c1 e c2 costanti arbitrarie.
Il contributo di Jacobi fu quello di concepire una teoria che collegava le soluzioni dell'equazione di Euler all'analisi della variazione seconda. Ciò gli consentì di utilizzare la funzione u(x), data dalla [7], per risolvere l'equazione differenziale di Legendre, ma Jacobi non si limitò a tale risultato, già di per sé notevole: utilizzando ancora la [7], egli introdusse una nuova trasformazione per la variazione seconda I2, ottenendo di nuovo la forma standard definita positiva di Legendre. Con la sua teoria Jacobi intendeva soprattutto affrontare il problema variazionale nel caso più generale, quello nel quale l'integranda della [1] contiene derivate rispetto alla variabile x di ordine superiore al primo.
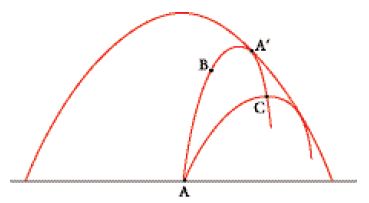
Le numerose ricerche che furono intraprese sotto lo stimolo dell'articolo di Jacobi, riguardarono prevalentemente lo studio della trasformazione della variazione seconda. I principali contributi in tal senso si devono a Charles-Eugène Delaunay nel 1841, Simon Spitzer nel 1854 e Ludwig Otto Hesse nel 1857. Tuttavia nel suo articolo Jacobi aveva considerato, anche se brevemente, un altro aspetto del problema variazionale che, una volta approfondito, diede origine alla cosiddetta 'teoria dei punti coniugati'. Il problema è essenzialmente il seguente: le curve che minimizzano l'integrale [1] devono essere soluzioni dell'equazione di Euler V=0; indicata allora con y=y(x,α) la soluzione generale di tale equazione, dipendente anch'essa dalla costante arbitraria α, si richiede alla y(x,α) di passare per gli estremi A e B (fig. 1).
A tale scopo, si considera una soluzione dell'equazione di Euler 'vicina' alla precedente, ossia y(x,α+δα), passante per i punti A e C; se C coincide con B (nel punto A′ della fig. 1) si ha che sia y(x,α) sia y(x,α+δα) soddisfano le condizioni agli estremi. In tal caso è chiaro che δy=(∂y/∂α)δα è una variazione ammissibile, cioè una variazione per la quale δy(a)=δy(b)=0. In accordo con l'intuizione iniziale di Jacobi, con questa scelta di δy si ha δV=0 e ciò implica che anche la variazione seconda I2 sia nulla. È allora evidente che in questa situazione niente assicura più l'esistenza di un minimo, in quanto la variazione terza, a sua volta, può (in generale) assumere segno sia positivo sia negativo.
Se ci si muove dal punto iniziale A lungo una curva soluzione y=y(x,α), si può immaginare di arrivare infine in un secondo punto A′ per il quale passano due curve arbitrariamente vicine che soddisfano l'equazione di Euler e le corrispondenti condizioni agli estremi. Un punto siffatto, che non può mai essere superato da una curva che minimizzi l'integrale variazionale, è quello che è stato definito 'punto coniugato'. Geometricamente, A′ si trova sull'inviluppo delle curve estremali passanti per il punto A. Nella fig. 1 il punto C si trova sulla curva ABA′ oltre il punto A′, ed è chiaro che sia la curva ABA′C sia la curva AC sono soluzioni del problema variazionale tra i punti A e C. Analiticamente ciò si traduce nel fatto che non esistono funzioni della forma [7] che si annullino in due punti dell'intervallo dato [a,b]. È dunque mediante lo studio della [7] che è possibile determinare i limiti entro i quali cercare una soluzione del problema variazionale.
Jacobi illustrò la necessità di tali restrizioni richiamandosi al moto di una particella che ruota attorno a un centro di attrazione, la cui traiettoria (ellittica) si deduce dal principio variazionale di minima azione. Nelle lezioni tenute nei primi anni Quaranta e pubblicate postume nelle Vorlesungen (Lezioni, 1866), Jacobi fornì un esempio ancora più semplice, considerando una singola particella vincolata a muoversi sulla superficie di una sfera, ma non soggetta ad alcuna altra forza. In questa ipotesi il principio di minima azione implica che la traiettoria della particella sia una geodetica, ossia una curva di lunghezza minima sulla superficie della sfera. Pertanto la particella si muove su archi di cerchi massimi, che si trovano intersecando la sfera con piani passanti per il suo centro. Se il moto inizia da un punto A e procede lungo un cerchio massimo per una ampiezza angolare di 180°, la particella raggiunge un punto C coniugato di A; se il secondo estremo B coincide con C o lo supera, allora non è difficile dimostrare che esistono altri cammini campione di lunghezza minore o al più uguale.
Mayer
È bene comunque sottolineare che ad attrarre l'attenzione dei matematici nei venticinque anni successivi alla pubblicazione dell'articolo di Jacobi fu, prevalentemente, il problema dell'individuazione della forma della variazione seconda I2 e non la teoria dei punti coniugati. Ciò vale anche per l'articolo di Hesse del 1857, il quale tuttavia contiene un'intera sezione dove si dimostra che, se l'integrale [1] è della forma
allora la non esistenza di un punto coniugato nell'intervallo [a,b] implica la validità della trasformazione della variazione seconda I2. In altre parole, se nell'intervallo [a,b] non vi è alcun punto coniugato ad a, allora le condizioni necessarie per poter trasformare la variazione seconda sono valide. Tuttavia la teoria di Jacobi si riferisce prevalentemente al caso più generale di un integrale variazionale della forma
(con n≤2) e Hesse non tentò di estendere il suo risultato a questo tipo di integrale. In effetti, nel caso generale, non era affatto comprensibile in quale modo si potesse collegare la teoria dei punti coniugati al problema della trasformazione della variazione seconda.
Fu il matematico tedesco Adolph Mayer, a chiarire questo problema teorico e a proporne una soluzione soddisfacente nella sua Habilitationsschrift del 1866; due anni dopo pubblicò i suoi risultati in un articolo nella rivista di Crelle. Mayer era nato nel 1839 in una facoltosa famiglia di Lipsia e dal 1862 al 1865 aveva studiato all'Università di Königsberg. L'interesse per il calcolo delle variazioni fu stimolato tra il 1864 e il 1865 dalle lezioni tenute dal matematico Friedrich Richelot, il quale gli suggerì l'argomento per l'Habilitationsschrift. Durante l'attività presso l'Università di Lipsia, Mayer fece parte attivamente dell'ambiente matematico tedesco, contribuendo a diffondere le idee di Sophus Lie sulla teoria delle trasformazioni e dirigendo la rivista "Mathematische Annalen".
La descrizione dettagliata dei risultati raggiunti da Mayer nel 1866 non rientra fra gli scopi propostici, tuttavia è possibile accennare ad alcuni aspetti del contesto analitico generale in cui egli svolse le sue ricerche. Proseguendo il lavoro di Alfred Clebsch, un altro matematico legato alla scuola di Königsberg, Mayer formulò il problema fondamentale variazionale secondo l'approccio di Lagrange. Il 'problema di Lagrange' considera n variabili y1,…,yn, dipendenti dalla variabile x, e l'integrale variazionale della forma
Le variabili yi (1≤i≤n) soddisfano m equazioni differenziali ausiliarie della forma
[9] Φk(x,y1,…,yn,y1(1),…,yn(1))=0 (1≤k≤m).
Il problema consiste nel determinare n curve y1,…,yn che rendano massimo o minimo l'integrale [8] e che soddisfino anche le m condizioni [9]. Nel 1797 e nel 1806 Lagrange aveva mostrato come ottenere le corrispondenti equazioni differenziali variazionali mediante l'ausilio di un'opportuna funzione F. Essa si ottiene per mezzo della cosiddetta 'regola dei moltiplicatori': si moltiplica ciascuna delle equazioni Φk=0 per una funzione λk(x) (detta moltiplicatore) e poi si definisce la funzione F nel modo seguente:
La soluzione del problema deve soddisfare la [9] e le equazioni di Euler associate alla funzione integranda F:
È bene ricordare che qualsiasi problema variazionale [1] che coinvolga una sola variabile indipendente (la x), è riconducibile a un problema di Lagrange la cui funzione integranda dipenda solamente dalle derivate del primo ordine di n variabili dipendenti y1,…,yn. Per esempio, il problema dell'ottimizzazione dell'integrale ∫baf (x,y,y(1),y(2))dx, nel quale la funzione integranda dipende anche dalle derivate seconde di y, è equivalente al problema di Lagrange che ottimizza l'integrale
sottoponendo la coppia di funzioni y1 e y2 al vincolo y1(1)−y2=0. Clebsch, nel lavoro del 1858, mostrò come estendere la teoria della trasformazione di Jacobi al contesto generale del problema di Lagrange. E fu proprio muovendo dall'analisi di Clebsch della variazione seconda che Mayer studiò il legame tra punti coniugati e condizioni che giustificano la trasformazione della variazione seconda. Per ottenere i suoi risultati, Mayer fece uso di tecniche specifiche per l'integrazione di equazioni variazionali definite da Hamilton e Jacobi. Tutto ciò evidenzia come la Habilitationsschrift di Mayer del 1866 costituisca, per profondità concettuale e raffinatezza tecnica, uno dei lavori più importanti del suo tempo.
Weierstrass
Prima del contributo di Karl Theodor Wilhelm Weierstrass, nello studio dei problemi variazionali si adottava tradizionalmente un approccio introdotto da Lagrange: studiare lo sviluppo in serie di Taylor della funzione integranda della [1]. Weierstrass ebbe invece l'idea, del tutto originale, di esaminare una famiglia (o 'campo') di soluzioni dell'equazione di Euler allo scopo di individuare tecniche e condizioni sufficienti ad assicurare l'esistenza di un massimo o di un minimo per l'integrale variazionale [1]. Lagrange, nel ricavare l'equazione differenziale di Euler per mezzo del suo operatore δ, aveva implicitamente assunto che i termini in δy e δy(1) dominassero lo sviluppo in serie di f(x,y+δy,y(1)+δy(1)). Questa ipotesi implica che i termini quadratici e di ordine superiore sia in δy che in δy(1) possono essere trascurati; ne deriva che entrambe queste grandezze devono essere sufficientemente piccole. In seguito, anche Legendre, Lagrange e Jacobi assunsero implicitamente la stessa ipotesi nello studio della variazione seconda. Tale assunzione, in effetti, era alla base della teoria classica della variazione seconda; seguendo la terminologia standard moderna ‒ che si deve a Kneser ‒ tale teoria si riferisce a una 'classe di variazioni deboli', ossia un insieme di curve campione che differiscono poco (per posizione e inclinazione) dalla curva data.
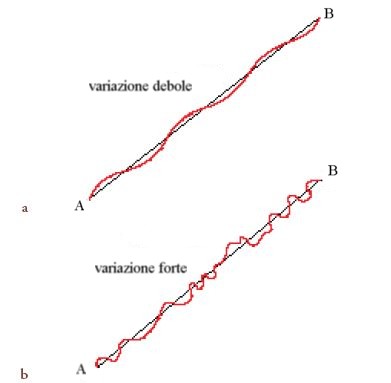
Con il suo nuovo approccio, illustrato nelle lezioni tenute a Berlino nel 1879 e mai pubblicate, Weierstrass ampliò la classe di 'curve ammissibili', includendovi le curve la cui direzione si discosta di una quantità fissata dalla direzione della curva data. Tale innovazione può essere compresa considerando il seguente problema: determinare, nel piano, la curva di lunghezza minima che collega due punti A e B fissati (fig. 2).
Risolvendo l'equazione di Euler si ha che la soluzione del problema è costituita dalla retta che unisce A e B. La teoria variazionale classica considerava come curve campione quelle che si discostano poco dalla retta, non soltanto per la posizione, ma anche nella loro inclinazione (fig. 2a); invece la tecnica di Weierstrass consente di adottare come curve campione anche gli archi che, pur restando vicini alla retta, possano rapidamente oscillare attorno a essa (fig. 2b). Esistono altre situazioni, meno semplici ma ugualmente importanti, in cui è possibile mostrare che la stessa curva che rende massimo (o minimo) l'integrale [1] rispetto alla classica (più ristretta) famiglia di curve campione può non essere più ottimale se i valori di [1] si confrontano sulla famiglia più vasta introdotta da Weierstrass.
Negli anni Settanta del XIX sec. vi erano ormai precisi motivi tecnici che sollecitavano l'introduzione di famiglie più ampie di variazioni (ossia di curve campione), ma il calcolo delle variazioni subì un profondo cambiamento per ragioni di metodo ancor più generali. Oggi nel calcolo delle variazioni è ben chiara la distinzione logica tra condizioni necessarie e condizioni sufficienti per l'esistenza di una soluzione, tuttavia in passato questa distinzione non era altrettanto evidente, almeno fino a Weierstrass. In effetti, prima del suo apporto, si assumeva sempre, implicitamente, che qualsiasi problema variazionale avesse soluzione e se ne deduceva l'esistenza dal fatto che certe equazioni o certe condizioni fossero soddisfatte. I matematici dell'epoca, ottenendo condizioni che oggi indicheremmo come necessarie, ritenevano invece di aver dimostrato l'esistenza della soluzione del problema. Se alcuni esempi particolari ‒ forniti da Weierstrass ‒, mostravano che non sempre un problema variazionale ha soluzione si trattava di rafforzare opportunamente le condizioni in modo da escludere quei casi eccezionali.
Come si è già detto, le classiche condizioni di Euler, Legendre e Jacobi venivano ottenute mediante tecniche di sviluppi in serie che, a loro volta, necessitavano implicitamente della classe delle variazioni deboli. D'altra parte, se si pensa alle premesse metodologiche generali dalle quali partivano i ricercatori che in base a tali condizioni isolavano e determinavano gradualmente una soluzione, si comprende perché essi non si fossero preoccupati di stabilire a priori la classe di funzioni campione. È bene ricordare che anche il nuovo 'approccio basato sull'idea di campo' di Weierstrass faceva uso sia di sviluppi in serie sia della classe di variazioni deboli per ottenere molte delle condizioni necessarie che la soluzione deve soddisfare. Sembra comunque ragionevole pensare che Weierstrass fosse spinto ad ampliare la classe delle variazioni da ragioni di carattere metodologico del tutto generali, legate soprattutto alla chiara consapevolezza della distinzione tra condizioni necessarie e condizioni sufficienti.
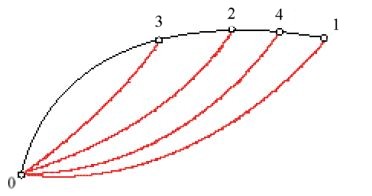
Weierstrass ipotizzò che la curva y0=y0(x), soluzione del problema variazionale, potesse trovarsi in una fascia o regione (Flächenstreifen) del piano interamente formata da una famiglia di soluzioni dell'equazione di Euler (tra le quali y0), e tale che ogni suo punto fosse collegabile al punto iniziale da una e una sola curva di quella famiglia. Nella fig. 3, tratta dalle lezioni di Weierstrass, è illustrata tale famiglia per l'arco 01; considerati i punti 3, 2, 4, esiste una e una sola soluzione dell'equazione di Euler che unisce 0 a 3, 0 a 2, 0 a 4. Nel Lehrbuch der Variationsrechnung (Trattato di calcolo delle variazioni), pubblicato nel 1900, Kneser diede formalmente a tale particolare famiglia di curve il nome di 'campo di estremali'. L'esistenza di un campo è assicurata se in tutta la regione considerata vale il criterio di Jacobi. Indicata con p(x,y) la pendenza che assume l'unica curva estremale passante per il punto di coordinate x e y, Weierstrass introdusse la funzione E, o 'funzione eccesso' (detta anche 'funzione di Weierstrass'), così definita:
Egli mostrò che se la condizione
[13] E(x,y,p,y(1))≥0
è soddisfatta su ogni curva campione y=y(x), allora la soluzione y0=y0(x) del problema variazionale rende minimo l'integrale [1]. In seguito, il metodo di Weierstrass subì sostanziali modifiche a opera di diversi matematici, tra i quali si distinse indubbiamente David Hilbert, che nel 1900, per ottenere più agevolmente la condizione sufficiente [13], introdusse il suo famoso 'invariante integrale'. Sia:
e y(x) una curva campione coincidente con y0(x) nei punti x=a e x=b; la differenza ∣y(x)−y0(x)∣ è piccola, ma ∣y(1)(x)−y0(1)(x)∣ può non esserlo. Considerato allora l'integrale:
Hilbert dimostrò che I* non dipende dal particolare cammino, ossia che esso assume lo stesso valore su una qualsiasi curva y(x) purché questa coincida con la curva y0 negli estremi a e b dell'intervallo di integrazione. Lungo la curva y0=y0(x) si ha y0(1)(x)=p(x,y0(x)) e pertanto su essa I*=I. Ne segue che la variazione ΔI è
da cui:
Così, se la condizione
[18] E(x,y,p(x,y),y(1))≥0
è soddisfatta su tutti gli archi campione y=y(x), allora l'integrale [1] assume sulla curva y0=y0(x) il valore minimo.
La teoria di Hamilton-Jacobi
Oggi la teoria di Hamilton-Jacobi è presentata dai libri di testo in termini molto astratti e formali, nell'ambito di tecniche per la trasformazione di coordinate: in realtà essa possiede una struttura concettuale ben più ricca e interessante. William R. Hamilton, durante le sue ricerche di meccanica analitica condotte negli anni Trenta del XIX sec., ebbe l'idea di considerare un certo integrale come una funzione dipendente dai suoi due estremi di integrazione. Ciò gli fu possibile perché la curva su cui valutava l'integrale era ottenuta analiticamente come soluzione delle equazioni del moto. Hamilton dimostrò che l'integrale, considerato come funzione degli estremi (la cosiddetta 'funzione principale'), soddisfa due equazioni differenziali alle derivate parziali del primo ordine. La sua analisi, pur richiamandosi a idee e tecniche proprie del calcolo delle variazioni, fu impiegata nell'ambito della meccanica analitica, una teoria ben consolidata. Hamilton nel 1834, con molta modestia rispetto all'importanza dei risultati ottenuti, affermava in una lettera al suo amico William Whewell di aver "rivoluzionato la meccanica". Jacobi, infatti, partì da quella che riteneva una "bellissima idea" di Hamilton, per sviluppare una teoria più generale. Jacobi si concentrò soprattutto sul problema dell'integrazione di equazioni differenziali. Con l'uso della teoria delle equazioni alle derivate parziali, egli dimostrò che le soluzioni delle equazioni del moto (equazioni differenziali ordinarie del secondo ordine) possono ottenersi anche risolvendo un'equazione alle derivate parziali del primo ordine, nota come equazione di Hamilton-Jacobi. Di seguito riportiamo uno schema che intende dare solamente un'idea, per sommi capi, delle principali intuizioni scientifiche di Hamilton e Jacobi. Considerato l'integrale variazionale S associato a una data funzione f(x,y,y(1)):
la variazione di S, su un arco di curva il cui estremo b può variare in entrambe le direzioni x e y del piano, è data dalla formula
Se la curva che unisce gli estremi a e b è un estremale dell'integrale [19], deve soddisfare l'equazione di Euler e la [20] si riduce alla
La [21] è la formula generale della variazione prima quando il secondo estremo della curva è libero di variare nel piano e viene detta 'formula dell'estremo libero'. Se si pone b=x essa diventa:
Definendo la funzione H con la relazione
la [22] si scrive
L'integrale S, valutato su una curva estremale, può considerarsi una funzione di x e y, cioè S=S(x,y); pertanto:
Confrontando la [24] con la [25] si ottiene
Combinando infine queste due equazioni e usando la seconda per eliminare y(1), si ottiene la seguente equazione differenziale alle derivate parziali:
Oggi H è detta 'funzione hamiltoniana' e la [27] è conosciuta come equazione di Hamilton-Jacobi associata al problema. Jacobi dimostrò che integrare l'equazione differenziale ordinaria di Euler equivale a determinare una soluzione completa dell'equazione differenziale alle derivate parziali [27] (per soluzione completa si intende una soluzione che contenga una sola costante arbitraria non additiva).
La bellezza della teoria di Hamilton-Jacobi risulta dal modo in cui riesce a unire settori dell'analisi tra loro così diversi, quali la meccanica analitica, la teoria delle equazioni differenziali (tanto ordinarie quanto alle derivate parziali), il calcolo delle variazioni e la geometria differenziale. In particolare, la teoria di Hamilton-Jacobi ha storicamente svolto un ruolo fondamentale nel calcolo delle variazioni e precisamente nello studio della variazione seconda. Infatti Clebsch e Mayer espressero le equazioni variazionali di Euler in forma canonica e, integrandole, ottennero una trasformazione della variazione seconda. Ancor più significativa è l'importanza che la teoria di Hamilton-Jacobi ha avuto nella teoria dei campi estremali. L'idea di Hamilton di considerare un certo integrale come funzione degli estremi di integrazione contiene implicitamente un concetto di grande portata che, nel 1904, Oskar Bolza definì 'integrale di campo'.
Anche se Hilbert non spiegò in quale modo fosse giunto alla definizione del suo integrale invariante, è evidente il legame logico di tale definizione con alcuni concetti della teoria di Hamilton-Jacobi, come si deduce, per esempio, dall'esame del caso qui sotto illustrato. Considerato l'integrale
dove si assume che S sia valutato lungo l'unica curva estremale che unisce il punto iniziale a, fissato, al punto finale (x,y), variabile, si ha che S(a,b)=I. Se δy=dy e δx=dx, dalla formula [21] dell'estremo libero si ottiene:
Nella [29] il valore di y(1) nel punto (x,y) è uguale alla pendenza p(x,y) della curva estremale nello stesso punto. Basta ora svolgere alcuni calcoli per verificare quanto osservò Hilbert, e cioè che la [29] è un differenziale esatto se e soltanto se la curva estremale passante per (x,y) soddisfa l'equazione di Euler in quel punto. Infatti, se si riscrive dS nella forma
si ha:
Nella [31] y(1) indica la pendenza della curva campione y=y(x) nel punto (x,y). Pertanto l'integrale variazionale, valutato tra a e b, è dato dalla formula
Il termine a sinistra della [32] è proprio I, mentre quello a destra è I*; ciò equivale a dire che I* è invariante.
Il problema dell'esistenza delle soluzioni
Anche se finora sono stati trattati esclusivamente gli integrali variazionali del tipo [1], che coinvolgono una sola variabile (la x), non è difficile estendere la teoria a problemi variazionali che presentino più di una variabile indipendente. Sia R una regione del piano xy, u=u(x,y) una funzione definita in R e vincolata ad assumere valori prefissati sulla frontiera C di R, p=∂u/∂x e q=∂u/∂y le sue derivate parziali; si supponga di voler trovare il massimo o il minimo dell'integrale
[33] ∬Rf (x,y,u,p,q)dx dy.
La soluzione di questo problema variazionale deve soddisfare l'equazione differenziale di Euler
Per esempio, considerata la funzione
in questo caso l'equazione di Euler per la funzione f si riduce alla cosiddetta 'equazione del potenziale' o di Laplace per la funzione u:
Nel XIX sec. il problema della determinazione di una funzione che, in una regione del piano, fosse soluzione dell'equazione [36] e assumesse sulla sua frontiera valori prefissati interessava sia chi si occupava di teoria del potenziale sia i matematici impegnati in ricerche di analisi complessa. In entrambe queste discipline si era soliti affermare l'esistenza di una tale funzione deducendola dal fatto che essa fosse soluzione di un 'ben noto' problema di calcolo delle variazioni. Sostenitori di questo orientamento erano, per esempio, George Green, William Thomson e Peter Gustav Lejeune Dirichlet nella teoria del potenziale, Georg Friedrich Bernhard Riemann in analisi complessa. In tal modo il calcolo delle variazioni divenne garante dell'esistenza di una funzione utilizzata in altri settori dell'analisi matematica. Quel tipo di ragionamento fu chiamato da Riemann 'principio di Dirichlet'. Tuttavia nel 1870 Weierstrass osservò che non sempre un problema del calcolo delle variazioni ammette soluzione. Egli considerò come esempio l'integrale
nel quale y è una funzione (generica) che nei punti x=−1 e x=+1 assume valori distinti e fissati. Weierstrass mostrò che, sebbene sia possibile trovare funzioni ammissibili y=y(x) che rendano arbitrariamente piccolo l'integrale [37], nessuna di esse è una curva estremale (ossia nessuna rende uguale a zero tale integrale). L'osservazione di Weierstrass mise in discussione la validità del principio di Dirichlet come metodo generale di analisi per affermare a priori l'esistenza di talune funzioni. In effetti, per un certo periodo di tempo tale principio risultò screditato, fino a quando Hilbert, nella famosa conferenza tenuta a Parigi nel 1900, auspicò (nel problema 20) ulteriori ricerche sulla questione dell'esistenza di soluzioni di problemi variazionali. In diversi articoli pubblicati tra il 1901 e il 1906 Hilbert recuperò il principio di Dirichlet mostrando che, con opportune ipotesi, il problema variazionale ha sempre una soluzione. Questa volta, per garantire la validità di tale affermazione, Hilbert adottò il cosiddetto 'metodo diretto' del calcolo delle variazioni: invece di ricavare le equazioni differenziali di Euler e tentare di risolverle, è possibile mostrare direttamente l'esistenza di una soluzione del problema variazionale ottenendola come limite di una opportuna successione di funzioni ammissibili. Il lavoro di Hilbert inaugurò un vasto programma di ricerche che ha permeato il calcolo delle variazioni durante tutto il XX sec., nel quale le questioni di esistenza delle soluzioni hanno avuto un ruolo predominante.
Bibliografia
Bolza 1904: Bolza, Oskar, Lectures on the calculus of variations, Chicago, University of Chicago Press, 1904.
Bottazzini 1986: Bottazzini, Umberto, The higher calculus. A history of real and complex analysis from Euler to Weierstrass, translated by W. von Egmond, Berlin-New York, Springer, 1986 (ed. orig.: Il calcolo sublime. Storia dell'analisi matematica da Euler a Weierstrass, Torino, Boringhieri, 1981).
Fraser 1996: Fraser, Craig, Jacobi's result (1837) in the calculus of variations and its reformulation by Otto Hesse (1857). A study in the changing interpretation of mathematical theorems, in: History of mathematics and education. Ideas and experiences, hrsg. von Hans N. Jahnke, Norbert Knoche und Michael Otte, Göttingen, Vandenhoeck und Ruprecht, 1996, pp. 149-172.
Goldstine 1980: Goldstine, Herman H., A history of the calculus of variations from the 17th through the 19th century, New York-Heidelberg-Berlin, Springer, 1980.
Hankins 1980: Hankins, Thomas L., Sir William Rowan Hamilton, Baltimore, Johns Hopkins University Press, 1980.
Monna 1975: Monna, Antonie F., Dirichlet's principle. A mathematical comedy of errors and its influence on the development of analysis, Utrecht, Oosthoek, Scheltema & Holkema, 1975.
Nakane 1991: Nakane, Michiyo, The role of the three-body problem in construction of characteristic function for mechanics by W. R. Hamilton, "Historia scientiarum", s. 2, 1, 1991, pp. 27-38.
Thiele 1997a: Thiele, Rüdiger, Über die Variationsrechnung in Hilberts Werken zur Analysis, "Zeitschrift für Geschichte der Naturwissenschaft, Technik und Medizin", 5, 1997, pp. 23-42.
‒ 1997b: Thiele, Rüdiger, On some contributions to field theory in the calculus of variations from Beltrami to Carathéodory, "Historia mathematica", 24, 1997, pp. 281-300.
Todhunter 1861: Todhunter, Isaac, A history of the progress of the calculus of variations during the nineteenth century, Cambridge-London, Macmillan, 1861 (rist.: A history of the calculus of variations during the nineteenth century, New York, Chelsea Publ. Co., 1962).