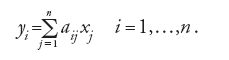L'Ottocento: matematica. Calcolo geometrico

L'Ottocento: matematica. Calcolo geometrico

Calcolo geometrico

Uno degli aspetti che hanno caratterizzato lo sviluppo della matematica nell'Ottocento è rappresentato dagli studi che portarono alla costituzione del calcolo geometrico. Queste ricerche ebbero come obiettivo la creazione di un calcolo di tipo algebrico che prendeva direttamente in considerazione enti geometrici elementari considerati sinteticamente (punti, segmenti, ecc.). In realtà già nell'Algebra (1550, 1572) di Rafael Bombelli e nella Géométrie (1637) di René Descartes si trovano tentativi di realizzare un calcolo tra segmenti non orientati in base al quale, per esempio, il prodotto tra due segmenti dà per risultato un segmento (e non una superficie). Tuttavia queste tendenze furono sviluppate solamente nella prima metà dell'Ottocento, a opera soprattutto di William R. Hamilton (1805-1865) e Hermann Günther Grassmann (1809-1877).

Tra le principali problematiche che, tra la fine del Settecento e il primo Ottocento, condussero ai sistemi di calcolo geometrico si possono individuare: la geometria di posizione, il calcolo baricentrico e la rappresentazione geometrica dei numeri complessi.

Il calcolo baricentrico

di Paolo Freguglia

La Géométrie de position (1803) di Lazare Carnot (1753-1823) rappresentò il riferimento culturale di molti tra quelli che proposero il calcolo geometrico, in particolare, di Giusto Bellavitis. Per Carnot "la geometria di posizione ha per principale oggetto la ricerca della connessione tra le rispettive posizioni delle diverse parti di una figura e i loro valori comparativi" (Carnot 1803a, p. 1). Queste connessioni si articolano mediante due tipi di correlazioni: quella di costruzione e quella di posizione. La prima consiste, per esempio, nello stabilire, tra i punti di due figure piane assegnate, una corrispondenza relativa alla costruzione medesima delle figure (per es., avere la stessa base o la stessa altezza), mentre la seconda conserva la posizione che i vari punti hanno nelle rispettive figure correlate: così, due triangoli possono essere messi in corrispondenza costruttiva se hanno la stessa altezza, ma possono non essere correlati per posizione qualora il piede dell'altezza del primo cada all'interno della base e quello dell'altezza del secondo all'esterno.

Carnot concepiva la geometria di posizione in un modo ben diverso da quello di Karl Georg Christian von Staudt, che nella Geometrie der Lage (Geometria di posizione, 1847) si riferiva alla geometria proiettiva. Alla geometria di posizione, come formulata da Carnot, sono invece legati i lavori di Simon-Antoine-Jean L'Huillier (élémens d'analyse géométrique et d'analyse algébrique appliquées à la recherche des lieux géométriques, 1809) e di Gabriel Lamé (Examen des différentes méthodes employées pour résoudre les problémes de géométrie, 1818). Carnot affronta nella sua opera del 1803 anche la determinazione del baricentro di una figura piana o solida. È però con August Ferdinand Möbius (1790-1868) che al calcolo baricentrico viene dedicata l'opera storicamente più significativa di quel periodo, cioè Der barycentrische Calcul: ein neues Hülfsmittel zur analytischen Behandlung der Geometrie (Il calcolo baricentrico: un nuovo strumento per la trattazione analitica della geometria, 1827). Carnot e L'Huillier, osserva Möbius, hanno cercato di "determinare il baricentro nell'ambito della geometria elementare considerando non corpi, superfici e linee, ma piuttosto sistemi di punti pesanti; per evitare ogni riferimento alla meccanica, chiamano 'punto delle medie distanze' il baricentro di un sistema di punti pesanti, infatti la sua distanza da un qualunque piano è uguale alla media delle distanze di tutti i punti del sistema dallo stesso piano. Tutti devono riconoscere i progressi che essi in questo modo hanno fatto compiere alla geometria" (Möbius 1827, pp. III, IV).

La determinazione di un punto particolare come il baricentro di un sistema di punti dipende dunque dai valori, cioè dai 'pesi', che sono associati ai punti. Così, dati tre punti di un piano e assegnati a essi dei pesi (cioè coefficienti numerici) possiamo calcolarne il baricentro. Al variare dei coefficienti varierà pure la posizione del baricentro, che potrà quindi descrivere curve di vario tipo. Analogamente avviene per lo spazio. Triangolo e tetraedro possono dunque essere presi come sistemi di riferimento rispettivamente per il piano e per lo spazio. Per costruire il proprio 'calcolo baricentrico' Möbius comincia con il considerare segmenti orientati, tali che AB+BA=0 e BC+CA+AB=0, se i punti A, B, C appartengono a una stessa retta. Tuttavia Möbius non presenta la regola di addizione per segmenti orientati non collineari (cioè la cosiddetta 'regola del parallelogramma').

Se A,B,C,D sono quattro punti ai quali sono rispettivamente associati i 'pesi' a, b, c, d, il relativo baricentro T si può calcolare mediante la seguente espressione: aA+bB+cC+dD= =(a+b+c+d)T.

Oltre che per i punti e per i segmenti, Möbius propose leggi di calcolo anche per le figure piane e solide orientate, realizzando un primo tentativo di calcolo geometrico che andava oltre le tecniche proposte da Carnot e L'Huillier.

La rappresentazione geometrica dei numeri complessi

di Paolo Freguglia

Nella Géométrie de position Carnot aveva sostenuto che i numeri immaginari, così come i numeri negativi, erano utili creazioni della nostra mente che non avevano un'esistenza naturale. Le convinzioni di Carnot aiutano a comprendere l'atteggiamento di quei matematici, in particolare di ambito culturale francese, che si occuparono della natura dei numeri complessi. L'idea di concepire l'unità immaginaria ε come l'unità perpendicolare all'unità reale e tale che ε²=−1 compare per la prima volta nel saggio di Caspar Wessel (1745-1818) Om Directionens analytiske Betegning (Saggio sulla rappresentazione analitica della direzione) pubblicato nel 1798 nelle "Nye samling af det Kongelige Danske Videnskabernes Selsksabs Skrifter". In verità già John Wallis (1685), Abraham de Moivre (1707), Euler (1748, 1777) e Gauss (1799) avevano pensato in maniera più o meno esplicita alla possibilità di una rappresentazione geometrica dei numeri immaginari. Il lavoro di Wessel, un agrimensore di origine norvegese, vissuto in Danimarca, rimase quasi sconosciuto per un secolo. Nondimeno, esso è storicamente significativo in quanto tratta di segmenti orientati nello spazio tridimensionale e delle loro rotazioni, temi questi che si ritroveranno sviluppati indipendentemente mezzo secolo più tardi nelle ricerche di William R. Hamilton.

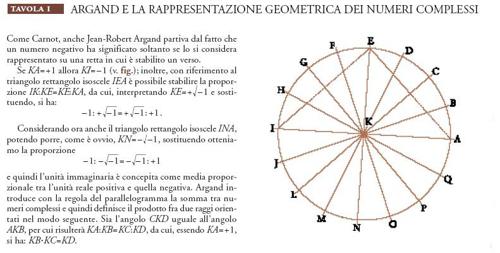
Nel 1806 apparve anonimo a Parigi l'opuscolo Essai sur une manière de représenter les quantités imaginaires dans les constructions géométriques. In realtà era stato scritto dallo svizzero Jean-Robert Argand (1768-1822). L'identità dell'autore divenne nota in seguito alla pubblicazione nelle "Annales de Mathématiques" di Joseph Diez Gergonne (1771-1859), nel 1813, di un lavoro di Jacques-Frédéric Français (1775-1833), professore alla Scuola imperiale di artiglieria e del genio.

A conclusione di quel contributo, ispirato alle concezioni della Géométrie de position, Français proponeva una rappresentazione geometrica dei numeri complessi, riconoscendo tuttavia che le idee presentate non erano sue, ma appartenevano a qualche altro autore non meglio identificato.

A questo punto Argand scrisse alla redazione della rivista di Gergonne rivendicando la paternità e presentando una memoria in cui riassumeva i risultati essenziali contenuti nel suo saggio anonimo del 1806. A questa fece seguito una serie di note di Français, Argand e di altri matematici, tra i quali Servois, che chiarirono meglio sul piano tecnico l'argomento e le relative questioni di priorità. Così Lacroix segnalò a qualche altro matematico, lettore delle "Annales", un lavoro di Adrien-Quentin Buée del 1806 al quale farà riferimento Bellavitis.

Nella nota di Français si trova fra l'altro enunciato il seguente teorema: "Tutte le radici di un'equazione di grado qualunque sono reali e possono essere rappresentate con segmenti dati in grandezza e in posizione". Questo teorema implicitamente vuol affermare che i numeri complessi non esistono se non come espressione linguistica e che essendo rappresentabili geometricamente nel piano, sono individuati da coppie di numeri reali. Come sosteneva d'altronde Argand (1806, p. 12), i numeri complessi sono impiegati proficuamente, non conducono a ragionamenti errati e anzi contribuiscono a una maggiore completezza nella soluzione dei problemi: ecco perché bisognava dar loro una rappresentazione adeguata e conforme a quella dei numeri reali.

Anche per Giusto Bellavitis (1803-1880), come si è accennato, fu determinante l'influenza della Géométrie de position. Professore di matematica al liceo di Vicenza e poi ordinario di geometria descrittiva nell'Università di Pavia a partire dal 1845, manifestò fin dai suoi primi studi, l'obiettivo di contribuire al programma geometrico tracciato e prospettato da Carnot. Il calcolo delle equipollenze, proposto da Bellavitis in una serie di lavori a partire dal 1832, costituisce uno strumento per ottenere geometricamente l'algebra dei numeri complessi e contemporaneamente un completo calcolo geometrico piano. Come scriveva Bellavitis nel Saggio sull'algebra degli immaginarii (1852):

Il tipo o, come si disse, la rappresentazione delle quantità immaginarie, fu data da parecchi analisti molto prima che io ne deducessi il mio metodo delle equipollenze; anche Cauchy la adopera non rade volte, ma sempre come un mezzo per esprimere più chiaramente qualche circostanza relativa alle quantità immaginarie, non già come l'essenziale e unica definizione delle medesime: io invece la prenderò come la vera definizione e da essa dedurrò le proprietà degli immaginari. (p. 247)

Pur avendo forma diversa, in concreto le tecniche di Bellavitis non differivano molto da quelle di Argand e dei matematici sopra ricordati; non fa eccezione C.V. Mourey, autore di un saggio dal titolo piuttosto bizzarro La vraie théorie des quantités négatives et des quantités prétendues imaginaires dediée aux amis de l'évidence, pubblicato nel 1828.

I quaternioni di Hamilton

di Paolo Freguglia

Tra i contributi al nascente calcolo geometrico vanno ricordati quelli di Adhémar-Jean-Claude Barré de Saint-Venant, in particolare quello del 1845 dal titolo Mémoire sur les sommes et les différences géométriques, et sur leur usage pour simplifier la Mécanique. In questo lavoro Saint-Venant presentava elementi di calcolo vettoriale e nozioni del tutto equivalenti a quelle di prodotto vettoriale e prodotto misto, nonché applicazioni alla meccanica. Altrettanto significativo è il Mémoire sur les clefs algébriques (1847) nel quale Cauchy presenta le cosiddette 'chiavi algebriche'; queste richiamano alla mente alcune concezioni di Hermann Günther Grassmann il quale, peraltro, sollevò polemiche per questioni di plagio.

Al 1843 risale la pubblicazione dei fondamenti della teoria dei quaternioni di William R. Hamilton che in seguito pubblicò numerosi altri lavori sull'argomento e in particolare i due impegnativi volumi Lectures on quaternions (1853) ed Elements of quaternions (1866).

La teoria dei quaternioni deve essere considerata come uno sviluppo del calcolo tra segmenti orientati (dal piano allo spazio) e un tentativo di estensione della nozione di numero complesso. Dal 1828 al 1843 Hamilton aveva pensato a una possibile definizione di moltiplicazione fra due vettori tridimensionali che potesse soddisfare la proprietà commutativa come accade per i numeri reali e i numeri complessi. Ciò che alla fine ottenne, tuttavia, doveva proprio negare la validità di questa fondamentale proprietà. Per Hamilton il calcolo dei quaternioni risultava essere una struttura sia algebrica sia geometrica, ossia contemporaneamente un apparato teorico mediante il quale si poteva realizzare la concezione, di ispirazione kantiana, in base alla quale l'algebra doveva essere intesa come scienza del tempo puro e la geometria come scienza dello spazio puro. La nozione di quaternione non investì soltanto l'ambito matematico; nelle sue applicazioni divenne anche la chiave di lettura dell'universo fisico: lo strumento forse più adeguato per attuare quella visione meccanicistico-deterministica cui Hamilton di fatto mostra di credere al di là dei suoi riferimenti alla filosofia di Kant.

Le applicazioni dei quaternioni alla meccanica rappresentano uno degli aspetti più considerati da Hamilton e dai suoi allievi, in particolare da Peter Guthrie Tait (1831-1901). La nozione di vettore, che ha la stessa provenienza concettuale, fu considerata da Hamilton teoricamente subordinata a quella di quaternione. Ciò nonostante tale vettore fosse necessario, perlomeno sotto l'aspetto di segmento orientato, per la definizione di quaternione.

Oltre Tait, molti matematici mostrarono interesse per la teoria dei quaternioni sia per accoglierla favorevolmente sia per respingerla, ampliando talora l'apparato concettuale e introducendo altre forme di numeri ipercomplessi. Vanno quanto meno rammentati Arthur Cayley, William K. Clifford, James C. Maxwell, Josiah W. Gibbs, Oliver Heaviside e Ferdinand Georg Frobenius. In un lavoro intitolato Linear associative algebra e pubblicato nel 1870, Benjamin Peirce analizza le 'algebre lineari' a quel tempo conosciute. La linearità è una proprietà che scaturisce dal fatto che il prodotto di due unità fondamentali, quali, per esempio, i e j, dà come risultato una terza unità fondamentale k e che, per esempio, i²=j²=k²=ijk=−1. Non si ottiene mai, quindi, come risultato un termine al quadrato o ad altra potenza. Queste algebre, rispetto alla 'somma' si comportano come l'algebra ordinaria, mentre rispetto al 'prodotto' godono della proprietà associativa, ma non di quella commutativa. Nel già citato lavoro del 1870 Peirce introduce altresì le nozioni di elemento 'nilpotente' e di elemento 'idempotente', studiandone le proprietà.

Il calcolo vettoriale di Grassmann

di Gert Schubring

I lavori fondamentali di Grassmann hanno la particolarità di non basarsi su opere precedenti né di essere influenzati da idee di altri matematici, con l'unica eccezione di Justus Grassmann, il padre di Hermann, che come lui era professore di matematica al ginnasio e autore di manuali per la scuola molto originali e autonomi. Grassmann affermò che la sua nozione di prodotto in geometria sviluppava un'idea di suo padre, il quale, impegnato anch'egli nella questione sempre più controversa in matematica di quanto fosse possibile o ammissibile la moltiplicazione in geometria, aveva deciso in favore di un'interpretazione algebrica delle operazioni geometriche. La motivazione principale che Grassmann forniva, tuttavia, era quella di considerare in geometria grandezze negative. I concetti che egli espresse hanno quindi origine nello stesso ambito concettuale nel quale avevano trovato stimolo Carnot, Argand, Bellavitis e Hamilton: "La spinta iniziale nacque dalla considerazione di quantità negative in geometria. Consideravo due spostamenti AB e BA come grandezze opposte: ne seguiva che se A, B e C sono punti di una retta, allora AB+BC=AC è sempre vera, sia che AB e BC siano orientati nello stesso senso, sia che siano orientati in senso opposto, cioè anche se C giace tra A e B" (Grassmann 1844 [1995, p. 9]).

Per questi nuovi enti geometrici che attualmente vengono definiti 'vettori', Grassmann stabilì dapprima l'operazione di somma. Tale operazione era resa possibile dal fatto che oltre alla lunghezza si teneva conto anche della direzione del segmento e non soltanto di quelle opposte, ma in generale di tutte le direzioni del piano.

Egli introdusse poi l'operazione di moltiplicazione come generalizzazione della costruzione del rettangolo, che già tradizionalmente e anche da suo padre, era stata vista come l'equivalente del prodotto aritmetico. Grassmann non si limitava più soltanto al rettangolo, ma considerava, includendo di nuovo la direzione, anche il parallelogramma come un prodotto di segmenti adiacenti e orientati. La novità e la singolarità di tale nozione di prodotto consisteva nel fatto che esso non era più commutativo, bensì anticommutativo.

Stabilito così un calcolo vettoriale, la vera conquista di Grassmann fu che, pur operando con oggetti geometrici, non ci si limitava, come i matematici di cui si è finora parlato, allo spazio a tre dimensioni, o come Hamilton, che in questo segue Lagrange, a quattro, ma si consideravano più in generale spazi di dimensioni qualunque. Il superamento della frontiera della rappresentazione spaziale e l'audace generalizzazione furono rese possibili senza dubbio dal fatto che Grassmann non rifletteva soltanto su operazioni algebriche o geometriche, ma che queste per lui erano solamente applicazioni particolari. In effetti, egli voleva elaborare, con un'audacia sorprendente per i contemporanei, una 'teoria generale della forma' come fondamento di tutti i rami della matematica, teoria nella quale operazioni astratte fossero studiate senza riferimento a significati concreti.

I lavori di Grassmann fornirono un contributo particolare al nuovo orientamento della matematica che si andava sviluppando soprattutto in Prussia e nella Germania del Nord contribuendo alla nascita della matematica pura. Lo stesso Grassmann intendeva diffondere questa nuova matematica: la sua teoria delle forme doveva essere la disciplina fondamentale della matematica pura, dalla quale escludeva la geometria e la meccanica, considerandole come applicazioni.

Nella teoria delle forme si poneva il problema di scoprire le leggi generali di connessione (Verknüpfung) degli elementi, cioè le leggi delle operazioni. In primo luogo, Grassmann distingue tra operazioni sintetiche e operazioni analitiche (queste ultime inverse delle prime), come pure tra connessioni di diverso ordine o rango. Come possibili proprietà delle connessioni egli considera l'associatività, la commutatività e la distributività. Dopo una parte generale segue il significato della connessione sintetica del primo ordine come operazione di addizione, della connessione analitica come sottrazione e le corrispondenti connessioni del secondo ordine come moltiplicazione e rispettivamente divisione. Come sottolinea Grassmann, già nella nozione generale di connessione del secondo ordine, la commutatività e l'associatività non sono richieste, per cui nella nuova Ausdehnungslehre (scienza dell'estensione) saranno presenti forme di moltiplicazione non commutativa.

Sulla base della teoria generale delle forme Grassmann elabora questa nuova branca della matematica, l'Ausdehnungslehre, fondata sulla geometria; in quest'ultima molti concetti trovano la loro motivazione. Il concetto fondamentale è quello di Ausdehnungsgrösse, o 'grandezza estensiva', generata dal movimento continuo di un punto. A queste forme estensive del primo ordine si possono applicare le connessioni dell'addizione e della sottrazione (la somma vettoriale). Segue la costruzione di sistemi di ordine superiore: si considera l'insieme degli elementi ottenuti generando segmenti in due modi diversi come sistema del secondo ordine (che corrisponde al piano); analogamente per il sistema del terzo ordine. Tuttavia, mentre la geometria si deve limitare a questo spazio infinito tridimensionale, Grassmann sottolinea come la scienza astratta dell'Ausdehnungslehre non sia sottoposta a tali limitazioni e come si possano generare sistemi di ordine comunque elevato.

Per questi sistemi n-dimensionali, che seguendo Riemann saranno in seguito chiamati 'varietà', Grassmann studia e sviluppa in modo completo le operazioni (connessioni) della sua teoria delle forme, stabilendo in modo dettagliato e coerente un 'calcolo geometrico'.

Riguardo alla somma vettoriale già considerata da altri matematici, l'addizione e la sottrazione non presentano novità, a parte il fatto che la dimensione non è limitata. Il risultato veramente innovativo sta soprattutto nelle connessioni del secondo ordine, cioè nella moltiplicazione. Grassmann elabora una notevole quantità di connessioni moltiplicative in modo da soddisfare i numerosi requisiti delle varietà n-dimensionali; tutta una serie di forme moltiplicative saranno soltanto abbozzate: le più note e utili sono il prodotto esterno e il prodotto interno o prodotto scalare.

Il prodotto interno, che a partire da vettori dello stesso ordine ha per risultato uno scalare, fu introdotto nella rielaborazione della Ausdehnungslehre del 1862, la cosiddetta A₂. Il prodotto esterno è quello che occupa sempre lo spazio maggiore. Esso è caratterizzato da tre proprietà:

a) l'ordine, vale a dire la dimensione, dei fattori aumenta e, precisamente, l'ordine del prodotto è la somma degli ordini dei fattori;

b) è anticommutativo: cambiando l'ordine dei fattori il prodotto cambia di segno: ab=−ba. Il motivo per cui si ottiene questa proprietà, insolita per i contemporanei, si spiega con il fatto che le grandezze estensive (i vettori) oltre a una lunghezza posseggono anche una direzione. Il prodotto esterno ‒ la denominazione si riferisce all'aumento di dimensione (Grassman 1844, par. 36) ‒ ha quindi tanto un contenuto 'algebrico', la lunghezza come valore assoluto, quanto uno 'geometrico', il seno dell'angolo tra le due direzioni: ab=∣a∥b∣sen(ab);

c) può essere nullo anche se i fattori sono entrambi non nulli e ciò accade quando i due fattori sono 'simili', ovvero, in linguaggio moderno, sono 'linearmente dipendenti'.

Grassmann descrive in dettaglio come operare con questo prodotto. Oltre al prodotto tra due grandezze estensive egli tratta anche quello tra una grandezza numerica (un numero ordinario) e una estensiva. Considera le grandezze numeriche come rapporti, 'veri quozienti' di grandezze omogenee, sottolineando che per lui le grandezze numeriche non sono numeri discreti ma, in quanto quozienti, sono grandezze continue, cioè in pratica numeri reali. Ciò mostra come con il suo calcolo geometrico Grassmann volesse risolvere un vecchio problema ancora irrisolto, ossia moltiplicare liberamente tra loro grandezze qualunque. Il programma di più ampia portata per questo problema era stato sviluppato da François Viète: il prodotto da questi definito implicava anche l'aumento della dimensione.

Non fu tuttavia possibile a Grassmann stabilire una completa analogia tra calcolo geometrico e operazioni aritmetico-algebriche. Solamente per alcune connessioni moltiplicative egli discute di una corrispondente connessione analitica. Per il prodotto esterno egli presenta una 'divisione esterna' ma, come spiega egli stesso, nemmeno la divisione esterna era confrontabile con la divisione aritmetica. Intanto, per via della non commutatività della moltiplicazione occorre distinguere tra una divisione a destra e una a sinistra: A/B. denota il fattore C che come secondo fattore connesso con B dà A, e che quindi soddisfa la relazione BC=A; A/.B analogamente per C come primo fattore, cioè CB=A.

In secondo luogo, il quoziente non è univocamente determinato, in quanto oltre a un fattore C, anche C+X, per ogni addendo X linearmente dipendente da B, dà lo stesso prodotto. Inoltre, nella divisione esterna fattori uguali nel dividendo e nel divisore non si possono semplificare.

La seconda importante connessione-moltiplicazione è costituita dal prodotto interno. Il prodotto interno di una unità, cioè di un vettore della base con sé stessa è 1, mentre il prodotto interno di due unità diverse è zero. In questo modo Grassmann può dedurre le proprietà di ortogonalità negli spazi vettoriali. Il prodotto interno di due grandezze estensive ha per grandezze dello stesso ordine m una forma particolarmente semplice:

[1] ∑α_rβ_r=α₁β₁+α₂β₂+…+α_mβ_m.

Qui si presuppone che una grandezza estensiva, ovvero un vettore, si possa rappresentare come combinazione lineare di m grandezze del primo ordine e questo spiega perché l'Ausdehnungslehre, che è una generalizzazione della geometria, sia diventata il punto di partenza per lo sviluppo dell'algebra lineare. Questa, a sua volta, nella seconda metà del XX sec., avrebbe, almeno per un determinato periodo, completamente soppiantato la geometria. Grassmann aveva già introdotto tutti i concetti fondamentali e dimostrato i teoremi dell'algebra lineare (l'esistenza di una base di 'unità', dipendenza e indipendenza lineare, il teorema di scambio e le proprietà dimensionali del prodotto vettoriale). Il prodotto interno ha acquisito un significato centrale nell'algebra lineare come prodotto scalare o forma bilineare definita positiva; si ha infatti per un vettore a=(α₁,α₂,…,α_n,):

Tav. IV

Ironia della sorte, il prodotto esterno per grandezze estensive dell'Ausdehnungslehre, un'opera motivata geometricamente, diventerà invece la base dell'algebra multilineare che, in particolare nell'opera di Bourbaki, è la teoria modello della matematica astratta. Lo stesso Grassmann aveva già messo in rilievo, considerandolo un risultato centrale, la multilinearità del prodotto esterno (Tav. IV).

Nella letteratura su Grassmann viene sempre deplorata la scarsa o tardiva accoglienza della sua opera. Non si considera però abbastanza il fatto che, nel campo scientifico, le innovazioni fondamentali non ricevono in generale un'accoglienza immediata e che l'introduzione di una teoria generale delle forme come pure il superamento della limitazione a tre o quattro dimensioni con le varietà n-dimensionali furono effettivamente innovazioni di grande portata. Da questo punto di vista si può in realtà parlare di un'accoglienza notevolmente rapida poiché essa ebbe luogo già alla fine degli anni Cinquanta e nei primi anni Sessanta, mentre già a partire dal 1894 verranno pubblicate le opere complete di Grassmann. Sotto un altro aspetto si può invece parlare di problemi di accoglienza: poiché al tempo di Grassmann il processo di algebrizzazione e quindi di separazione del concetto di numero da quello di grandezza, aveva già compiuto molti progressi, è chiaro che la motivazione di fondare su basi coerenti la moltiplicazione tra grandezze in generale non era più un problema particolarmente sentito.

Che l'elaborazione di Grassmann del calcolo geometrico abbia avuto effetti relativamente rapidi è confermato dal fatto che tutta una serie di nozioni a lui dovute furono presto riprese e sviluppate. Uno di tali sviluppi è dato dal concetto di numero ipercomplesso, denominato anche sistema ipercomplesso. I numeri ipercomplessi sono elementi di un'algebra finito-dimensionale, associativa con unità, su un campo (che inizialmente fu quello dei numeri reali). Essi nascono come generalizzazione dei numeri complessi; le operazioni con tali numeri corrispondono a trasformazioni geometriche nel piano e quindi si trovano già nell'Ausdehnungslehre. Ricerche specifiche sui numeri ipercomplessi erano cominciate negli anni Sessanta, con Karl Theodor Wilhelm Weierstrass e Hermann Hankel. Come è stato dimostrato, Weierstrass aveva già lavorato a un teorema fondamentale nel quale tutte le operazioni con numeri ipercomplessi avvengono componente per componente in sottospazi di dimensione uno o due; dal momento però che non tutte le ipotesi erano generali, negli anni Ottanta nacque un dibattito tra i matematici tedeschi riguardo a una versione rigorosa del teorema.

Un ulteriore sviluppo concerne il nucleo centrale del programma di Grassmann, il calcolo geometrico. Tale sviluppo è legato all'opera di William K. Clifford (1845-1879), il quale lo introdusse nelle algebre che da lui prendono il nome e con le quali sono precisati specificatamente concetti che Grassmann non aveva trattato in dettaglio come quello di rotazione e della corrispondente moltiplicazione, fornendo con questa sistemazione la realizzazione completa di un'algebra geometrica.

Le matrici

A partire dal 1840 ca. si sviluppò una nuova teoria in stretta relazione con il calcolo vettoriale, la teoria delle matrici. I primi elementi di questa teoria si trovano in Lagrange e Gauss; lavori più approfonditi in James J. Sylvester (1814-1897) e Arthur Cayley (1821-1895). Fu Sylvester a coniare nel 1850 l'espressione 'matrice'. Due sono le fonti principali di tale teoria: le ricerche sulle forme bilineari, già presenti nell'algebra lineare di Grassmann, e le trasformazioni lineari:

La teoria si deve soprattutto a Cayley, che mise in luce le proprietà fondamentali dell'algebra delle matrici: somma e prodotto di matrici, moltiplicazione di una matrice per uno scalare e condizioni per l'esistenza di una matrice inversa A^-1. La teoria delle matrici si evolverà in stretta relazione con la teoria dei determinanti e degli invarianti, ma il suo grande sviluppo e, in particolare, le fruttuose applicazioni in fisica teorica, si avranno soltanto nel Novecento.

Bibliografia

Bellone 1976: Bellone, Enrico, Il mondo di carta. Ricerche sulla seconda rivoluzione scientifica, Milano, EST Mondadori, 1976.

Bloor 1981: Bloor, David, Hamilton and Peacock on the essence of algebra, in: Social history of nineteenth century mathematics, edited by Herbert Mehrtens, Henk Bos and Ivo Schneider, Boston Birkhäuser, 1981.

Bos 2001: Bos, Henk J.M., Redefining geometrical exactness. Descartes' transformation of the early modern concept of construction, New York, Springer, 2001.

Freguglia 1976: Freguglia, Paolo, I quaternioni: una chiave di lettura dell'universo, "Memorie di scienze fisiche e naturali dei Rendiconti dell'Accademia Nazionale delle Scienze detta dei XL", s. 5, v. IX, parte II, pp. 211-216.

‒ 1992: Freguglia, Paolo, Dalle equipollenze ai sistemi lineari, il contributo italiano al calcolo geometrico, Urbino, Quattro Venti, 1992.

Hestenes 1996: Hestenes, David, Grassmann's vision, in: Hermann Günther Grassmann (1809-1877). Visionary mathematician, scientist and neohumanist scholar, edited by Gert Schubring, Dordrecht-Boston-London, Kluwer Academic, 1996, pp. 243-254.

Lützen 2001: Lützen, Jesper, Julius Pedersen, Karl Weierstrass, Hermann Amandus Schwarz and Richard Dedekind on hypercomplex numbers, in: Around Caspar Wessel and the geometric representation of complex numbers, edited by Jesper Lützen, Copenhagen, Det Kongelige Danske Videnskabernes Selskab, 2001, pp. 223-254.

Schubring 1996a: Hermann Günther Grassmann (1809-1877). Visionary mathematician, scientist and neohumanist scholar, edited by Gert Schubring, Dordrecht-Boston-London, Kluwer Academic, 1996.

‒ 1996b: Schubring, Gert, Introduction. Reflections on the complex history of Grassmann's reception, in: Hermann Günther Grassmann (1809-1877). Visionary mathematician, scientist and neohumanist scholar, edited by Gert Schubring, Dordrecht-Boston-London, Kluwer Academic, 1996, pp. ix-xxix.

‒ 2003: Schubring, Gert, A case study in generalization: the notion of multiplication, activity and sign-grounding mathematics education. Festschrift for Michael Otte, edited by Michael Hoffmann, Johannes Lenhard and Falk Seeger, Dordrecht, Kluwer Academic, 2003.

Sinègre 1995: Sinègre, L., Les quaternions et le mouvement du solide autour d'un point fixe chez Hamilton, "Revue d'histoire des mathématiques", 1, 1995.