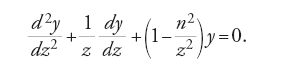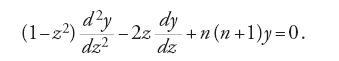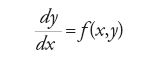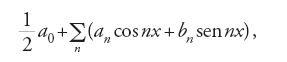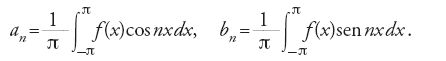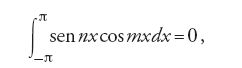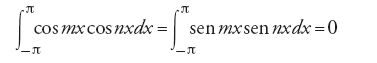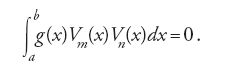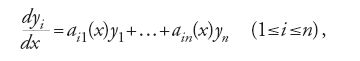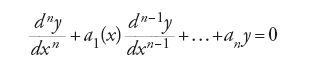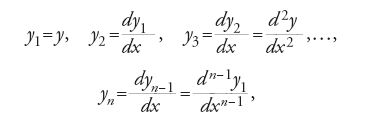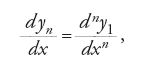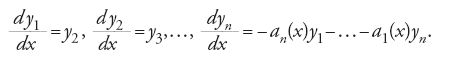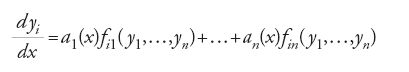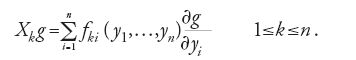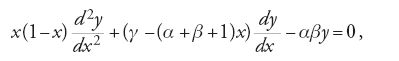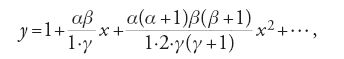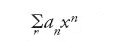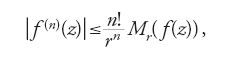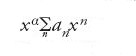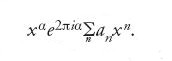L'Ottocento: matematica. Equazioni differenziali ordinarie

L'Ottocento: matematica. Equazioni differenziali ordinarie

Equazioni differenziali ordinarie

Variabili reali

Durante il XVIII sec. i matematici avevano risolto un numero crescente di equazioni differenziali ordinarie di vario tipo: equazioni lineari di ordine qualunque e a coefficienti costanti, non lineari del primo ordine, sistemi di equazioni differenziali lineari del primo ordine e così via. Nei casi in cui le soluzioni non erano disponibili 'in forma chiusa', ossia come polinomi nelle funzioni elementari, si cercava di determinarle tramite serie di potenze. Inoltre, nella seconda metà del Settecento cominciò a svilupparsi la più sofisticata teoria delle equazioni alle derivate parziali. Queste ultime sono equazioni differenziali in due o più variabili indipendenti che spesso venivano risolte con il metodo della separazione delle variabili. Poiché molti fenomeni fisici si rappresentano con equazioni differenziali alle derivate parziali del secondo ordine e la ricerca di sistemi di coordinate adeguati conduce a equazioni differenziali ordinarie (espresse in una forma spesso non familiare), erano state individuate nuove classi di equazioni differenziali ordinarie del secondo ordine accrescendo così ulteriormente l'importanza dei metodi di soluzione tramite serie di potenze. In questi problemi la fisica suggeriva ciò che i metodi formali confermavano: la soluzione generale di un'equazione del secondo ordine è esprimibile come combinazione di due sue soluzioni linearmente indipendenti e una soluzione particolare è determinata se sono noti i valori che la funzione incognita e la sua derivata prima assumono in corrispondenza di valori specifici delle variabili indipendenti.

Un'equazione differenziale ordinaria che si presenta in fenomeni diversi (per es., le oscillazioni di una catena sospesa) è l'equazione di Bessel, in cui n è un parametro

La storia dell'equazione di Bessel mostra una caratteristica importante per molti capitoli significativi della matematica pura e applicata: le soluzioni fanno parte di una piccola ma crescente classe di funzioni 'note'. Intorno al 1800 questa classe includeva le funzioni polinomiali (in una sola variabile), alcune semplici funzioni algebriche e le funzioni logaritmiche, esponenziali e trigonometriche. Una nuova funzione si può considerare nota non appena venga definito un numero sufficiente di sue proprietà quali, tipicamente, i suoi sviluppi in serie di potenze e la loro convergenza, buone approssimazioni numeriche e alcuni comportamenti qualitativi (come il numero degli zeri posseduti dalla funzione e il suo comportamento asintotico). Una conoscenza di questo tipo consente un uso agevole della funzione nell'analisi di determinati problemi; tuttavia è evidente che tale analisi richiede sempre competenza e capacità di valutazione: quelle abilità, cioè, che lezioni, corsi e libri possono diffondere a vasto raggio.

Analogamente, l'equazione del calore in coordinate polari sferiche conduce all'equazione differenziale ordinaria di Legendre di seguito riportata:

L'equazione di Legendre venne presto inclusa in una famiglia di equazioni differenziali conosciute come 'equazioni ipergeometriche' e costituisce un momento importante nella storia delle equazioni differenziali ordinarie nel campo complesso.

La riformulazione di Augustin-Louis Cauchy (1789-1857) della teoria delle equazioni differenziali è caratteristica del metodo, proprio del XIX sec., di analisi rigorosa all'interno di un paradigma strettamente numerico. In effetti, i matematici delle generazioni successive hanno attribuito a Cauchy il merito della prima fondazione adeguata dell'argomento. Cauchy espresse con grande chiarezza il suo punto di vista, secondo il quale una serie di potenze non ha alcun significato se non viene specificato il suo corrispondente raggio di convergenza. In altre parole, data una serie di potenze della forma ∑_na_nxⁿ (con x reale), o della forma ∑_na_nzⁿ (con z complesso), egli poneva l'accento sulla necessità di individuare l'insieme dei valori di x o di z per i quali la somma della serie è un valore finito. Egli aveva dimostrato che, se si escludono i casi banali, un tale insieme è sempre un intervallo della forma −M⟨x⟨M o un cerchio definito dalla relazione ∣z∣⟨R. Per esempio, la serie geometrica ∑^∞_n=₀aⁿxⁿ (nella quale si ha a_n=aⁿ, con a numero positivo fissato) converge nell'intervallo −1/a⟨x⟨1/a al valore 1/(1−ax). Cauchy sosteneva che una serie di potenze deve essere studiata all'interno del suo cerchio di convergenza, dimostrando che in questa regione possono essere applicati gli usuali processi dell'analisi; per esempio, si può differenziare la serie termine a termine, e la serie risultante converge alla derivata della funzione definita dalla serie di potenze originaria. In altre parole, Cauchy poneva l'accento sulle serie di potenze che definiscono funzioni (perché convergenti), eliminando altresì dall'analisi quei ragionamenti e quei metodi che le trattavano come espressioni algebriche formali.

Nel 1823, nelle sue lezioni all'École Polytechnique, Cauchy fornì la prima dimostrazione rigorosa dell'esistenza di una soluzione per un'equazione differenziale del primo ordine, lineare o non lineare; le lezioni preliminari erano state dedicate alla critica e alla sistematizzazione del lavoro dei suoi predecessori. Egli definiva i concetti di soluzione generale, particolare e singolare. In questo contesto, caratterizzava la relazione tra soluzione generale e particolare come relazione di dipendenza da un parametro: pertanto le soluzioni singolari (se esistono), si presentano come inviluppo di una famiglia di soluzioni particolari. Egli chiariva poi la dipendenza della soluzione particolare dalle condizioni iniziali arrivando a riformulare il problema stesso della risoluzione di un'equazione differenziale. Tale problema consiste nel trovare una soluzione dell'equazione, note determinate condizioni iniziali. Prima di Cauchy, i matematici davano per scontata l'esistenza di una soluzione generale e la loro ricerca era rivolta alla determinazione della sua forma generale; Cauchy richiese, invece, la dimostrazione dell'esistenza della soluzione particolare (una volta fissate le condizioni iniziali). In accordo con la sua teoria delle serie di potenze, Cauchy riteneva che la soluzione fosse definita soltanto nell'intorno di un dato punto. L'importanza di questa affermazione risiede nel fatto che con essa viene reso più chiaro il significato di soluzione di un'equazione differenziale, così da poter affrontare in modo diretto sia le questioni di natura teorica sia quelle di natura pratica (senza perdersi nelle nebbie dello sviluppo in serie di potenze). Per tale motivo questo problema, e altri analoghi nella teoria delle equazioni ordinarie e alle derivate parziali, vengono oggi detti 'problemi di Cauchy'.

Il metodo di Cauchy, nel caso da lui considerato, era quello di pervenire a un'approssimazione della soluzione in modo formale, per poi imporre all'equazione differenziale condizioni tali che la soluzione approssimata avesse senso dal punto di vista analitico. Questo metodo formale è detto 'metodo delle differenze finite'.

Cauchy considera un'equazione differenziale della forma

e ipotizza che, sotto certe condizioni sulla funzione f, sia possibile determinare una successione di punti x0,x1,…,x_n (per i quali le differenze x_n−x_n−1 siano arbitrariamente piccole) tali che la corrispondente successione y0,y1,…,y_n soddisfi la relazione

[4]  y_n-y_n-1=(x_n-x_n-1)f(x_n-1'y_n-1).

Ciò implica che la pendenza (yn−yn−1)/(xn−xn−1)=f(xn−1,yn−1) può essere resa arbitrariamente vicina al valore richiesto dall'equazione differenziale. Ne deriva che i punti (x_n,y_n) sono arbitrariamente vicini alla curva che è soluzione dell'equazione: è così dimostrata l'esistenza della soluzione. Anche Sylvestre-François Lacroix, e persino Leonhard Euler, avevano già trattato questo argomento in alcuni lavori, ma con finalità essenzialmente euristiche, mentre in Cauchy esso assume un ruolo fondamentale. Egli dimostra inoltre che il metodo delle differenze finite consente anche di individuare una maggiorazione dell'errore di approssimazione dei punti (x_n,y_n), trasformando così una semplice dimostrazione di esistenza in un efficace strumento di matematica applicata. In modo ancor più notevole, Cauchy affermava che, fissate certe condizioni iniziali, se esiste una soluzione della [3], questa necessariamente è unica.

Non è il caso di trattare in questa sede i dettagli delle argomentazioni di Cauchy, che necessitavano talvolta di maggiore precisione, perché questo lavoro, come spesso accadde con le sue ricerche, non era stato adeguatamente pubblicato. L'onore della prima pubblicazione della dimostrazione dell'esistenza di una soluzione di un'equazione differenziale spetta a Joseph Liouville (1809-1882), il quale usò il metodo delle approssimazioni successive per provare la risolubilità di un'equazione differenziale lineare ordinaria del secondo ordine. È lecito pertanto avanzare qualche dubbio sul fatto che l'abate François-Napoléon-Marie Moigno, nella sua opera Leçons de calcul différentiel et de calcul intégral, rédigées d'après les méthodes [...] de Cauchy (1840-1861) ‒ che, come indica il titolo, trae spunto prevalentemente dai metodi di Cauchy ‒ abbia correttamente attribuito a quest'ultimo il metodo delle approssimazioni successive: come evidenzia Jesper Lützen (1990), Moigno utilizza tale metodo limitatamente alle equazioni differenziali del secondo ordine (delle quali si era appunto occupato Liouville), mentre il metodo di Cauchy si applica alle equazioni differenziali del primo ordine. La materia è senz'altro discutibile, se si considera che il metodo delle approssimazioni successive sarebbe stato riscoperto nei suoi tratti essenziali da Picard circa sessant'anni dopo, ed è per questa ragione che di frequente viene citato sotto il suo nome. Si noti che nel 1830, durante il suo volontario esilio da Parigi, Cauchy elaborò un altro metodo, applicabile solo alle equazioni differenziali in una variabile complessa. Tuttavia, nel XIX sec. l'attenzione crescente per le funzioni di una variabile complessa era tale che questa distinzione di metodi veniva perlopiù ignorata, e i matematici successivi a Cauchy si riferirono spesso, in modo impreciso, ai metodi generali da lui definiti per provare l'esistenza di soluzioni delle equazioni differenziali. Questa imprecisione è giustificata, se costituisce un riconoscimento generale dei successi di Cauchy, al quale va il merito di aver posto al centro della ricerca matematica il problema dell'esistenza delle soluzioni.

Il problema che nel 1830 aveva attirato l'attenzione del ventunenne Liouville riguardava un fenomeno fisico di grande interesse per i suoi contemporanei e quindi in grado di stimolare un giovane brillante: la teoria della propagazione del calore. Qualche tempo prima Jean-Baptiste-Joseph Fourier (1768-1830) aveva stabilito l'equazione differenziale alle derivate parziali che governa il flusso del calore in un corpo omogeneo e individuato i metodi per risolverla. Tali metodi ponevano l'accento sulla possibilità di rappresentare qualunque funzione per mezzo di serie trigonometriche. In seguito, la vasta portata di questa idea si rivelò in una serie di complessi e delicati problemi analitici che, da quel momento in poi, sono stati al centro della riflessione degli analisti; le idee di Fourier possono essere comunque considerate come uno dei contributi più importanti alla matematica pura e applicata dall'invenzione del calcolo in poi. In sintesi, Fourier aveva mostrato che una funzione f(x), definita in un intervallo che (senza perdere di generalità) si può supporre uguale a [−π,π], è rappresentabile mediante una serie infinita della forma:

dove i coefficienti a_n e b_n sono dati da

La dimostrazione di Fourier si basa sul fatto che

a meno che n=m, nel qual caso entrambi gli integrali [8] sono uguali a π. Le [7] e [8] sono note come relazioni di ortogonalità delle funzioni trigonometriche (la terminologia è quella della teoria degli spazi di Hilbert ed è stata introdotta all'inizio del XX secolo).

Partendo dalle relazioni precedenti, Fourier aveva dimostrato che, se nell'equazione alle derivate parziali che descrive il flusso del calore si passa a coordinate sferiche polari, si ottiene un'equazione differenziale che si può risolvere mediante serie trigonometriche. Egli aveva generalizzato questo approccio al problema di una barra cilindrica immersa in un fluido a temperatura costante, anch'esso risolubile con il metodo della separazione delle variabili. L'equazione differenziale ordinaria che ne risulta è in realtà un caso particolare dell'equazione di Bessel, della quale tuttavia le soluzioni non sono funzioni trigonometriche.

Nel 1836 un protégé di Fourier, Charles-François Sturm, che era anche amico di Liouville, iniziò una serie di lavori nei quali il metodo di separazione delle variabili era applicato all'equazione del calore per un corpo non omogeneo. In questo caso si ottiene un'equazione differenziale ordinaria del secondo ordine, ma con un tipo differente di condizioni al contorno. Ciò che si cerca è una funzione che soddisfi l'equazione differenziale su un intervallo [a,b] e che assuma valori prescritti agli estremi dell'intervallo. I metodi di Cauchy garantiscono l'esistenza di infinite soluzioni aventi il valore prescritto all'estremo a, ma queste curve, in corrispondenza dell'altro estremo b, non hanno un valore predeterminato.

Il lavoro di Sturm ispirò Liouville che lo pubblicò in uno dei primi volumi del giornale da lui fondato e i due autori pubblicarono successivamente un'intera serie di articoli. Il problema che affrontarono era questo: data un'equazione differenziale della forma (k(x)V′(x))′+ (g(x)r−λ(x))V(x)=0 (dove l'apice ′ significa derivata rispetto a x), con x variabile nell'intervallo [a,b], determinare una sua soluzione che soddisfi le condizioni al contorno k(x)V′(x)−hV(x)=0, per x=a, e k(x)V′(x) +HV(x)=0 per x=b. Le funzioni k(x), g(x) e λ(x) sono note, così come le costanti positive h e H; r è un parametro che può essere modificato in modo che il problema ammetta soluzione.

Sturm si concentrò sulla ricerca delle proprietà del parametro r e delle funzioni soluzione associate, mentre Liouville si occupò del problema, che possiamo dire 'di tipo Fourier', di esprimere funzioni arbitrarie in termini di soluzioni di questa equazione differenziale (di fatto, aggiungendole alla lista delle funzioni note). Entrambi arrivarono a dimostrare che le soluzioni hanno molte proprietà in comune con le funzioni trigonometriche.

In particolare Sturm provò l'esistenza di infiniti valori di r per i quali l'equazione differenziale ha soluzioni non banali. Indichiamo questi valori di r con r1⟨r2⟨…⟨r_n⟨… e le corrispondenti soluzioni con V1,V2,…,V_n,…; Sturm dimostrò anche che tra due zeri consecutivi arbitrari di V_n esiste uno zero di V_n−1, così che gli zeri si intrecciano proprio come gli zeri delle funzioni cosnx e cos(n−1)x. Inoltre è soddisfatta una proprietà di ortogonalità:

Liouville trovò espressioni asintotiche per valori grandi di r e per la V_n associata; inoltre provò l'esistenza di una grande classe di funzioni sviluppabili in serie di potenze di V_n.

L'equazione di Sturm-Liouville, al pari di quella di Bessel, e in effetti come quasi tutte le equazioni differenziali importanti introdotte all'epoca in fisica matematica, è lineare. Questo significa, in termini matematici, che somme e multipli (secondo una costante) di soluzioni sono ancora soluzioni e, in termini fisici, che le soluzioni possono essere sovrapposte. Le equazioni differenziali non lineari non godono di queste proprietà e quindi sono molto più difficili da studiare: esse pertanto hanno svolto un ruolo secondario nella fisica matematica del XIX sec., mentre i risultati matematici ottenuti furono dovuti prevalentemente alla teoria delle funzioni di variabile complessa.

Le poche opportunità di impiego nelle applicazioni sono conseguenza della scarsità di risultati teorici significativi; affrontando un problema non lineare, un matematico dell'Ottocento poteva di solito fare poco più che cercare di risolverlo con una successione di approssimazioni lineari, valida per un piccolo intervallo di valori della variabile indipendente. Questo metodo, sviluppato estensivamente da Sir William Thomson e Peter Guthrie Tait, da Edward J. Routh e dal russo Nikolaj Egorovič Žukovskij, procede approssimando l'equazione differenziale tramite la considerazione dei soli termini del primo ordine nelle variabili dipendenti. Le equazioni lineari che ne derivano possono allora essere risolte, ma occorre fare attenzione a non introdurre nelle soluzioni, con la suddetta procedura, errori incontrollabili. Lo stesso può dirsi oggi in relazione a molti problemi, per esempio quello delle previsioni meteorologiche: esiste una differenza cruciale nel basare una previsione per il tempo di mercoledì sul tempo che si è effettivamente verificato martedì o sulla previsione di lunedì circa il tempo di martedì. Ma in questa sede ci si occuperà invece del primo serio tentativo di superamento del metodo delle approssimazioni lineari e di analisi globale delle equazioni differenziali non lineari in una variabile reale.

Sistemi di equazioni differenziali

Un insieme di n equazioni differenziali ordinarie e lineari del primo ordine nelle n funzioni y1,…,y_n

viene detto sistema lineare di equazioni differenziali ordinarie del primo ordine. Tali sistemi si presentano comunemente in matematica. In particolare, è sempre possibile scrivere un'equazione differenziale ordinaria lineare

come un sistema lineare. Infatti, se si definiscono n variabili y1,y2,…,y_n nel modo seguente:

cosicché

l'equazione differenziale [11] si trasforma nel sistema lineare di equazioni differenziali ordinarie del primo ordine

Nel XVIII sec. d'Alembert e Lagrange avevano studiato i sistemi di equazioni differenziali nel caso particolare di coefficienti a_ij costanti, nella speranza di individuare combinazioni lineari delle funzioni originali per le quali le equazioni avessero la forma

[15] dy_i/dx=a_iiy_i (1≤i≤n).

Le [15] ammettono le ovvie soluzioni y_i=A_ie^aiix. Le funzioni originali sono pertanto combinazioni lineari di queste ultime. Tale caratteristica costituisce un'importante sorgente di idee per l'algebra lineare e per la teoria delle matrici. L'utilizzo dei sistemi lineari di equazioni differenziali ordinarie a coefficienti costanti divenne sistematico con la teoria di Weierstrass dei divisori elementari e con la teoria di Jordan delle forme canoniche per le matrici.

Una generalizzazione del concetto di sistema lineare è stata studiata da Sophus Lie (1842-1899). Essa consiste di un insieme di n equazioni della forma

con 1≤i≤n. Lie era interessato all'analisi delle corrispondenti n trasformazioni infinitesimali su funzioni delle n variabili y1,y2,…,y_n, definite dalle relazioni

L'analisi delle trasformazioni [17] ha svolto un ruolo importante nell'elaborazione da parte di Lie di quella che egli poi definì come 'teoria dei gruppi di trasformazioni'.

Variabili complesse

Lo studio delle equazioni differenziali ordinarie lineari nel campo complesso, cioè per una funzione complessa di variabile complessa, è legato intimamente alla storia della teoria delle funzioni di variabili complesse. Questo è chiaramente vero per quanto riguarda il lavoro di Cauchy, ma è vero soprattutto per la teoria che venne elaborata per una singola equazione o, per meglio dire, per una singola famiglia di equazioni, la cosiddetta equazione ipergeometrica (e.i.g.):

dove le costanti α, β, γ possono essere reali o complesse e le variabili possono essere entrambe reali o entrambe complesse. La serie di potenze:

detta serie ipergeometrica (s.i.g.), rappresenta una delle sue soluzioni; nel caso in cui tale serie converga si dice che essa rappresenta una funzione ipergeometrica (f.i.g.). La e.i.g. fu introdotta nella sua forma attuale da Gauss il quale la mise in connessione con la nascente teoria degli integrali ellittici e delle funzioni ellittiche. L'equazione fu descritta nuovamente da Riemann nel 1857 come parte della sua formulazione della teoria delle funzioni di variabile complessa; inoltre Christian Felix Klein e altri mostrarono che da tale equazione proveniva la maggior parte delle equazioni differenziali ordinarie lineari della fisica matematica (se non tutte). Lo studio di Riemann rappresentò il caso paradigmatico per tutte le equazioni differenziali ordinarie nel dominio complesso, come Fuchs illustrò nella sua esauriente esposizione dell'argomento nel 1866. Sulla base di questo lavoro, nei primi anni Ottanta del XIX sec., Poincaré mostrò che ogni equazione differenziale (algebrica) aveva soluzioni in termini di funzioni da lui definite nel corso di una vasta generalizzazione della teoria delle funzioni di variabili complesse.

Anche alla luce della solida concatenazione di sviluppi che va da Gauss a Poincaré appare più opportuno qui non rispettare la cronologia ponendo il lavoro di Cauchy fuori dall'ordine temporale.

Cauchy e il metodo dei maggioranti

Nel 1835 Cauchy, allora a Praga, pubblicò una memoria litografata che forniva un nuovo metodo per stabilire l'esistenza di soluzioni di equazioni differenziali. Egli cominciò con una serie di potenze che rappresentava la soluzione formalmente; tale serie veniva ottenuta sostituendo una serie di potenze della forma

nell'equazione e risolvendo le relazioni di ricorrenza che si stabilivano in tal modo tra gli a_n. Pur così facendo Cauchy sostenne che questo metodo non poteva essere di alcuna utilità a meno che non fosse possibile stabilire la convergenza della serie, almeno in qualche intorno delle condizioni iniziali. A questo scopo egli riconsiderò il suo metodo dei maggioranti (calcul des limites) introdotto in un'altra memoria litografata del 1831, pubblicata a Torino. In quella memoria Cauchy aveva mostrato come ottenere stime per il limite superiore dei coefficienti dello sviluppo in serie di potenze di una funzione di una variabile complessa. Nella memoria di Praga stabilì inoltre le disuguaglianze che ancora oggi portano il suo nome:

dove f è continua sul disco di centro z e raggio r, mentre M_r(f(z)) denota il valore massimo del modulo sul perimetro di quel disco. Da queste disuguaglianze segue automaticamente la convergenza della serie di potenze su un disco opportuno (dipendente dall'equazione differenziale e dalle condizioni iniziali).

A uno sguardo moderno può sembrare strano che Cauchy dimostrasse nel 1835 un teorema che aveva già stabilito nel 1824 sotto condizioni più deboli (nel 1835 la funzione che definisce l'equazione differenziale deve essere analitica). Ma, come ha evidenziato Christian Gilain nella sua accurata edizione (Cauchy 1981), per Cauchy lo scopo era lo stesso: stabilire l'esistenza delle soluzioni ed esibire approssimazioni arbitrariamente vicine a esse. Da questo punto di vista il secondo metodo risulta senza dubbio più veloce e, in un periodo storico nel quale le funzioni erano considerate comunemente analitiche in modo naturale, la perdita di generalità non venne notata. Né possiamo dire che questa apparente confusione abbia causato una qualche difficoltà matematica ai lettori di Cauchy. Ma, dato che la memoria di Torino non fu mai pubblicata adeguatamente (sebbene quella di Praga fosse stata ristampata nel 1840), l'attribuzione di questo o di quel risultato a Cauchy è stata inevitabilmente soggetta a errore e solo di recente tale situazione è stata chiarita.

Gauss e l'equazione ipergeometrica

Gauss pubblicò la prima parte dei suoi studi sull'equazione ipergeometrica nel 1812. Tale lavoro si basava su uno studio durato molti anni. La seconda parte del testo fu trovata nel vasto Nachlass gaussiano. Il lavoro pubblicato considera x come una variabile complessa e contiene le primissime argomentazioni rigorose riguardanti la convergenza di una serie di potenze; inoltre, viene mostrato che molte delle funzioni note possono essere considerate come casi speciali o casi limite di funzioni ipergeometriche. Tuttavia, almeno a partire dal 1800, Gauss aveva collegato la e.i.g. con lo studio dei periodi di un integrale ellittico considerato come funzione di un parametro, osservando che i periodi soddisfano l'equazione di Legendre (essa stessa un caso speciale della e.i.g). Egli quindi sviluppò la teoria delle serie di potenze in una variabile complessa in modo sufficiente per studiare i periodi di un integrale ellittico nel caso in cui il parametro sia complesso, guidato in questo dalla sua teoria generale della e.i.g. In tal senso il suo lavoro, sebbene non pubblicato, sorpassa per importanza quello di Abel.

Nel 1836, Kummer riprese, in un certo senso, il tema della seconda parte del lavoro di Gauss e diede un resoconto sistematico delle soluzioni della e.i.g. e delle loro connessioni con altre classi di funzioni, come quella delle funzioni ellittiche. In particolare, egli ottenne un insieme di 24 soluzioni per lipergeometrica che non solo forniscono insiemi di basi per soluzioni in ogni punto, ma descrivono il loro prolungamento analitico sulla sfera complessa nel caso in cui la variabile sia complessa (tuttavia in questa fase nel lavoro di Kummer la variabile è reale).

Riemann e le questioni di monodromia

La risposta più profonda allo studio di Gauss della e.i.g. venne da Riemann il quale, nel suo lavoro del 1857, colse l'opportunità di spiegare, tra le altre cose, le relazioni tra le 24 soluzioni di Kummer dal punto di vista complesso. Egli mostrò che la e.i.g. per una variabile complessa y, considerata come funzione complessa della variabile complessa x, può essere pensata come una equazione differenziale con tre punti singolari (per convenzione posti in 0, 1 e ∞) dove le soluzioni sono ramificate. Esiste una relazione lineare fra tre rami qualsiasi e il comportamento relativo ai punti di diramazione che è determinato dai coefficienti della e.i.g. In effetti, come mostrava il metodo di Cauchy, fissati valori arbitrari per x0, per y e dy/dx in x0, esistono due soluzioni in serie di potenze linearmente indipendenti valide in un certo intorno di x0 e un'unica combinazione di esse che prende i valori dati per y e dy/dx in x0. Così i coefficienti α, β, γ determinano il comportamento di una base di soluzioni rispetto al prolungamento analitico ovunque, inclusi gli intorni dei punti di diramazione.

In effetti Riemann mostrò che è sufficiente conoscere la natura del prolungamento analitico in due dei tre punti di diramazione dal momento che il prolungamento analitico intorno a tutti e tre i punti non deve avere effetto. Inoltre, il prolungamento analitico è specificato dicendo quale combinazione dei vettori della base è ottenuta conducendo, per esempio, ogni singolo vettore della base intorno ai punti di diramazione 0 e 1. Questa informazione sarà espressa mediante una certa matrice di costanti in ogni punto di diramazione, matrice i cui elementi dipendono da α, β e γ (più tardi dette da Hermite 'matrici di monodromia'). Ne segue che i coefficienti α, β, γ determinano le matrici e così la natura globale della soluzione come superficie di Riemann (con, magari, un numero infinito di fogli). In particolare, le complicate argomentazioni usate da Kummer potevano ora essere viste in modo più naturale.

Ancora più notevole è il fatto che Riemann mostrò inoltre che le matrici di monodromia determinano i coefficienti della e.i.g. Ciò aprì la strada alle ricerche relative al problema di stabilire quale equazione differenziale o famiglia di equazioni differenziali avesse una data superficie di Riemann come superficie di Riemann delle proprie soluzioni; tale questione fu sollevata da Hilbert nel 1900 come uno dei suoi famosi 23 problemi.

Equazioni differenziali lineari: il contributo di Fuchs

Il lavoro di Riemann rappresentò una diretta ispirazione, per Immanuel Lazarus Fuchs (1833-1902), uno studente sia di Weierstrass che di Kummer a Berlino. Per la sua Habilitationsschrift (la qualifica che permetteva di insegnare in una università tedesca) Fuchs presentò un lavoro sulle equazioni differenziali lineari ordinarie nel campo complesso. Weierstrass aveva recentemente chiarito la distinzione tra le funzioni di variabile complessa che hanno poli e le funzioni che presentano ciò che egli chiamò punti singolari essenziali. Una funzione complessa f(z) ha un polo in z=z0 se 1/f(z0) è uguale a zero; essa ha un punto singolare essenziale se né f(z0) né 1/f(z0) possono essere definiti. Fuchs cercò quindi di determinare quali fossero le equazioni differenziali lineari ordinarie che ammettevano soluzioni che, nel caso peggiore, avessero punti di diramazione e poli logaritmici ma nessun punto singolare essenziale. Egli scoprì che si poteva caratterizzare questa classe di equazioni in modo esplicito (tali equazioni, infatti, sono oggi dette di classe fuchsiana) e la e.i.g. era proprio un'equazione di questo tipo ‒ in effetti la sola equazione del secondo ordine con tre punti singolari di questa classe. In generale per l'equazione differenziale lineare di ordine n Fuchs trovò che la specificazione della posizione dei punti di diramazione e della monodromia non era sufficiente a individuare esattamente l'equazione differenziale; rimanevano nei coefficienti dell'equazione differenziale dei parametri liberi, i quali vennero in seguito chiamati parametri accessori. Mentre molte questioni relative a questi parametri accessori rimangono senza risposta ancora oggi, i risultati di cui sopra procurarono a Fuchs la reputazione di essere uno dei più brillanti allievi di Weierstrass e, nonostante una serie di lavori successivi cosparsi di errori, egli ritornò a Berlino come professore ordinario, succedendo a Kummer.

Nel suo lavoro Fuchs fece un uso considerevole delle matrici di monodromia in ogni punto singolare. Autori successivi mostrarono come lo studio di queste matrici potesse essere considerevolmente semplificato usando la teoria di Jordan delle forme canoniche. Nel caso più semplice una matrice di monodromia può essere diagonalizzata. Gli elementi sulla diagonale sono relativi ai termini principali delle serie di potenze le quali rappresentano le soluzioni in un intorno del punto di diramazione. In effetti il prolungamento analitico di

effettuato compiendo un giro intorno all'origine produce come risultato

Così un elemento sulla diagonale di x^αe2^πiα implica un certo comportamento per una soluzione. Altri autori, in particolar modo Ferdinando Georg Frobenius, semplificarono presto il metodo di risoluzione trovando una strada diretta per la determinazione degli α: ma tale metodo funziona sistematicamente solo per le equazioni della classe fuchsiana.

Uno dei lavori successivi di Fuchs solleva una questione interessante: si chiede quale classe di equazioni differenziali abbia tutte le sue soluzioni algebriche (praticamente il miglior comportamento possibile). Hermann Amandus Schwarz rispose per primo a questa questione relativamente all'e.i.g. In seguito Fuchs diede risposte parziali per l'equazione generale del secondo ordine che furono più tardi corrette da Klein e Paul A. Gordan in modo indipendente; inoltre, Camille Jordan diede una risposta per ldifferenziale del terzo ordine (Klein trovò poi un caso mancante). I metodi di Klein e Jordan misero in evidenza l'importanza di considerare il gruppo generato dalle matrici di monodromia (le soluzioni sono tutte algebriche se questo gruppo è finito) e rappresentarono un punto significativo in cui la nuova teoria dei gruppi si dimostrò superiore ai metodi, più vecchi, della teoria degli invarianti (usati da Fuchs e Gordan). La risposta di Klein mise in evidenza anche una sorprendente interpretazione geometrica: i gruppi finiti che si possono presentare con la suddetta procedura sono solamente quelli associati ai solidi regolari o platonici (più i cosiddetti gruppi ciclici e gruppi diedrali).

Bibliografia

Anosov 1994: Anosov, Dmitrij Viktorovič - Bolibruch, Andrej A., The Riemann-Hilbert problem, Braunschweig, Vieweg, 1994.

Barrow-Green 1997: Barrow-Green, June, Poincaré and the three body problem, Providence (R.I.), American Mathematical Society; London, London Mathematical Society, 1997.

Gilain 1977: Gilain, Christian, La théorie géométrique des équations différentielles de Poincaré et l'histoire de l'analyse, (Diss.), Paris, 1977.

Gray 1985: Gray, Jeremy J., Linear differential equations and group theory from Riemann to Poincaré, Boston-Basel, Birkhäuser, 1985 (2. ed.: 2000).

Lützen 1990: Lützen, Jesper, Joseph Liouville, 1809-1882. Master of pure and applied mathematics, New York-Berlin, Springer, 1990.

Maz'ya 1998: Maz'ya, Vladimir G. - Shaposhnikova, Tatyana, Jacques Hadamard. A universal mathematician, Providence (R.I.), American Mathematical Society; London, London Mathematical Society, 1998.