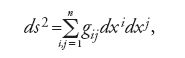L'Ottocento: matematica. La geometria non euclidea
L'Ottocento: matematica. La geometria non euclidea
La geometria non euclidea
Alla base dei suoi Elementi Euclide aveva posto un certo numero di definizioni (o 'termini') e di assiomi (o 'nozioni comuni') e cinque postulati. Oggi non esiste più alcuna differenza tra assiomi e postulati, in quanto tutti rappresentano proposizioni assunte come vere e poste alla base di una teoria. All'epoca di Euclide, invece, gli assiomi erano considerati enunciati generalmente ammessi, propri di ogni ragionamento logico, mentre i postulati enunciavano proprietà specifiche della disciplina che si andava a trattare (in questo caso la geometria). Il V postulato degli Elementi euclidei affermava che "Se una retta venendo a cadere su due rette forma gli angoli interni e dalla stessa parte minori di due retti, le due rette prolungate illimitatamente verranno a incontrarsi da quella parte in cui sono gli angoli la cui somma è minore di due retti". Se α+β è minore di due angoli retti, allora le due linee rette, se prolungate, si incontrano in un punto P.
Dubbi sull'evidenza di questo postulato furono avanzati già dai primi commentatori dell'opera euclidea, e per oltre duemila anni i matematici cercarono invano di dimostrarne la validità a partire dagli altri postulati e assiomi. Infatti, le loro dimostrazioni chiamavano tacitamente in causa ipotesi che erano in realtà equivalenti al postulato da dimostrare, come per esempio, le seguenti:
a) la somma degli angoli di un triangolo è sempre uguale a due angoli retti;
b) esistono figure simili non congruenti;
c) per tre punti del piano non allineati passa sempre una circonferenza;
d) una perpendicolare e un'obliqua a una stessa retta si incontrano sempre in un punto in cui l'obliqua forma con la retta un angolo acuto (postulato dell'obliqua);
e) dati una retta e un punto fuori di essa, esiste una e una sola retta passante per il punto e parallela alla retta data (postulato dell'unicità della parallela).
In epoca moderna, particolarmente interessante è stato il tentativo di dimostrazione del padre gesuita Girolamo Saccheri (1667-1733). Nell'Euclides ab omni naevo vindicatus, pubblicato l'anno della sua morte, Saccheri cercava di emendare gli Elementi euclidei da alcuni 'nei', tra i quali figurava proprio il V postulato, ed era convinto di essere riuscito nell'impresa. In realtà la sua 'dimostrazione' condotta per assurdo (a partire cioè dall'ipotesi di falsità del postulato) era viziata da errore. Nel suo affannoso tentativo di giungere a una contraddizione che gli consentisse di provare la verità del V postulato, Saccheri riuscì comunque, suo malgrado, a stabilire un certo numero di teoremi e proprietà di quella che oggi si chiama geometria non euclidea.
Dopo la morte di Saccheri, verso la metà del Settecento si cimentò nell'impresa Johann Heinrich Lambert (1728-1777) la cui Theorie der Parallellinien (Teoria delle parallele) ricorda l'Euclides e le cui considerazioni si basano su ragionamenti molto simili a quelli di Saccheri. Tuttavia, a differenza del gesuita, Lambert sembra fosse consapevole della debolezza delle proprie speculazioni, e forse per questo motivo si astenne dal pubblicare il libro, che venne edito solamente nel 1786.
Anche Adrien-Marie Legendre (1752-1833) lavorò per circa vent'anni al problema delle parallele e raccolse i risultati delle sue ricerche negli éléments de géométrie (1794), un classico di geometria che conobbe diverse edizioni. Ciascuna di esse (la dodicesima e ultima è del 1813) è corredata da appendici che presentano presunte dimostrazioni del postulato delle parallele, ognuna delle quali assume come veri enunciati che sono in realtà equivalenti al V postulato stesso. Le numerose strade tentate da Legendre lo portavano a supporre l'esistenza di triangoli simili non congruenti, oppure ad ammettere la possibilità di costruire una circonferenza per tre punti dati, o ad altri enunciati ancora, tutti equivalenti al postulato euclideo. A partire dai primi quattro postulati di Euclide, Legendre riuscì per esempio a dimostrare che la somma degli angoli di un triangolo non può superare i due angoli retti e che l'area di un triangolo è sempre proporzionale al suo difetto angolare (cioè alla differenza tra due angoli retti e la somma degli angoli del triangolo). Cercò allora di costruire un triangolo con area doppia e dunque difetto angolare doppio di quelli di un triangolo dato. Il suo scopo era quello di costruire triangoli con difetti angolari sempre maggiori in modo che la somma dei loro angoli tendesse a zero. Un risultato che, secondo Legendre, era assurdo dal momento che la somma degli angoli di un triangolo avrebbe dovuto uguagliare due angoli retti; il che era equivalente al postulato delle parallele. Tuttavia Legendre si accorse che la sua costruzione si riduceva a dimostrare che, per un punto dato all'interno di un angolo di 60°, è sempre possibile tracciare una retta che incontri entrambi i lati dell'angolo. Tale proposizione però, a sua volta, richiedeva il V postulato euclideo per essere dimostrata. Dunque, dopo oltre duemila anni dalla redazione degli Elementi e nonostante le intense ricerche svolte la dimostrazione di quel postulato era ancora una questione aperta e costituiva un oggetto di studio più che mai attuale per i matematici.
Geometria 'astrale' e 'Disquisitiones generales'
Mentre a Parigi Legendre cercava di dimostrare il postulato delle parallele, a Gottinga il giovane Carl Friedrich Gauss (1777-1855) avanzava forti dubbi sulla possibilità della sua dimostrazione in appunti e lettere indirizzate ad amici. Fin da ragazzo Gauss si era reso conto che le difficoltà incontrate dai matematici erano insite nella natura stessa del problema. All'amico Farkas Bólyai (1775-1856), che gli inviava una 'dimostrazione' del V postulato, Gauss rispondeva nel dicembre del 1799: "la via sulla quale mi sono messo non conduce al fine che si cerca, e che tu affermi avere raggiunto, ma conduce piuttosto a mettere in dubbio l'esattezza della geometria. Sono, è vero, arrivato a parecchie cose, che dalla maggior parte sarebbero ritenute come una valida dimostrazione, ma che, ai miei occhi, non provano, per così dire, 'nulla' (in Bonola 1906, p. 59).
Il nucleo del problema, intuito da Gauss, è il seguente: poiché non è possibile provare il V postulato a partire dagli altri assiomi e postulati euclidei, esso può dunque essere o non essere inserito ‒ come postulato ‒ all'interno del sistema ipotetico-deduttivo elaborato da Euclide. Nel caso in cui lo si escluda o lo si sostituisca con un altro postulato, si ottengono nuove geometrie diverse da quella euclidea. Così, per esempio, se invece del V postulato di Euclide si assume il seguente postulato: "Dati una retta r e un punto P fuori di essa, allora esistono almeno due rette passanti per P e che non incontrano la retta" si ottiene quella che oggi si chiama 'geometria iperbolica'. Come si vede nella fig. 2, se RR′ e SS′ sono le due rette parallele a r passanti per P, tutte le rette per P contenute negli angoli RPS′ e R′PS non incontrano la retta r. Nel caso euclideo le due rette RR′ e SS′ coincidono e torna così a essere valido il postulato dell'unicità della parallela.
Gauss partiva da una simile concezione di parallelismo per dimostrare alcuni notevoli risultati di geometria 'astrale' (l'odierna geometria iperbolica), alcuni dei quali ‒ come la transitività del parallelismo ‒ validi anche in geometria euclidea. Un elemento distintivo della nuova geometria era la necessità di introdurre una certa costante che compariva con insistenza nelle formule. Questa stessa costante era stata introdotta in una breve nota che il giurista Ferdinand Karl Schweikart (1780-1859) aveva fatto pervenire a Gauss. Schweikart vi sosteneva che esistono due tipi di geometria: la euclidea, valida 'in senso ristretto', e la astrale, valida cioè per distanze molto grandi, di scala cosmica. Schweikart considerava un triangolo rettangolo isoscele la cui altezza, pur aumentando al crescere dei lati, non poteva superare un certo segmento, che chiamava 'costante'; la geometria euclidea valeva nell'ipotesi che questa costante fosse infinitamente grande.
Visto l'entusiasmo del princeps mathematicorum verso le sue ricerche, Schweikart esortò il nipote Franz Adolph Taurinus (1794-1874), anch'egli giurista, a proseguire in questo tipo di studi. Nonostante fosse intimamente convinto della validità del postulato euclideo, e impaziente di dimostrarlo, Taurinus riuscì a ottenere alcuni risultati fondamentali di una nuova geometria, da lui chiamata 'logaritmico-sferica', di fatto equivalente ‒ come la geometria astrale ‒ alla geometria non euclidea iperbolica.
Queste nuove geometrie presentavano intime connessioni con altri campi di ricerca, che appassionavano Gauss: la geodesia teorica e la teoria delle superfici. Intorno al 1820 Gauss era stato incaricato di compiere il rilevamento topografico del Ducato di Hannover, un impegno che lo assorbì per oltre dieci anni. Dal punto di vista teorico si trattava di costruire una rete di triangoli che 'ricoprissero' l'intera regione e avessero lati e angoli di grandezze note. Il lavoro sul campo stimolò gli interessi teorici di Gauss in più direzioni. Innanzi tutto, egli si trovò ad affrontare il cosiddetto problema delle carte geografiche e rese note le sue idee rispondendo alla seguente questione, posta nel 1822 dalla Det Kongelige Danske Videnskabernes Selskab (Reale Accademia Danese delle Scienze) di Copenaghen: "rappresentare una superficie su un'altra in modo che le due superfici siano simili nelle loro parti infinitesime". Si trattava, dunque, di trovare una legge di trasformazione tra due superfici (per es., tra un ellissoide e un piano, come nel caso delle carte geografiche) che mantenesse inalterata ('conforme', come si dice oggi) l'ampiezza degli angoli.
La teoria delle superfici era un argomento estremamente fecondo fino ad allora esplorato soltanto in parte. Le idee di Gauss, esposte nelle Disquisitiones generales circa superficies curvas (1828), hanno un profondo carattere innovativo e rappresentano una tappa fondamentale nello sviluppo della geometria differenziale. Egli considerava le superfici da un nuovo punto di vista, non come 'contorni di corpi' ma piuttosto quali 'corpi di cui una dimensione è infinitamente piccola'. Una specie di velo 'flessibile ma inestensibile', deformabile senza strappi o piegature. Questo punto di vista permetteva di definire le proprietà essenziali della superficie, come le linee geodetiche (ossia le linee di minimo percorso sulla superficie che uniscono due punti dati) e la misura di curvatura, un concetto che era già stato introdotto da Leonhard Euler (1707-1783), in maniera intrinseca, senza far riferimento allo spazio tridimensionale in cui la superficie era immersa. Allo scopo Gauss associava alla superficie un'espressione differenziale detta 'prima forma fondamentale' o 'elemento lineare', che fornisce la distanza tra due punti infinitamente vicini generalizzando l'usuale concetto di distanza. È la prima forma fondamentale che caratterizza la superficie a essa associata: oltre a permettere di ottenere la misura di curvatura in ogni suo punto, offre criteri per la classificazione delle superfici. Due superfici che possono trasformarsi l'una nell'altra mediante una semplice deformazione (senza strappi o piegature) sono da ritenersi 'essenzialmente identiche'. Gauss provava infatti il seguente theorema egregium: "Se una superficie curva si sviluppa sopra una qualsiasi altra superficie, la misura di curvatura in ogni suo punto resta invariata" (Gauss 1828 [1863-1933, IV, p. 237]). Così, per esempio, un cilindro e un piano possono 'svilupparsi' uno sull'altro mediante una semplice flessione; ne segue che entrambi hanno curvatura nulla.
L'ultima parte delle Disquisitiones presenta notevoli connessioni con la geometria non euclidea. I rilevamenti topografici, in particolare le triangolazioni del Ducato di Hannover, avevano portato Gauss a considerare 'triangoli geodetici' (ossia triangoli i cui lati sono linee geodetiche della superficie) su una superficie curva e a porre in relazione la somma degli angoli di quei triangoli con la loro misura di curvatura. Quando la curvatura è nulla, la somma degli angoli del triangolo uguaglia due angoli retti; da ciò discende il V postulato di Euclide e dunque tutta la geometria euclidea. Tuttavia, su una superficie con curvatura diversa da zero non valgono i teoremi della geometria euclidea, come l'unicità della parallela, i criteri di similitudine dei triangoli e il teorema di Pitagora. Gauss dimostrava in particolare che la differenza tra la somma degli angoli di un triangolo geodetico e due angoli retti uguaglia proprio la misura totale di curvatura del triangolo. Pertanto, su superfici a curvatura costante, la somma degli angoli di un triangolo geodetico sarà maggiore o minore di due angoli retti a seconda che la curvatura della superficie sia positiva oppure negativa. Nel primo caso si è in presenza della geometria ellittica, nel secondo di quella iperbolica.
I fondatori della geometria non euclidea
Nelle pagine conclusive delle Disquisitiones Gauss riportava le misure, da lui stesso effettuate, degli angoli del triangolo geodetico avente per vertici le tre cime di Brocken, Hohehagen e Inselberg (il cui lato maggiore è dell'ordine del centinaio di chilometri). I calcoli rivelavano che l'errore commesso, supponendo che il triangolo fosse disteso su un piano anziché sulla superficie terrestre, era 'impercettibile'. Restava tuttavia aperto il problema di verificare quale geometria fosse la più adatta a descrivere porzioni di spazio infinitesime o infinitamente grandi; una scelta che veniva subordinata alla nostra esperienza nello spazio. Lo stesso Gauss scriveva nel 1817 all'astronomo Heinrich Wilhelm Mathias Olbers (1758-1840) che la necessità della nostra geometria non può essere dimostrata e, di conseguenza, "si deve annoverare la geometria non con l'aritmetica, che è puramente a priori, ma piuttosto con la meccanica" (Gauss 1863-1933, VIII, p. 177). Un punto di vista che si contrapponeva con forza alle idee sostenute in quegli anni dai seguaci della filosofia kantiana. Nella Kritik der reinen Vernunft (Critica della ragion pura, 1781), infatti, Immanuel Kant (1724-1804) aveva sostenuto che lo spazio non è un concetto costruito empiricamente, ma una rappresentazione necessaria a priori.
Del resto, l'atteggiamento filosofico che discende dalla teoria kantiana della conoscenza corrispondeva alla radicata convinzione, vecchia di oltre duemila anni, secondo la quale la geometria euclidea coincideva con la vera geometria dello spazio. Il timore delle 'strida dei Beoti', come Gauss chiamava in una lettera le voci di coloro che si opponevano alla nuova geometria, era ai suoi occhi una buona motivazione per non pubblicare alcuno scritto sull'argomento. Forse non fu semplicemente una casualità il fatto che Schweikart e Taurinus fossero matematici dilettanti e che i fondatori della geometria non euclidea, Nikolaj Ivanovič Lobačevskij (1793-1856) e János Bólyai (1802-1860), appartenessero ad ambienti accademici in qualche modo periferici.
La convinzione di Gauss che l'esperienza indichi quali sono i veri assiomi geometrici era stata condivisa anche da Lobačevskij, professore all'Università di Kazan in Russia, fin dalle sue prime riflessioni sui principî della geometria, risalenti al 1817. Come Gauss, anche Lobačevskij annoverava la geometria, al pari della meccanica, tra le scienze empiriche. Del resto, egli affermava nei Novye načala geometrii s polnoj teoriej parallel´nych (Nuovi principî della geometria con una teoria completa delle parallele) che nello spazio noi percepiamo soltanto il movimento. Sebbene la geometria euclidea rappresenti in maniera accurata lo spazio percepito dai nostri sensi, egli continuava, "non si può garantire che non possa mostrarsi sensibilmente falsa anche prima di andare al di là del mondo a noi visibile" (Lobačevskij 1835-38 [1994, p. 22]).
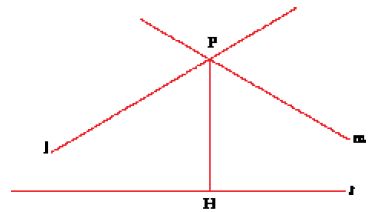
Nei Novye načala Lobačevskij sviluppava inizialmente la geometria 'assoluta', ossia quella parte della geometria che è indipendente dal V postulato euclideo e solamente in seguito, nella sezione dedicata alla congruenza dei triangoli, distingueva i due casi, quando la somma degli angoli di un triangolo è uguale, oppure è minore di due retti, e dimostrava che nel secondo caso tutti i triangoli rettangoli con gli stessi angoli sono uguali. In questa geometria immaginaria non vale più la teoria euclidea della similitudine e addirittura tutti i triangoli simili sono congruenti. Tale geometria è caratterizzata dal fatto che le linee uscenti da un punto o intersecano una data retta nel medesimo piano, o non si incontrano mai con essa, per quanto vengano prolungate. Con riferimento alla fig. 4, a dividere le schiere delle secanti e delle non secanti (dette anche 'iperparallele') alla retta r passante per il punto P, vi sono due rette (la l e la m) che si dicono parallele. Inoltre, se H è il piede della perpendicolare da P a r e p è la distanza PH, l'angolo π(p) si dice angolo di parallelismo. Se π(p) è un angolo retto, allora siamo nel caso della geometria euclidea, altrimenti per la geometria iperbolica π(p) è minore di un angolo retto.
Lobačevskij mostrava che in questa nuova geometria il luogo dei punti perpendicolare a un fascio di rette parallele non è una retta, come nella geometria euclidea, ma una curva, che egli chiamava 'oriciclo', e che può pensarsi come il limite di un cerchio quando il suo centro si allontana all'infinito nella direzione delle rette del fascio. La formula fondamentale che mette in relazione gli archi di due oricicli con le loro distanze è s′=sex, dove a e b sono due oricicli, x la loro distanza e s, s′ le lunghezze di due diversi archi.
Nella geometria euclidea e=1, e dunque s=s′ (due rette parallele sono equidistanti). Nella geometria immaginaria si ha invece e>1. Prendendo e uguale alla base del logaritmo neperiano, Lobačevskij individuava una 'unità di misura assoluta dei segmenti', fissando x uguale al logaritmo del rapporto s′/s. Era questa la 'costante assoluta' di cui parlavano Schweikart, Taurinus e Gauss. In maniera del tutto simile Lobačevskij definiva poi l'orisfera come la figura cui tende una sfera all'aumentare del suo raggio; nella geometria euclidea essa è un piano, mentre nella geometria immaginaria è una superficie curva sulla quale valgono i teoremi della geometria ordinaria, una volta che alla parola retta si sostituisca la parola oriciclo.
Le opere di Lobačevskij ebbero scarsa diffusione e le sue idee tardarono ad affermarsi. Il suo primo lavoro a stampa, O načalach geometrii (Sui principî della geometria) apparve tra il 1829 e il 1830 in lingua russa in una rivista poco nota di Kazan. Anche Voobražaemaja geometrija (La geometria immaginaria, 1835) e i Novye načala, pubblicati anch'essi a Kazan, passarono quasi del tutto inosservati. Destarono invece un certo interesse la traduzione francese di La geometria immaginaria, apparsa nel 1837 sulla celebre rivista tedesca "Journal für die reine und angewandte Mathematik" e il volume Geometrische Untersuchungen zur Theorie der Parallellinien (Ricerche geometriche sulla teoria delle parallele), edito a Berlino nel 1840 e letto dallo stesso Gauss.
Non era certo a conoscenza delle rivoluzionarie idee di Lobačevskij il giovane ungherese János Bólyai, figlio di Farkas, compagno di studi e amico di Gauss a Gottinga. Fin dal 1823 János aveva sviluppato una geometria indipendente dal postulato euclideo, del tutto analoga a quella di Lobačevskij, e in una lettera al padre affermava risolutamente di aver "scoperto cose sì belle che ne sono rimasto abbagliato, e si dovrebbe sempre rimpiangere se andassero perdute. Quando le vedrete, lo riconoscerete voi pure. Nell'attesa non vi posso dire altro che questo: ho dal nulla creato un nuovo universo" (in Bonola 1906, pp. 88-89). Mentre Lobačevskij aveva posto l'accento sul problema dei principî della geometria, János Bólyai aveva soprattutto sviluppato la 'geometria dello spazio assolutamente vera', cioè quella parte della geometria i cui teoremi valgono sia nel contesto euclideo sia in quello non euclideo e aveva in particolare dimostrato che nella geometria non euclidea si poteva anche trovare la quadratura del cerchio (costruire cioè un segmento di lunghezza pari a π).
La risposta di Farkas appare straordinariamente profetica, se si pensa ai lavori di Lobačevskij che saranno pubblicati in quegli anni e alle contemporanee ricerche di Gauss. Esortava il figlio ad affrettarsi "a rendere di pubblica ragione" le sue scoperte "perché le idee passano facilmente da uno all'altro, che in seguito potrebbe pubblicarle rivendicandone la paternità" e, d'altra parte "c'è anche qualche verità in ciò, che parecchie cose hanno un'epoca, nella quale esse sono scoperte allo stesso tempo in più luoghi. [...] Poiché ogni lotta scientifica è solo una gran guerra, alla quale non so quando seguirà la pace, si deve, quando si può, vincere, poiché qui il vantaggio spetta al primo" (ibidem, p. 89). Tuttavia, soltanto nel 1832 János Bólyai riuscì a pubblicare le sue idee nell'Appendix scientiam spatii absolute veram exhibens, un'appendice a un'opera geometrica del padre.
Proprio in quegli anni, superando le perplessità sull'opportunità di rendere pubbliche le proprie riflessioni sulla geometria non euclidea, Gauss aveva cominciato a scrivere alcune note sull'argomento che furono ritrovate successivamente tra le sue carte. Uno sforzo reso inutile dall'apparizione dell'Appendix di Bólyai. Un mese dopo aver ricevuto questa pubblicazione, Gauss scriveva all'amico Farkas che lodare questo lavoro "sarebbe lodare me stesso" giacché i risultati ottenuti da János "coincidono quasi interamente con le mie meditazioni, che hanno occupato in parte la mia mente da trenta a trentacinque anni a questa parte". Anche se Gauss concludeva affermando di essere "estremamente contento" per esser stato preceduto "in modo così notevole dal figlio del mio vecchio amico" (ibidem, p. 90), János vide nella lettera del princeps mathematicorum un tentativo di plagio che lo amareggiò al punto da non pubblicare più nulla sull'argomento. Soltanto dopo la morte di Gauss, la stampa del suo fitto carteggio rese giustizia delle sue affermazioni.
La lezione di Riemann
Nel giugno 1854 Georg Friedrich Bernhard Riemann (1826-1866) discuteva a Gottinga, alla presenza di Gauss, la sua lezione di abilitazione Über die Hypothesen welche der Geometrie zugrunde liegen (Sulle ipotesi che stanno alla base della geometria), universalmente riconosciuta come uno dei più profondi e, allo stesso tempo, criptici lavori nella storia della matematica. La confusione tra concetti metrici e topologici, oltre alla mancanza di una chiara definizione di 'grandezza pluriestesa' stavano, secondo Riemann, alla base delle difficoltà incontrate dai matematici nello studio dei fondamenti della geometria. Tale oscurità non era stata superata 'da Euclide fino a Legendre'. Nella lezione di Riemann una grandezza pluriestesa, che ha inizialmente il significato di un generico insieme di punti, viene poi dotata di una struttura geometrica che prefigura il moderno concetto di varietà riemanniana. In termini moderni, uno spazio a n-dimensioni senza cuspidi o altri punti irregolari (in linguaggio matematico liscio) è una varietà se nell'intorno di ogni suo punto si possono introdurre coordinate e se i sistemi di coordinate così definiti si 'raccordano bene' tra loro. Per affrontare lo studio delle varietà n-dimensionali Riemann introduceva la nozione fondamentale di elemento lineare
dove gij è una matrice simmetrica definita positiva, denominata in seguito 'tensore metrico'. Nel caso di una superficie (n=2), questa relazione si riduce alla prima forma fondamentale data da Gauss nelle Disquisitiones generales.
Come Gauss, anche Riemann adottava un punto di vista intrinseco e determinava le proprietà fondamentali di una varietà n-dimensionale a partire dall'espressione del suo elemento lineare. Riemann non si limitava comunque a estendere le definizioni e i risultati di Gauss relativi alla teoria delle superfici al caso più generale delle varietà. Egli si proponeva infatti di trovare le proprietà essenziali dello spazio, quelle da porre a fondamento di una teoria geometrica che parlasse davvero del mondo fisico in cui viviamo. Il fatto che i corpi nello spazio si possano muovere liberamente (ossia che le lunghezze e gli angoli di una figura restino inalterati durante il moto) costituiva secondo Riemann una caratteristica intrinseca dello spazio. Le uniche varietà che soddisfano questa 'ipotesi', secondo cui le figure possono assumere qualsiasi posizione senza subire deformazioni, sono le varietà a curvatura costante. Se infatti la curvatura fosse variabile (come, per es., le immagini della realtà attraverso uno specchio convesso) le figure varierebbero di forma e di dimensione e non sarebbe più possibile misurare un corpo mediante un altro; in altre parole, gli strumenti di misura sarebbero inutilizzabili perché suscettibili di variazione.
Per le varietà a curvatura costante in ogni punto, il concetto di curvatura che Riemann definiva si poteva considerare "come la misura di quanto la varietà si allontana dalla planarità in quel punto, in quella direzione" (Riemann 1867a [1994, p. 12]), sottolineando la completa analogia tra la sua teoria e quella gaussiana: nel caso di una superficie curva la misura di curvatura di Riemann coincide infatti con quella di Gauss. La nozione di curvatura sarà estesa dallo stesso Riemann a una varietà qualsiasi (anche con curvatura non costante) in un lavoro del 1861, pubblicato postumo nel 1876, dove verrà introdotta un'espressione denominata in seguito 'tensore di curvatura di una varietà'.
Lo spazio euclideo tridimensionale è dunque una varietà a tre dimensioni, la cui curvatura è nulla in ogni punto. Dalle misurazioni astronomiche sembra discendere che la geometria euclidea sia 'garantita dall'esperienza', ossia che il nostro spazio sia effettivamente euclideo e a tre dimensioni. Tuttavia, continuava Riemann, fino a quel momento era stata esplorata soltanto una piccola porzione di Universo, quella "accessibile ai nostri telescopi". Nulla dunque impediva di pensare che nell'infinitamente grande, così come nell'infinitamente piccolo, "le relazioni metriche dello spazio non si accordino con i postulati [euclidei] della geometria; ammissione questa che si renderebbe di fatto necessaria, se permettesse di spiegare in modo più semplice i fenomeni" (ibidem, p. 19). Quando si considerava "l'incommensurabilmente grande", a parere di Riemann bisognava "distinguere l'illimitato dall'infinito; l'uno appartiene alle relazioni d'estensione, l'altro alle relazioni metriche" (ibidem, p. 17). Se infatti la curvatura dello spazio fosse positiva, anche se piccolissima, esso assumerebbe la forma di una sfera, pur se di raggio molto grande e dunque localmente approssimabile a un piano. Nel caso in cui un punto percorra una geodetica sulla superficie sferica (dunque un cerchio massimo) non v'è dubbio che, prima o poi, esso si troverà a passare per le stesse posizioni. Lo spazio sarebbe finito (perché è una sfera) ma non limitato, perché il punto potrebbe percorrere la geodetica un numero anche infinito di volte. Come affermava Riemann: "L'illimitatezza dello spazio possiede dunque una certezza empirica maggiore di qualsiasi esperienza esterna. Da qui non consegue affatto però l'infinitezza" (ibidem, p. 18). Sebbene nella sua lezione egli non facesse alcun riferimento alle geometrie non euclidee, le sue affermazioni spiegano perché oggi si parli di geometria di Riemann per indicare la geometria non euclidea che ha come modello una superficie sferica (modello di Riemann).
Dopo la pubblicazione della memoria di Riemann, Hermann von Helmholtz (1821-1894) si impegnò a fondo allo scopo di divulgare le nuove idee negli ambienti colti di tutta Europa. Anche se 'in sede empirica' la validità della geometria euclidea aveva trovato ampie conferme, egli non esitò a formulare la possibilità che lo spazio fosse dotato di curvatura non nulla. Nella celebre conferenza Über den Ursprung und die Bedeutung der geometrischen Axiome (Sull'origine e il significato degli assiomi geometrici) tenuta nel 1870, Helmholtz immaginò esseri dotati di intelletto, che vivono in un mondo a due dimensioni. Egli osservava che se tali esseri costruissero la loro geometria, attribuirebbero naturalmente al loro spazio due sole dimensioni, aggiungendo che esseri viventi su una superficie sferica, dotati delle nostre stesse facoltà logiche, formulerebbero un sistema di assiomi geometrici del tutto diverso dal nostro.
Il modello di Beltrami e la diffusione della geometria non euclidea
Nello stesso anno in cui fu pubblicata la memoria di Riemann vide la luce un altro scritto di enorme interesse per i fondamenti della geometria, il Saggio di interpretazione della geometria non-euclidea di Eugenio Beltrami (1835-1900). Allievo di Francesco Brioschi (1824-1897) e Luigi Cremona (1830-1903), Beltrami fu nominato nel 1862 professore di algebra complementare e geometria analitica all'Università di Bologna, senza aver mai conseguito la laurea. Oltre alla geometria non euclidea, i suoi campi di ricerca riguardavano la geometria delle curve e delle superfici e la fisica matematica (meccanica, teoria del potenziale, teoria dell'elasticità, campi elettrici ed elettromagnetici). Il Saggio, direttamente ispirato alle idee di Gauss e Lobačevskij, era stato redatto nel 1867 e poi 'lasciato dormire' in seguito a un'obiezione di tipo metodologico avanzata da Cremona. La lettura della lezione di Riemann indusse tuttavia Beltrami a pubblicare il suo scritto "perché sostanzialmente in accordo con alcune delle idee di Riemann" (in Loria 1901, p. 416), come egli scriveva ad Angelo Genocchi (1817-1889). E ai critici della nuova geometria Beltrami faceva notare che "la critica profonda dei principî non può mai nuocere alla solidità dell'edificio scientifico, quando pure non conduca a scoprirne e riconoscerne meglio le basi vere e proprie" (Beltrami 1868 [1902-20, I, p. 374]).
Per dare maggior concretezza alle proprie affermazioni, Beltrami cercava un 'substrato reale' alla geometria di Lobačevskij, ossia un modello euclideo del piano iperbolico. A partire dall'espressione dell'elemento lineare di una superficie con curvatura costante negativa, Beltrami otteneva un modello proiettivo della geometria di Lobačevskij-Bólyai, in cui il piano iperbolico corrisponde all'interno di un cerchio C (detto 'cerchio limite'); due geodetiche secanti del piano di Lobačevskij corrispondono a due corde del cerchio (a e b) che si intersecano in un punto interno a C; due geodetiche parallele (nel senso di Lobačevskij) si interpretano come due corde (b e c) che hanno un punto in comune sulla circonferenza di C; mentre due geodetiche non secanti (iperparallele) corrispondono a due corde (a e c) che non si intersecano né all'interno del cerchio né sulla circonferenza.
Questo modello proiettivo della geometria iperbolica proposto da Beltrami e ripreso da Christian Felix Klein (1849-1925), che in alcuni lavori editi tra il 1871 e il 1873 lo arricchì definendo esplicitamente l'espressione della distanza tra due punti, è oggi noto con il nome di modello di Beltrami-Klein. Tale modello, che non rispetta né le distanze né l'ampiezza degli angoli, non soddisfaceva del tutto Beltrami, che si proponeva invece di fornire una rappresentazione il più possibile 'fedele' del piano iperbolico. Nel Saggio Beltrami mostrava infatti che la geometria di Lobačevskij-Bólyai coincideva con la geometria su una particolare superficie dello spazio euclideo, la pseudosfera, introdotta e studiata da Ernst Ferdinand Adolf Minding (1806-1885) in un articolo del 1840. Tale superficie, la cui curvatura è in ogni punto costante e negativa, è generata dalla rotazione di una curva, detta 'trattrice', intorno al proprio asintoto. La trattrice è il luogo dei punti M tali che la tangente alla curva in M taglia l'asse delle y in un punto T con MT uguale a una costante assegnata. Ruotando la trattrice intorno al proprio asintoto (l'asse delle y) si ottiene la pseudosfera.
Tramite un opportuno dizionario, Beltrami traduceva tutti i teoremi della geometria iperbolica sulla superficie pseudosferica. Tuttavia la sua interpretazione era valida solo localmente, come osservarono Helmholtz, Klein e Genocchi che posero seriamente in dubbio la validità globale del modello di Beltrami, cioè il fatto che il piano iperbolico potesse essere totalmente rappresentato sulla pseudosfera. Beltrami si oppose sempre con forza alle loro critiche. In particolare, il 13 marzo 1869 egli scriveva al matematico francese Guillaume-Jules Hoüel (1823-1886) di aver avuto "un'idea bizzarra", ovvero quella di "tentare di costruire materialmente la superficie pseudosferica sulla quale si realizzano i teoremi della geometria non euclidea" (in Boi 1998, p. 80). In effetti, uno di questi suoi modelli di carta (la 'cuffia di Beltrami') è conservato presso il Dipartimento di matematica dell'Università di Pavia. Dopo la morte di Beltrami, in un articolo del 1901 David Hilbert (1862-1943) dimostrò rigorosamente che il modello di Beltrami è valido solo localmente.
A un attento studio della memoria di Riemann era ispirato un secondo lavoro di Beltrami, la Teoria fondamentale degli spazii di curvatura costante (1869), in cui egli mostrava che la planimetria di Lobačevskij-Bólyai coincide con la geometria delle superfici di curvatura costante negativa: gli oricicli altro non sono che le linee geodetiche con centro all'infinito, mentre le orisfere sono le sfere geodetiche con centro all'infinito, ossia le superfici i cui raggi formano un sistema di geodetiche parallele. L'articolo di Beltrami conteneva anche una prima trattazione accurata della geometria sferica sviluppata con i metodi e gli strumenti della geometria differenziale.
Il modello presentato da Beltrami nel Saggio contribuì in modo notevole alla diffusione della geometria non euclidea: la possibilità di visualizzare definizioni e teoremi della geometria iperbolica su una superficie euclidea rendeva la nuova geometria più comprensibile e intuitiva. Inoltre, un importante teorema dimostrato da Klein nel 1871 affermava che la geometria euclidea e le geometrie non euclidee sono casi particolari (o sottogeometrie) di un'altra teoria più generale, la geometria proiettiva. Dunque, la possibilità di inquadrare le geometrie non euclidee all'interno di teorie ben consolidate ‒ quali erano la geometria differenziale e quella proiettiva ‒ faceva sì che esse non venissero più considerate alla stregua di bizzarre costruzioni geometriche, ma che assumessero un proprio status teorico.
Nonostante questi notevoli risultati, le geometrie non euclidee stentavano comunque ad affermarsi. All'atteggiamento critico dei filosofi kantiani, allora prevalenti, si aggiungeva il fatto che le nuove teorie geometriche non avevano trovato significative applicazioni in matematica, né avevano contribuito alla risoluzione di problemi aperti. La svolta avvenne a partire dal 1882, quando Jules-Henri Poincaré (1854-1912), ispirandosi al modello di Beltrami, si rese conto che la geometria non euclidea iperbolica svolgeva un ruolo determinante nella teoria delle equazioni differenziali ordinarie e nella teoria delle funzioni fuchsiane. Il lavoro di Poincaré gettò una luce nuova sulla geometria non euclidea, che da quel momento è entrata a pieno titolo a far parte della ricerca matematica più avanzata.
Bibliografia
Agazzi 1998: Agazzi, Evandro - Palladino, Dario, Le geometrie non euclidee e i fondamenti della geometria dal punto di vista elementare, Brescia, La Scuola, 1998.
Barbarin 1928: Barbarin, Paul, La géométrie non euclidienne, 3. ed., Paris, Gauthier-Villars, 1928 (1. ed.: 1902).
Boi 1992: 1830-1930. A century of geometry, edited by Luciano Boi, Dominique Flament and Jean-Michel Salanskis, Berlin, Springer, 1992.
‒ 1998: La découverte de la géométrie non euclidienne sur la pseudosphère. Les lettres d'Eugenio Beltrami à Jules Hoüel (1868-1881), introduction, notes et commentaires critiques par Luciano Boi, Livia Giacardi et Rossana Tazzioli, Paris, Blanchard, 1998.
Bonola 1906: Bonola, Roberto, La geometria non euclidea. Esposizione storico-critica del suo sviluppo, Bologna, Zanichelli, 1906.
Bottazzini 1990: Bottazzini, Umberto, Il flauto di Hilbert. Storia della matematica moderna e contemporanea, Torino, Utet, 1990 (3. ed.: 1998).
‒ 1995: Bottazzini, Umberto - Tazzioli, Rossana, Naturphilosophie and its role in Riemann's mathematics, "Revue d'histoire des mathématiques", 1, 1995, pp. 3-38.
Dombrowski 1979: Dombrowski, Paul, Differential geometry. 150 years after Carl Friedrich Gauss' Disquisitiones generales circa superficies curvas, "Asterisque", 62, 1979, pp. 97-153.
Fano 1935: Fano, Gino, Geometria non euclidea. Introduzione geometrica alla teoria della relatività, Bologna, Zanichelli, 1935.
Freguglia 1982: Freguglia, Paolo, Fondamenti storici della geometria, Milano, Feltrinelli, 1982.
Gray 1979: Gray, Jeremy J., Ideas of space: Euclidean, non-euclidean and relativistic, Oxford, Clarendon, 1979.
Kline 1991: Kline, Morris, Storia del pensiero matematico, a cura di Alberto Conte, Torino, Einaudi, 1991, 2 v. (ed. orig.: Mathematical thought from ancient to modern times, New York, Oxford University Press, 1972).
Loria 1901: Loria, Gino, Eugenio Beltrami e le sue opere matematiche, "Bibliotheca mathematica", s. 2, 3, 1901, pp. 392-440.
Pont 1986: Pont, Jean-Claude, L'aventure des parallèles. Histoire de la géométrie non euclidienne. Précurseurs et attardés, Bern-Frankfurt a.M., Lang, 1986.
Reich 1973: Reich, Karin, Die Geschichte der Differentialgeometrie von Gauss bis Riemann (1828-1868), "Archive for history of exact sciences", 11, 1973, pp. 273-382.
Rozenfeld 1988: Rozenfeld, Boris Abramovič, A history of non-euclidean geometry. Evolution of the concept of a geometrical space, New York, Springer, 1988 (ed. orig.: Istorija neevklidovoi geometrii. Razvitie ponjatija o geometričeskom prostranstve, Moskvà, Nauka, 1976).
Scholz 1980: Scholz, Erhard, Geschichte des Mannigfaltigkeitsbegriffs von Riemann bis Poincaré, Basel-Boston, Birkhäuser, 1980.
Tazzioli 2000: Tazzioli, Rossana, Riemann. Alla ricerca della geometria della natura, Milano, Le Scienze, 2000.
‒ 2002: Tazzioli, Rossana, Gauss. Principe dei matematici e scienziato poliedrico, Milano, Le Scienze, 2002.
Torretti 1978: Torretti, Roberto, Philosophy of geometry from Riemann to Poincaré, Dordrecht-Boston, Reidel, 1978.