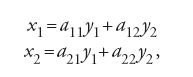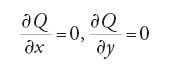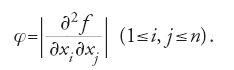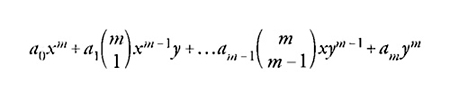L'Ottocento: matematica. Teoria degli invarianti

L'Ottocento: matematica. Teoria degli invarianti

Teoria degli invarianti

L'algebra del XIX sec. ebbe uno sviluppo intenso che coprì numerosi domini. Nuove entità matematiche come gruppi, anelli e campi emersero gradualmente e, specialmente nella seconda metà del secolo, in relazione all'uso di metodi algebrici nella teoria dei numeri e nella geometria. L'argomento classico della ricerca continuò a essere principalmente lo studio delle equazioni polinomiali: tecniche per risolverle e proprietà delle loro soluzioni. Strettamente collegato a tali ricerche fu lo studio di invarianti algebrici di espressioni omogenee in più variabili, il settore della matematica che incarna, più di ogni altro, lo spirito della ricerca algebrica nel XIX secolo.

I primi sviluppi in Inghilterra

La teoria degli invarianti algebrici fu un campo di studio estremamente attivo nella seconda metà del XIX sec., e il lavoro di Carl Friedrich Gauss (1777-1855) sulle forme quadratiche binarie, pubblicato nel 1801 nelle Disquisitiones arithmeticae, contiene già le prime osservazioni relative a tale problematica. Il vero sviluppo della teoria, però, iniziò soltanto dopo il 1840, quando apparvero i lavori di George Boole (1815-1864) in Inghilterra e di Ludwig Otto Hesse (1811-1874) in Germania.

Il contributo di Boole traeva spunto dallo studio di Joseph-Louis Lagrange (1736-1813) sulle trasformazioni lineari di polinomi omogenei. Data una forma binaria omogenea f(x₁,x₂) di grado n con coefficienti a_i e una trasformazione lineare T:

risulta definita implicitamente una nuova forma T(f) di grado n, nelle variabili y₁ e y₂, T(f)=F(y₁,y₂) con coefficienti b_i che sono funzioni razionali, lineari nelle a_i e di grado n nelle a_ij. Un'espressione algebrica n-aria I, si dice un 'invariante' se

[2]  I(a₁,a₂,…a_n)=δ^rI(b₁,b₂,…b_n),

dove r è un intero qualsiasi e δ=a₁₁a₂₂−a₁₂a₂₁. Questa definizione può essere generalizzata a forme in più di due variabili e anche a più di due forme; si possono considerare inoltre invarianti dei coefficienti e delle variabili insieme (covarianza e controvarianza).

Nel 1841 Boole pubblicò una memoria nella quale discusse, per la prima volta, un caso particolare di tale questione. Partendo dalla forma quadratica binaria

[3] Q=ax²+2bxy+cy²,

e utilizzando il sistema

egli considerò θ(Q)=b²−ac, il discriminante della forma quadratica, e dimostrò che θ(Q)=δ^rθ(T(Q)), dove, necessariamente, la trasformazione T deve essere non singolare. Egli dimostrò inoltre un analogo risultato relativo a forme cubiche binarie.

Boole dava inizio così a una linea di ricerca nella quale fu ben presto seguito da Arthur Cayley (1821-1895) che, nel 1845, pubblicò On the theory of linear transformations, il primo di una lunga serie di studi dedicati al calcolo di relazioni algebriche tra i coefficienti di forme di grado superiore. Le relazioni considerate da Cayley erano definite da condizioni simili a quelle studiate da Boole, ma fu Cayley a usare per esse il termine 'invarianti' e a sviluppare tecniche efficaci, anche se piuttosto laboriose, per trovare diversi invarianti di una data forma. Egli scoprì inoltre che diversi invarianti della stessa forma soddisfano a volte opportune relazioni, per le quali, nel 1853, James J. Sylvester conierà il termine 'sizigie'.

Sono esempi di invarianti della quartica binaria

[5] A=ax⁴+4bx³y+6cx²y²+4dxy³+ey⁴,

u=ae−4bd+3c² e v=ace−ad²−eb²−c³+2bcd, scoperti rispettivamente da Cayley e Boole; un terzo invariante per questa forma è una combinazione polinomiale dei due precedenti: z=u³+27v².

Cayley e Sylvester, che mantennero per tutta la vita un rapporto di stretta amicizia, inaugurarono con la loro collaborazione scientifica una prolifica tradizione di ricerca sugli invarianti, della quale fanno parte Edwin B. Elliot, Herbert W. Turnbull, George Salmon in Gran Bretagna, Charles Hermite e Camille Jordan in Francia, Francesco Brioschi in Italia e Fabian Franklin negli Stati Uniti. Cayley formulò ben presto il problema fondamentale che avrebbe impegnato i matematici coinvolti nella ricerca in questo nuovo campo: trovare tutti gli invarianti di una data forma e, più precisamente, un insieme minimale di invarianti che avrebbe consentito di costruire completamente, usando le relative sizigie in modo opportuno, il sistema in questione. Il lavoro degli studiosi britannici si focalizzò sull'elaborazione di algoritmi per la ricerca di determinati invarianti in casi particolari, così come in Germania, dove però i ricercatori, pur perseguendo obiettivi simili a quelli dei loro colleghi britannici, elaborarono tecniche differenti e più efficaci.

Hesse e la scuola tedesca

In Germania gli sviluppi più importanti nella ricerca sugli invarianti scaturirono dal lavoro di Hesse in geometria benché, prima di lui, idee simili fossero state sviluppate da Ferdinand Gotthold Eisenstein (1823-1852) in teoria dei numeri, nel tentativo di generalizzare la teoria di Gauss delle forme quadratiche al caso cubico. Eisenstein aveva infatti formulato una procedura per associare a una classe di forme cubiche forme quadratiche corrispondenti, mostrando che proprietà invarianti di queste ultime avrebbero potuto essere utilizzate per dedurle da quelle cubiche.

L'approccio di Hesse aveva invece origine da un problema di natura geometrica: lo studio dei punti critici nelle curve piane del terzo ordine. Egli utilizzò per tale studio quello che oggi è noto come determinante hessiano:

Da considerazioni puramente geometriche sui punti di flesso della curva di equazione f=0 (f è in questo caso un polinomio omogeneo), Hesse, che non conosceva i risultati di Boole, dimostrò nel 1844 che se f si trasforma in T(f), allora φ(f)=δ²φ(T(f)).

A partire dal 1848 Siegfried Heinrich Aronhold (1819-1884), uno studente di Hesse, proseguì lo studio di queste tematiche in termini puramente algebrici distaccandole da una diretta interpretazione geometrica. Aronhold approfondì in seguito la sua conoscenza dei lavori di Cayley e Sylvester, adottandone in gran parte la terminologia. Nei successivi decenni lo sviluppo di questa impostazione molto diversa nella ricerca e nello studio degli invarianti lo condusse a conquiste notevoli. Tra i suoi seguaci, i più importanti furono Rudolf Alfred Clebsch, Paul A. Gordan e Max Noether, i quali diedero vita in Germania a un'importante scuola il cui metodo, noto come 'simbolico', intendeva evitare, almeno parzialmente, alcuni dei noiosi calcoli espliciti che caratterizzavano i lavori di Cayley, di Sylvester e dei loro seguaci. Mentre questi avrebbero scritto una forma binaria di grado m

operando quindi direttamente per trovarne gli invarianti, la notazione simbolica avrebbe consentito l'uso di espressioni equivalenti più succinte:

[8] (a₁x₁+a₂x₂)^m

e anche di quella estremamente concisa a^m. Un tipico teorema avrebbe quindi asserito che un invariante di questa forma binaria può scriversi come:

[9]  (ab)^α(ac)^β(bd)^γ…a^pb^qc^r…

dove a, b, c, d, e così via, sono differenti rappresentazioni simboliche della stessa forma e (ab) rappresenta il determinante a₁b₂−a₂b₁. Il numero dei fattori a, b, c,… che compaiono nel prodotto deve essere uguale a un multiplo di m. Aronhold fu il primo a esprimere la relazione fra prodotti simbolici di questo tipo e le forme cubiche ternarie derivanti dal lavoro di Hesse, mentre Clebsch ne dimostrò, nel 1861, la validità nel caso generale di grado e numero di variabili arbitrari.

L'approccio simbolico della scuola tedesca permetteva di derivare espressioni formali che semplificavano molto le manipolazioni nei calcoli sugli invarianti. Così, per esempio, è semplice dimostrare con la notazione precedente che

[10] a(bc)+b(ca)+c(ab)=0.

Un'altra identità, più complessa e molto utile, deducibile dalla precedente è

[11] b²(ca)²+c²(ab)²−a²(bc)²=2bc(ab)(ac).

Gordan e Hilbert

Dopo il 1860 i risultati più importanti nella teoria degli invarianti furono ottenuti grazie a manipolazioni simboliche di questo tipo. L'esempio principale è la dimostrazione del teorema di finitezza per forme binarie, pubblicata nel 1868 da Paul A. Gordan, a lungo la maggiore autorità del settore. Egli dimostrò che, per ogni sistema di forme binarie di grado arbitrario, si può trovare un sottosistema finito tale che ogni invariante del sistema di partenza può essere scritto come combinazione razionale di forme del sottosistema. Usando il metodo simbolico Gordan riuscì anche a fornire, mediante calcoli laboriosi, 'il sistema di forme base minimale' nel caso delle forme di quinto e sesto grado. Negli anni seguenti furono dimostrate varie parziali generalizzazioni del teorema di Gordan e furono apportati miglioramenti e semplificazioni alla dimostrazione originale; furono, inoltre, notevolmente migliorate le tecniche per il calcolo degli invarianti. La completa generalizzazione del teorema di Gordan rimase tuttavia una questione aperta per molti anni: dimostrare l'esistenza di una base finita per ogni sistema di invarianti di grado arbitrario e in un numero qualsiasi di variabili. Questo problema fu affrontato da David Hilbert (1862-1943) in una serie di articoli che rappresentarono un significativo punto di svolta nella teoria degli invarianti.

Tra il 1888 e il 1889, e con maggiori dettagli nel 1890, Hilbert pubblicò i primi lavori che gli valsero il riconoscimento internazionale. In essi dimostrò una versione generale del teorema della base finita per classi arbitrariamente grandi di forme di qualsiasi grado in un numero qualunque di variabili. Gordan era uno dei referees del lavoro di Hilbert e sollevò serie riserve sulla sua dimostrazione, che in effetti, a differenza della propria per il caso binario, non mostrava come la base richiesta potesse essere costruita, dimostrandone soltanto l'esistenza con un argomento basato sulla reductio ad absurdum, la cui legittimità era ben lontana dall'essere accettata unanimemente. Questa iniziale reazione negativa si attenuò tuttavia presto, se non altro perché già nel 1893 Hilbert fornì una dimostrazione molto più costruttiva del suo teorema di finitezza, che era peraltro già stato semplificato dallo stesso Gordan. Un altro aspetto importante dell'approccio di Hilbert era l'uso innovativo di idee precedentemente introdotte nella teoria dei numeri da Leopold Kronecker (1823-1891) e nello studio di funzioni algebriche da Richard Dedekind e Heinrich Weber in un articolo del 1882 scritto in collaborazione.

Hilbert stesso fu il primo a valutare il significato storico del proprio lavoro sulla teoria degli invarianti; in un articolo che ne esaminava gli sviluppi, letto a suo nome al Congresso Internazionale dei matematici tenutosi a Chicago nel 1893, egli descrisse tre momenti distinti attraverso i quali, nella sua concezione, le teorie matematiche si svilupperebbero: l'ingenuo, il formale e il critico. Nel caso della teoria degli invarianti Hilbert considerava i lavori di Cayley e Sylvester tipici del momento ingenuo, quelli di Gordan e Clebsch del momento formale, mentre il suo lavoro rappresentava il momento critico. Inoltre, nello stesso articolo Hilbert aveva esplicitamente affermato di aver portato a termine tutti i maggiori obiettivi della teoria degli invarianti, abbandonandone in effetti subito dopo lo studio. Il giudizio di Hilbert è stato spesso ripreso e accettato acriticamente. La teoria degli invarianti e l'approccio algoritmico caratteristico dei suoi primi esponenti furono considerati conclusi dopo i risultati di Hilbert, aprendo così il campo all'ascesa della nuova algebra astratta, basata sulle strutture.

Alcuni studiosi della teoria degli invarianti videro nei risultati di Hilbert nuove strade di ricerca per la disciplina, piuttosto che un punto terminale. Benché il numero dei matematici coinvolti in questo settore di studio e la quantità delle ricerche pubblicate diminuissero notevolmente dopo il 1900, la teoria degli invarianti non scomparve completamente e nel 1933 Eduard Study (1862-1930) compilò un nuovo manuale in cui criticava l'impostazione hilbertiana. Study affermava che la sola generalizzazione astratta, esemplificata dal lavoro di Hilbert, non poteva sostituire la 'vera matematica', ossia quella algoritmica rappresentata dai metodi di Aronhold e Clebsch. Bisogna inoltre ricordare che nella lista dei 23 problemi di Hilbert, il quattordicesimo chiede di dimostrare la finitezza di alcuni tipi di sistemi di invarianti. Relativamente pochi sforzi, tuttavia, sembrano essere stati diretti verso la soluzione di questo particolare problema fino agli anni Cinquanta del XX sec., quando fu trovato un sistema del tipo richiesto nel quattordicesimo problema per il quale non esiste una base finita.

Bibliografia

Crilly 1986: Crilly, Tony, The rise of Cayley's invariant theory (1841-1862), "Historia mathematica", 13, 1986, pp. 241-254.

Fisch 1994: Fisch, Menachem, The emergency which has arrived. The problematic history of nineteenth-century British algebra. A programmatic outline, "British journal for the history of science", 27, 1994, pp. 247-276.

Gray 1997: Gray, Jeremy J., Algebraic geometry between Noether and Noether. A forgotten chapter in the history of algebraic geometry, "Revue d'histoire des mathématiques", 3, 1997, pp. 1-48.

Parshall 1989: Parshall, Karen H., Towards a history of nineteenth-century invariant theory, in: The history of modern mathematics, edited by David E. Rowe and John McCleary, Boston, Academic Press, 1989-1994, 3 v.; v. I: Ideas and their reception, 1989, pp. 157-206.

‒ 1990: Parshall, Karen H., The one-hundredth anniversary of the death of invariant theory?, "Mathematical intelligencer", 12, 1990, pp. 10-16.